Ferromagnetic Mass Localization in Check Point Configuration Using a Levenberg Marquardt Algorithm
Abstract
:1. Introduction
2. The Localization Procedure
2.1. The Levenberg Marquardt Algorithm
2.2. The Tracking Algorithm
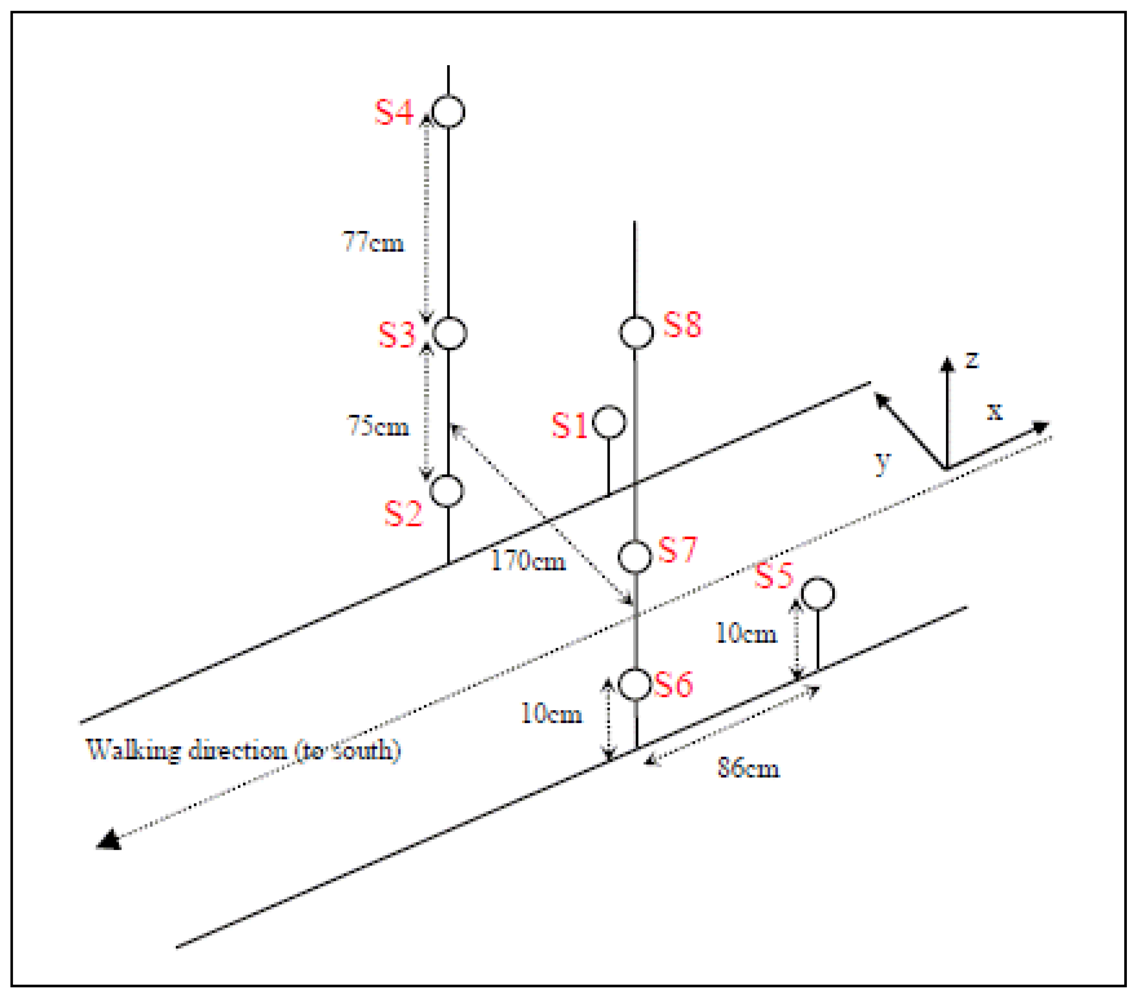
2.3. Experimental Setups
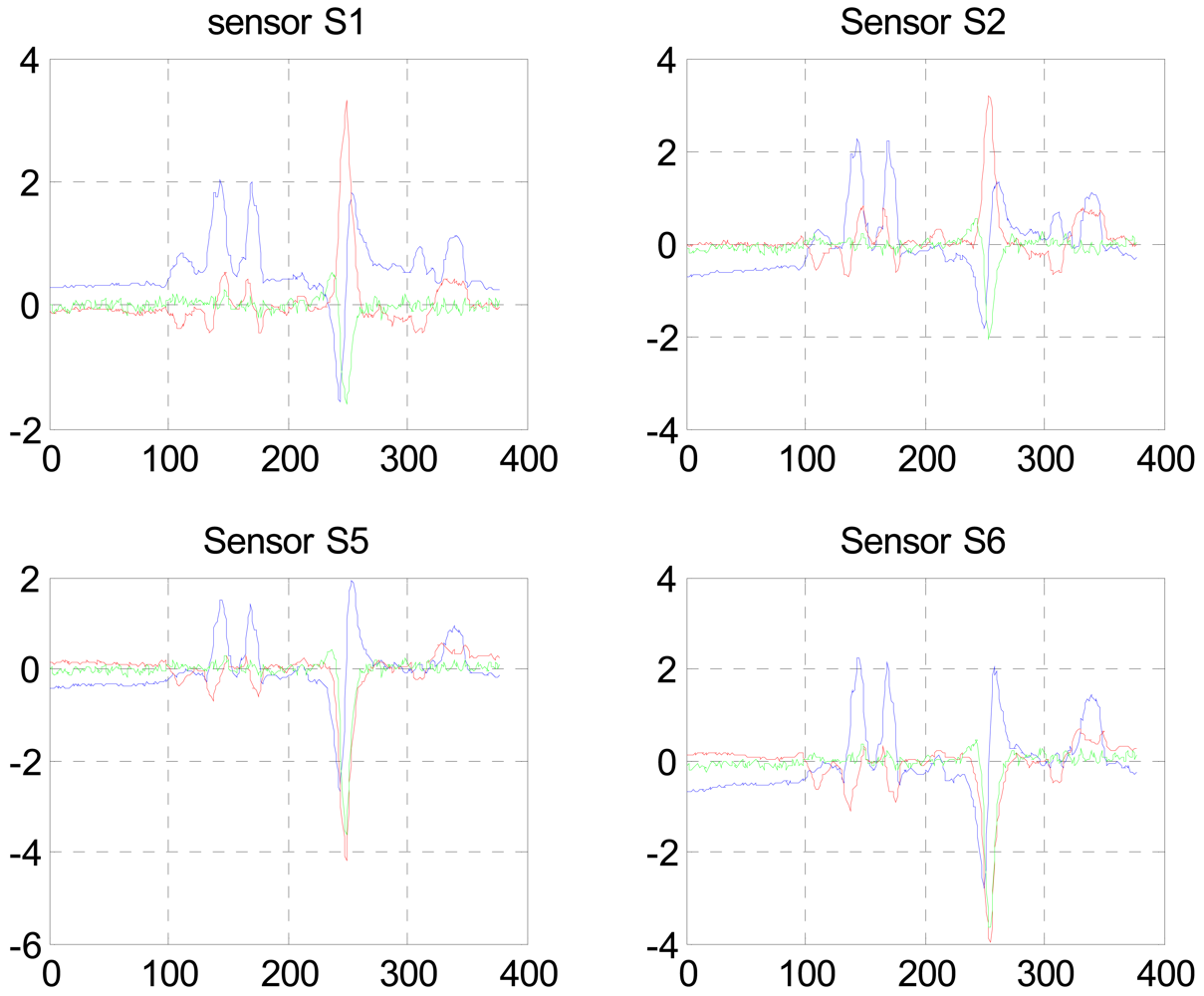
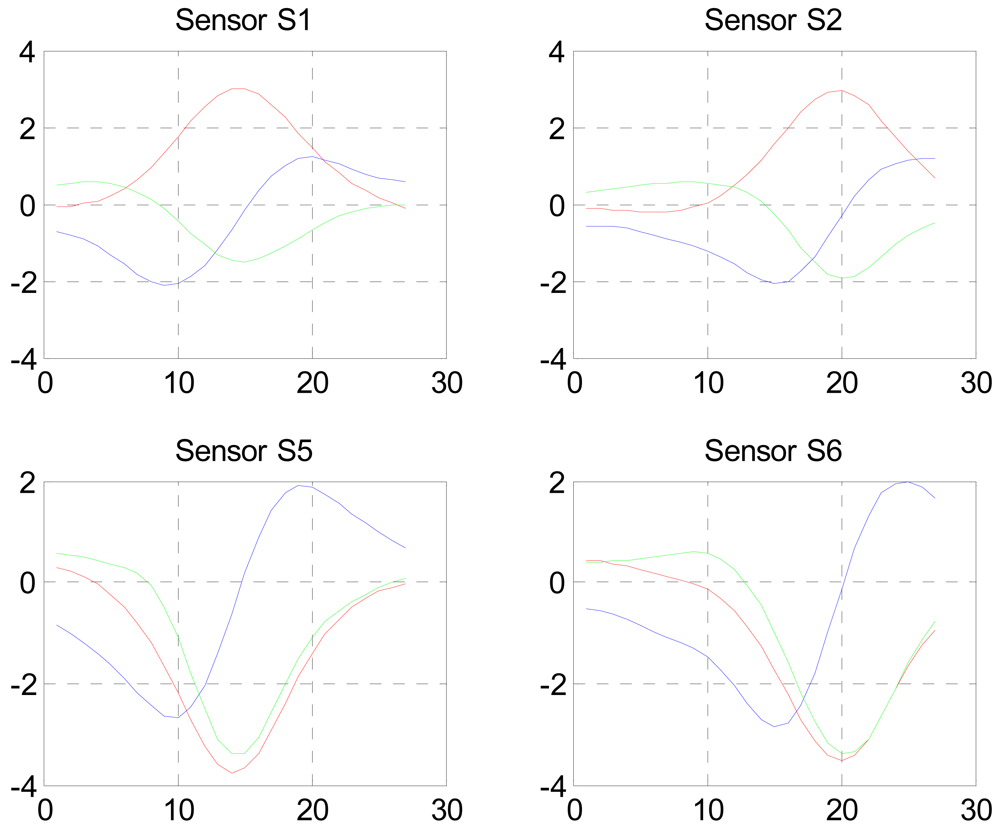
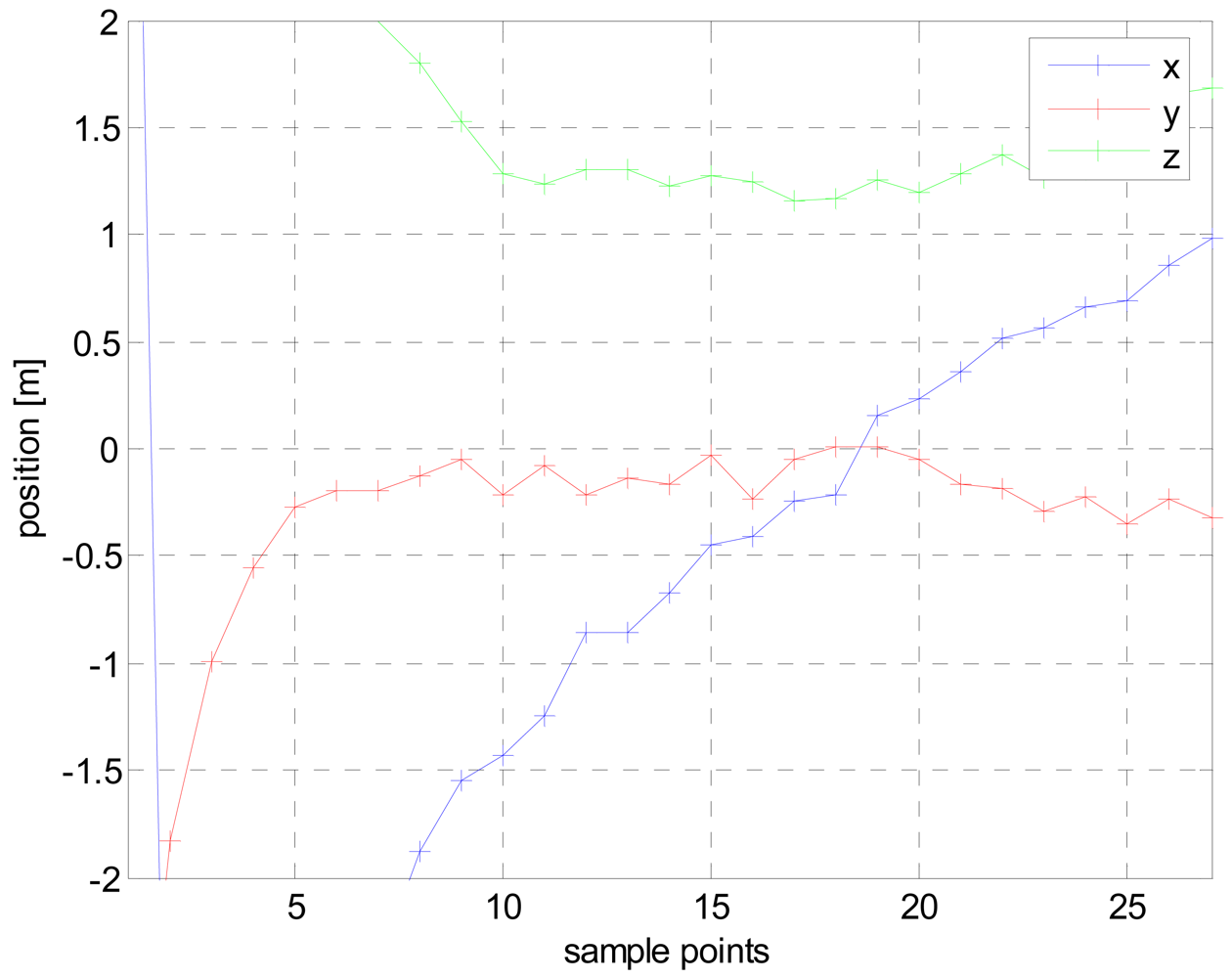
2.4. Tracking Demonstration
3. Algorithm Performance Analysis
4. Conclusions
References and Notes
- Wynn, W.M. Detection, Localization and Charactezation of Static Magnetic-Dipole Sources. In Detection and Identification of Visually Obscured Targets; Baum, C.E., Ed.; Taylor and Francis: Philadelphia, PA, USA, 1999; pp. 337–374. [Google Scholar]
- Kozick, R.J.; Sadler, B.M. Algorithms for Tracking with an Array of Magnetic Sensors. Proceedings of the Fifth IEEE Sensors Array and Multichannel Signal Processing Worskshop, SAM 2008, Darmstadt, Germany, July 21-23, 2008; pp. 423–427.
- Nara, T.; Suzuki, S.; Ando, S. A Closed-Form Formula for Magnetic Dipole Localization by Measurement of Its magnetic Field and Spatial Gradients. IEEE Trans. Magn. 2006, 42, 3291–3293. [Google Scholar]
- Murray, I.B.; McAulay, A.D. Magnetic Detection and Localization Using Multichannel Levinson-Durbin Algorithm. Process. Sens. Fusion Target Recognit. XIII 2004, 5429, 5429–5434. [Google Scholar]
- Scholz, B; Schwierz, G. Probability-based current dipole localization from biomagnetic fields. IEEE Trans. Biomed. Eng. 1994, 41, 35–42. [Google Scholar]
- Sherman, J.T.; Lubkert, J.K.; Popovic, R.S.; Disilvestro, M.R. Characterization of a Novel Magnetic Tracking System. IEEE Trans. Magn. 2007, 43, 2725–2727. [Google Scholar]
- Dassot, G.; Blanpain, R.; Flament, B.; Jauffret, C. Process for determining the position of a moving object using magnetic gradientmetric measurements. US Patent 6,539,327, 2003. [Google Scholar]
- Mauriello, P.; Patella, D. Localization of Magnetic Sources Underground by a Probability Tomography Approach. Prog. Electromagn. Res. M 2008, 3, 27–56. [Google Scholar]
- Birsan, M. Unscented Particle Filter for Tracking a Magnetic Dipole Target. Proceedings of OCEANS, 2005, Proceedings of MTS/IEEE, Washington, D.C.; WA, USA, September 17-23, 2005; pp. 1656–1659.
- Kiyuna, T.; Kamijo, K.; Yamazaki, T. Multiple-Dipole Source Localization Based on Information Criteria. NEC Res. Devel. 1997, 38, 139–148. [Google Scholar]
- Sheinker, A.; Lerner, B.; Salomonski, N.; Ginzburg, B.; Frumkis, L.; Kaplan, B. Localization and Magnetic Moment Estimation of a Ferromagnetic Target by Simulated Annealing. Meas. Sci. Technol. 2007, 18, 3451–3457. [Google Scholar]
- Cauffet, G.; Caldora-Costa, M.; Coulomb, J.L.; Bongiraud, J.P.; LeThiec, P. Localization and Identification of a Magnetic Dipole by the Application of Genetic Algorithm. Eur. J. Elec. Eng. 2001, 4, 55–63. [Google Scholar]
- Sheinker, A.; Salomonski, N.; Ginzburg, B.; Frumkis, L.; Kaplan, B. Remote Sensing of a Magnetic Target Utilizing Based Incremental Learning. Sens. Actuat. 2008, 143, 215–223. [Google Scholar]
- Weiss, E.; Ginzburg, B; Ram-Cohen, T.; Zafrir, H.; Alimi, R.; Salomonski, N.; Sharvit, J. High Resolution Marine Survey of Shallow Water Littoral Area. Sensors 2007, 7, 1697–1712. [Google Scholar]
- Perry, A.R.; Czipott, P.V.; Beevor, S.P.; Hanley, G.A. Innovations in Weapons Detector Portal Technology. Proceedings of Sensors and Command Control Communications and Intellingence (C3I) Technologies, Orlando, FL, USA, April 21-25, 2003; pp. 362–371.
- Merlat, L.; Naz, P. Magnetic Localization and Identification of Vehicles. Proceedings of Unattended Ground Sensor Technologies and Applications V, Orlando, FL, USA, April 21-25, 2003; pp. 174–185.
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and NonLinear Equations.; Soc. for Industrial & Applied Math: Philadelphia, PA, USA, 1983. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-linear Problems in Least Squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Marquardt, D.W. An Algorithm for the Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, A.W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing., 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Plotkin, A.; Paperno, E.; Vasserman, G.; Segev, R. Magnetic Tracking of Eye Motion in Small Fast Moving Animals. IEEE Trans. Magn. 2008, 44, 4492–4496. [Google Scholar]
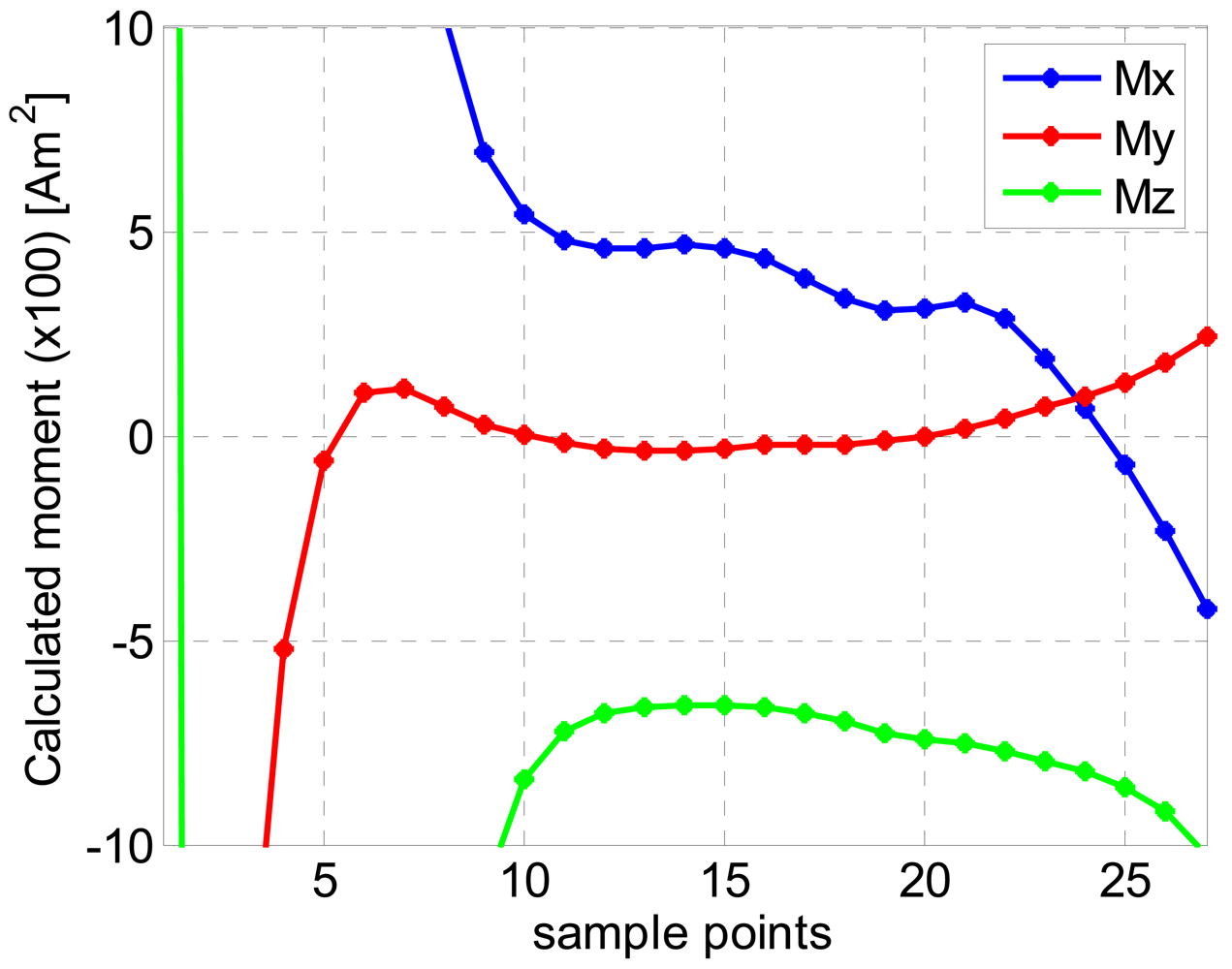
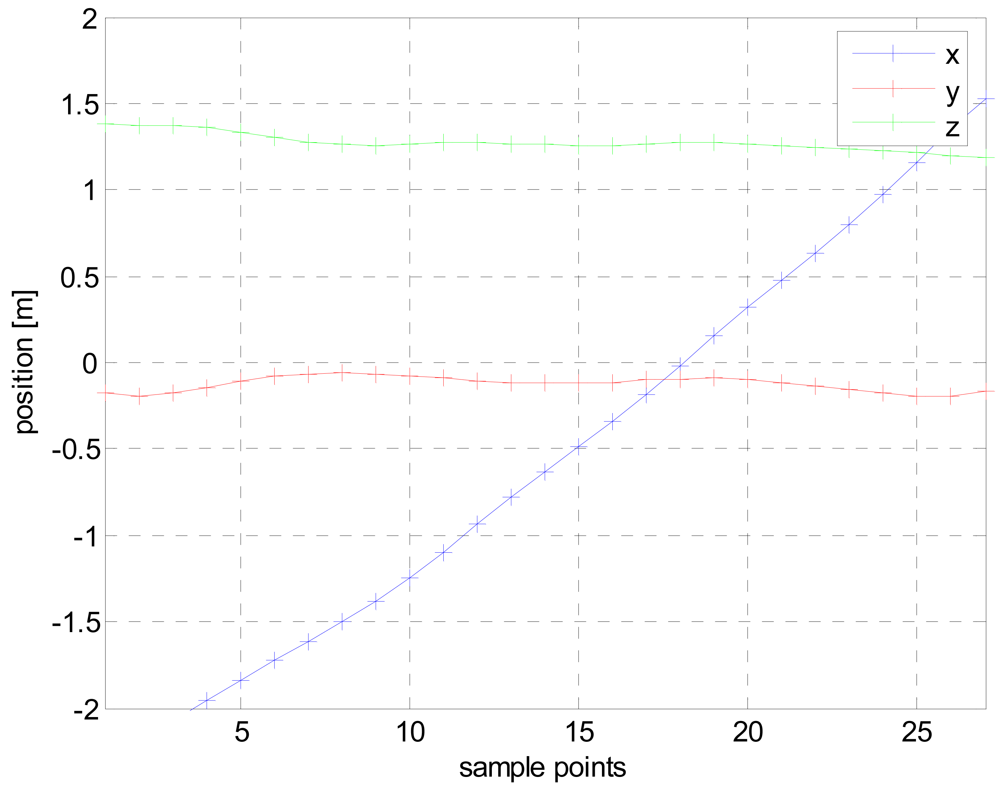
| Target | Horizontal setup | Vertical setup | ||
|---|---|---|---|---|
| 2 sensors | 4 sensors | 3 sensors | 4 sensors | |
| Large | 80% | 90% | 100% | 100% |
| Medium | 60% | 85% | 90% | 100% |
| Small | 45% | 75% | 100% | 100% |
| Target | Horizontal setup | Vertical setup | ||
|---|---|---|---|---|
| 2 sensors | 4 sensors | 3 sensors | 4 sensors | |
| Large | 90% | 80% | 95% | 90% |
| Medium | 85% | 80% | 100% | 100% |
| Small | 70% | 65% | 95% | 80% |
| Horizontal setup | Vertical setup | |||
|---|---|---|---|---|
| 2 sensors | 4 sensors | 3 sensors | 4 sensors | |
| Large | 6.4 ±1.8 | 6.9 ±1.5 | 6.3 ±1.3 | 6.1 ±1.3 |
| Medium | 2.6 ±2.0 | 2.0 ± 1.7 | 2.7 ±0.9 | 2.4 ±0.7 |
| Small | 1.1 ± 0.8 | 0. 8 ± 0.4 | 0.7 ± 0.4 | 0.7 ± 0.2 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alimi, R.; Geron, N.; Weiss, E.; Ram-Cohen, T. Ferromagnetic Mass Localization in Check Point Configuration Using a Levenberg Marquardt Algorithm. Sensors 2009, 9, 8852-8862. https://doi.org/10.3390/s91108852
Alimi R, Geron N, Weiss E, Ram-Cohen T. Ferromagnetic Mass Localization in Check Point Configuration Using a Levenberg Marquardt Algorithm. Sensors. 2009; 9(11):8852-8862. https://doi.org/10.3390/s91108852
Chicago/Turabian StyleAlimi, Roger, Nir Geron, Eyal Weiss, and Tsuriel Ram-Cohen. 2009. "Ferromagnetic Mass Localization in Check Point Configuration Using a Levenberg Marquardt Algorithm" Sensors 9, no. 11: 8852-8862. https://doi.org/10.3390/s91108852




