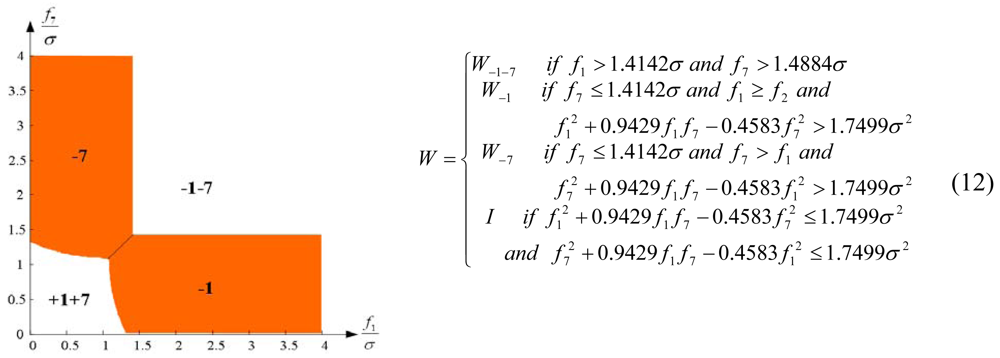1. Introduction
The reliability of any system can be enhanced by fault detection, isolation, and accommodation (FDIA). FDI methods have been studied since the 1960s in various areas of engineering problems. The reviews [
1-
3] and books [
4,
5] and references therein introduce various methods of FDI and diverse applications in engineering problems.
To make them reliable and enhance their navigation accuracy, inertial navigation systems (INS) often use redundant sensors. Numerous studies have been performed on the use of redundant inertial sensors in FDI, and there are many FDI papers on hardware redundancy, such as those based on look-up tables and the squared error (SE) method [
6,
7], generalized likelihood test(GLT) method [
8], optimal parity test(OPT) method[
9], multiple parity vector method [
10], and reduced-order parity method for double faults [
11].
Yang
et al. [
10,
12] suggested accommodation rules for single and double faults based on the error covariance of an estimated variable, which is related to the navigation accuracy of INS. These accommodation rules give decision criteria to determine whether faulty sensors should be excluded or not. Yang
et al. [
12] suggested accommodation rules for six inertial sensors. However, when six inertial sensors are used, a double fault can be detected, but the faults cannot be isolated in some cases. Accommodation rules for seven inertial sensors are suggested in [
13], which is a conference version of this paper and the accommodation rules are obtained for the simplest sensor configuration among the four configurations which provide the best navigation performance.
The present paper proves that when six inertial sensors are used, the isolation of a double fault cannot be achieved for some combinations of fault magnitudes whereas, when seven inertial sensors are used, isolation can be achieved for any double fault. The configuration which shows the best navigation performance is not unique. Actually, there are many configurations which provide minimum position errors. This paper proposes the four best configurations from the navigational viewpoint and provides accommodation rules for double faults for one of them. For the four best sensor configurations, the probability of correct isolation (PCI) is obtained and compared to select the configuration for which the accommodation rules are obtained. Considering the FDI performance and the complexity of the accommodation rule, we choose one sensor configuration among the four suggested configurations and provide accommodation rules for double faults.
This paper is organized as follows. The sensor configuration and null space of the measurement matrix are explained in Section 2. The fact that seven inertial sensors should be used to isolate any double fault is proved, and the four best sensor configurations for navigation performance are given in Section 3. For these four sensor configurations, the PCIs are simulated and compared with each other in Section 3. The accommodation rules for a double fault for seven inertial sensors are given in Section 4. The simulation results and conclusions are given in Sections 5 and 6, respectively.
2. Sensor Configuration and Null Space of Measurement Matrix
2.1. Sensor Configuration
Consider a typical measurement equation for redundant inertial sensors such as their acceleration or angular rate:
where:
m(t) = [m1 m2 … mn]T ∈ Rn : inertial sensor measurement.
H(t) = [h1 h2 … hn]T: n×3 measurement matrix of sensor configuration with rank(H) = 3.
x(t) ∈ R3 : triad-solution(acceleration or angular rate).
f(t) = [f1 f2 … fn]T ∈ Rn : fault vector.
ε(t) ∼ N(0n, σIn) : a measurement noise vector with normal distribution(white noise), all sensors are assumed to have the same noise characteristics.
N(x, y): Gaussian probability density function with mean x and standard deviation y.
The triad solution x(t) in (
1) can be obtained by the least square method from the measurement as follows:
The navigation accuracy of INS depends on the estimation error of the triad solution x(t), as shown in
Figure 1. The estimation error of the triad solution x(t) in (
1) depends on the matrix H. Harrison
et al. [
14] mentioned the condition which provides the least estimation error of x(t) resulting in the best navigation performance.
Lemma 1 [14]
Consider the measurement
Equation (1), where the matrix H ∈ R
n×3 denotes the sensor configuration. When the eigenvalues of H
TH are all equivalent to n/3, the sensor configuration provides the minimum estimation error of the triad solution x(t), which gives the best navigation performance.
2.2. Null Space of Measurement Matrix
A parity vector P(t) is obtained from the measurement using a matrix V as follows:
where the matrix V satisfies:
The following Lemma shows the well-known singular value decomposition (SVD) result.
Lemma 2
Suppose that n>3. Every matrix H ∈ Rn×3 with rank 3 can be transformed into the form H = UΛ = U[Σ 0]T= U1Σ
where U and Σ satisfy the following. UU* =U*U=In, U=[U1 U2], U1 ∈ Rn×3, U2 ∈ Rn×(n-3), Σ = diag{σ1, σ2, σ3} with σ1 > σ2 > σ3 > 0. ( )* denotes a complex conjugate transpose.
Measurement
Equation (1) can be described as follows:
and the parity vector can be obtained by multiplying U
2* on the left:
If we temporarily ignore the noise, we can obtain the null space projection of the fault f.
where U
2U
2* is the projector into the null space of the measurement matrix H. Thus, we can estimate the fault by using f̂
null.
3. Sensor Configuration for Seven Inertial Sensors
3.1. The Number of Sensors Required to Isolate a Double Fault
It is well-known that two faulty sensors can be isolated among six sensors. Gilmore
et al. [
6] mentioned that the symmetric configuration with six sensors arranged on dodecahedron enables self-contained failure isolation for up to two out of six sensors. This is correct when two faults occur at different times. However, in the case where two faults occur simultaneously, which is generally referred to as a double fault, the isolation of the two faults cannot be guaranteed, as will be proved in Theorem 1.
Theorem 1
Consider the measurement
Equation (1) with n=6. Suppose that the magnitude of the faults differ from each other, i.e., f
i ≠ f
j for i ≠ j. Then, the isolation of the double fault cannot always be achieved for some combinations of f
i and f
j.
Proof
Define a unit vector e
i for which only the i
th component is 1 and the other components are zero. Then we obtain double faults as follows:
The difference between f̂
jk and f̂
lmcan be zero for non-zero f
j, f
k, f
l and f
m since U
2U
2* has a maximum of three independent columns and, thus, there exist some combinations of f
j, f
k, f
l and f
m which make (
7) zero. Therefore, a double fault cannot be isolated for some combinations of f
i and f
j.
The simulation result for Theorem 1 can be seen in [
15]. If we need to isolate a double fault for any combination of f
i and f
j, seven sensors should be used.
Theorem 2
Consider the measurement
Equation (1) with n=7. Then, the isolation of a double fault can be achieved for all combinations of f
i and f
j.
Proof
Consider the double fault in (
6), where U
2 ∈ R
7×4. The difference value:
cannot be zero for non-zero combinations of f
j, f
k, f
l and f
m since U
2U
2* has a maximum of four independent columns. Thus, a double fault can be isolated for any combination of f
i and f
j.
Considering the result of Theorem 2, we need to use seven sensors to isolate double faults in any situation.
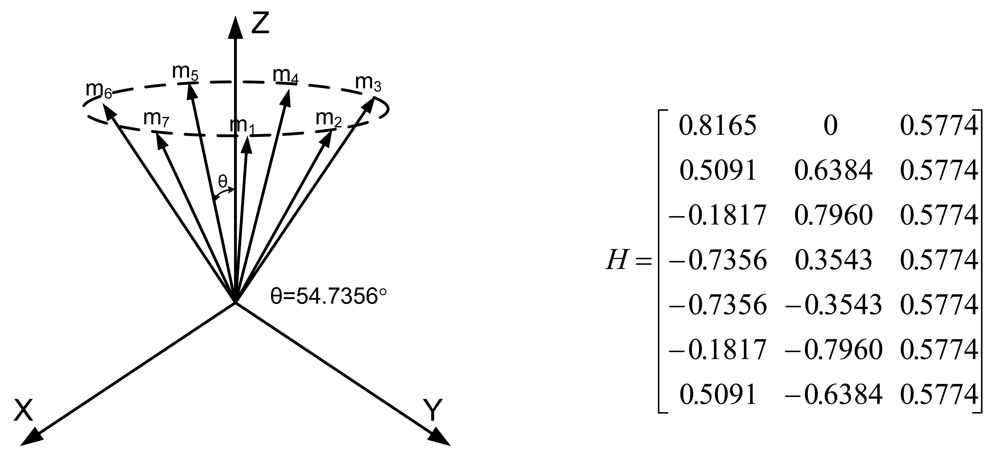
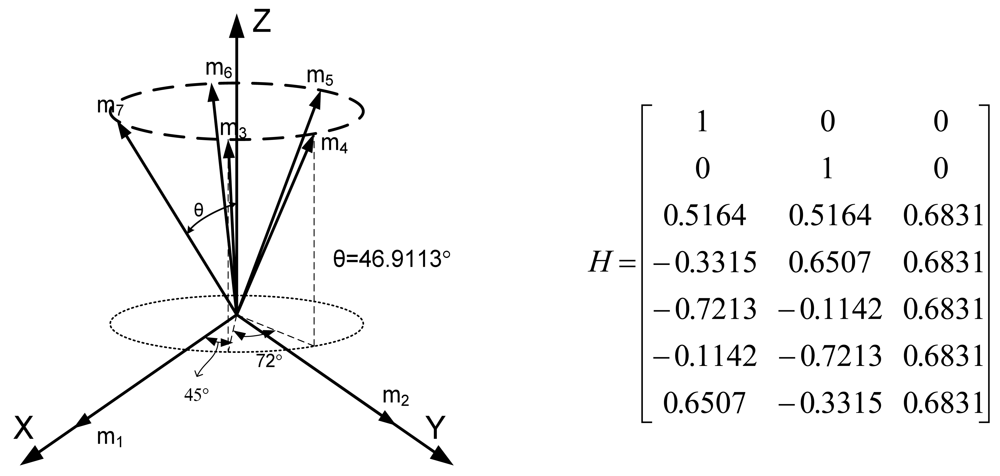
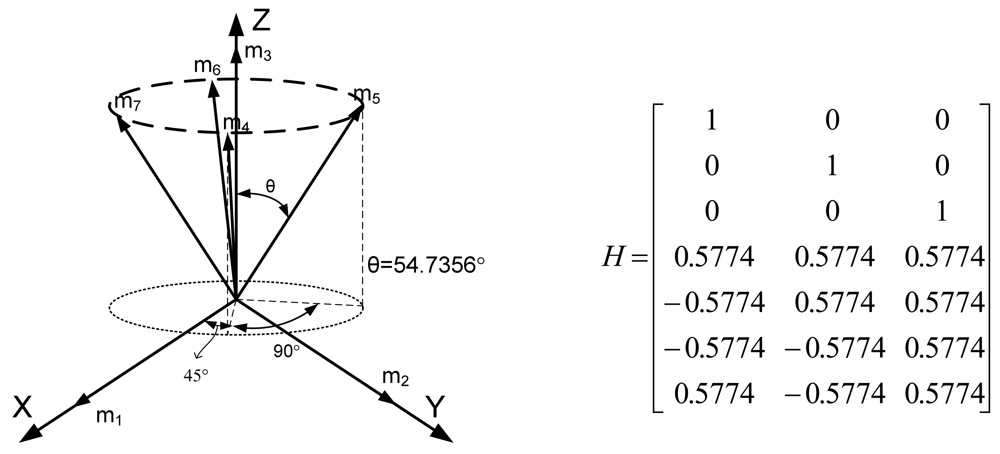
3.2. Four Sensor Configurations to Obtain Best Navigation Accuracy
Lemma 1 gives the condition for the sensor configuration to provide the least estimation error of x in (
2). Now we consider seven inertial sensors and there are many configurations which satisfy the condition, H
TH = 7/3 I
3. The configurations in
Figures 2 through
5 all satisfy the condition, H
TH = 7/3 I
3.
4. Accommodation Rule for Seven Inertial Sensors
4.1. Accommodation Rule for Single and Double Faults
In this section, the results of [
10,
12] are used for the accommodation rules for single and double faults.
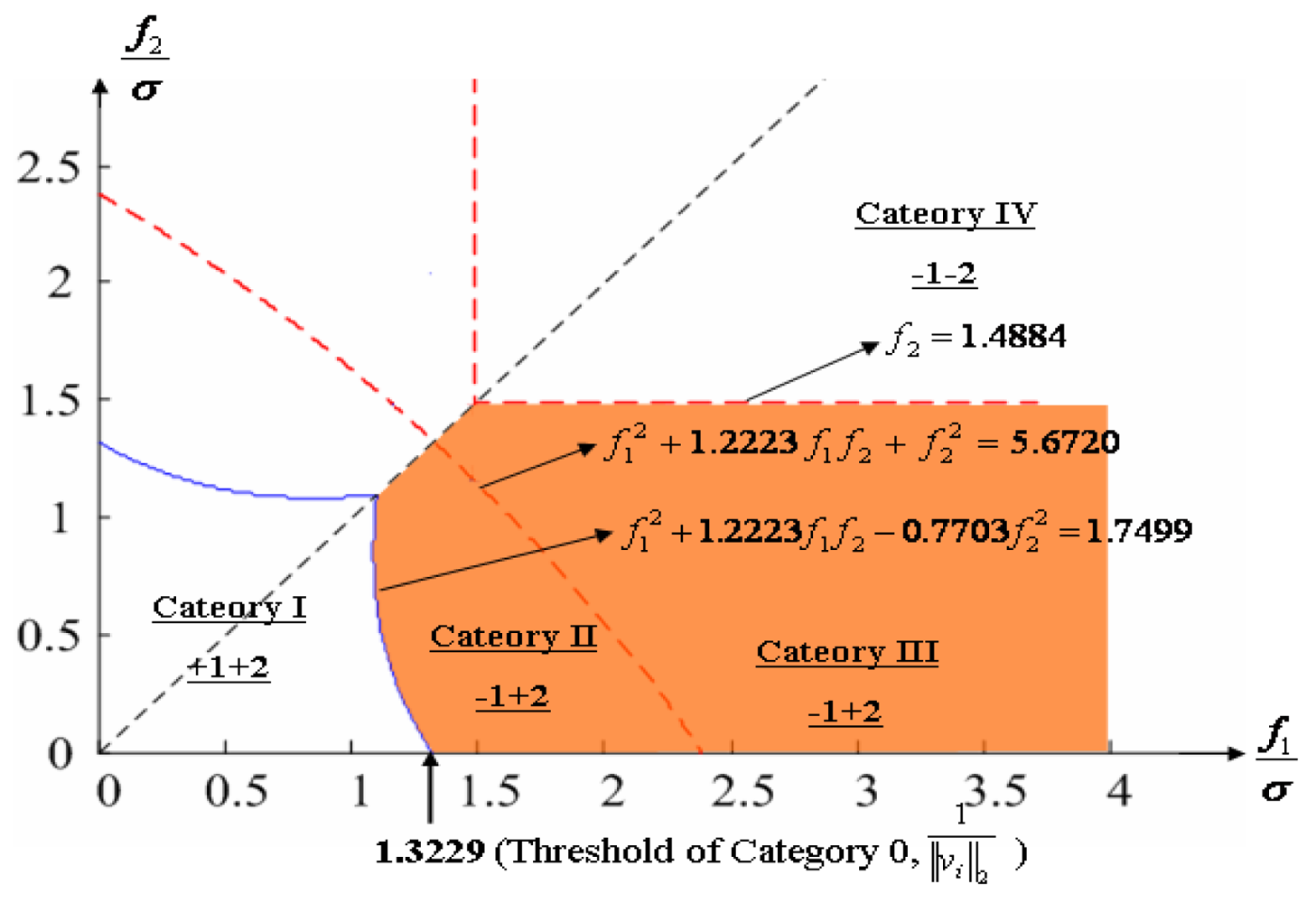
Category 0 [10]
When a single fault satisfies the following inequality
, the faulty sensor should be excluded. The vector v
i is the i
th column of matrix V in (
4).
Category I [12]
When double faults satisfy the following three inequalities:
| fj | < | fi |
where
and γ = 2 < (HTH)−1hi, (HTH)−1hi > < vi, vj >, Dij = ‖Vi‖2‖Vj‖2 − <Vi, Vj>2.
the two faulty sensors should not be excluded.
Category II [12]
When double faults satisfy the following three inequalities:
| fj | < | fi |
the i
th sensor should be excluded, but not the j
th sensor.
Category III [12]
When double faults satisfy the following three inequalities:
where
,
the i-th sensor should be excluded, but not the j-th sensor.
Category IV [12]
When double faults satisfy the following three inequalities:
the two faulty sensors should be excluded.
4.2. Accommodation Rule of Configuration 2
In Section 3.3, we choose sensor configuration 2, as shown in
Figure 7, considering the navigation performance, FDI performance, and the complexity of the accommodation rule, altogether.
In this case, the measurement matrix H is given in (8) and has the following relations:
Configuration 2 in
Figure 7 has six sensor input axes (i=1, …, 6) on the cone with angle 61.8745° from the Z-axis and one sensor input axis (i=7) on the Z-axis. There are four kinds of combinations of double fault. Three double fault combinations take place on the cone (f
i, i=1, …, 6) : adjacent double faults (f
i and f
i+1), double faults skipping a sensor (f
i and f
i+2), and double faults skipping two sensors (f
i and f
i+3). The other double fault combination takes place between the Z-axis (f
7) and one sensor on the cone (f
i, i=1, …, 6). For simplicity, we call these faults the 1
st and 2
nd, 1
st and 3
rd, 1
st and 4
th, and 1
st and 7
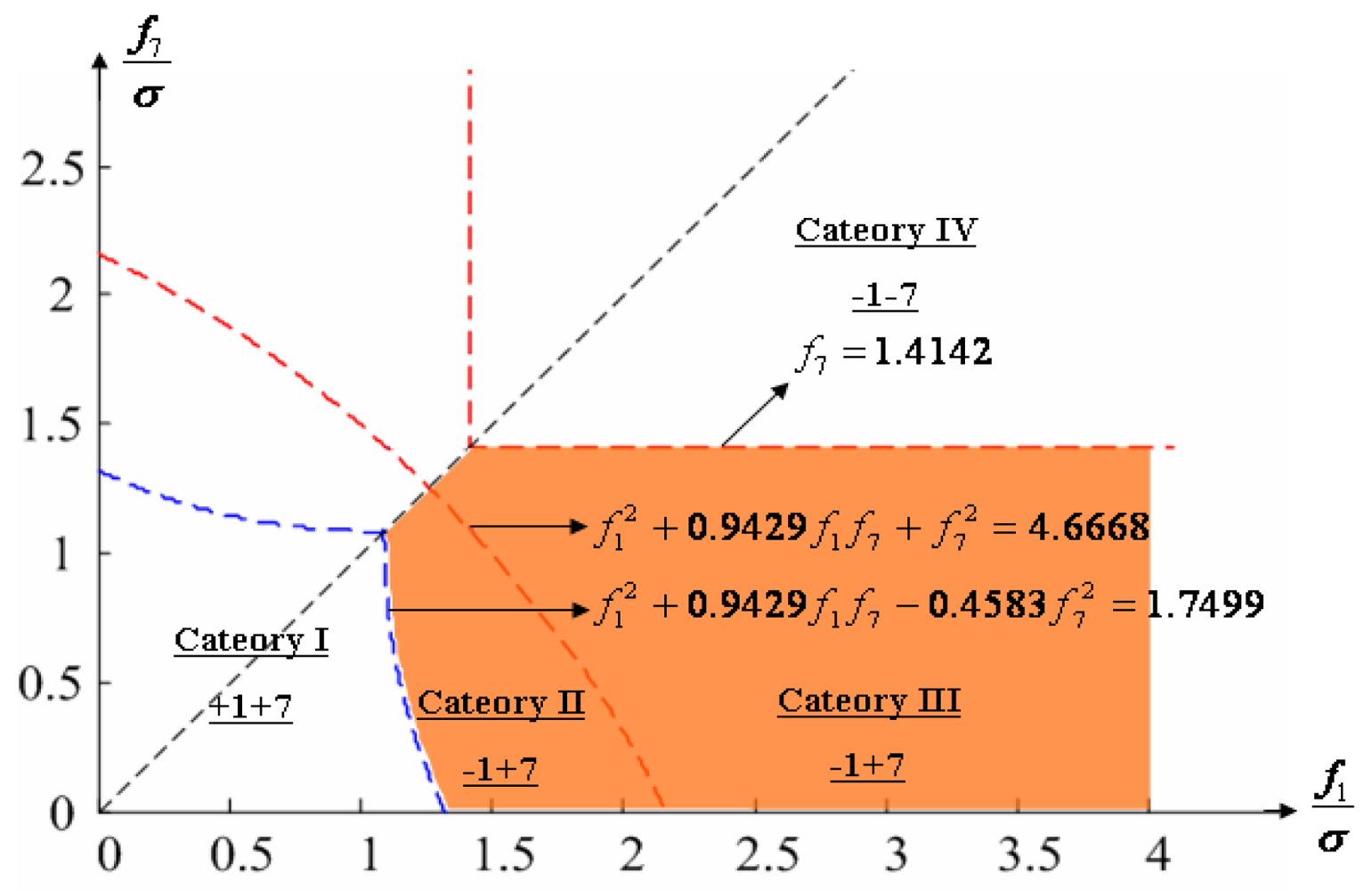
th faults, respectively. The regions of Category 0 through Category IV in Section 4.1 are shown in
Figures 8 through
11, respectively, where “-i” means that the i
th sensor should be excluded and “+j” means that the j
th sensor should be included.
4.3. Implementation of the Accommodation Rules: Update Matrix W
The accommodation rule is implemented by updating matrix W as in (9)–(12), where W
-i-j denotes the identity matrix with the i
th and j
th diagonal components having zero values, and W
-i denotes the identity matrix with the i
th diagonal component having zero value.
Figures 12 through
15 show the accommodation rule in the first quadrant.
5. Simulations for Accommodation Rules
In this section, Monte Carlo simulations are performed 10,000 times for each double fault combination to confirm that the accommodation rules are correct. Seven identical sensors are used with configuration 2 as shown in
Figure 7. For the measurement matrix H in (8), the matrix V satisfying VH = 0 and VV
T = I can be obtained by using the SVD method as follows:
where ‖v
i‖
2 = 0.7559 (i = 1,2, …, 7).
To show the navigation performance, the error covariance of the triad solution x is used. The covariance matrices are defined as follows:
Matrix C
+i+j denotes the error covariance of x̂ including the i
th and j
th sensor outputs and C
-i-j the error covariance of x̂ excluding the i
th and j
th sensors, and so on. It is known that the minimization of the trace of the error covariance matrix provides the best navigation performance. The traces of the error covariance matrices (13)–(15) will be calculated and compared with each other for the four accommodation rules, which results are shown in
Figures 17,
19,
21, and
23.
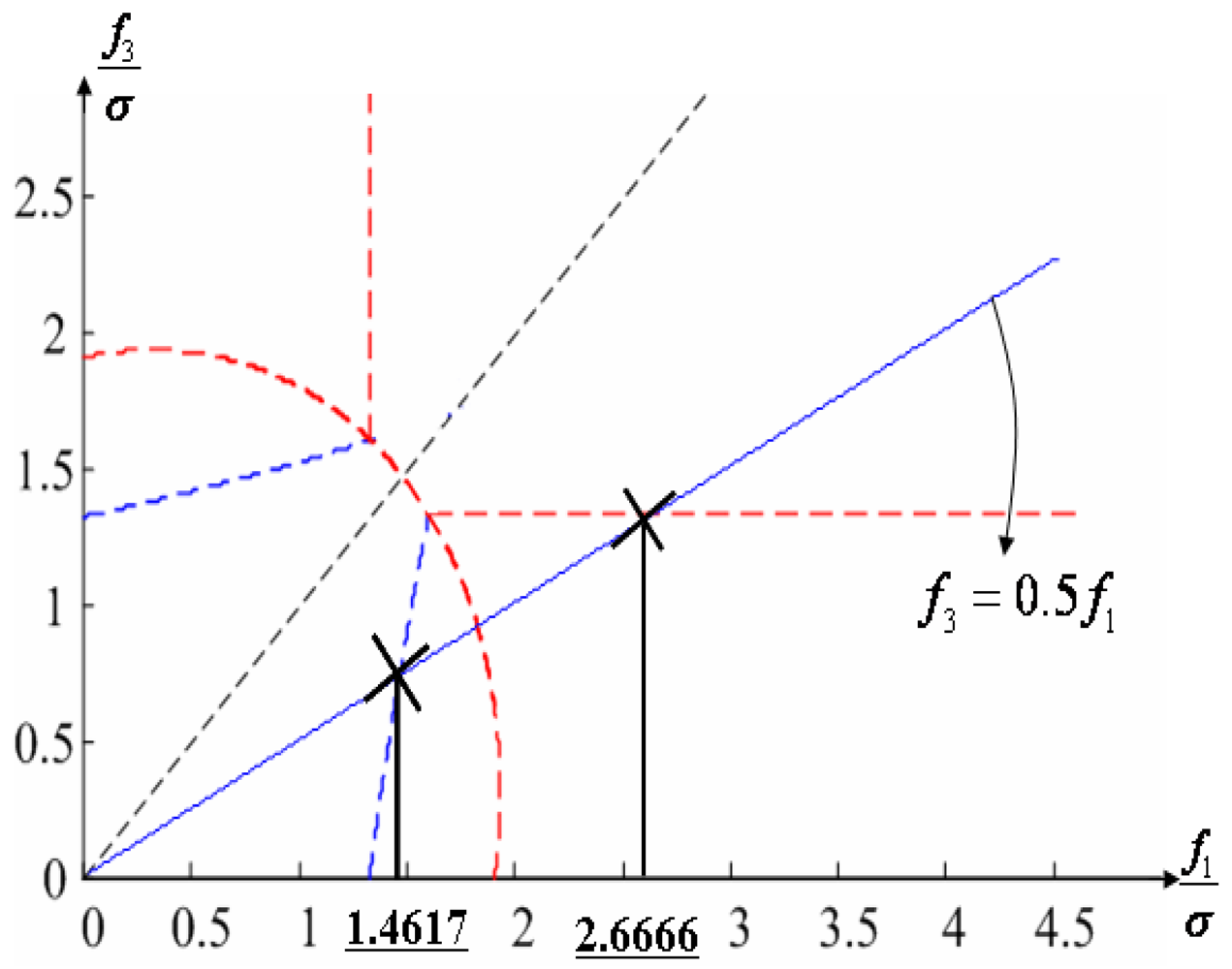
5.1. Double Fault of 1st and 2nd Sensors
Suppose that the first and second sensors have a fault such that f(t) = [f
1 f
2 0 0 0 0]
T with f
1 and f
2 being constants. Simulations are performed for each point on the linear line of f
2 = 0.5 f
1 as shown in
Figure 16, and the measurement noise is white Gaussian with mean 0 and variance σ = 1.
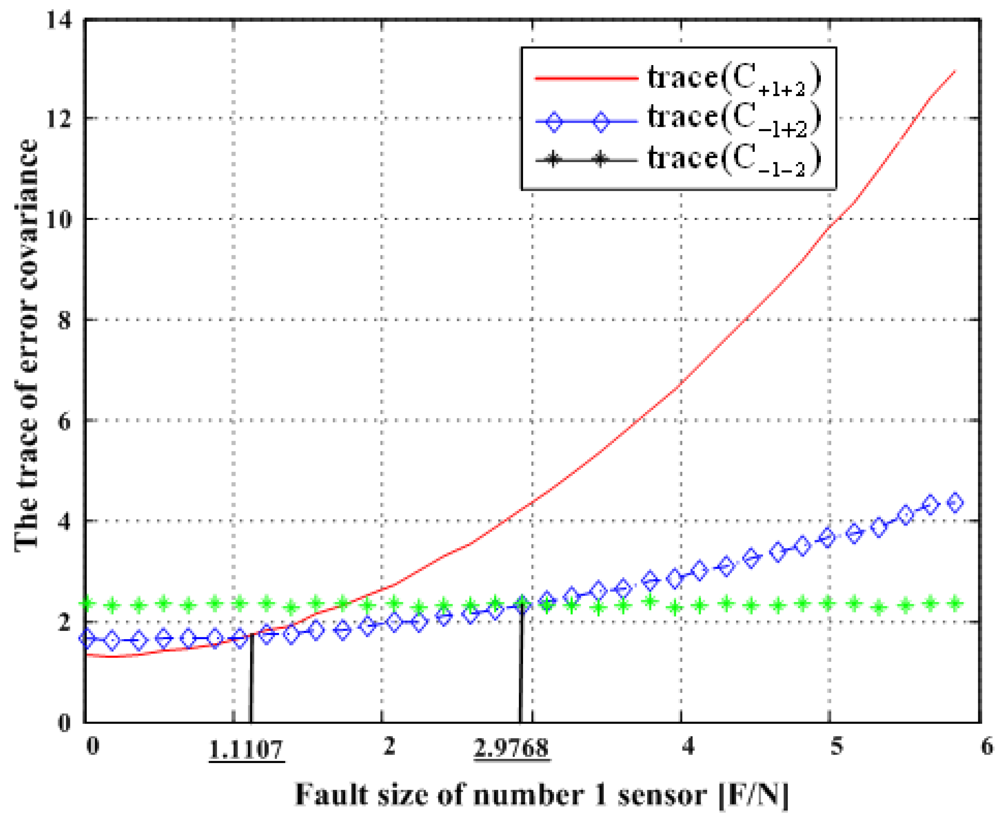
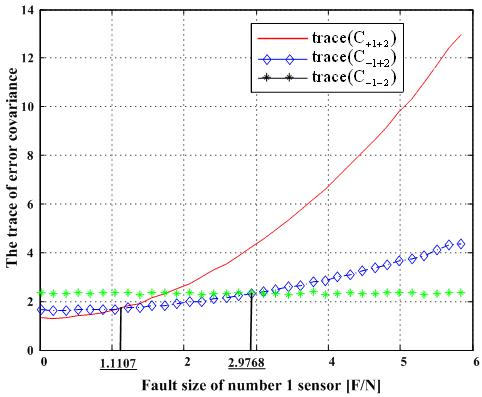
Figure 17 shows the results of the accommodation rule for a double fault according to the fault size in
Figure 16. When faults f
1 and f
2 belong to the region of Category I, the trace of C
+1+2 is the minimum among the three traces. This means that when faults f
1 and f
2 belong to the region of Category I, the two faulty sensors should be used to obtain the minimum estimation error, in other words, the best navigation accuracy. When faults f
1 and f
2 belong to the region of Categories II or III, the trace of C
-1+2 is the minimum, and when they belong to the region of Category IV, the trace of C
-1-2 is the minimum. In
Figure 16, the point at f
1 = 1.1107 is the boundary between Category I and II, and the point at f
1 = 2.2968 is the boundary between Category III and IV. These boundary points correspond to the crossover points between trace(C
+1+2) and trace(C
-1+2) and between trace(C
-1+2) and trace(C
-1-2), respectively, in
Figure 17.
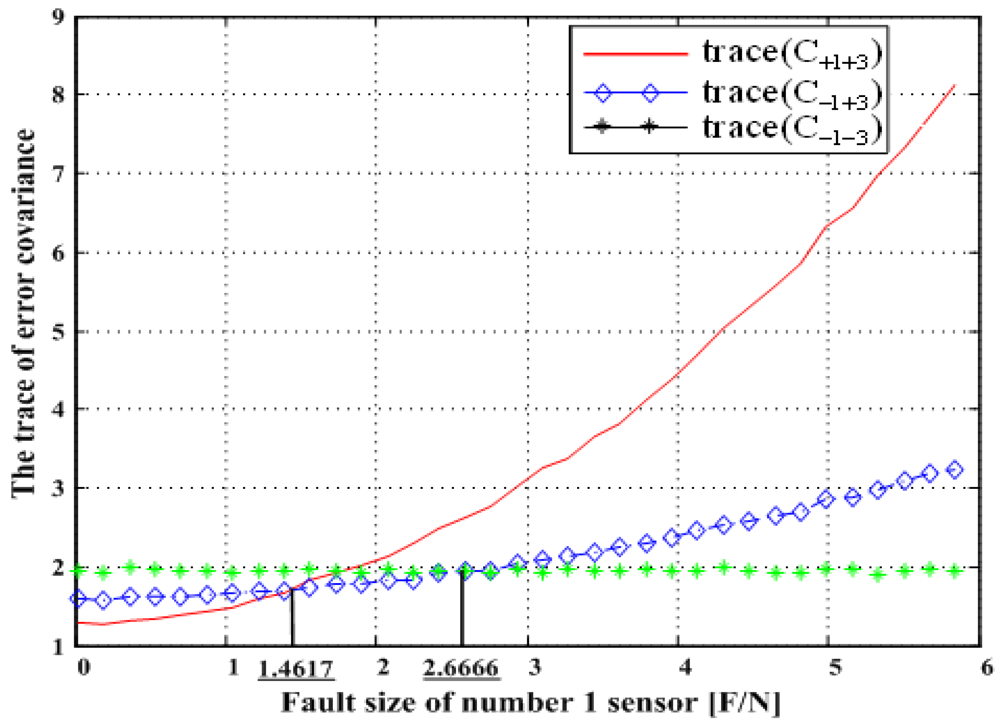
5.2. Double Fault of 1st and 3rd Sensor
Figure 19 shows the results of the accommodation rule for a double fault according to the fault size in
Figure 18. The results are the same as those in Section 5.1.
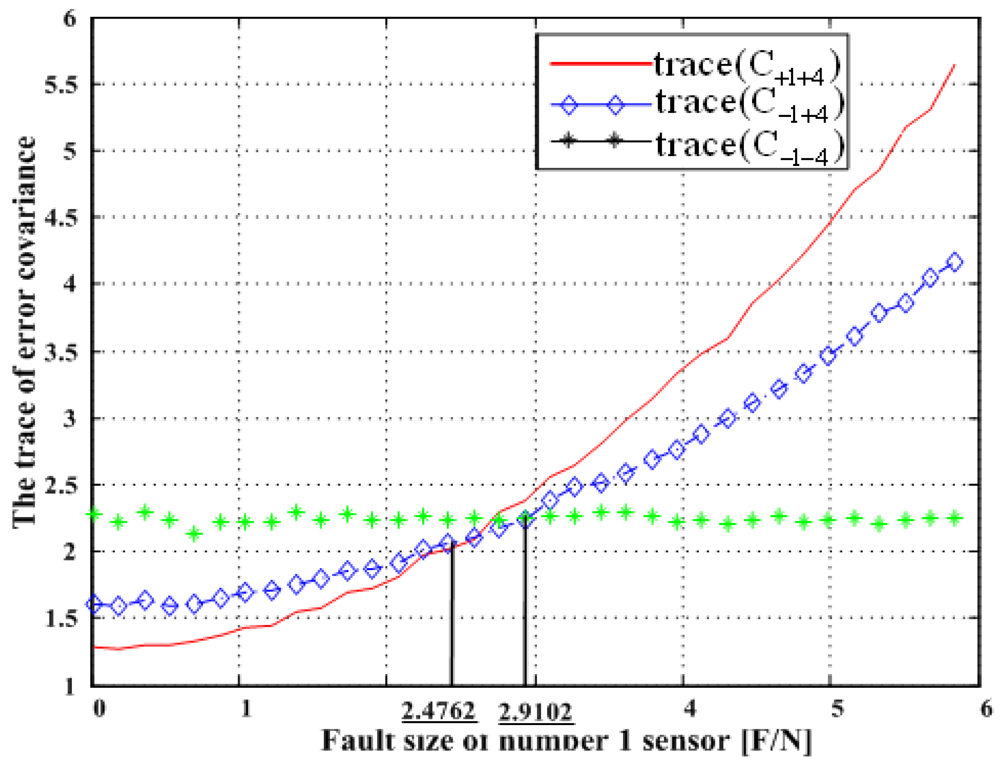
5.3. Double Fault of 1st and 4th Sensors
Figure 21 shows the results of the accommodation rule for a double fault according to the fault size in
Figure 20. The results are the same as those in section 5.1.
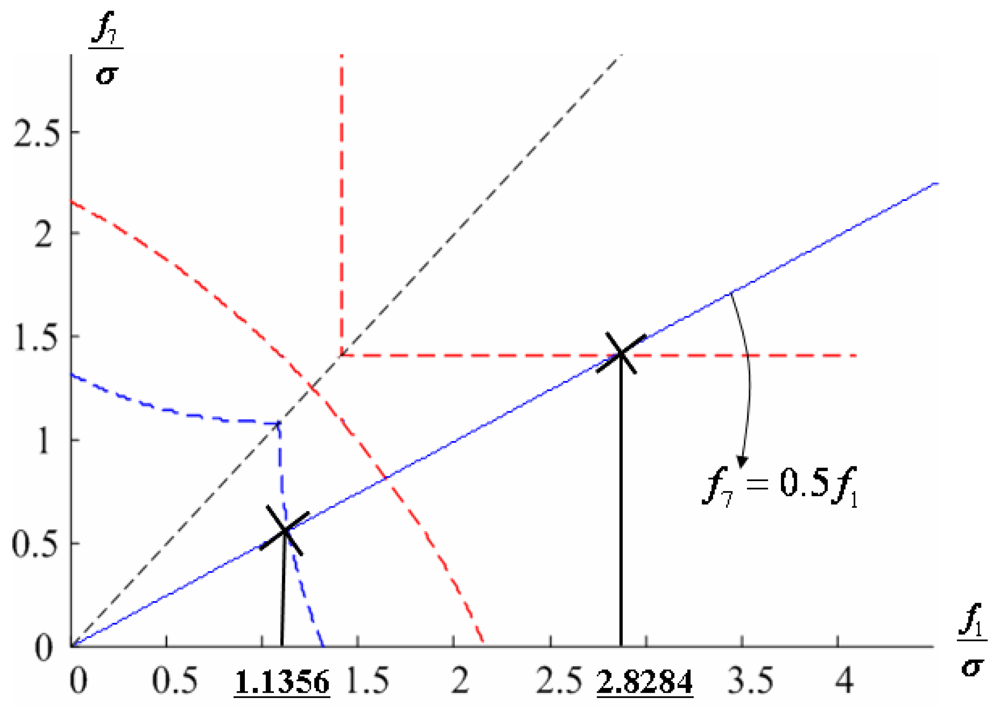
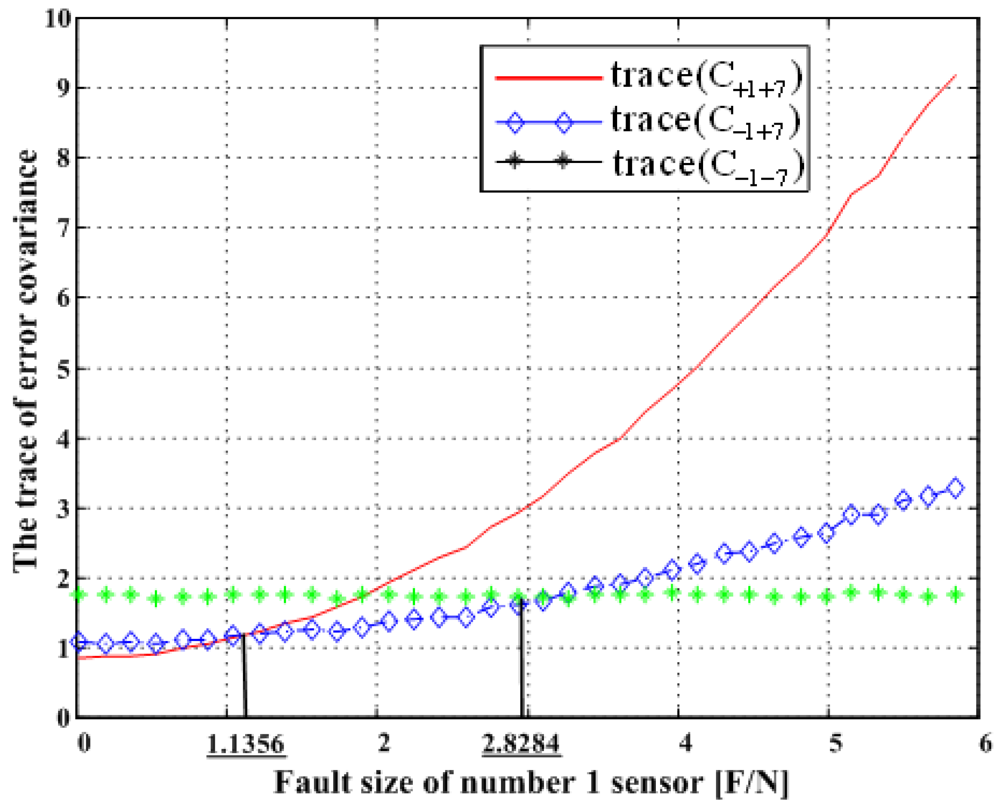
5.4. Double Fault of 1st and 7th Sensors
Figure 23 shows the results of the accommodation rule for a double fault according to the fault size in
Figure 22. The results are the same as those in Section 5.1.
6. Conclusions
For inertial navigation systems which use seven sensors, this paper proves that a double fault can be isolated for any combination of fault magnitudes. This paper suggests the four sensor configurations which provide the best navigation performance when seven sensors are used. The four sensor configurations are as follows: (1) cone configuration, (2) six sensor inputs on the cone surface and one sensor input on the center axis through the cone, (3) two sensors on the x and y axes, respectively, and the other five sensors on the cone surface with the z axis as center axis of the cone, (4) three sensors on the x, y, and z axes, respectively, and the other four sensors on the cone surface with the z axis as the center axis of the cone.
For these four configurations, the PCI is obtained for each sensor in order to compare their FDI performance. The Monte Carlo simulations indicate that configuration 4 shows the best PCI, but which is only slightly better than that of configuration (4). As explained in detail in Sections 3.3 and 4.2, configuration (2) has four sets of accommodation rules, while configuration (4) has 13. Thus, we chose configuration (2) after considering the complexity of the accommodation rule. For sensor configuration (2), four accommodation rules are obtained and a Monte Carlo simulation is performed. The Monte Carlo simulation shows that the suggested accommodation rules are correct and work well.