A Coupled Field Multiphysics Modeling Approach to Investigate RF MEMS Switch Failure Modes under Various Operational Conditions
Abstract
:1. Introduction
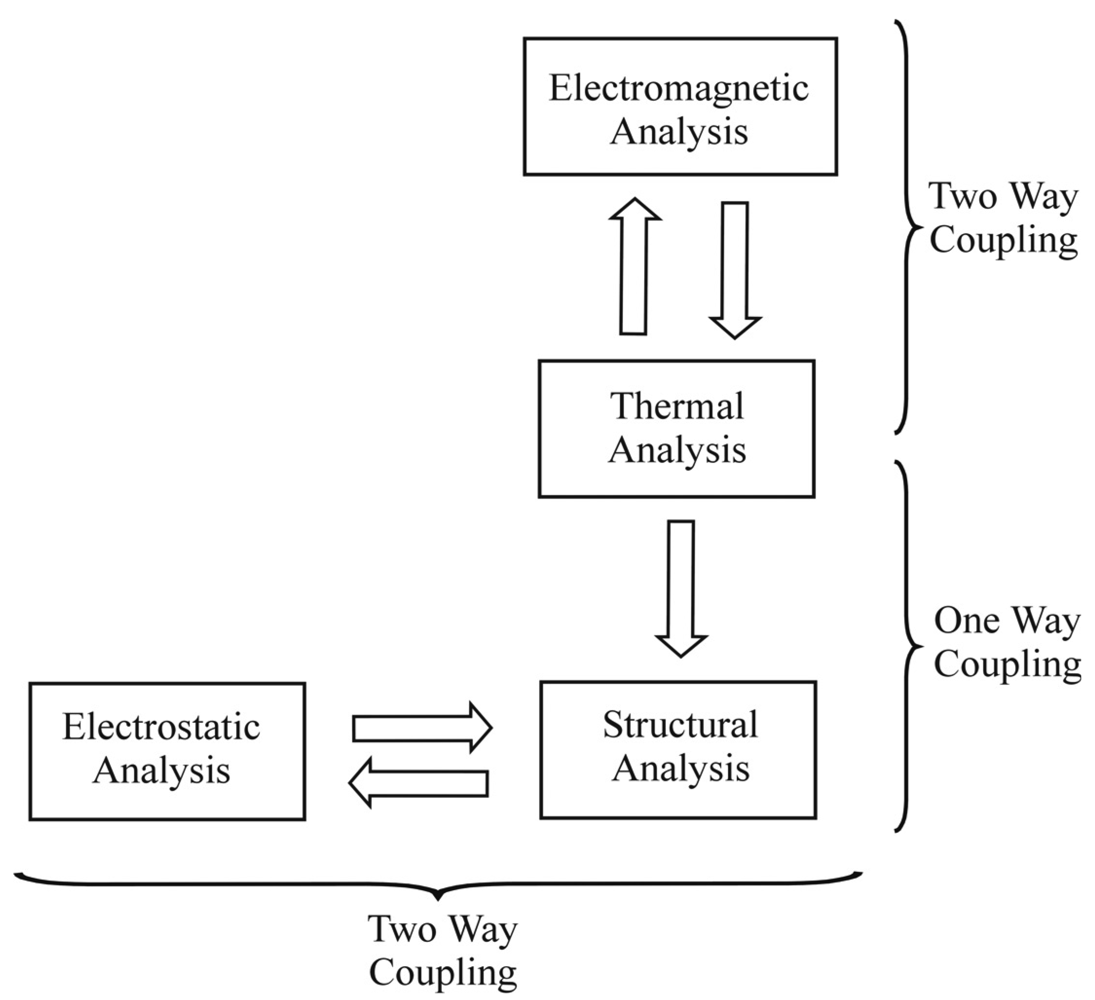
2. Coupled Field FE Analysis of RF MEMS Switch
2.1. EM-Thermal Fields Coupling
2.2. Thermal-Structural Fields Coupling
2.3. Structural-Electrostatic Fields Coupling
3. Automated-Substructuring Algorithm
4. Validation Examples
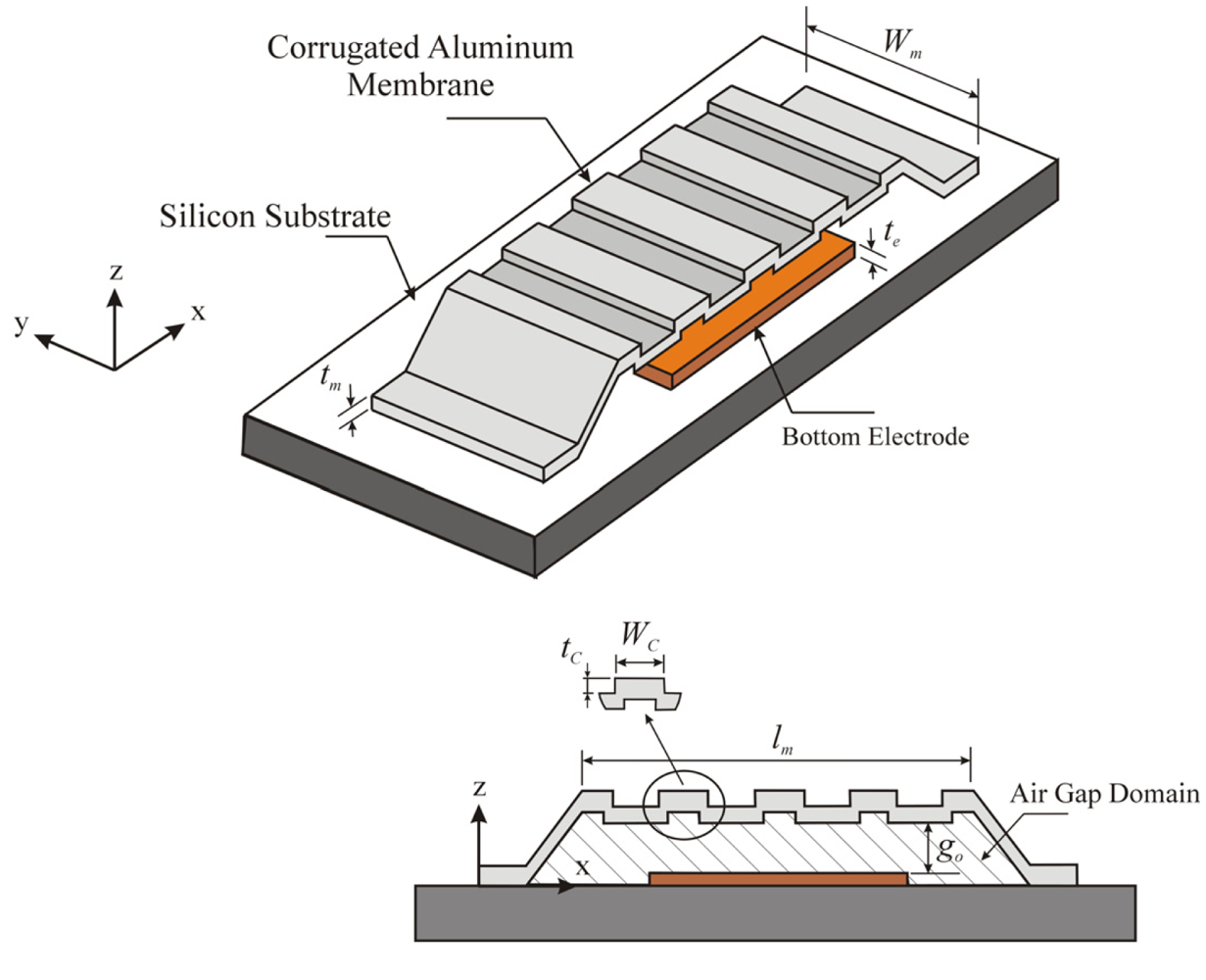
4.1. Example 1
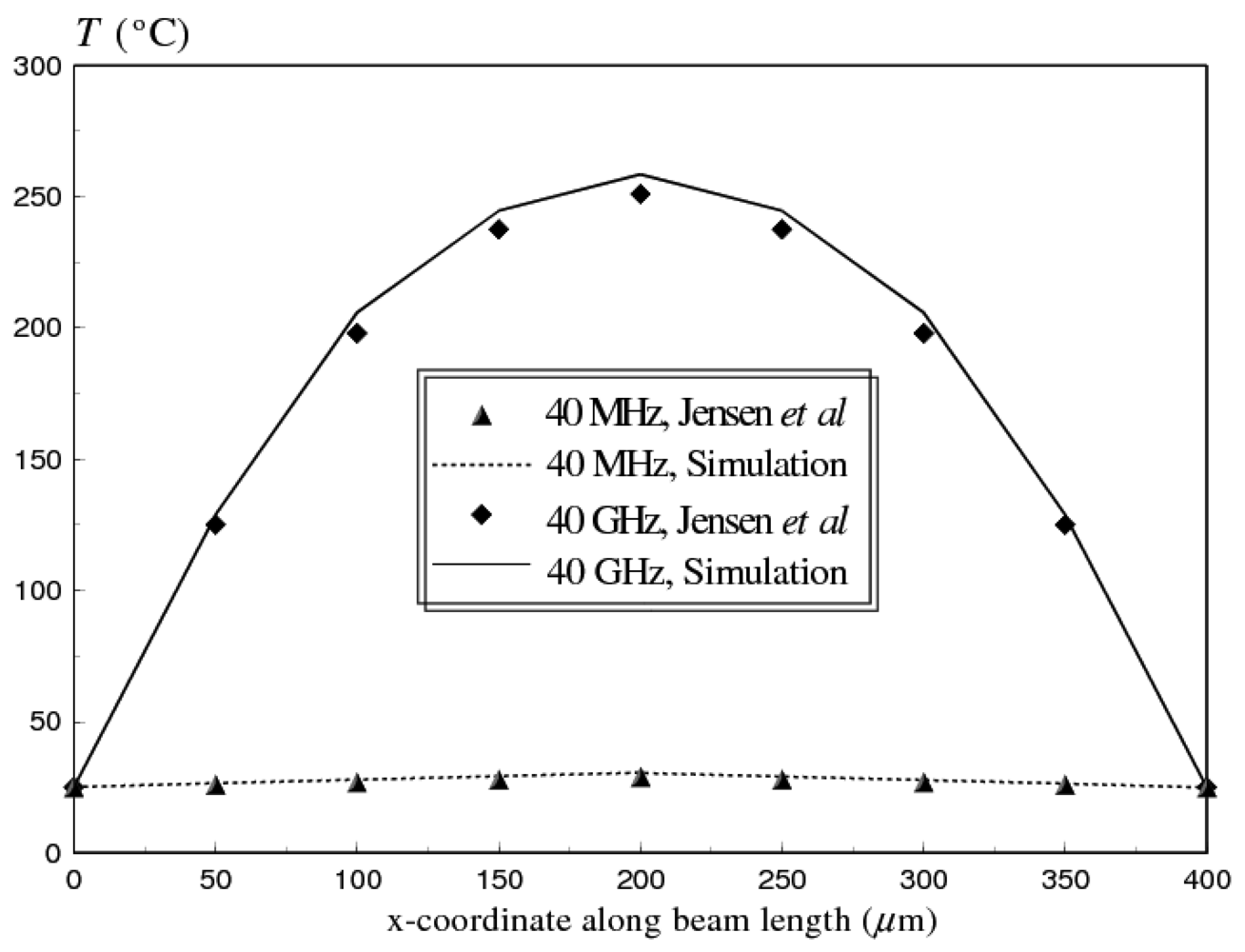
4.2. Example 2
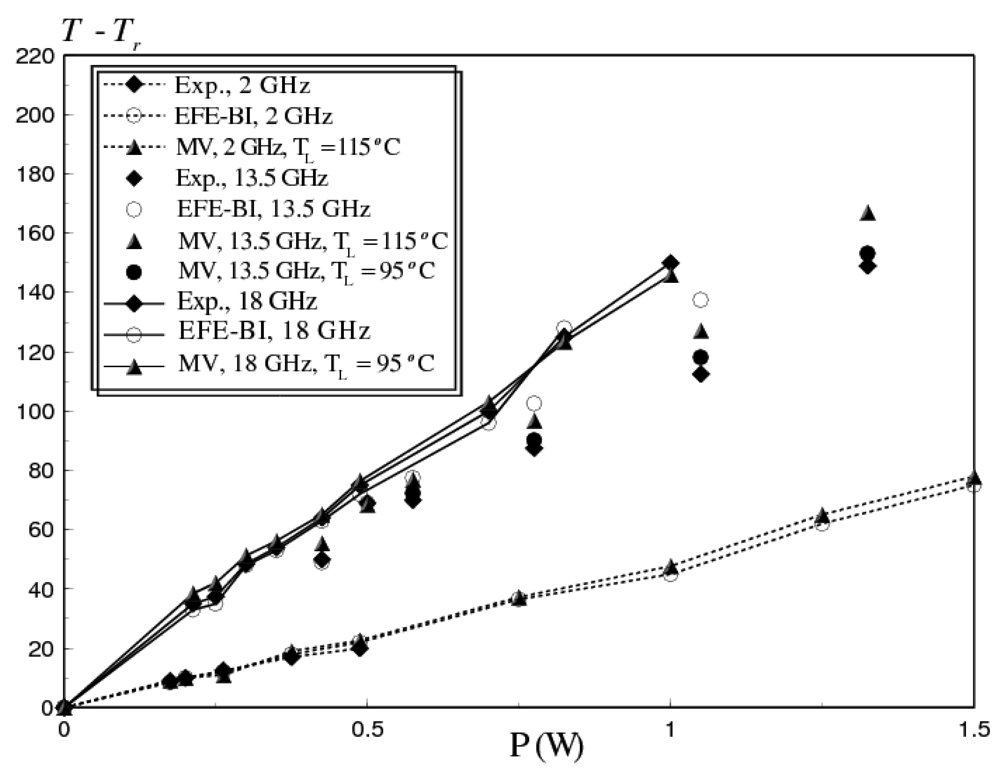
4.3. Example 3
5. Results and Discussion
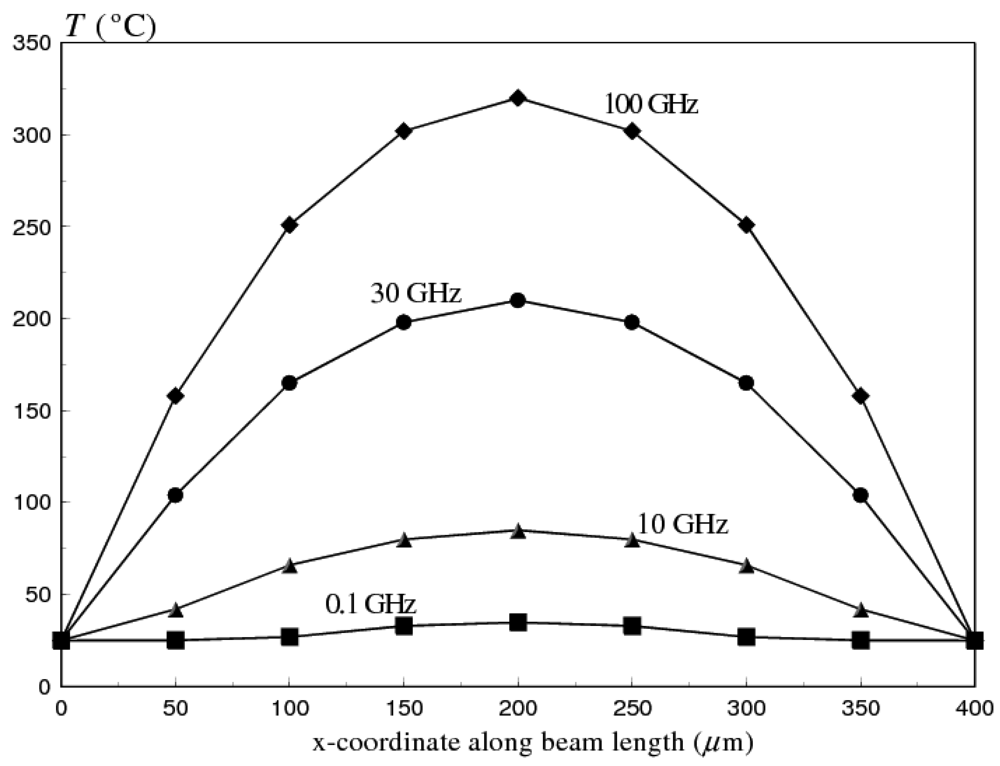
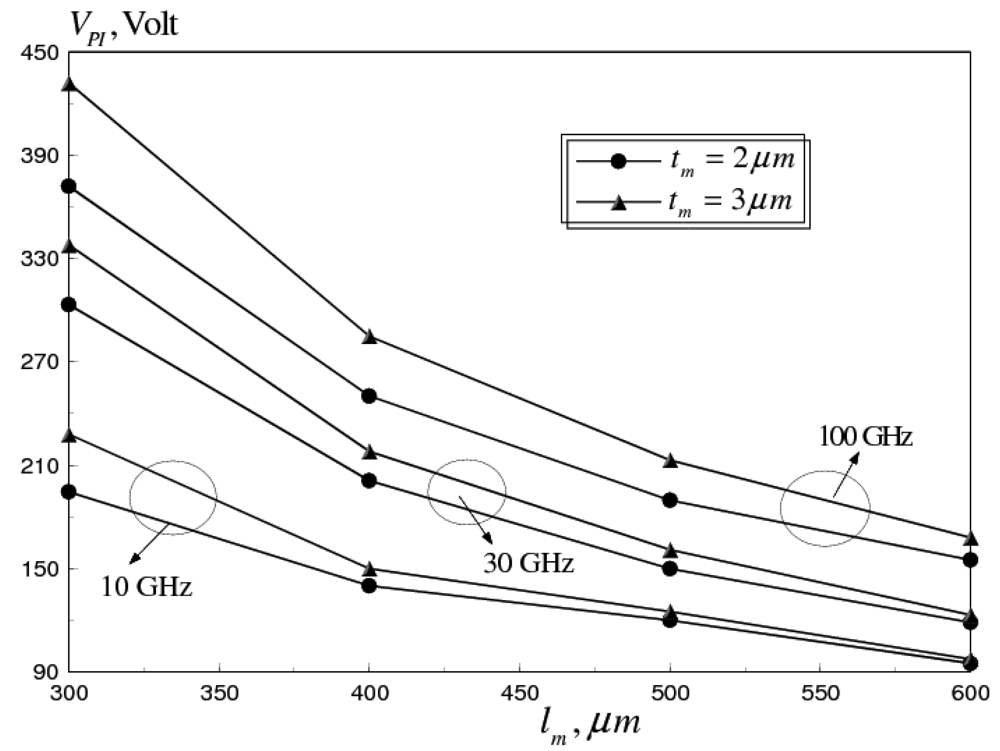
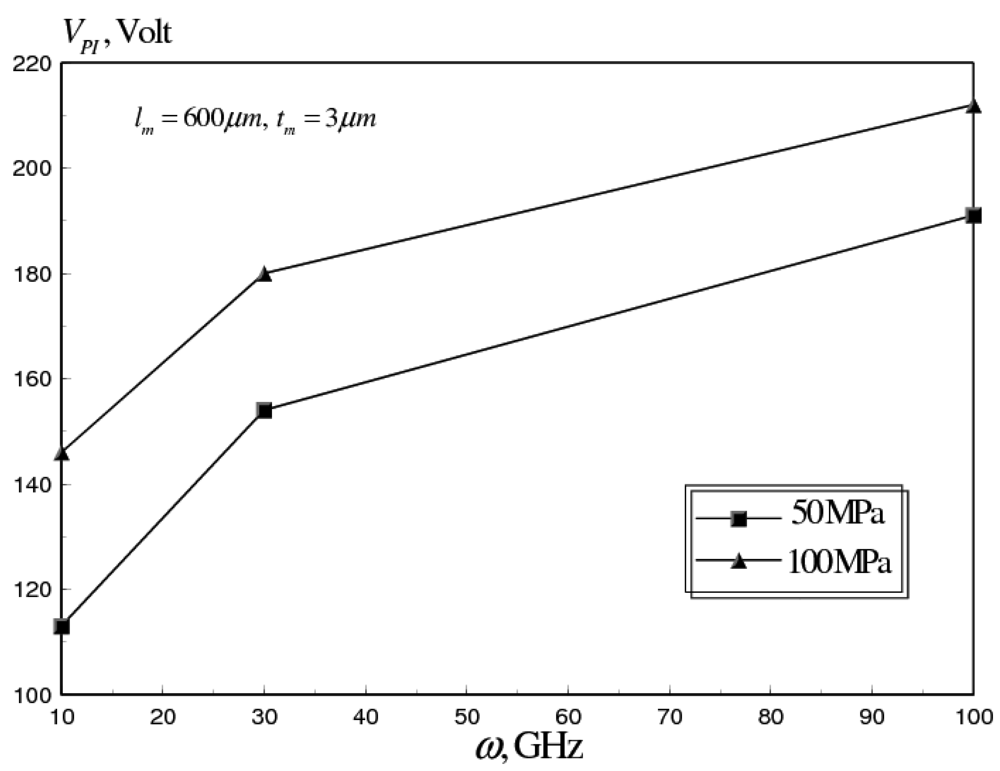
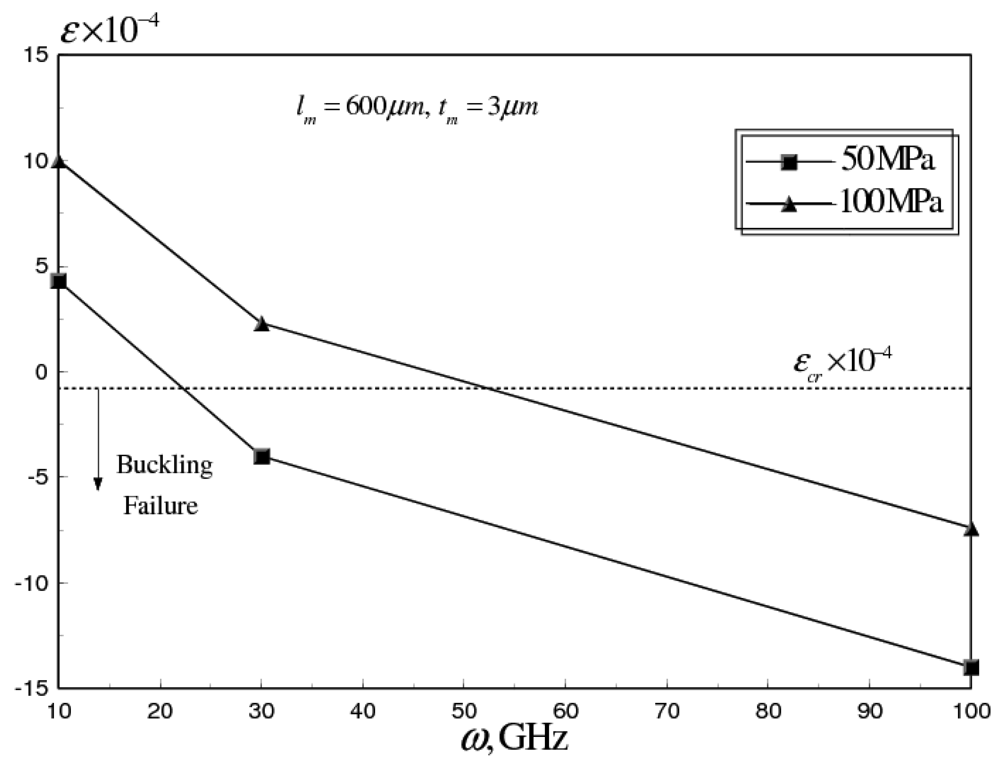
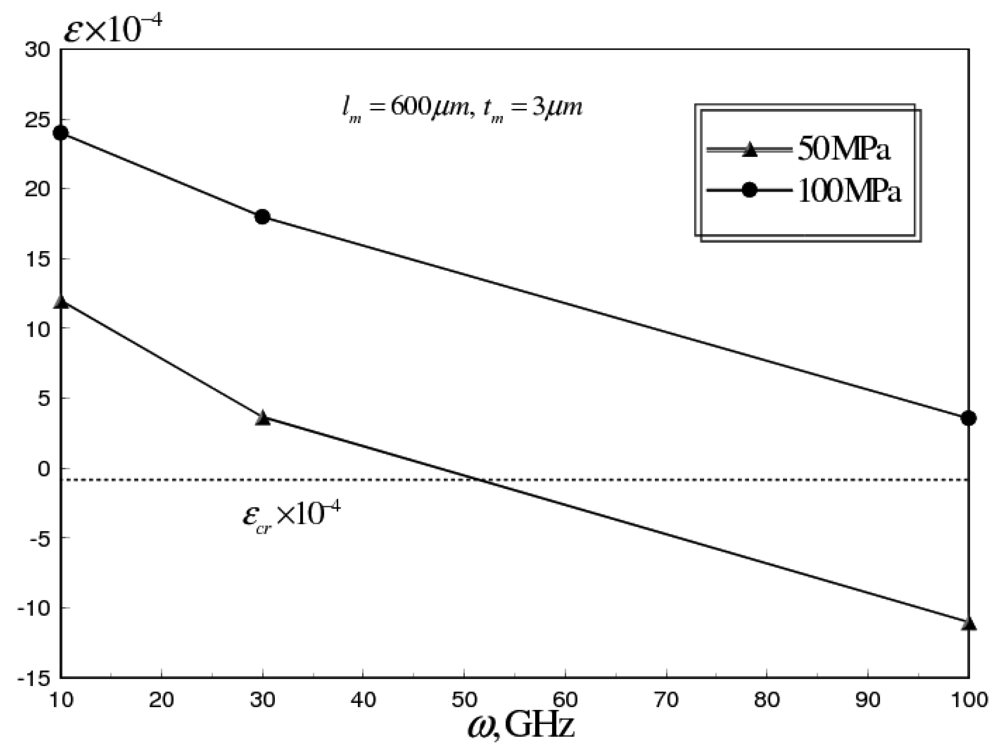
5.1. Effects of Operational Frequencies
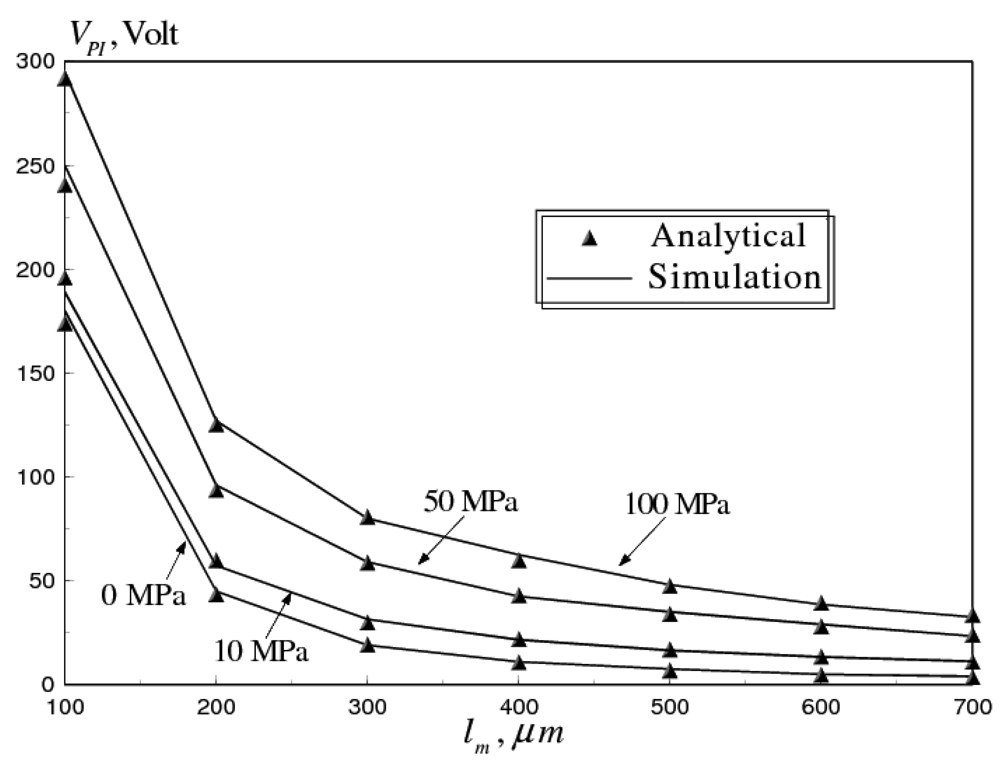
5.2. Effects of Residual Stresses
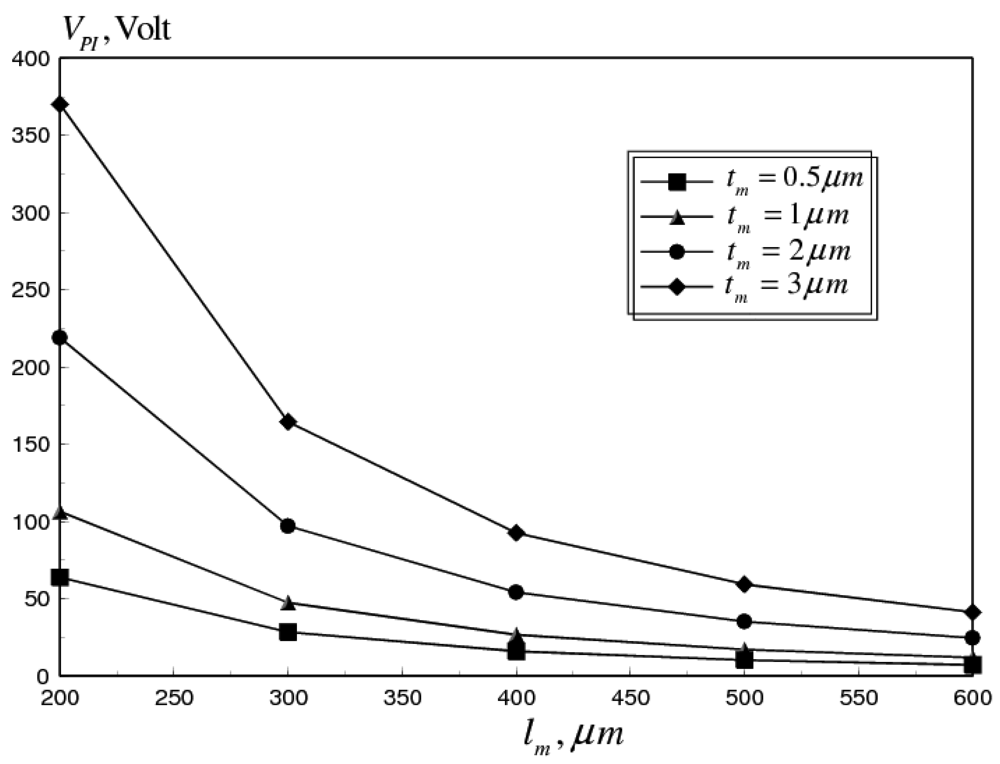
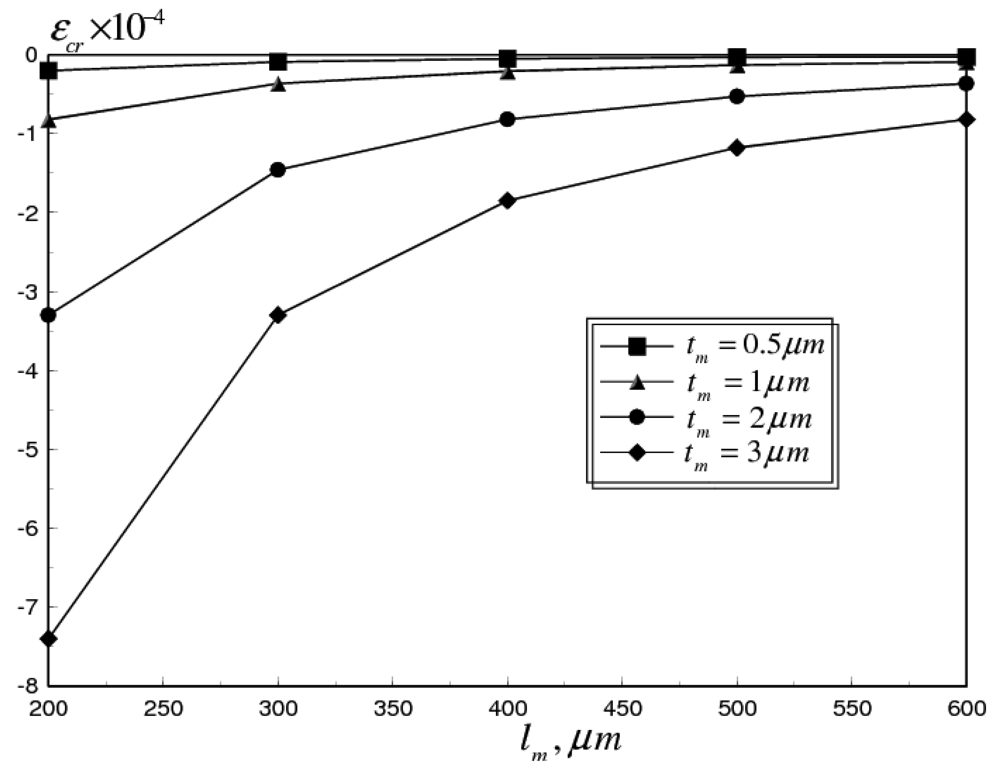
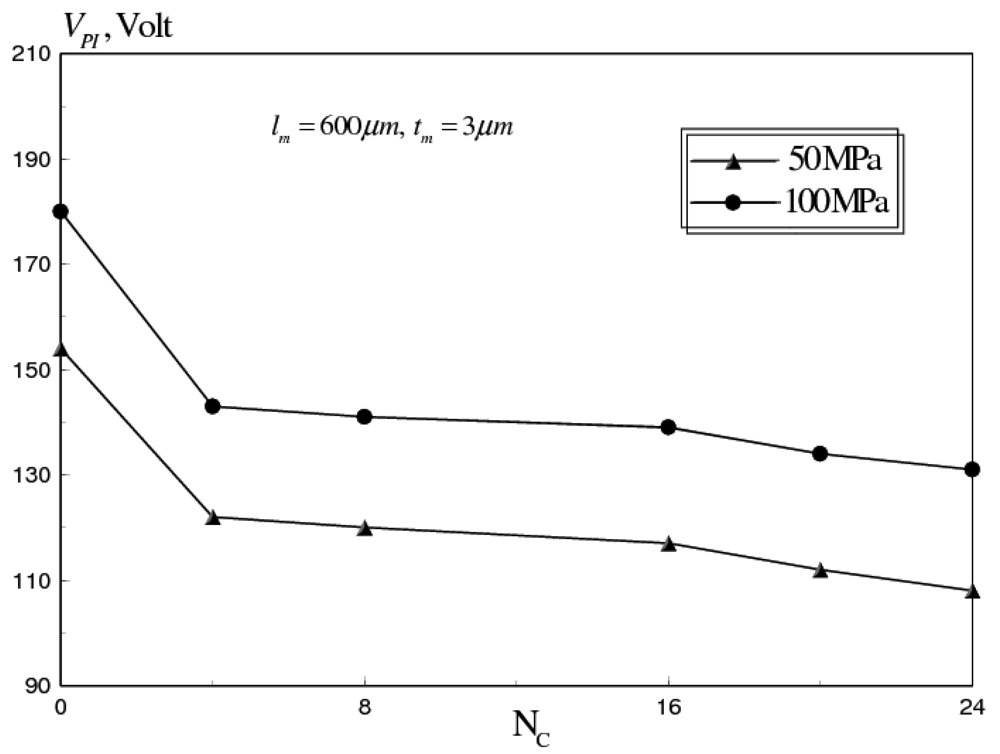
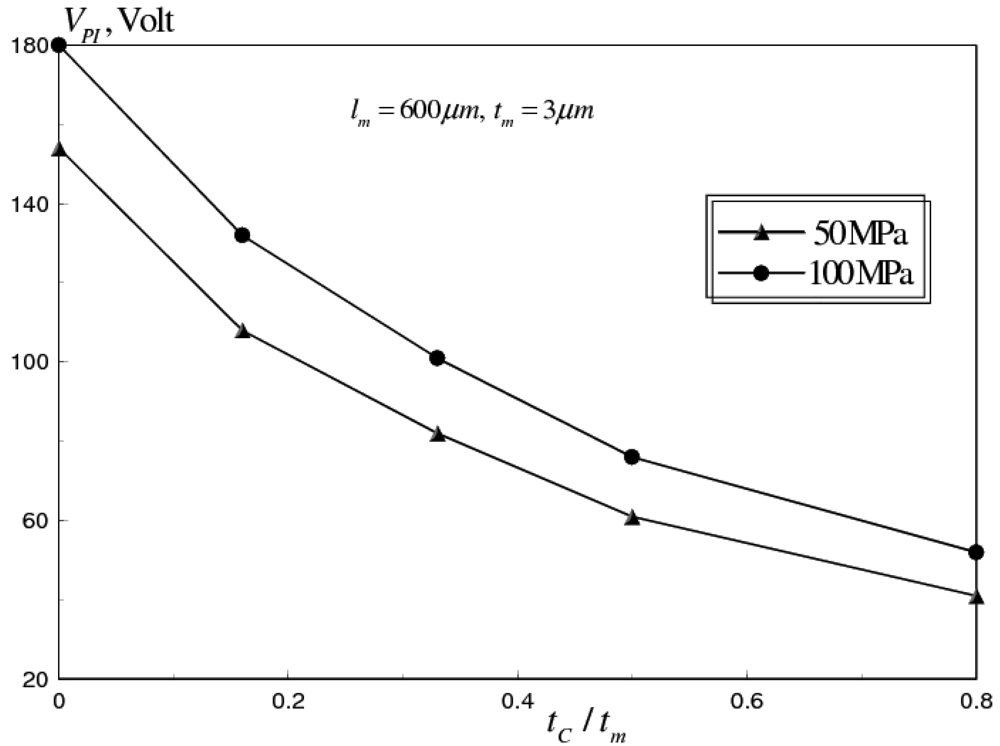
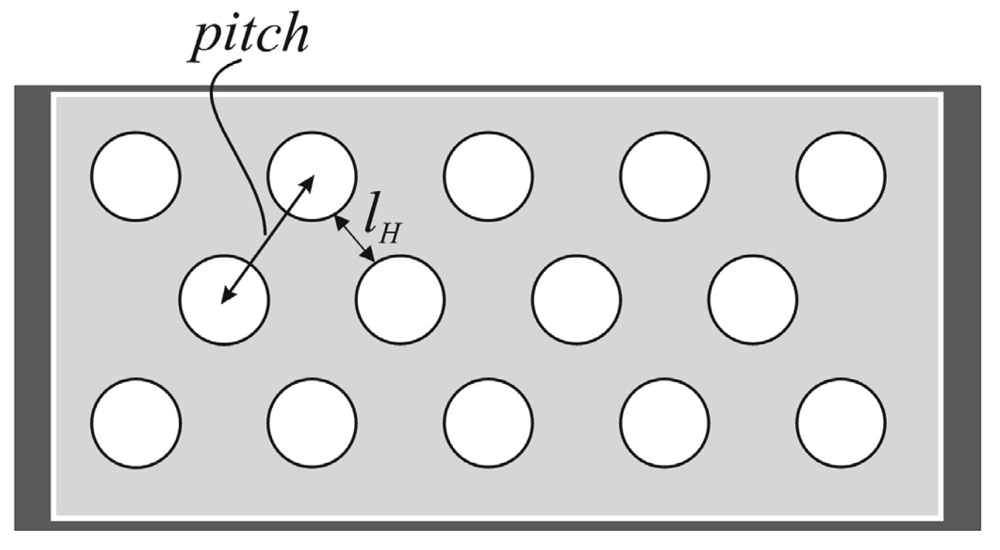
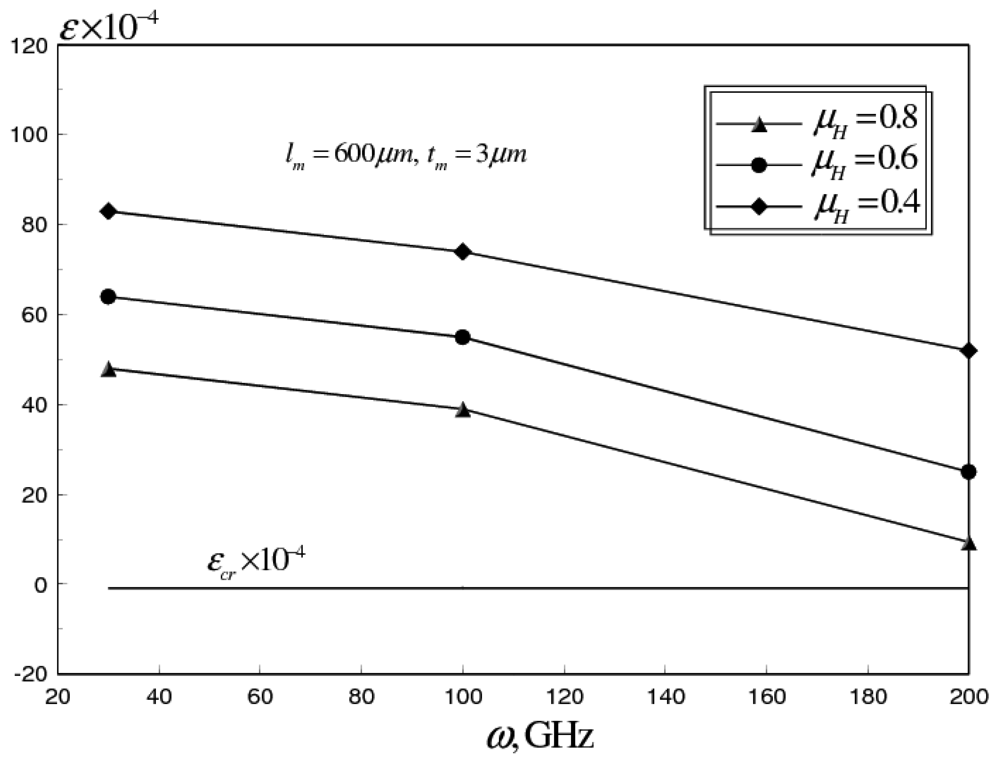
5.3. Mechanical Approaches
6. Conclusions
- The temperature rise at higher operational frequencies induces compressive stresses in the switch membrane of flat RF MEMS switches. The induced compressive stresses lead to buckling and device failure for ω ≥ 10 GHz. Moreover, the change in the deformation state of the switch leads to a dramatic increase in the required actuation voltages.
- In-plane tensile residual stresses generated during microfabrication counteract the induced compressive thermal stresses. In this sense, proper control of microfabrication residual stresses can increase the power carrying capacity of the RF switch. However, higher values of actuation voltages are exhibited because of the membrane stiffening effect.
- Membrane corrugations, at a distance from the support area can be used to maintain the actuation voltages at lower values. Therefore, using these membranes in conjunction with a proper control of microfabrication residual stresses, increase the reliable range of operation of the RF switch.
- A better design can be achieved by introducing holes to corrugated switch membranes. These holes help in reducing the effective Young's modulus of the switch membrane. This mainly would yield lower actuation voltages. Moreover, this reduction increases the positive residual axial strain component, which counteracts the compressive strains generated at higher frequencies. Therefore, the power handling capability of the RF switch can be increased considerably, without buckling, while maintaining a suitable actuation voltage. Our analysis of a corrugated switch membrane, with holes at a ligament efficiency of 0.4, shows that this design can increase the reliable operation of the RF switch to ω > 200 GHz.
Acknowledgments
References and Notes
- Goldsmith, C.; Ehmke, J.; Malczewski, A.; Pillans, B.; Eshelman, S.; Yao, Z.; Brank, J.; Eberly, M. Lifetime Characterization of Capacitive RF MEMS Switches. Proceedings of the IEEE International Microwave Symposium, Phoenix, AZ, USA, May 2001; pp. 227–230.
- Goldsmith, C.L.; Yao, Z.M.; Eshelman, S.; Denniston, D. Performance of low-loss RF MEMS capacitive switches. IEEE Microw. Guided. Wave Lett. 1998, 8, 269–271. [Google Scholar]
- Peroulis, D.; Pacheco, S.P.; Katehi, L.P.B. RF MEMS switches with enhanced power-handling capabilities. IEEE T. Microw. Theory 2004, 52, 59–68. [Google Scholar]
- Rebeiz, G.M. RF MEMS: Theory, Design and Technology; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Jensen, B.D.; Saitou, K.; Volakis, J.L.; Kurabayashi, K. Fully integrated electrothermal multidomain modeling of RF MEMS switches. IEEE Microw. Wireless Compon. Lett. 2003, 13, 364–366. [Google Scholar]
- Rizk, J.B.; Chaiban, E.; Rebeiz, G.M. Steady State Thermal Analysis and High-Power Reliability Considerations of RF MEMS Capacitive Switches. Proceedings of the IEEE MTT-S International Microwave Symposium, Seattle, WA, USA; 2002; pp. 239–242. [Google Scholar]
- Thiel, W.; Tornquist, K.; Reano, R.; Katehi, L.P.B. A Study of Thermal Effects in RF-MEM-Switches Using a Time Domain Approach. Proceedings of the IEEE MTT-S International Microwave Symposium, Seattle, WA, USA; 2002; pp. 235–238. [Google Scholar]
- Chen, S.; Baughn, T.V.; Yao, Z.J.; Goldsmith, C.L. A new in situ residual stress measurement method for a MEMS thin fixed-fixed beam structure. J. Microelectromech. Syst. 2002, 11, 309–316. [Google Scholar]
- Doerner, M.F.; Nix, W.D. Stresses and deformation processes in thin films on substrates. CRC Crit. Rev. Solid State Mater. Sci. 1988, 14, 225–268. [Google Scholar]
- Stadtmueller, M. Mechanical stress of CVD-dielectrics. J. Electrochem. Soc. 1992, 139, 3669–3674. [Google Scholar]
- ANSYS v10.1 Coupled Field Analysis Guide, User Manual.; ANSYS: Houston, TX, USA, 2005.
- Pamidighantam, S.; Puers, R.; Baert, K.; Tilmans, H.A.C. Pull-in voltage analysis of electrostatically actuated beam structures with fixed-fixed and fixed-free end conditions. J. Micromech. Microeng. 2002, 12, 458–464. [Google Scholar]
- Zhu, Y.; Espinosa, H.D. Effect of temperature on capacitive RF MEMS switch performance—A coupled-field analysis. J. Micromech. Microeng. 2004, 14, 1270–1279. [Google Scholar]
- Belendez, T.; Neipp, C.; Belendez, A. Large and small deflections of a cantilever beam. Eur. J. Phys. 2002, 23, 371–379. [Google Scholar]
- Chang, K. Microwave solid-state circuits and applications; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Palmer, H.B. The capacitance of a parallel plate capacitor by the Schwartz-Christoffel transformation. J. Electr. Eng. 1937, 56, 363–366. [Google Scholar]
- Sadek, K.; Moussa, W. Investigating the effect of deposition variation on the performance sensitivity of low-power gas sensors. Sens. Actuat. B - Chem. 2005, 107, 497–508. [Google Scholar]
- Farhat, C.; Lesoinne, M. Automatic partitioning of unstructured meshes for the parallel solution of problems in computational mechanics. Int. J. Numer. Meth. Eng. 1993, 36, 745–764. [Google Scholar]
- Hsieh, S.-H.; Paulino, G.H.; Abel, J.F. Recursive spectral algorithms for automatic domain partitioning in parallel finite element analysis. Comput. Meth. Appl. Mech. Eng. 1995, 121, 137–162. [Google Scholar]
- Wang, Z.; Jensen, B.D.; Chow, L.L.W.; Volakis, J.L.; Saitou, K.; Kurabayashi, K. Full-wave electromagnetic and thermal modeling for the prediction of heat-dissipation-induced RF-MEMS switch failure. J. Micromech. Microeng. 2006, 16, 157–164. [Google Scholar]
- Peroulis, D.; Pacheco, S.; Sarabandi, K.; Katehi, L.P.B. Tunable Lumped Components with Applications to Reconfigurable MEMS Filters. Proceedings of the 2001 IEEE MTT-S International Microwave Symposium, Phoenix, AZ, USA; 2001; pp. 341–344. [Google Scholar]
- Peroulis, D.; Pacheco, S.P.; Sarabandi, K.; Katehi, L.P.B. Electromechanical considerations in developing low-voltage RF MEMS switches. IEEE Trans. Microw. Theory 2003, 51, 259–270. [Google Scholar]

© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sadek, K.; Lueke, J.; Moussa, W. A Coupled Field Multiphysics Modeling Approach to Investigate RF MEMS Switch Failure Modes under Various Operational Conditions. Sensors 2009, 9, 7988-8006. https://doi.org/10.3390/s91007988
Sadek K, Lueke J, Moussa W. A Coupled Field Multiphysics Modeling Approach to Investigate RF MEMS Switch Failure Modes under Various Operational Conditions. Sensors. 2009; 9(10):7988-8006. https://doi.org/10.3390/s91007988
Chicago/Turabian StyleSadek, Khaled, Jonathan Lueke, and Walied Moussa. 2009. "A Coupled Field Multiphysics Modeling Approach to Investigate RF MEMS Switch Failure Modes under Various Operational Conditions" Sensors 9, no. 10: 7988-8006. https://doi.org/10.3390/s91007988



