Ship Detection in SAR Image Based on the Alpha-stable Distribution
Abstract
:1. Introduction
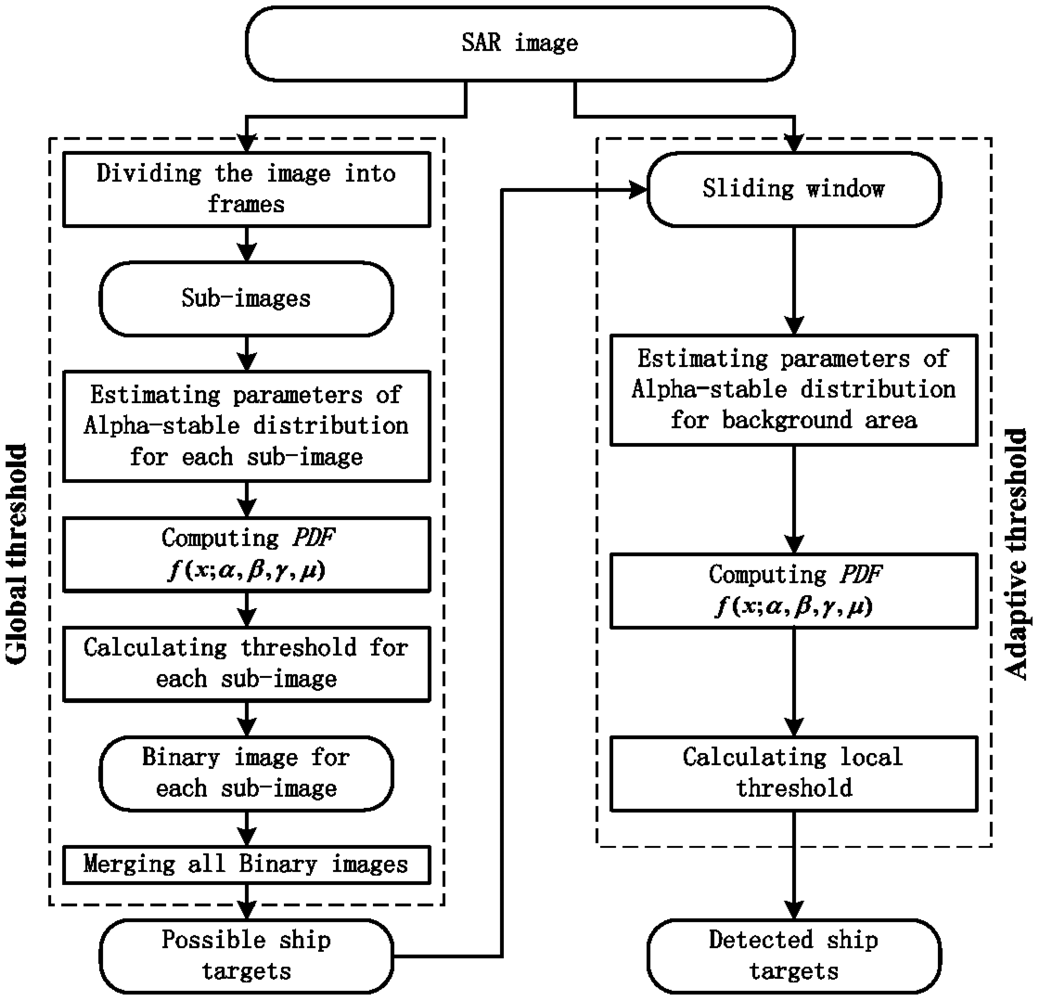
2. Methodology
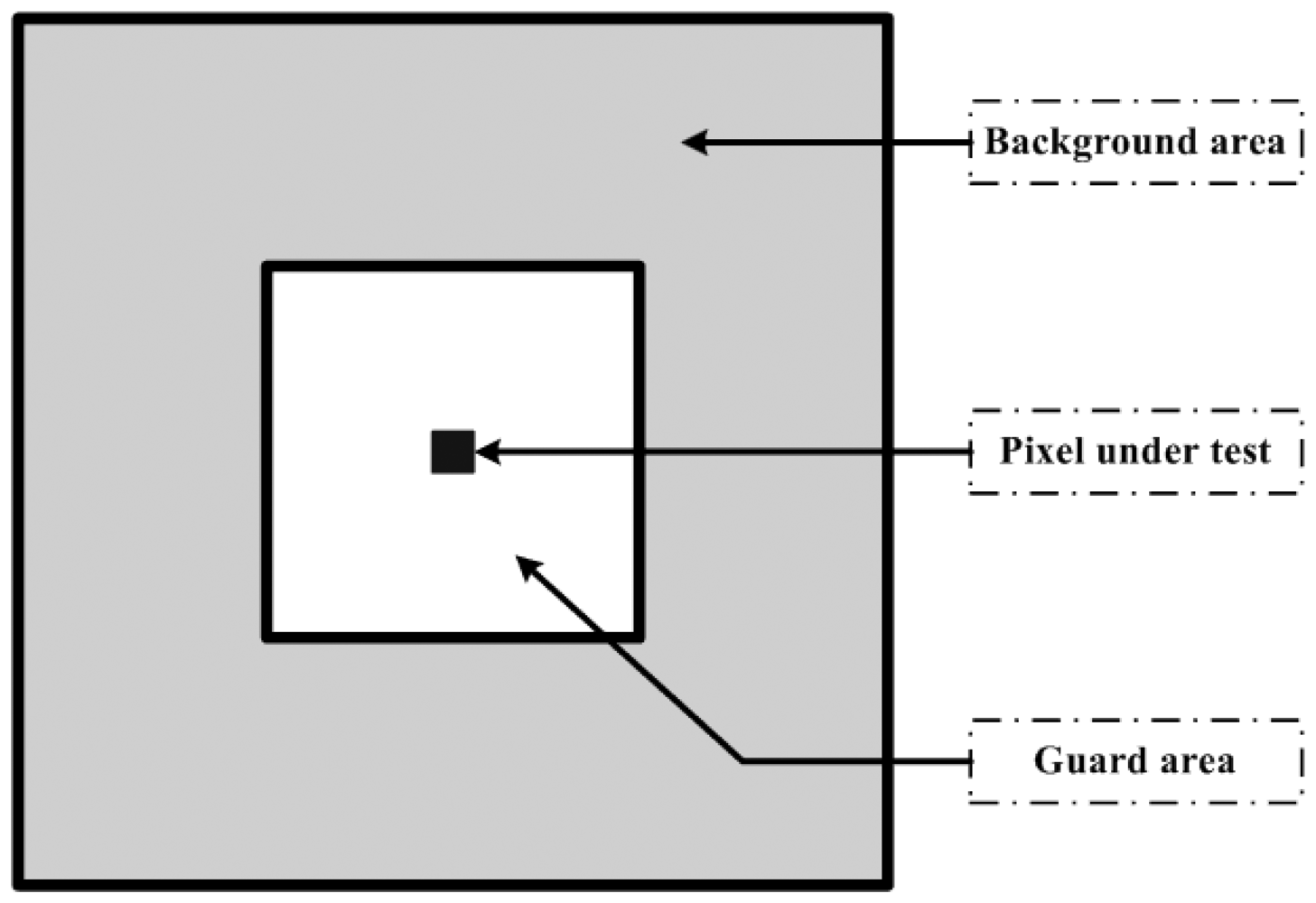
2.1. CFAR Based Ship Detection Algorithm
2.2. The Alpha-stable Distribution
2.3. CFAR Algorithm Based on the Alpha-stable Distribution
3. Experimental Results
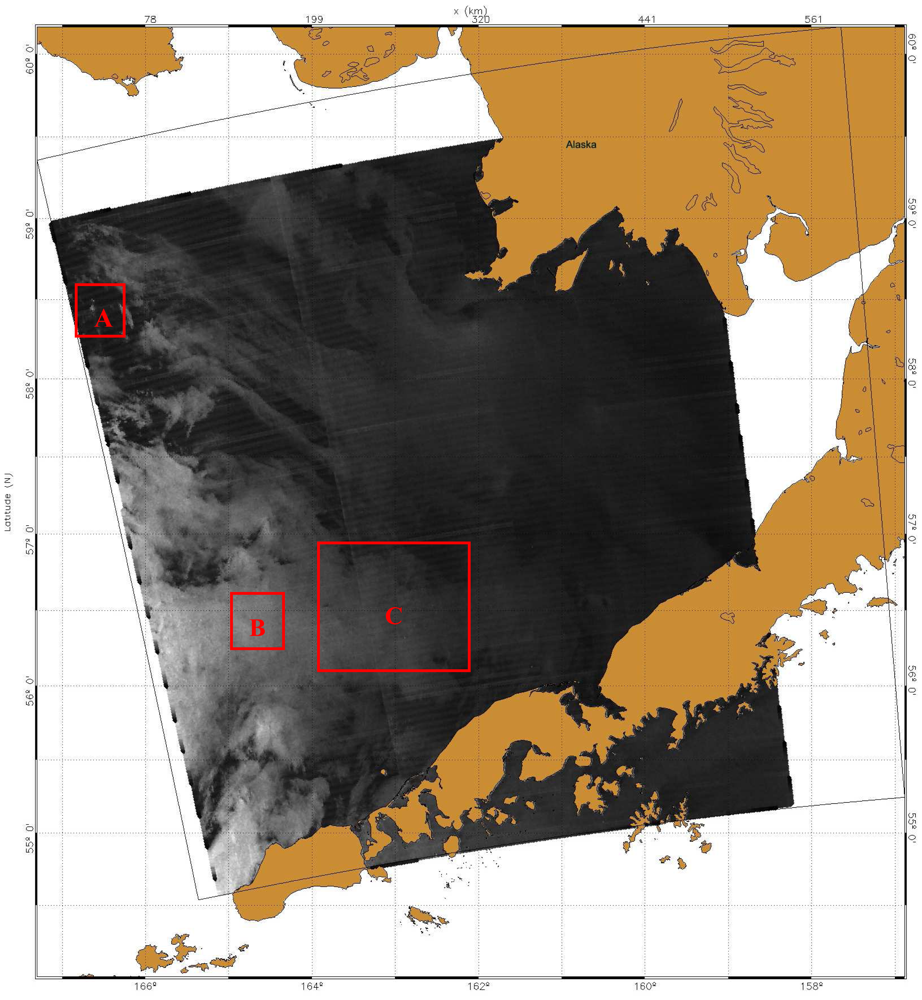
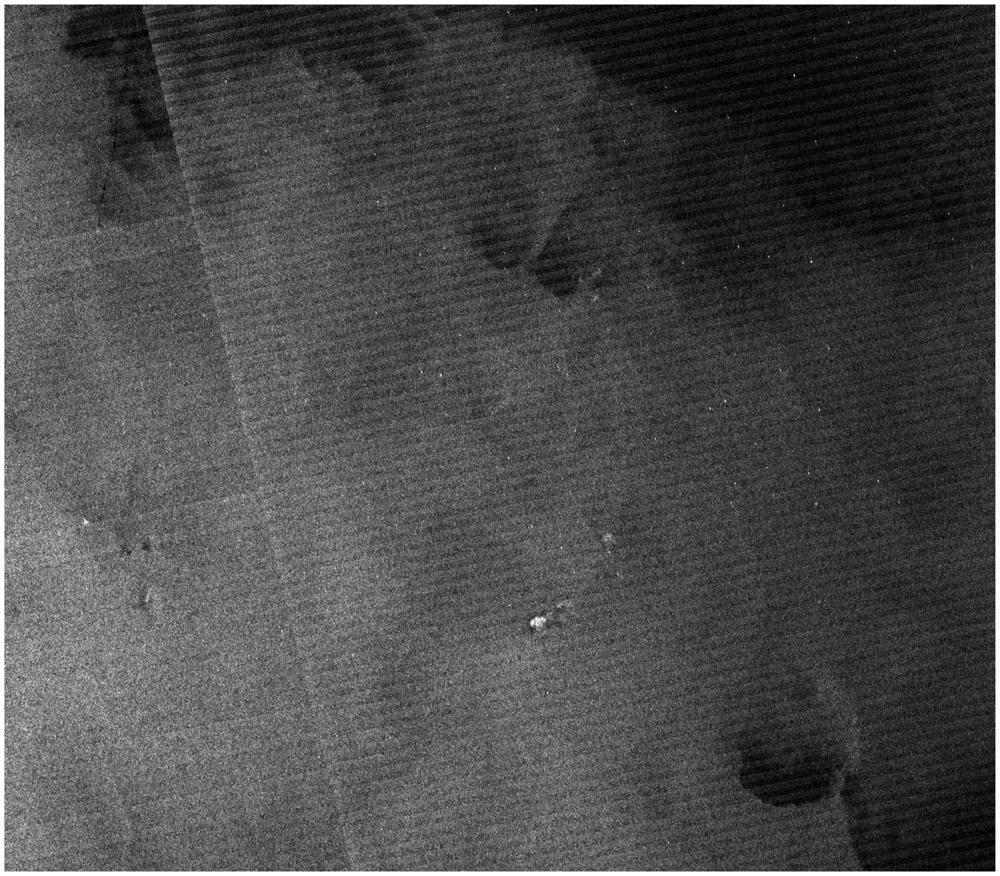
3.1. Study Areas and Data
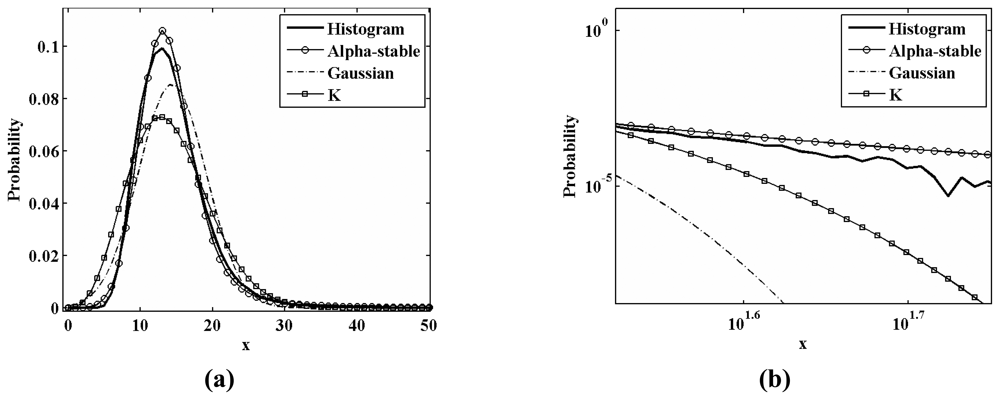
3.2. Test for Alpha-stable Distribution
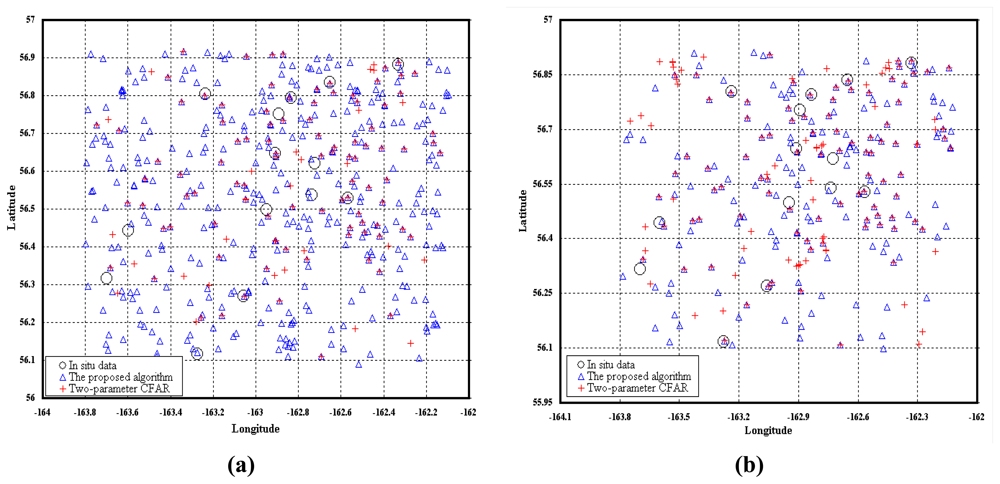
3.3. Validation of Ship Detection Results
4. Conclusions
Acknowledgments
References
- Wackerman, C.C.; Friedman, K.S.; Pichel, W.G.; Clemente-Colon, P.; Li, X. Automatic Detection of Ships in RADARSAT-1 SAR imagery. Canadian Journal of Remote Sensing 2001, 27(5), 568–577. [Google Scholar]
- Vachon, P.W.; Thomas, S.J.; Cranton, J.; Edel, H.R.; Henschel, M.D. Validation of Ship Detection by the RADARSAT Synthetic Aperture Radar and the Ocean Monitoring Workstation. Canadian Journal of Remote Sensing 2000, 26(3), 200–212. [Google Scholar]
- Eldhuset, K. An Automatic Ship and Ship Wake Detection System for Spaceborne SAR Images in Coastal Regions. IEEE Transactions on Geoscience and Remote Sensing 1996, 34(4), 1010–1019. [Google Scholar]
- Kuo, J.M.; Chen, K.S. The Application of Wavelets Correlator for Ship Wake Detection in SAR Images. IEEE Transactions on Geoscience and Remote Sensing 2003, 41(6), 1506–1511. [Google Scholar]
- Crisp, D.J. The State-of-the-Art in Ship Detection in Synthetic Aperture Radar Imagery.; Australian Government, Department of defence, 2004; p. 115. [Google Scholar]
- Wang, C.; Liao, M.; Li, X.; Jiang, L.; Chen, X. Ship detection algorithm in SAR images based on Alpha-stable model. Proceedings of SPIE 2007, 6786, 678611. [Google Scholar]
- Liao, M.; Wang, C.; Wang, Y.; Jiang, L. Using SAR Images to Detect Ships From Sea Clutter. IEEE Geoscience and Remote Sensing Letters 2008, 5(2), 194–198. [Google Scholar]
- Oktem, R.; Egiazarian, K.; Lukin, V.V.; Ponomarenko, N.N.; Tsymbal, O.V. Locally adaptive DCT filtering for signal-dependent noise removal. EURASIP Journal on Advances in Signal Processing 2007, 1–10. [Google Scholar]
- Principe, J.C.; Radisavljevic, A.; Fisher, J.; Hiett, M. Target Prescreening Based on a Quadratic Gamma Discriminator. IEEE Transactions on Aerospace and Electronic Systems 1998, 34(3), 706–715. [Google Scholar]
- Jiang, Q.; Wang, S.; Ziou, D.; Zaart, A.E.; Rey, M.T.; Benie, G.B.; Henschel, M. Ship detection in RADARSAT SAR imagery. IEEE International Conference on Systems, Man, and Cybernetics (SMC'98); 1998; 5, pp. 4562–4566. [Google Scholar]
- Pierce, R.D. RCS characterization using the alpha-stable distribution. IEEE National Radar Conference Proceedings; 1996; pp. 154–159. [Google Scholar]
- Banerjee, A.; Burlina, P.; Chellappa, R. Adaptive target detection in foliage-penetrating SAR images using alpha-stable models. IEEE Transactions on Image Processing 1999, 8(12), 1823–1831. [Google Scholar]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Imagery; Artech House: Norwood, Massachusetts, USA, 1998. [Google Scholar]
- Nikias, C.L.; Shao, M. Signal processing with Alpha-Stable Distributions and Applications; New York; Wiley, 1995. [Google Scholar]
- Kuruoglu, E.E.; Zerubia, J. Modeling SAR Images with a generalization of the Rayleigh distribution. IEEE Transactions on Image Processing 2004, 13(4), 527–533. [Google Scholar]
- Koutrouvelis, I.A. Regression-type estimation of the parameters of stable laws. Journal of American Statistical Association 1980, 75, 918–928. [Google Scholar]
- Nolan, J.P. Numerical Calculation of Stable Densities and Distribution Functions. Communications in Statistics - Stochastic Models 1997, 13, 759–774. [Google Scholar]
- Novak, L.M.; Owirka, G.J.; Netishen, C.M. Performance of a high-resolution polarimetric SAR automatic target recognition system. Lincoln Laboratory Journal 1993, 6(1), 11–23. [Google Scholar]


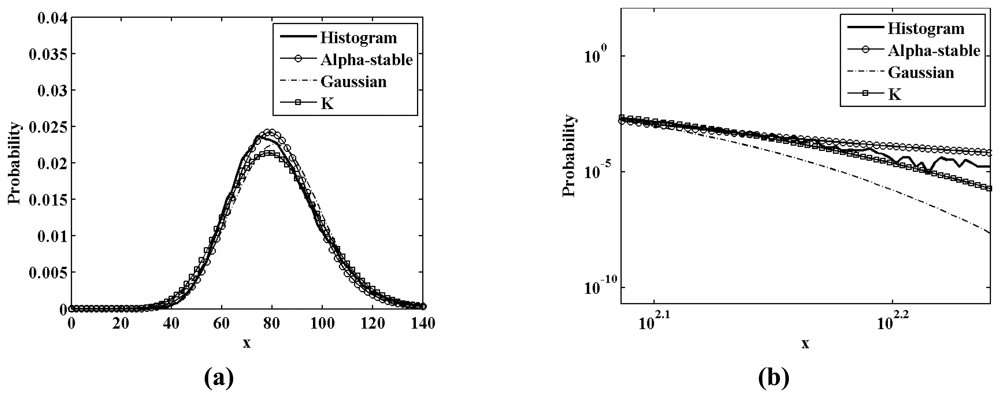
| Study Area | Distributions | Parameter 1 | Parameter 2 | Parameter 3 | Parameter 4 |
|---|---|---|---|---|---|
| A | Gaussian | μ= 14.3882 | σ= 4.6616 | - | - |
| K | L= 1.8140 | ν= 98.4250 | - | - | |
| Alpha-stable | α= 1.8067 | γ= 6.3132 | β= 1.0000 | μ= 14.7815 | |
| B | Gaussian | μ= 81.3233 | σ= 17.6446 | - | - |
| K | L= 5.0781 | ν= 98.4250 | - | - | |
| Alpha-stable | α= 1.9560 | γ= 129.9372 | β = 1.0000 | μ= 81.8972 |
| No. | Ship name | Date (GMT) | Time (GMT) | Latitude | Longitude | Ship length (m) | Wind speed (m/s) | Sea state |
|---|---|---|---|---|---|---|---|---|
| 1 | Gladiator | 2002-10-16 | 4:28:39 | 56.117 | -163.275 | 37.8 | 5.14 | 4 |
| 2 | Alliance | 2002-10-16 | 4:28:39 | 56.270 | -163.058 | 30.5 | 5.14 | 2 |
| 3 | Andronica | 2002-10-16 | 4:28:39 | 56.317 | -163.698 | 30.2 | - | 3 |
| 4 | Alaska Sea | 2002-10-16 | 4:28:39 | 56.443 | -163.598 | 33.5 | - | calm |
| 5 | Pavlof | 2002-10-16 | 4:28:39 | 56.497 | -162.948 | 50.6 | - | 1 |
| 6 | Handler | 2002-10-16 | 4:28:39 | 56.528 | -162.568 | 38.4 | 1.03 | calm |
| 7 | Sultan | 2002-10-16 | 4:28:39 | 56.538 | -162.737 | 39.6 | 5.14 | <3 |
| 8 | Argosy | 2002-10-16 | 4:28:39 | 56.646 | -162.910 | 37.8 | 5.14 | calm |
| 9 | Kelveen K | 2002-10-16 | 4:28:39 | 56.751 | -162.892 | 32.0 | 7.72 | 6 |
| 10 | Northwind | 2002-10-16 | 4:28:39 | 56.794 | -162.836 | 32.0 | 2.57 | <4 |
| 11 | Early Dawn | 2002-10-16 | 4:28:39 | 56.803 | -163.239 | 32.9 | 2.24 | 3 |
| 12 | Aleutian Beauty | 2002-10-16 | 4:28:39 | 56.839 | -162.652 | 29.9 | 2.57 | 1 |
| 13 | Big Blue | 2002-10-16 | 4:28:39 | 56.882 | -162.330 | 26.8 | 0 | <4 |
| No. | Ship name | The proposed algorithm (BW: 25×25, GW:9×9) | Two-parameter CFAR (BW:25×25, GW:9×9, SW:5×5) | The proposed algorithm (BW:41×41, GW:13×13) | Two-parameter CFAR (BW:41×41, GW:13×13, SW:5×5) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Detection | Distance (km) | Detection | Distance (km) | Detection | Distance (km) | Detection | Distance (km) | ||
| 1 | Gladiator | Yes | 0.356 | No | 9.351 | Yes | 0.356 | Yes | 0.356 |
| 2 | Alliance | Yes | 0.255 | Yes | 0.255 | Yes | 0.255 | Yes | 0.255 |
| 3 | Andronica | No | 3.211 | No | 3.211 | No | 3.211 | No | 3.211 |
| 4 | Alaska Sea | Yes | 0.786 | No | 4.710 | Yes | 0.786 | Yes | 1.555 |
| 5 | Pavlof | Yes | 1.740 | Yes | 1.740 | Yes | 1.740 | Yes | 1.740 |
| 6 | Handler | Yes | 0.186 | Yes | 0.186 | Yes | 0.186 | Yes | 0.186 |
| 7 | Sultan | Yes | 0.867 | No | 5.534 | Yes | 0.867 | No | 5.563 |
| 8 | Argosy | Yes | 0.914 | Yes | 0.914 | Yes | 0.914 | Yes | 0.914 |
| 9 | Kelveen K | Yes | 2.201 | Yes | 2.201 | Yes | 2.201 | Yes | 2.201 |
| 10 | Northwind | Yes | 0.261 | Yes | 0.261 | Yes | 0.261 | Yes | 0.261 |
| 11 | Early Dawn | Yes | 0.375 | Yes | 0.375 | Yes | 0.375 | Yes | 0.375 |
| 12 | Aleutian Beauty | Yes | 0.237 | Yes | 0.237 | Yes | 0.237 | Yes | 0.237 |
| 13 | Big Blue | Yes | 0.629 | Yes | 0.629 | Yes | 0.629 | Yes | 0.629 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, C.; Liao, M.; Li, X. Ship Detection in SAR Image Based on the Alpha-stable Distribution. Sensors 2008, 8, 4948-4960. https://doi.org/10.3390/s8084948
Wang C, Liao M, Li X. Ship Detection in SAR Image Based on the Alpha-stable Distribution. Sensors. 2008; 8(8):4948-4960. https://doi.org/10.3390/s8084948
Chicago/Turabian StyleWang, Changcheng, Mingsheng Liao, and Xiaofeng Li. 2008. "Ship Detection in SAR Image Based on the Alpha-stable Distribution" Sensors 8, no. 8: 4948-4960. https://doi.org/10.3390/s8084948





