Measurement of Mechanical Properties of Cantilever Shaped Materials
Abstract
:1. Introduction
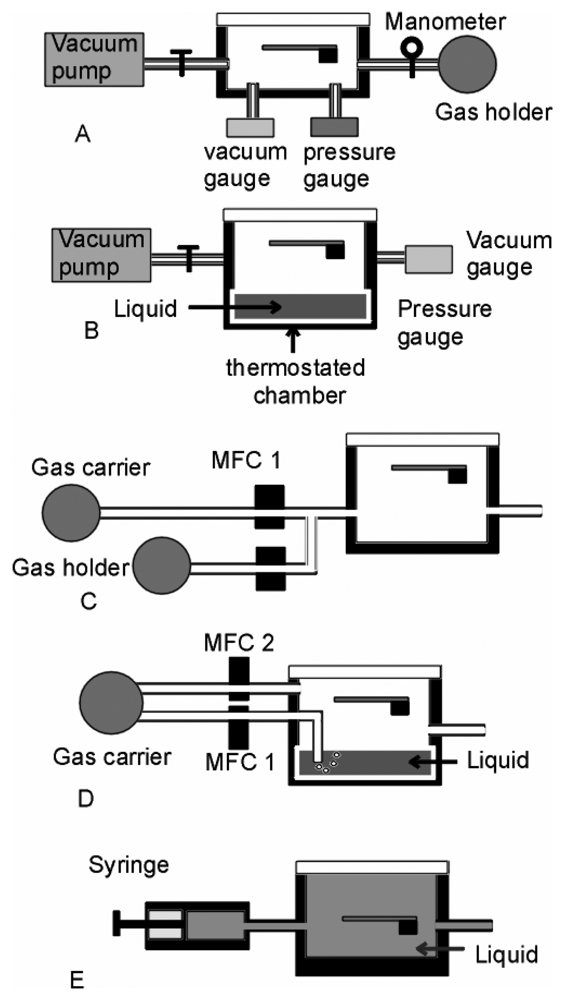
2. In situ measurements
Static Measurements
Dynamic Measurements
Measurements in Liquids
3. Elastic parameters
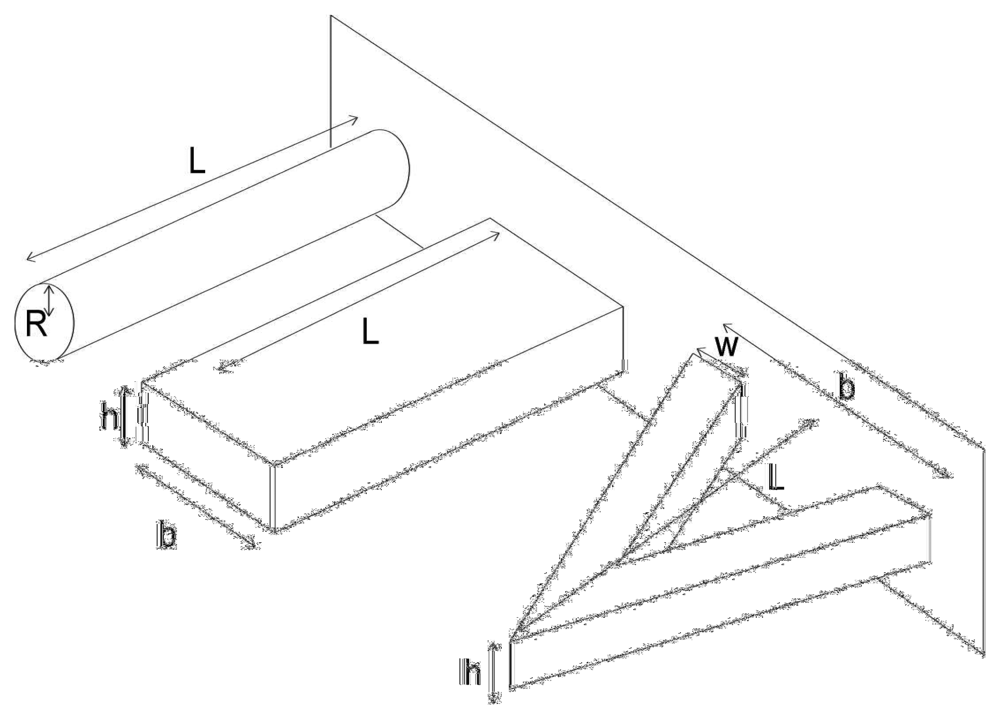
Static approach using single material cantilevers
| Cylindrical beam | Rectangular beam | V-shaped cantilever |
Static approach for a bilayer cantilever
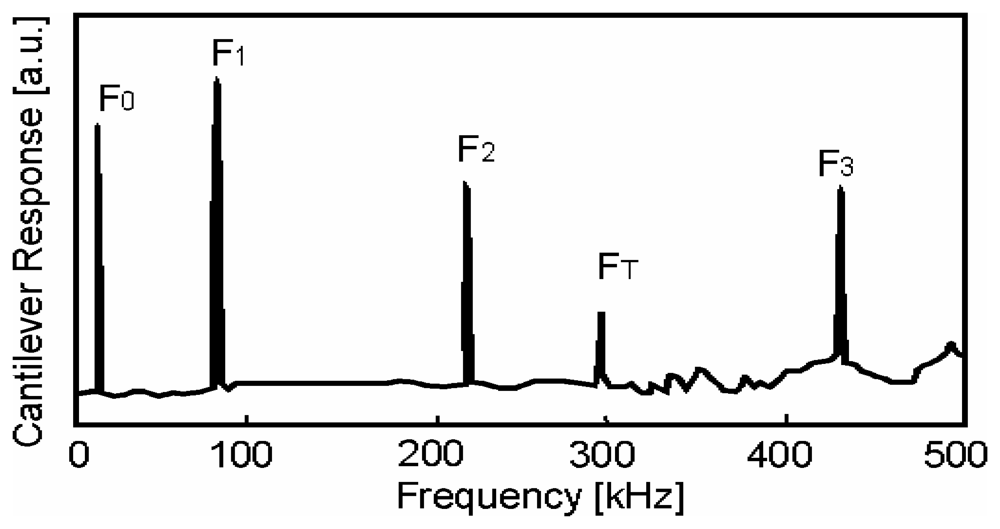
Dynamic approach for single material cantilevers
| Cylindrical beam | Rectangular beam | V-shaped cantilever | |
| Effective mass | m = 0.243PL(πR2) | m = 0.243PL(bh) | m = 0.163rL(bh) |
| Effective Young's modulus |
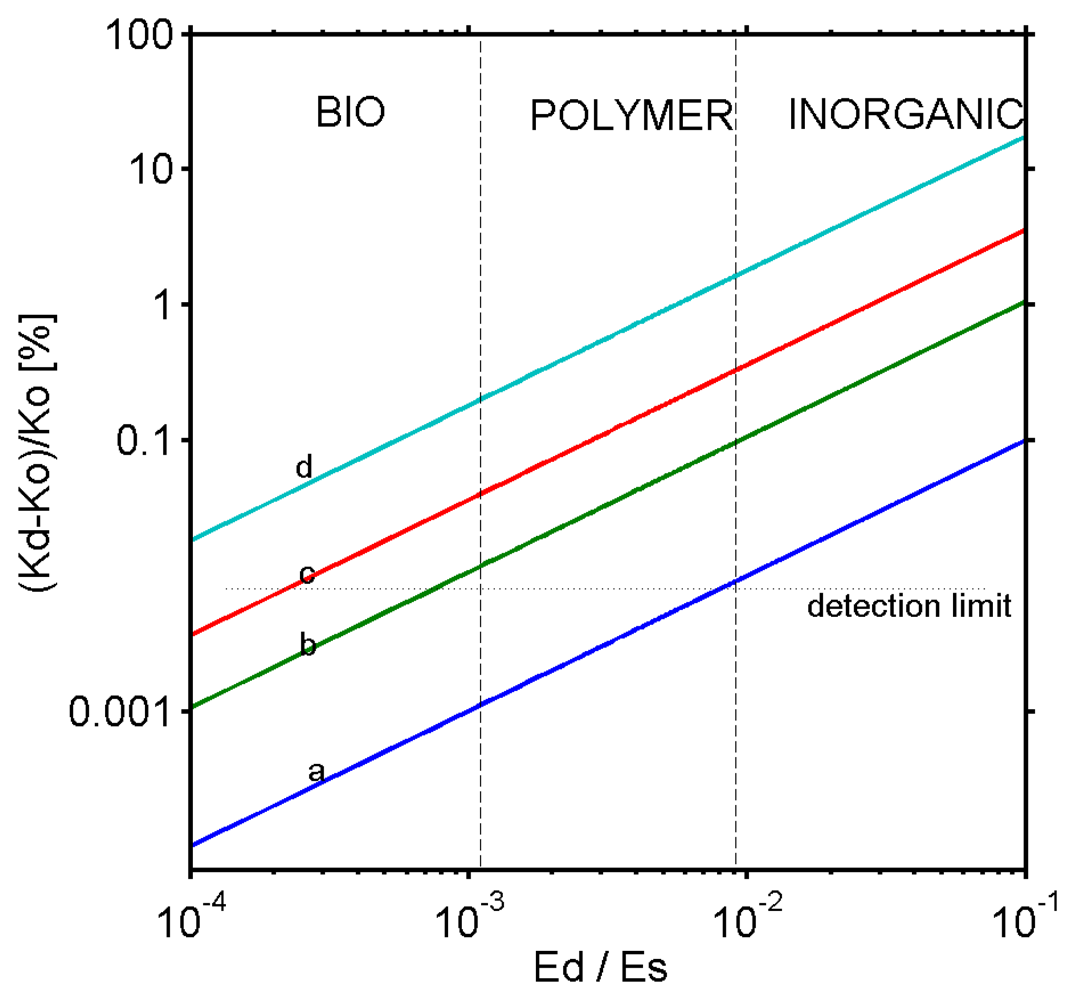
Dynamic approach using bilayer cantilevers
Poisson ratio
4. Inelastic parameters
Residual stress and yield strength
Surface stress
Internal friction, fracture and fatigue
- by fitting the vibration amplitude in frequency domain using the following formula:where ωf is the resonance frequency, Zp vertical extension of the piezoelectric crystal and Zc the displacement of the free end of the lever;
- by the direct use of the resonance peak by measuring its width Δf at the of the maximum amplitude and by applying the relation:
- by the decrement logarithmic curve d defined by, where n is the index of the nth peak after the lever has been displaced from its equilibrium position to oscillate freely while decaying exponentially back to its equilibrium position through a series of transient oscillations. Typically, Q can vary between 10 and 10000 depending on the nature of the cantilever.
5. Reliability of mechanical measurements
6. Measurement of the environmental properties of cantilevers
Temperature
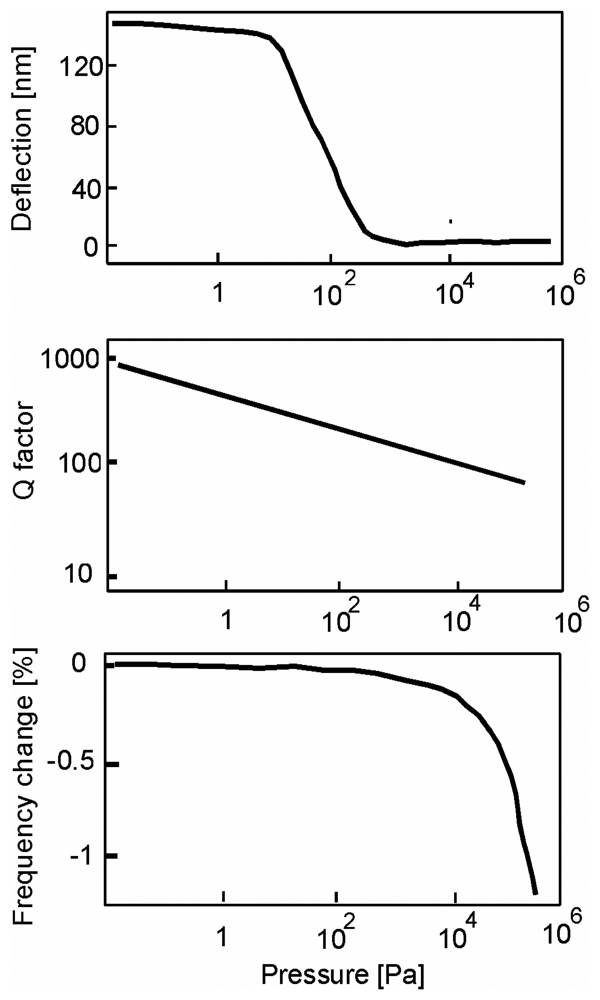
Pressure sensitivity, Knudsen's number, Reynold's number
In gases
In liquids [38, 138]
7. Applications
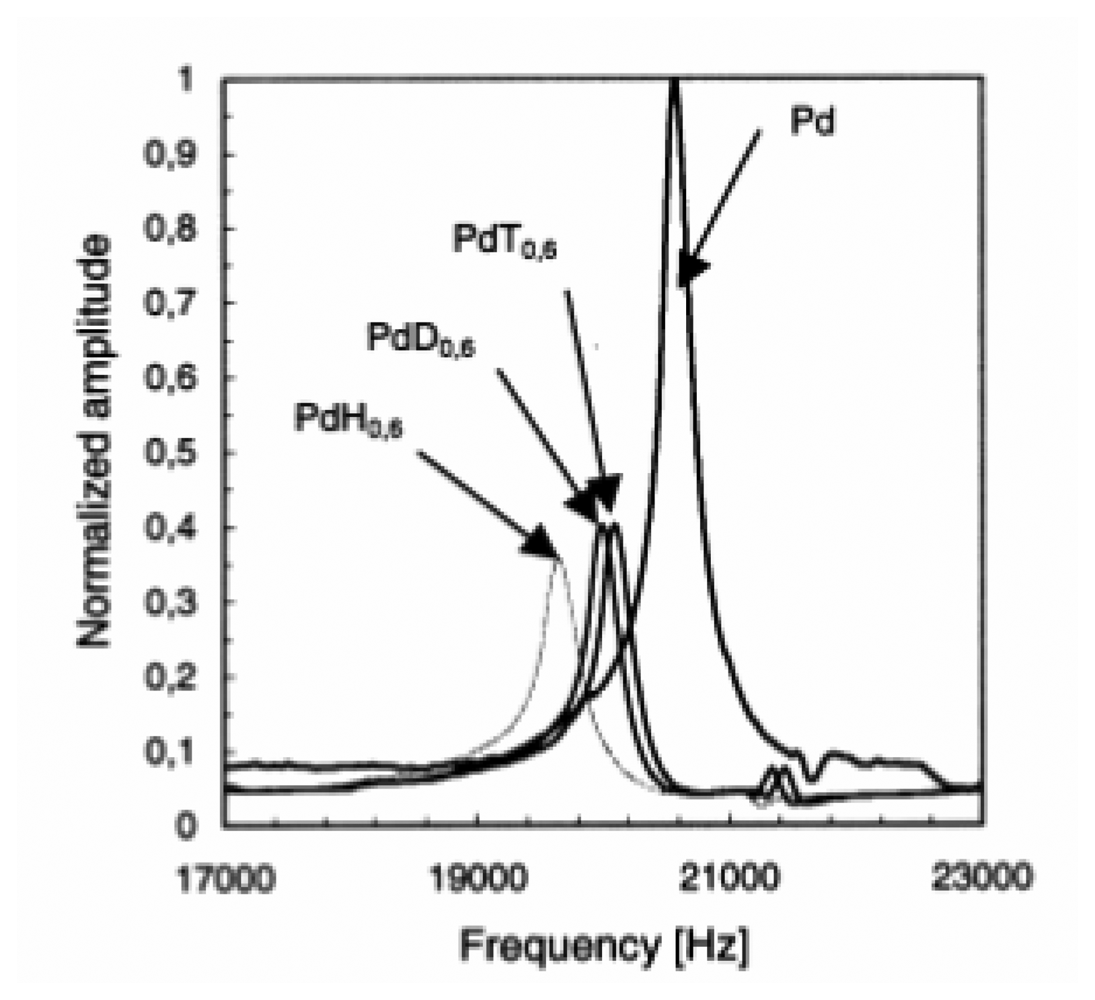
Palladium tritide cantilevers
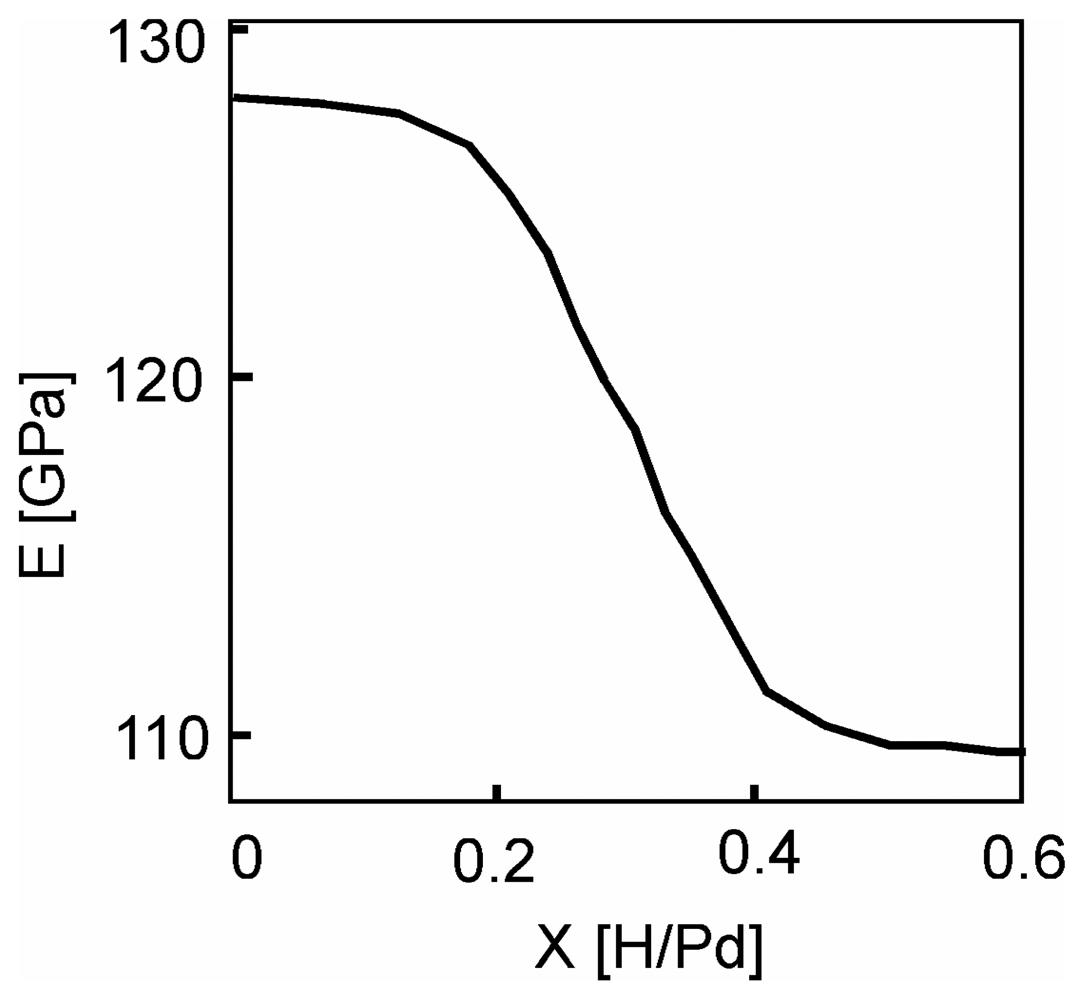
Isotopic effect (Hydrogen, Deuterium, Tritium) on Young's modulus
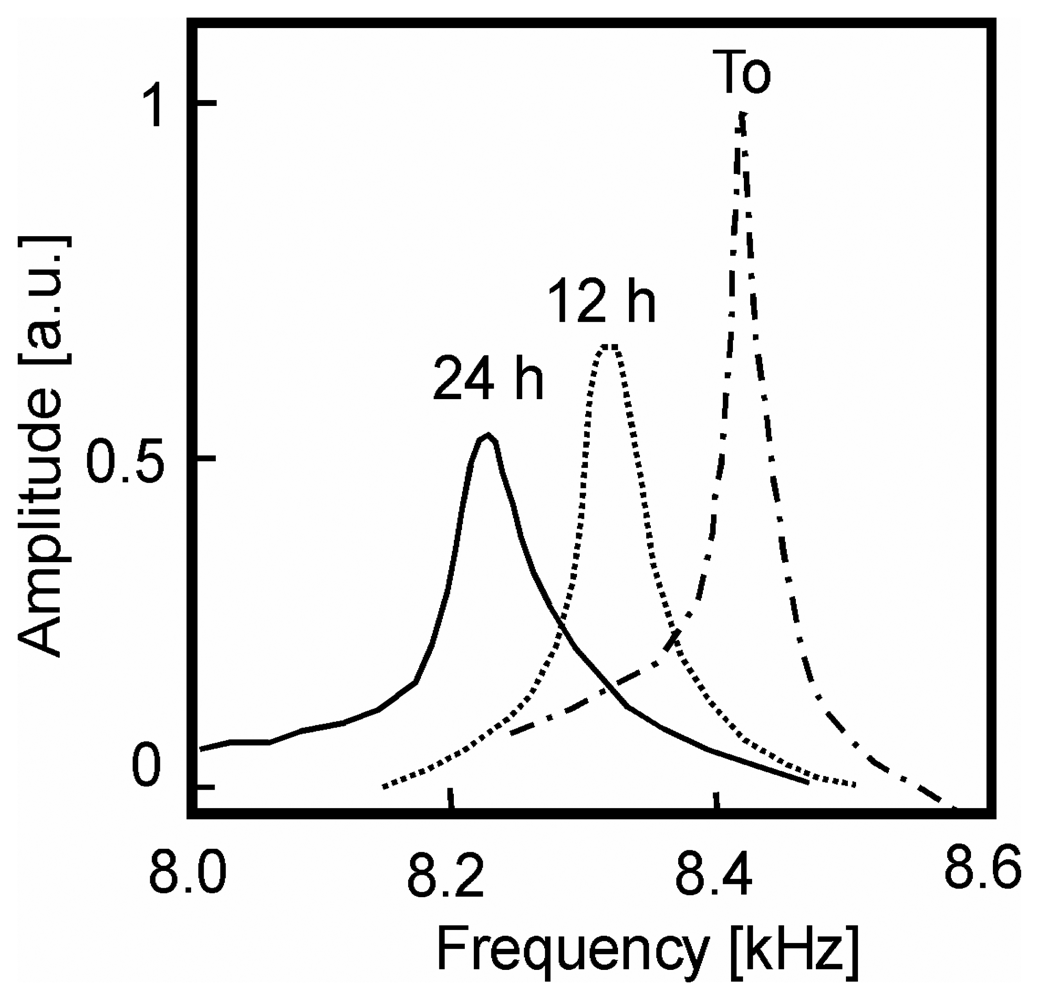
Ageing process of optical fibers
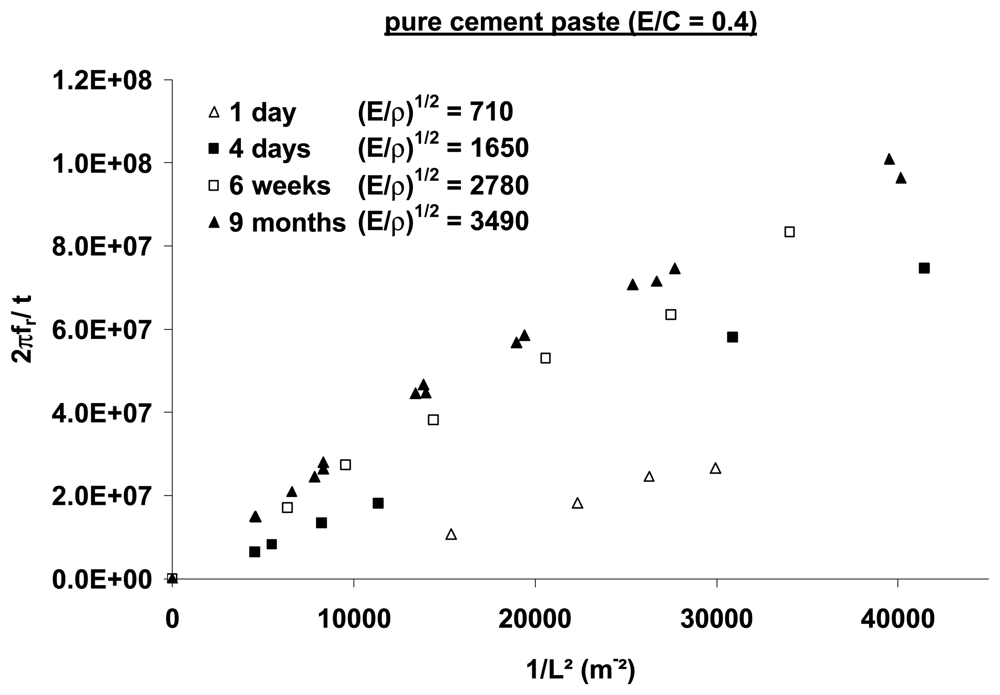
Strengthening of cement cantilevers
Measurement of changes in surface tension and film stress
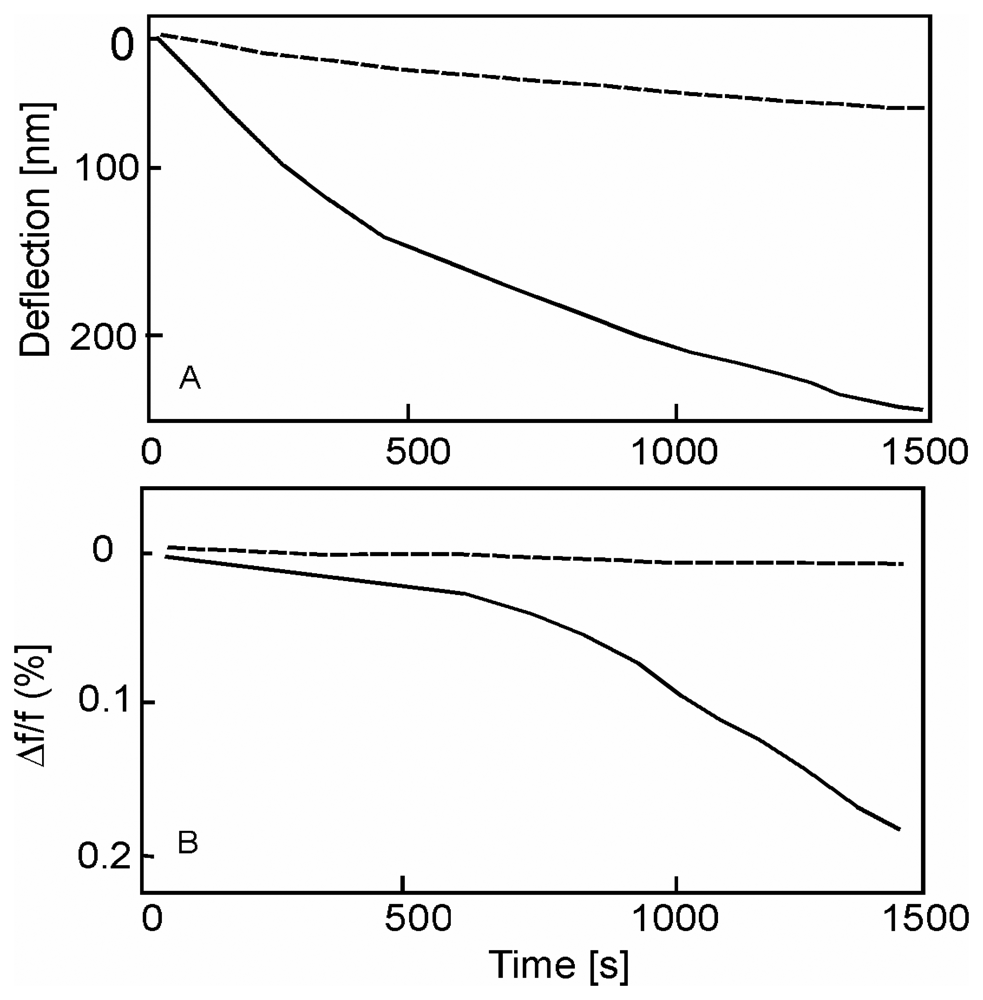
Irreversible surface tension induced by chemical etching
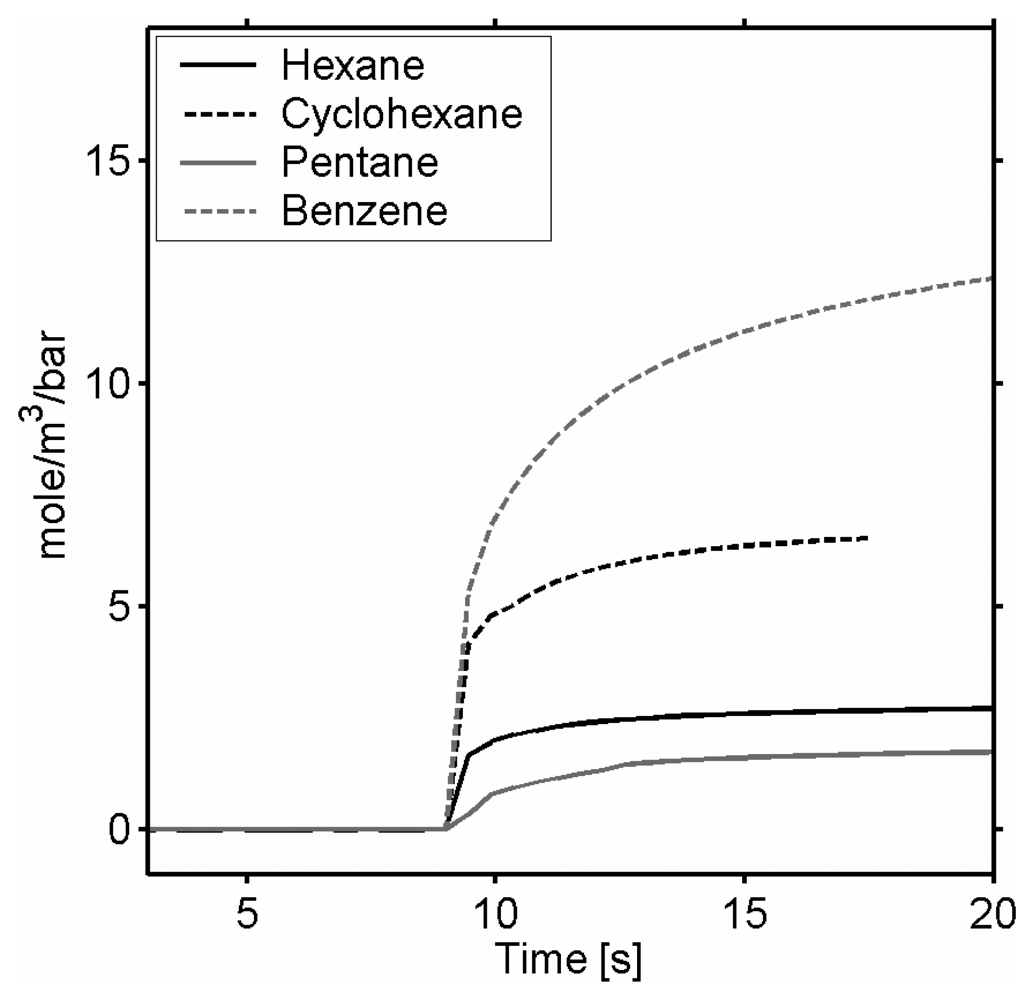
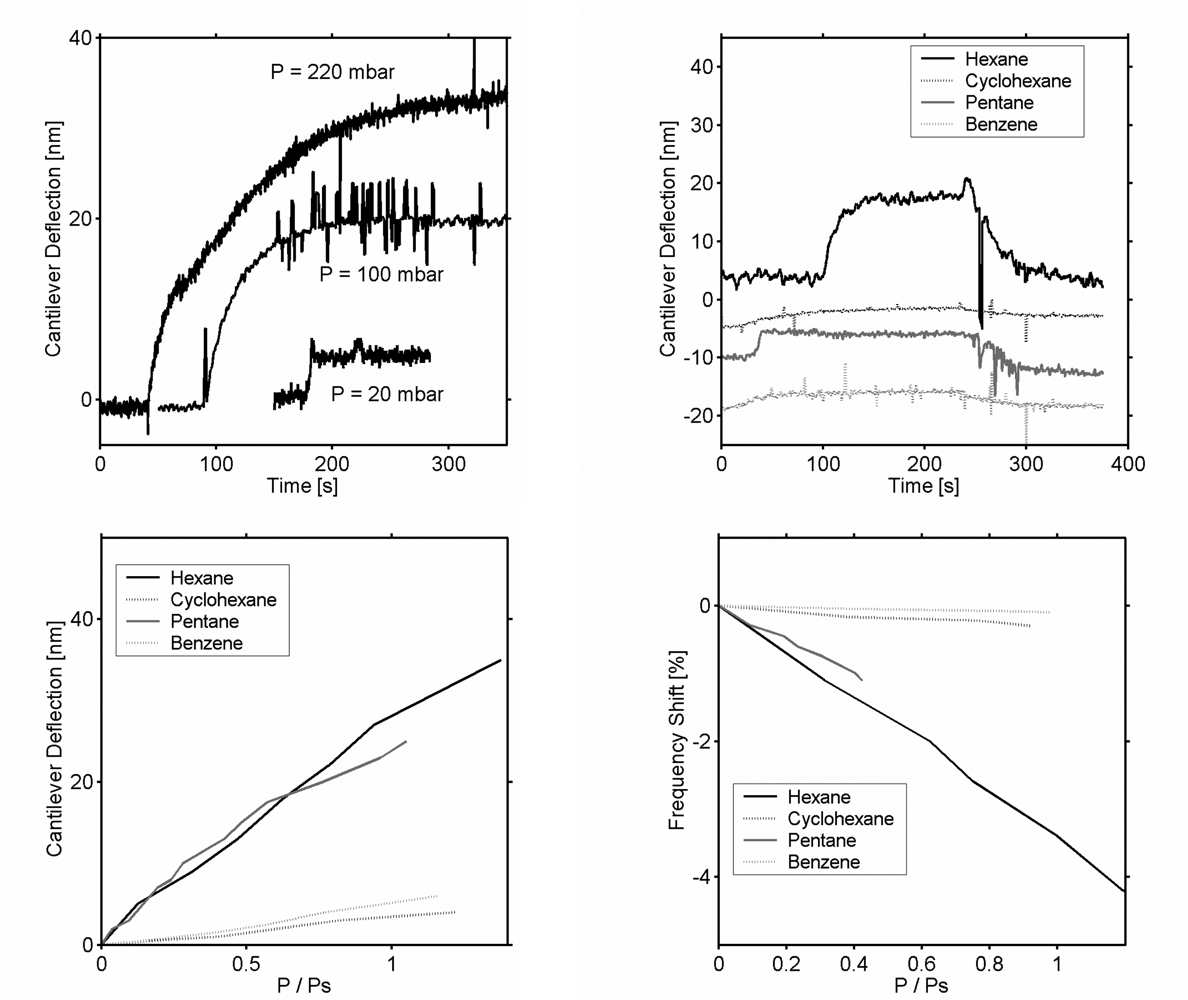
Film stress or swelling induced by chemical absorption
Conclusions
References
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic Force Microscope. Physical Review Letters 1986, 56(9), 930–933. [Google Scholar]
- Mertens, J.; Finot, E.; Thundat, T.; Fabre, A.; Nadal, M.H.; Eyraud, V.; Bourillot, E. Effects of temperature and pressure on microcantilever resonance response. Ultramicroscopy 2003, 97(1-4), 119–126. [Google Scholar]
- Barnes, J.R.; Stephenson, R.J.; Welland, M.E.; Gerber, C.; Gimzewski, J.K. Photothermal Spectroscopy with Femtojoule Sensitivity Using a Micromechanical Device. Nature 1994, 372(6501), 79–81. [Google Scholar]
- Jana, A.; Raman, A.; Dhayal, B.; Tripp, S.L.; Reifenberger, R.G. Microcantilever mechanics in flowing viscous fluids. Applied Physics Letters 2007, 90(11), 114110. [Google Scholar]
- Ilic, B.; Craighead, H.G.; Krylov, S.; Senaratne, W.; Ober, C.; Neuzil, P. Attogram detection using nanoelectromechanical oscillators. Journal of Applied Physics 2004, 95(7), 3694–3703. [Google Scholar]
- Yang, J.L.; Ono, T.; Esashi, M. Energy dissipation in submicrometer thick single-crystal silicon cantilevers. Journal of Microelectromechanical Systems 2002, 11(6), 775–783. [Google Scholar]
- Burg, T.P.; Manalis, S.R. Suspended microchannel resonators for biomolecular detection. Applied Physics Letters 2003, 83(13), 2698–2700. [Google Scholar]
- Gupta, A.; Akin, D.; Bashir, R. Single virus particle mass detection using microresonators with nanoscale thickness. Applied Physics Letters 2004, 84(11), 1976–1978. [Google Scholar]
- Verbridge, S.S.; Parpia, J.M.; Reichenbach, R.B.; Bellan, L.M.; Craighead, H.G. High quality factor resonance at room temperature with nanostrings under high tensile stress. Journal of Applied Physics 2006, 99(12), 013112. [Google Scholar]
- Han, W.H.; Lindsay, S.M.; Jing, T.W. A magnetically driven oscillating probe microscope for operation in liquids. Applied Physics Letters 1996, 69(26), 4111–4113. [Google Scholar]
- Ghatnekar-Nilsson, S.; Forsen, E.; Abadal, G.; Verd, J.; Campabadal, F.; Perez-Murano, F.; Esteve, J.; Barniol, N.; Boisen, A.; Montelius, L. Resonators with integrated CMOS circuitry for mass sensing applications, fabricated by electron beam lithography. Nanotechnology 2005, 16(1), 98–102. [Google Scholar]
- Finot, E.; Thundat, T.; Lesniewska, E.; Goudonnet, J.P. Measuring magnetic susceptibilities of nanogram quantities of materials using microcantilevers. Ultramicroscopy 2001, 86(1-2), 175–180. [Google Scholar]
- Raiteri, R.; Grattarola, M.; Butt, H.J.; Skladal, P. Micromechanical cantilever-based biosensors. Sensors and Actuators B-Chemical 2001, 79(2-3), 115–126. [Google Scholar]
- Thundat, T.; Oden, P.I.; Warmack, R.J. Microcantilever sensors. Microscale Thermophysical Engineering 1997, 1(3), 185–199. [Google Scholar]
- Lavrik, N.V.; Sepaniak, M.J.; Datskos, P.G. Cantilever transducers as a platform for chemical and biological sensors. Review of Scientific Instruments 2004, 75(7), 2229–2253. [Google Scholar]
- Ziegler, C. Cantilever-based biosensors. Analytical and Bioanalytical Chemistry 2004, 379(7-8), 946–959. [Google Scholar]
- Lechuga, L.M.; Tamayo, J.; Alvarez, M.; Carrascosa, L.G.; Yufera, A.; Doldan, R.; Peralias, E.; Rueda, A.; Plaza, J.A.; Zinoviev, K.; Dominguez, C.; Zaballos, A.; Moreno, M.; Martinez, C.; Wenn, D.; Harris, N.; Bringer, C.; Bardinal, V.; Camps, T.; Vergnenegre, C.; Fontaine, C.; Diaz, V.; Bernad, A. A highly sensitive microsystem based on nanomechanical biosensors for genomics applications. Sensors and Actuators B-Chemical 2006, 118(1-2), 2–10. [Google Scholar]
- Tian, F.; Hansen, K.M.; Ferrell, T.L.; Thundat, T. Dynamic microcantilever sensors for discerning biomolecular interactions. Analytical Chemistry 2005, 77(6), 1601–1606. [Google Scholar]
- Lang, H.P.; Baller, M.K.; Berger, R.; Gerber, C.; Gimzewski, J.K.; Battiston, F.M.; Fornaro, P.; Ramseyer, J.P.; Meyer, E.; Guntherodt, H.J. An artificial nose based on a micromechanical cantilever array. Analytica Chimica Acta 1999, 393(1-3), 59–65. [Google Scholar]
- Baller, M.K.; Lang, H.P.; Fritz, J.; Gerber, C.; Gimzewski, J.K.; Drechsler, U.; Rothuizen, H.; Despont, M.; Vettiger, P.; Battiston, F.M.; Ramseyer, J.P.; Fornaro, P.; Meyer, E.; Guntherodt, H.J. A cantilever array-based artificial nose. Ultramicroscopy 2000, 82(1-4), 1–9. [Google Scholar]
- Zhang, X.C.; Xu, B.S.; Wang, H.D.; Wu, Y.X.; Jiang, Y. Underlying mechanisms of the stress generation in surface coatings. Surface & Coatings Technology 2007, 201(15), 6715–6718. [Google Scholar]
- Grodzinski, P.; Silver, M.; Molnar, L.K. Nanotechnology for cancer diagnostics: promises and challenges. Expert Review of Molecular Diagnostics 2006, 6(3), 307–318. [Google Scholar]
- McCarthy, J.; Pei, Z.; Becker, M.; Atteridge, D. FIB micromachined submicron thickness cantilevers for the study of thin film properties. Thin Solid Films 2000, 358(1-2), 146–151. [Google Scholar]
- Subramanian, A.; Oden, P.I.; Kennel, S.J.; Jacobson, K.B.; Warmack, R.J.; Thundat, T.; Doktycz, M.J. Glucose biosensing using an enzyme-coated microcantilever. Applied Physics Letters 2002, 81(2), 385–387. [Google Scholar]
- Weeks, B.L.; Camarero, J.; Noy, A.; Miller, A.E.; Stanker, L.; De Yoreo, J.J. A microcantilever-based pathogen detector. Scanning 2003, 25(6), 297–299. [Google Scholar]
- Boettinger, W.J.; Johnson, C.E.; Bendersky, L.A.; Moon, K.W.; Williams, M.E.; Stafford, G.R. Whisker and hillock formation on Sn, Sn-Cu and Sn-Pb electrodeposits. Acta Materialia 2005, 53(19), 5033–5050. [Google Scholar]
- Campbell, G.A.; Mutharasan, R. Piezoelectric-excited millimeter-sized cantilever (PEMC) sensors detect Bacillus anthracis at 300 spores/mL. Biosensors & Bioelectronics 2006, 21(9), 1684–1692. [Google Scholar]
- Grogan, C.; Raiteri, R.; O'Connor, G.M.; Glynn, T.J.; Cunningham, V.; Kane, M.; Charlton, M.; Leech, D. Characterisation of an antibody coated microcantilever as a potential immuno-based biosensor. Biosensors & Bioelectronics 2002, 17(3), 201–207. [Google Scholar]
- Raiteri, R.; Nelles, G.; Butt, H.J.; Knoll, W.; Skladal, P. Sensing of biological substances based on the bending of microfabricated cantilevers. Sensors and Actuators B-Chemical 1999, 61(1-3), 213–217. [Google Scholar]
- Moulin, A.M.; O'Shea, S.J.; Welland, M.E. Microcantilever-based biosensors. Ultramicroscopy 2000, 82(1-4), 23–31. [Google Scholar]
- Marie, R.; Jensenius, H.; Thaysen, J.; Christensen, C.B.; Boisen, A. Adsorption kinetics and mechanical properties of thiol-modified DNA-oligos on gold investigated by microcantilever sensors. Ultramicroscopy 2002, 91(1-4), 29–36. [Google Scholar]
- Legay, G.; Finot, E.; Meunier-Prest, R.; Cherkaoui-Malki, M.; Latruffe, N.; Dereux, A. DNA nanofilm thickness measurement on microarray in air and in liquid using an atomic force microscope. Biosensors & Bioelectronics 2005, 21(4), 627–636. [Google Scholar]
- Thundat, T.; Finot, E.; Hu, Z.; Ritchie, R.H.; Wu, G.; Majumdar, A. Chemical sensing in Fourier space. Applied Physics Letters 2000, 77(24), 4061–4063. [Google Scholar]
- Ji, H.F.; Finot, E.; Dabestani, R.; Thundat, T.; Brown, G.M.; Britt, P.F. A novel self-assembled monolayer (SAM) coated microcantilever for low level caesium detection. Chemical Communications 2000, 6, 457–458. [Google Scholar]
- Lang, H.P.; Berger, R.; Battiston, F.; Ramseyer, J.P.; Meyer, E.; Andreoli, C.; Brugger, J.; Vettiger, P.; Despont, M.; Mezzacasa, T.; Scandella, L.; Guntherodt, H.J.; Gerber, C.; Gimzewski, J.K. A chemical sensor based on a micromechanical cantilever array for the identification of gases and vapors. Applied Physics a-Materials Science & Processing 1998, 66, S61–S64. [Google Scholar]
- Betts, T.A.; Tipple, C.A.; Sepaniak, M.J.; Datskos, P.G. Selectivity of chemical sensors based on micro-cantilevers coated with thin polymer films. Analytica Chimica Acta 2000, 422(1), 89–99. [Google Scholar]
- Tipple, C.A.; Lavrik, N.V.; Culha, M.; Headrick, J.; Datskos, P.; Sepaniak, M.J. Nanostructured microcantilevers with functionalized cyclodextrin receptor phases: Self-assembled monolayers and vapor-deposited films. Analytical Chemistry 2002, 74(13), 3118–3126. [Google Scholar]
- Thundat, T.G.; Oden, P.; Warmack, R.; Finot, E. Micromechanical transient sensor for measuring viscosity and density of a fluid. WO0122056 2001. [Google Scholar]
- Tang, Y.J.; Fang, J.; Xu, X.H.; Ji, H.F.; Brown, G.M.; Thundat, T. Detection of femtomolar concentrations of HF using an SiO2 microcantilever. Analytical Chemistry 2004, 76(9), 2478–2481. [Google Scholar]
- Mertens, J.; Finot, E.; Nadal, M.H.; Eyraud, V.; Heintz, O.; Bourillot, E. Detection of gas trace of hydrofluoric acid using microcantilever. Sensors and Actuators B-Chemical 2004, 99(1), 58–65. [Google Scholar]
- Maute, M.; Raible, S.; Prins, F.E.; Kern, D.P.; Ulmer, H.; Weimar, U.; Gopel, W. Detection of volatile organic compounds (VOCs) with polymer-coated cantilevers. Sensors and Actuators B-Chemical 1999, 58(1-3), 505–511. [Google Scholar]
- Hwang, K.S.; Lee, J.H.; Park, J.; Yoon, D.S.; Park, J.H.; Kim, T.S. In-situ quantitative analysis of a prostate-specific antigen (PSA) using a nanomechanical PZT cantilever. Lab on a Chip 2004, 4(6), 547–552. [Google Scholar]
- Kiesewetter, L.; Zhang, J.M.; Houdeau, D.; Steckenborn, A. Determination of Young Moduli of Micromechanical Thin-Films Using the Resonance Method. Sensors and Actuators a-Physical 1992, 35(2), 153–159. [Google Scholar]
- Finot, E. Local mechanical properties determined by atomic force microscopy. Annales De Chimie-Science Des Materiaux 2004, 29(3), 33–45. [Google Scholar]
- Rogers, J.A.; Maznev, A.A.; Banet, M.J.; Nelson, K.A. Optical generation and characterization of acoustic waves in thin films: Fundamentals and applications. Annual Review of Materials Science 2000, 30, 117–157. [Google Scholar]
- Fielding, S.M.; Sollich, P.; Cates, M.E. Aging and rheology in soft materials. Journal of Rheology 2000, 44(2), 323–369. [Google Scholar]
- Maboudian, R.; Carraro, C. Surface chemistry and tribology of MEMS. Annual Review of Physical Chemistry 2004, 55, 35–54. [Google Scholar]
- Jianqiang, H.; Changchun, Z.; Junhua, L.; Yongning, H. Dependence of the resonance frequency of thermally excited microcantilever resonators on temperature. Sensors and Actuators A: Physical 2002, 101(1-2), 37–41. [Google Scholar]
- Malzbender, J. Mechanical and thermal stresses in multilayered materials. Journal of Applied Physics 2004, 95(4), 1780–1782. [Google Scholar]
- Hsueh, C.H. Thermal stresses in elastic multilayer systems. Thin Solid Films 2002, 418(2), 182–188. [Google Scholar]
- Baek, C.W.; Kim, Y.K.; Ahn, Y.; Kim, Y.H. Measurement of the mechanical properties of electroplated gold thin films using micromachined beam structures. Sensors and Actuators a-Physical 2005, 117(1), 17–27. [Google Scholar]
- Godin, M.; Tabard-Cossa, V.; Grutter, P.; Williams, P. Quantitative surface stress measurements using a microcantilever. Applied Physics Letters 2001, 79(4), 551–553. [Google Scholar]
- Ibach, H.; Bach, C.E.; Giesen, M.; Grossmann, A. Potential-induced stress in the solid-liquid interface: Au(111) and Au(100) in an HClO4 electrolyte. Surface Science 1997, 375(1), 107–119. [Google Scholar]
- Kramer, D.; Viswanath, R.N.; Weissmuller, J. Surface-stress induced macroscopic bending of nanoporous gold cantilevers. Nano Letters 2004, 4(5), 793–796. [Google Scholar]
- Cherian, S.; Thundat, T. Determination of adsorption-induced variation in the spring constant of a microcantilever. Applied Physics Letters 2002, 80(12), 2219–2221. [Google Scholar]
- Dorignac, J.; Kalinowski, A.; Erramilli, S.; Mohanty, P. Dynamical response of nanomechanical oscillators in immiscible viscous fluid for in vitro biomolecular recognition. Physical Review Letters 2006, 96(18), 186105. [Google Scholar]
- Sader, J.E. Surface stress induced deflections of cantilever plates with applications to the atomic force microscope: Rectangular plates. Journal of Applied Physics 2001, 89(5), 2911–2921. [Google Scholar]
- Tsuchiya, T.; Tabata, O.; Sakata, J.; Taga, Y. Specimen size effect of tensile strength of surface-micromachined polycrystalline silicon thin films. Journal of Microelectromechanical Systems 1998, 7(1), 106–113. [Google Scholar]
- Wolter, O.; Bayer, T.; Greschner, J. Micromachined Silicon Sensors for Scanning Force Microscopy. Journal of Vacuum Science & Technology B 1991, 9(2), 1353–1357. [Google Scholar]
- Yasumura, K.Y.; Stowe, T.D.; Chow, E.M.; Pfafman, T.; Kenny, T.W.; Stipe, B.C.; Rugar, D. Quality factors in micron- and submicron-thick cantilevers. Journal of Microelectromechanical Systems 2000, 9(1), 117–125. [Google Scholar]
- Namazu, T.; Isono, Y.; Tanaka, T. Evaluation of size effect on mechanical properties of single crystal silicon by nanoscale bending test using AFM. Journal of Microelectromechanical Systems 2000, 9(4), 450–459. [Google Scholar]
- Li, X.X.; Ono, T.; Wang, Y.L.; Esashi, M. Ultrathin single-crystalline-silicon cantilever resonators: Fabrication technology and significant specimen size effect on Young's modulus. Applied Physics Letters 2003, 83(15), 3081–3083. [Google Scholar]
- Hua, F.; Cui, T.H.; Lvov, Y.M. Ultrathin cantilevers based on polymer-ceramic nanocomposite assembled through layer-by-layer adsorption. Nano Letters 2004, 4(5), 823–825. [Google Scholar]
- Bumbu, G.G.; Kircher, G.; Wolkenhauer, M.; Berger, R.; Gutmann, J.S. Synthesis and characterization of polymer brushes on micromechanical cantilevers. Macromolecular Chemistry and Physics 2004, 205(13), 1713–1720. [Google Scholar]
- Zhou, F.; Shu, W.M.; Welland, M.E.; Huck, W.T.S. Highly reversible and multi-stage cantilever actuation driven by polyelectrolyte brushes. Journal of the American Chemical Society 2006, 128(16), 5326–5327. [Google Scholar]
- Thaysen, J.; Yalcinkaya, A.D.; Vettiger, P.; Menon, A. Polymer-based stress sensor with integrated readout. Journal of Physics D-Applied Physics 2002, 35(21), 2698–2703. [Google Scholar]
- Conradie, E.H.; Moore, D.F. SU-8 thick photoresist processing as a functional material for MEMS applications. Journal of Micromechanics and Microengineering 2002, 12(4), 368–374. [Google Scholar]
- Calleja, M.; Tamayo, J.; Nordstrom, M.; Boisen, A. Low-noise polymeric nanomechanical biosensors. Applied Physics Letters 2006, 88(11), 113901. [Google Scholar]
- Calleja, M.; Tamayo, J.; Johansson, A.; Rasmussen, P.; Lechuga, L.M.; Boisen, A. Polymeric cantilever arrays for biosensing applications. Sensor Letters 2003, 1(1), 20–24. [Google Scholar]
- Johansson, A.; Calleja, M.; Rasmussen, P.A.; Boisen, A. SU-8 cantilever sensor system with integrated readout. Sensors and Actuators a-Physical 2005, 123-24, 111–115. [Google Scholar]
- Schwaiger, R.; Kraft, O. Size effects in the fatigue behavior of thin Ag films. Acta Materialia 2003, 51(1), 195–206. [Google Scholar]
- Lievers, W.B.; Pilkey, A.K.; Lloyd, D.J. The influence of iron content on the bendability of AA6111 sheet. Materials Science and Engineering a-Structural Materials Properties Microstructure and Processing 2003, 361(1-2), 312–320. [Google Scholar]
- Belaubre, P.; Guirardel, M.; Garcia, G.; Pourciel, J.B.; Leberre, V.; Dagkessamanskaia, A.; Trevisiol, E.; Francois, J.M.; Bergaud, C. Fabrication of biological microarrays using microcantilevers. Applied Physics Letters 2003, 82(18), 3122–3124. [Google Scholar]
- Son, D.; Jeong, J.H.; Kwon, D. Film-thickness considerations in microcantilever-beam test in measuring mechanical properties of metal thin film. Thin Solid Films 2003, 437(1-2), 182–187. [Google Scholar]
- Choi, D.H.; Kim, H.; Nix, W.D. Anelasticity and damping of thin aluminum films on silicon substrates. Journal of Microelectromechanical Systems 2004, 13(2), 230–237. [Google Scholar]
- Baselt, D.R.; Fruhberger, B.; Klaassen, E.; Cemalovic, S.; Britton, C.L.; Patel, S.V.; Mlsna, T.E.; McCorkle, D.; Warmack, B. Design and performance of a microcantilever-based hydrogen sensor. Sensors and Actuators B-Chemical 2003, 88(2), 120–131. [Google Scholar]
- Fabre, A.; Finot, E.; Demoment, J.; Contreras, S. Monitoring the chemical changes in Pd induced by hydrogen absorption using microcantilevers. Ultramicroscopy 2003, 97(1-4), 425–432. [Google Scholar]
- Belloy, E.; Sayah, A.; Gijs, M.A.M. Micromachining of glass inertial sensors. Journal of Microelectromechanical Systems 2002, 11(1), 85–90. [Google Scholar]
- Krauss, A.R.; Auciello, O.; Gruen, D.M.; Jayatissa, A.; Sumant, A.; Tucek, J.; Mancini, D.C.; Moldovan, N.; Erdemir, A.; Ersoy, D.; Gardos, M.N.; Busmann, H.G.; Meyer, E.M.; Ding, M.Q. Ultrananocrystalline diamond thin films for MEMS and moving mechanical assembly devices. Diamond and Related Materials 2001, 10(11), 1952–1961. [Google Scholar]
- Czaplewski, D.A.; Sullivan, J.P.; Friedmann, T.A.; Carr, D.W.; Keeler, B.E.N.; Wendt, J.R. Mechanical dissipation in tetrahedral amorphous carbon. Journal of Applied Physics 2005, 97(2), 023517. [Google Scholar]
- Banthia, N.; Nandakumar, N. Crack growth resistance of hybrid fiber reinforced cement composites. Cement & Concrete Composites 2003, 25(1), 3–9. [Google Scholar]
- Yoshihara, H. Simple estimation of critical stress intensity factors of wood by tests with double cantilever beam and three-point end-notched flexure. Holzforschung 2007, 61(2), 182–189. [Google Scholar]
- South, J.T.; Case, S.W.; Reifsnider, K.L. Effects of thermal aging on the mechanical properties of natural rubber. Rubber Chemistry and Technology 2003, 76(4), 785–802. [Google Scholar]
- Muhlstein, C.L.; Howe, R.T.; Ritchie, R.O. Fatigue of polycrystalline silicon for microelectromechanical system applications: crack growth and stability under resonant loading conditions. Mechanics of Materials 2004, 36(1-2), 13–33. [Google Scholar]
- Hierlemann, A.; Brand, O.; Hagleitner, C.; Baltes, H. Microfabrication techniques for chemical/biosensors. Proceedings of the Ieee 2003, 91(6), 839–863. [Google Scholar]
- Johnstone, R.W.; Parameswaran, M. Theoretical limits on the freestanding length of cantilevers produced by surface micromachining technology. Journal of Micromechanics and Microengineering 2002, 12(6), 855–861. [Google Scholar]
- Davis, Z.J.; Abadal, G.; Kuhn, O.; Hansen, O.; Grey, F.; Boisen, A. Fabrication and characterization of nanoresonating devices for mass detection. Journal of Vacuum Science & Technology B 2000, 18(2), 612–616. [Google Scholar]
- Fabre, A.; Finot, E.; Demoment, J.; Contreras, S.; Goudonnet, J.P. Microscale technique for in situ measurement of elastic parameters of materials under reactive atmosphere. Review of Scientific Instruments 2001, 72(10), 3914–3920. [Google Scholar]
- McGovern, J.P.; Shih, W.Y.; Shih, W.H. In situ detection of Bacillus anthracis spores using fully submersible, self-exciting, self-sensing PMN-PT/Sn piezoelectric microcantilevers. Analyst 2007, 132(8), 777–783. [Google Scholar]
- Tse, L.A.; Hesketh, P.J.; Rosen, D.W.; Gole, J.L. Stereolithography on silicon for microfluidics and microsensor packaging. Microsystem Technologies-Micro-and Nanosystems-Information Storage and Processing Systems 2003, 9(5), 319–323. [Google Scholar]
- Erickson, D.; Li, D. Q. Integrated microfluidic devices. Analytica Chimica Acta 2004, 507(1), 11–26. [Google Scholar]
- Mertens, J.; Alvarez, M.; Tamayo, J. Real-time profile of microcantilevers for sensing applications. Applied Physics Letters 2005, 87(23), 234102. [Google Scholar]
- Lee, J.; Beechem, T.; Wright, T.L.; Nelson, B.A.; Graham, S.; King, W.P. Electrical, thermal, and mechanical characterization of silicon microcantilever heaters. Journal of Microelectromechanical Systems 2006, 15(6), 1644–1655. [Google Scholar]
- Lee, C.; Itoh, T.; Suga, T. Self-excited piezoelectric PZT microcantilevers for dynamic SFM -with inherent sensing and actuating capabilities. Sensors and Actuators a-Physical 1999, 72(2), 179–188. [Google Scholar]
- Voiculescu, I.; Zaghloul, M.E.; McGill, R.A.; Houser, E.J.; Fedder, G.K. Electrostatically actuated resonant microcantilever beam in CMOS technology for the detection of chemical weapons. Ieee Sensors Journal 2005, 5(4), 641–647. [Google Scholar]
- Chen, B.Y.; Yeh, M.K.; Tai, N.H. Accuracy of the spring constant of atomic force microscopy cantilevers by finite element method. Analytical Chemistry 2007, 79(4), 1333–1338. [Google Scholar]
- Butt, H.J.; Siedle, P.; Seifert, K.; Fendler, K.; Seeger, T.; Bamberg, E.; Weisenhorn, A.L.; Goldie, K.; Engel, A. Scan Speed Limit in Atomic Force Microscopy. Journal of Microscopy-Oxford 1993, 169, 75–84. [Google Scholar]
- Burnham, N.A.; Chen, X.; Hodges, C.S.; Matei, G.A.; Thoreson, E.J.; Roberts, C.J.; Davies, M.C.; Tendler, S.J.B. Comparison of calibration methods for atomic-force microscopy cantilevers. Nanotechnology 2003, 14(1), 1–6. [Google Scholar]
- Neumeister, J.M.; Ducker, W.A. Lateral, Normal, and Longitudinal Spring Constants of Atomic-Force Microscopy Cantilevers. Review of Scientific Instruments 1994, 65(8), 2527–2531. [Google Scholar]
- Clifford, C.A.; Seah, M.P. The determination of atomic force microscope cantilever spring constants via dimensional methods for nanomechanical analysis. Nanotechnology 2005, 16(9), 1666–1680. [Google Scholar]
- Jelenic, G.; Saje, M. A Kinematically Exact Space Finite Strain Beam Model - Finite-Element Formulation by Generalized Virtual Work Principle. Computer Methods in Applied Mechanics and Engineering 1995, 120(1-2), 131–161. [Google Scholar]
- Fang, W.L. Determination of the elastic modulus of thin film materials using self-deformed micromachined cantilevers. Journal of Micromechanics and Microengineering 1999, 9(3), 230–235. [Google Scholar]
- Petersen, K.E.; Guarnieri, C.R. Youngs Modulus Measurements of Thin-Films Using Micromechanics. Journal of Applied Physics 1979, 50(11), 6761–6766. [Google Scholar]
- Min, Y.H.; Kim, Y.K. In situ measurement of residual stress in micromachined thin films using a specimen with composite-layered cantilevers. Journal of Micromechanics and Microengineering 2000, 10(3), 314–321. [Google Scholar]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids 2003, 51(8), 1477–1508. [Google Scholar]
- Lee, J.H.; Kim, T.S.; Yoon, K.H. Effect of mass and stress on resonant frequency shift of functionalized Pb(Zr0.52Ti0.48)O-3 thin film microcantilever for the detection of C-reactive protein. Applied Physics Letters 2004, 84(16), 3187–3189. [Google Scholar]
- Evans, D.R.; Craig, V.S.J. Sensing cantilever beam bending by the optical lever technique and its application to surface stress. Journal of Physical Chemistry B 2006, 110(11), 5450–5461. [Google Scholar]
- Zhang, Y.; Ren, Q.; Zhao, Y.P. Modelling analysis of surface stress on a rectangular cantilever beam. Journal of Physics D-Applied Physics 2004, 37(15), 2140–2145. [Google Scholar]
- Sader, J.E. Surface stress induced deflections of cantilever plates with applications to the atomic force microscope: V-shaped plates. Journal of Applied Physics 2002, 91(11), 9354–9361. [Google Scholar]
- Huang, S.S.; Zhang, X. Extension of the Stoney formula for film-substrate systems with gradient stress for MEMS applications. Journal of Micromechanics and Microengineering 2006, 16(2), 382–389. [Google Scholar]
- Desikan, R.; Lee, I.; Thundat, T. Effect of nanometer surface morphology on surface stress and adsorption kinetics of alkanethiol self-assembled monolayers. Ultramicroscopy 2006, 106(8-9), 795–799. [Google Scholar]
- Stephan, A.C.; Finot, E.L.; Ji, H.F.; Pinnaduwage, L.A.; Thundat, T. Micromechanical measurement of active sites on silicon nitride using surface free energy variation. Ultramicroscopy 2002, 91(1-4), 1–8. [Google Scholar]
- Dick, L.A.; McFarland, A.D.; Haynes, C.L.; Van Duyne, R.P. Metal film over nanosphere (MFON) electrodes for surface-enhanced Raman spectroscopy (SERS): Improvements in surface nanostructure stability and suppression of irreversible loss. Journal of Physical Chemistry B 2002, 106(4), 853–860. [Google Scholar]
- Shafer-Peltier, K.E.; Haynes, C.L.; Glucksberg, M.R.; Van Duyne, R.P. Toward a glucose biosensor based on surface-enhanced Raman scattering. Journal of the American Chemical Society 2003, 125(2), 588–593. [Google Scholar]
- Harms, U.; Gaertner, M.; Schutze, A.; Bewilogua, K.; Neuhauser, H. Elastic and anelastic properties, internal stress and thermal expansion coefficient of cubic boron nitride films on silicon. Thin Solid Films 2001, 385(1-2), 275–280. [Google Scholar]
- Romig, A.D.; Dugger, M.T.; McWhorter, P.J. Materials issues in microelectromechanical devices: science, engineering, manufacturability and reliability. Acta Materialia 2003, 51(19), 5837–5866. [Google Scholar]
- Bermudo, J.; Osendi, M.I.; Li, M.; Reece, M.J. Cyclic fatigue behaviour of silicon nitride materials. Journal of the European Ceramic Society 1997, 17(15-16), 1855–1860. [Google Scholar]
- Prabhakar, S.; Vengallatore, S. Thermoelastic damping in bilayered micromechanical beam resonators. Journal of Micromechanics and Microengineering 2007, 17(3), 532–538. [Google Scholar]
- Khan, A.; Philip, J.; Hess, P. Young's modulus of silicon nitride used in scanning force microscope cantilevers. Journal of Applied Physics 2004, 95(4), 1667–1672. [Google Scholar]
- Pan, C.H. A novel method for determining Young's modulus of thin films by micro-strain gauges. Microsystem Technologies-Micro-and Nanosystems-Information Storage and Processing Systems 2005, 11(2-3), 151–157. [Google Scholar]
- Buchaillot, L.; Farnault, E.; Hoummady, M.; Fujita, H. Silicon nitride thin films Young's modulus determination by an optical non destructive method. Japanese Journal of Applied Physics Part 2-Letters 1997, 36(6B), L794–L797. [Google Scholar]
- Drummond, C.J.; Senden, T.J. Characterization of the Mechanical-Properties of Thin-Film Cantilevers with the Atomic-Force Microscope. In Interfaces Ii; Trans Tech Publications Ltd; Zurich, 1995; Vol. 189, pp. 107–113. [Google Scholar]
- Fritz, T.; Griepentrog, M.; Mokwa, W.; Schnakenberg, U. Determination of Young's modulus of electroplated nickel. Electrochimica Acta 2003, 48(20-22), 3029–3035. [Google Scholar]
- Levy, R.; Maaloum, M. Measuring the spring constant of atomic force microscope cantilevers: thermal fluctuations and other methods. Nanotechnology 2002, 13(1), 33–37. [Google Scholar]
- Hutter, J.L.; Bechhoefer, J. Calibration of Atomic-Force Microscope Tips. Review of Scientific Instruments 1993, 64(7), 1868–1873. [Google Scholar]
- Schaffer, T.E. Calculation of thermal noise in an atomic force microscope with a finite optical spot size. Nanotechnology 2005, 16(6), 664–670. [Google Scholar]
- Cleveland, J.P.; Manne, S.; Bocek, D.; Hansma, P.K. A Nondestructive Method for Determining the Spring Constant of Cantilevers for Scanning Force Microscopy. Review of Scientific Instruments 1993, 64(2), 403–405. [Google Scholar]
- Gibson, C.T.; Weeks, B.L.; Abell, C.; Rayment, T.; Myhra, S. Calibration of AFM cantilever spring constants. Ultramicroscopy 2003, 97(1-4), 113–118. [Google Scholar]
- Tortonese, M. Cantilevers and tips for atomic force microscopy. Ieee Engineering in Medicine and Biology Magazine 1997, 16(2), 28–33. [Google Scholar]
- Bonaccurso, E.; Butt, H.J. Microdrops on atomic force microscope cantilevers: Evaporation of water and spring constant calibration. Journal of Physical Chemistry B 2005, 109(1), 253–263. [Google Scholar]
- Tsui, Y.C.; Doyle, C.; Clyne, T.W. Plasma sprayed hydroxyapatite coatings on titanium substrates Part 1: Mechanical properties and residual stress levels. Biomaterials 1998, 19(22), 2015–2029. [Google Scholar]
- Ding, W.Q.; Guo, Z.Y.; Ruoff, R.S. Effect of cantilever nonlinearity in nanoscale tensile testing. Journal of Applied Physics 2007, 101(3), 034316. [Google Scholar]
- Chui, B.W.; Stowe, T.D.; Ju, Y.S.; Goodson, K.E.; Kenny, T.W.; Mamin, H.J.; Terris, B.D.; Ried, R.P.; Rugar, D. Low-stiffness silicon cantilevers with integrated heaters and piezoresistive sensors for high-density AFM thermomechanical data storage. Journal of Microelectromechanical Systems 1998, 7(1), 69–78. [Google Scholar]
- Datskos, P.G.; Rajic, S.; Senesac, L.R.; Datskou, I. Fabrication of quantum well microcantilever photon detectors. Ultramicroscopy 2001, 86(1-2), 191–206. [Google Scholar]
- Senesac, L.R.; Corbeil, J.L.; Rajic, S.; Lavrik, N.V.; Datskos, P.G. IR imaging using uncooled microcantilever detectors. Ultramicroscopy 2003, 97(1-4), 451–458. [Google Scholar]
- Nelson, B.A.; King, W.P. Temperature calibration of heated silicon atomic force microscope cantilevers. Sensors and Actuators A: Physical 2007, 140(1), 51–59. [Google Scholar]
- Finot, E.; Lacroute, Y.; Bourillot, E.; Rouessac, V.; Durand, J. Thermomechanical behavior of coated tapered optical fibers for scanning force microscopy. Journal of Applied Physics 2004, 95(9), 5137–5144. [Google Scholar]
- McLoughlin, N.; Lee, S.L.; Hahner, G. Simultaneous determination of density and viscosity of liquids based on resonance curves of uncalibrated microcantilevers. Applied Physics Letters 2006, 89(18), 184106. [Google Scholar]
- Chelidze, D.; Liu, M. Dynamical systems approach to fatigue damage identification. Journal of Sound and Vibration 2005, 281(3-5), 887–904. [Google Scholar]
- Fabre, A.; Finot, E.; Demoment, M.; Contreras, S. In situ measurement of elastic properties of PdHx, PdDx, and PdTx. Journal of Alloys and Compounds 2003, 356, 372–376. [Google Scholar]
- Fabre, A.; Decamps, B.; Finot, E.; Penisson, J.M.; Demoment, J.; Thiebaut, S.; Contreras, S.; Percheron-Guegan, A. On the correlation between mechanical and TEM studies of the aging of palladium during tritium storage. Journal of Nuclear Materials 2005, 342(1-3), 101–107. [Google Scholar]
- Mertens, J.; Finot, E.; Bourillot, E.; Fabre, A.; Goudonnet, J.P. Study of the surface reactivity of optical fibers under aging conditions by flexural resonance. Journal of Vacuum Science & Technology B 2001, 19(6), 2095–2103. [Google Scholar]
- Finot, E.; Lesniewska, E.; Mutin, J. C.; Goudonnet, J.P. Investigations of surface forces between gypsum microcrystals in air using atomic force microscopy. Langmuir 2000, 16(9), 4237–4244. [Google Scholar]
- Finot, E.; Lesniewska, E.; Goudonnet, J.P.; Mutin, J.C. Correlation between surface forces and surface reactivity in the setting of plaster by atomic force microscopy. Applied Surface Science 2000, 161(3-4), 316–322. [Google Scholar]
- Finot, E.; Lesniewska, E.; Mutin, J.C.; Goudonnet, J.P. Investigations of surface forces between gypsum crystals in electrolytic solutions using microcantilevers. Journal of Chemical Physics 1999, 111(14), 6590–6598. [Google Scholar]
- Garrault, S.; Finot, E.; Lesniewska, E.; Nonat, A. Study of C-S-H growth on C3S surface during its early hydration. Materials and Structures 2005, 38(278), 435–442. [Google Scholar]
- Mertens, J.; Finot, E.; Heintz, O.; Nadal, M.H.; Eyraud, V.; Cathelat, A.; Legay, G.; Bourillot, E.; Dereux, A. Changes in surface stress, morphology and chemical composition of silica and silicon nitride surfaces during the etching by gaseous HF acid. Applied Surface Science 2007, 253(11), 5101–5108. [Google Scholar]
- Dumay, B.; Finot, E.; Theobald, M.; Legaie, O.; Durand, J.; Baclet, P.; Goudonnet, J.P. Structure of amorphous hydrogenated carbon films prepared by radio frequency plasma enhanced chemical vapor deposition. An analogy with the structure zone model developed for metals. Journal of Applied Physics 2002, 92(11), 6572–6581. [Google Scholar]
- Finot, E.; Roualdes, S.; Kirchner, M.; Rouessac, V.; Berjoan, R.; Durand, J.; Goudonnet, J.P.; Cot, L. Surface investigation of plasma membranes post-treated by CF4/Ar plasma. Applied Surface Science 2002, 187(3-4), 326–338. [Google Scholar]
Notations
a lattice parameter (m) b cantilever width (m) f flexural resonance frequency (Hz) f′ flexural resonance frequency (Hz) after coating fT flexural resonance frequency (Hz) h cantilever thickness (m) hf film thickness (m) ℓ distance from the cantilever end (m) ℓs distance from surface molecules (m) Δσ differential surface stress (N/m) m cantilever mass (kg) t time (s) tdyn adsorption time under flow (s) x position along the cantilever (m) A cross section area of the cantilever (m2) C vapor concentration (molecules/liter) E Young's modulus (N/m2) Ef Young's modulus of the film (N/m2) E* reduced Young's modulus (N/m2) E′ storage modulus (N/m2) E″ loss modulus (N/m2) D intrinsic damping of the cantilever (internal loss) DF fluid damping F force (N) G shear modulus I inertia momentum (m4) K spring constant of cantilever (N/m) Ko bare cantilever spring constant (N/m) KD bilayer cantilever spring constant (N/m) L cantilever length (m) M molar mass of the gas (g/mol) P pressure (N/m2) Q quality factor Rσ curvature radius caused by intrinsic stress (m) Ro curvature radius caused before coating (m) Re Reynold's number Rg constant of perfect gas S active surface area of the cantilever (m2) ΔT temperature change (K) U interfacial energy (J/m2) V flow rate (liter/min) W adsorption capacity (molecules/μm2) Z vibration amplitude of the c: cantilever and the p: piezoelectric (m) α thermal expansion coefficient (K-1) ε strain σ stress (N/m2) σY yield strength (N/m2) σF fracture strength (N/m2) σf film normal stress (N/m2) σR residual stress (N/m2) σRf residual stress of the film (N/m2) σS surface stress (N/m) l mean free path of molecules (m) Kn Knudsen number ϕ phase angle between E′ and E″ (°) d decrement logarithmic η gas viscosity mass density of the cantilever (kg/m3) peff effective mass density of the bilayer cantilever (kg/m3) ν Poisson ratio ω pulsation (Hz) QCM Quartz Crystal Microbalance MEMS Micro Electro Mechanical System MFC Mass Flow Controller PDMS Polydimethylsiloxane PMMA Polymethylmetaacrylate SAW Surface Acoustic Wave
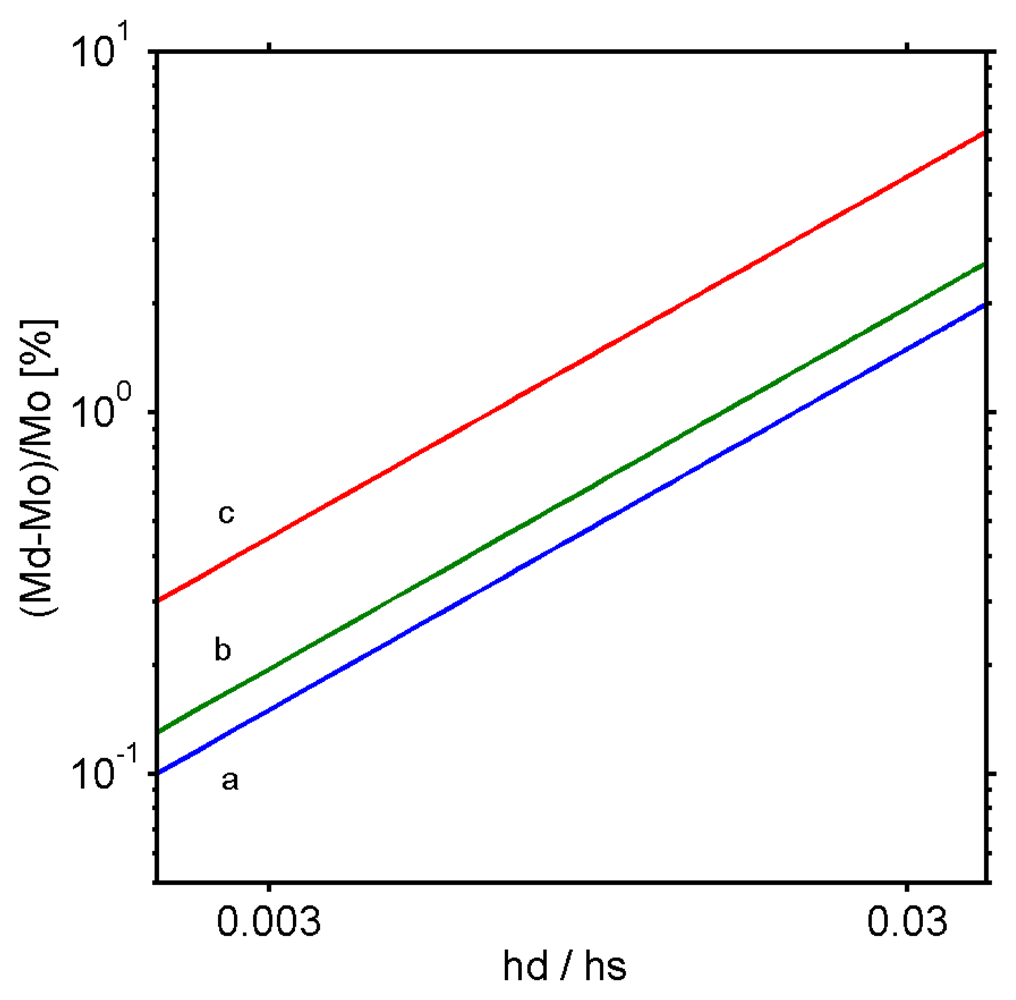
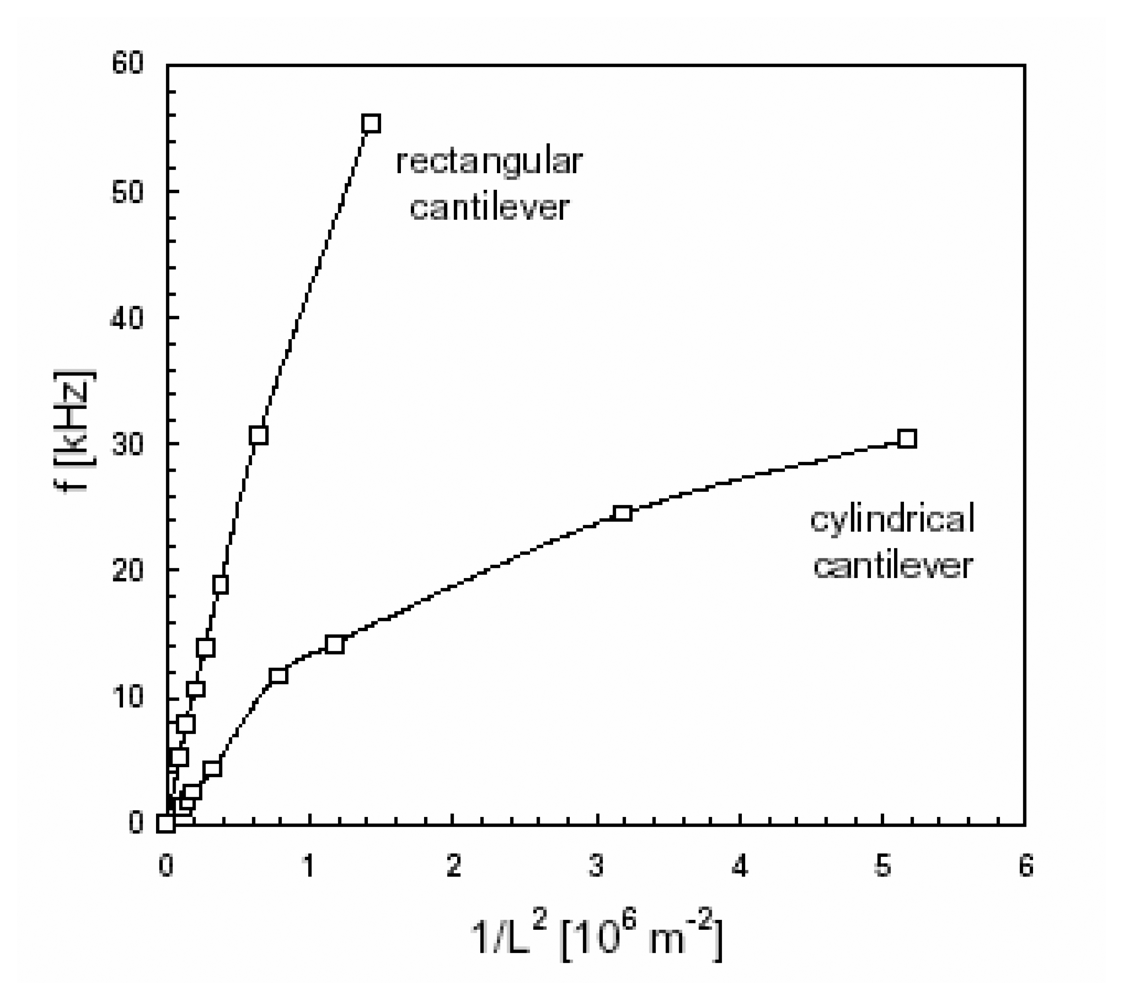
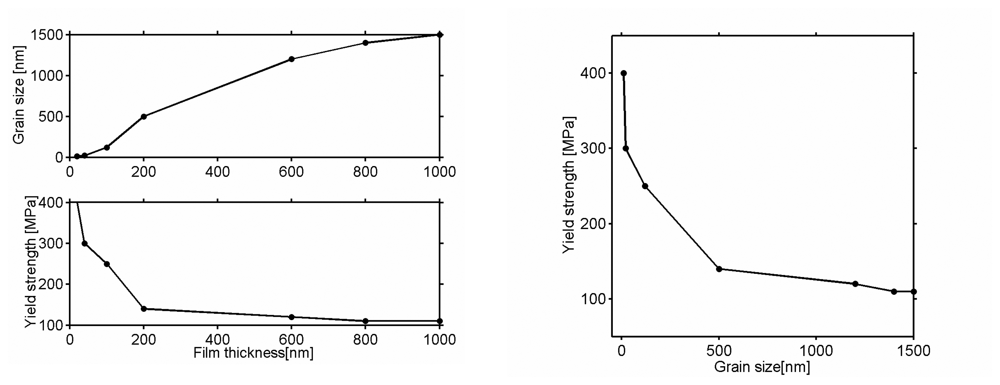
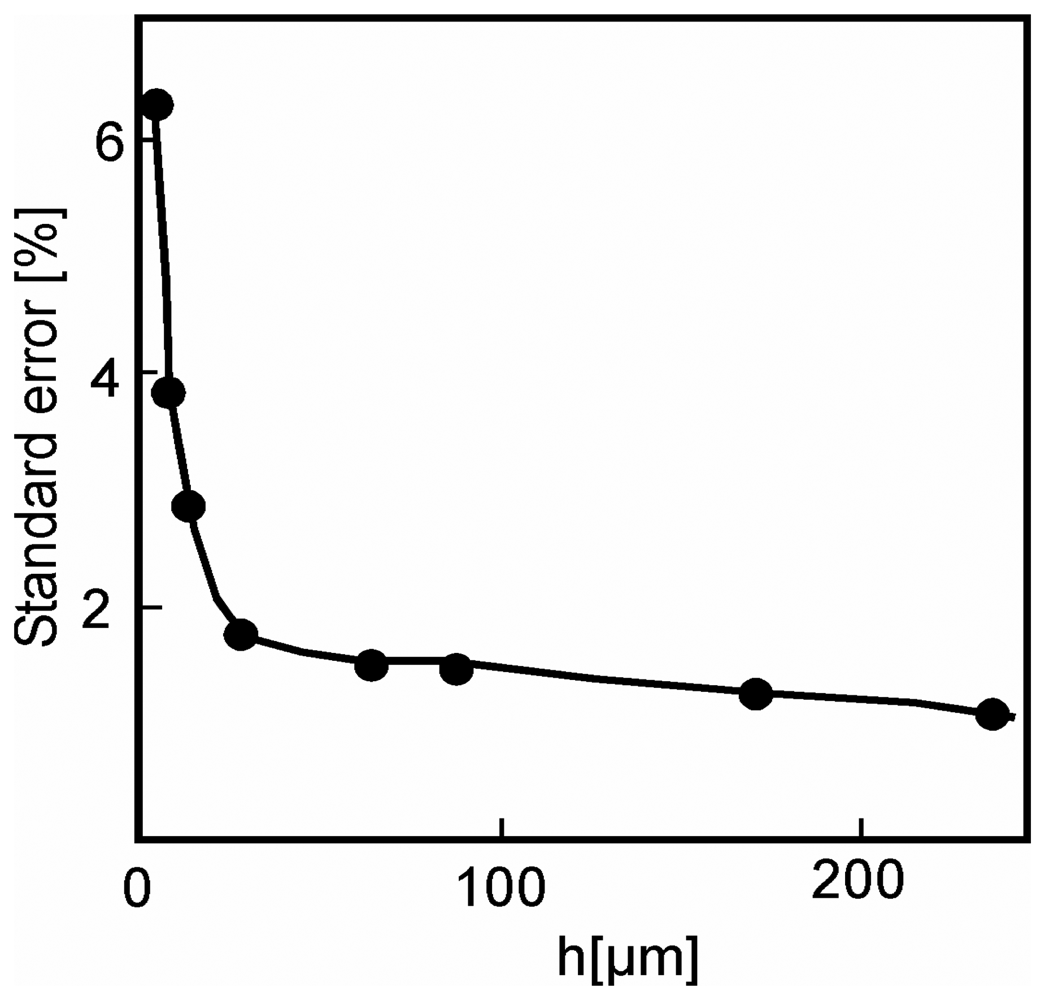
| E [84] | ν | s Y (MPa) | s F(MPa) | |
|---|---|---|---|---|
| LB film | anisotropic 0.3 - 2.5 | anisotropic 0.1- 0.8 | 15-35 | |
| Rubber | 0.01 - 0.1 | 0.5 | 4-12 | 25 |
| Polystyrene | 2 | 0.35 | 30 | 30 |
| Aluminum | 70 | 0.33 | 50 | 710-1000 |
| Silicon | 150 | 0.17 | 300 | 700 |
| Single Carbon nanotube | 1000 | 0.17 | not reached | not reached |
| n | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| b/L=0.2 | 6.85 | 19.1 | 36.4 | 62.4 |
| b/L=0.1 | 6.44 | 18 | 35.4 | 57 |
| d/L=0.03 | 6.05 | 16.9 | ||
| d/L=0.03 | 6.19 | 17.3 | ||
| Theory | 6.27 | 17.6 | 34.4 | 56.9 |
| Au | Cu | Pd | Fe | |
|---|---|---|---|---|
| Cantilever | 6.85 | 19.1 | 36.4 | 62.4 |
| Ultrasonic | 6.44 | 18 | 35.4 | 57 |
| (Δm/m)/(Δf/f) (%) | Biopolymer Ef= 0.1 GPa, ρf= 1000 kg/m3 | Inorganic/polymer Ef= 10 GPa, ρf= 1500 kg/m3 | Metal Ef= 100 GPa, ρf= 2000 kg/m3 |
|---|---|---|---|
| hf/h = 3.10-3 | 99.4% | 71.4% | 24.8% |
| hf/h = 3.10-2 | 99.3% | 70,2% | 23.9% |
| hf/h = 3.10-1 | 98.9% | 58.5% | 19,5% |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Finot, E.; Passian, A.; Thundat, T. Measurement of Mechanical Properties of Cantilever Shaped Materials. Sensors 2008, 8, 3497-3541. https://doi.org/10.3390/s8053497
Finot E, Passian A, Thundat T. Measurement of Mechanical Properties of Cantilever Shaped Materials. Sensors. 2008; 8(5):3497-3541. https://doi.org/10.3390/s8053497
Chicago/Turabian StyleFinot, Eric, Ali Passian, and Thomas Thundat. 2008. "Measurement of Mechanical Properties of Cantilever Shaped Materials" Sensors 8, no. 5: 3497-3541. https://doi.org/10.3390/s8053497





