Three-Dimensional Transport Modeling for Proton Exchange Membrane(PEM) Fuel Cell with Micro Parallel Flow Field
Abstract
:1. Introduction
2. Numerical Models
2.1 Model assumptions
- 1)
- The gas mixture is incompressible, ideal fluid
- 2)
- The flow in the flow channel is laminar
- 3)
- Isothermal condition
- 4)
- Butler - Volmer kinetics for electrochemical reaction rate
2.2 Governing equation
1) Mass conservation equation
2) Momentum conservation equation
3) Species conservation equation
2.3 Water transport equation
1) Electro-osmotic drag flux
2) Back diffusion flux
3) Current density and membrane ion Conductivity
2.4 Numerical algorithm
2.5 Numerical simulation model
3. Discussions
4. Conclusions
- 1)
- Hydrogen and oxygen were supplied to the membrane by diffusion mechanism rather than convection transport. Pressure drop was 11 Pa at anode and 22.5 Pa at the cathode flow channel for 0.5V, and a higher pressure drop at the cathode side is thought to be caused by the higher flow rate of oxygen at the cathode.
- 2)
- The amount of water in cathode channel was determined by the water formation due to the electrochemical reaction plus the electro-osmotic mass flux directing toward the cathode side.
- 3)
- It is very important to model the back diffusion and electro-osmotic mass flux accurately since the two flux were closely correlated with each other and have greatly influenced the determination of ionic conductivity of the membrane, which directly affected the performance of the fuel cell.
- 4)
- Since our model was only a single-phase model, it has some limitations in representing water flooding phenomena properly. However, a comparison of the relative performances of fuel cells with different flow configurations may give the data necessary for designing the micro flow channel.
References
- Kazim, A.; Liu, H.T.; Forges, P. Modeling of performance of PEM fuel cells with conventional and interdigitated flow fields. J. Appl. Electrochem. 1999, 29, 1409–1416. [Google Scholar]
- Nguyen, T. V. Modeling two-phase flow in the porous electrodes of proton exchange membrane fuel cells using the interdigitated flow fields. May 1999.
- Wood, D.L.; Yi, J. S.; Nguyen, T. V. Effect of direct liquid water injection and interdigitated flow field on the performance of proton exchange membrane fuel cells. Electrochem. Acta. 1998, 43, 3795–3809. [Google Scholar]
- Lee, P.H.; Cho, S. A.; Han, S. S.; Hwang, S. S. Performance characteristics of proton exchange membrane fuel cell(PEMFC) with interdigitated flow channel. International J. Automotive Technology. 2007, 8, 761–769. [Google Scholar]
- Bernardi, D.M.; Verbrugge, M. W. Mathematical model of a gas diffusion electrode bonded to polymer electrolyte. AIChE J. 1992, 37, 1151–1163. [Google Scholar]
- Bernardi, D.M.; Verbrugge, M. W. Mathematical model of the solid polymer-electrolyte fuel cell. J. Electrochem. Soc. 1992, 139, 2477–2491. [Google Scholar]
- Springer, T.E.; Zawodzinski, T. A.; Gottesfeld, S. Polymer electrolyte fuel cell model. J. Eletrochem. Soc. 1999, 138, 2334–2342. [Google Scholar]
- Fuller, T.E.; Newman, I. Water thermal management in solid polymer electrolyte fuel cells. J. Eletrochem. Soc. 1998, 146, 1218–1225. [Google Scholar]
- Nguyen, T.V.; White, R. E.; Water, A. Heat management model for proton exchange membrane fuel cells. J. Electrochem. Soc. 1993, 140, 2178–2186. [Google Scholar]
- Gurau, V.; Liu, H.; Kakac, S. Two-dimensional model for proton exchange membrane fuel cells. AIChE J. 1998, 44, 2410–2422. [Google Scholar]
- Kumar, A.; Reddy, R.G. Modeling of polymer electrolyte membrane fuel cell with metal form in the flow-field of the bipolar/end plate. J. Power Sources. 2003, 114, 54–62. [Google Scholar]
- Shimpalee, S.; Dutta, S.; Lee, W. K.; Van Zee, J. W. Effect of humidity on PEM fuel cell performance part II - mumerical simulation. In Proceeding of ASME IMECH, TN, HTD; Nashville, USA, 1999; Volume 364-1, pp. 367–374. [Google Scholar]
- Um, S.; Wang, C.Y. Three-dimensional analysis of transport and electrochemical reactions in polymer electrolyte fuel cells. J. Power Socrces. 2004, 125, 40–51. [Google Scholar]
- Wang, L.; Husar, A.; Zhou, T.; Liu, H. A parametric study of PEM fuel cell performances. International Journal of Hydrogen Energy. 2003, 28, 1263–1272. [Google Scholar]
- Sivertsen, B.R.; Djilali, N. CFD-based modeling of proton exchange membrane fuel cells. J. Power Sources. 2005, 141, 65–78. [Google Scholar]
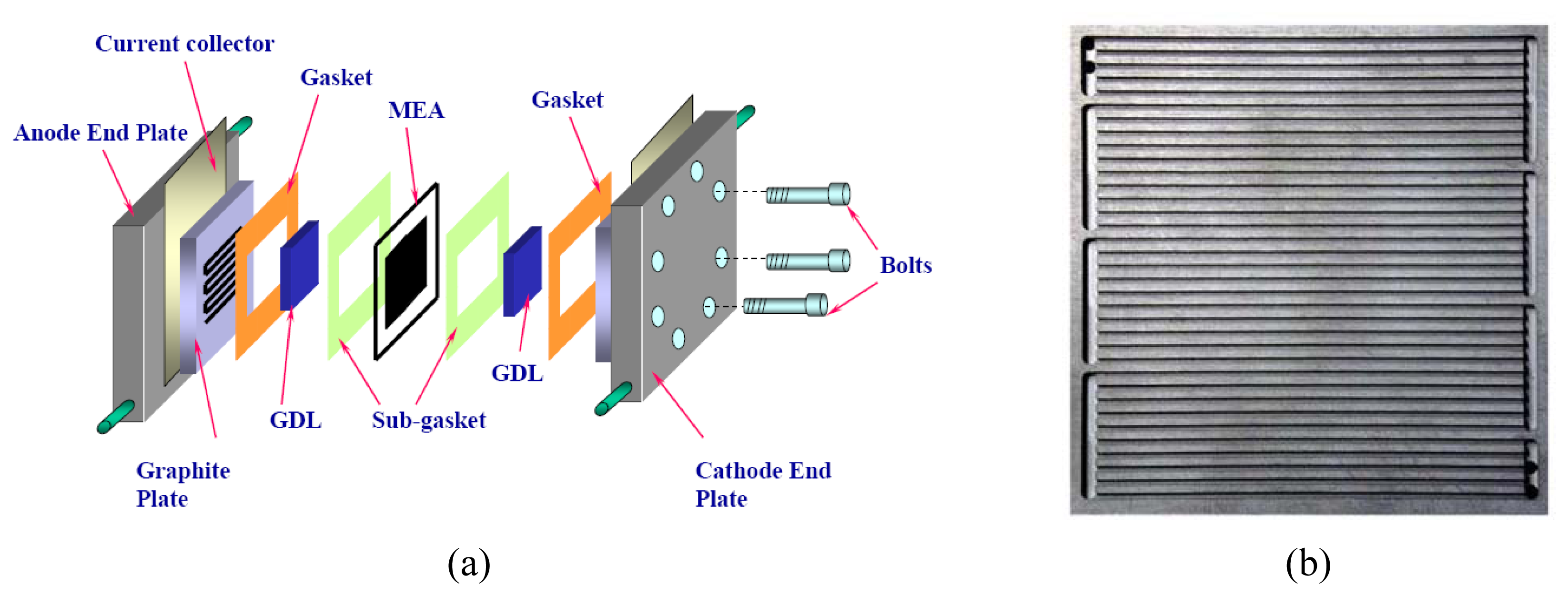
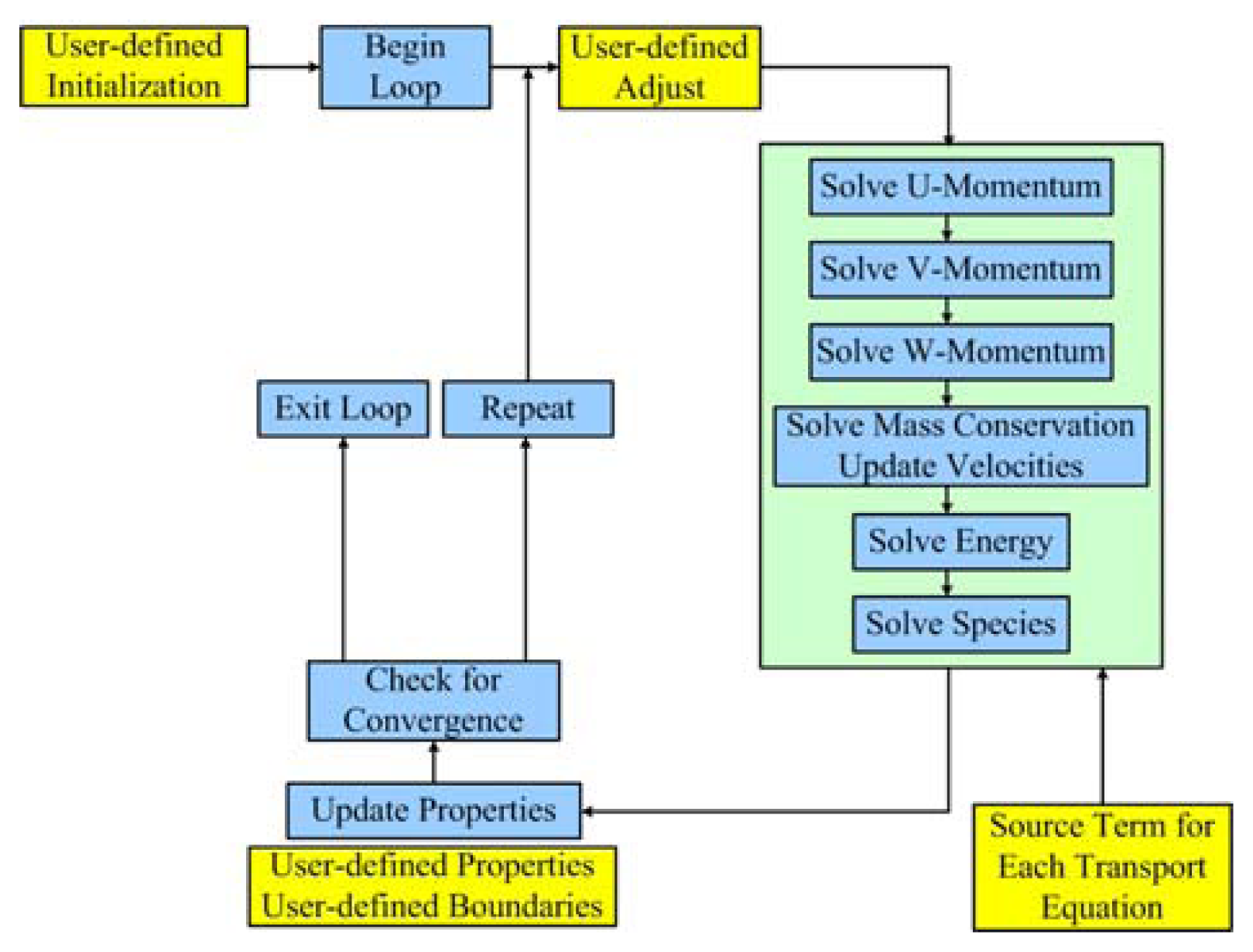
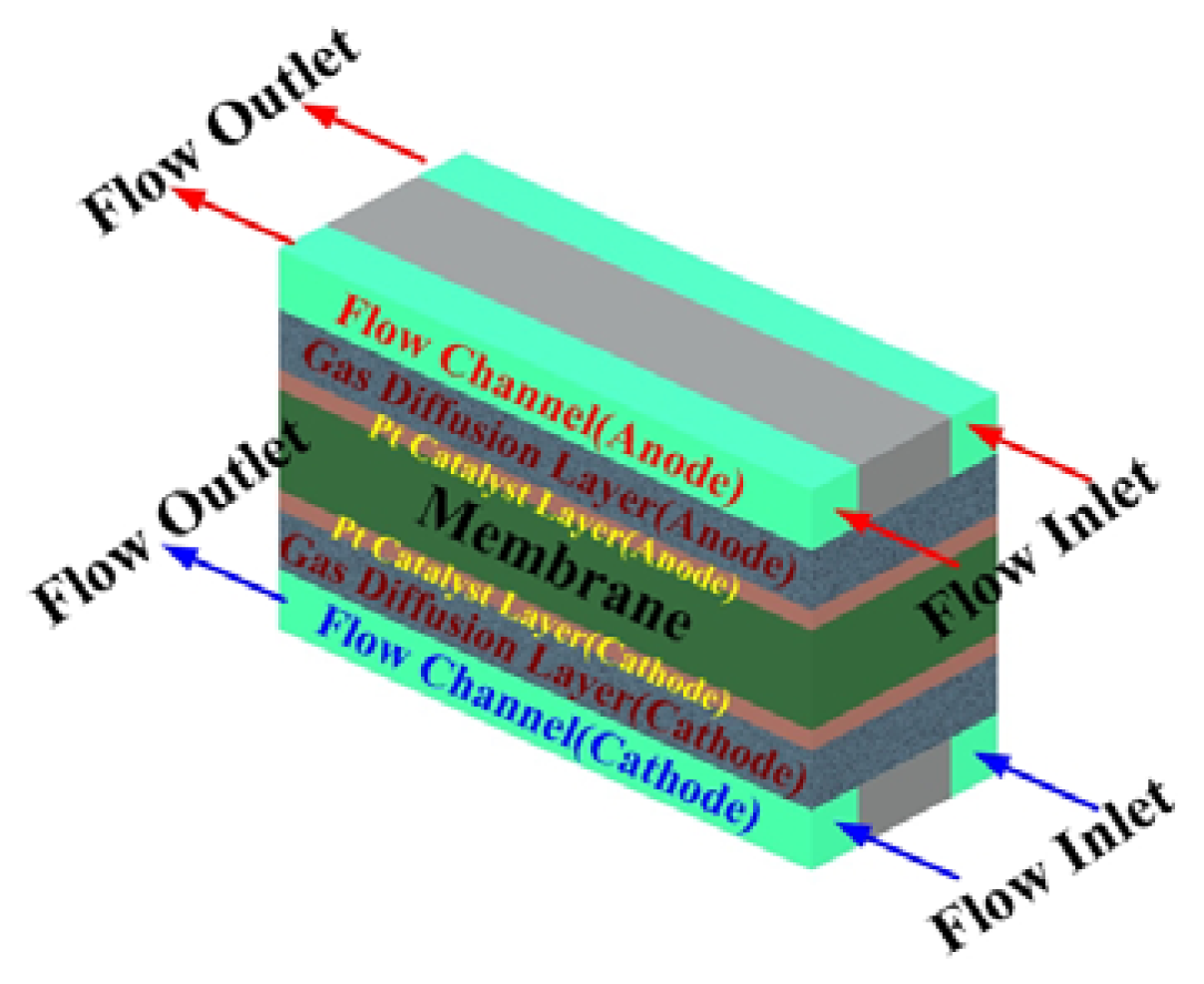
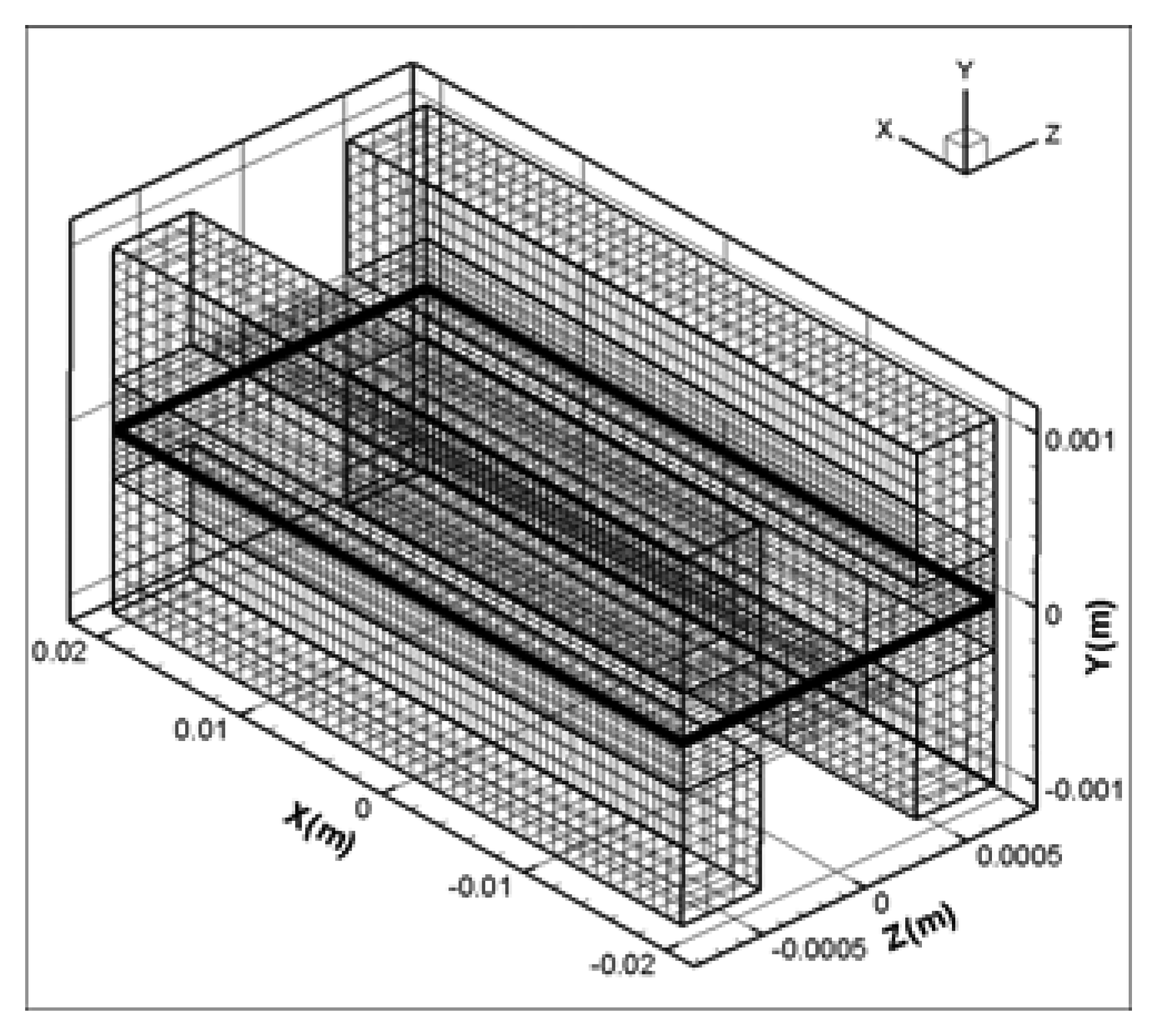
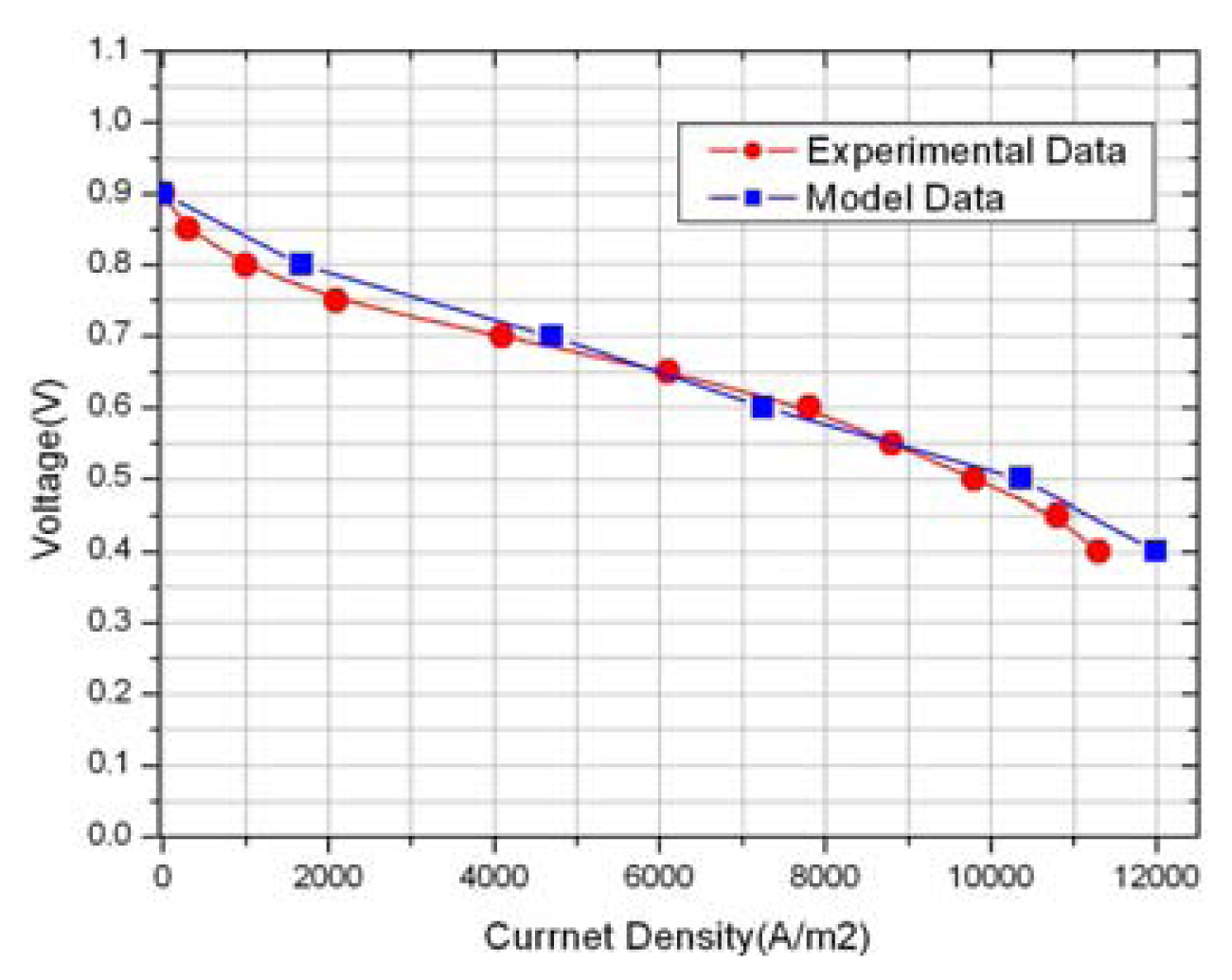
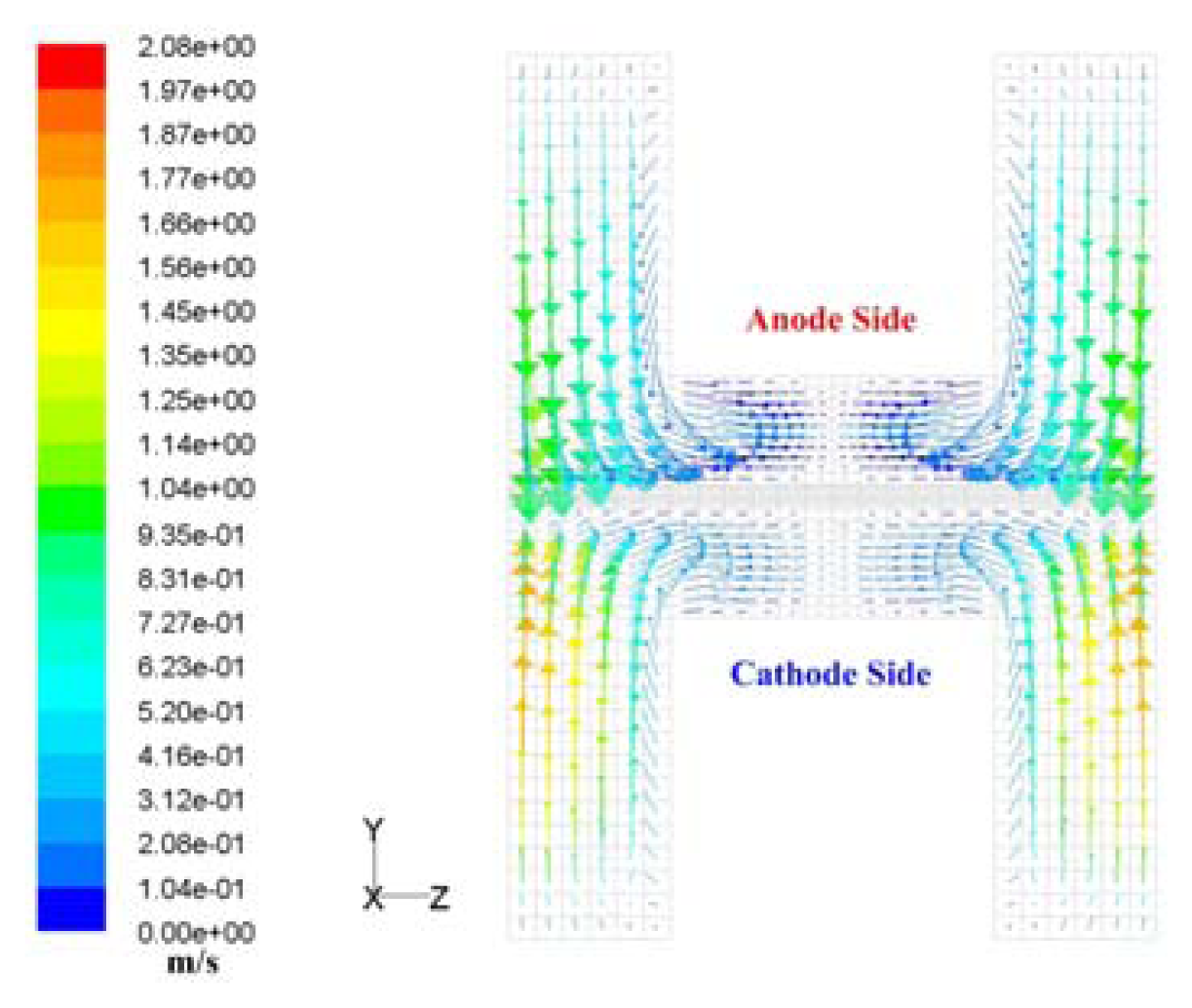
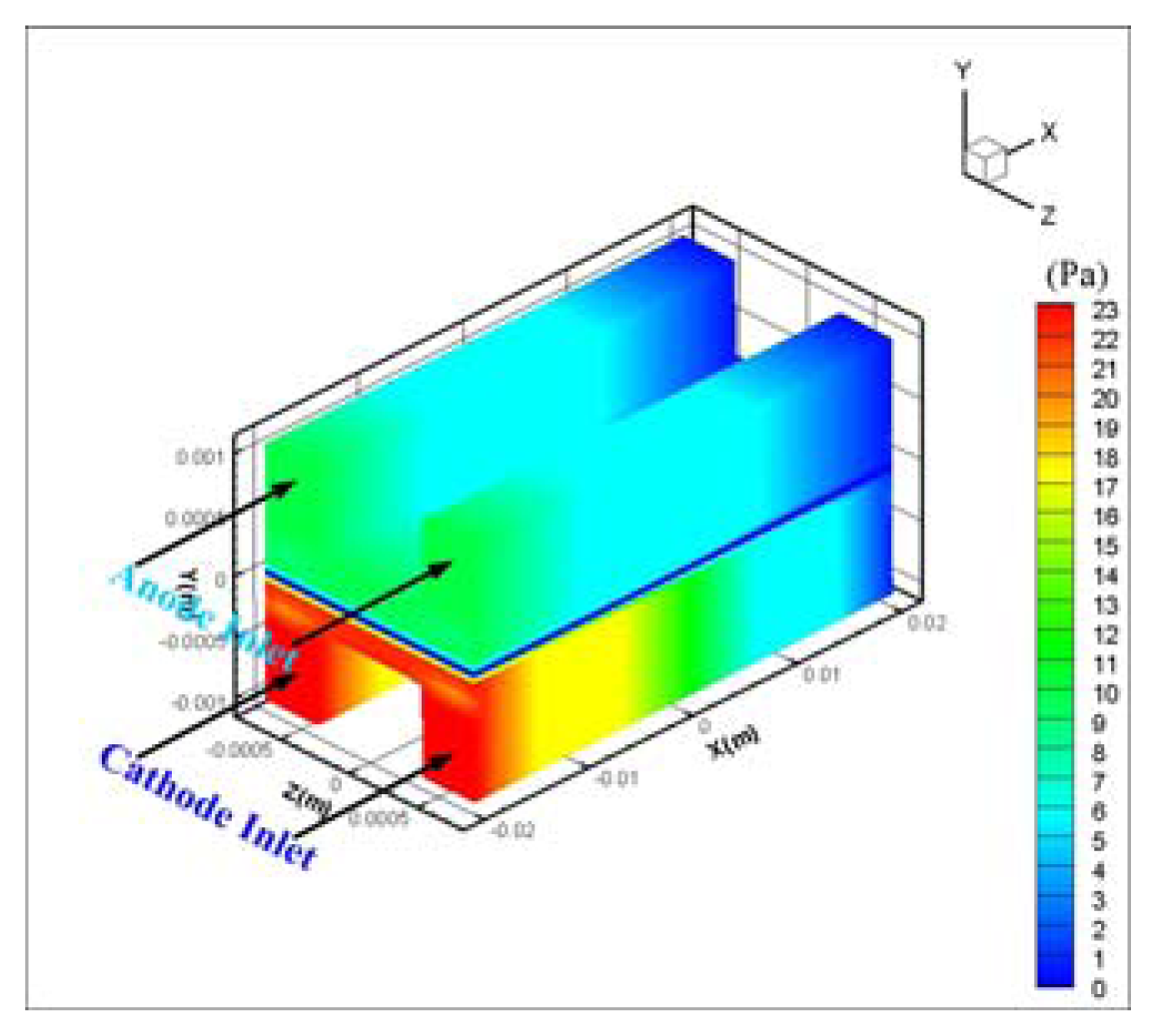
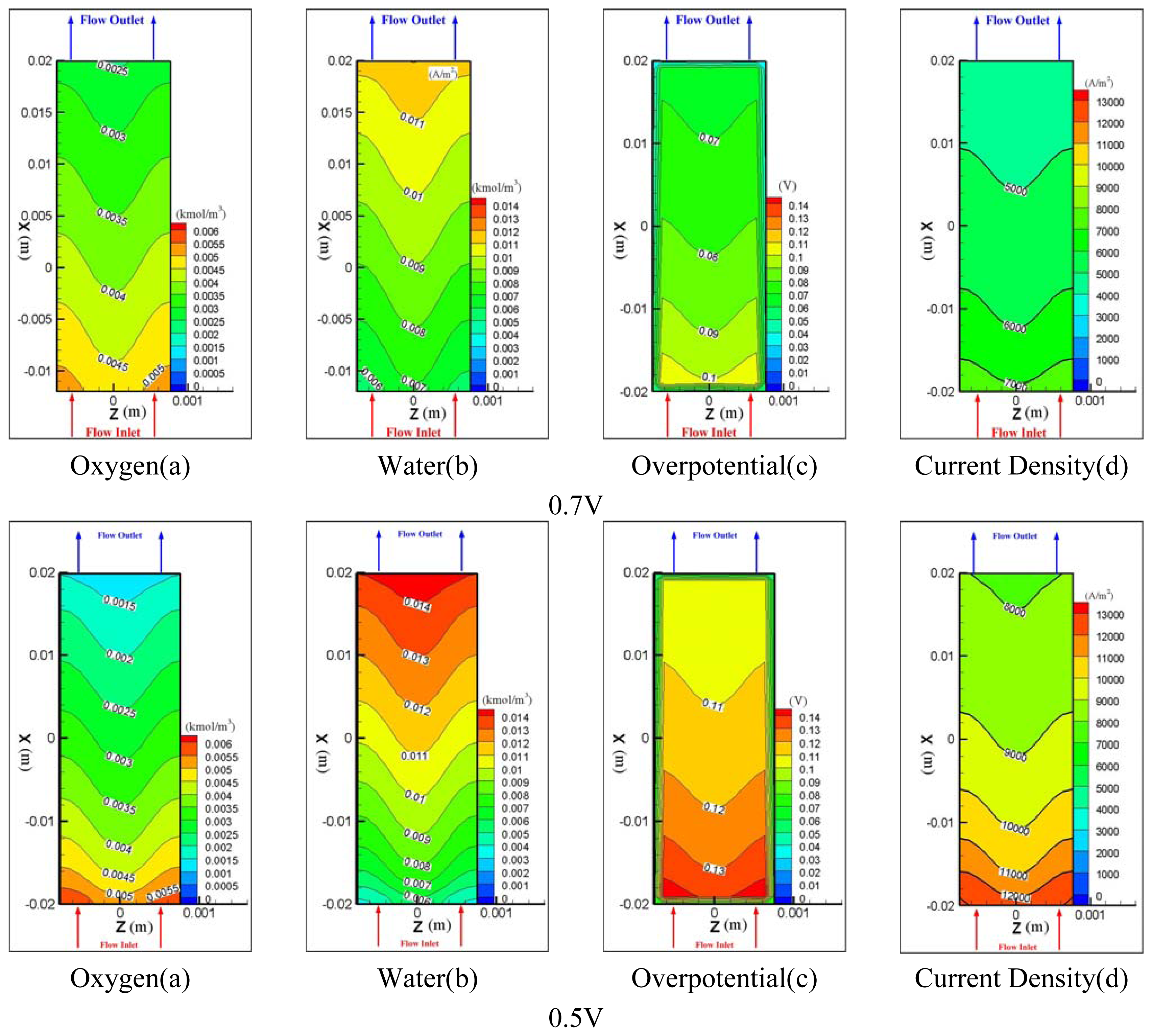
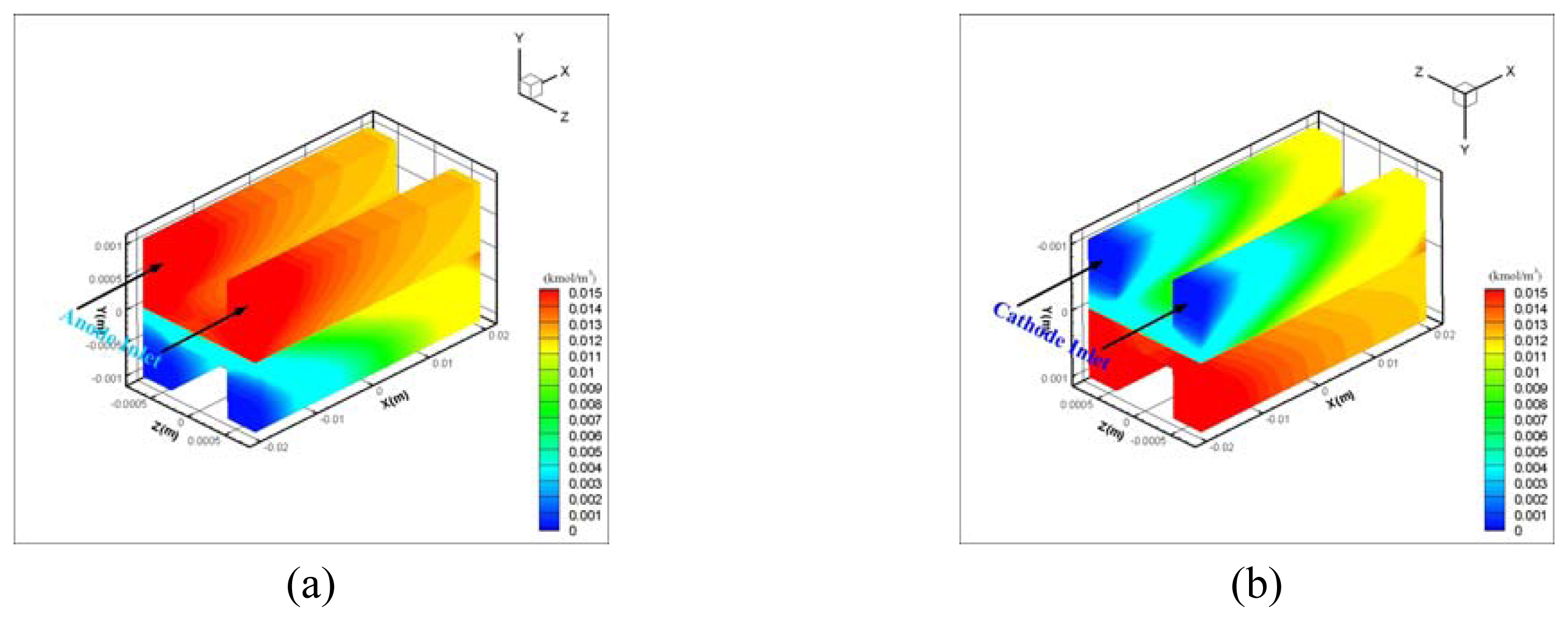
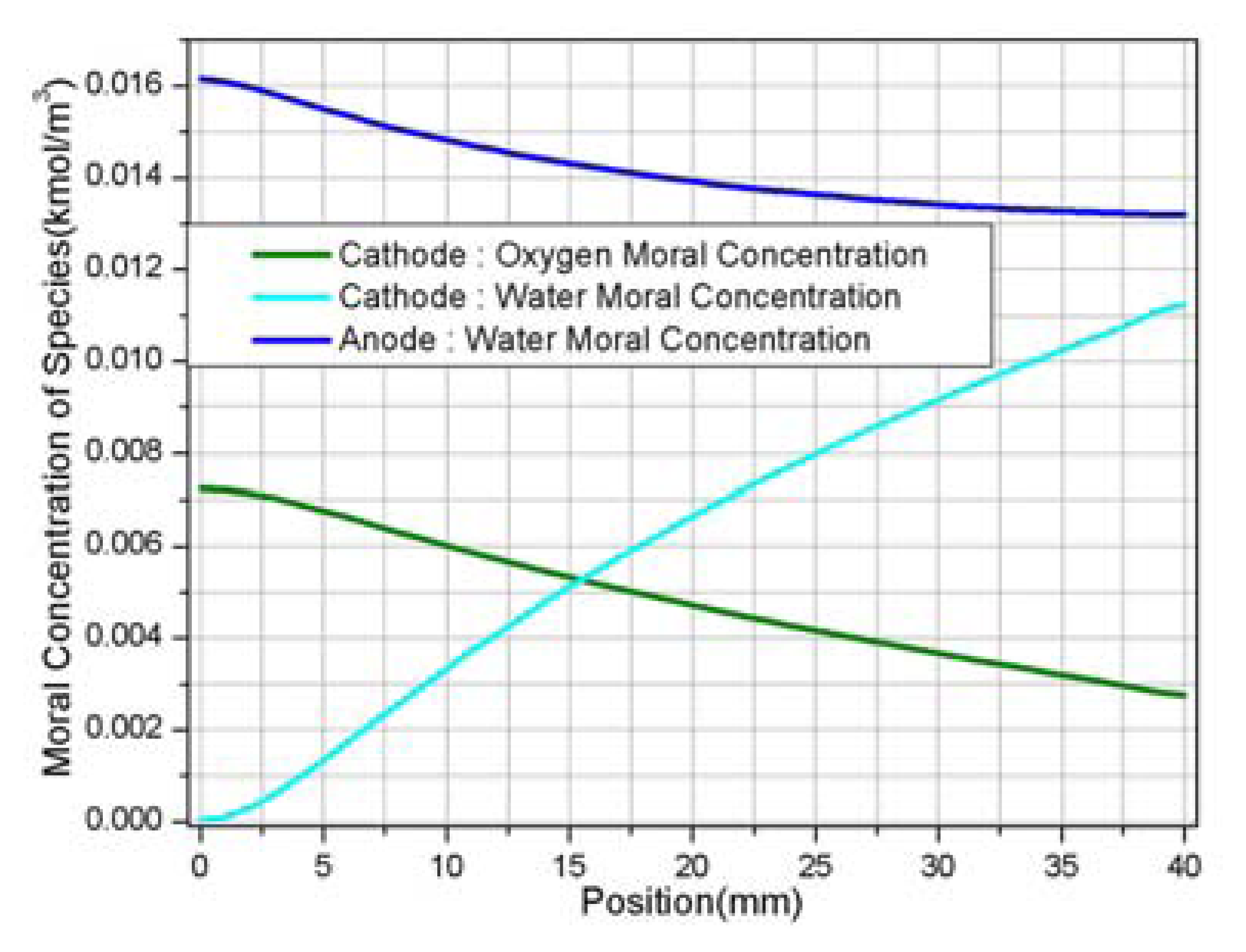
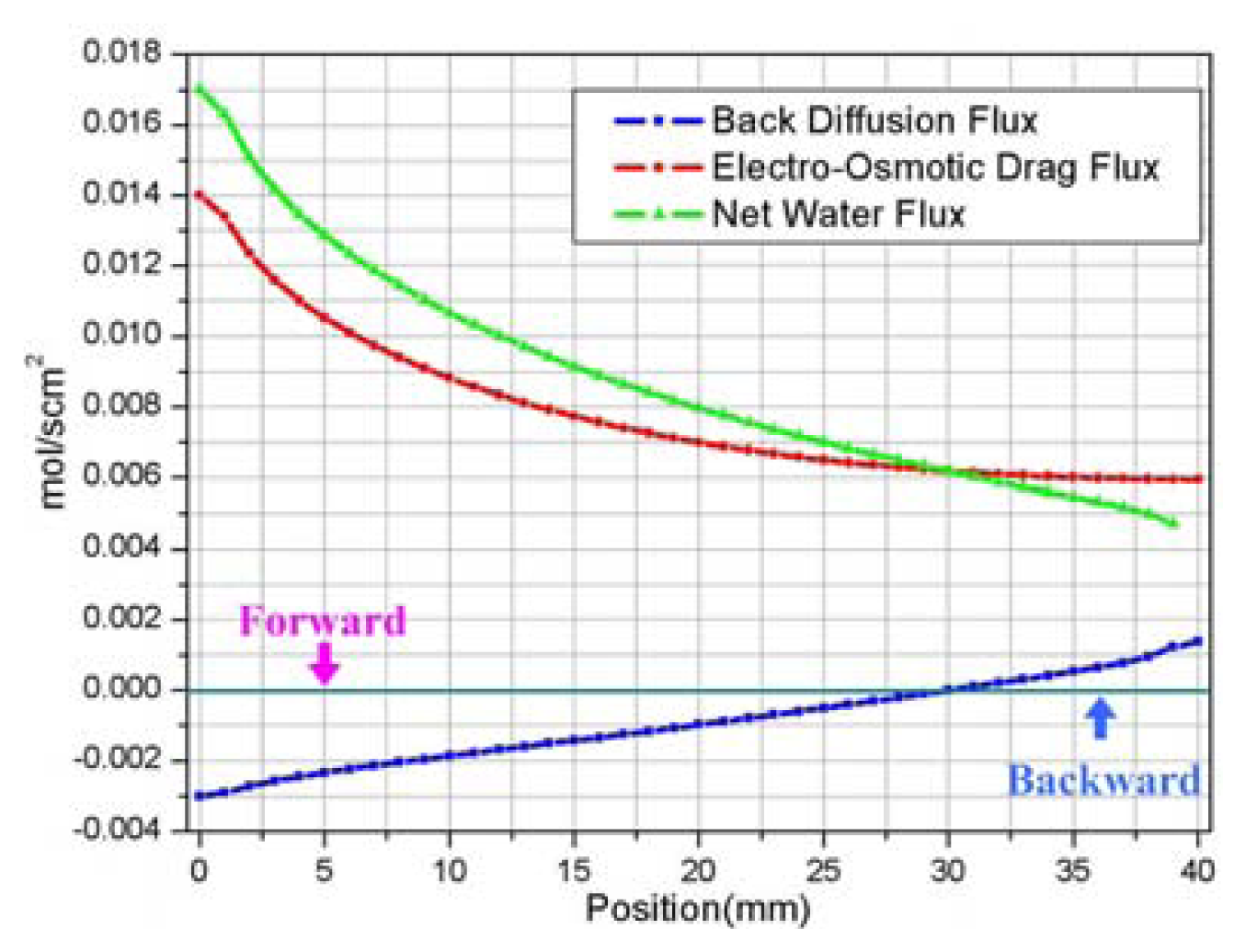
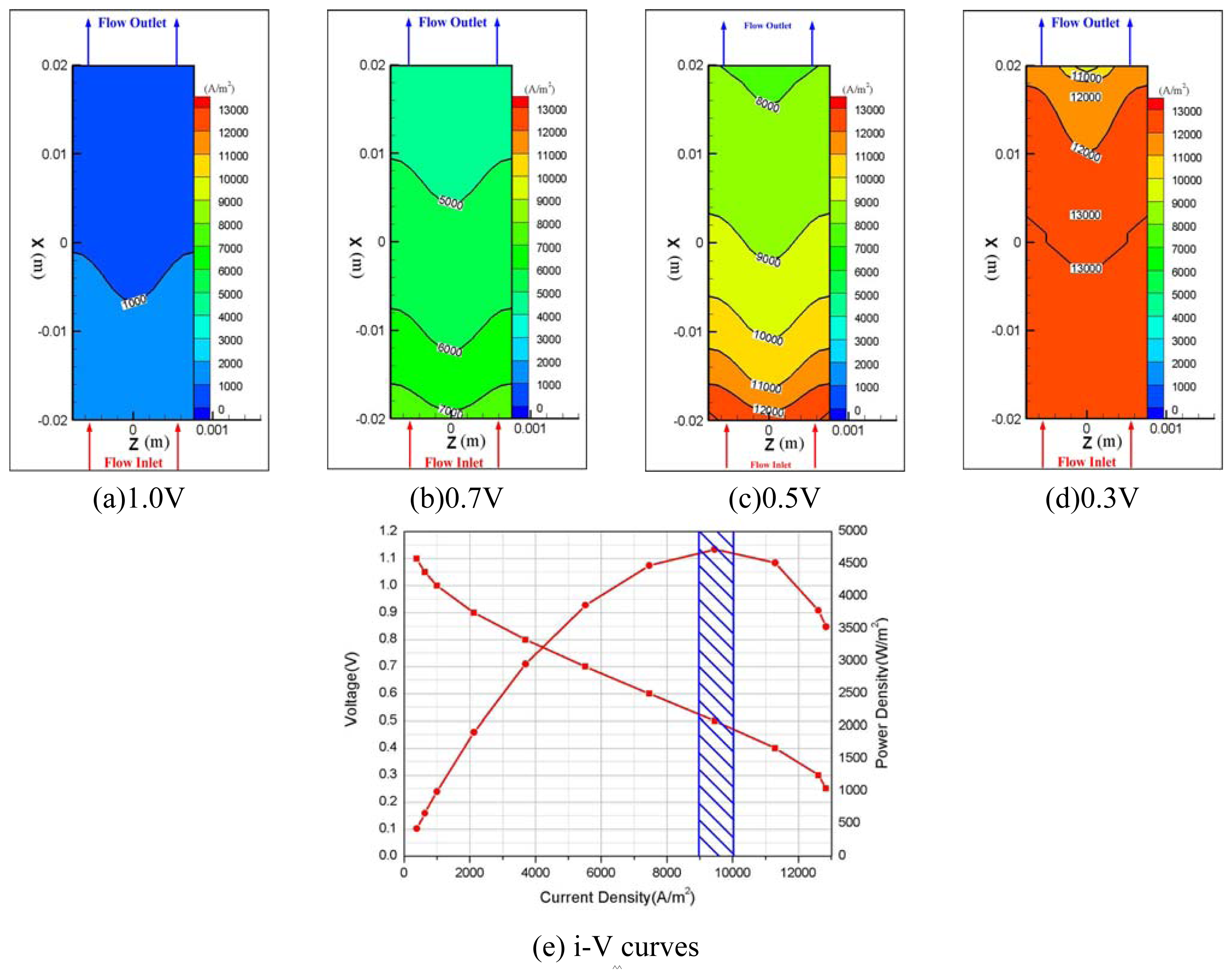
| Description | Value | Description | Value |
|---|---|---|---|
| Channel length (mm) | 40 | Cathode side pressure (atm) | 1 |
| Channel width (μm) | 762 | Anode stoichiometric number | 1.5 |
| Channel height (μm) | 762 | Cathode stoichiometric number | 2.0 |
| GDL thickness (μm) | 254 | O2 / N2 ratio | 0.21/0.79 |
| Catalyst layer thickness (μm) | 28.7 | H2 inlet mass fraction, Anode(%) | 11.54 |
| Cell temperature (K) | 353.2 | H2O inlet mass fraction, Anode(%) | 88.46 |
| Anode side pressure (atm) | 1 | O2 inlet mass fraction, Cathode (%) | 23.3 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Lee, P.H.; Han, S.S.; Hwang, S.S. Three-Dimensional Transport Modeling for Proton Exchange Membrane(PEM) Fuel Cell with Micro Parallel Flow Field. Sensors 2008, 8, 1475-1487. https://doi.org/10.3390/s8031475
Lee PH, Han SS, Hwang SS. Three-Dimensional Transport Modeling for Proton Exchange Membrane(PEM) Fuel Cell with Micro Parallel Flow Field. Sensors. 2008; 8(3):1475-1487. https://doi.org/10.3390/s8031475
Chicago/Turabian StyleLee, Pil Hyong, Sang Seok Han, and Sang Soon Hwang. 2008. "Three-Dimensional Transport Modeling for Proton Exchange Membrane(PEM) Fuel Cell with Micro Parallel Flow Field" Sensors 8, no. 3: 1475-1487. https://doi.org/10.3390/s8031475




