A Review of Interface Electronic Systems for AT-cut Quartz Crystal Microbalance Applications in Liquids
Abstract
:1. Introduction
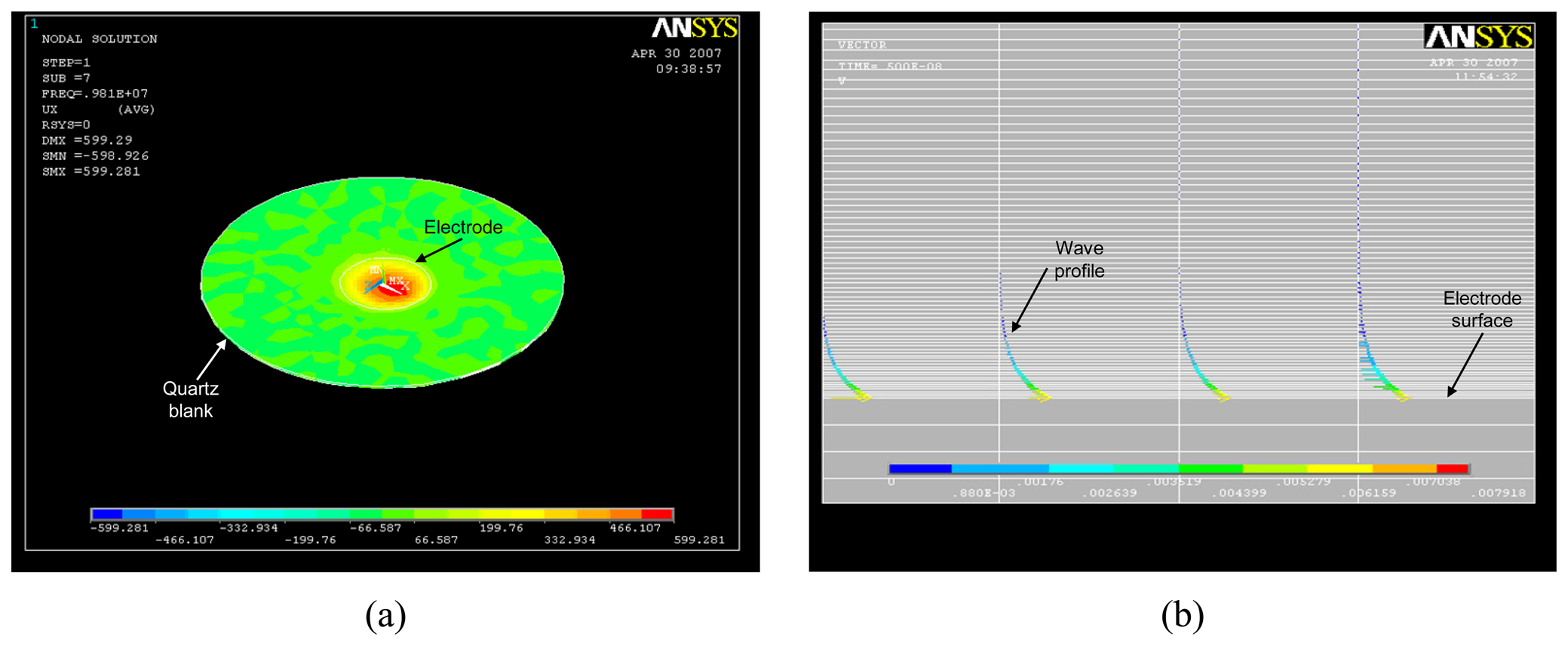
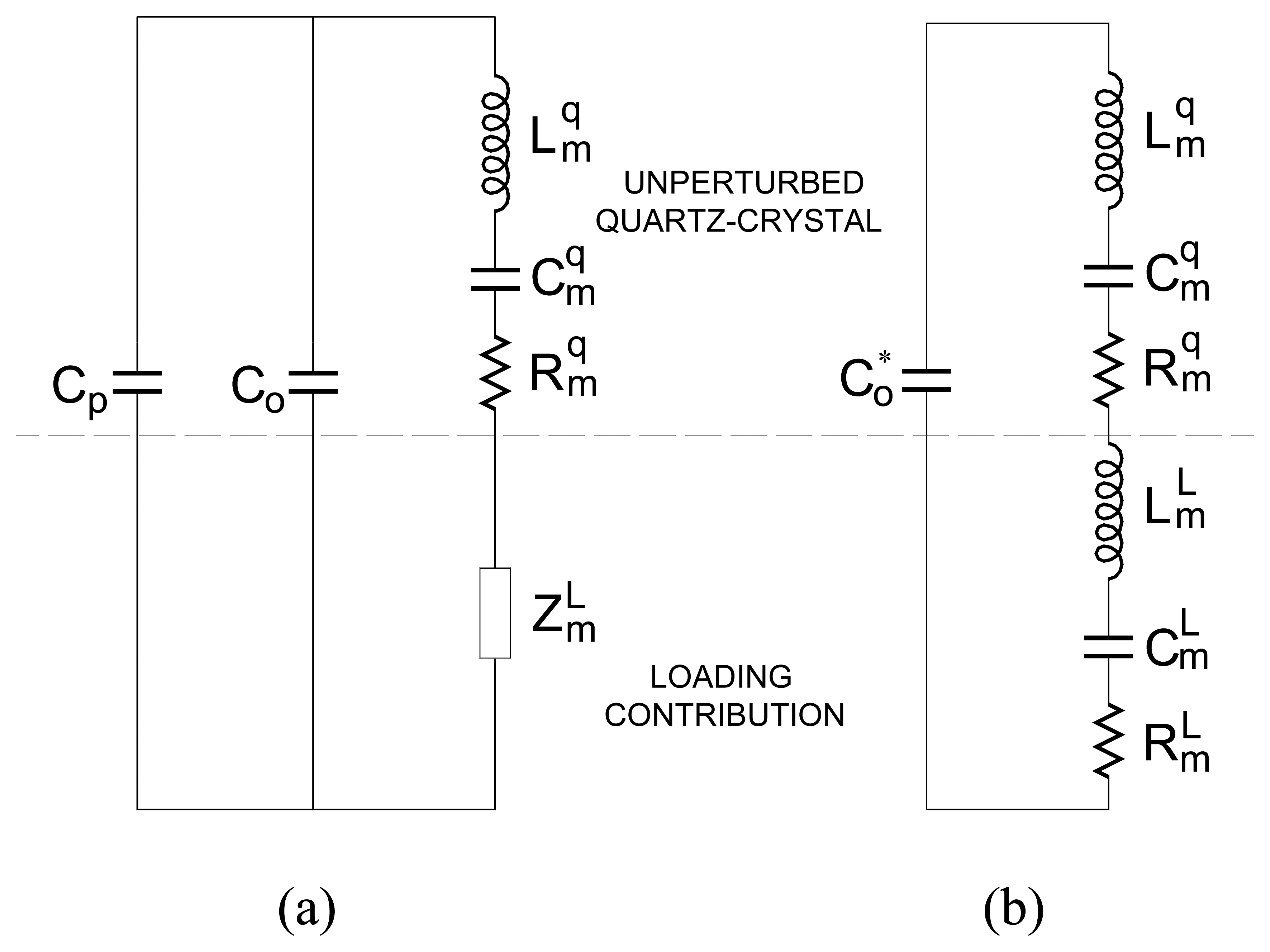
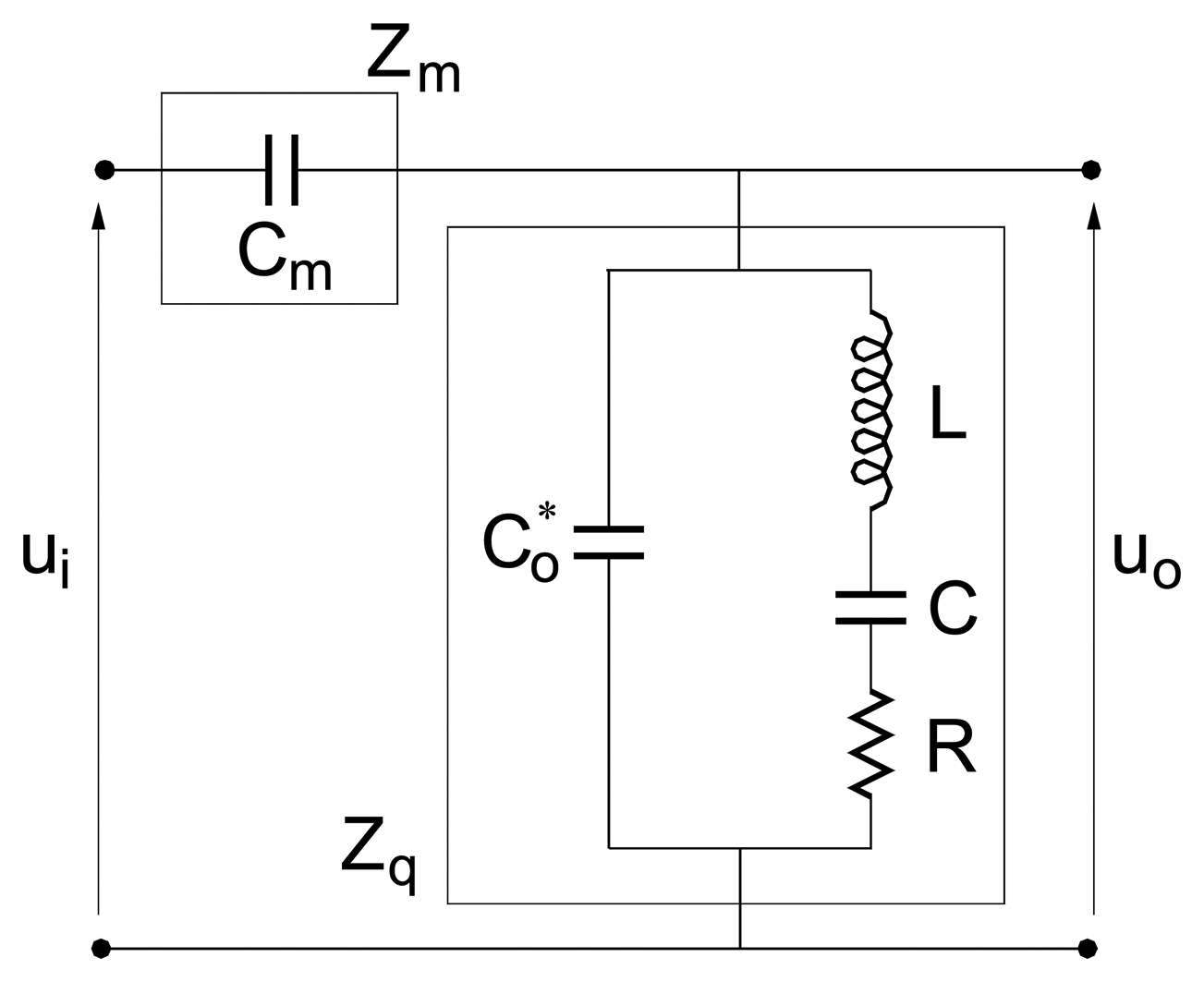
2. A Suitable Electrical Model for a QCM Sensor
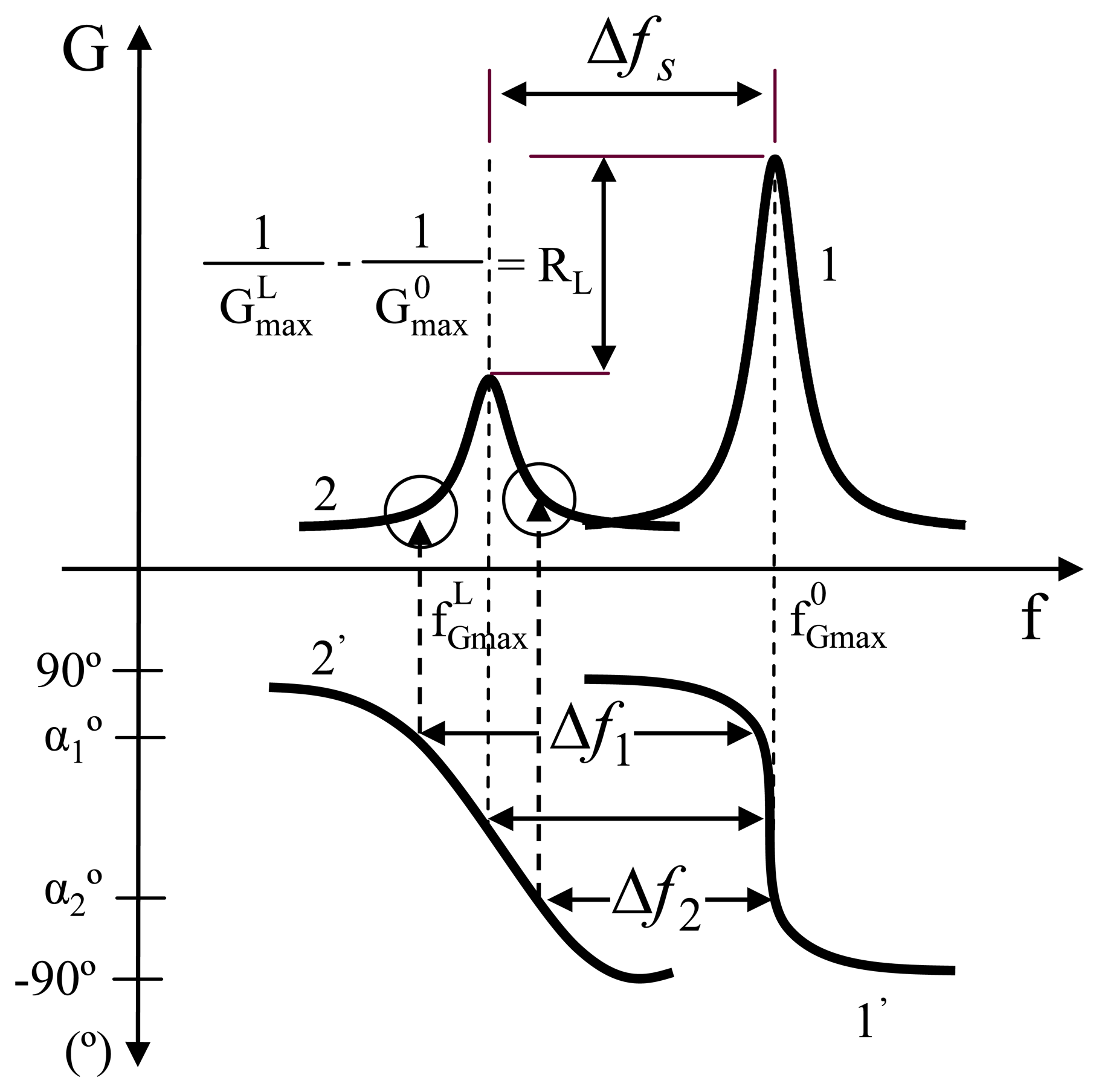
3. QCM Sensor Parameters
4. Systems for Sensor Parameter Characterization
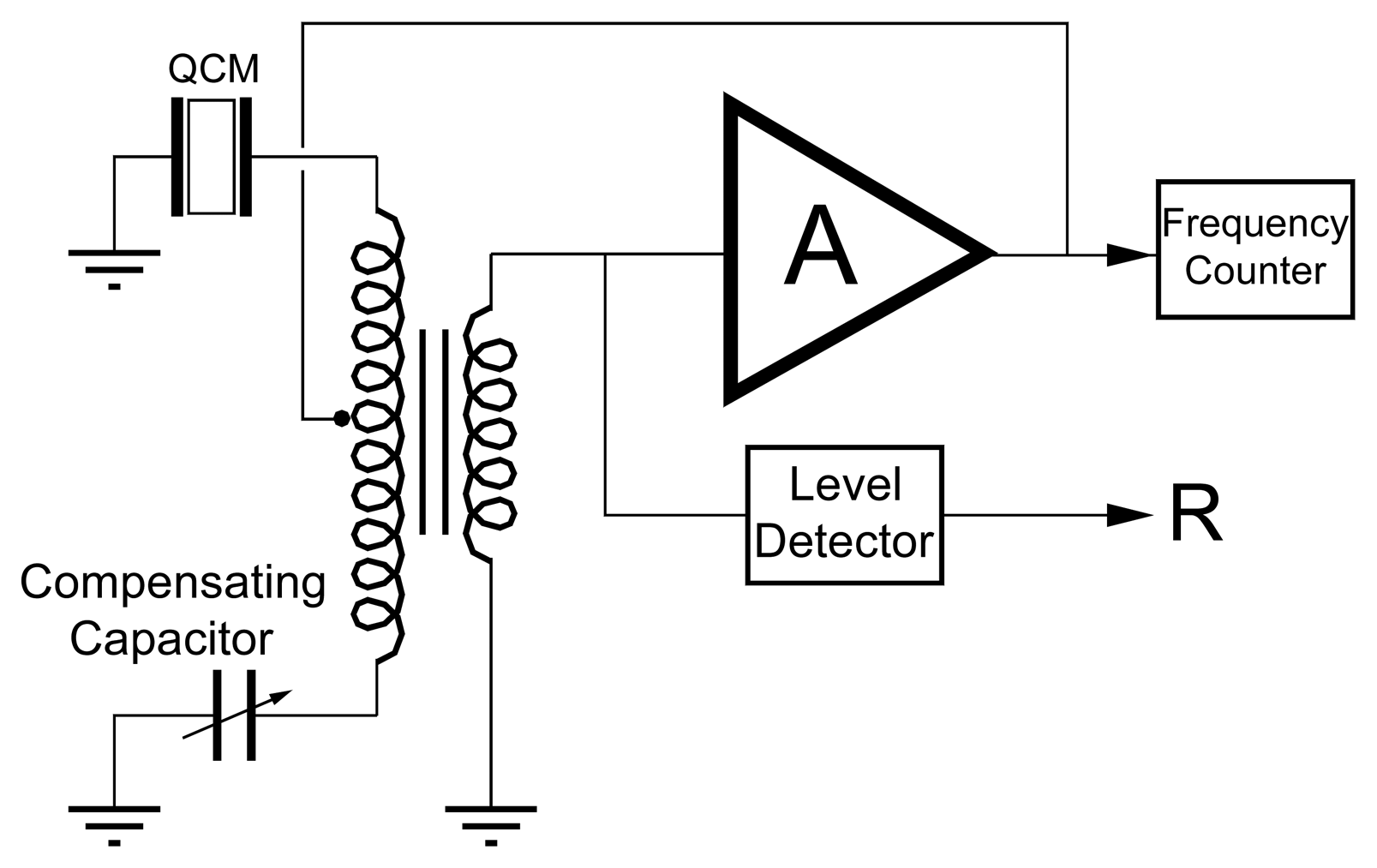
4.1 Impedance or Network Analysis
- The device is measured in isolation and no external circuitry influences the electrical behavior of the sensor.
- Parasitic influences can be excluded by calibration due to passive operation of the sensor.
- Differentiated information in relation to diverse contributions of the load can be obtained by measuring both the conductance and the susceptance of the sensor over a range of frequencies around resonance.
- Its high cost and large dimensions of the associated equipment prevent its use for in situ or remote measurements.
- The connection between the sensor and the equipment is sometimes difficult to accomplish such as in electrochemical or biological applications where it is convenient to ground one of the quartz electrodes.
- It is not suitable for simultaneous multiple sensor characterization. Sometimes a multiplexing interface is used for a sequential connection of different sensors to the same analyzer, but it can perturb the device response.
4.1.1 Adapted Impedance Spectrum Analyzers
- The information of the phase and magnitude of the sensor impedance is carried out in the amplitude of low frequency signals; this makes easier and more accurate their acquisition.
- Because the signal of interest is formed as the difference between two coherent signals, any additive source of noise is cancelled.
- The differential form of the signal permits to increase the sensitivity in case of heavy loaded resonators. Effectively, within a certain range, an increase in the modulating frequency increases the difference g(ω+)-g(ω-); it creates an amplifying effect while maintaining the noise and then the signal to noise ratio is improved.
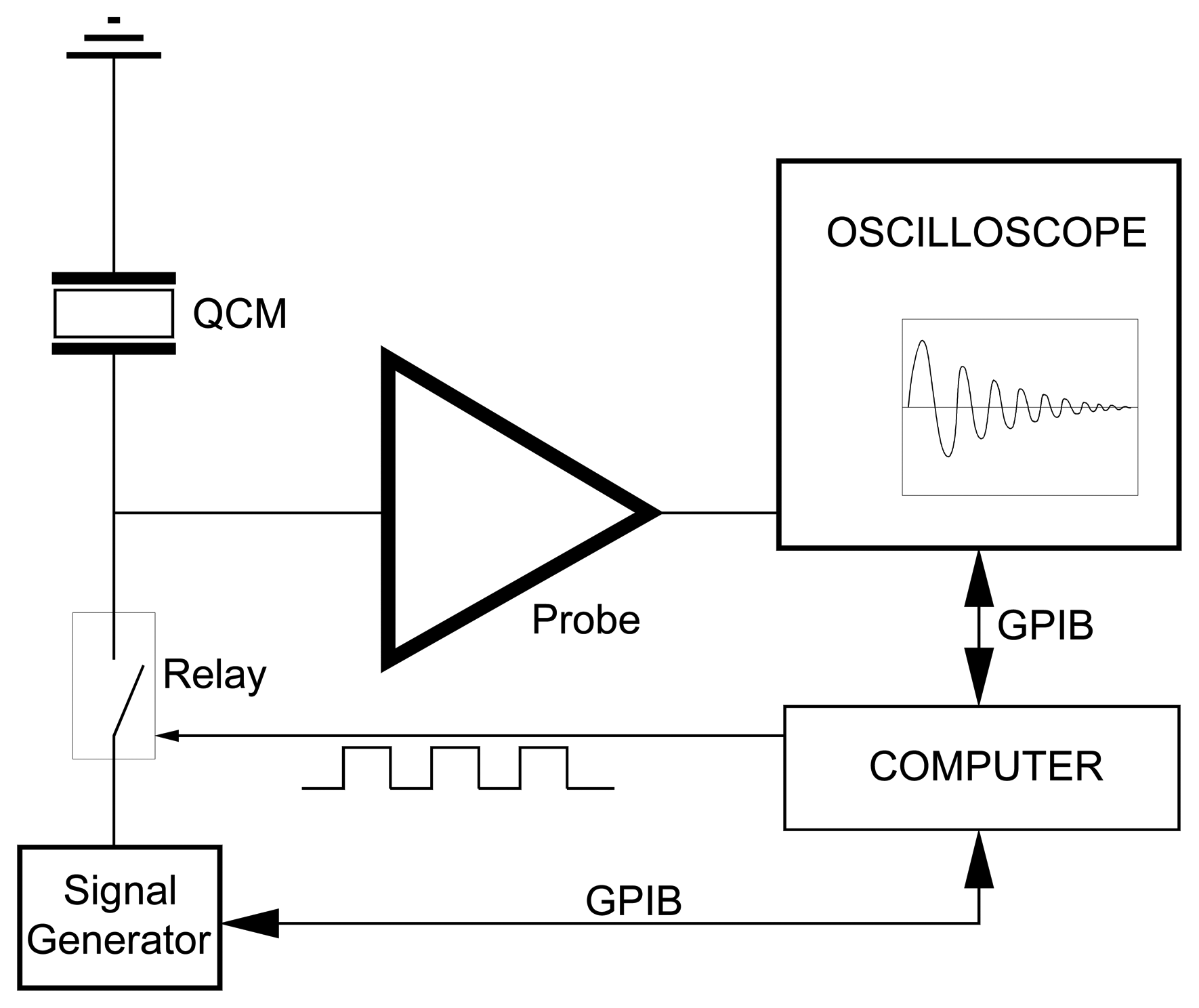
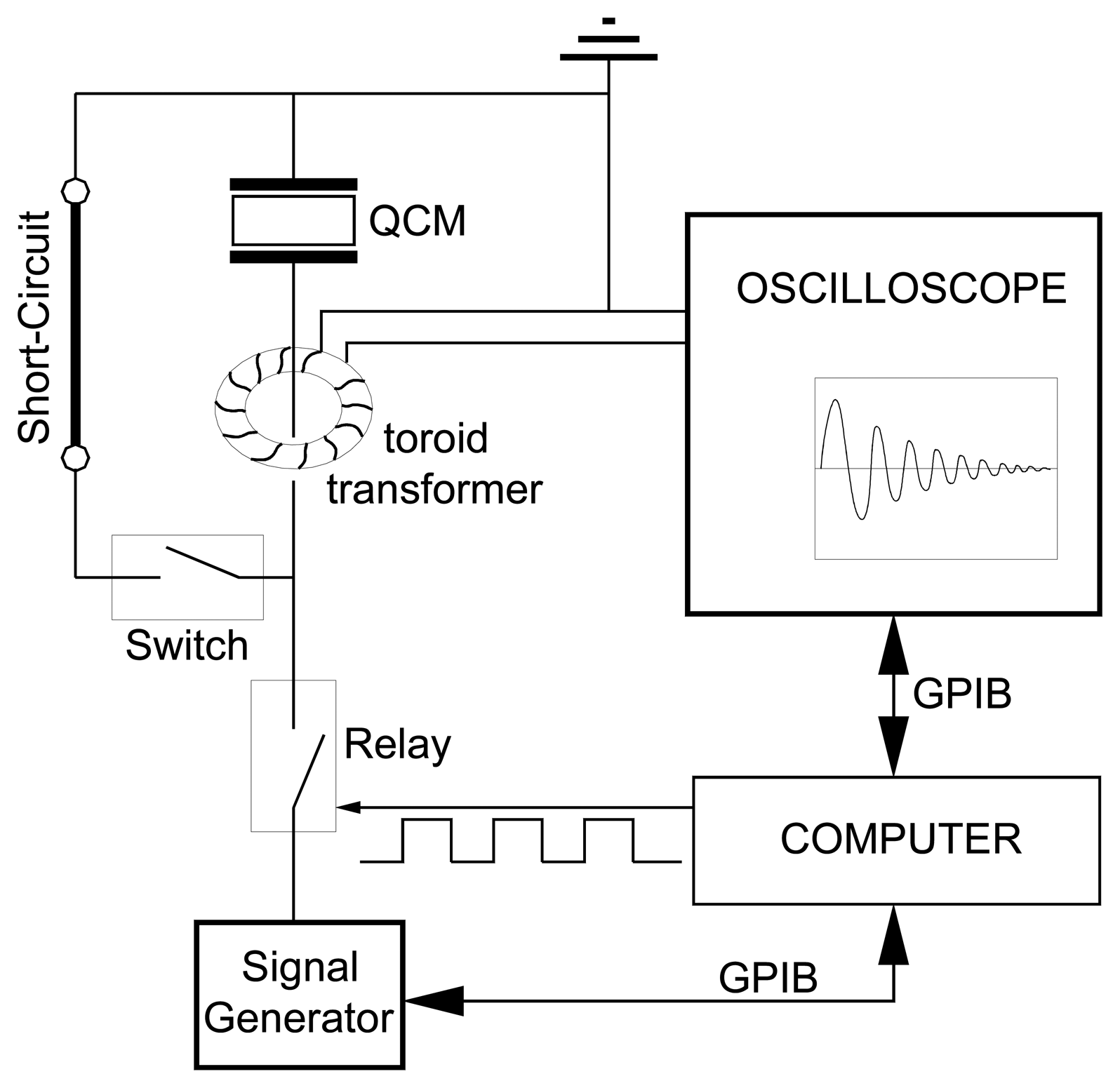
4.2 Decay Methods
4.3 Oscillators
4.3.1 Problem associated with the determination of the MSRF and the motional resistance
4.3.2 Oscillators for QCM Sensors. Overview
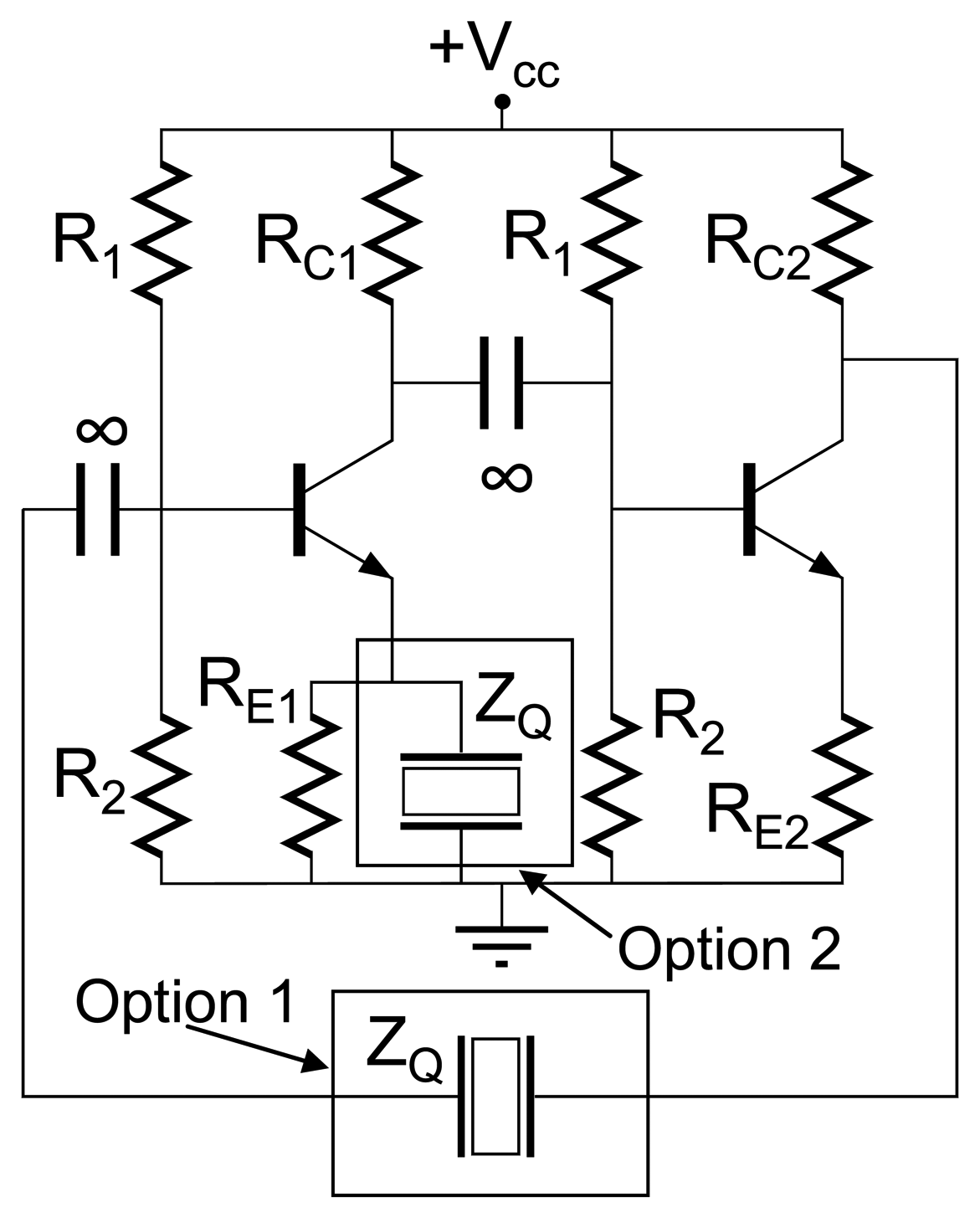
A. Emitter coupled crystal oscillator
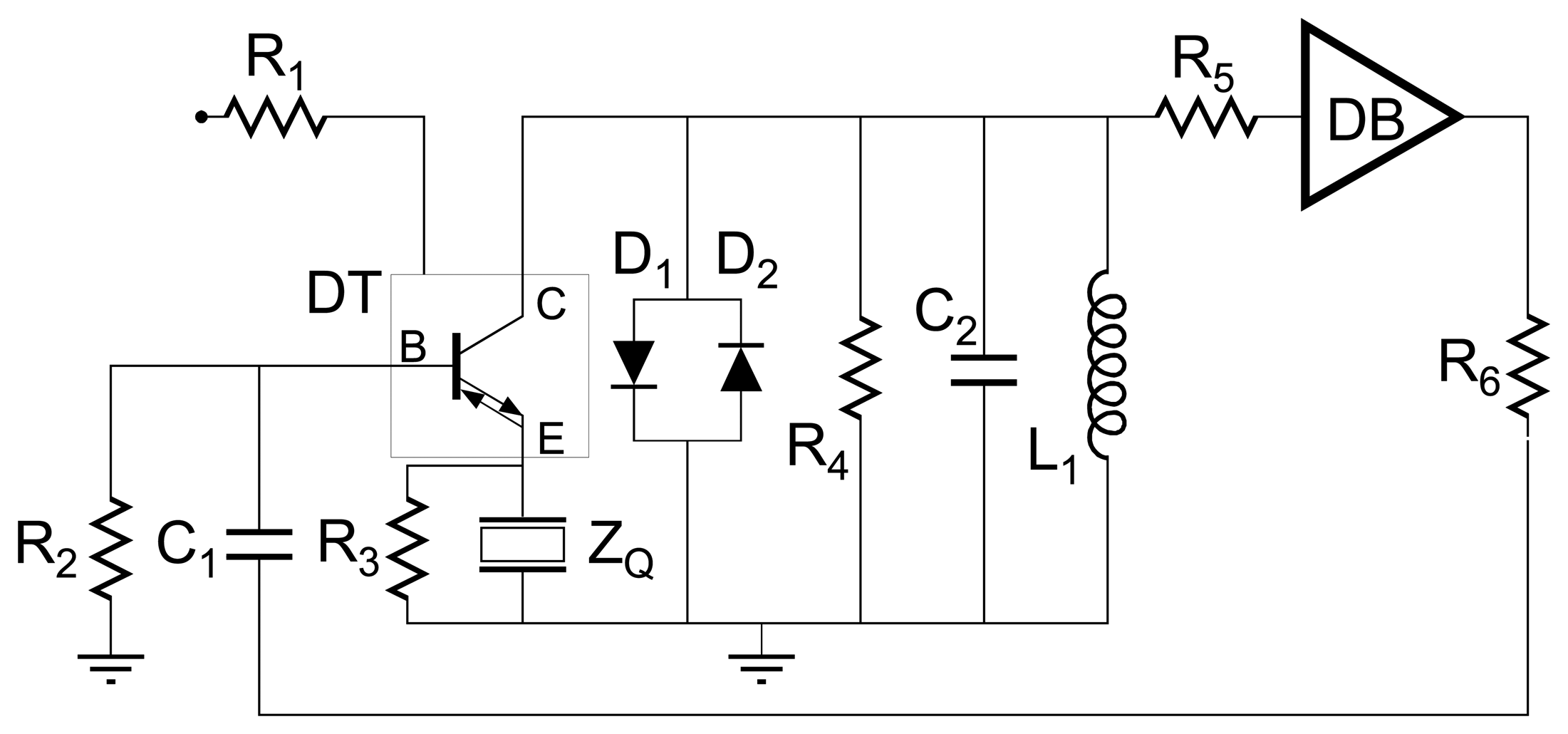
B. Bridge oscillators
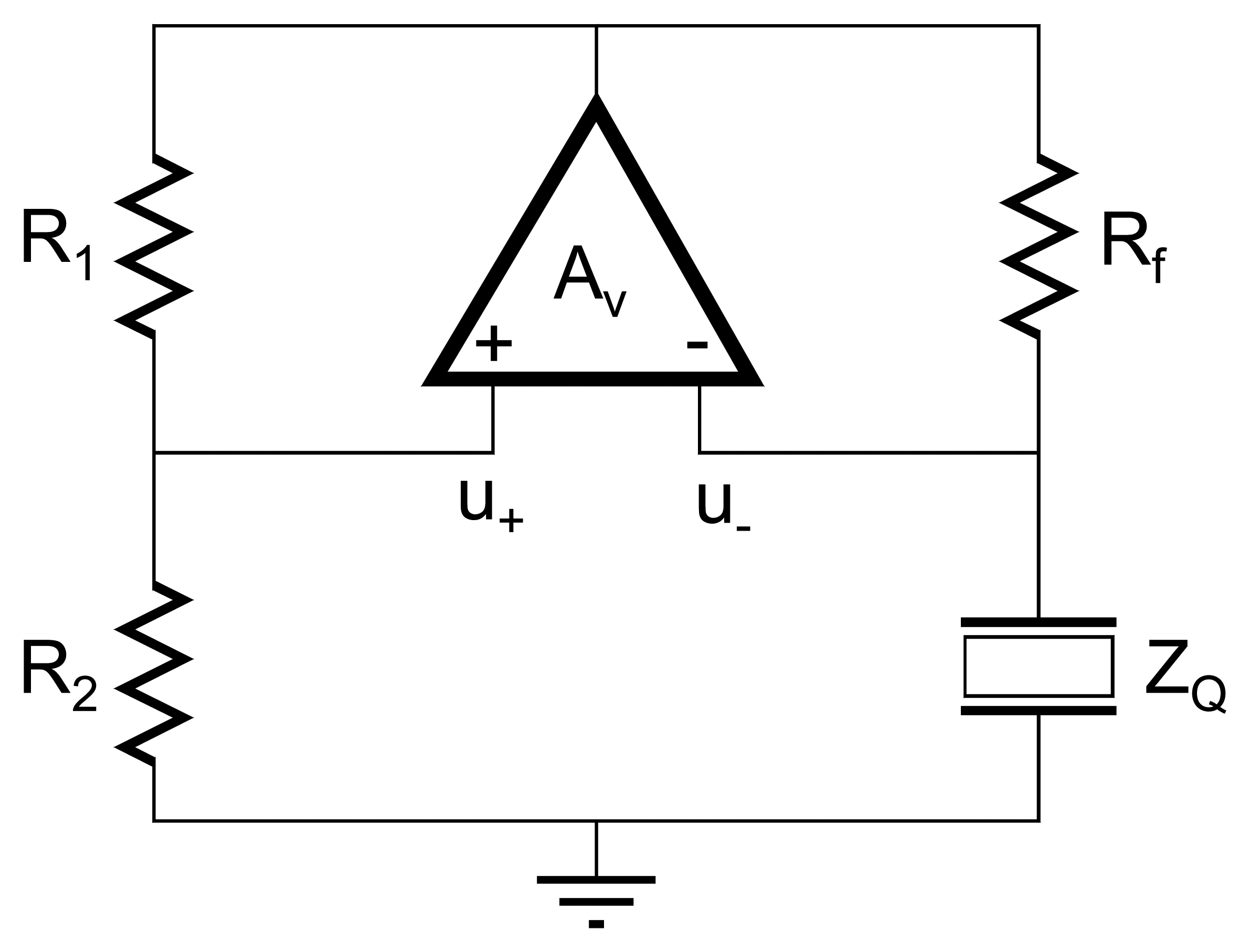
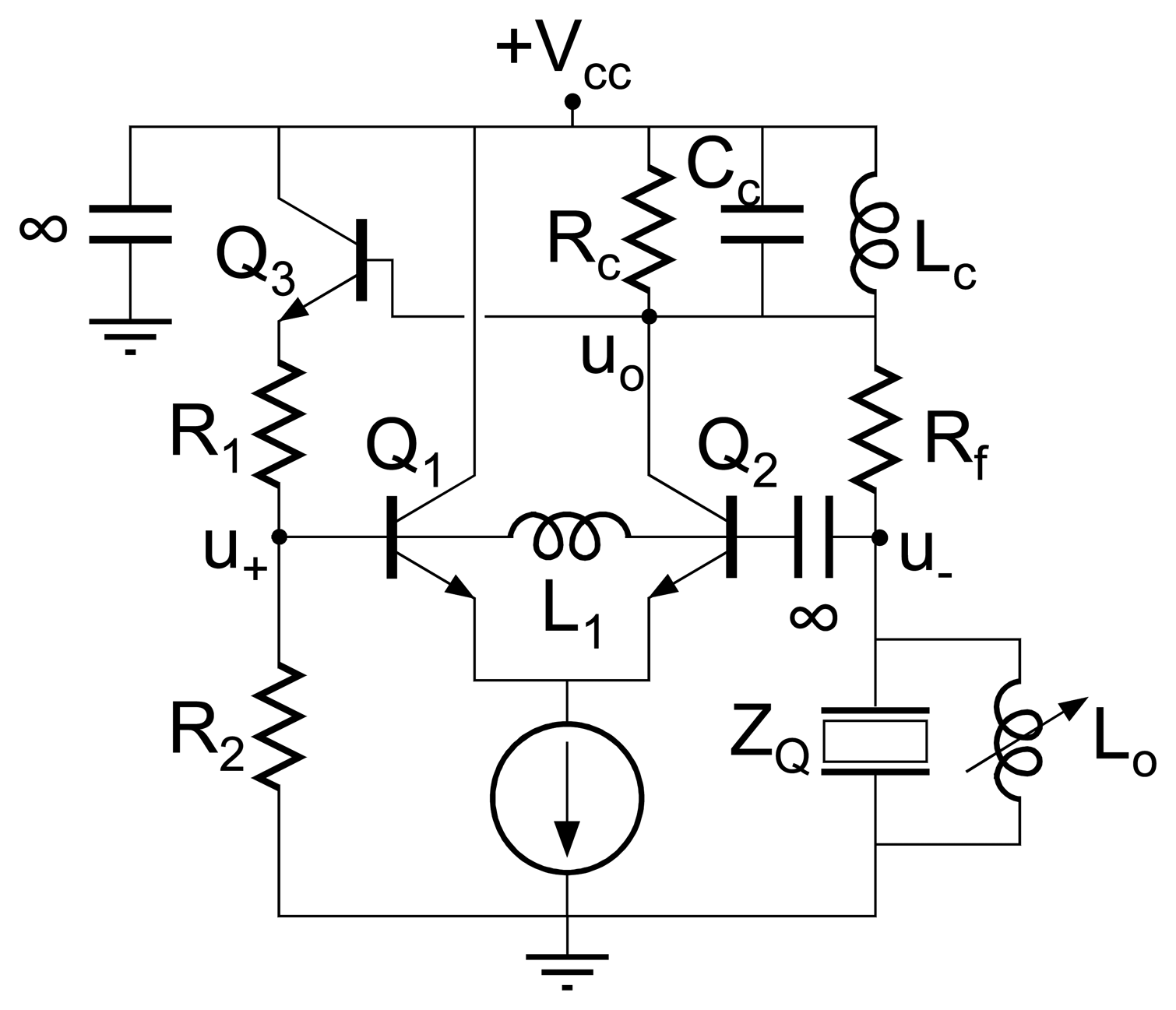
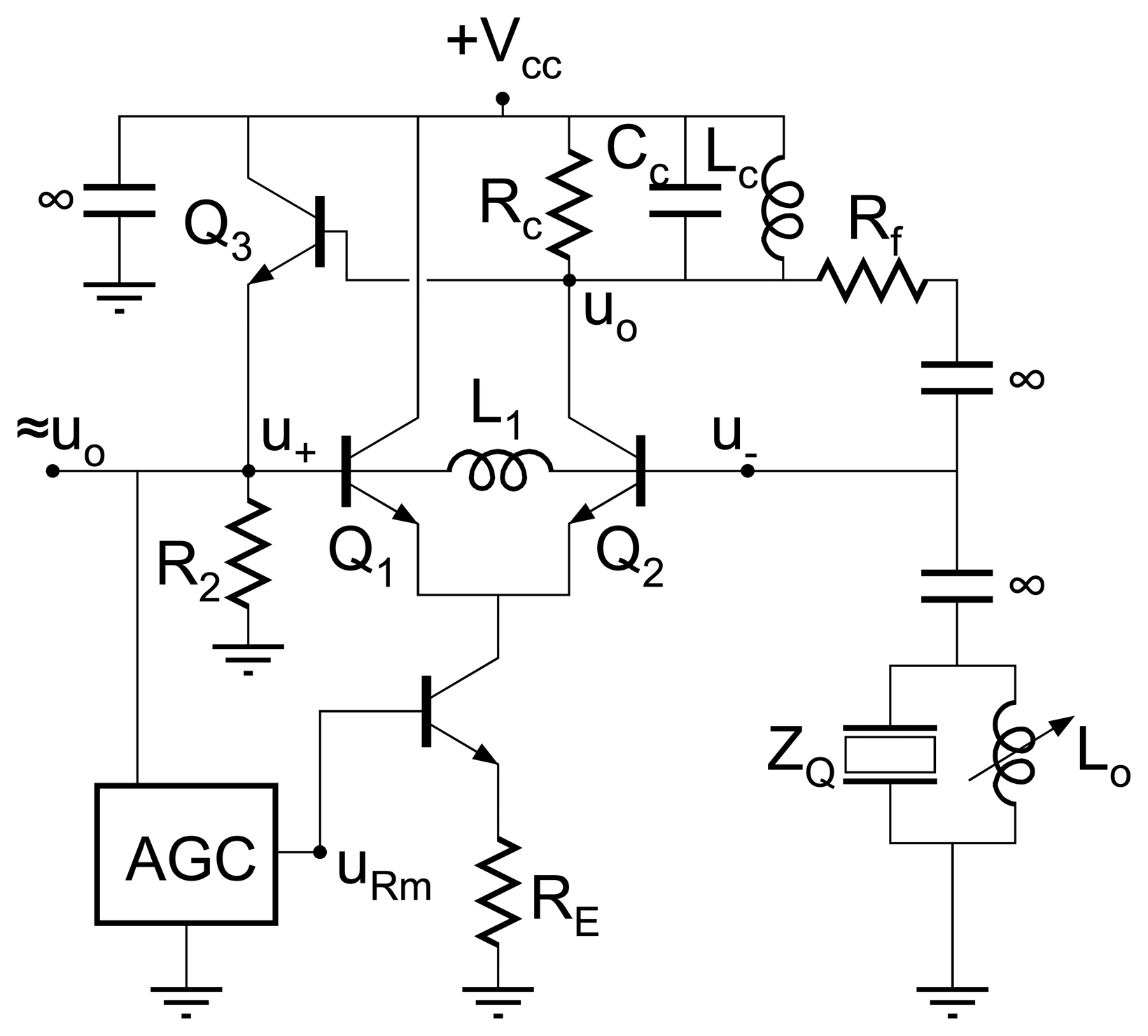
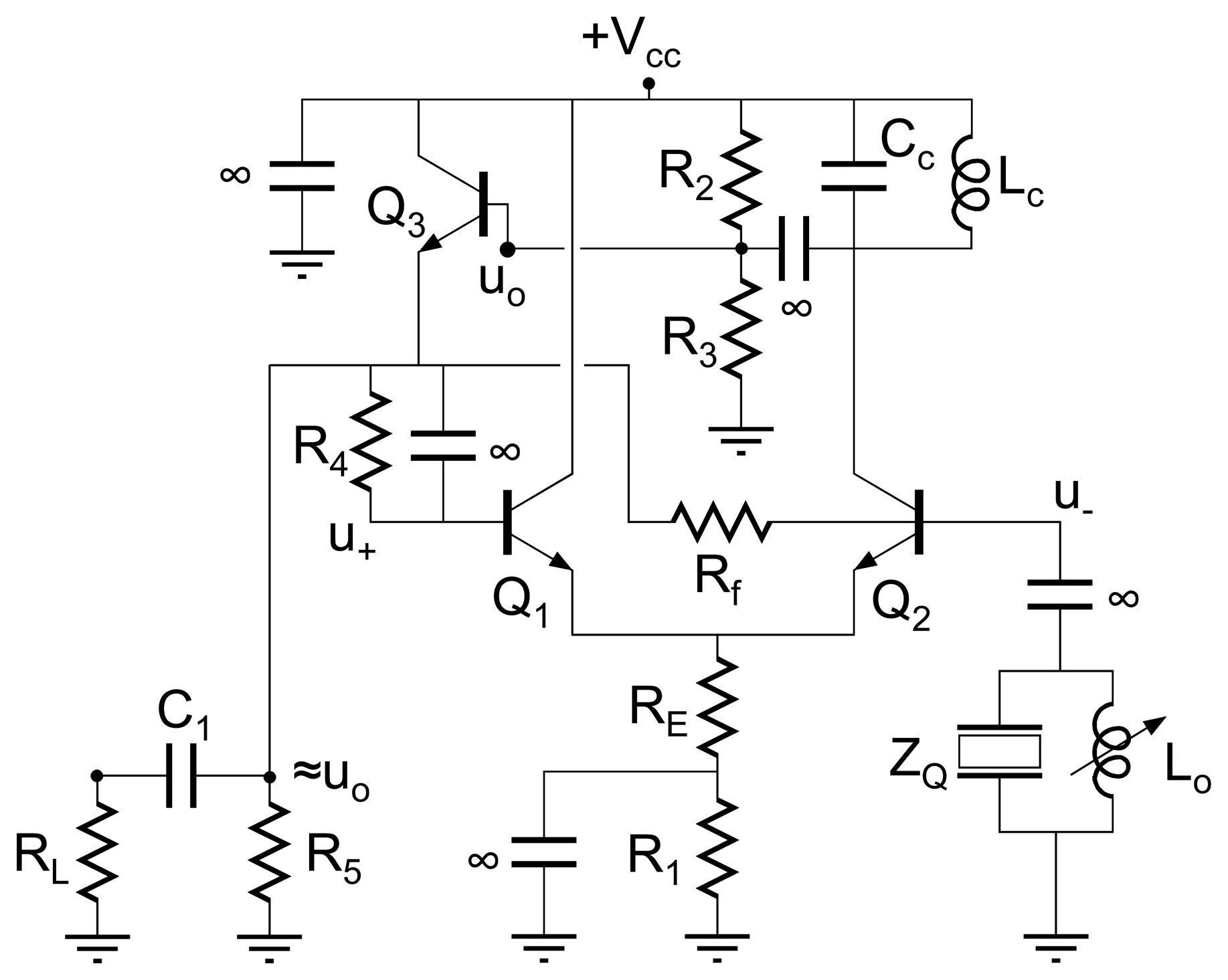
C. Balanced bridge oscillator
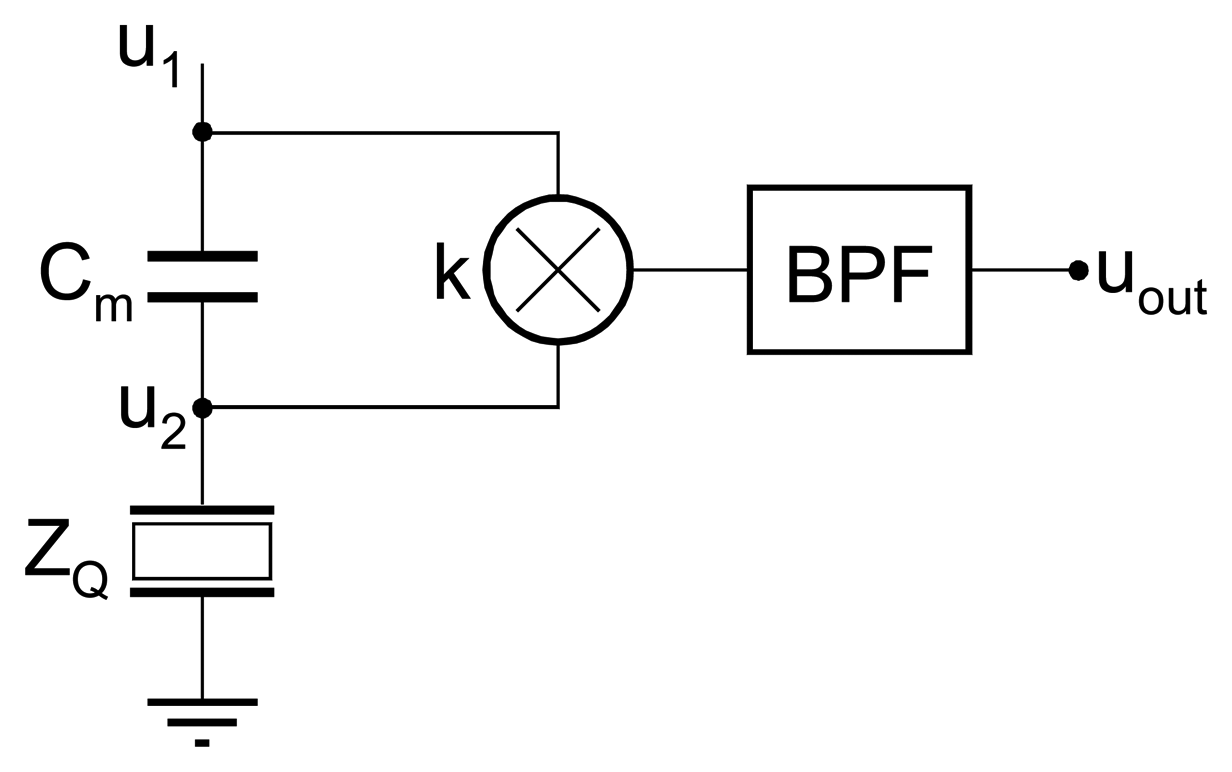
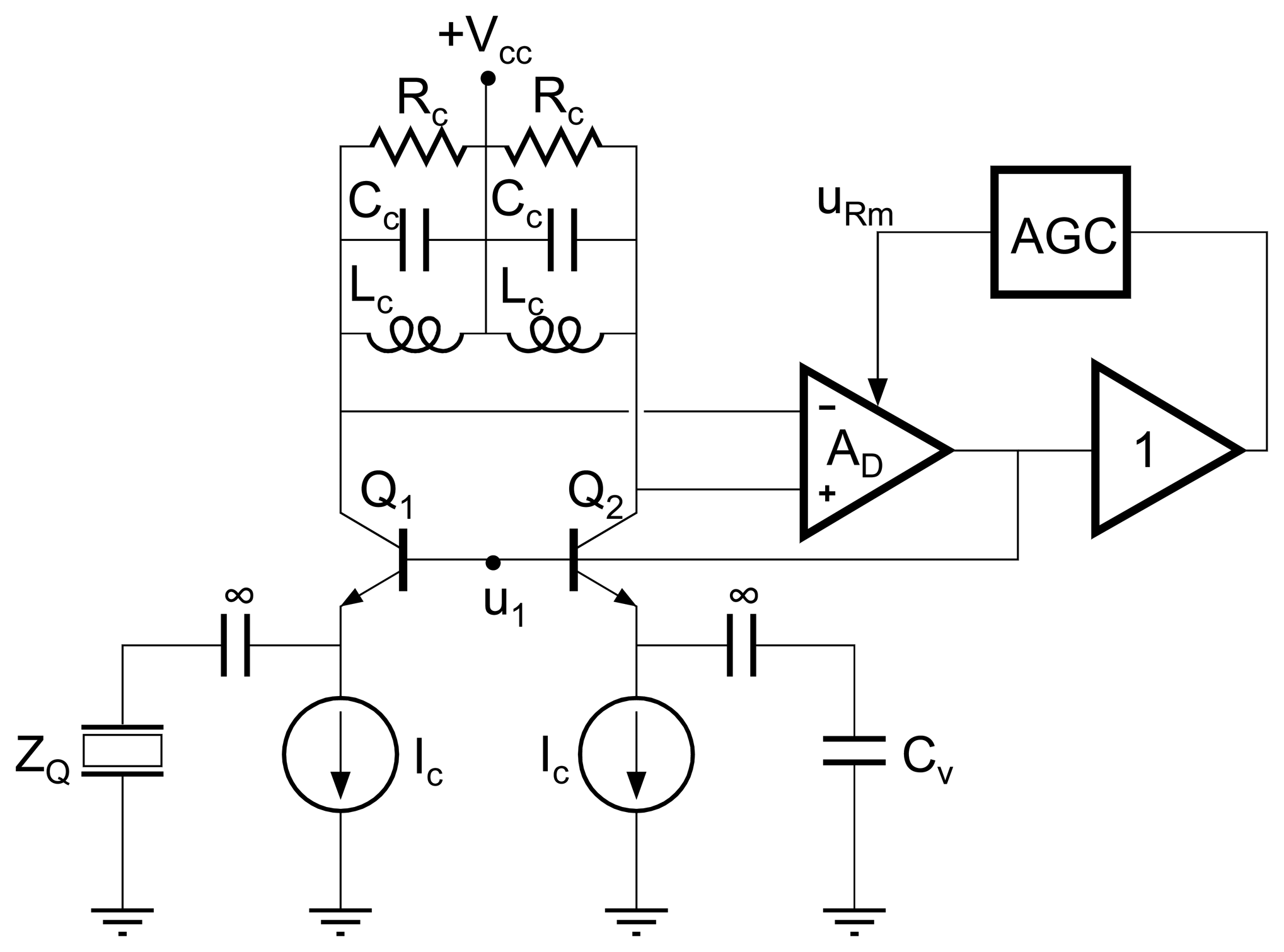
4.4 Lock-in Techniques
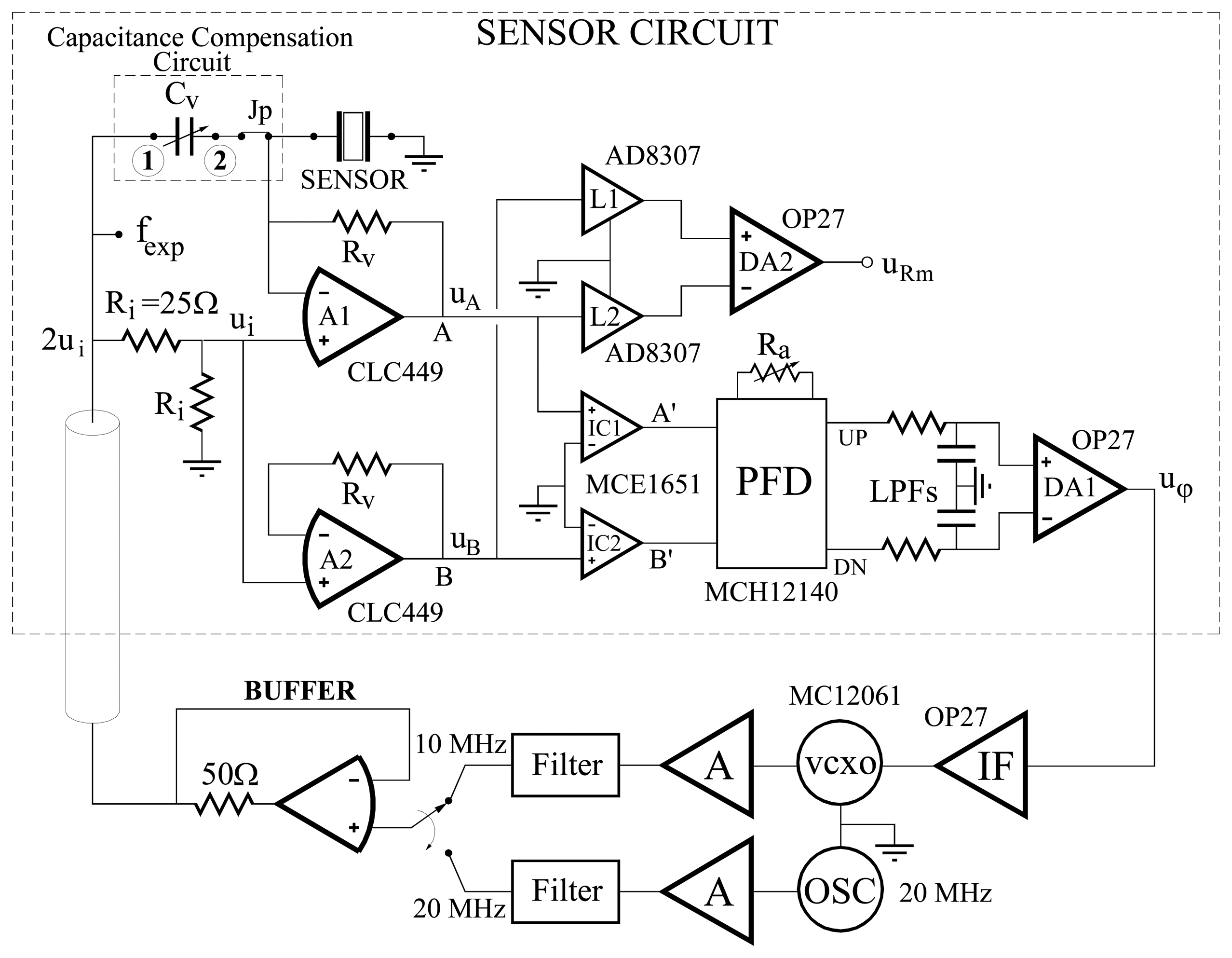
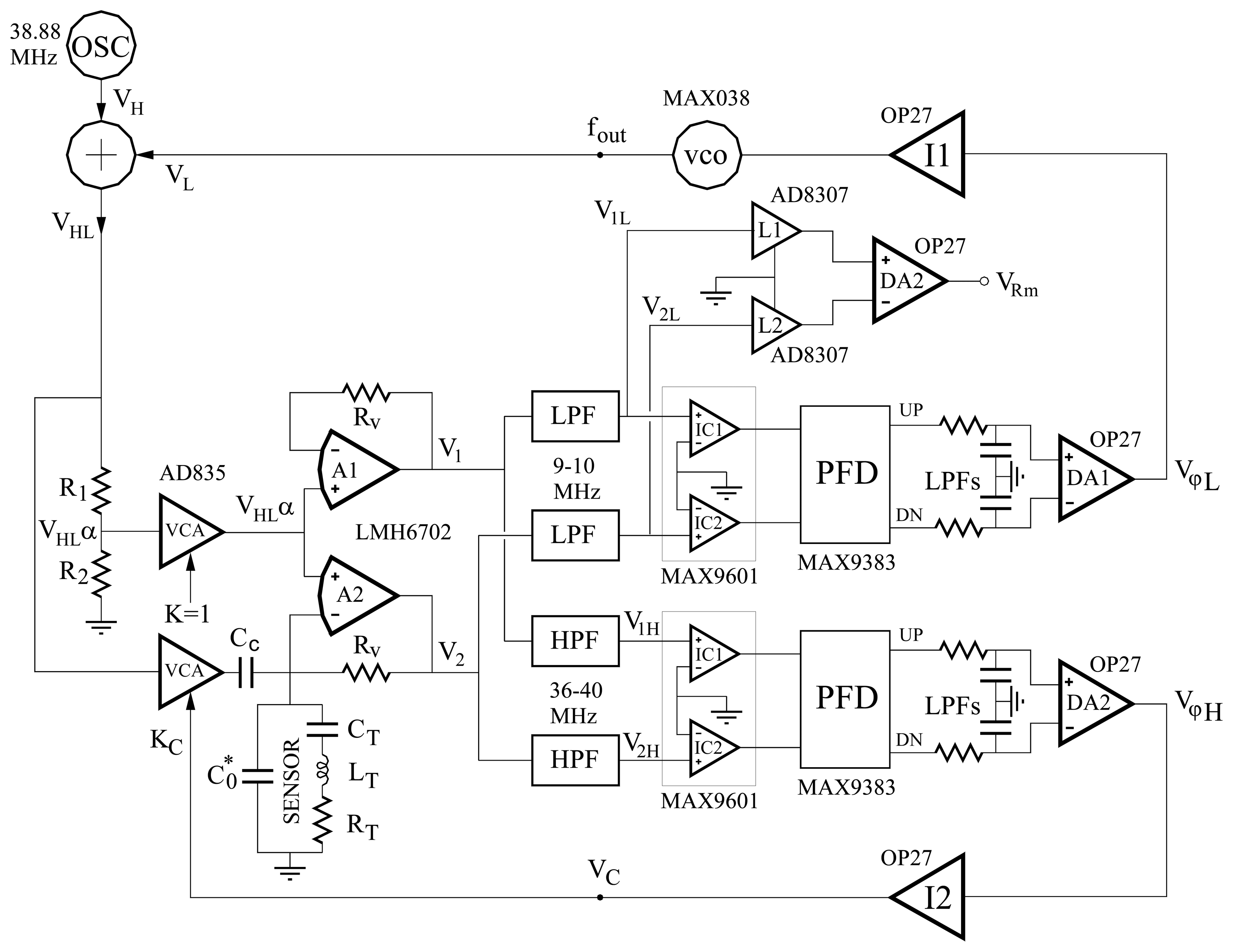
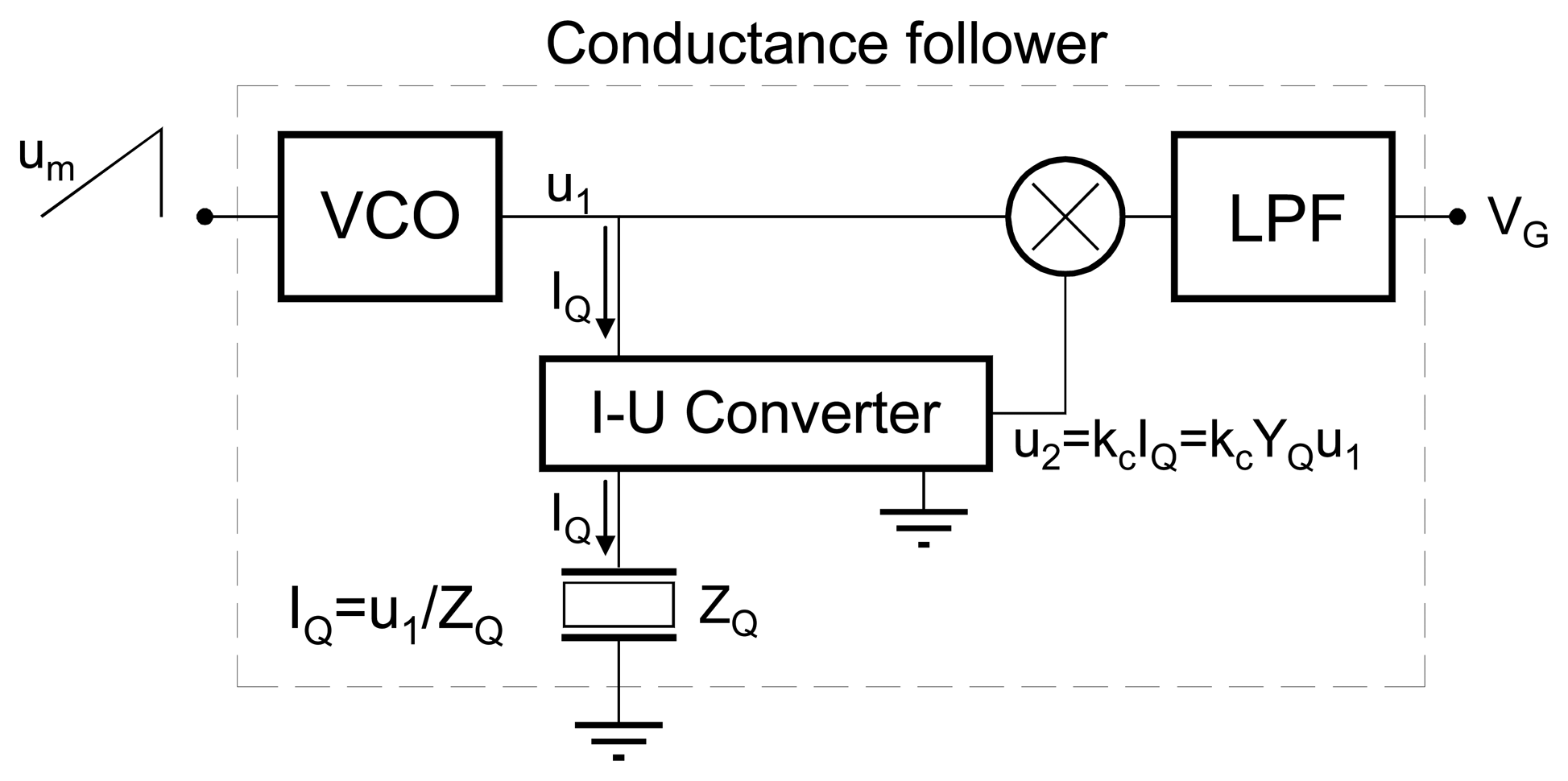
4.4.1 Phase-locked loop techniques with parallel capacitance compensation
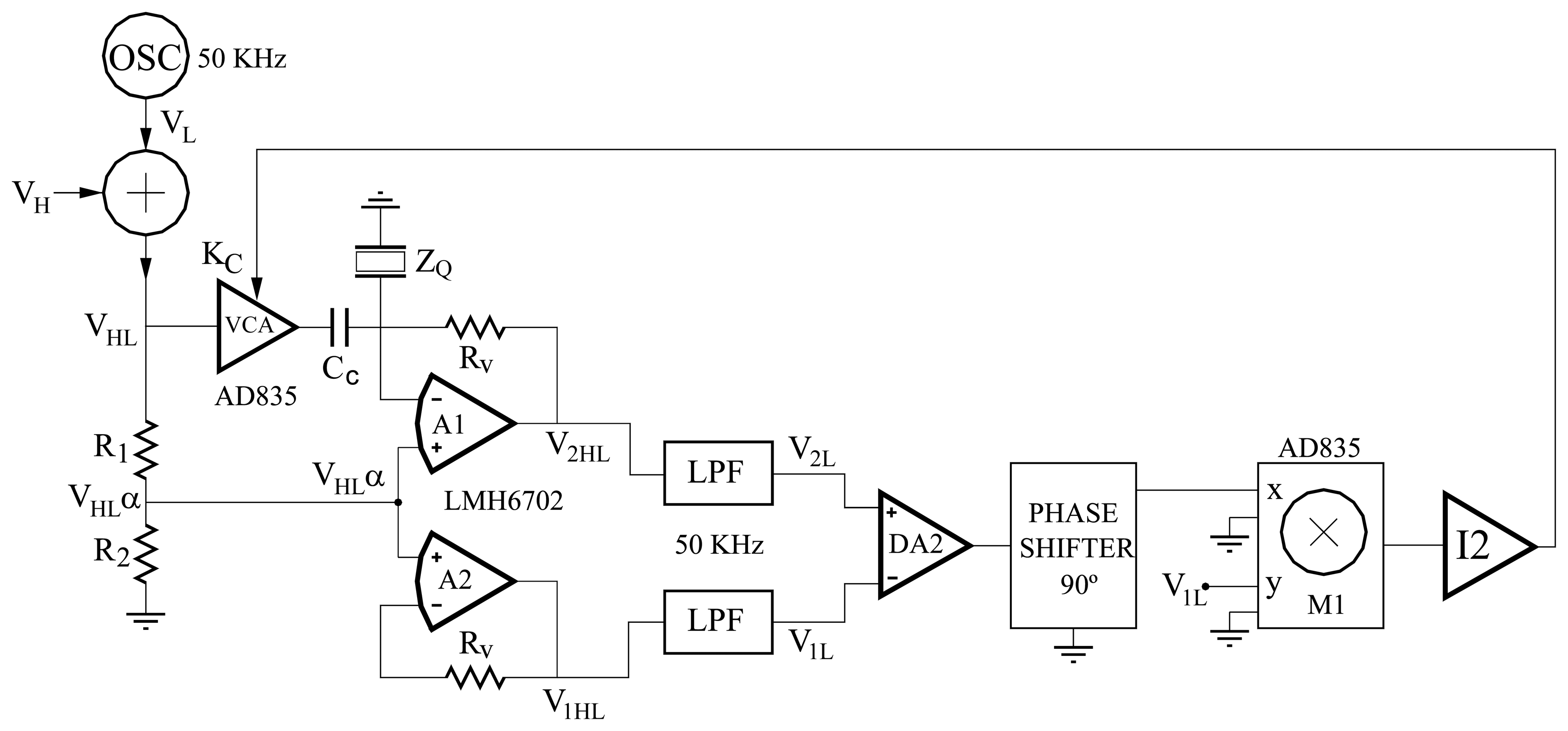
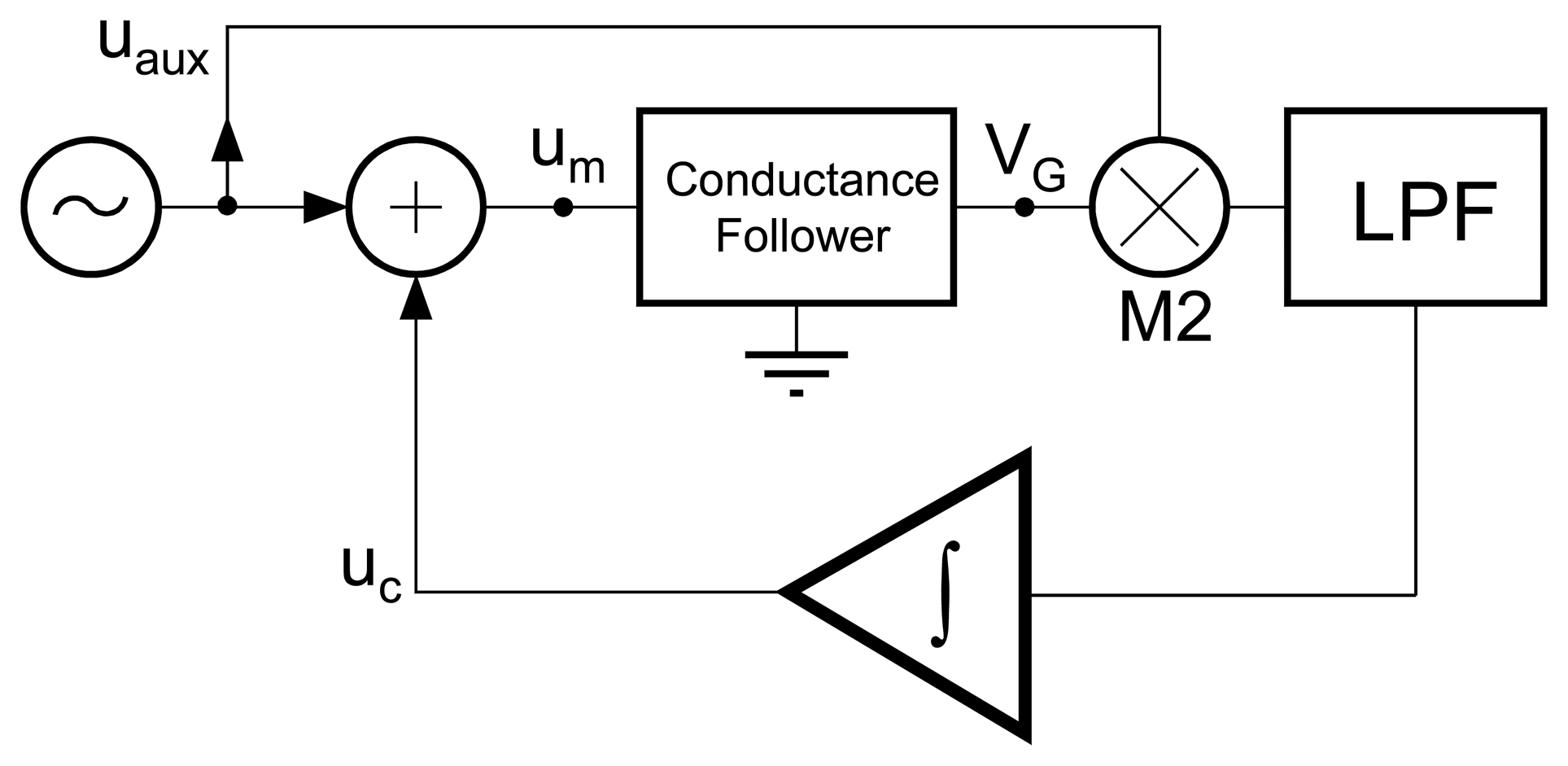
4.4.2 Lock-in Techniques at Maximum Conductance Frequency
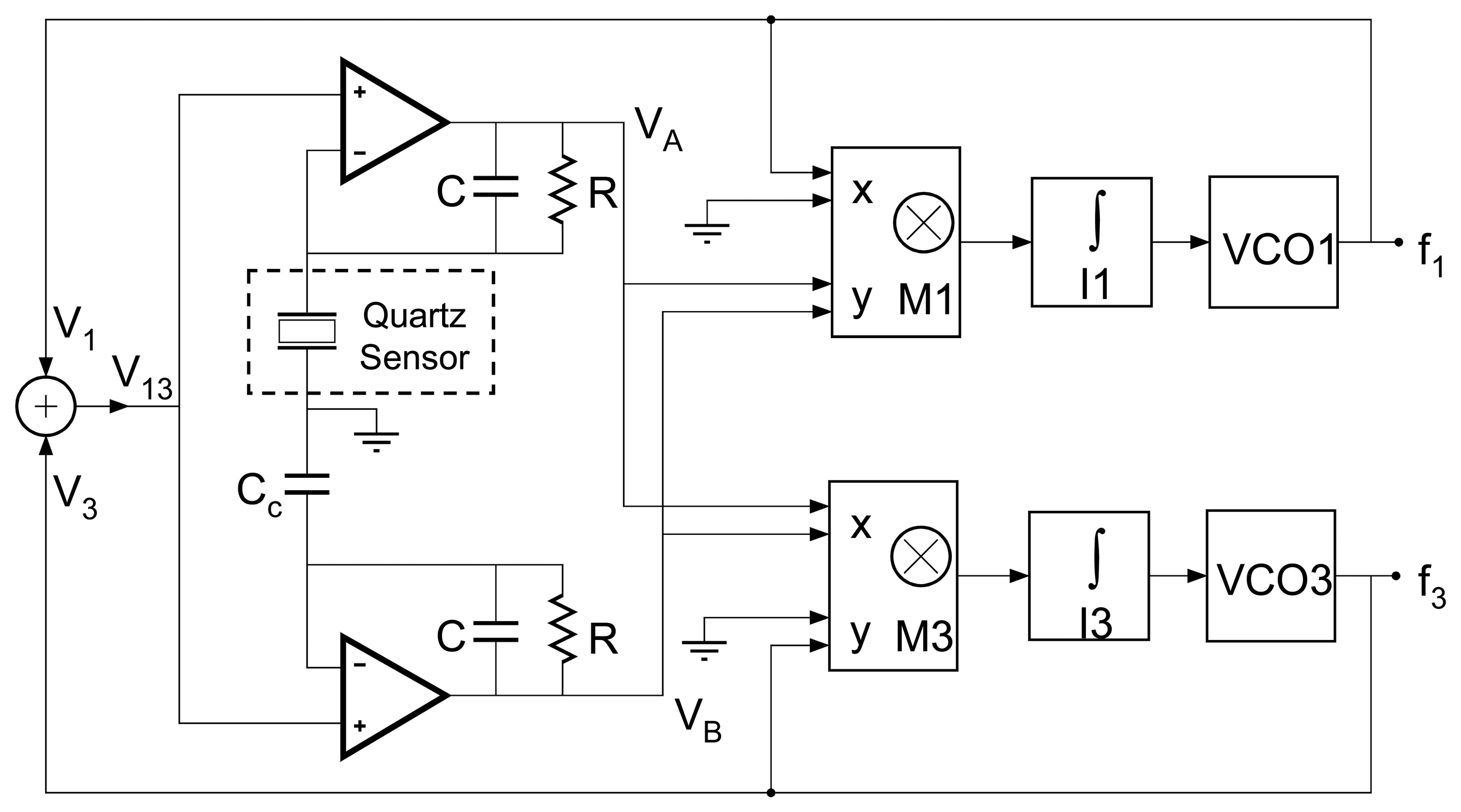
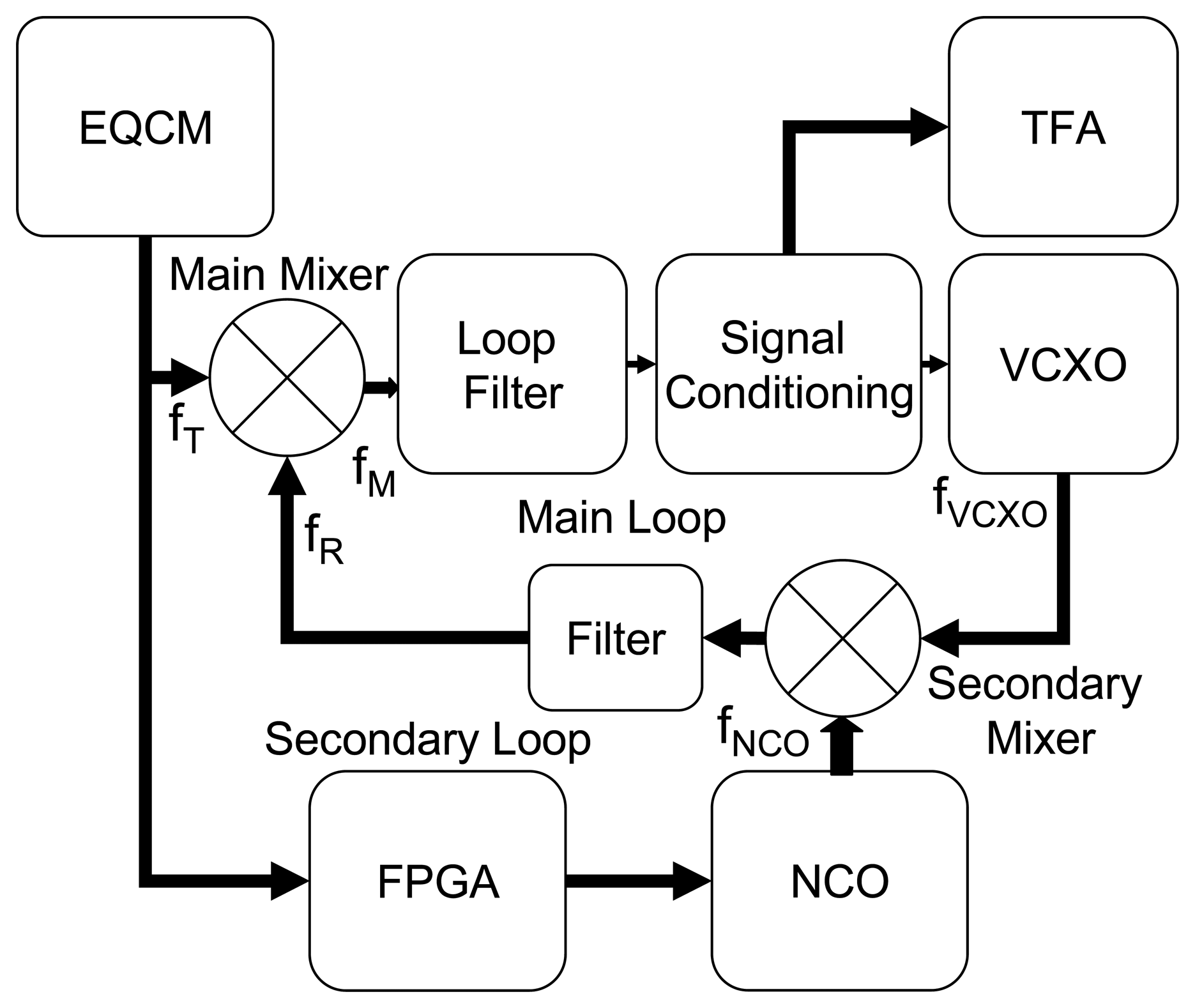
4.5 Interface Circuits for Fast QCM Applications
5. Conclusions
Acknowledgments
References and Notes
- Czanderna, A.W.; Lu, C. Applications of Piezoelectric Quartz Crystal Microbalances; Czanderna, A.W., Lu, C., Eds.; Elsevier: Amsterdam, 1984; Volume 7, pp. 1–393. [Google Scholar]
- Konash, P.L.; Bastiaans, G.J. Piezoelectric crystals as detectors for liquid chromatography. Analytical Chemistry 1980, 52, 1929–1931. [Google Scholar] [CrossRef]
- Kanazawa, K.K.; Gordon, J.G., II. The oscillation frequency of a quartz resonator in contact with a liquid. Analytica Chimica Acta 1985, 175, 99–105. [Google Scholar] [CrossRef]
- Reed, C.E.; Kanazawa, K.K.; Kaufman, J.H. Physical description of a viscoelastically loaded AT-cut quartz resonator. Journal of Applied Physics 1990, 68(5), 1993–2001. [Google Scholar] [CrossRef]
- Kurosawa, S.; Tawara, E. Oscillating frequency of piezoelectric quartz crystal in solutions. Analytica Chimica Acta 1990, 230(1), 41–49. [Google Scholar] [CrossRef]
- Schumacher, R. The quartz microbalance: a novel approach to the in-situ investigation of interfacial phenomena at the solid/liquid junction. Angew. Chem. Int. Ed. In English 1990, 29(4), 329–343. [Google Scholar] [CrossRef]
- Davis, K. A.; Leary, T.R. Continuous liquid-phase piezoelectric biosensor for kinetic immunoassays. Anal. Chem. 1989, 61, 1227–1230. [Google Scholar] [CrossRef]
- Shana, Z.A.; Radtke, D.E. Theory and applications of quartz resonator as a sensor for viscous-liquids. Analytica Chimica Acta 1990, 231(2), 317–320. [Google Scholar] [CrossRef]
- Behling, C.; Lucklum, R.; Hauptmann, P. Possibilities and limitations in quantitative determination of polymer shear parameters by TSM resonators. Sensors and Actuators A 1997, 61, 260–266. [Google Scholar]
- Behling, C.; Lucklum, R.; Hauptmann, P. The non-gravimetric quartz crystal resonator response and its application for polymer shear moduli determination. Meas. Sci. Technol. 1998, 9, 1886–1893. [Google Scholar] [CrossRef]
- Lucklum, R.; Behling, C.; Hauptmann, P. Role of mass accumulation and viscoelastic film properties for the response of acoustic-wave-based chemical sensors. Anal. Chem. 1999, 71, 2488–2496. [Google Scholar] [CrossRef]
- Jiménez, Y.; Otero, M.; Arnau, A. Piezoelectric Transducer and Applications, 2nd Ed.; Arnau, A., Ed.; 2008; Springer-VerlagBerlin: Heidelberg. [Google Scholar]
- Martin, S.J.; Granstaff, V. E.; Frye, G.C. Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Lee, S.W.; Hinsberg, W.D.; Kanazawa, K.K. Determination of the viscoelastic properties of polymer films using a compensated phase-locked oscillator circuit. Anal. Chem. 2002, 74(1), 125–131. [Google Scholar] [CrossRef]
- Arnau, A.; Jiménez, Y.; Sogorb, T. Thickness shear mode quartz crystal resonators in viscoelastic fluid media. J. Appl. Phys. 2000, 88, 4498–4506. [Google Scholar] [CrossRef]
- Gabrielli, C.; Perrot, H.; Rose, D.; Rubin, A.; Pham, M.C.; Piro, B. New frequency/voltage converters for ac-electrogravimetric measurements based on fast quartz crystal microbalance. Review Scientific Instruments 2007, 78, 6. [Google Scholar]
- Janshoff, A.; Galla, H.-J.; Steinem, C. Piezoelectric mass-sensing devices as biosensors-an alternative to optical biosensors? Angew. Chem. Int. Ed. 2000, 39, 4004–4032. [Google Scholar]
- A survey of the 2001 to 2005 quartz crystal microbalance biosensor literature: applications of acoustic physics to the analysis of biomolecular interactions. Journal of Molecular Recognition 2007, 20(3), 154–184. [CrossRef]
- Camesano, T.A.; Liu, Y.T.; Datta, M. Measuring bacterial adhesion at environmental interfaces with single-cell and single-molecule techniques. Advances in Water Resources 2007, 30, 1470–1491. [Google Scholar]
- Lazcka, O.; Del Campo, F.J.; Muñoz, F.X. Pathogen detection: A perspective of traditional methods and biosensors. Biosensors & Bioelectronics 2007, 22(7), 1205–1217. [Google Scholar] [CrossRef]
- Hug, T.S. Biophysical methods fro monitoring cell-substrate interactions in drug discovery. Assay and Drug Development Technologies 2003, 1(3), 479–488, PubMed 15090185. [Google Scholar]
- Dickert, FL.; Lieberzeit, P.; Hayden, O. Sensor strategies for micro-organism detection – from physical principles to imprinting procedures. Analytical and Bioanalytical Chemistry 2003, 377(3), 540–549. [Google Scholar] [CrossRef]
- Marx, KA. Quartz crystal microbalance: A useful tool for studying thin polymer films and complex biomolecular systems at the solution-surface interface. Biomacromolecules 2003, 4(5), 1099–1120. [Google Scholar] [CrossRef]
- Fahnrich, KA.; Pravda, M.; Guilbault, GG. Immunochemical detection of polycyclic aromatic hydrocarbons (PAHs). Analytical Letters 2002, 35(8), 1269–1300. [Google Scholar] [CrossRef]
- Wegener, J.; Janshoff, A.; Steinem, C. The quartz crystal microbalance as a novel means to study cell-substrate interactions in situ. Cell Biochemistry and Biophysics 2001, 34(1), 121–151. [Google Scholar] [CrossRef]
- O'Sullivan, CK.; Guilbault, G.G. Commercial quartz crystal microbalances – theory and applications. Biosensors & Bioelectronics 1999, 14, 663–670. [Google Scholar]
- O'Sullivan, CK.; Vaughan, R.; Guilbault, GG. Piezoelectric immunosensors – theory and applications. Analytical Letters 1999, 32(12), 2353–2377. [Google Scholar]
- Bizet, K.; Grabielli, C.; Perrot, H. Biosensors based on piezoelectric transducers. Analusis EurJAC 1999, 27, 609–616. [Google Scholar]
- Arnau, A.; Ferrari, V.; Soares, D.; Perrot, H. Piezoelectric Transducers and Applications, 2nd Ed.; Arnau, A., Ed.; 2008; Springer-Verlag: Berlin Heidelberg. [Google Scholar]
- Ni, R.; Zhang, XB.; Liu, W.; Shen, GL.; Yu, RQ. Piezoelectric quartz crystal sensor array with optimized oscillator circuit for analysis of organic vapours mixtures. Sensors and Actuators B 2003, 88, 198–204. [Google Scholar]
- Lucklum, R.; Soares, D.; Kanazawa, K.K. Piezoelectric Transducers and Applications, 2nd Ed.; Arnau, A., Ed.; Springer-Verlag: Berlin-Heidelberg, 2008; Chapter 3; p. 63, in press. [Google Scholar]
- Arnau, A.; Jiménez, Y.; Sogorb, T. An extended Butterworth-Van Dyke model for QCM applications in viscoelastic fluid media. IEEE Trans. Ultrason, Ferroelect. Freq. Contr. 2001, 48, 1367–1382. [Google Scholar] [CrossRef]
- Barnes, C. Development of quartz crystal-oscillators for under liquid sensing. Sensors and Actuators A-Physical 1991, 29(1), 59–69. [Google Scholar] [CrossRef]
- IEC Standard, publication 444-1. Measurement of quartz crystal unit parameters by zero phase technique in a pi-network (Part 1). International Electrotechnical Commission 1986. [Google Scholar]
- Arnau, A.; Sogorb, T.; Jiménez, Y. A new method for continuous monitoring of series resonance frequency and simple determination of motional impedance parameters for loaded quartz crystal resonators. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2001, 48, 617–623. [Google Scholar]
- Cady, W.G. Piezoelectricity: an introduction to the theory and applications of electromechanical phenomena in crystals; Dover Publication, Inc.: New York, 1964. [Google Scholar]
- Buttry, D.A.; Ward, D.W. Measurements of interfacial processes at electrode surfaces with the electrochemical quartz crystal microbalance. Chem. Rev. 1992, 92(6), 1355–1379. [Google Scholar] [CrossRef]
- Jiménez, Y.; Fernández, R.; Torres, R.; Arnau, A. A contribution to solve the problem of coating properties extraction in quartz crystal microbalance applications. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2006, 53(5), 1057–1072. [Google Scholar] [CrossRef]
- Zhang, C.; Vetelino, J.F. Bulk acoustic wave sensors for sensing measurand-induced electrical property changes in solutions. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2001, 48(3), 773–778. [Google Scholar] [CrossRef]
- Ferrari, V.; Lucklum, R. Piezoelectric Transducers and Applications, 2nd Ed.; Arnau, A., Ed.; Springer-Verlag: Berlin-Heidelberg, 2008; Chapter 2; p. 39, in press. [Google Scholar]
- Lucklum, R.; Hauptmann, P. Determination of polymer shear modulus with quartz crystal resonators. Faraday Discussions 1997, 107, 123–140. [Google Scholar] [CrossRef]
- Montoya, A.; Ocampo, A.; March, C. Piezoelectric Transducers and Applications, 2nd Ed.; Arnau, A., Ed.; Springer-Verlag: Berlin-Heidelberg, 2008; Chapter 12; p. 289, in press. [Google Scholar]
- Cernosek, R. W.; Martin, S. J.; Hillman, A. R.; Bandey, H.L. Comparison of lumped-element and transmission-line models for thickness-shear-mode quartz resonator sensors. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 1998, 45, 1399–1407. [Google Scholar] [CrossRef]
- Johannsmann, D.; Mathauer, K. Viscoelastic properties of thin films probed with a quartz crystal resonator. Physical Review B 1992, 46(12), 7808–7815. [Google Scholar] [CrossRef]
- Yang, M.; Thompson, M. Interfacial properties and the response of the Thickness-Shear-Mode acoustic wave sensor in Liquids. Langmuir 1993, 9, 802–811. [Google Scholar] [CrossRef]
- Yang, M.; Thompson, M. Acoustic network analysis and equivalent circuit simulation of the Thickness-Shear-Mode acoustic wave sensor in liquid phase. Analytica Chimica Acta 1993, 282, 505–515. [Google Scholar] [CrossRef]
- Noël, M.; Topart, P.A. High frequency impedance analysis of quartz microbalances I. General considerations. Analytical Chemistry 1994, 66(4), 484–491. [Google Scholar]
- Eichelbaum, F.; Borngräber, R.; Schröder, J.; Lucklum, R.; Hauptmann, P. Interface circuits for quartz crystal microbalance sensors. Rev. Sci. Instrum. 1999, 70, 2537–2545. [Google Scholar] [CrossRef]
- Schmid, M.; Benes, E.; Sedlaczek, R. A computer-controlled system for the measurement of complete admittance spectra of piezoelectric resonators. Meas. Sci. Technol. 1990, 1, 970–975. [Google Scholar]
- Schröder, J.; Borngräber, R.; Lucklum, R.; Hauptmann, P. Network analysis based interface electronics for quartz crystal microbalance. Review Scientific Instruments 2001, 72, 2750–2755. [Google Scholar]
- Schröder, J.; Borngräber, R.; Eichelbaum, F.; Hauptmann, P. Advanced interface electronics and methods for QCM. Sensors and Actuators A 2002, 97-98, 543–547. [Google Scholar]
- Auge, J.; Dierks, K.; Eichelbaum, F.; Hauptmann, P. High-speed multi-parameter data acquisition and web-based remote access to resonant sensors and sensor arrays. Sensors and Actuators B 2003, 95, 32–38. [Google Scholar]
- Doerner, S.; Schneider, T.; Schröder, J.; Hauptmann, P. Universal impedance spectrum analyzer for sensor applications. Proceedings of IEEE Sensors 2003, 1, 596–594. [Google Scholar]
- Schnitzer, R.; Reiter, C.; Harms, KC.; Benes, E.; Gröschl, M. A general-purpose online measurement system for resonant BAW sensors. IEEE Sensors Journal 2006, 6(5), 1314–1322. [Google Scholar] [CrossRef]
- Torres, R.; Arnau, A.; Perrot, H.; García, J.; Grabielli, C. Analog-Digital Phase-Locked Loop for alternating current quartz electrogravimetry. Electronics Letters 2006, 42, 1272–1273. [Google Scholar]
- Kurosawa, S.; Kitajima, H.; Ogawa, Y.; Muratsugu, M.; Nemoto, E.; Kamo, N. Resonant Frequency of a Piezoelectric Quartz Crystal in Contact with Solutions. Analytica Chimica Acta 1993, 274, 209–217. [Google Scholar] [CrossRef]
- Calvo, E.J.; Etchenique, R.; Barlett, P.N.; Singhal, K.; Santamaría, C. Quartz crystal impedance studies at 10 MHz of viscoelastic liquids and films. Faraday Discuss 1997, 107, 141–157. [Google Scholar] [CrossRef]
- Kankare, J.; Loikas, K.; Salomaki, M. Method for measuring the losses and loading of a quartz crystal microbalance. Analytical Chemistry 2006, 78, 1875–1882. [Google Scholar] [CrossRef]
- Rodahl, M.; Kasemo, B. A simple setup to simultaneously measure the resonant frequency and the absolute dissipation factor of a quartz crystal microbalance. Rev. Sci. Instrum. 1996, 67, 3238–3241. [Google Scholar] [CrossRef]
- Rodahl, M.; Kasemo, B. Frequency and dissipation-factor responses to localized liquid deposits on a QCM electrode. Sensors and Actuators B 1996, 37, 111–116. [Google Scholar] [CrossRef]
- Rodahl, M.; Hook, F.; Kasemo, B. QCM operation in liquids: An explanation of measured variations in frequency and Q factor with liquid conductivity. Anal. Chem. 1996, 68, 2219–2227. [Google Scholar] [CrossRef]
- Edwardsson, M.; Rodalh, M.; Kasemo, B.; Hook, F. A dual-frequency QCM-D setup operating at elevated oscillation amplitudes. Anal. Chem. 2006, 77, 4918–4926. [Google Scholar] [CrossRef]
- Parzen, B.; Ballato, A. Design of crystal and other harmonic oscillators; John Wiley & Sons: New York, 1983; p. 454. [Google Scholar]
- Frerking, M.E. Crystal oscillator design and temperature compensation; Van Nostrand Reinhold: New York, 1978; p. 240. [Google Scholar]
- Ehahoun, H.; Gabrielli, C.; Keddam, M.; Perrot, H.; Rousseau, P. Performances and limits of a parallel oscillator for electrochemical quartz crystal microbalances. Anal Chem. 2002, 74, 1119–1127. [Google Scholar] [CrossRef]
- Barnes, C. Some new concepts on factors influencing the operational frequency of liquid-immersed quartz microbalances. Sensors and Actuators A-Physical 1992, 30(3), 197–202. [Google Scholar] [CrossRef]
- Tiean, Z.; Nie, L.H. On equivalent-circuits of piezoelectric quartz crystals in a liquid and liquid properties I. Theoretical derivation of equivalent-circuit and effects of density and viscosity of liquids. Journal of Electroanalytical Chemistry 1990, 293, 1–18. [Google Scholar]
- Auge, J.; Hauptmann, P.; Eichelbaum, F.; Rösler, S. Quartz crystal microbalance sensor in liquids. Sensor and Actuators B 1994, 18-19, 518–522. [Google Scholar]
- Bottom, V.E. Introduction to Quartz Crystal Unit Design; Van Nostrand: New York, 1982. [Google Scholar]
- Hayward, G. Viscous interaction with oscillating piezoelectric quartz crystals. Analytica Chimica Acta 1992, 264(1), 23–30. [Google Scholar] [CrossRef]
- Hayward, G.; Chu, G.Z. Simultaneous measurement of mass and viscosity using piezoelectric quartz crystals in liquid-media. Analytica Chimica Acta 1994, 288(3), 179–185. [Google Scholar] [CrossRef]
- Wessendorf, K.O. The lever oscillator for use in high resistance resonator applications. Proceedings of the 1993 IEEE International Frequency Control Symposium 1993, 711–717. [Google Scholar]
- Chagnard, C.; Gilbert, P.; Watkins, A. N.; Beeler, T.; Paul, D.W. An electronic oscillator with automatic gain control: EQCM applications. Sensors and Actuators B 1996, 32, 129–136. [Google Scholar] [CrossRef]
- Paul, D.W.; Beeler, T.L. Piezoelectric sensor Q-loss compensation. US Patent No. 4788466, 1998. [Google Scholar]
- Borngräber, R.; Schröder, J.; Lucklum, R.; Hauptmann, P. Is an oscillator-based measurement adequate in a liquid environment? IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2002, 49(9), 1254–1259. [Google Scholar] [CrossRef]
- Martin, S. J.; Spates, J. J.; Wessendorf, K. O.; Schneider, T. W.; Huber, R. J. Resonator/oscillator response to liquid loading. Anal. Chem. 1997, 69, 2050–2054. [Google Scholar] [CrossRef]
- Arnau, A.; Sogorb, T.; Jiménez, Y. Circuit for continuous motional series resonant frequency and motional resistance monitoring of quartz crystal resonators by parallel capacitance compensation. Rev. Sci. Instrum. 2002, 73(7), 2724–2737. [Google Scholar] [CrossRef]
- Rodriguez-Pardo, L.; Fariña, J.; Gabrielli, C.; Perrot, H.; Brendel, R. Resolution in quartz oscillator circuits for high sensitivity microbalance sensors in damping media. Sensors and Actuators B 2004, 103, 318–324. [Google Scholar] [CrossRef]
- Rodriguez-Pardo, L.; Fariña, J.; Gabrielli, C.; Perrot, H.; Brendel, R. Sensitivity, noise, and resolution in QCM sensors in liquid media. IEEE Sensors Journal 2005, 5(6), 1251–1257. [Google Scholar] [CrossRef]
- Rodriguez-Pardo, L.; Fariña, J.; Gabrielli, C.; Perrot, H.; Brendel, R. Quartz crystal oscillator circuit for high resolution microgravimetric sensors. Electronics Letters 2006, 42(18), 1065–1067. [Google Scholar] [CrossRef]
- Soares, D. A quartz microbalance with the capability of viscoelasticity measurements for in-situ electrochemical investigations. Meas. Sci. Technol. 1993, 4, 549–553. [Google Scholar]
- Fruböse, C.; Doblhofer, K.; Soares, D. Impedance analysis of the quartz micro-balance signal. Ber. Bunsenges. Phys. Chem. 1993, 97, 475–478. [Google Scholar]
- Wessendorf, K.O. Oscillator circuit for use with high loss quartz resonator sensors. US Patent No. 5416448, 1995. [Google Scholar]
- Wessendorf, K.O. The active bridge oscillator. Proceeding of IEEE International Frequency Control Symposium 1998, 361–369. [Google Scholar]
- Wessendorf, K.O. The active-bridge oscillator for use with liquid loaded QCM sensors. Proceedings of IEEE International Frequency Control Symposium and PDA Exhibition 2001, 400–407. [Google Scholar]
- Benes, E.; Gröschl, M.; Burger, W.; Schmid, M. Sensors based on piezoelectric resonators. Sensors and Actuators A 1995, 48, 1–21. [Google Scholar] [CrossRef]
- Benes, E.; Schmid, M.; Gröschl, M.; Berlinger, P.; Nowotny, H.; Harms, K.C. Solving the cable problem between crystal sensor and electronics by use of a balanced bridge oscillator circuit. Proceedings of the Joint Meeting of the European Frequency and Time Forum and the IEEE International Frequency Control Symposium 1999, 2, 1023–1026. [Google Scholar]
- Soares, D.; Kautek, W.; Fruböse, C.; Doblhofer, K. The electrochemical quartz crystal microbalance in media of changing viscoelastic properties, and the design and characterization of suitable driver electronics. Ber. Bunsenges. Phys. Chem. 1994, 98(2), 219–228. [Google Scholar]
- Auge, J.; Hauptmann, P.; Hartmann, J.; Rösler, S.; Lucklum, R. New design from QCM sensors in liquids. Sensors and Actuators B 1995, 24-25, 43–48. [Google Scholar]
- Matthys, R.J. Crystal oscillator circuits, Revised Ed.; Krieger: Malabar, 1992; p. 251. [Google Scholar]
- Data Sheet OPA660 (PDS-1072E); Burr-Brown: Tucson, 1995.
- Henn, Ch. New ultrahigh-speed circuit techniques with analog ICs. AB-183; Burr-Brown: Tucson, 1995. [Google Scholar]
- Benjaminson, A. Balanced feedback oscillators. Proceedings of the 38th Annual Symposium on Frequency Control 1984, 327–333. [Google Scholar]
- Benjaminson, A. A crystal oscillator with bidirectional frequency control and feedback ALC. Proceedings of the 40th Annual Symposium on Frequency Control 1986, 344–349. [Google Scholar]
- Wessendorf, K.O. Active bridge oscillator. 2001. [Google Scholar]
- Geelhood, S.; Frank, C.W.; Kanazawa, K. Acoustic Wave Sensor Worshop 3; Taos, New Mexico, 2001. [Google Scholar]
- Behrends, R.; Kaatze, U. A high frequency shear wave impedance spectrometer for low viscosity liquids. Meas. Sci. Technol. 2001, 12, 519–524. [Google Scholar] [CrossRef]
- Ferrari, V.; Marioli, D.; Taroni, A. Oscillator circuit configuration for quartz crystal-resonator sensors subject to heavy acoustic load. Electron. Lett. 2000, 36(7), 610–612. [Google Scholar] [CrossRef]
- Ferrari, V.; Marioli, D.; Taroni, A. Improving the accuracy and operating range of quartz microbalance sensors by purposely designed oscillator circuit. IEEE Trans. Instrum. Meas. 2001, 50, 1119–1122. [Google Scholar] [CrossRef]
- Arnau, A.; Sogorb, T.; Jiménez, Y. A continuous motional series resonant frequency monitoring circuit and a new method of Determining Butterworth – Van Dyke Parameters of a Quartz Crystal Microbalance in Fluid Media. Review of Scientific Instruments 2000, 71, 2563–2571. [Google Scholar] [CrossRef]
- Arnau, A.; García, J.V.; Jiménez, Y.; Ferrari, V.; Ferrari, M. Improved Electronic Interfaces for Heavy Loaded at Cut Quartz Crystal Microbalance Sensors. Proceedings of Frequency Control Symposium Joint with the 21st European Frequency and Time Forum. IEEE International 2007, 357–362, Extended version submitted to Review of Scientific Instruments. [Google Scholar]
- Ferrari, V.; Marioli, D.; Taroni, A. ACC oscillator for in-liquid quartz microbalance sensors. Proceedings of IEEE Sensors 2003, 2, 849–854. [Google Scholar]
- Ferrari, M.; Ferrari, V.; Marioli, D.; Taroni, A.; Suman, M.; Dalcanale, E. In-liquid sensing of chemical compounds by QCM sensors coupled with high-accuracy ACC oscillator. IEEE Trans. Instrum. Meas. 2006, 55(3), 828–834. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Kanazawa, K.K. Dual-harmonic oscillator for quartz crystal resonator sensors. Solid-State Sensors, Actuators and Microsystems Conference 2007, TRANSDUCERS 2007. International; 10-14 June 2007. 241–244, Extended version in press in Sensors and Actuators A. [Google Scholar]
- Nakamoto, T.; Kobayasi, T. Development of circuit for measuring both Q variation and resonant frequency shift of quartz crystal microbalance. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 1994, 41(6), 806–811. [Google Scholar] [CrossRef]
- Jakoby, B.; Art, G.; Bastemeijer, J. A novel analog readout electronics for microacoustic thickness shear-mode sensors. IEEE Sensors Journal 2005, 5(5), 1106–1111. [Google Scholar] [CrossRef]
- Torres, R.; Arnau, A.; Perrot, H. Electronic System for Experimentation in AC Electrogravimetry II: Implemented Design. Revista EIA 2007, 7, 63–73. [Google Scholar]
- Torres, R. Instrumental techniques for improving the measurements based on Quartz Crystal Microbalances. Ph.D. Thesis, Universidad Politécnica de Valencia, 2007. [Google Scholar]
- Torres, R.; García, J. V.; Arnau, A.; Perrot, H.; Gabrielli, C. Improved frequency/voltage converters for fast QCM applications. Submitted for review to Scientific Instruments.

© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Arnau, A. A Review of Interface Electronic Systems for AT-cut Quartz Crystal Microbalance Applications in Liquids. Sensors 2008, 8, 370-411. https://doi.org/10.3390/s8010370
Arnau A. A Review of Interface Electronic Systems for AT-cut Quartz Crystal Microbalance Applications in Liquids. Sensors. 2008; 8(1):370-411. https://doi.org/10.3390/s8010370
Chicago/Turabian StyleArnau, Antonio. 2008. "A Review of Interface Electronic Systems for AT-cut Quartz Crystal Microbalance Applications in Liquids" Sensors 8, no. 1: 370-411. https://doi.org/10.3390/s8010370
APA StyleArnau, A. (2008). A Review of Interface Electronic Systems for AT-cut Quartz Crystal Microbalance Applications in Liquids. Sensors, 8(1), 370-411. https://doi.org/10.3390/s8010370



