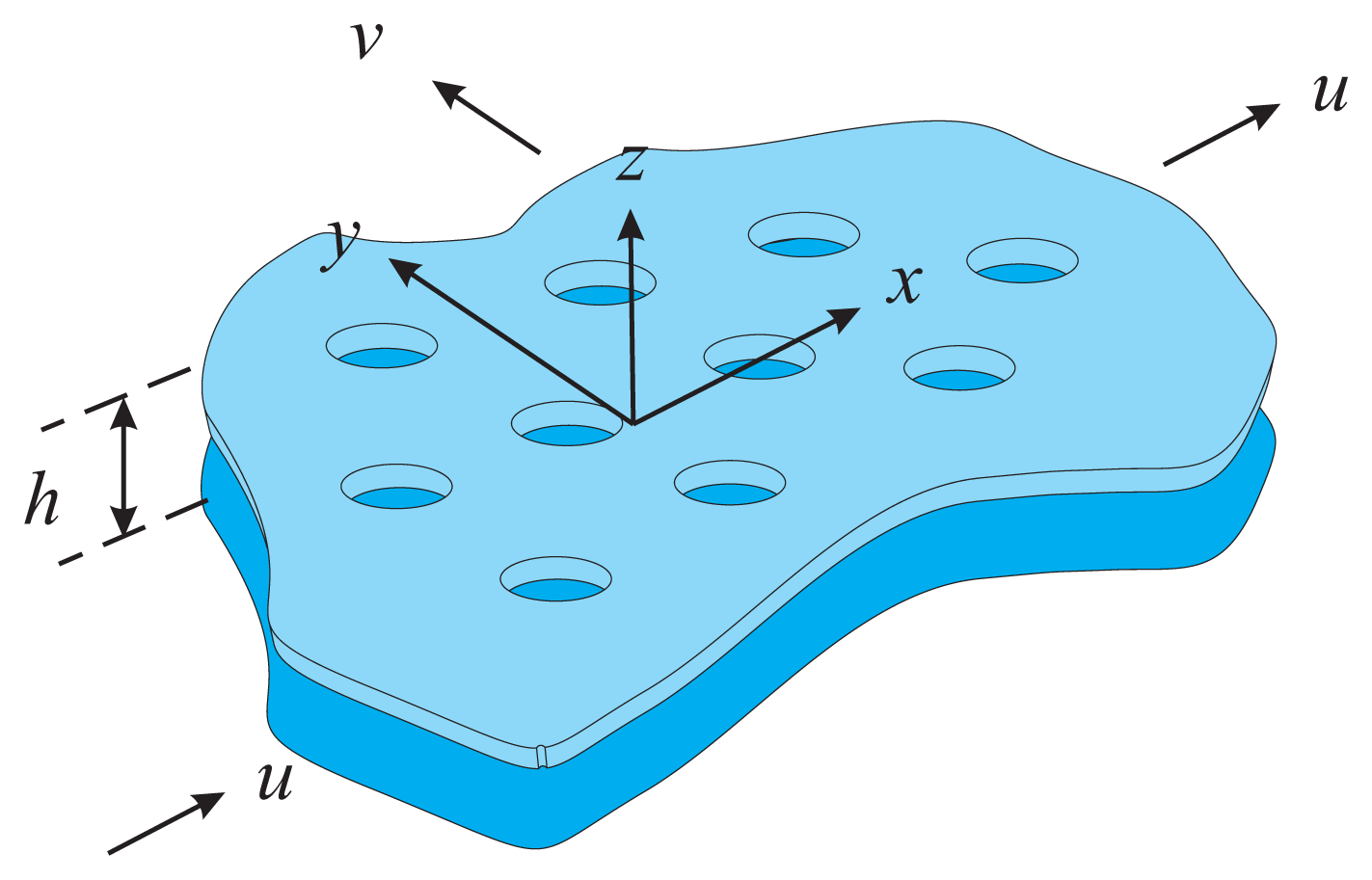
1. Introduction
Perforations are used in oscillating microelectromechanical (MEM) sensors and actuators to control damping due to gas for desired frequency-domain operation. Practical MEM devices using perforations include microphones [
1], capacitive switches [
2,
3], and resonators [
4].
The perforations reduce damping in a squeeze-film structure considerably: the characteristic dimensions are reduced from the outer dimensions of the surface to the separation of the perforations. Also, the cut-off frequency (when the spring and damping forces are equal) rises considerably due to the perforations. Often this cut-off frequency in perforated structures is much higher than the operating frequencies of interest, which simplifies the design of such devices since only the damping forces need to be considered in the device design.
3D flow simulations are needed in solving perforation problems generally. However, accurate 3D simulation of the Navier-Stokes (N-S) equation is, in practice, impossible due to the huge number of elements needed, especially in cases where the number of perforations is relatively large. The number of perforations may vary from a few holes to a grid of thousands of holes. Moreover, the N-S equations are limited to the region of a slightly rarefied gas (slip-flow region). Accurate modelling of these structures requires the consideration of rarefied gas flow in tiny flow channels and around the structure.
Different methods that reduce the 3D flow problem into 2D are available, depending on the boundary conditions, number of perforations, the relative hole size
s0/
h (
s0 is the hole diameter and
h is the height of the air gap) and the perforation ratio (ratio of the perforated area and the surface area). If the
s0/
h-ratio is large, the flow resistance of the perforation is insignificant (unless the perforations are relatively long). In the case of a few relatively large perforations, the problem reduces to a 2D problem that can be solved from the Reynolds equation by considering the holes as additional boundary conditions [
5,
6]. Open edge corrections [
7] might need to be considered in this case. On the other hand, if the number of holes is large, and the perforation ratio is not small, the horizontal flow from the damper borders is insignificant (also caused by closed damper borders), and the pressure patterns around each perforation are identical. In this case, the damping can be determined solely from a single perforation and its surroundings, called a perforation cell. A simple analytic model for such a cell by Skvor [
8] has been used in modelling perforations in a microphone's backplate. When the
s0/
h-ratio cannot be considered large, the flow resistance of the perforations must be included in the model. Homentcovschi and Miles [
9], have derived such an analytic model considering the compressibility and inertial effects. Perforation cell models over a wide range of perforation ratios and hole lengths well below the cut-off frequency are given in [
10,
11].
If the
s0/
h ratio and the perforation ratio are not large, such that the flow from the damper borders is considerable, a more complicated model is required. In the case of a regular grid of perforations, the flow resistance of the perforation cell can be solved and homogenised over the damper surface. This flow problem can be modelled with the extended Reynolds equation that contains an additional pressure leakage term [
12–
16]. This homogenisation method is usable, but it has its limitations, especially if the number of perforations is small. A mixed-level approach has also been published [
17], and a hybrid method combining N-S and Reynolds equations has been presented by da Silva et al. [
18]. Flow resistances of perforations with different shapes were studied by Homentcovschi and Miles [
19]. A compact analytic model for rectangular dampers having an uniform perforation was given in [
10]. The model was verified with FEM simulations at frequencies well below the cut-off frequency.
The models referenced above assume motion normal to the surfaces, and the squeezing force in the air gap makes the gas flow. A different problem where the perforated surface moves tangentially to the surfaces has been discussed in [
20].
We have presented a Perforation Profile Reynolds (PPR) method [
21] for damping problems where the homogenisation method is not accurate. These are characterized by, e.g., a moderate number of perforations, complex shaped perforations, and non-uniform distribution and sizes of perforations.
In this paper, we present improvements to this method. Flow admittance profiles that vary across the perforations are used instead of constant profiles. Also, an improved perforation cell model [
10] has been used instead of a simple theoretical long-channel model with theoretical end corrections. Besides translational motion, the verifications include also torsional motion. This paper also shows how the perforation cell model [
10] can be utilised in a homogenisation method with a FEM solver.
The method was verified with 3D FEM simulations using a N-S solver. Simulations of a parallel-plate damper with 16 to 64 square perforations were performed for various perforation ratios. Only incompressible flow is considered here, since time-harmonic reference N-S simulation with sufficient accuracy is not realistic.
3. Verification
Several perforated dampers in perpendicular and rotating motion are simulated both with the 3D N-S solver with slip conditions and with the time-harmonic PPR solver. Both solvers are implemented in the multiphysical simulation software Elmer [
27].
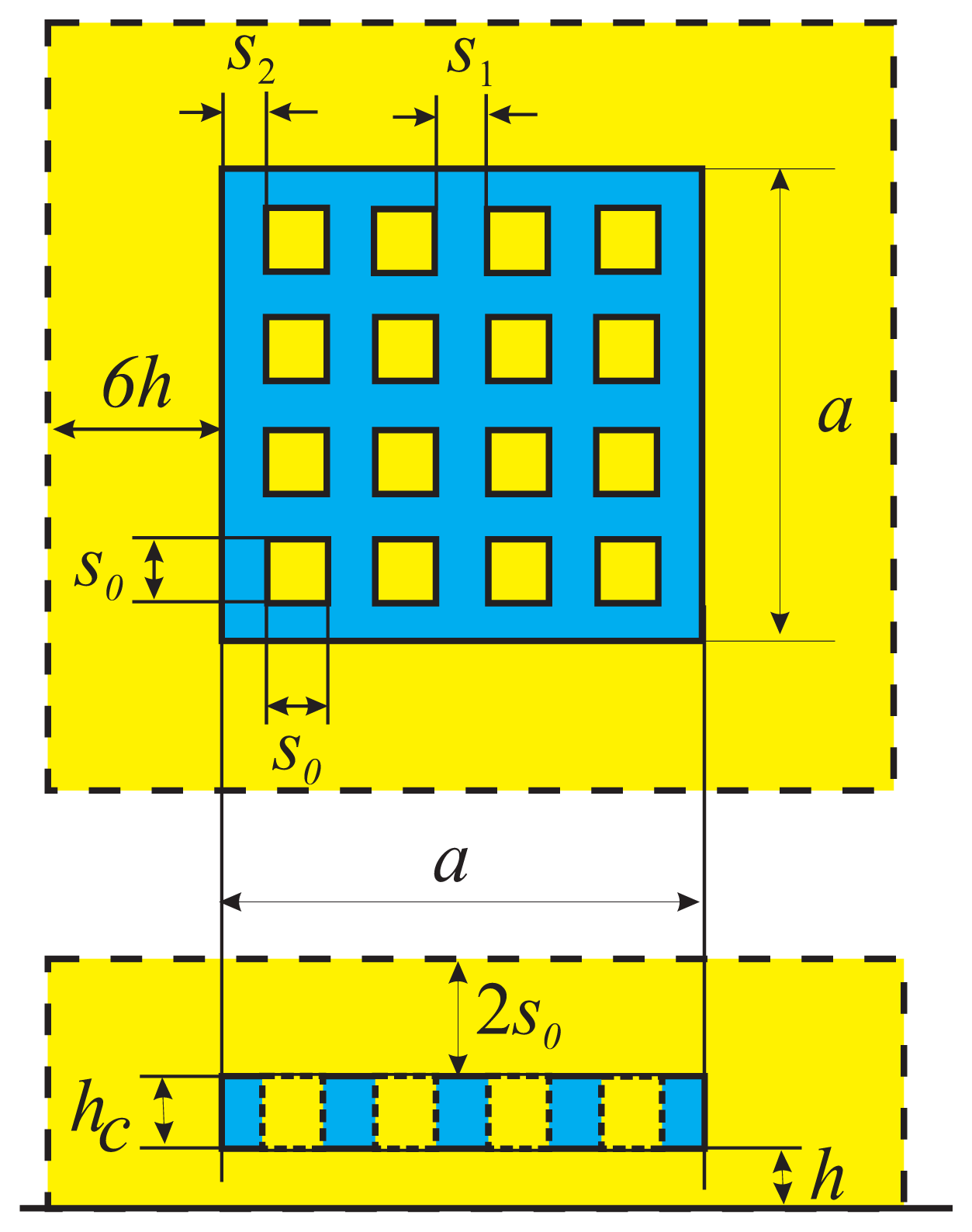
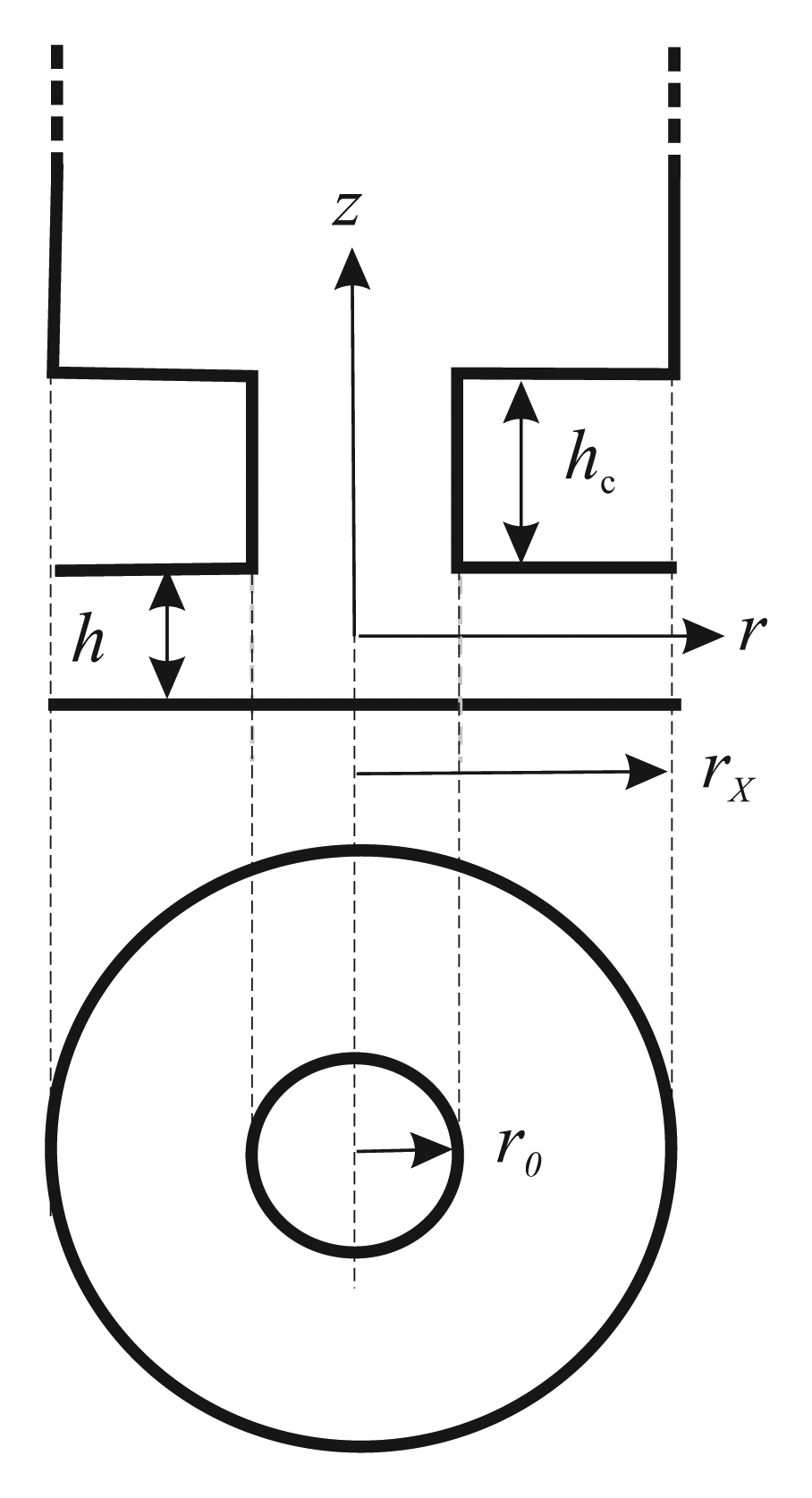
The surface is a square, and it consists of
N square holes. The distance between the edges of two adjacent holes is
s1, as is the distance from the edges of the holes to the edges of the damper
s2 =
s1. The perforation pitch is
sx =
s0 +
s1. A comparison is made well below the cut-off frequency, that is, the compressibility of the gas is ignored (
Ch = 0). The simplifies the N-S simulations, since response to a constant velocity is calculated. The dimensions are summarised in
Table 1 and one of the four structures is shown in
Fig. 4.
3.1. 3D simulations
First, full 3D N-S simulations of the structure are performed to generate reference data for the methods presented in this paper. The simulations can be performed relatively reliably, thanks to the small number of holes and the symmetry of the structure. Slip boundary conditions are used for the surfaces. The simulated gas volume is extended around the damper: free space around and above the damper are 6h and 2s0, respectively. A mesh of 450 000 elements is used. Both translational and torsional motion cases were simulated.
The number of elements (450 000) in the 3D N-S simulations was in practice the maximum that could be performed considering the computing time and the memory consumption. The computer used was Sun Fire 25K. Simulating each (of 432) topology took between one and two hours and 6 Gb of memory.
To estimate the accuracy of the results, simulations with 250 000 elements were made, too. Comparative results are discussed later in this paper.
3.2. PPR solver
The PPR
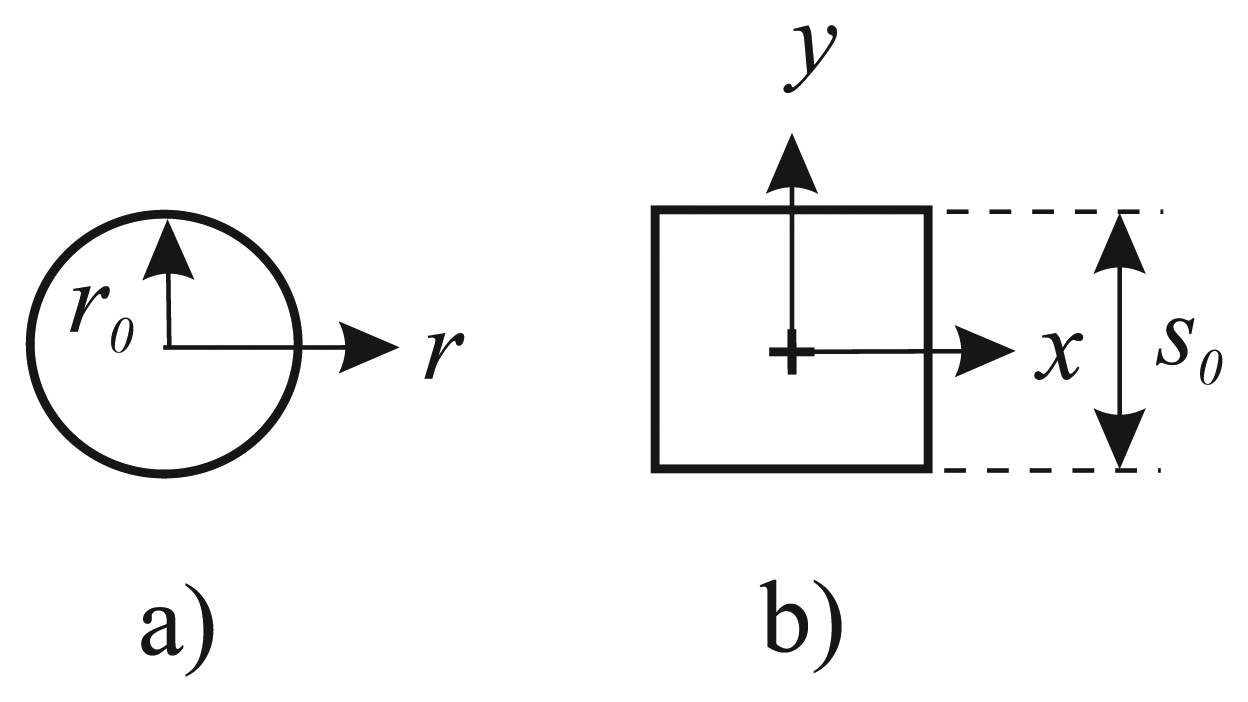
Equation (2) is solved with a time-harmonic PPR solver. For each square hole, the specific admittance for a circular hole specified in
Eq. (11) with an effective radius of
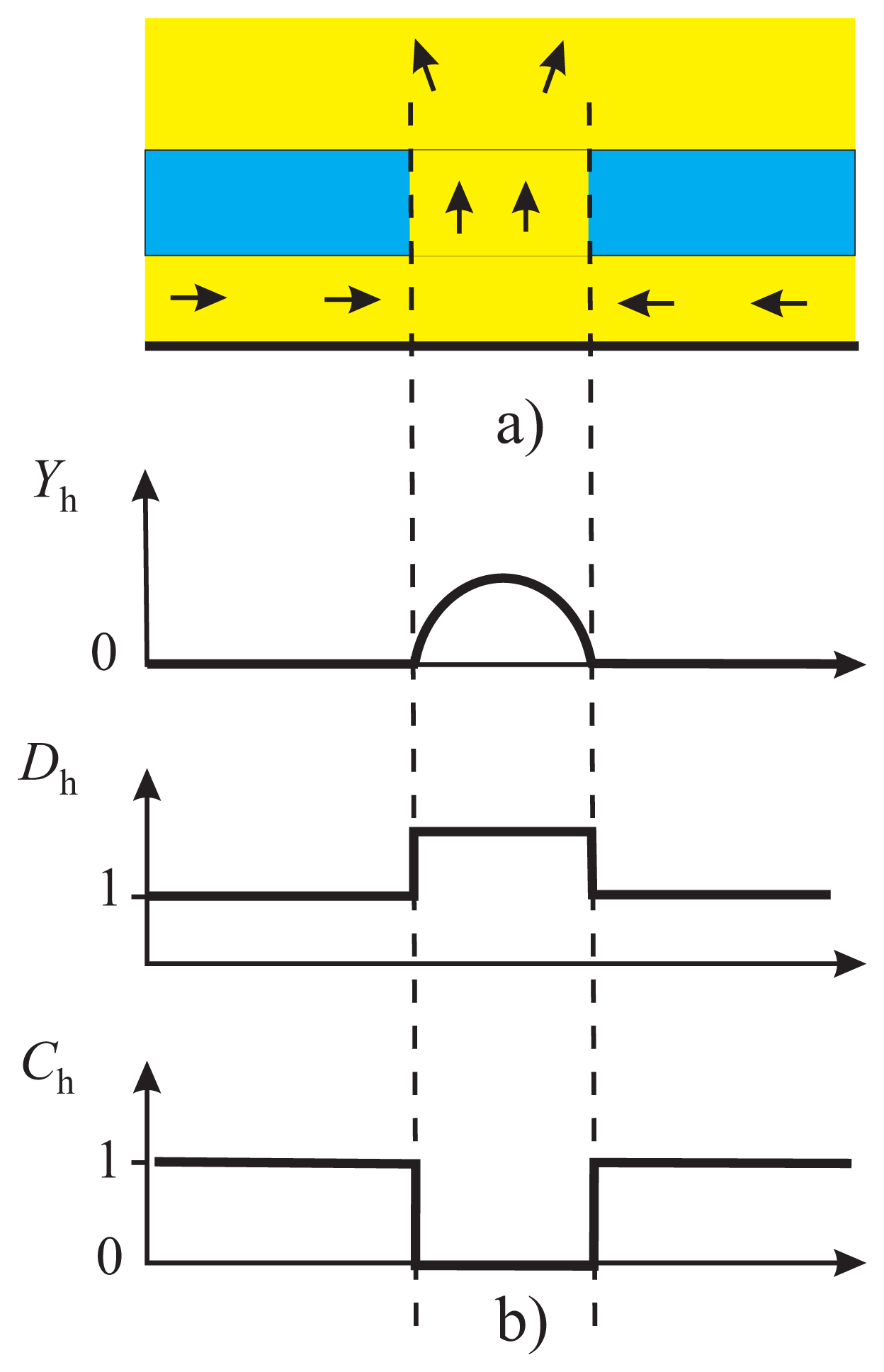
r0 is used. The PPR solver also includes the compressibility of the gas in the air gap. The compressibility of the perforations can also be included specifying a complex-valued specific admittance. This is essential in modelling, e.g., closed perforations. Compressibility profile is not needed here, since steady flow calculations are made.
We use Dh = 1 since there is no model available for the diffusivity profile. The friction surface for the flow under the hole is reduced by half, and this could justify setting Dh = 2. However, the changes in the flow profile will introduce additional losses that justify decreasing the diffusivity.
Considering the edge effects at the outer borders of the structure is essential for accurate results. Each border of the structure is extended by an amount 0.65
h(1 +3.3
Kn,ch), as suggested in [
7]. The borders of the perforations are not modified in this method, since the diffusivity profile at the perforation effectively builds an “edge effect”: the flow admittance at the border of the perforation is small, forcing gas to flow horizontally in a viscous channel close to the border.
Both translational and torsional motion cases are simulated. Each of the simulations with the Reynolds solver with 20 000 elements took about 10 seconds.
3.3. PPR method
First, the structure is set into translational motion with a velocity of vz = 1 m/s. The mechanical resistance, or the damping coefficient is Zm = F/vz, where F is the force acting on the ground surface. A mesh of 20 000 elements is used.
The damping coefficients are compared with the ones from the N-S simulations as a function of the perforation ratio
The maximum relative errors in the damping coefficient are shown in
Table 2, and
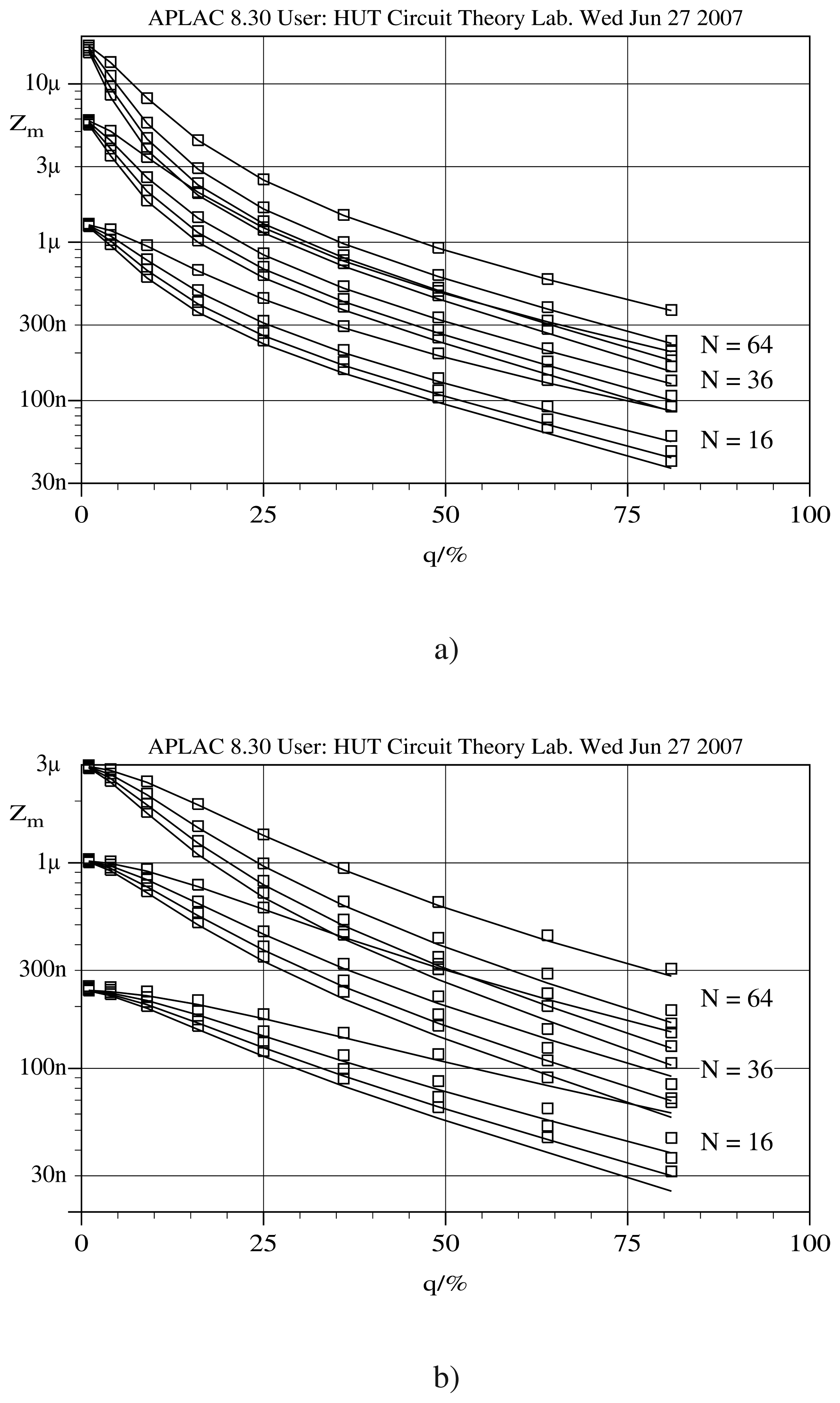
Fig. 5 shows the damping coefficients as a function of the perforation ratio
q for air gaps of 1
μm and 2
μm. In
Fig. 6, the simulated pressure profiles are compared.
Next, the structure is set into torsional motion about the
y-axis with a velocity of
vz= 1 m/s at
x =
a/2. The torsional resistance, or the torsional damping coefficient is
Zt =
τ/
ωz, where
τ is the twisting moment acting on the ground surface and
ωz =
vz/(
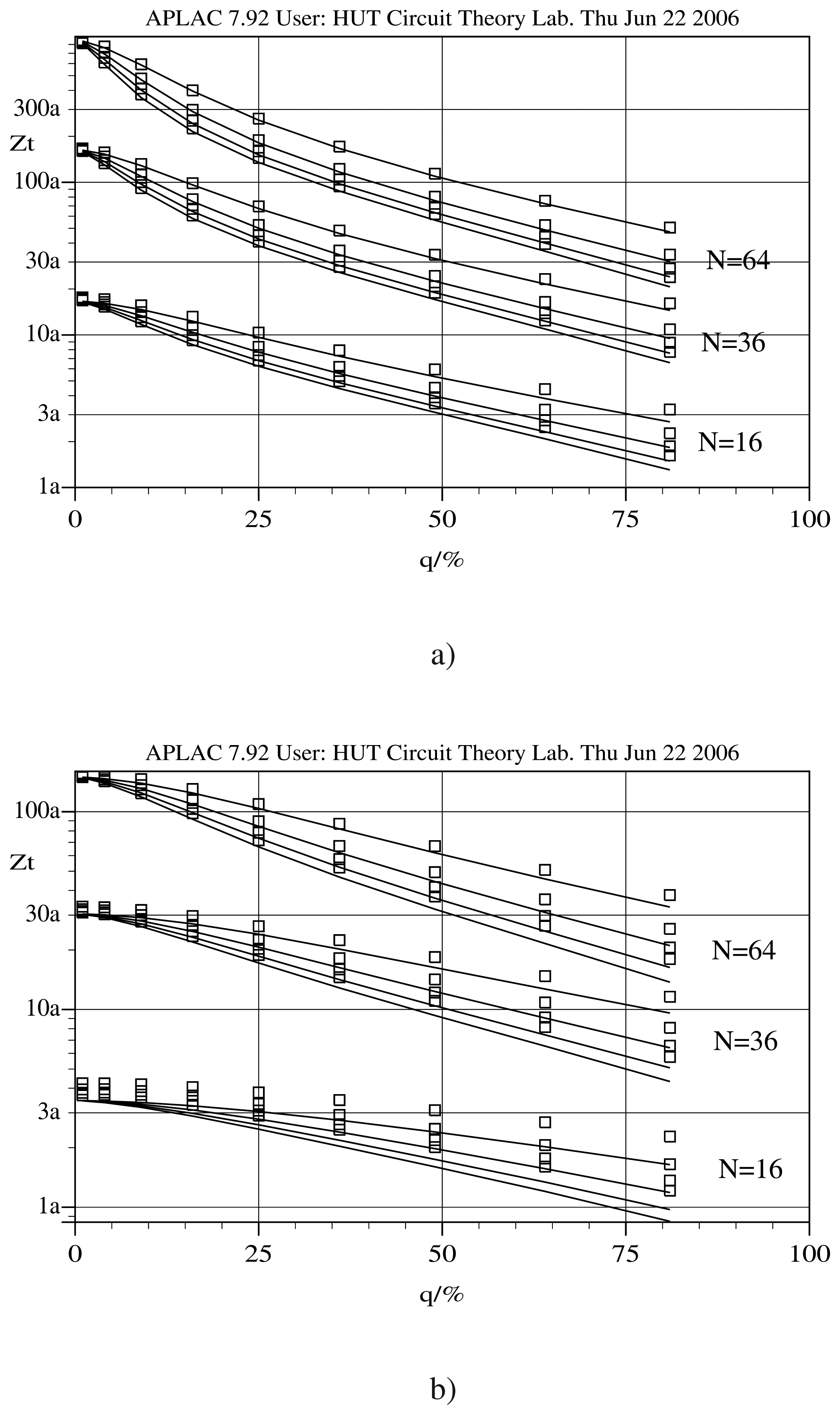
a/2) is angular velocity. A mesh of 20000 elements is used. The maximum relative errors in the torsional motion are shown in
Table 3.
Figure 7 shows the torsional damping coefficients as a function of the perforation ratio for air gaps of 1
μm and 2
μm.
3.4. Homogenisation method
The extended Reynolds equation is solved for perpendicularly moving rectangular surfaces. The perforation cell admittance calculated from
Eq. (17) is used in the simulation. The diffusivity coefficient
Dh = 1 is used. Each damper border is extended by 0.65
h(1 + 3.3
Kn,ch). The quarter of the rectangular surface is meshed having 5000 elements.
Table 4 shows the maximum relative errors of the homogenisation method.
4. Discussion
4.1. Comparison between methods
Table 2 shows the errors of the PPR method compared with the 3D FEM simulations for translational motion. The maximum relative error in the damping force in translational motion is below 10%, except for the case of strong perforation (
q ≥ 49%). The PPR model generally underestimates the damping. This is probably due to the fact that additional drag forces acting on the sidewalls and on the top surface are ignored in the model. These forces contribute most when the surface is the thickest (
hc = 5
μm) and the surface area is the smallest (
N = 16).
In the case of torsional motion,
Table 3, the accuracy of the model is approximately the same as for translational motion for
N = 64. The contribution of the drag forces can be seen in the results of smaller surfaces in
Fig. 7. In the torsional motion the drag forces acting on the sidewalls are relatively stronger. For small
q, the change in the height of the surface changes the damping force for
N = 16 in the N-S simulations, see
Fig. 7b). The surface height clearly changes the damping coefficient (N-S simulations) even for very small perforation ratios. This change cannot be explained by the change in the perforation length, since the damping due to perforations is negligible for very small perforation ratios.
To analyse the importance of the varying pressure profile at the perforations, a set of PPR simulations was performed using a constant specific admittance
Y̅ci of the perforations. The results are summarised in
Table 5. Comparison with results in
Table 2 reveals that errors of both models are approximately the same for small perforation ratios, but the error of the constant specific admittance model is considerably larger if
q > 16%.
The maximum relative errors of the homogenisation method (
Table 4) are also approximately below 10% for
N ≥ 16 and
q < 49 %, but the PPR results are much better for small perforation ratios. However, the homogenisation method gives better results when
N ≥ 16 for
q ≥ 50%. This was an expected result. For an inhomogeneous perforation, where the distribution and sizes of the perforations vary, the determination of the perforation cell might be difficult. In such a case, the generation of the variable perforation admittance profile is not a trivial task. On the other hand, if the number of perforations is large (hundreds or thousands of holes) the element sizes in the PPR method will grow intolerably. In this case, the homogenisation method is superior since the required element count is independent of the number of perforations.
4.2. Rarefied gas effects
The verification in this paper is limited to the slip-flow region just to make the comparison with 3D solutions possible. The PPR method itself is valid for arbitrary gas rarefaction as long as the model for Yh is valid. The comparison is made in the region where the validity of the slip conditions is questionable (Kn,sl < 0.14, Kn,ch < 0.14). In spite of the small additional error in the results, the comparison is justified since slip flow models are used in both cases. The consideration of the slip correction is essential for accurate results for the micromechanical structures simulated. If the rarefied gas effects are ignored (Kn,sl = Kn,ch = 0), the error in the damping force would increase by about 40 % and 15 % for air gaps of 1 μm and 2 μm, respectively.
4.3. Maximum frequency of the model
In squeeze-film dampers, the compressibility of the gas will change the damping coefficient at higher frequencies. The cut-off frequency specifies a frequency when the viscous and compressibility (spring-) forces are equal. For perforated dampers, the small-frequency assumption made in this paper is generally a valid, since the perforation increases the cut-off frequency considerably.
The cut-off frequency due to compressibility can be estimated by calculating the ratio between the viscous and compressibility forces in a perforation cell [
10]. This is quite straightforward after assuming that the perforation ratio is high enough that all gas flows through perforations (not from the damper borders). However, the cut-off frequency might be so high that the inertial effects should also be considered. In estimating the validity the complex flow resistance due to inertia should be considered. In [
10] the maximum frequency for a perforation cell is estimated.
There is no limitation in the method that prevents compressibility from being accounted for. In this case, a complex-valued specific admittance profile and compressibility profile Ch are both needed for the PPR solver. For verifying this case a 3D linearised time-harmonic N-S solver may be used.
4.4. Accuracy of 3D N-S simulations
The 3D simulations were very challenging. A lot of computing resources were used to have the data, still the results are not perfect. To estimate the error in the simulations with 450 000 elements, a comparison is made to simulations with 250 000 elements. The results are shown in
Table 6.
When the perforation ratio is large, the relative difference is the largest. This indicates that the selection of the meshing was not very good for large perforations.
The comparison shows that damping coefficients with 250 000 elements are generally larger than with 450 000 elements. It is then expected that the damping coefficients become smaller when the element count is increased. When considering such fictitious simulations and studying the maximum relative errors of the PPR method in
Table 2, the magnitudes of the relative errors become generally smaller.
5. Conclusions
A straightforward method solving perforation problems with a 2D PPR solver was presented. Damping coefficients of a large number of perforated dampers were solved with the PPR method and they were compared with 3D N-S simulation results with very good agreement. Compared to direct N-S simulations, the PPR method offers orders of magnitudes faster simulation times and less memory consumption. The maximum relative errors for translational motion for N ≥ 16 were about 10 % and 20 % for perforation ratios 1%…36% and 1%…81%, respectively.
Perforations were modelled with their specific admittance profile. Both, constant and spatially varying admittance profiles at the perforations were used. It was shown that the errors were smaller when a varying admittance profile was used. Uniform diffusivity profile (Dh = 1) was assumed. A further study is needed to resolve if a non-trivial profile could be extracted form FEM simulations, and if the utilization of this profile would improve the accuracy of the model.
The PPR method was also compared with the homogenisation method. The results were almost as good (maximum relative error about 10%) for N ≥ 16 for small perforation ratios (q < 36%).
The square perforations were approximated with a model for a cylindrical perforation cell. It is expected that a model for a square cell [
11] could improve the accuracy of PPR and homogenisation methods, especially at high perforation ratios.
The fringe flow effects due to the sidewalls and the upper surface clearly contributed the damping coefficient for small s0/h ratios. This was seen in the results for dampers with a small number of holes, since in these cases the surface area was also relatively small.
Incompressible flow was assumed. For a squeeze-film damper this sounds like a very limiting assumption. But due to the perforations, the cut-off frequency is significantly higher than in the non-perforated case. Thus the valid frequency range of the incompressible damper model is relatively wide. Further increase of the frequency range is not trivial, since, besides the compressibility effects, the inertia of the gas should be considered. Also, the thermal aspects should be considered since isothermal assumptions will not be sufficient due to the high cut-off frequencies.
The method needs to be verified in cases where the gas compressibility and inertia are considered. However, this is not easy, since the time-harmonic analysis of the 3D structure with a sufficient accuracy will be very challenging. Extraction and usage of non-uniform perforation profiles and coupling between perforations will be studied in the future.