Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices
Abstract
:1. Introduction
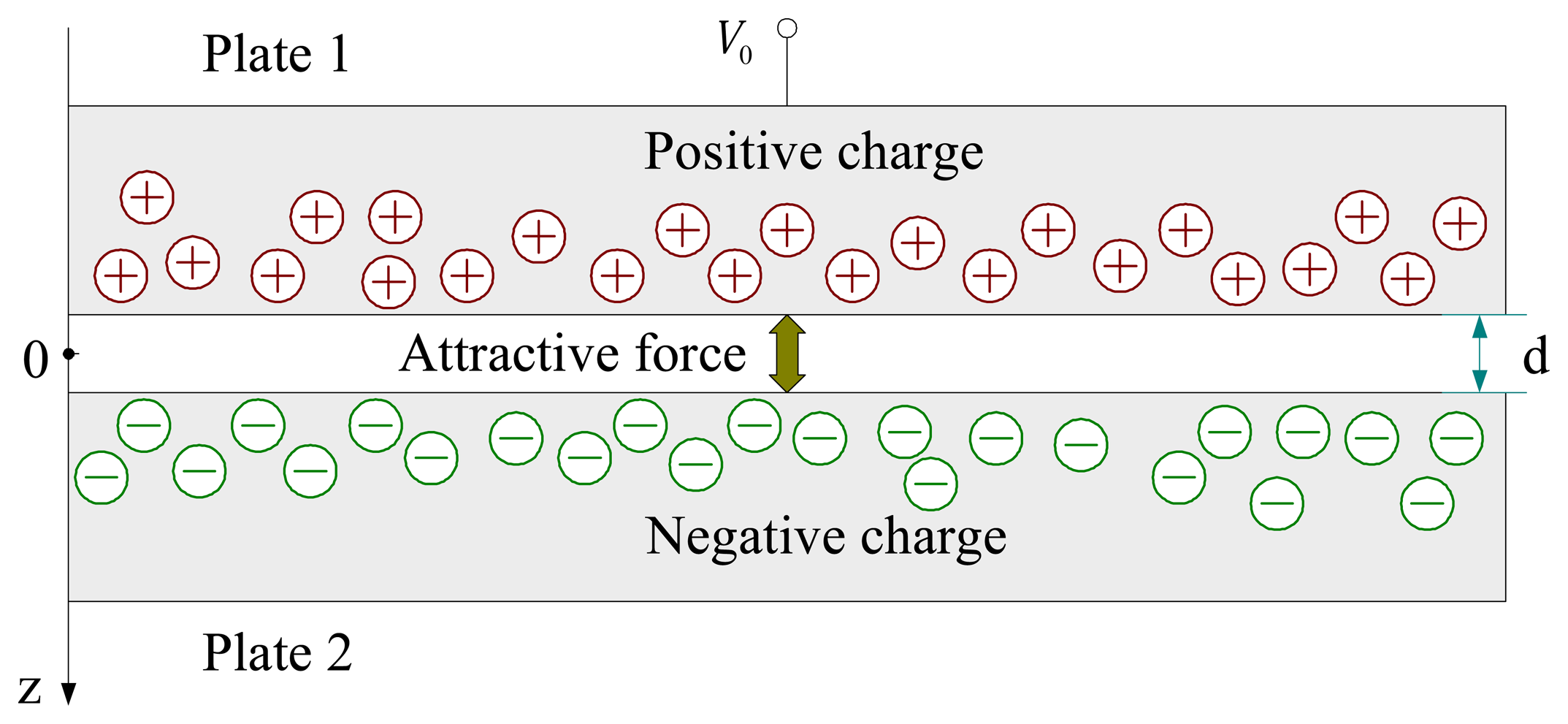
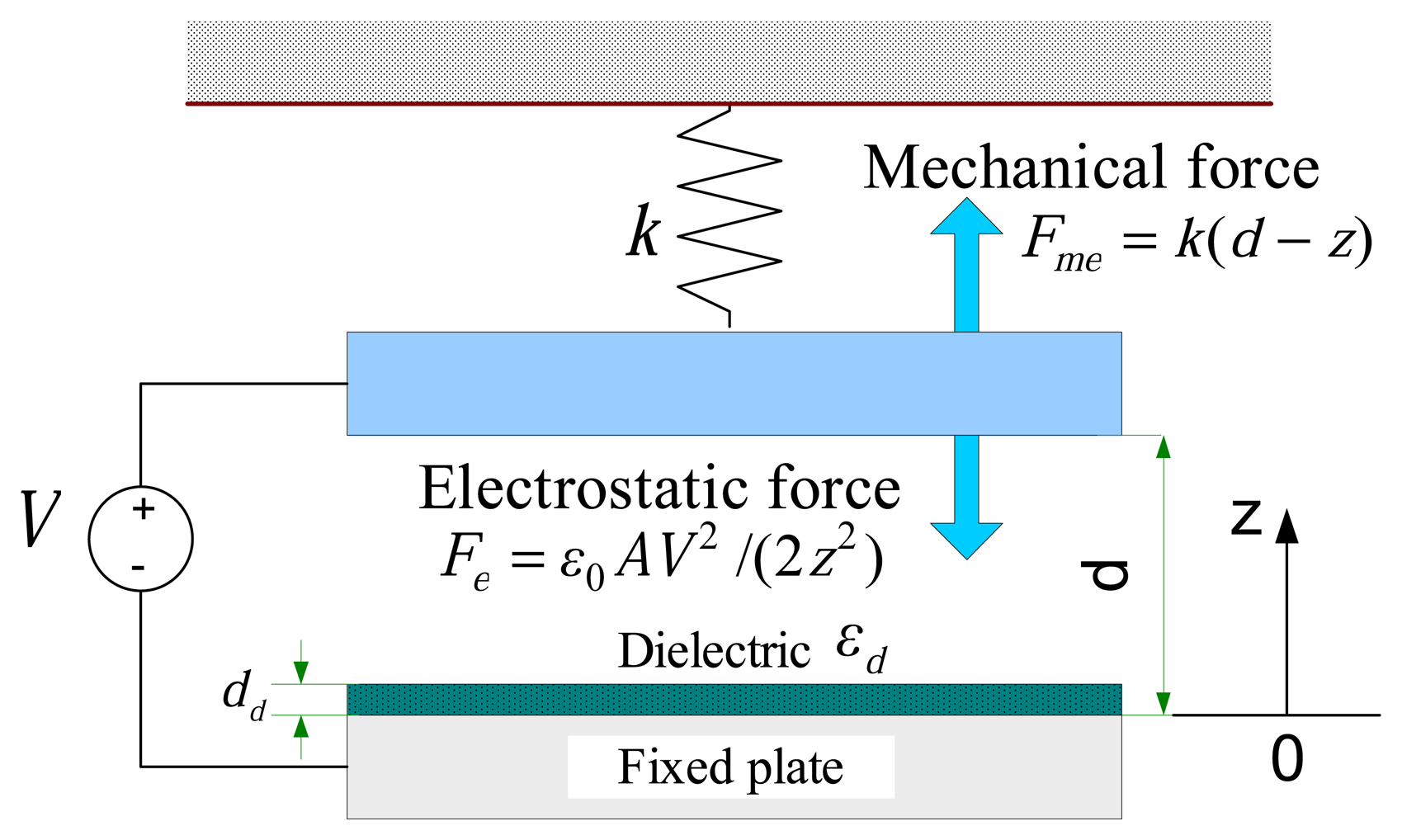
2. Physical model
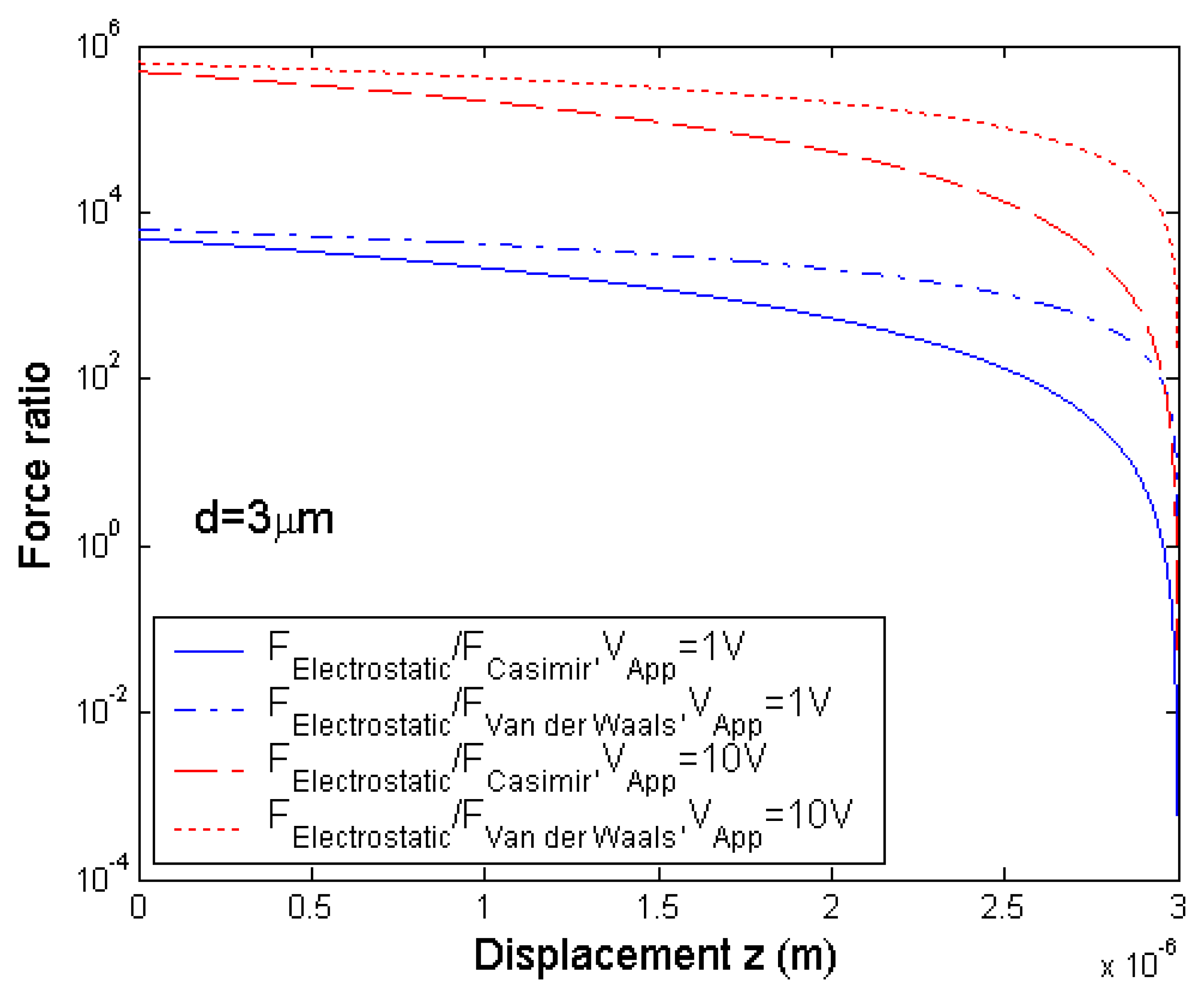
3. Scaling effect
4. Stability analysis
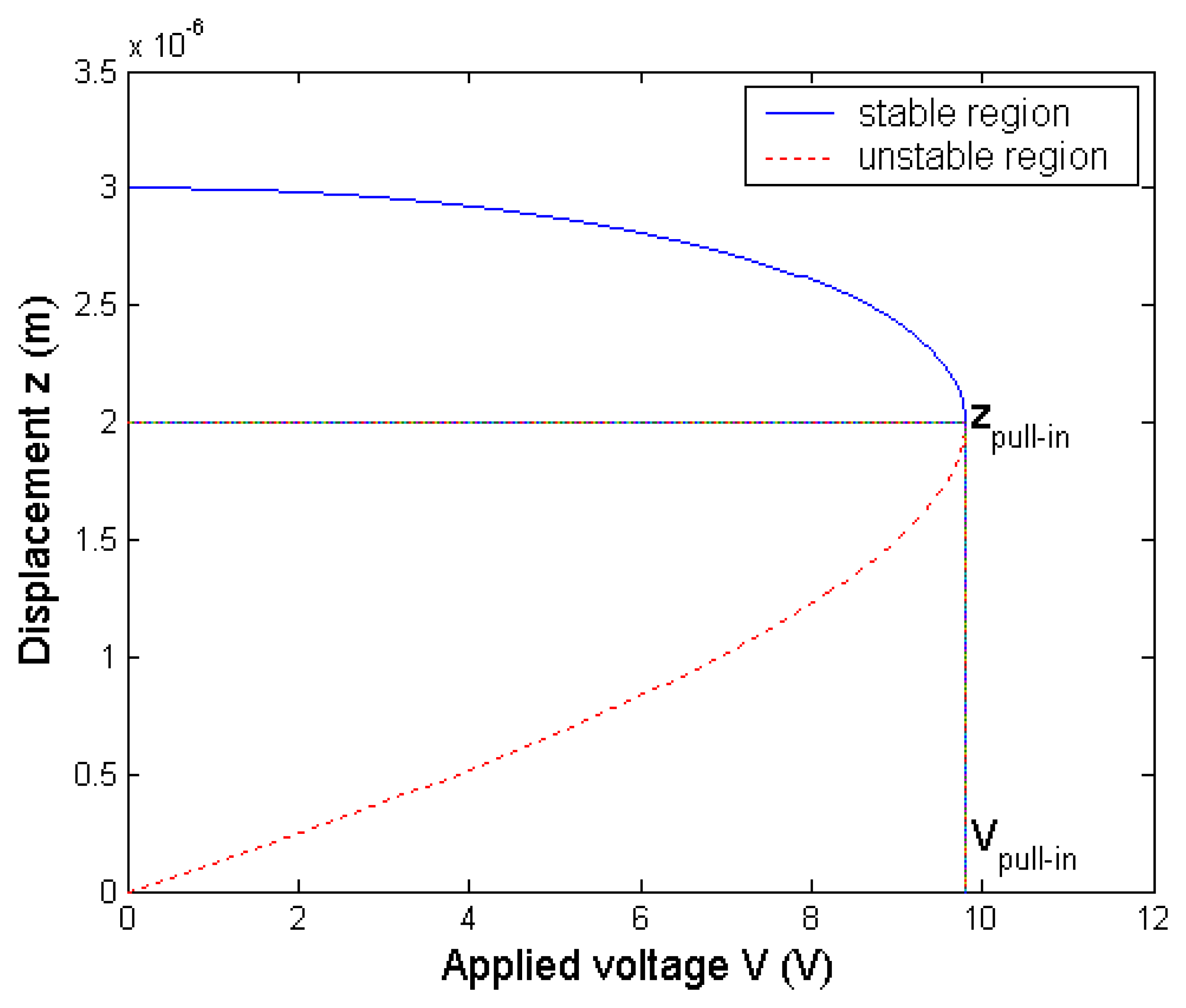
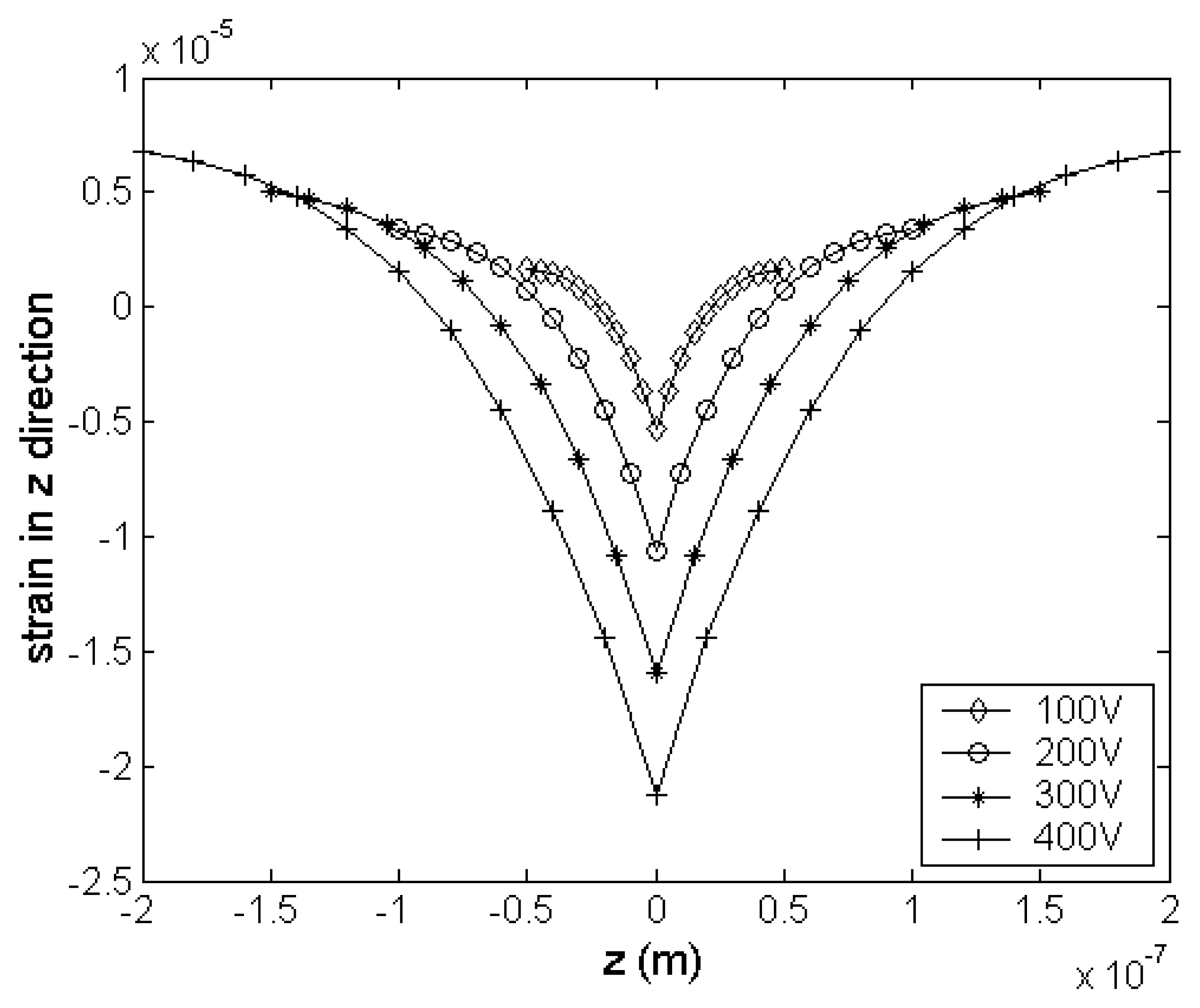
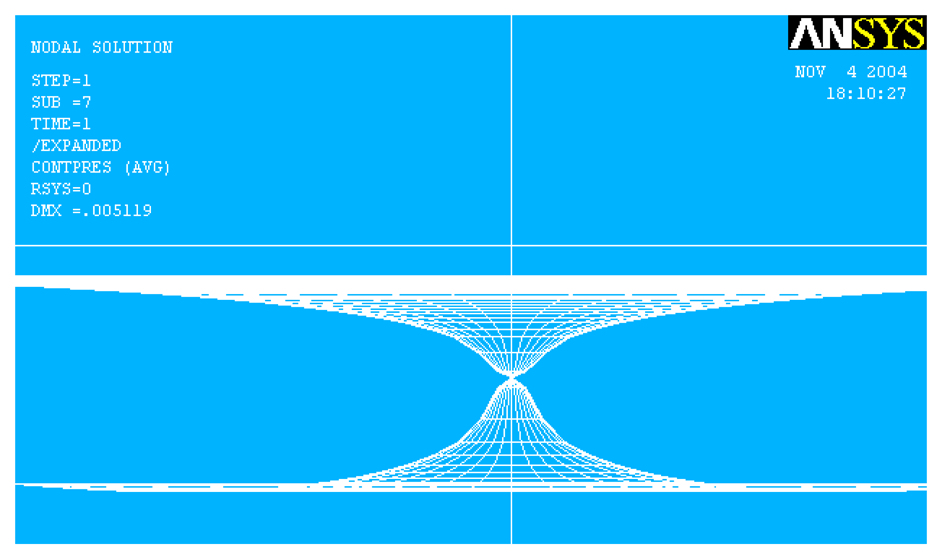
4.1. Pull-in effect
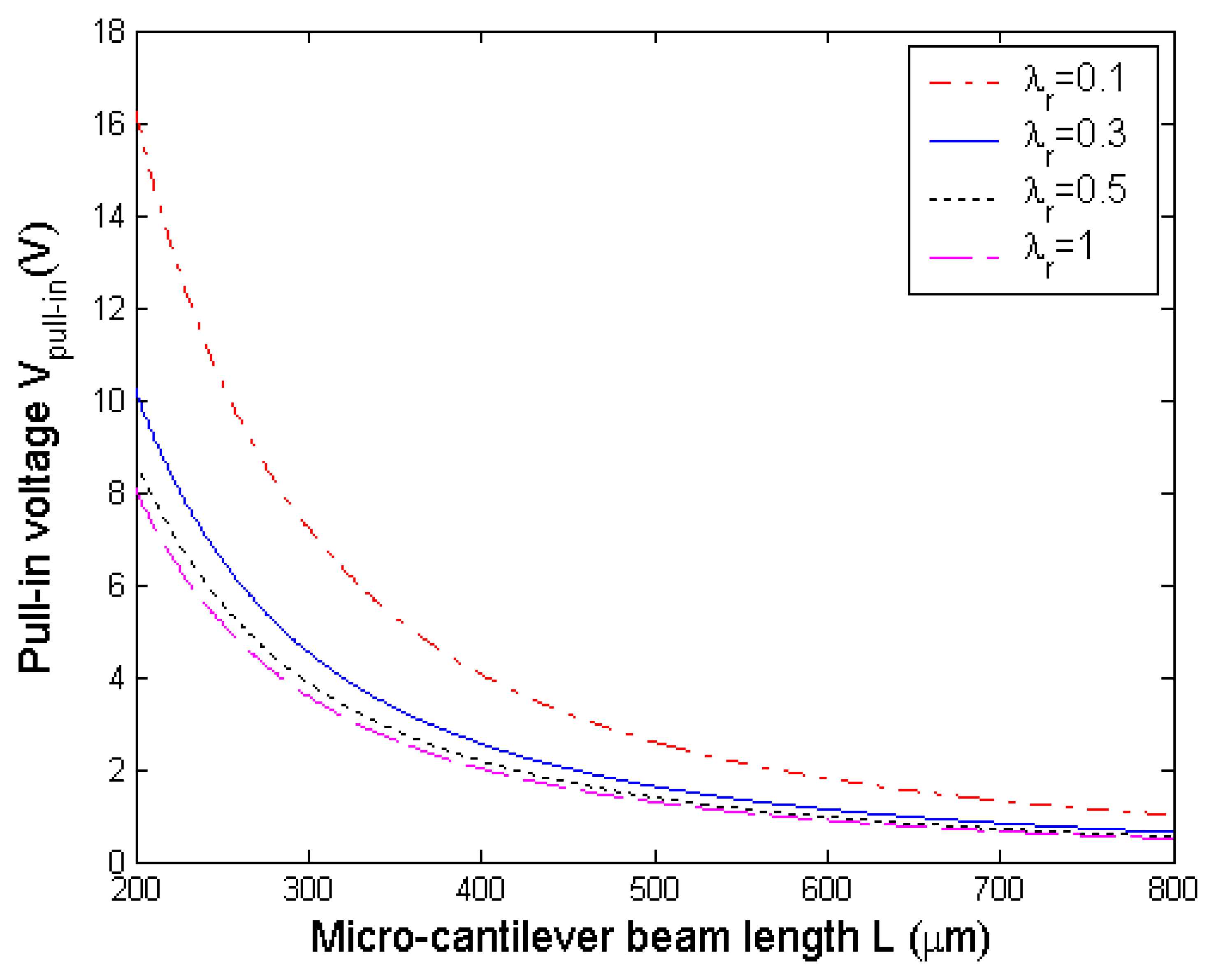
4.2. Effects on the pull-in voltage
4.2.1. Effect of effective stiffness keff
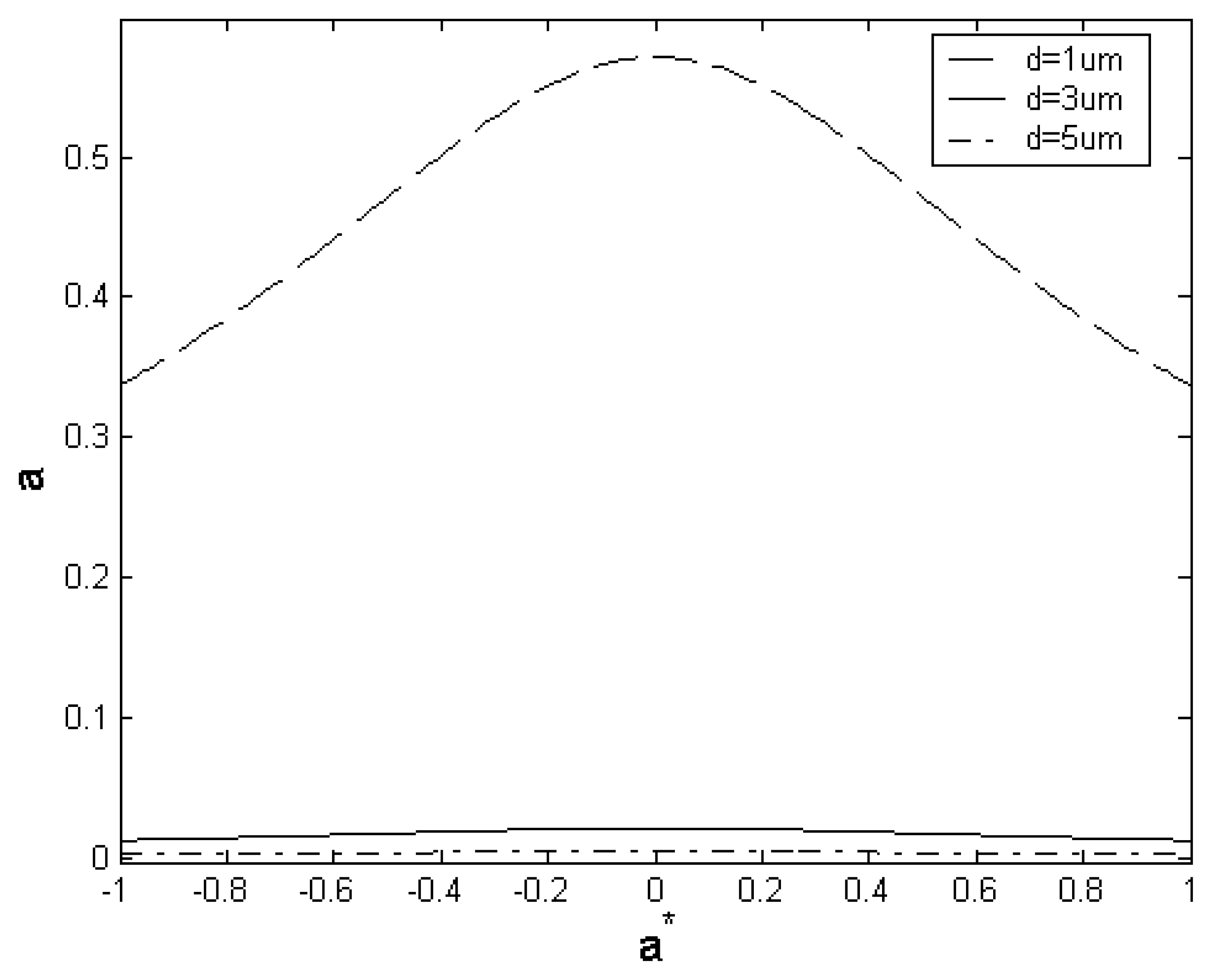
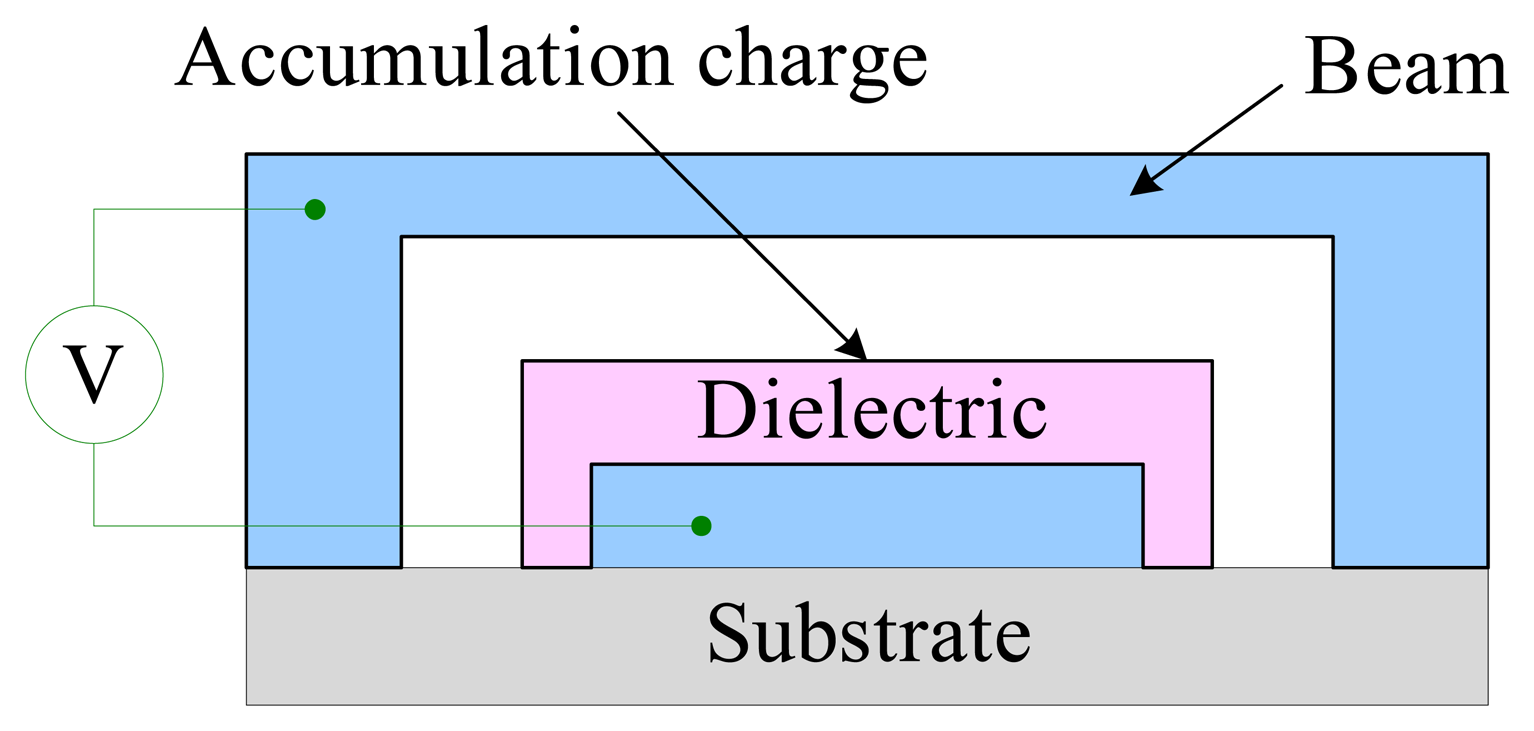
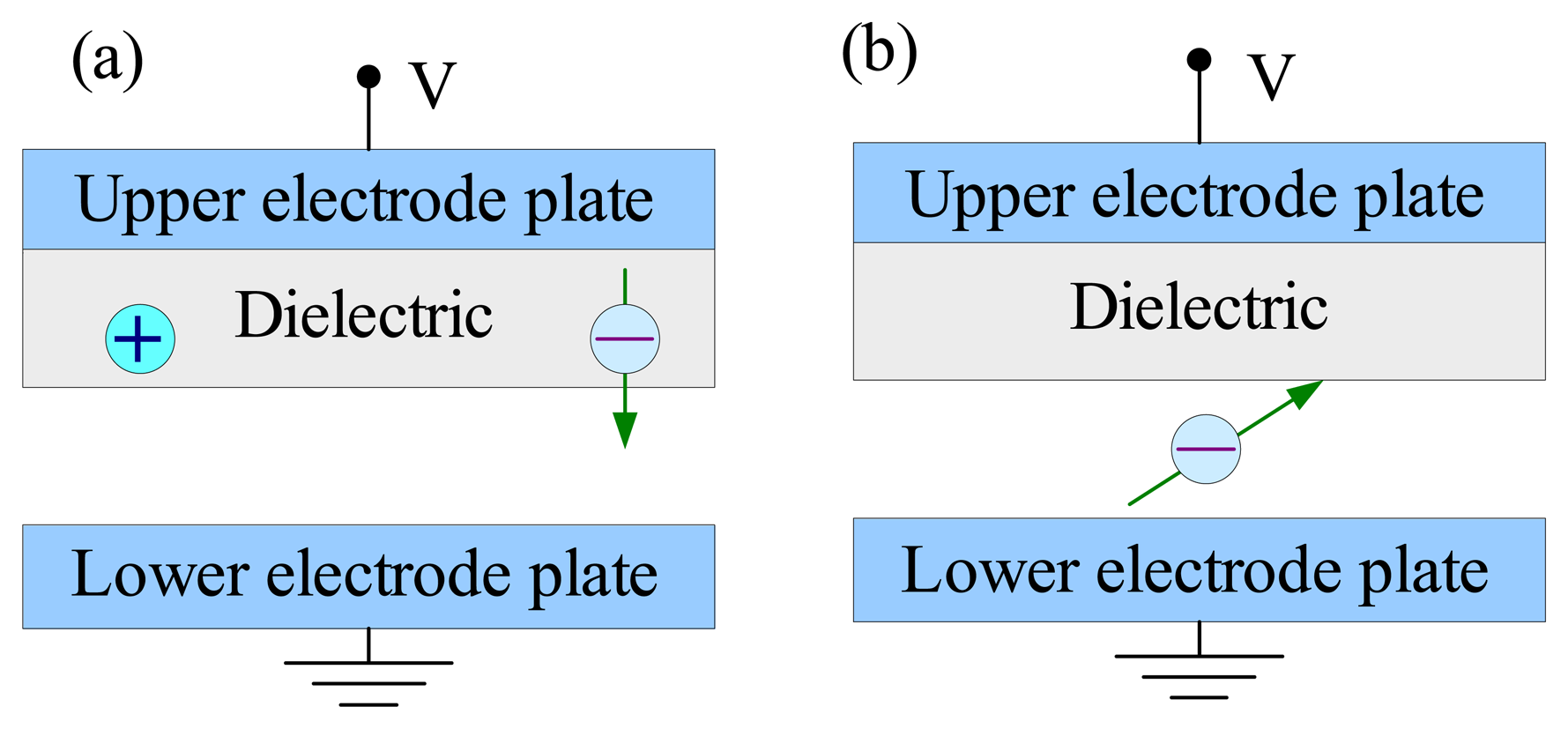
4.2.2. Effect of dielectric charging
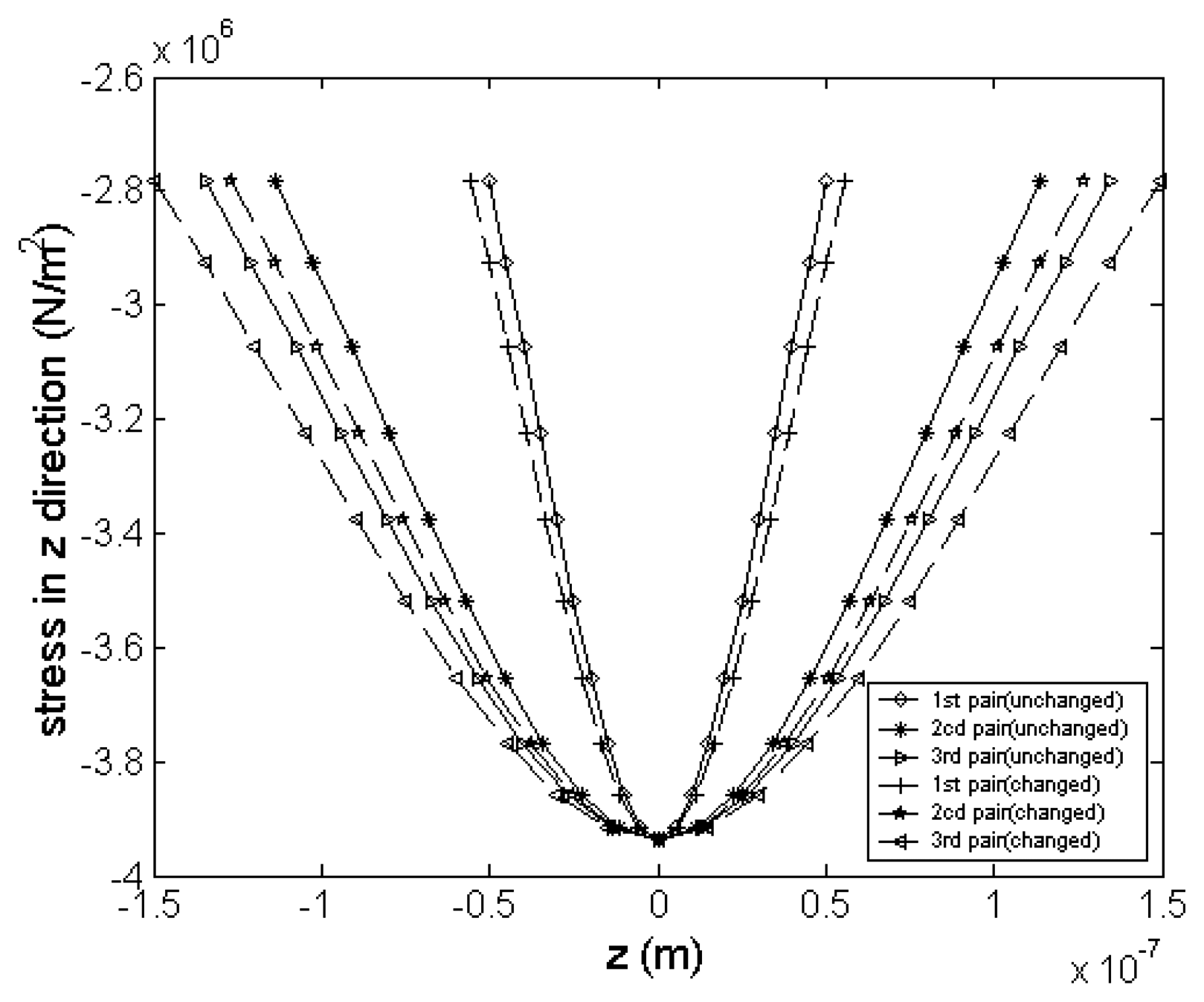
4.2.3. Effect of stress gradient
4.2.4. Effect of temperature
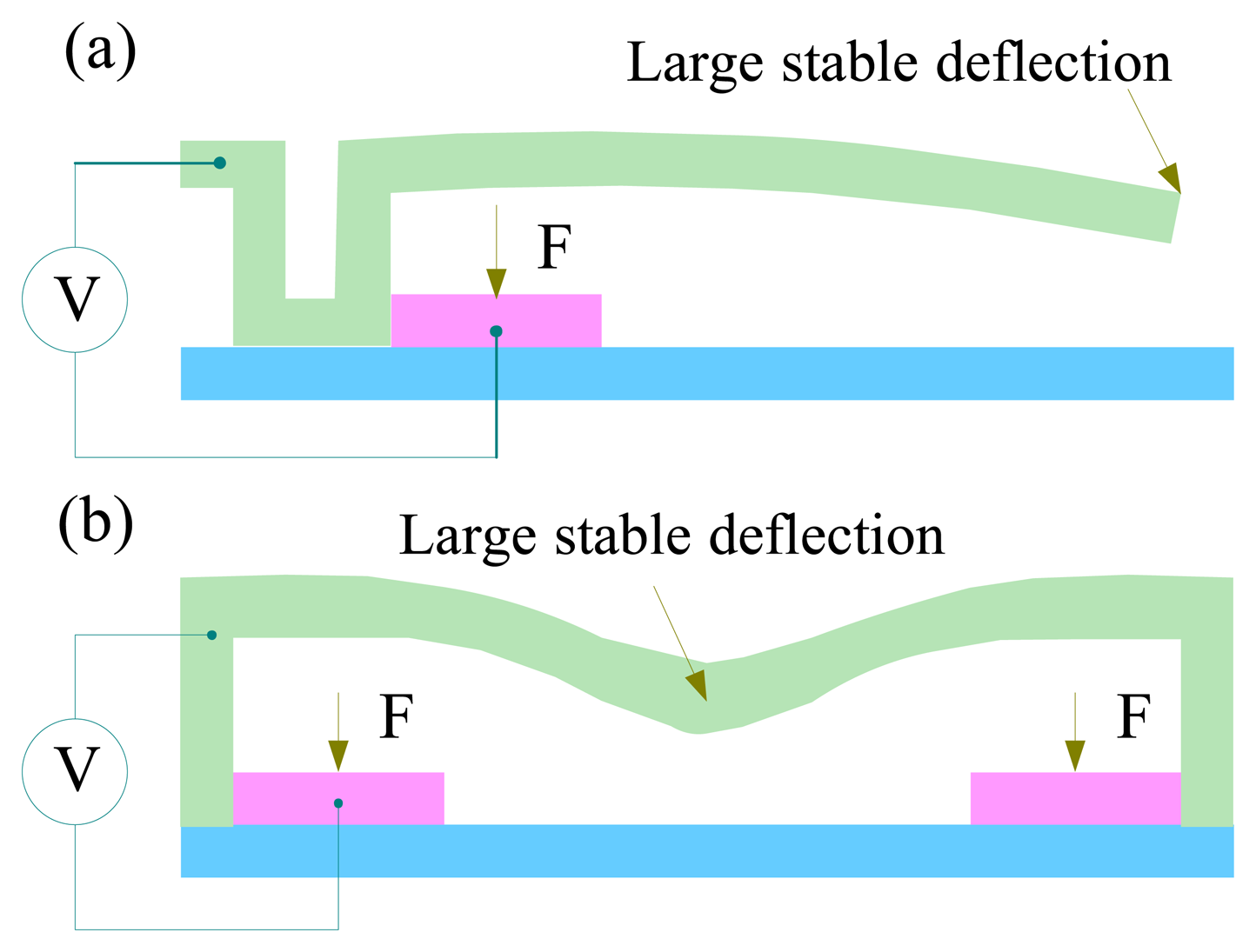
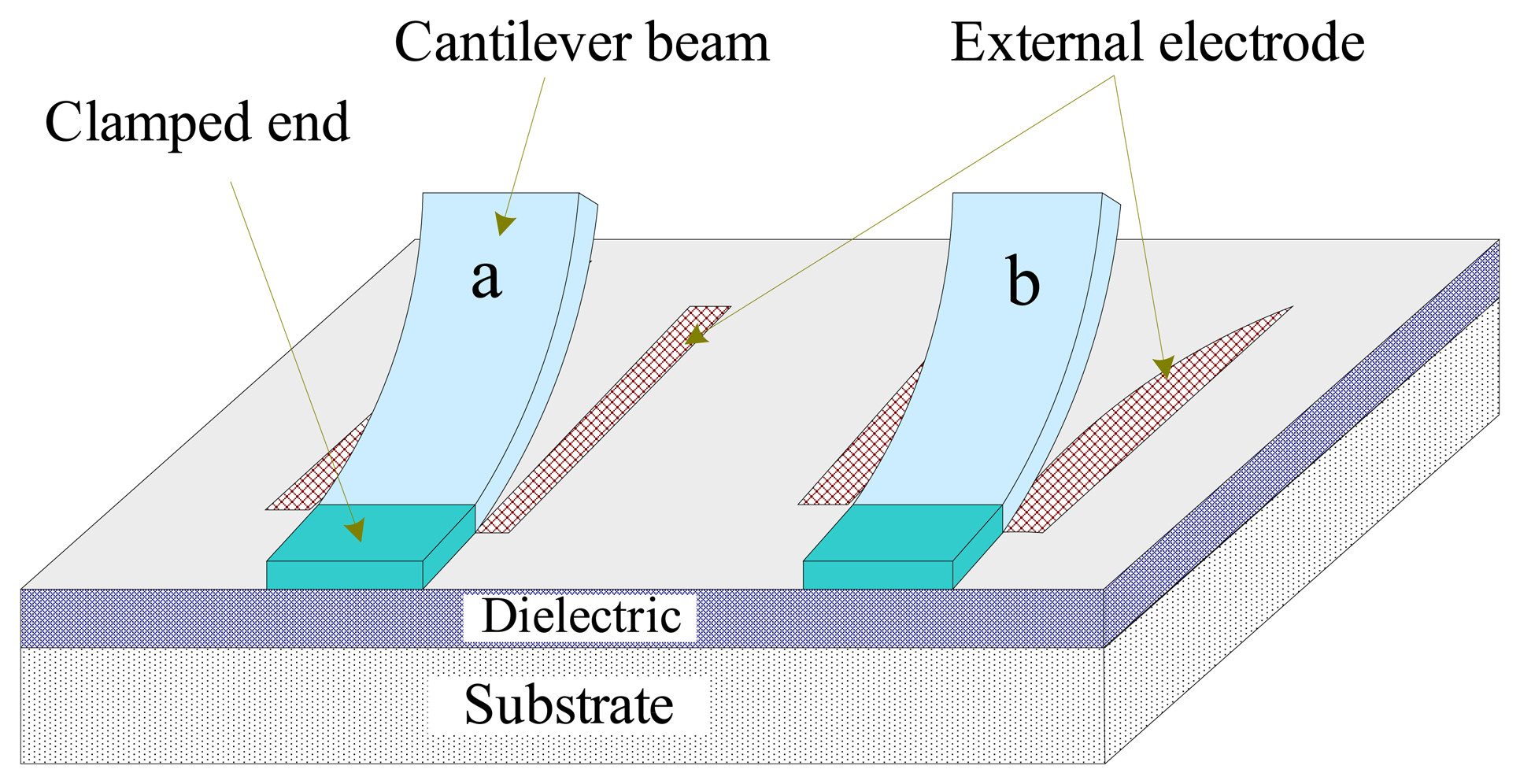
4.2.5. Extending the travel range
5. Nonlinearity analysis
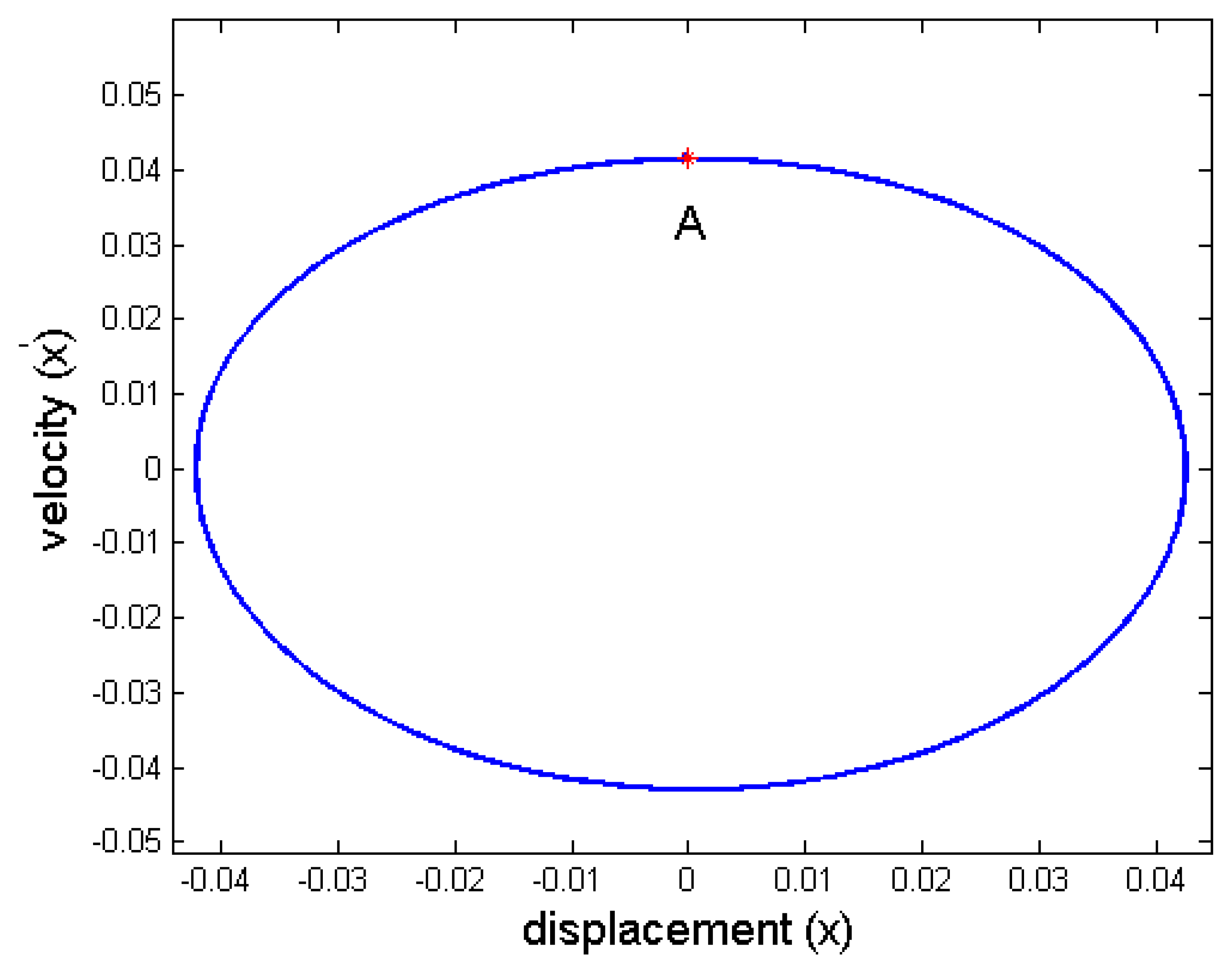
5.1. Resonance response
5.2. Inherent nonlinear effect
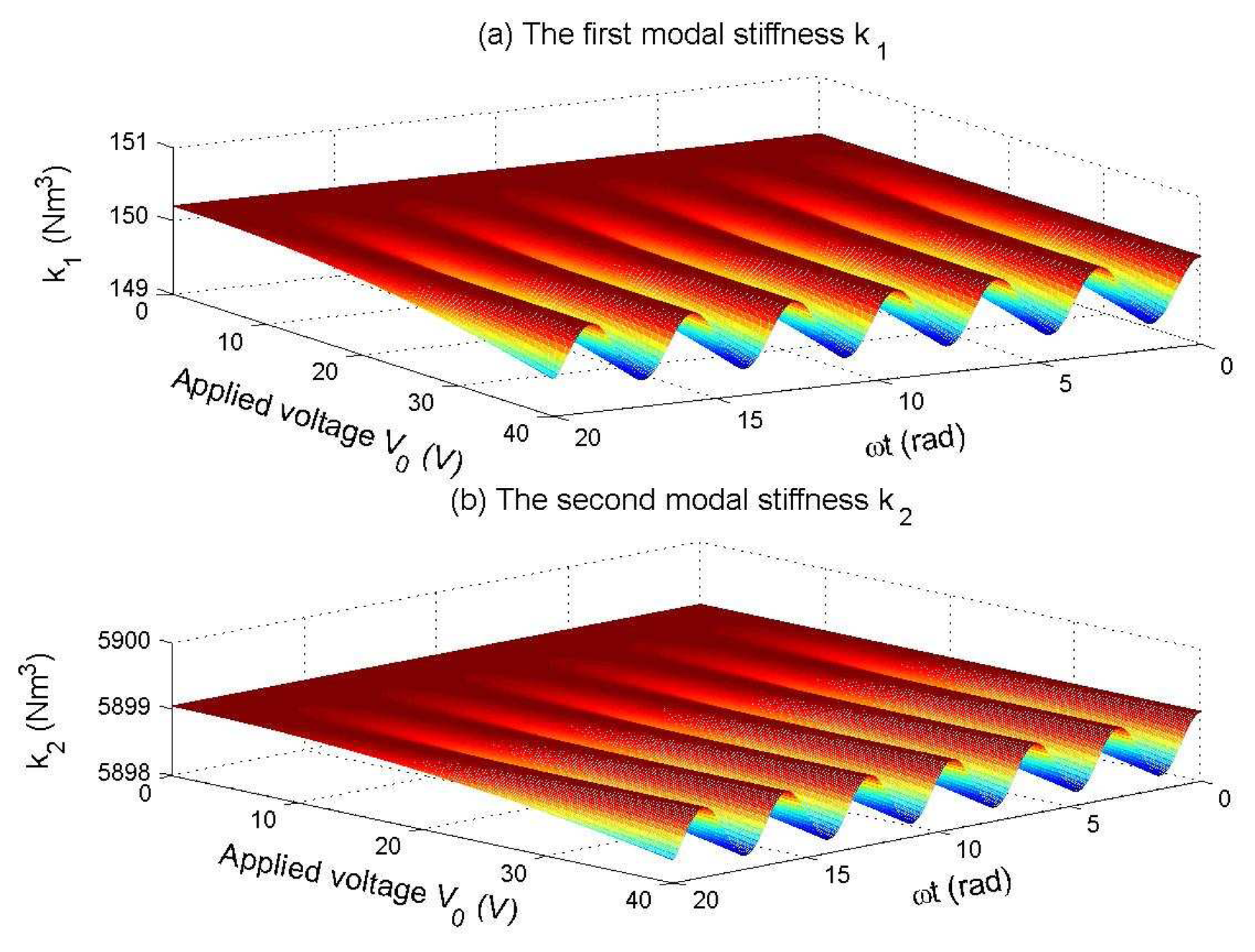
5.3. Stiffness softened effect
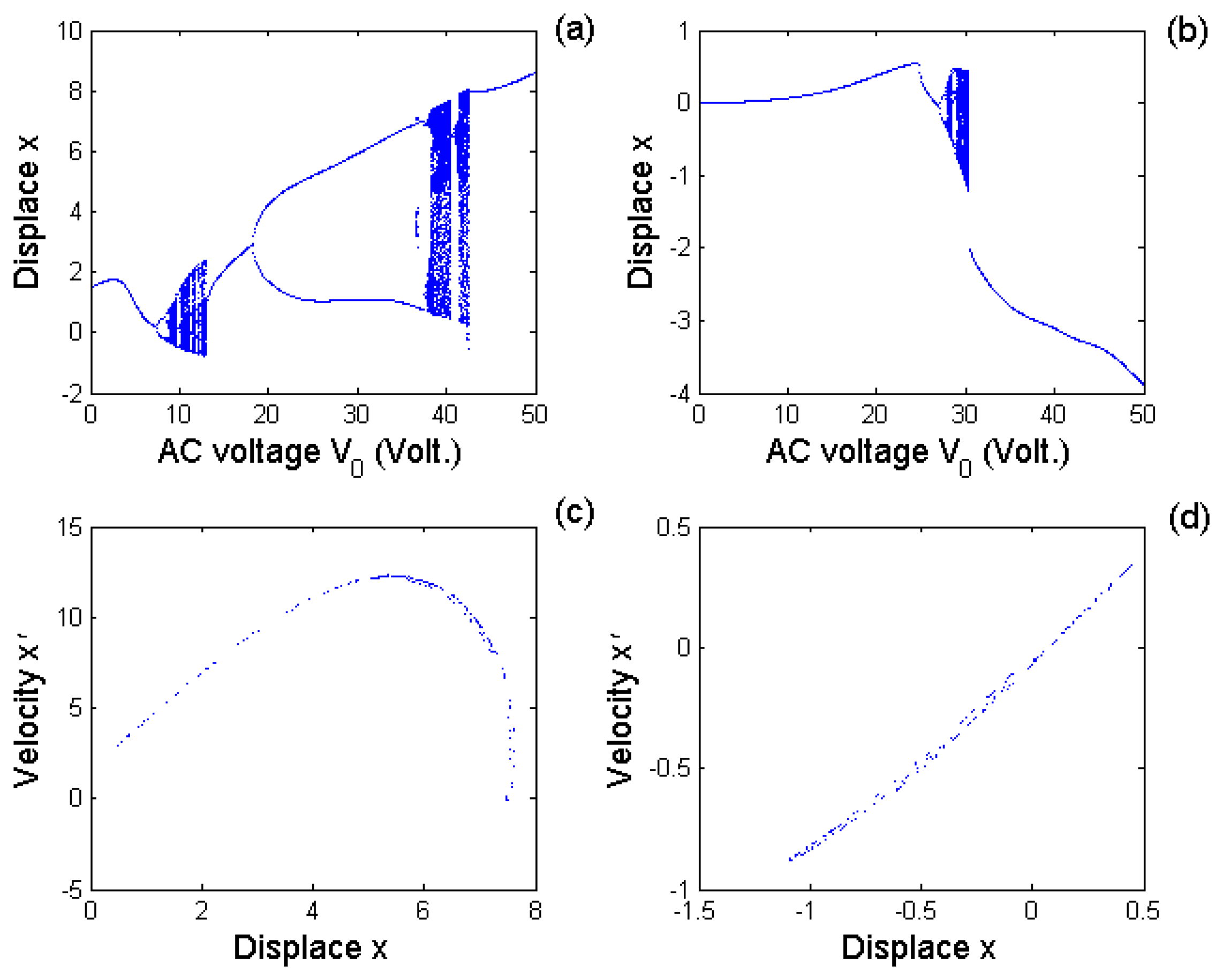
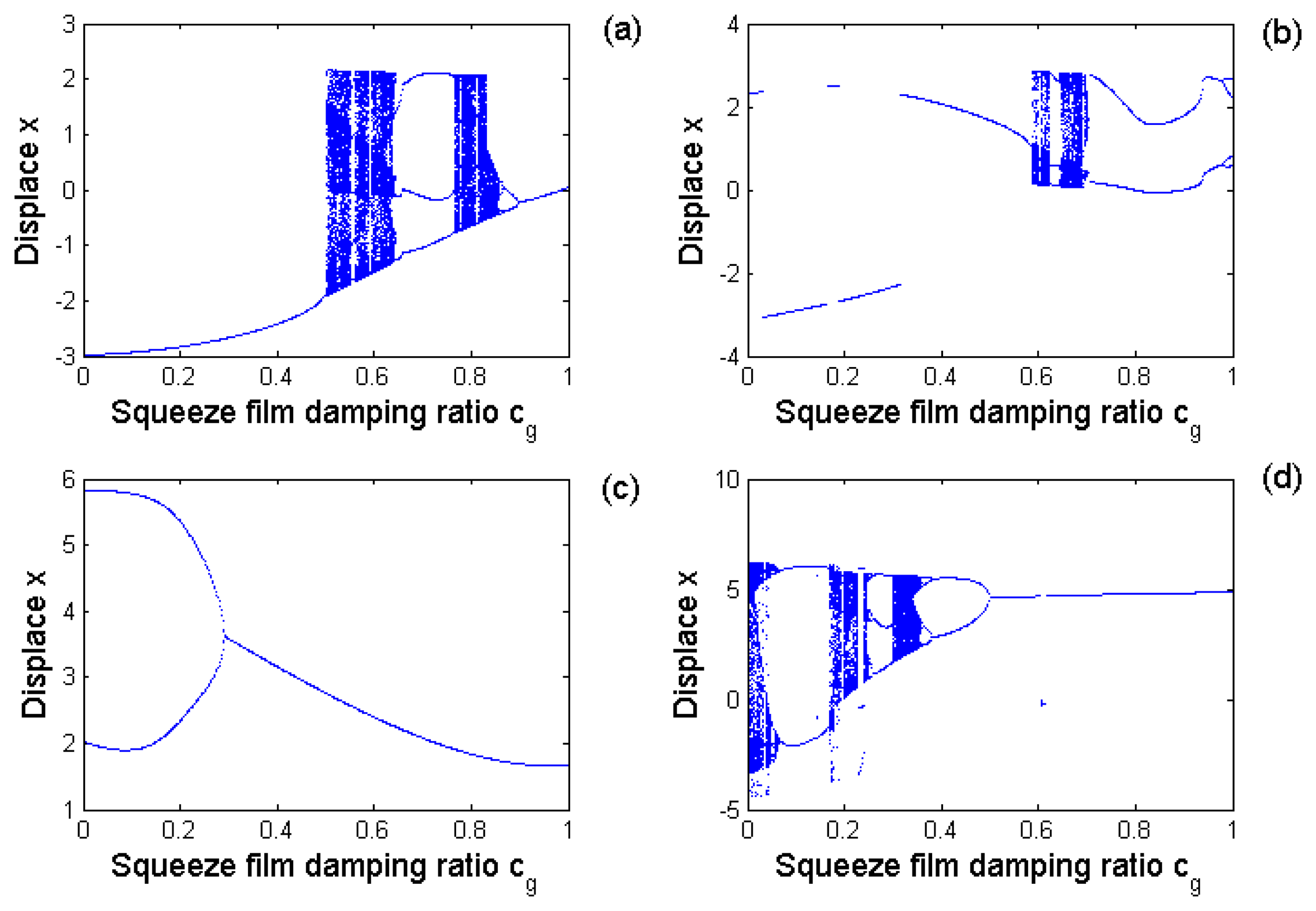
5.4. Coupled nonlinear effect
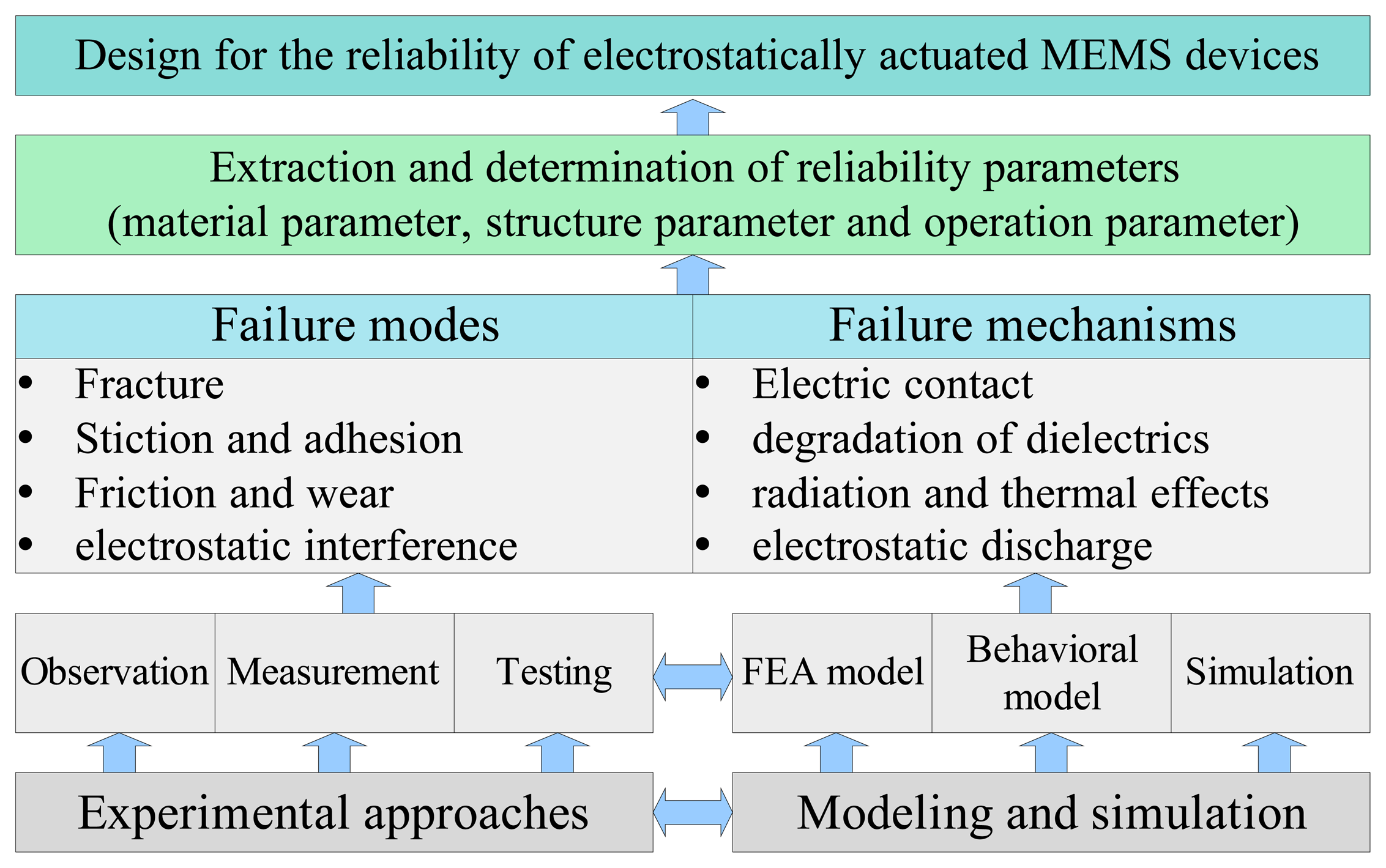
6. Reliability analysis
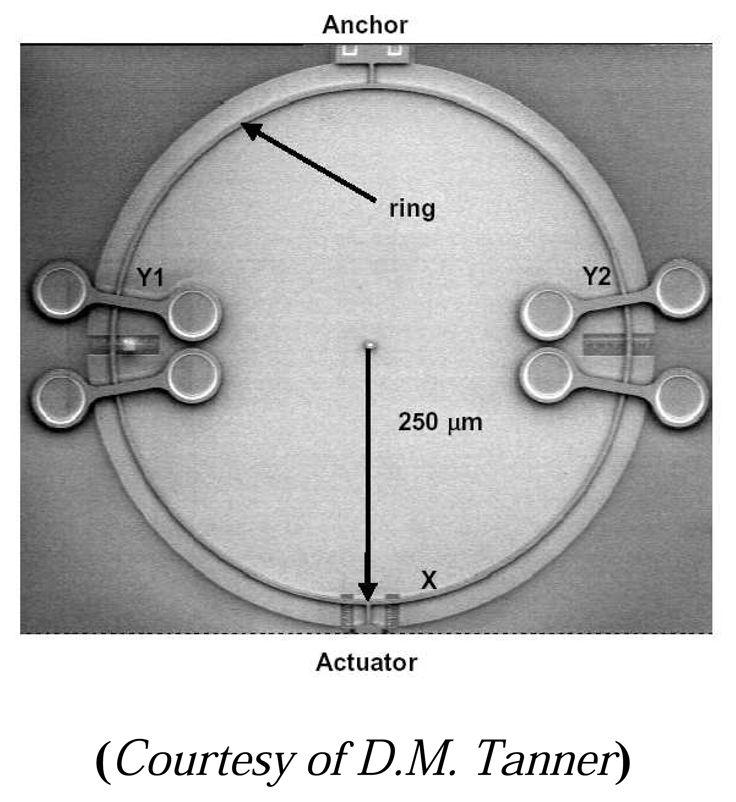
6.1. Failure models and mechanisms
6.1.1. Fracture
6.1.2. Stiction and adhesion
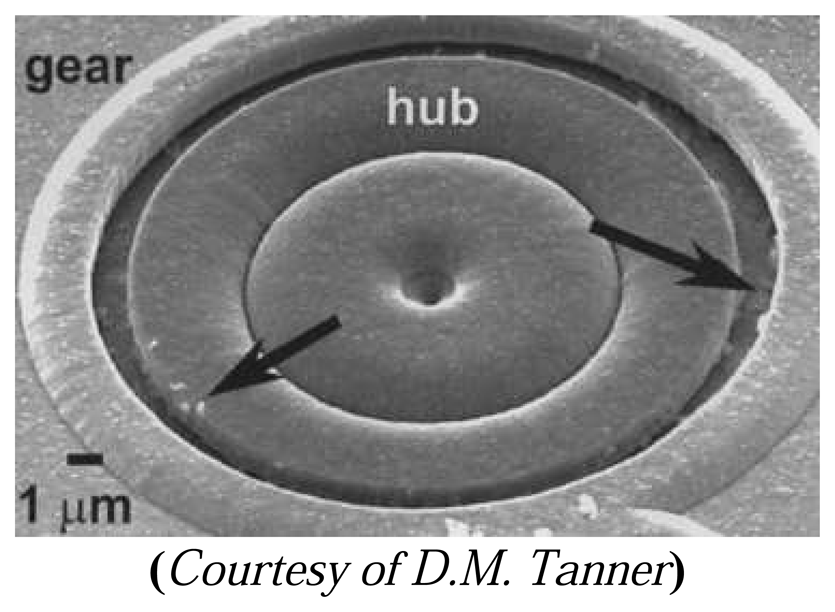
6.1.3. Friction and wear
6.1.4. Dielectric charging and breakdown
(1) Electrostatic interference
(2) Radiation effect
(3) Breakdown voltage
(4) Lifetime prediction
(5) Methods to reduce the effects of charging
6.1.5. Environmentally induced failure mechanisms
(1) Anodic oxidation
(2) Electrostatic discharge
6.2. Approaches to failure analysis
6.2.1. Selection of materials
6.2.2. Modeling and simulation
6.2.3. Experimental techniques
(1) Observation
(2) Measurement
(3) Testing
7. Conclusions
Acknowledgments
References
- Huber, J.E.; Fleck, Z.A.; Ashby, M.F. The selection of mechanical actuators based on performance indices. Proc R Soc London Ser A 1997, 453, 2185–2205. [Google Scholar]
- Zhou, Shu-Ang. On forces in microelectromechanical systems. International Journal of Engineering Science 2003, 41, 313–335. [Google Scholar]
- Price, R.H.; Wood, J.E; Jacobsen, S.C. Modelling considerations for electrostatic forces in electrostatic microactuators. Sensors and Actuators 1989, 20, 107–114. [Google Scholar]
- Hu, Y.C.; Chang, C.M.; Huang, S.C. Some design considerations on the electrostatically actuated microstructures. Sensors and Actuators A 2004, 112, 155–161. [Google Scholar]
- Pamidighantam, S.; Puers, R.; Baert, K.; Tilmans, H.A.C. Pull-in voltage analysis of electrostatically actuated beam structures with fixed-fixed and fixed-free end conditions. J Micromech Microeng 2002, 12, 454–464. [Google Scholar]
- Sasayama, T.; Suzuki, S.; Tsuchitani, S.; Koide, A.; Suzuki, M.; Ichikawa, N.; Nakazawa, T. Highly reliable silicon micromachined physical sensors in mass production. Sensors and Actuators A 1996, 54, 714–717. [Google Scholar]
- Bao, M.H.; Yang, H.; Yin, H.; Shen, S.Q. Effects of electrostatic forces generated by the driving signal on capacitive sensing devices. Sensors and Actuators A 2000, 24, 213–219. [Google Scholar]
- Lee, S.; Ramadoss, R.; Buck, M.; Bright, V.M.; Gupta, K.C.; Lee, Y.C. Reliability testing of flexible printed circuit-based RF MEMS capacitive switches. Microelectronics Reliability 2004, 44, 245–250. [Google Scholar]
- MoCarthy, B.; Adams, G.G.; McGruer, N.E.; Potter, D. A dynamical model, including contact bounce, of an electrostatically actuated microswitch. J Microelectromech Syst 2002, 11, 276–283. [Google Scholar]
- Millet, O.; Bernardoni, P.; Regnier, S.; Bidaud, P.; Tsitsiris, E.; Collard, D.; Buchaillot, L. Electrostatic actuated micro gripper using an amplification mechanism. Sensors and Actuators A 2004, 114, 371–378. [Google Scholar]
- Schiele, I.; Huber, J.; Hillerich, B.; Kozlowski, F. Surface-micromachined electrostatic microrelay. Sensors and Actuators A 1998, 66, 345–354. [Google Scholar]
- Mehregany, M.; Nagarkar, P.; Senturia, S.D.; Lang, J.H. Operation of microfabricated harmonic and ordinary side-drive motors. Proc. 3rd. IEEE MEMS Workshop, Napa Valley, CA, Feb. 1990; pp. 1–8.
- Tavrow, L.S.; Bart, S.F.; Lang, J.H. Operational characteristics of microfabricated electric motors. Sensors and Actuators A 1992, 35, 33–44. [Google Scholar]
- Ishihara, H.; Arai, F.; Fukuda, T. Micro mechatronics and micro actuators. IEEE/ASME Transactions on Mechatronics 1996, 1(1), 68–79. [Google Scholar]
- Zhang, W.M.; Meng, G.; Li, H.G. Electrostatic micromotor and its reliability. Microelectronics Reliability 2005, 45, 1230–1242. [Google Scholar]
- Hung, E.S.; Senturia, S.D. Extending the travel range of analog-tuned electrostatic actuators. J Microelectromech Syst 1999, 8(4), 497–505. [Google Scholar]
- Osterberg, P.M.; Senturia, S.D. M-test: a test chip for MEMS material property measurement using electrostatically actuated test structures. J Microelectromech Syst 1997, 6(2), 107–118. [Google Scholar]
- Zhang, W.M.; Meng, G. Nonlinear dynamic analysis of electrostatically actuated resonant MEMS sensors under parametric excitation. IEEE Sensors Journal 2007, 7(3), 370–380. [Google Scholar]
- Castaner, L.M.; Senturia, S.D. Speed-energy optimization of electrostatic actuators based on pull-in. J Microelectromech Syst 1999, 8, 290–298. [Google Scholar]
- Castaner, L.; Rodriguez, A.; Pons, J.; Senturia, S.D. Pull-in time energy product of electrostatic actuators: comparison of experiments with simulation. Sensors and Actuators A 2000, 83, 263–269. [Google Scholar]
- Quevy, E.; Bigotte, P.; Collard, D.; Buchaillot, L. Large stroke actuation of continuous membrane for adaptive optics by 3D self-assembled microplates. Sensors and Actuators A 2002, 95, 183–195. [Google Scholar]
- Chan, E.K.; Dutton, R.W. Electrostatic micromechanical actuator with extended range of travel. J Microelectromech Syst 2000, 9, 321–328. [Google Scholar]
- Nadal-Guardia, R.; Dehe, A.; Aigner, R.; Castaner, L.M. Current drive methods to extend the range of travel of electrostatic microactuators beyond the voltage pull-in point. J Microelectromech Syst 2002, 11, 255–263. [Google Scholar]
- Legtenberg, R.; Gilbert, J.; Senturia, S.D.; Elwenspoek, M. Electrostatic curved electrode actuators. J Microelectromech Syst 1997, 6, 257–265. [Google Scholar]
- Tang, W.C.; Nguyen, T.C.H.; Judy, M.W.; Howe, R.T. Electrostatic comb drive of lateral polysilicon resonators. Sensors and Actuators A 1990, 21-23, 323–331. [Google Scholar]
- Ye, W.; Mukherjee, S.; Macdonald, N.C. Optimal shape design of an electrostatic comb drive in microelectromechanical systems. J Microelectromech Syst 1998, 7, 16–26. [Google Scholar]
- Busta, H.; Amantea, R.; Furst, D.; Chen, J.M.; Turowski, M.; Mueller, C. A MEMS shield structure for controlling pull-in forces and obtaining increased pull-in voltages. J Micromech Microeng 2001, 11, 720–725. [Google Scholar]
- Zhang, W.M.; Meng, G. Nonlinear dynamical system of micro-cantilever under combined parametric and forcing excitations in MEMS. Sensors and Actuators A 2005, 119, 291–299. [Google Scholar]
- Liu, S.; Davidson, A.; Lin, Q. Simulating nonlinear dynamics and chaos in a MEMS cantilever using Poincare mapping. IEEE Transducers'03, the 12th International Conference on Solid State Sensors, Actuators and Microsystems, Boston, June 8-12 2003; pp. 1092–1095.
- Adams, S.G.; Bertsch, F.M.; Shaw, K.A.; MacDonald, N.C. Independent tuning of linear and nonlinear stiffness coefficients. J Microelectromech Syst 1998, 7(2), 172–180. [Google Scholar]
- Zhang, W.; Baskaran, R.; Turner, K.L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sensors and Actuators A 2002, 102, 139–150. [Google Scholar]
- Li, G.; Aluru, N.C. Linear, nonlinear and mixed-regime analysis of electrostatic MEMS. Sensors and Actuators A 2001, 91, 278–291. [Google Scholar]
- Aluru, N.R.; White, J. An efficient numerical technique for electromechanical simulation of complicated microelectromechanical structures. Sensors and Actuators A 1997, 58, 1–11. [Google Scholar]
- Younis, M.I.; Abdel-Rahman, E.M.; Nayfeh, A. A reduced-order model for electrically actuated microbeam-based MEMS. J Microelectromech Syst 2003, 12(5), 672–680. [Google Scholar]
- Senturia, S.D.; Harris, R.M.; Johnson, B.P.; Kim, S.; Nabors, K.; Shulman, M.A.; White, J.K. A computer-aided design system for microelectromechanical systems (MEMCAD). J Microelectromech Syst 1992, 1, 3–13. [Google Scholar]
- Li, G.Y.; Wang, L. Influence of bonding parameters on electrostatic force in anodic wafer bonding. Thin Solid Films 2004, 462-463, 334–338. [Google Scholar]
- Zhang, W.M.; Meng, G. Contact dynamics between the rotor and bearing hub in an electrostatic micromotor. Microsystem Technologies 2005, 11, 438–443. [Google Scholar]
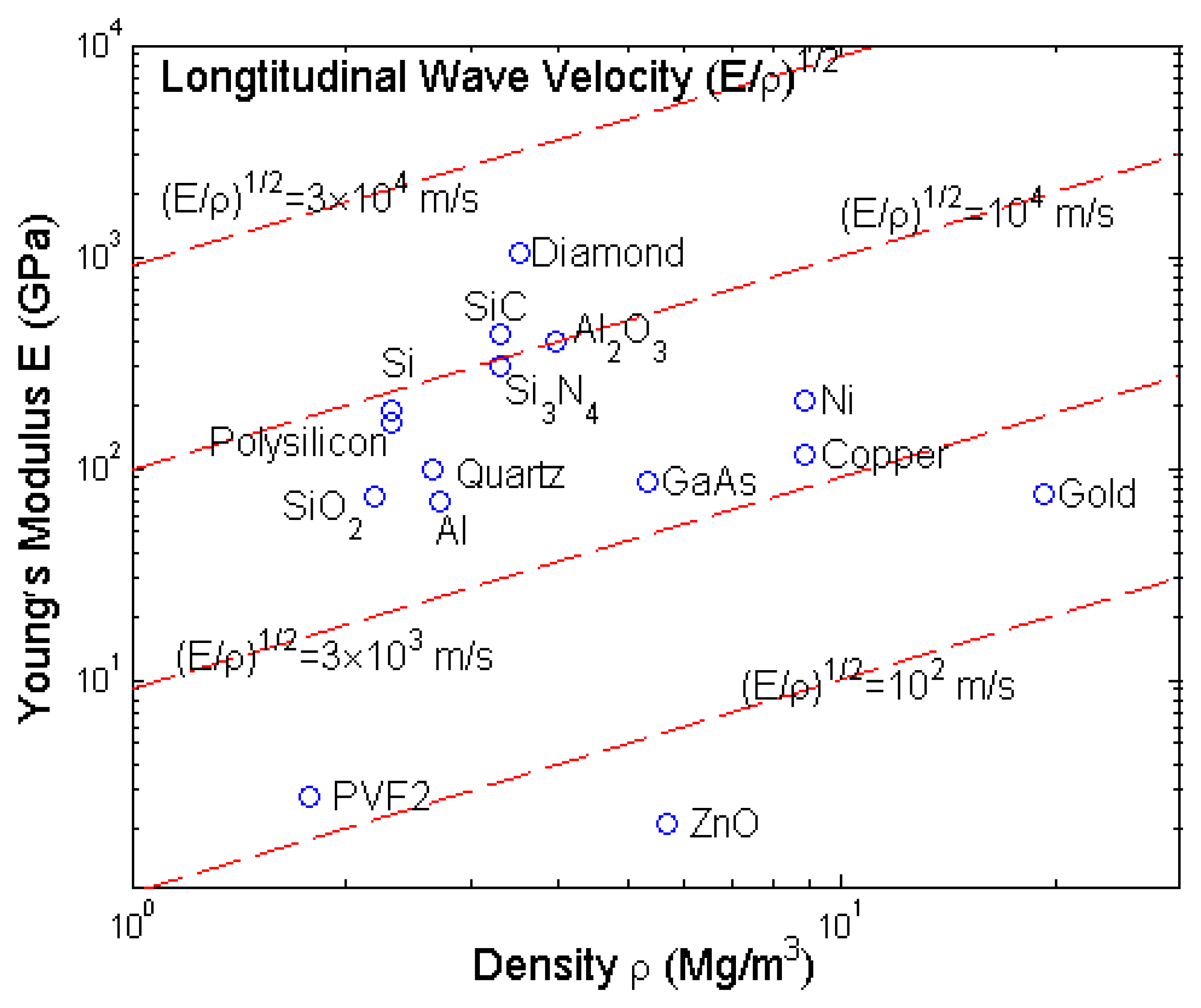
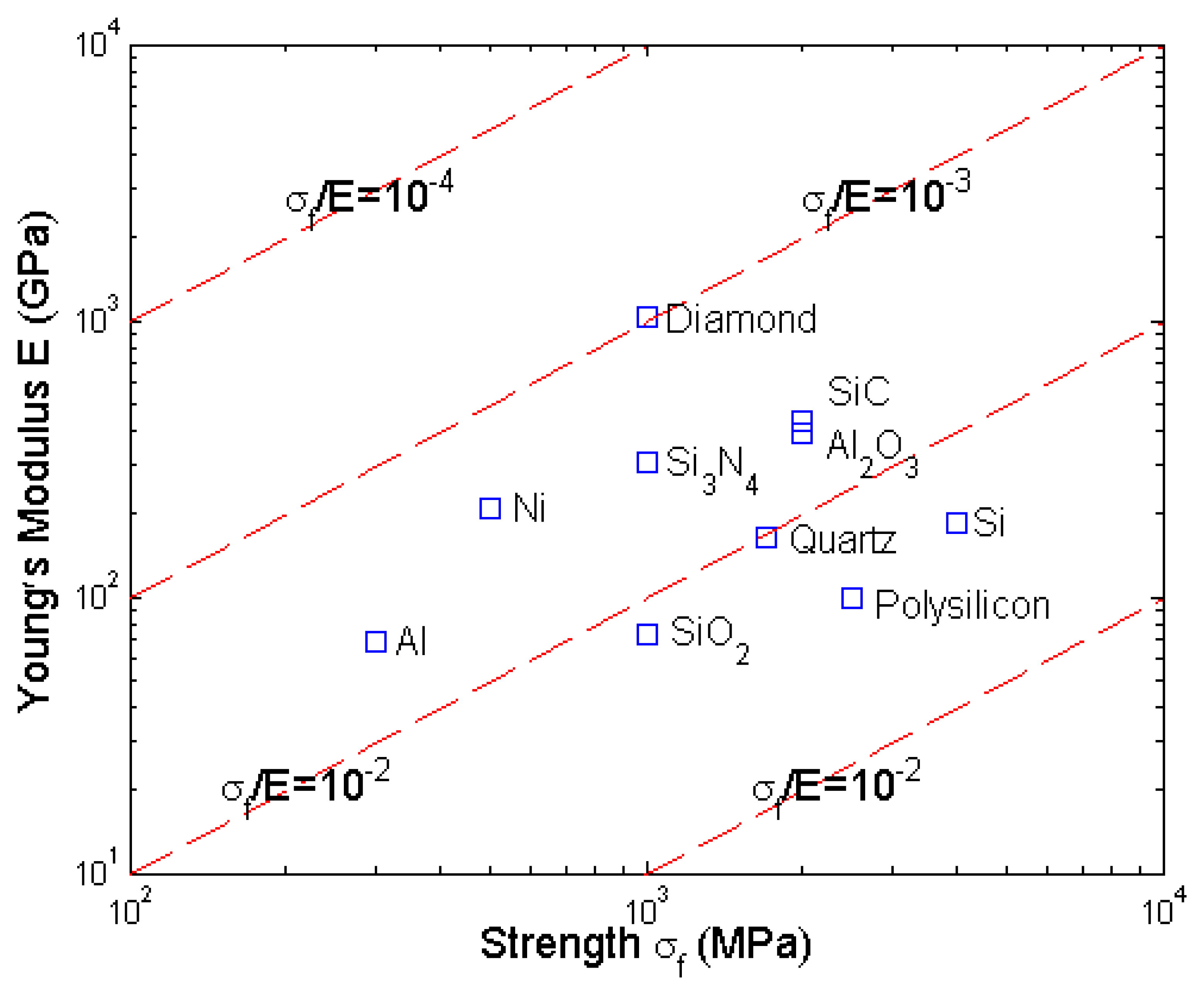
- Srikar, V.T.; Spearing, S.M. Materials selection for microfabricated electrostatic actuators. Sensors and Actuators A 2003, 102, 279–285. [Google Scholar]
- Zhang, W.M.; Meng, G. Stability, bifurcation and chaos analyses of a high-speed micro-rotor system with rub-impact. Sensors and Actuators A: Physical 2006, 127(1), 163–178. [Google Scholar]
- Srikar, V.T.; Spearing, S.M. Materials selection in micromechanical design: an application of the Ashby approach. J Microelectromech Syst 2003, 12(1), 3–10. [Google Scholar]
- Zhang, W.M.; Meng, G. Numerical simulation of sliding wear between the rotor bushing and ground plane in micromotors. Sensors and Actuators A: Physical 2006, 126, 15–24. [Google Scholar]
- Spearing, S.M. Materials issues in microelectromechanical systems (MEMS). Acta mater 2000, 48, 179–196. [Google Scholar]
- Li, B.Q.; Zhu, C.C.; Liu, J.H. Electrostatic force influenced by space charge in submicrometer or nanometer silicon microstructures. J Micromech Microeng 1999, 9, 319–323. [Google Scholar]
- Trimmer, W.S.N. Microrobots and Micromechanical Systems. Sensors and Actuators 1989, 19(3), 267–287. [Google Scholar]
- Peirs, J.; Reynaerts, D.; Brussel, H.V. Scale effects and thermal considerations for micro-actuators. Proceedings of the 1998 IEEE International Conference on Robotics & Automation, Leuven, Belgium, May 1998; pp. 1516–21.
- Fischer, M.; Giousouf, M.; Schaepperle, J.; Eichner, D.; Weinmann, M. Electrostatically deflectable polysilicon micromirrors-dynamic behaviour and comparison with the results from FEM modeling with ANSYS. Sensors and Actuators A 1998, 67, 89–95. [Google Scholar]
- Wibbeler, J.; Pfeifer, G.; Hietschold, M. Parasitic charging of dielectric surfaces in capacitive microelectromechanical systems (MEMS). Sensors and Actuators A 1998, 71(1-2), 74–80. [Google Scholar]
- O'Mahony, C.; Duane, R.; Hill, M.; Mathewson, A. Low-voltage micromechanical test structures for measurement of residual charge in dielectrics. Electronics Letters 2005, 41(7), 409–410. [Google Scholar]
- Lafontan, X.; Pressecq, F.; Beaudoin, F.; Rigo, S.; Dardalhon, M.; Roux, J.-L.; Schmitt, P.; Kuchenbecker, J.; Baradat, B.; Lellouchi, D.; Le-Touze, C.; Nicot, J.-M. The advent of MEMS in space. Microelectronics Reliability 2003, 43, 1061–1083. [Google Scholar]
- Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. Full characterization of pull-in single-sided clamped beams. Sensors and Actuators A 2004, 110, 301–309. [Google Scholar]
- Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. Compensation of temperature effects on the pull-in voltage of microstructures. Sensors and Acutators A 2004, 115, 351–356. [Google Scholar]
- Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. The pull-in of symmetrically and asymmetrically driven microstructures and the use in dc voltage references. Proc. of IMTC02, Anchorage, USA, 21-23 May 2002; Vol. 1, pp. 759–764.
- Tada, H.; Kumpel, A.E.; Lathrop, R.E.; Slanina, J.B.; Nieva, P.; Zavracky, P.; Miaoulis, I.N.; Wong, P.Y. Thermal expansion coefficient of polycrystalline silicon and silicon dioxide thin films at high temperatures. J Appl Phys 2000, 87, 4189–4193. [Google Scholar]
- Burns, D.M.; Bright, V.M. Nonlinear flexture for stable deflection of an electrostatically actuated micromirror. Proc. of the SPIE on Microelectronics Structures and MEMS for Optical Processing III 1997, 3226, 125–135. [Google Scholar]
- Rosa, M.A.; Bruyker, D.D.; Volkel, A.R.; Peeters, E. A novel external electrode configuration for the electrostatic actuation of MEMS based devices. J Micromech Microeng 2004, 14, 446–451. [Google Scholar]
- Seeger, J.I.; Boser, B.E. Dynamics and control of parallel-plate actuators beyond the electrostatic instability. Proc. of the Transducers; 1999; pp. 474–477. [Google Scholar]
- Chu, P.B.; Pister, K.S.J. Analysis of closed-loop control of parallel plate electrostatic microgrippers. Proc. of the IEEE International Conference on Robotics and Automation; 1994; pp. 820–825. [Google Scholar]
- Sun, Y.; Piyabongkarn, D.; Sezen, A.; Nelson, B.J.; Rajamani, R. A high-aspect-ratio two-axis electrostatic microactuator with extended travel range. Sensors and Actuators A 2002, 102, 49–60. [Google Scholar]
- Gilbert, J.R.; Senturia, S.D. Two-phase actuators: stable zipping devices without fabrication of curved structures. Solid-State Sensor and Actuator Workshop (Hilton Head, SC) 1996, 98–100. [Google Scholar]
- Legtenberg, R.; Berenschot, E.; Elwenspoek, M.; Fluitman, J. Electrostatic curved electrode actuators. IEEE Workshop on Micro Electro Mechanical Systems (MEMS)'95, Amsterdam; 1995; pp. 37–42. [Google Scholar]
- Bochobza-Degani, O.; Elata, D.; Nemirovsky, Y. A general relation between the ranges of stability of electrostatic actuators under charge or voltage control. Appl Phys Lett 2003, 82, 302–304. [Google Scholar]
- Chu, P.B.; Nelson, P.R.; Tachiki, M.L.; Pister, K.S. Dynamics of polysilicon parallel-plate electrostatic actuator. Sensors and Actuators A 1996, 52, 216–220. [Google Scholar]
- Veijola, T.; Kuisma, H.; Lahdenpera, J. The influence of gas-surface interaction on gas film damping in a silicon accelerometer. Sensors and Actuators A 1998, 66, 83–92. [Google Scholar]
- Starr, J.B. Squeeze-film damping in solid-state accelerometers. Proc. IEEE Solid State Sensor and Actuator Workshop, Hilton Head Island, SC, USA, June 4-7 1990; pp. 44–47.
- Walraven, J.A. Failure Mechanisms in MEMS. ITC International Test Conference, Charlotte, NC, USA, September 30-October 02, 2003; pp. 808–812.
- Spengen, W.M.V.; Puers, R.; Wolf, I.D. A physical model to predict stiction in MEMS. J Micromech Microeng 2002, 12, 702–713. [Google Scholar]
- Knudson, A.R.; Buchner, S.; McDonald, P.; Stapor, W.J.; Campbell, A.B.; Grabowski, K.S.; Knies, D.L.; Lewis, S.; Zhao, Y. The effects of radiation on MEMS accelerometers. IEEE Trans Nucl Sci Indian Wells, CA, USA; 1996; 43, pp. 3122–3126. [Google Scholar]
- Gabriel, K.J.; Behi, F.; Mahadevan, R. In-Situ Friction and Wear Measurements in Integrated Polysilicon Mechanisms. Sensors and Actuators A 1990, 21-23, 184–188. [Google Scholar]
- Tanner, D.M.; Miller, W.M.; Peterson, K.A.; Dugger, M.T.; Eaton, W.P.; Irwin, L.W.; Senft, D.C.; Smith, N.F.; Tangyunyong, P.; Miller, S.L. Frequency dependence of the lifetime of a surface micromachined microengine driving a load. Microelectronics Reliability 1999, 39, 401–414. [Google Scholar]
- Kahn, H.; Tayebi, N.; Ballarini, R.; Mullen, R.L.; Heuer, A.H. Fracture toughness of polysilicon MEMS devices. Sensors and Actuators A 2000, 82, 274–280. [Google Scholar]
- Komvopoulos, K. Surface engineering and microtribology for microelectromechanical systems. Wear 1996, 200(1-2), 305–327. [Google Scholar]
- Spengen, W.M.V. MEMS reliability from a failure mechanisms perspective. Microelectronics Reliability 2003, 43, 1049–1060. [Google Scholar]
- Shea, H.R.; Gasparyan, A.; Chan, H.B.; Arney, S.; Frahm, R.E.; Lopez, D.; Jin, S.; McConnel, R.P. Effects of electrical leakage currents on MEMS reliability and performance. IEEE Transactions on Device and Materials Reliability 2004, 4(2), 198–207. [Google Scholar]
- Schanwald, L.P.; Schwank, J.R.; Sniegowski, J.J.; Albuquerque, N.M. Radiation effects on surface micromachined comb drives and microengines. IEEE Trans Nucl Sci 1998, 45, 2789–2798. [Google Scholar]
- Mcclure, S.S.; Edmonds, L.D.; Mihailovich, R.; Johnston, A. Radiation effects in microelectromechanical systems (MEMS): RF relay. IEEE Transactions on Nuclear Science 2002, 49(6), 3197–3202. [Google Scholar]
- Madou, M.J. Fundamentals of Microfabrication: The Science of Miniaturization, 2nd ed.; Cleveland, OH; CRC Press, 2002. [Google Scholar]
- http://home.earthlink.net/∼jimlux/hv/paschen.htm (online).
- Dhariwal, R.S.; Torres, J.M.; Desmulliez, M.P.Y. Electric field breakdown at micrometer separations in air and nitrogen at atmospheric pressure. IEE Proc Sci Meas Technol 2000, 147(5), 261–265. [Google Scholar]
- Torres, J.M.; Dhariwal, R.S. Electric field breakdown at micrometre separations in air and vacuum. Microsystem Technologies 1999, 6, 6–10. [Google Scholar]
- Spengen, W.M.V.; Puers, R.; Mertens, R.; Wolf, I.D. A comprehensive model to predict the charging and reliability of capacitive RF MEMS switches. J Micromech Microeng 2004, 14, 514–521. [Google Scholar]
- Zafar, S.; Callegari, A.; Gusev, E.; Fischetti, M.V. Charge trapping in high k gate dielectric stacks. Proc Int Electron Devices Meeting (IEDM); 2002; p. 517. [Google Scholar]
- Ehmke, J.; Goldsmith, C.; Yao, Z.; Eshelman, S. Method and apparatus for switching high frequency signals. U.S. Patent 6, 391, 675, 21 May 2002. [Google Scholar]
- Shea, H.R.; White, C.; Gasparyan, A.; Comizzoli, R.B.; Abusch-Magder, C.; Arney, S. Anodic oxidation and reliability of poly-Si MEMS electrodes at high voltages and in high relative humidity. In Proc SPIE, MEMS Reliability for Critical Applications; Lawton, R., Ed.; 2000; vol. 4180, pp. 117–122. [Google Scholar]
- Plass, R.A.; Walraven, J.A.; Tanner, D.M.; Sexton, F.W. Anodic oxidation-induced delamination of the SUMMiT polysilicon nitride interface. In Proc SPIE, Reliability, Testing, and Characterization of MEMS/MOEMS II; Ramesham, R., Tanner, D. M., Eds.; 2003; vol. 4980, pp. 81–86. [Google Scholar]
- Lewerenz, H.J. Anodic oxides on silicon. Electrochimica Acta 1992, 37, 847–864. [Google Scholar]
- Romig, J.A.D.; Dugger, M.T.; McWhorter, P.J. Materials issues in microelectromechanical devices: science, engineering, manufacturability and reliability. Acta Materialia 2003, 51, 5837–5866. [Google Scholar]
- Ashby, M.F. Materials Selection in Mechanical Design.; Oxford, U.K; Butterworth-Heinemann, 1999. [Google Scholar]
- Zhang, W.M.; Meng, G. Active vibration control of micro-cantilever beam in MEMS., IEEE International Conference on Intelligent Mechatronics and Automation, Chengdu, China, August 26-31 2004; pp. 272–276.
- Zettler, T. Integrated circuit fabrication compatible three-mask tungsten process for micromotors and gears. Sensors and Actuators A 1994, 44, 159–163. [Google Scholar]
- Reyntjens, S.; Puers, R. A review of focused ion beam applications in microsystem technology. J Micromech Microeng 2001, 11, 287–300. [Google Scholar]
- Walraven, J.A.; Peterson, K.A.; Tangyunyong, P.; Dugger, M.T.; Miller, S.L. MEMS reliability: Infrastructure, test structures, experiments, and failure modes; Sandia National Laboratories: Albuquerque, NM, Sandia Rep. SAND 2000-0091.
- Ashursta, W.R.; Boerb, M.P.D.; Carraroa, C.; Maboudian, R. An investigation of sidewall adhesion in MEMS. Applied Surface Science 2003, 212-213, 735–741. [Google Scholar]
- Larsen, K.P.; Rasmussen, A.A.; Ravnkilde, K.T.; Ginnerup, M.; Hansen, O. MEMS device for bending test: measurements of fatigue and creep of electroplated nickel. Sensors and Actuators A 2003, 103, 156–164. [Google Scholar]


| Force | Formulation | Scaling | Description |
|---|---|---|---|
| Electrostatic force | [L2] | Ef : electric field strength ε0 : permittivity A : surface area (Normal) | |
| [L0] | V : applied voltage d : gap (MEMS) | ||
| Electromagnetic force | [L2] | μ0 : permeability B : magnetic density | |
| Ac: area of cross section of coil | |||
| Piezoelectric force | [L2] | L : length E : Young's modules | |
| ΔL: strain | |||
| Lorentz force | FL = I (L × B) | [L2] | I: current density |
| Thermal expansion force | [L2] | L : length E : Young's modules | |
| ΔL: strain T: temperature | |||
| Inertial force | [L3] | m : mass t : time x : displacement | |
| cv : viscosity coefficient A : | |||
| Viscosity force | [L3] | surface area t : time x : displacement | |
| Elastic force | [L2] | L : length E : Young's modules | |
| ΔL: strain A : cross section area | |||
| Friction force | Ff = μN | [L2] | μ : friction coefficient N : normal force |
| Failure mode | Failure mechanism | Example | Reference |
|---|---|---|---|
| Stiction and adhesion | Surface contact | Comb finger actuator, beam | [65, 66] |
| Electrostatic interference | Electrical contact | Electrostatic micromotor | [12, 15] |
| Dielectric changing and breakdown | Nuclear radiation | Accelerometer, RF MEMS switch | [8, 47, 67] |
| Wear and friction | Surface contact and rubbing | Micro-motor, microengine | [68, 69] |
| Fracture | Intrinsic and applied stress | comb finger actuator | [70] |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Zhang, W.-M.; Meng, G.; Chen, D. Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices. Sensors 2007, 7, 760-796. https://doi.org/10.3390/s7050760
Zhang W-M, Meng G, Chen D. Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices. Sensors. 2007; 7(5):760-796. https://doi.org/10.3390/s7050760
Chicago/Turabian StyleZhang, Wen-Ming, Guang Meng, and Di Chen. 2007. "Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices" Sensors 7, no. 5: 760-796. https://doi.org/10.3390/s7050760




