Simulation of Optical Microfiber Loop Resonators for Ambient Refractive Index Sensing
Abstract
:1. Introduction
2. Theory
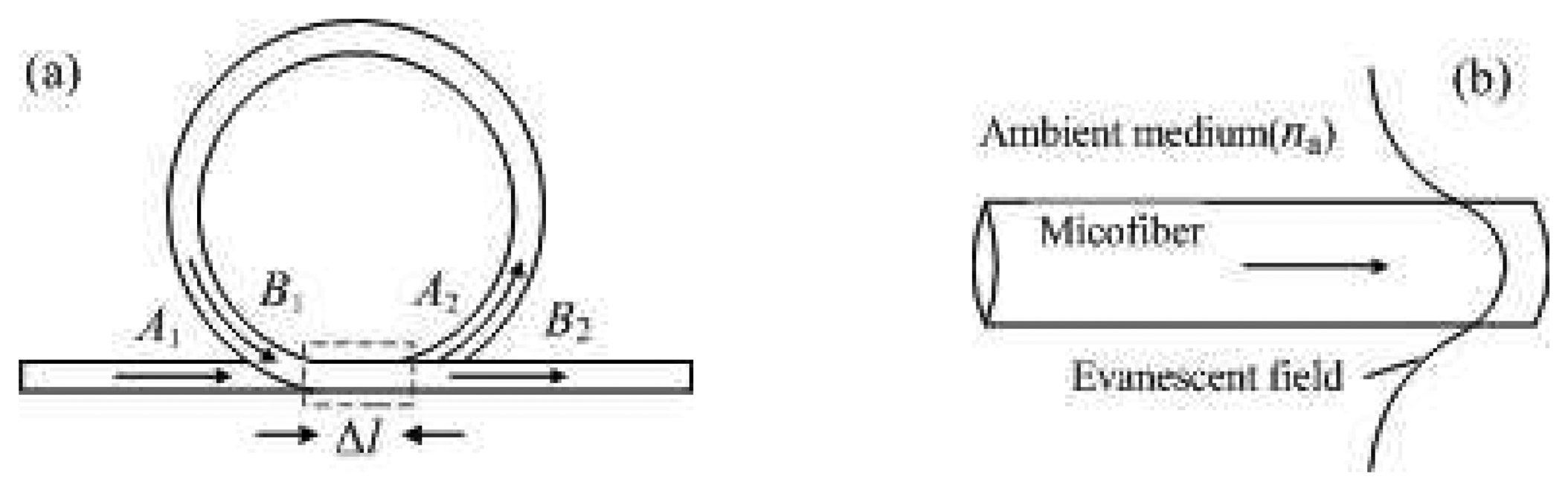
2.1. Fundamental s of an MLR
2.2. Sensing Parameters
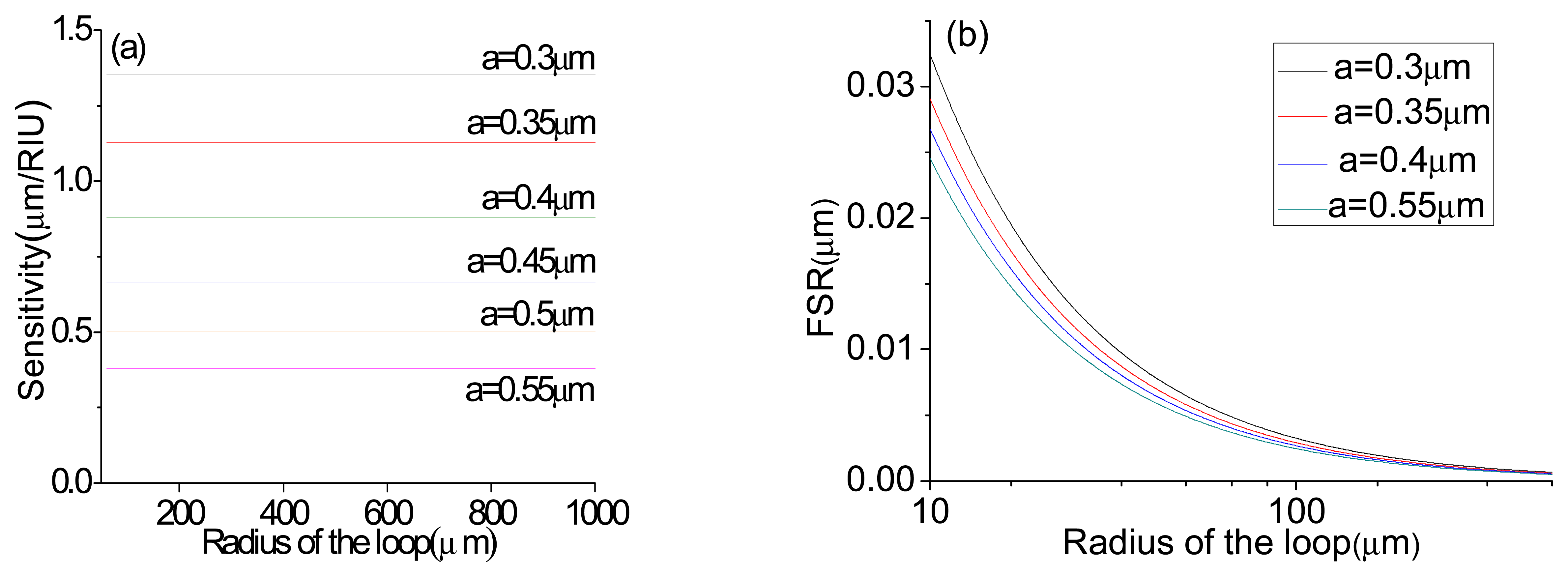
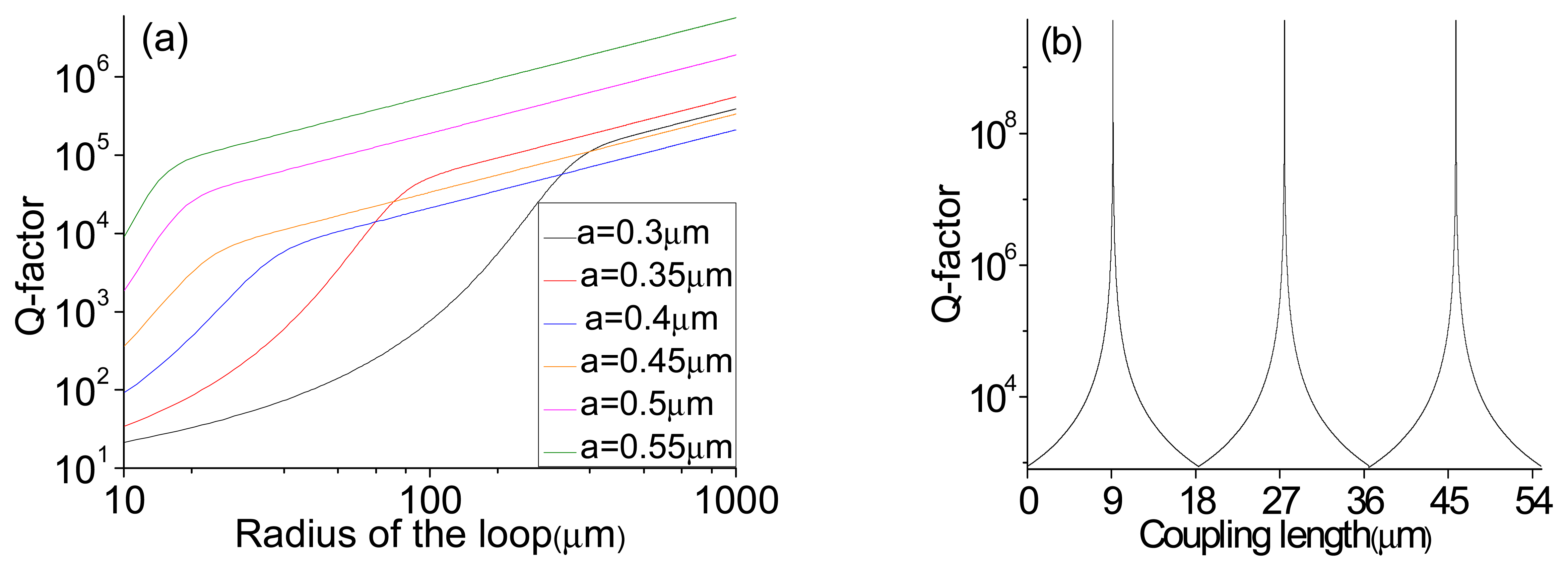
3. Optimization of the Structural Parameters of the MLR for Ambient Refractive Index Sensing
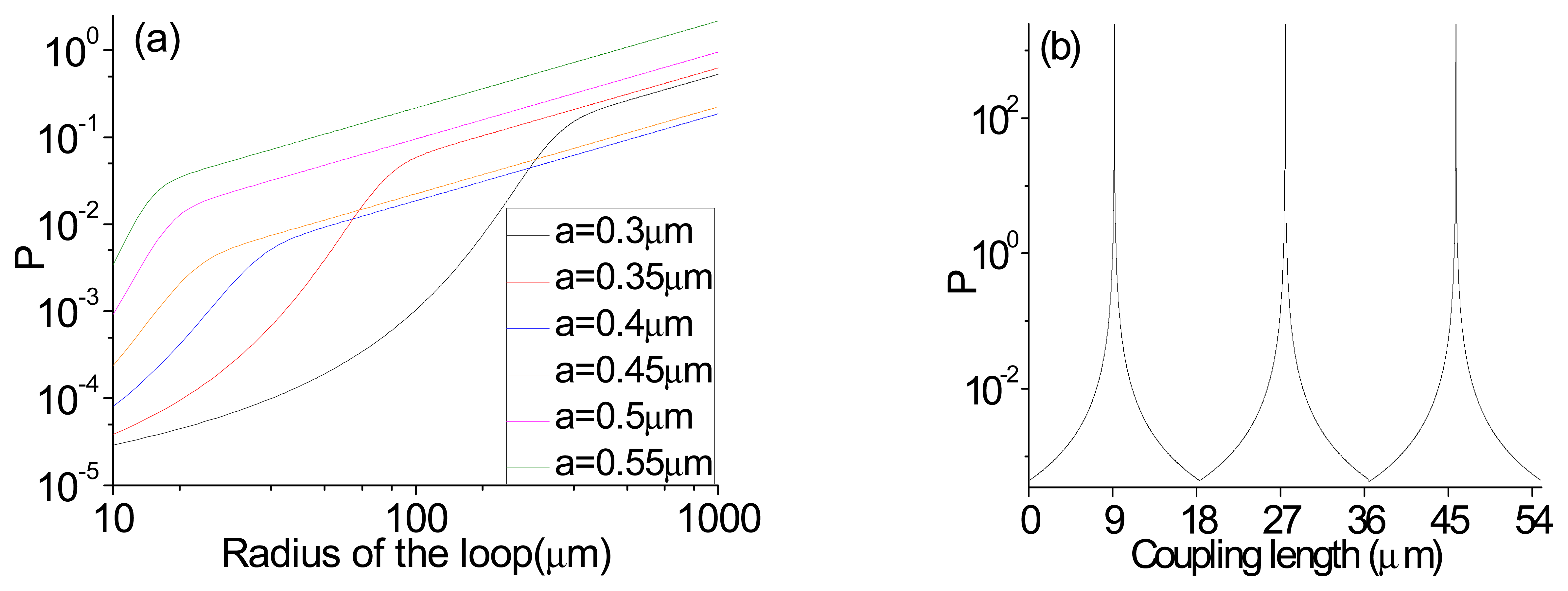
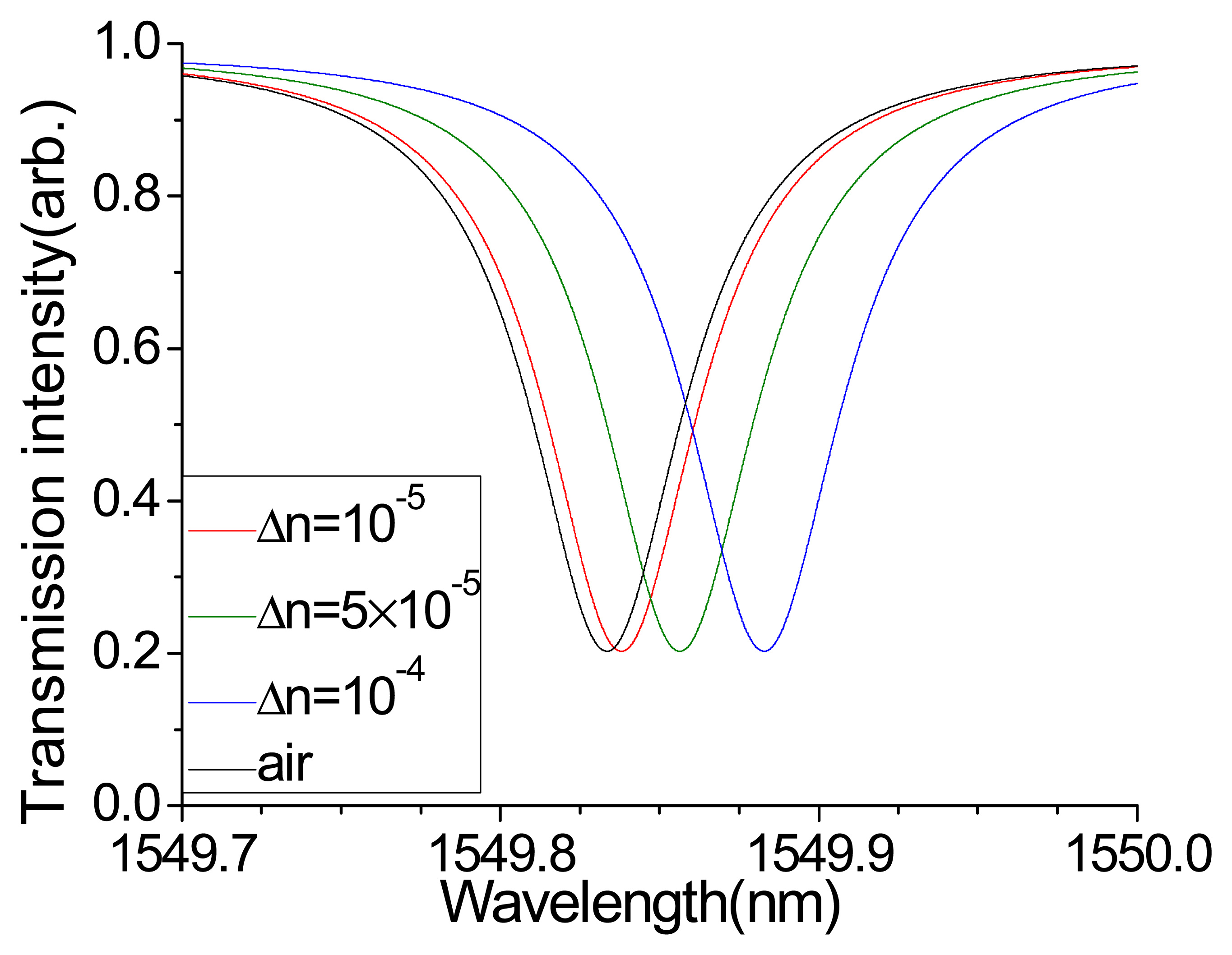
4. Simulation of Sensing an Extreme Small Variation of Ambient Refractive Index
5. Conclusion
Acknowledgments
References
- Tong, L.; Ashcom, J.B.; He, S.L.; Lou, J.Y.; Shen, M.Y.; Maxwell, I.; Mazur, E. Subwavelength-diameter silica wires for low-loss optical waveguiding. Nature 2003, 426, 816–819. [Google Scholar]
- Brambilla, G.; Finazz, V.; Richardson, D. J. Ultra-low-loss optical fiber nanotapers. Opt. Express 2004, 12, 2258–2263. [Google Scholar]
- Leon-Saval, S.G.; Birks, T. A.; Wadsworth, W. J.; Russell, P. St. J. Supercontinuum generation in submicron fibre waveguides. Opt. Express 2004, 12, 2864–2869. [Google Scholar]
- Sumetsky, M.; Dulashko, Y.; Hale, A. Fabrication and study of bent and coiled free silica nanowires: Self-coupling microloop optical interferometer. Opt. Express 2004, 12, 3521–3531. [Google Scholar]
- Law, M.; Sirbuly, D.J.; Johnson, J.C.; Goldberger, J.; Saykally, R.J.; Yang, P.D. Nanoribbon waveguides for subwavelength photonics integration. Science 2004, 305, 1269–1273. [Google Scholar]
- Brambilla, G.; Xu, F.; Feng, X. Fabrication of optical fiber nanowires and their optical and mechanical Characterization. Electron. Lett. 2006, 42, 517–51. [Google Scholar]
- Foster, M.A.; Gaeta, A. L. Soliton-effect compress of supercontinuum to few-cycle durations in photonic nanowires. Opt. Express 2005, 13, 6848–6855. [Google Scholar]
- Gattass, R.R.; Svacha, G. T.; Tong, L.; Mazur, E. Supercontinuum generation in submicrometer diameter silica fibers. Opt. Express 2006, 14, 9048–9014. [Google Scholar]
- Lou, J.; Tong, L.; Ye, Z. Modeling of silica nanowires for optical sensing. Opt. Express 2005, 13, 213–2140. [Google Scholar]
- Villatoro, J.; Monzon-hernandez, D. Fast detection of hydrogen with nano fiber tapers coated with ultra thin palladium layers. Opt. Express 2004, 13, 5087–5092. [Google Scholar]
- Polynkin, P.; Polykin, A.; Peyghambarian, N.; Mansuripur, M. Evanescent field-based optical fiber sensing devices for measuring the refractive index of liquid in microfluidic channels. Opt. Lett. 2005, 30, 1273–1275. [Google Scholar]
- Sumetsky, M. Optical fiber microcoil resonator. Opt. Experss 2004, 12, 2303–2316. [Google Scholar]
- Sumetsky, M.; Dulashko, Y.; Fini, J.M.; Hale, A. Optical microfiber loop resonator. Appl. Phys. Lett. 2005, 86, 161108. [Google Scholar]
- Sumetsky, M. Uniform coil optical resonator and waveguide: Transmission spectrum,eigenmodes, and dispersion relation. Opt. Express 2005, 13, 4331–4340. [Google Scholar]
- Sumetsky, M.; Dulashko, Y.; Fini, J. M.; Hale, A.; DiGiovanni, D. J. Demonstration of a microfiber loop resonator. Optical Fiber Communications Conference, Anaheim, CA; 2005. Postdeadline Paper PDP10. [Google Scholar]
- Sumetsky, M.; Dulashko, Y.; Hale, A.; DiGiovanni, D.J. The microfiber loop resonator: theory, experiment, and application. J. Lightw. Technol. 2006, 24, 242–250. [Google Scholar]
- Jiang, X.; Tong, L.; Vienne, G.; Guo, X. Demonstration of optical knot resontors. Appl. Phys. Lett. 2006, 88, 223501. [Google Scholar]
- Vahala, K. J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar]
- Niehusmann, J.; Vorckel, A.; Bolivar, P.H.; Wahlbrink, T.; Henschel, W.; Kurz, H. Ultrahighquality-factor silicon-on-insulator microring resonator. Opt. Lett. 2004, 29, 2861–2863. [Google Scholar]
- Chao, C. Y.; Guo, L. J. Design and optimization of microring resonators in biochemical sensing applications. J. Lightw. Technol. 2006, 24, 1395–1402. [Google Scholar]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Chapman & Hall: London, 1983. [Google Scholar]
- Stokes, L. F.; Chodorow, M.; Shaw, H. J. All-single-mode fiber resonator. Opt. Lett. 1982, 7, 288–290. [Google Scholar]
- Schwelb, O. Transmission, group delay, and dispersion in single-ring optical resonators and add/drop filters - A tutorial overview. J. Lightw. Technol. 2004, 22, 1380–1394. [Google Scholar]
- Little, B. E.; Chu, S. T.; Haus, H. A.; Foresi, J.; Laine, J. P. Microring resonator channel dropping filters. J. Lightw. Technol. 1997, 15, 998–1005. [Google Scholar]
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Shi, L.; Xu, Y.; Tan, W.; Chen, X. Simulation of Optical Microfiber Loop Resonators for Ambient Refractive Index Sensing. Sensors 2007, 7, 689-696. https://doi.org/10.3390/s7050689
Shi L, Xu Y, Tan W, Chen X. Simulation of Optical Microfiber Loop Resonators for Ambient Refractive Index Sensing. Sensors. 2007; 7(5):689-696. https://doi.org/10.3390/s7050689
Chicago/Turabian StyleShi, Lei, Yonghao Xu, Wei Tan, and Xianfeng Chen. 2007. "Simulation of Optical Microfiber Loop Resonators for Ambient Refractive Index Sensing" Sensors 7, no. 5: 689-696. https://doi.org/10.3390/s7050689



