Rapid SINS Two-Position Ground Alignment Scheme Based on Piecewise Combined Kalman Filter and Azimuth Constraint Information
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Piecewise Combined Time-Invariant Linear System Model
2.2. The Conventional SINS Two-Position Alignment Model
2.3. The Conventional Augmented Observation Model Based on Angular Rate Measurements
2.4. The Piecewise Combined Kalman Filter for Improved Two-Position Initial Alignment
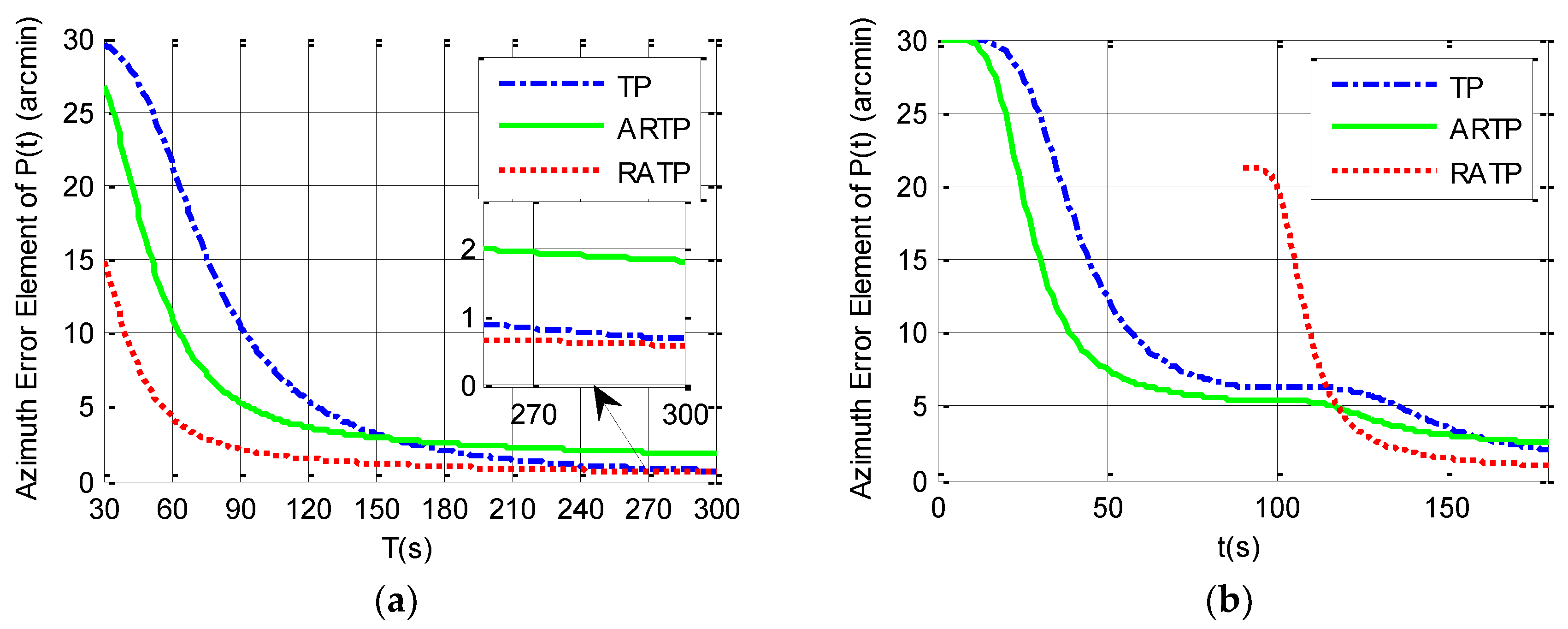
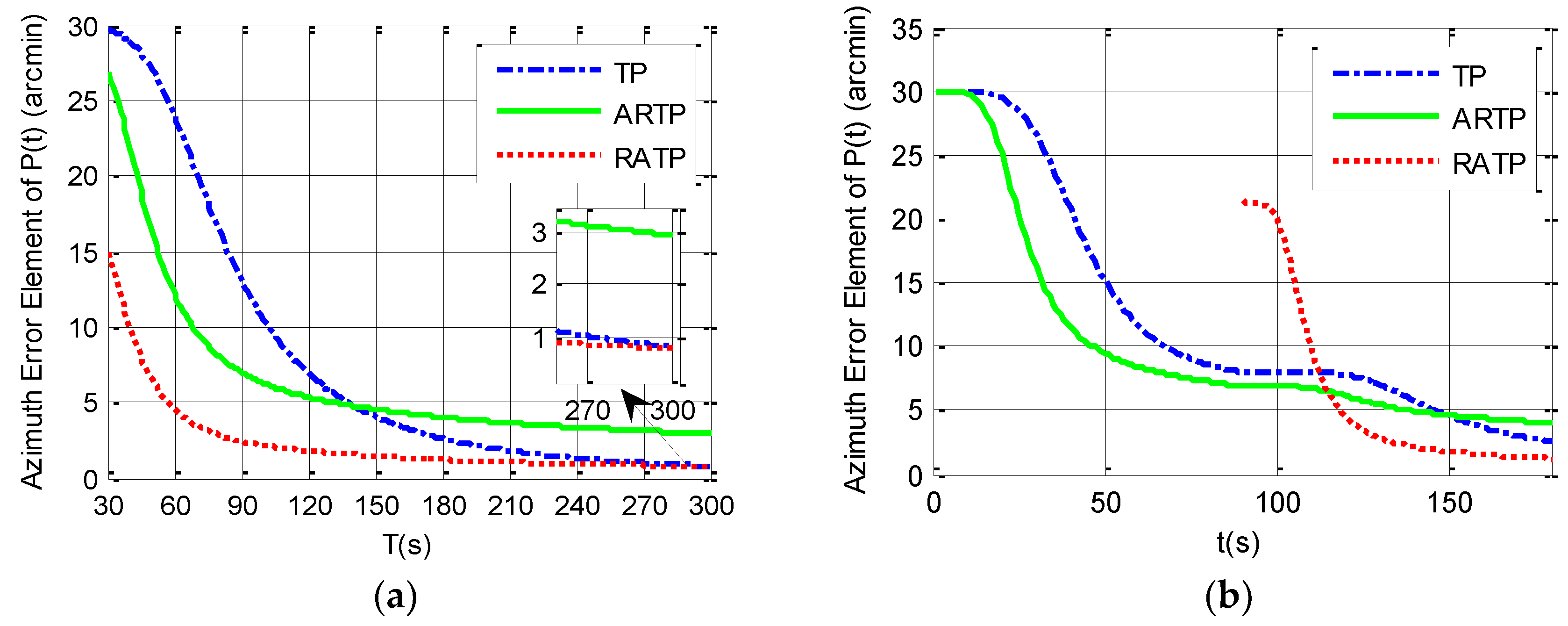
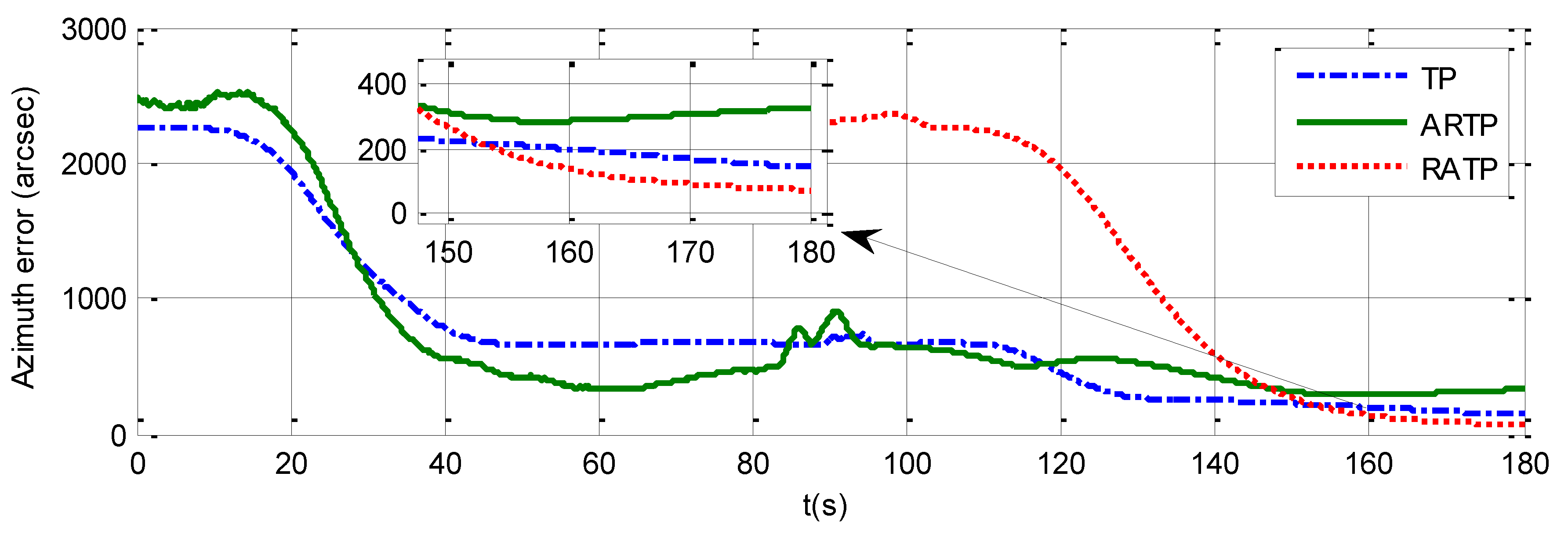
2.5. Comparison of Simulation Results among Different Alignment Schemes
3. Results and Discussion
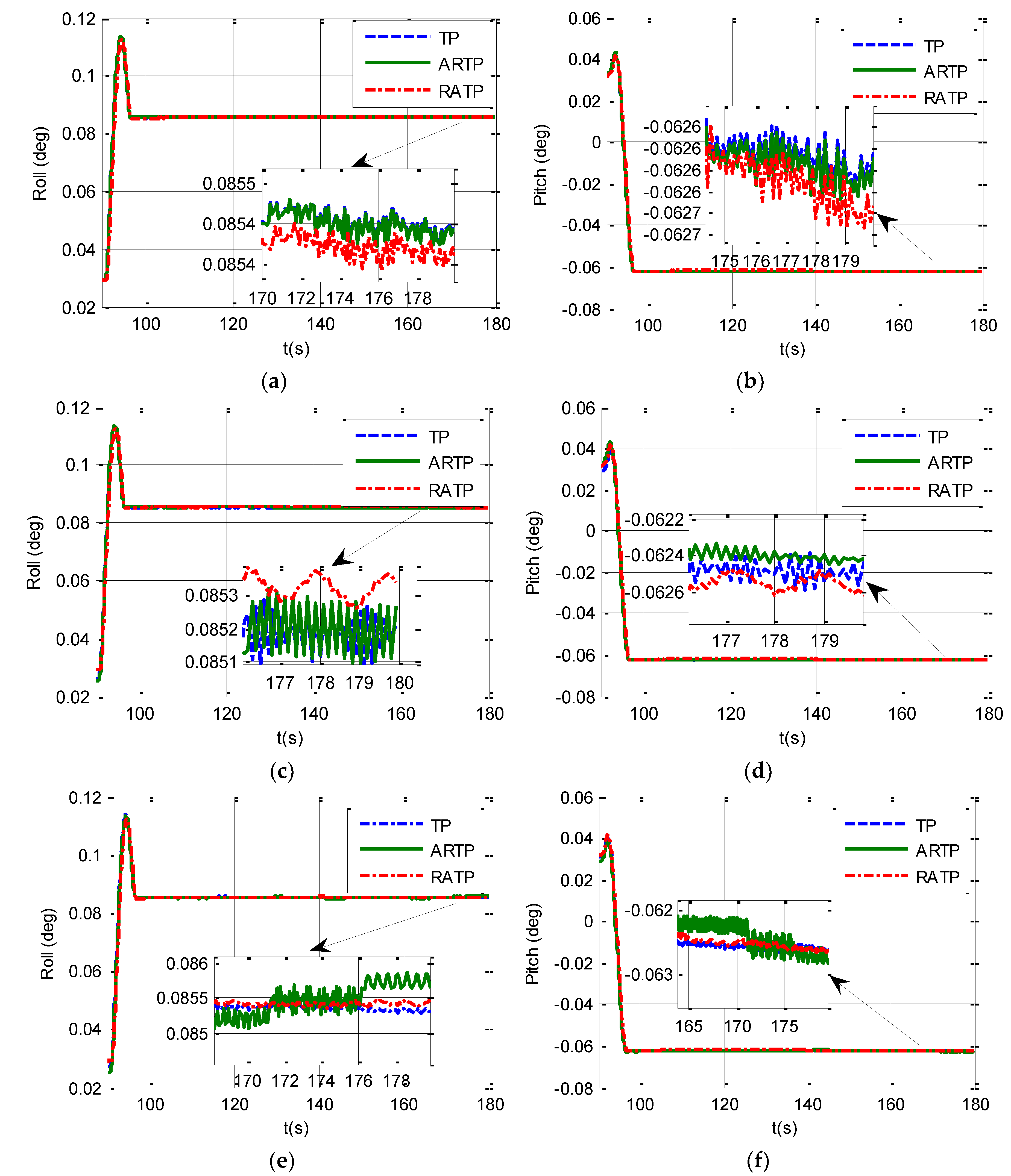
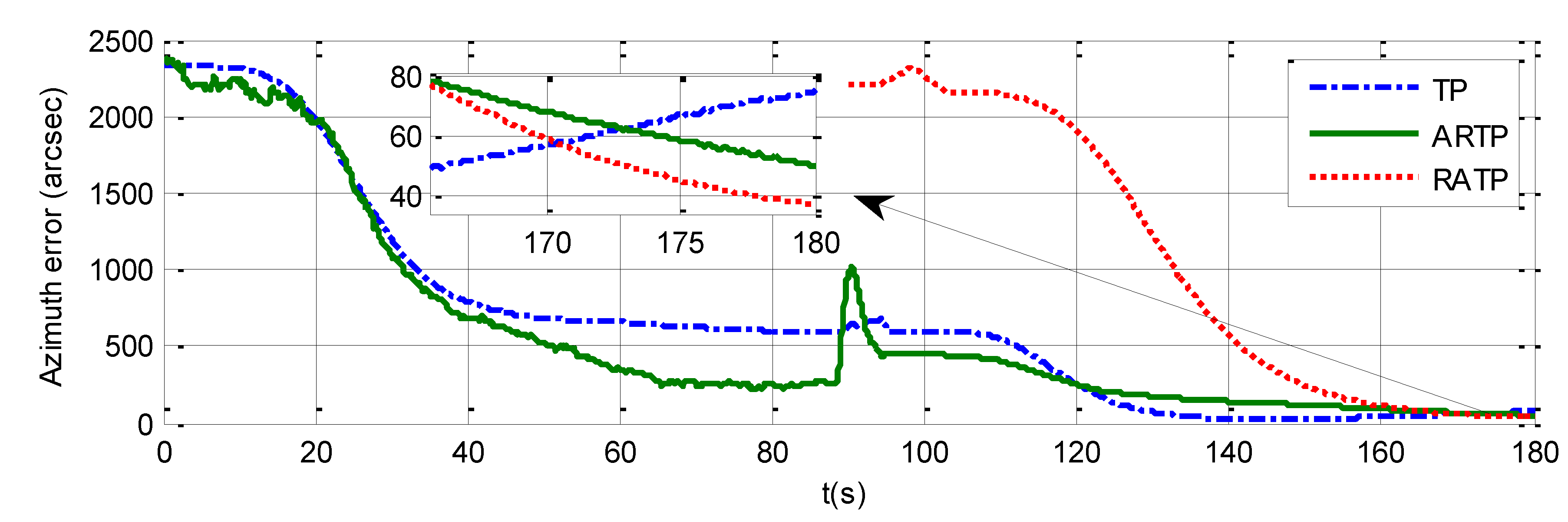
Two-Position Initial Alignment Experiment
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- El-Sheimy, N.; Nassar, S.; Noureldin, A. Wavelet de-noising for IMU alignment. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 32–39. [Google Scholar] [CrossRef]
- Silson, P.M.G. Coarse Alignment of a Ship’s Strapdown Inertial Attitude Reference System Using Velocity Loci. IEEE Trans. Instrum. Meas. 2011, 60, 1930–1941. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, H.; Wu, M.; Hu, X.; Hu, D. Observability of Strapdown INS Alignment: A Global Perspective. IEEE Trans. Aerosp. Electron. Syst. 2011, 48, 78–102. [Google Scholar]
- Jiang, Y.F.; Lin, Y.P. Error estimation of INS ground alignment through observability analysis. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 92–97. [Google Scholar] [CrossRef]
- Malakar, B.; Roy, B.K. Application of Bilinear Recursive Least Square Algorithm for Initial Alignment of Strapdown Inertial Navigation System. In Advanced Computing, Networking and Informatics; Springer: New York, NY, USA, 2014; Volume 1, pp. 1–8. [Google Scholar]
- Zhao, L.; Guan, D.; Cheng, J.; Xu, X.; Fei, Z. Coarse Alignment of Marine Strapdown INS Based on the Trajectory Fitting of Gravity Movement in the Inertial Space. Sensors 2016, 16, 1714. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, S.; Tsukioka, S.; Yoshida, H.; Hyakudome, T.; Ishikawa, A. Accuracy Improvement of an Inertial Navigation System Brought about by the Rotational Motion. In Proceedings of the OCEANS 2007-Europe, Aberdeen, UK, 18–21 June 2007. [Google Scholar]
- Tucker, T.; Levinson, E. The AN/WSN-7B Marine Gyrocompass/Navigator. In Proceedings of the 2000 National Technical Meeting of The Institute of Navigation, Anaheim, CA, USA, 26–28 January 2000; pp. 348–357. [Google Scholar]
- Mao, Y.L.; Chen, J.B.; Song, C.L.; Yin, J.Y. Single-Axis Rotation Modulation of SINS. Appl. Mech. Mater. 2013, 313, 643–646. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Y.; Hu, X.; Hu, D. Optimization-based alignment for inertial navigation systems: Theory and algorithm. Aerosp. Sci. Technol. 2011, 15, 1–17. [Google Scholar] [CrossRef]
- Barbour, N. Inertial components—Past, present, and future. In Proceedings of the AIAA Guidance, Navigation, & Control Conference & Exhibit, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Cheng, J.; Li, M.; Guan, D.; Wang, T.; Zhang, W. Research on Nonlinear Comprehensive Calibration Algorithm for the Single-Axis Rotation Inertial Navigation System Based on Modified Unscented Kalman Filter. J. Comput. Theor. Nanosci. 2017, 14, 1535–1542. [Google Scholar] [CrossRef]
- Acharya, A.; Sadhu, S.; Ghoshal, T.K. Improved self-alignment scheme for SINS using augmented measurement. Aerosp. Sci. Technol. 2011, 15, 125–128. [Google Scholar] [CrossRef]
- Gao, W.X.; Miao, L.J.; Mao-Lin, N.I. A Fast Initial Alignment Method with Gyro Angular Rate Information. J. Astronaut. 2010, 31, 1596–1601. [Google Scholar]
- Xiong, J.; Guo, H.; Yang, Z.H. A Two-Position SINS Initial Alignment Method Based on Gyro Information. Adv. Space Res. 2014, 53, 1657–1663. [Google Scholar] [CrossRef]
- Chang, G. Fast two-position initial alignment for SINS using velocity plus angular rate measurements. Adv. Space Res. 2015, 56, 1331–1342. [Google Scholar] [CrossRef]
- Che, Y.; Wang, Q.; Gao, W.; Yu, F. An Improved Inertial Frame Alignment Algorithm Based on Horizontal Alignment Information for Marine SINS. Sensors 2015, 15, 25520–25545. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Hai, Z.; Gao, D.; Meng, Y.; Wu, W. A Stationary North-Finding Scheme for an Azimuth Rotational IMU Utilizing a Linear State Equality Constraint. Sensors 2015, 15, 4368–4387. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, X.; Song, Q.; Yan, Y.; Liu, Y.; Wang, L. A novel self-alignment method for SINS based on three vectors of gravitational apparent motion in inertial frame. Measurement 2015, 62, 47–62. [Google Scholar] [CrossRef]
- Xia, X.-W.; Sun, Q. Initial Alignment Algorithm Based on the DMCS Method in Single-Axis RSINS with Large Azimuth Misalignment Angles for Submarines. Sensors 2018, 7, 2123. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Duan, T.; Wang, L. A modified rapid alignment method of SINS based on measurement augmentation. Optik 2018, 170, 492–505. [Google Scholar] [CrossRef]
- Chang, L.; Li, J.; Chen, S. Initial Alignment by Attitude Estimation for Strapdown Inertial Navigation Systems. IEEE Trans. Instrum. Meas. 2015, 64, 784–794. [Google Scholar] [CrossRef]
- Lee, J.G.; Park, C.G.; Park, H.W. Multiposition alignment of strapdown inertial navigation system. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 1323–1328. [Google Scholar] [CrossRef]
- Chung, D.; Lee, J.G.; Chan, G.P.; Park, H.W. Strapdown INS error model for multiposition alignment. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1362–1366. [Google Scholar] [CrossRef]
- Yu, H.; Wu, W.; Wu, M.; Meng, Y.; Ming, H. Stochastic Observability-Based Analytic Optimization of SINS Multiposition Alignment. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2181–2192. [Google Scholar] [CrossRef]
- Chung, D.; Park, C.G.; Lee, J.G. Observability analysis of strapdown inertial navigation system using Lyapunov transformation. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volume 1, pp. 23–28. [Google Scholar]
- Cho, H.; Lee, M.H.; Ryu, D.G.; Lee, K.S.; Lee, S.H.; Lee, H.C.; Park, H.G.; Won, J.S. A Two-Stage Initial Alignment Technique for Underwater Vehicles Dropped from a Mother Ship. Int. J. Precis. Eng. Manuf. 2013, 14, 2067–2073. [Google Scholar] [CrossRef]
- Bar-Itzhack, I.Y.; Berman, N. Control theoretic approach to inertial navigation systems. J. Guid. Control Dyn. 1988, 11, 237–245. [Google Scholar] [CrossRef]
- Rogers, R.M. Applied Mathematics in Integrated Navigation Systems, 3rd ed.; American Institute of Aeronautics & Astronautics Inc.: Reston, VA, USA, 2007. [Google Scholar]
- Dai, H.; Dai, S.; Cong, Y.; Zhao, G.; Wu, G. Rapid transfer alignment of laser SINS using quaternion based angular measurement. Optik 2013, 124, 4364–4368. [Google Scholar] [CrossRef]
- Goshen-Meskin, D.; Bar-Itzhack, I.Y. Observability analysis of piece-wise constant systems with application to inertial navigation. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990. [Google Scholar]
- Goshen-Meskin, D.; Bar-Itzhack, I. Observability analysis of piece-wise constant systems. I. Theory. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 1056–1067. [Google Scholar] [CrossRef]




| 28.21° | |
|---|---|
| Bias instability of gyros Constant bias of gyros | |
| Angular random walk of gyros | |
| Bias instability of accelerometers Constant bias of accelerometers | 20 µg 100 µg |
| Noise power spectrum density of accelerometers | |
| Process noise covariance parameters in | , |
| Measurement noise covariance parameters of TP in | |
| Measurement noise covariance parameters of ARTP in | , (Con.1), (Con.2), (Con.3) |
| Measurement noise covariance parameters of RATP in | , (Con.1), (Con.2) (Con.3) |
| Initial error covariance parameters of TP and ARTP in | |
| Initial error covariance parameters of RATP in |
| Condition | ||||||
|---|---|---|---|---|---|---|
| TP | ARTP | RATP | TP | ARTP | RATP | |
| Con.1 | 1.51 | 1.01 | 0.72 | 0.54 | 0.50 | 0.40 |
| Con.2 | 2.06 | 2.55 | 0.96 | 0.67 | 1.81 | 0.58 |
| Con.3 | 2.61 | 4.01 | 1.21 | 0.80 | 2.93 | 0.78 |
| Laser gyro | Zero-bias stability | |
| Angle random walk | ||
| Quartz pendulous accelerometer | Zero-bias stability | |
| Noise power spectrum density | ||
| Sampling frequency |
| Num | TP (arcsec) | ARTP (arcsec) | RATP (arcsec) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Con.1 | Con.2 | Con.3 | Con.1 | Con.2 | Con.3 | Con.1 | Con.2 | Con.3 | |
| 1 | −110.26 | −199.00 | 272.94 | −95.08 | −52.74 | −94.134 | −1.76 | 45.31 | 144.47 |
| 2 | −38.26 | 56.85 | −183.61 | 9.02 | −148.55 | 51.26 | 34.64 | 10.83 | −69.82 |
| 3 | 110.46 | −24.70 | 34.60 | 7.41 | 78.65 | 59.75 | 3.39 | −58.99 | 14.40 |
| 4 | −70.55 | 237.23 | 68.07 | −59.90 | −334.08 | −66.70 | −40.21 | −53.06 | 90.46 |
| 5 | 6.14 | −73.86 | −254.07 | 35.43 | 217.33 | −132.19 | −59.04 | 12.49 | −127.33 |
| 6 | 102.48 | 3.48 | 62.07 | 103.11 | 239.40 | 182.01 | 62.99 | 43.42 | −52.17 |
| 7 | −96.24 | −18.10 | −124.30 | −4.95 | −7.66 | −476.15 | −8.63 | −20.32 | −50.61 |
| 8 | −84.72 | −91.60 | −20.84 | −85.77 | −157.55 | −14.43 | −78.16 | −85.72 | 65.65 |
| 9 | 18.52 | 100.76 | −39.40 | 29.03 | −83.69 | −191.20 | 28.56 | 37.15 | −107.95 |
| 10 | 104.79 | 130.65 | 112.16 | 81.13 | 101.39 | 508.14 | 44.86 | 77.35 | 85.82 |
| 11 | −55.33 | −97.28 | 91.85 | −45.65 | −54.37 | −142.47 | −22.21 | −40.75 | −50.62 |
| 12 | 124.49 | −24.43 | −19.46 | 26.22 | 201.87 | −316.57 | 35.58 | 32.29 | 57.71 |
| STD value | 89.26 | 117.23 | 141.83 | 61.96 | 174.01 | 254.55 | 43.75 | 50.75 | 87.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wu, W.; Wang, M. Rapid SINS Two-Position Ground Alignment Scheme Based on Piecewise Combined Kalman Filter and Azimuth Constraint Information. Sensors 2019, 19, 1125. https://doi.org/10.3390/s19051125
Zhang L, Wu W, Wang M. Rapid SINS Two-Position Ground Alignment Scheme Based on Piecewise Combined Kalman Filter and Azimuth Constraint Information. Sensors. 2019; 19(5):1125. https://doi.org/10.3390/s19051125
Chicago/Turabian StyleZhang, Lu, Wenqi Wu, and Maosong Wang. 2019. "Rapid SINS Two-Position Ground Alignment Scheme Based on Piecewise Combined Kalman Filter and Azimuth Constraint Information" Sensors 19, no. 5: 1125. https://doi.org/10.3390/s19051125




