Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation
Abstract
:1. Introduction
2. Nonlinear Information Weighted Consensus Filters
| Algorithm 1 Extended Information Weighted Consensus Filter |
|
2.1. Extended Information Weighted Consensus Filter
2.2. Square-Root Central Difference Information Weighted Consensus Filter
| Algorithm 2 Square-Root Central Difference Information Weighted Consensus Filter (SRCDIWCF) |
|
2.3. Square-Root Unscented Information Weighted Consensus Filter
2.4. Square-Root Cubature Information Weighted Consensus Filter
3. Nonlinear Dynamic Hybrid Consensus Filters
| Algorithm 3 Square-Root Central Difference Dynamic Hybrid Consensus Filter (SRCDDHCF) |
|
4. Simulation
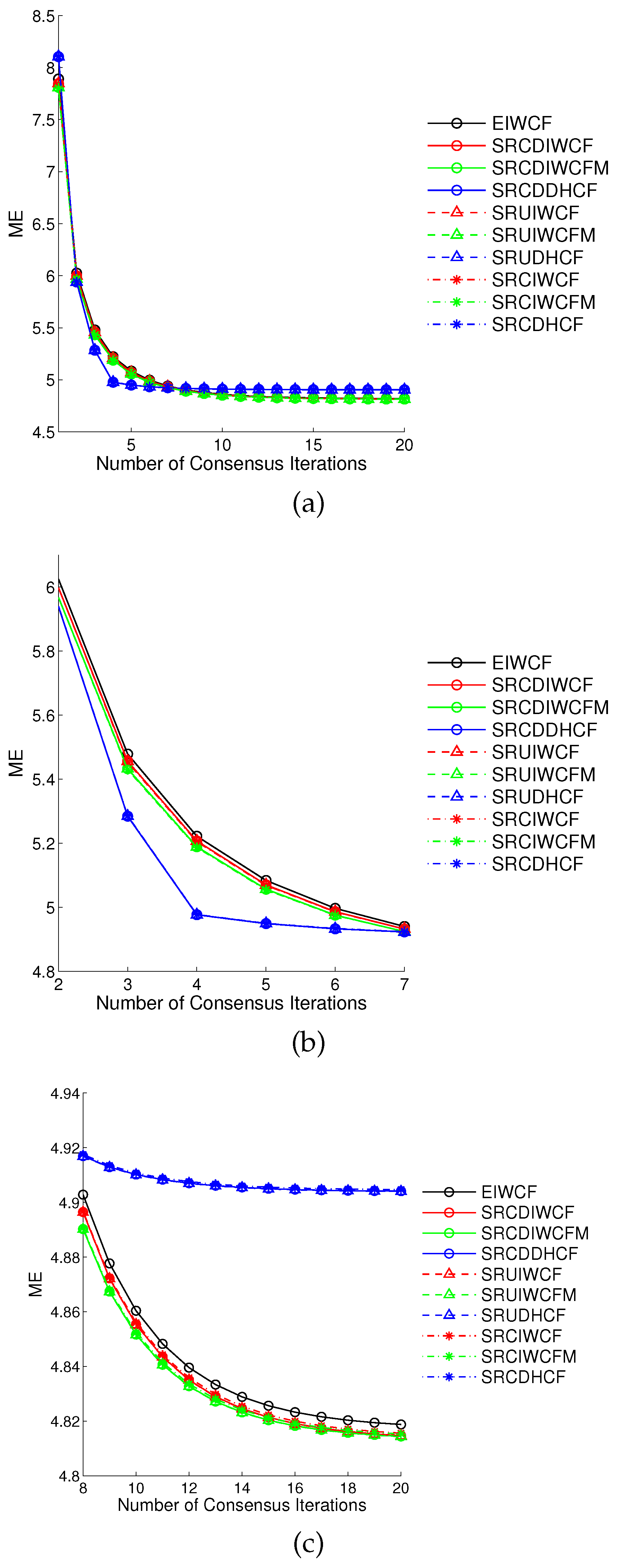
4.1. Normal Measurement
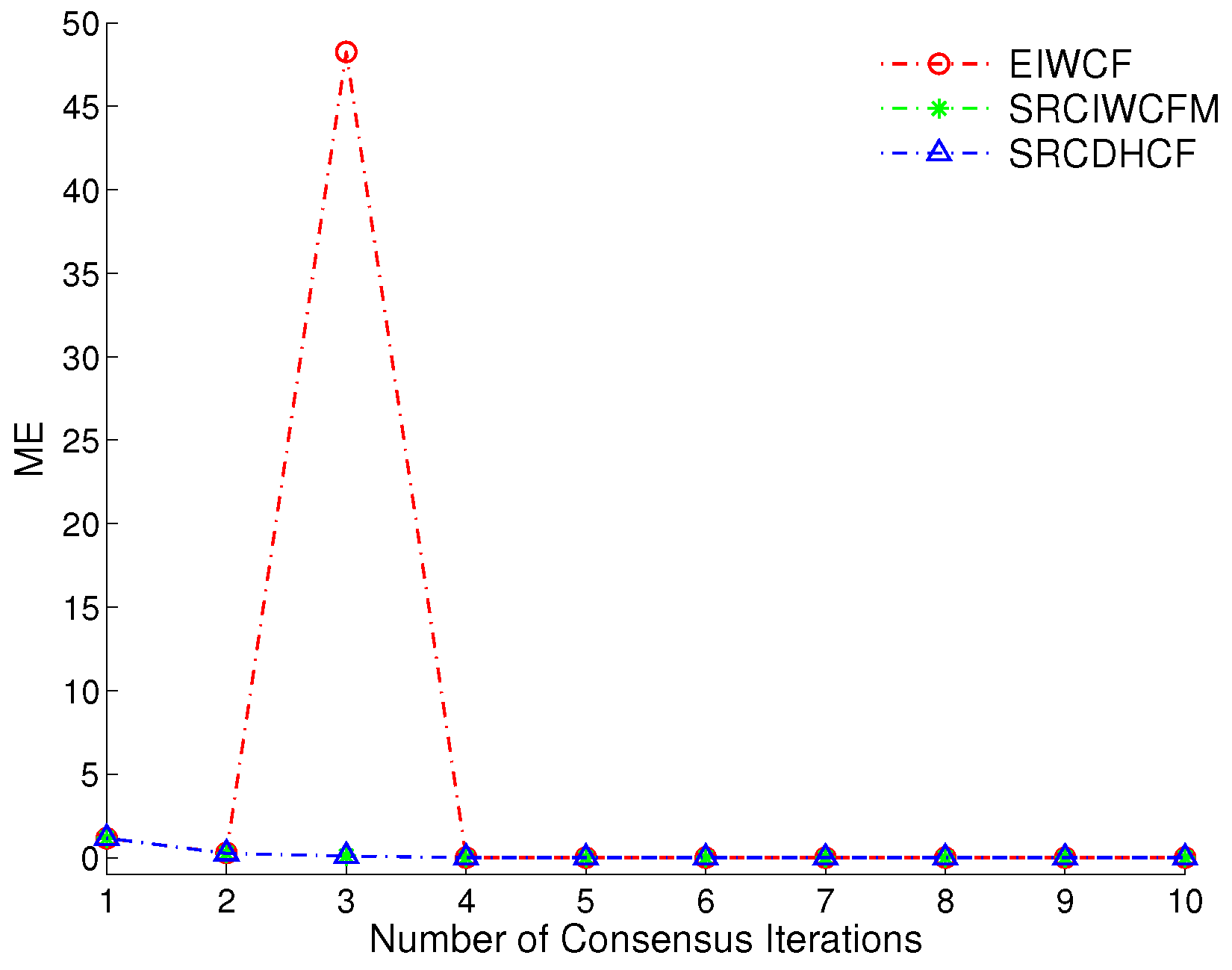
4.2. Ill Condition: Near Perfect Measurement
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kamal, A.T.; Farrell, J.A.; Roy-Chowdhury, A.K. Information weighted consensus filters and their application in distributed camera networks. IEEE Trans. Autom. Control 2013, 58, 3112–3125. [Google Scholar] [CrossRef]
- Casbeer, D.W.; Beard, R.W. Multi-static radar target tracking using information consensus filters. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; pp. 1–9. [Google Scholar]
- Wang, L.; Zhang, Q.; Zhu, H.; Shen, L. Adaptive consensus fusion estimation for MSN with communication delays and switching network topologies. In Proceedings of the 2010 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 2087–2092. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Aragues, R.; Cortes, J.; Sagues, C. Distributed consensus on robot networks for dynamically merging feature-based maps. IEEE Trans. Robot. 2012, 28, 840–854. [Google Scholar] [CrossRef]
- Li, W.; Jia, Y. Consensus-based distributed multiple model ukf for jump markov nonlinear systems. IEEE Trans. Autom. Control 2012, 57, 230–236. [Google Scholar]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Kamal, A.T.; Farrell, J.A.; Roy-Chowdhury, A.K. Information weighted consensus. In Proceedings of the IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 2732–2737. [Google Scholar]
- Olfati-Saber, R. Distributed Kalman filter with embedded consensus filters. In Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference (CDC-ECC ’05), Seville, Spain, 12–15 December 2005; pp. 8179–8184. [Google Scholar]
- Casbeer, D.W.; Beard, R. Distributed information filtering using consensus filters. In Proceedings of the American Control Conference, Hyatt Regency Riverfront, St. Louis, MO, USA, 10–12 June 2009; pp. 1882–1887. [Google Scholar]
- Battistelli, G.; Chisci, L.; Mugnai, G.; Farina, A.; Graziano, A. Consensus-based linear and nonlinear filtering. IEEE Trans. Autom. Control 2015, 60, 1410–1415. [Google Scholar] [CrossRef]
- Katragadda, S.; Sanmiguel, J.C.; Cavallaro, A. Consensus protocols for distributed tracking in wireless camera networks. In Proceedings of the 2014 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014; pp. 1–8. [Google Scholar]
- Chen, Y.; Zhao, Q. A Novel Square-Root Cubature Information Weighted Consensus Filter Algorithm for Multi-Target Tracking in Distributed Camera Networks. Sensors 2015, 15, 10526–10546. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Woergoetter, F.; Markelic, I. Square-Root Sigma-Point Information Filtering. IEEE Trans. Autom. Control 2012, 57, 2945–2950. [Google Scholar] [CrossRef]
- Guo, Z.; Li, S.; Wang, X.; Heng, W. Distributed Point-Based Gaussian Approximation Filtering for Forecasting-Aided State Estimation in Power Systems. IEEE Trans. Power Syst. 2016, 31, 2597–2608. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S.; Lall, S. A scheme for robust distributed sensor fusion based on average consensus. In Proceedings of the International Conference on Information Processing in Sensor Networks, Los Angeles, CA, USA, 25–27 April 2005; pp. 63–70. [Google Scholar]
- Ilic, N.; Stankovic, M.S.; Stankovic, S.S. Adaptive consensus-based distributed target tracking in sensor networks with limited sensing range. IEEE Trans. Control Syst. Technol. 2014, 22, 778–785. [Google Scholar] [CrossRef]
- Ito, K.; Xiong, K. Gaussian filters for nonlinear filtering problems. IEEE Trans. Autom. Control 2000, 45, 910–927. [Google Scholar] [CrossRef]
- Merwe, R.V.D. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Ph.D. Thesis, Oregen Health & Science University, Portland, OR, USA, 2004. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Lee, D.j. Nonlinear Estimation and Multiple Sensor Fusion Using Unscented Information Filtering. IEEE Signal Process. Lett. 2008, 15, 861–864. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Liu, Y.; He, Y.; Wang, H. Squared-root cubature information consensus filter for non-linear decentralised state estimation in sensor networks. IET Radar Sonar Navig. 2014, 8, 931–938. [Google Scholar]
- Van der Merwe, R.; Wan, E.A. The square-root unscented Kalman filter for state and parameter-estimation. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 6, pp. 3461–3464. [Google Scholar]
- Bharani Chandra, K.P.; Chandra, B.; Gu, D.W.; Postlethwaite, I. Square root cubature information filter. IEEE Sens. J. 2013, 13, 750–758. [Google Scholar] [CrossRef]
- Arasaratnam, I. Sensor Fusion with Square-Root Cubature Information Filtering. Intell. Control Autom. 2013, 2013, 11–17. [Google Scholar] [CrossRef]
- Särkkä, S.; Solin, A. On continuous-discrete cubature Kalman filtering. In Proceedings of the 2012 16th IFAC Symposium on System Identification (SYSID 2012), Brussels, Belgium, 11–13 July 2012; Volume 16, pp. 1210–1215. [Google Scholar]
- Wang, S.; Feng, J.; Tse, C.K. A class of stable square-root nonlinear information filters. IEEE Trans. Autom. Control 2014, 59, 1893–1898. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Q.; An, Z.; Lv, P.; Zhao, L. Distributed Multi-Target Tracking Based on the K-MTSCF Algorithm in Camera Networks. IEEE Sens. J. 2016, 16, 5481–5490. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Chen, G.; Yu, W. Consensus Tracking of Multi-Agent Systems With Lipschitz-Type Node Dynamics and Switching Topologies. IEEE Trans. Circuits Syst. I 2013, 61, 1–13. [Google Scholar] [CrossRef]
- Wen, G.; Yu, W.; Hu, G.; Cao, J.; Yu, X. Pinning synchronization of directed networks with switching topologies: A multiple lyapunov functions approach. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3239–3250. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Tian, G. Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation. Sensors 2017, 17, 800. https://doi.org/10.3390/s17040800
Liu G, Tian G. Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation. Sensors. 2017; 17(4):800. https://doi.org/10.3390/s17040800
Chicago/Turabian StyleLiu, Guoliang, and Guohui Tian. 2017. "Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation" Sensors 17, no. 4: 800. https://doi.org/10.3390/s17040800
APA StyleLiu, G., & Tian, G. (2017). Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation. Sensors, 17(4), 800. https://doi.org/10.3390/s17040800




