On Using Maximum a Posteriori Probability Based on a Bayesian Model for Oscillometric Blood Pressure Estimation
Abstract
: The maximum amplitude algorithm (MAA) is generally utilized in the estimation of the pressure values, and it uses heuristically obtained ratios of systolic and diastolic oscillometric amplitude to the mean arterial pressure (known as systolic and diastolic ratios) in order to estimate the systolic and diastolic pressures. This paper proposes a Bayesian model to estimate the systolic and diastolic ratios. These ratios are an improvement over the single fixed systolic and diastolic ratios used in the algorithms that are available in the literature. The proposed method shows lower mean difference (MD) with standard deviation (SD) compared to the MAA for both SBP and DBP consistently in all the five measurements.1. Introduction
There is an increasing need to offer health care devices within the homes of senior patients. This has led to an increasing demand on home blood pressure monitors. Oscillometric measurements have recently gained popularity and are used in blood pressure (BP) monitors, which are now readily available on the market [1–9]. Although vendors of oscillometric BP monitors rarely disclose their algorithms, and the determination of oscillometric systolic blood pressure (SBP) and diastolic blood pressure (DBP) values has been declared controversial [1], the maximum amplitude algorithm (MAA) is one of the most popular algorithms for estimation of arterial blood pressure (ABP) using the oscillometric measurement [2–4]. The MAA approximates the mean blood pressure as the cuff pressure (CP) at which the maximum oscillation in amplitude occurs and then linearly relates the SBP and DBP to this mean pressure using heuristically obtained ratios [2,3,5]. These ratios are utilized to determine the time points at which the cuff pressure (CP) coincides with the systolic and diastolic pressures, respectively [5]. Even though estimation of the ABP is possible employing oscillometric blood pressure estimation, it is subject to various errors since the systolic and diastolic blood pressures or the systolic and diastolic ratios are determined only using quasi-empirical methods [2,4,10]. Moreover, there has been almost no study that tries to estimate the theoretical relationship between the ratios [5]. Currently, the fixed ratios of SBP and DBP are used to determine the SBP and DBP estimates based on the maximum amplitude (MA) obtained through MAA. Although the SBP and DBP ratios (SBPR and DBPR) in the conventional method are assumed to be fixed, this assumption is not valid [5,6,10–12]. For example, Moraes et al. [11] suggested that the SBPR and DBPR vary in relation to the SBP, DBP, and mean blood pressure. More recently, the error mechanisms of the fixed-ratio for estimating SBP and DBP was found by Liu et al. [10]. Specifically, the fixed ratio may be viewed as a value dependent on the measurements obtained for a specified group of subjects by minimizing the mean absolute error relative to reference auscultatory measurements. If the ratios obtained from one group are utilized for another group, one would not be able to acquire reliable blood pressure estimates. Thus, the MAA derived by a single group-based ratio is not adequate to accurately determine the SBP and DBP because they are subject to significant continuous variability over time [13]. For this reason, it is necessary to develop a methodology that can accurately measure blood pressure based on the oscillometric measurement. Therefore, to obtain a more generalized ratio, this paper proposes a methodology to determine the ratios for systolic and diastolic blood pressures using a Bayesian model for individual subjects. This ratio is an improvement over the single fixed SBPR and DBPR used in the algorithms which are available in the literature.
The organization of this paper is as follows. In Section 2, the data used in the study is described, and the Bayesian model principles and the conventional methodology used in this paper are explained. In Section 3, the experimental results and discussion obtained from the proposed method are presented. In Section 4, conclusions drawn based on the results are presented.
2. Methods
The proposed methodology assumes generalized Gaussian distribution [14] which includes not only the Gaussian distribution but also the Laplacian distribution to find more efficient parametric modeling for the a posteriori distribution of the SBPR and DBPR, which are used to estimate the SBP and DBP for each individual subject. The methodology also assumes that the ratios are random variables unlike the existing approaches in the literature where they are considered to be deterministic. This paper chooses the value of the likelihood function that maximizes the a posteriori probability. An equally likely a prior is used that creates a likelihood function using the blood pressure values obtained through the MAA algorithm for each prior. It then chooses the likelihood value that maximizes the a posteriori probability obtained using Bayes' model. As a result, the mean difference (MD) and the standard deviation (SD) [15] of the SBP and DBP estimate obtained with the SBPR and DBPR using the Bayesian model were compared with the MD and SD of the estimates obtained using the conventional MAA method.
2.1. Conventional MAA Concepts
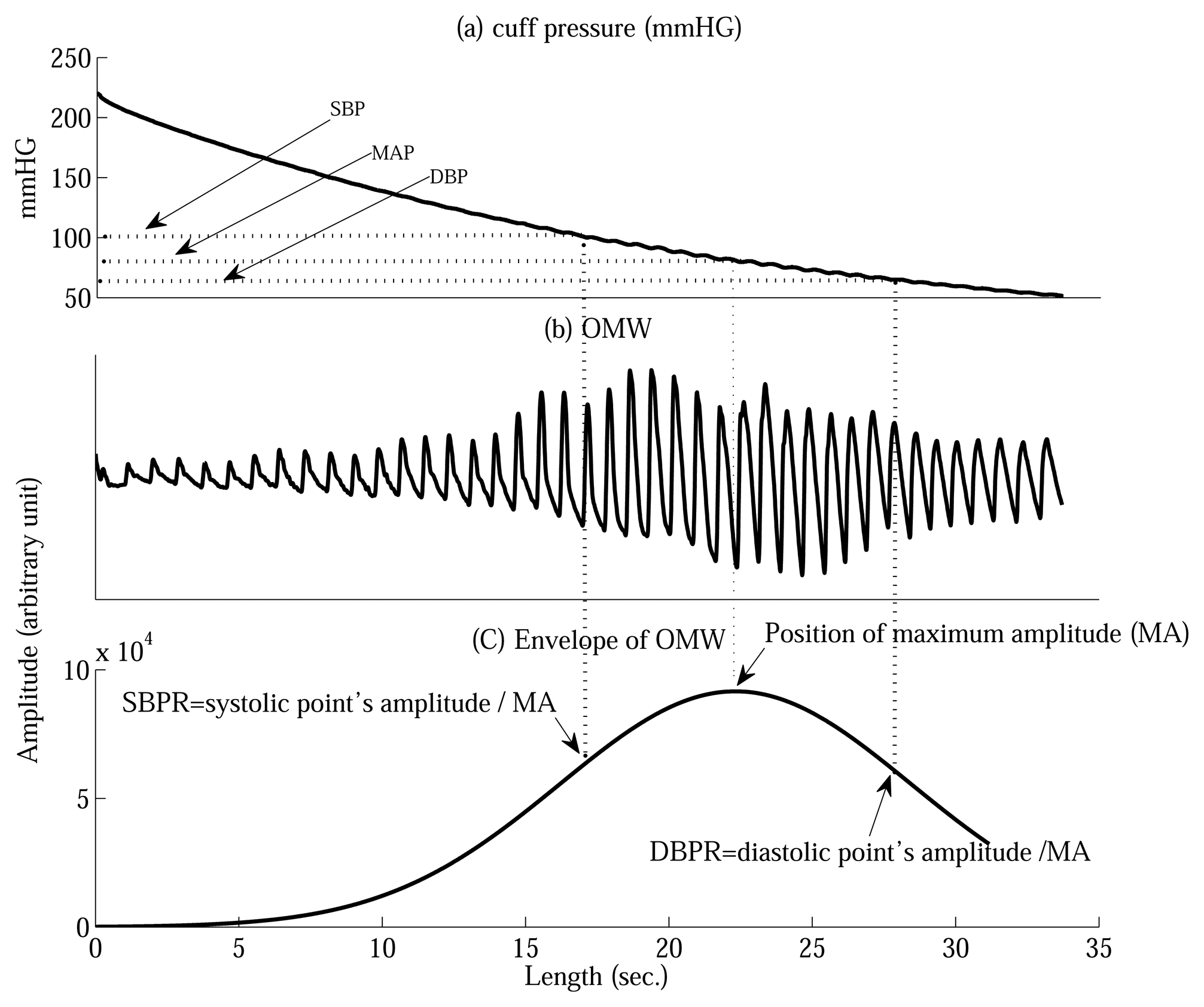
Based on the oscillometric BP envelope, the MAA is widely used to estimate the SBP and DBP, which utilizes SBPR and DBPR to find the points which correspond to SBP and DBP. The amplitude of the maximum point is multiplied by the fixed SBPR and DBPR obtained experimentally [2,3,5].
2.2. Blood Pressure Estimation Using Bayesian Model
For any ith subject and any jth measurement, the systolic and diastolic ratios are defined as follows:
Let crs and crd be the vectors of the possible candidates for the SBPR and DBPR.
The a posterior probability (POP) for every l, l = 1, · · ·, K is
The likelihoods of each ratio are the values of the measurement distribution at a measurement value, where are the ratios of the pressure values obtained from the reference auscultatory measurement and the maximum amplitude (MA), as given by Equation (15). The goal is to find the SBPR, cr(l)s(i,j) that maximizes the likelihood ratio, for the available SBP reference measurements for each subject. The same idea is used for obtaining the DBPR. Since two reference auscultatory measurements are available, the average SBP and DBP measurement is used as the reference to obtain the SBPR and DBPR. We also apply the Laplacian (L) model [14] to obtain the likelihoods of each ratio such that
The reference SBPR and DBPR are obtained for the jth measurement of the ith subject as follows:
The following procedure is used for obtaining the SBP and DBP estimates using the conventional approach. The OMW is recovered using the CP and the pulse derivative waveform (PDW) [8] is obtained. The local maxima of the OMW are used in order to build an envelope. The envelope of the OMW is then smoothed using cubic spline interpolation [19] that is commonly used to reduce interference such as movement artifacts from the oscillometric BP envelope [4]. Based on the MA and the CP, SBP and DBP are determined using the conventional experimentally obtained systolic and diastolic ratios [5] which are 0.70 and 0.45, respectively [4].
The SBP and DBP estimates are also obtained using Bayesian inference [18] and then the results of the conventional MAA and the proposed method are compared.
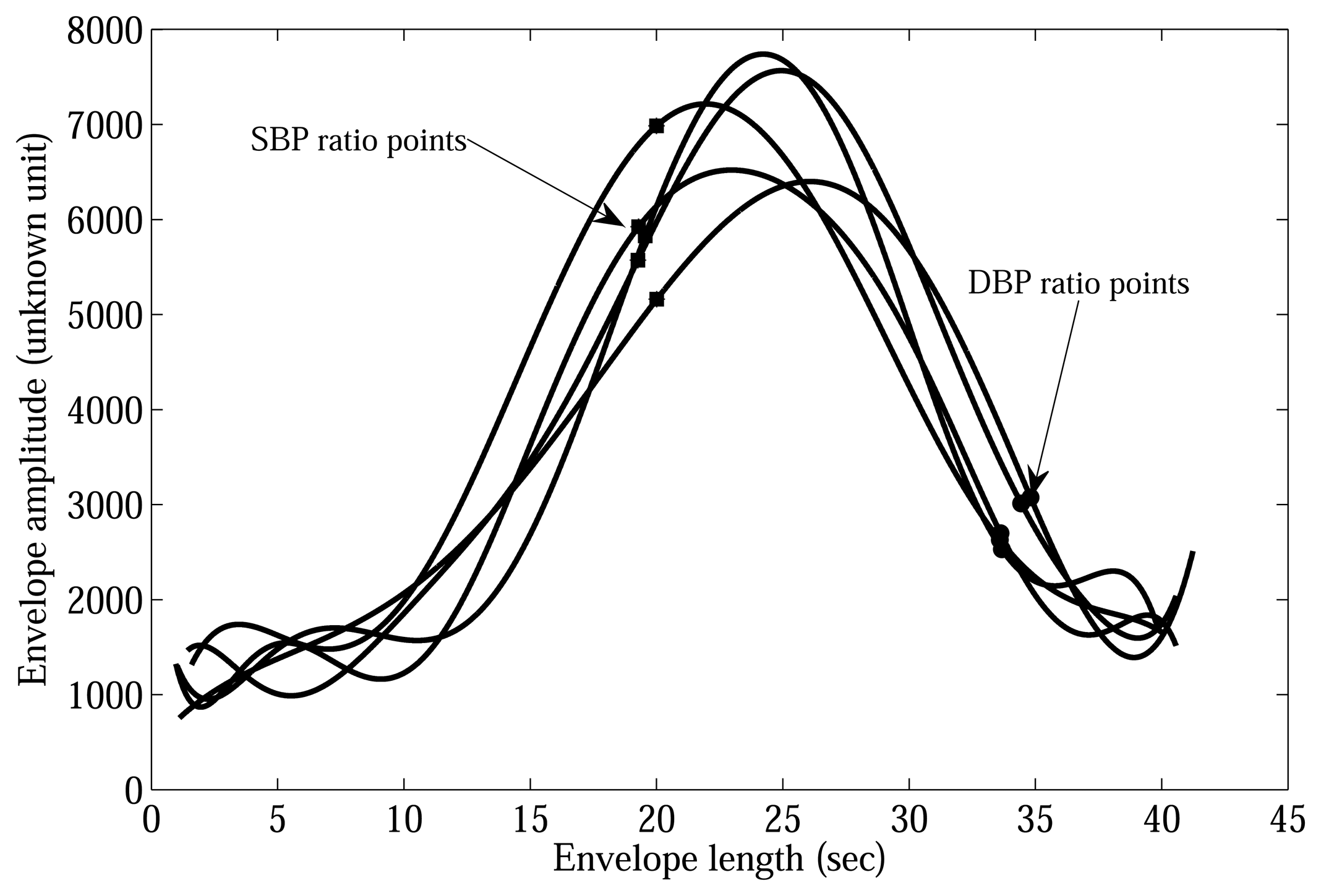
The following step by step procedure is used to estimate the SBP and DBP ratios using the Bayesian approach as shown Figure 4.
- (1)
As the first step, the ranges of the systolic and diastolic ratios used in the proposed method are initially found experimentally [2,3] and the PP is defined as shown in Equations (7) and (8).
- (2)
The SBP and DBP estimates are obtained using both the MA value and the fixed a priori ratios of SBP and DBP
- (3)
The reference SBPR and DBPR are obtained using the reference auscultatory measurement, which itself is obtained using the cuff pressure, reference auscultatory measurement, and maximum amplitude for each subject.
- (4)
The a priori likelihoods are obtained as shown in Equation (11) to Equation (12).
- (5)
The calculation of POP is performed to determine the final ratio of SBP and DBP in Equations (9) and (10).
- (6)
The SBPR and DBPR that produced the maximum a posteriori probability in Equation (17) are taken as the best ratio for the measurement. As the estimation of the SBPR and DBPR is based on the a priori probability and the likelihood function, the final ratios are presented as the maximum a posteriori probability.
Similarly, the ratio for the DBP, can also be obtained. Using these ratios, the SBP and DBP estimates are obtained. In the method above, each measurement will produce one SBPR and DBPR.
3. Experimental Results and Discussion
3.1. Subjects and Data Collection
The local research ethics committee approved the research, and all subjects provided informed consent prior to the BP measurement according to the protocol of the institutional research ethics board. The oscillometric measurements for this study were provided by Biosign Technologies Inc. (Toronto, Ontario, Canada). The experimental data set was acquired from 85 healthy subjects aged from 12 to 80, out of which thirty seven were females and forty eight were males. No recruited subject had any history of cardiovascular disease. Five sets of oscillometric BP measurements were obtained from each volunteer (5 × 85 = 425 total measurements: duration range to record a single measurement: 31–95 s, duration median: 55 s) using a wrist worn UFIT® blood pressure device [4,20,21] (Biosign Technologies Inc., Toronto, Ontario, Canada) in accordance with the recommendations of the ANSI/AAMI SP 10 standard [15]. Specifically, the two nurse readings are averaged to provide one SBP and one DBP reading as the reference which is an auscultatory method (mmHG) considered the standard protocol for noninvasive BP measurement [15]. The data set provided contains relatively stable nurse readings, in that the maximum difference between the two nurses is no more than 2 mmHG. This again satisfies the recommendations of the ANSI/AAMI SP 10 standard, which requires the mean difference to be no more than 5 mmHG. Nurse reading of SBP ranged from 78 to 147 mmHG and DBP ranged from 42 to 99 mmHG across all subjects. Specifically, our procedure of our BP measurements consists of an oscillometric blood pressure recoding, followed by readings of SBP and DBP with help of two trained nurse after a one minute pause. This is then followed by another one minute pause. The procedure is repeated again four more time to make the recoding of five measurements. For data collection, each subject sat well and upright posture in a chair where the UFIT monitor's cuff is strapped to the left wrist of the subject, which is raised to heart level. Another cuff, which is the component of the auscultatory, is placed on the upper left arm also at heart level.
In this paper, only five measurements of each subject were assumed to be available and were used to implement was used as the true estimate. In Tables 1 and 2, we presents the averaged (over 85 subjects) systolic blood pressure (SBP) and diastolic blood pressure (DBP) estimates for a sequence of five measurements determined by the proposed algorithm as well as the corresponding averaged systolic and diastolic ratios obtained through the proposed method for the five measurements. The standard deviation of the estimates is provided in brackets. Tables 3 and 4 contain the average results obtained using the proposed individualized ratios for 85 subjects using the five measurements. The proposed methods are referred to as the maximum amplitude algorithm using Bayesian with Gaussian (MAABG) and the maximum amplitude algorithm using Bayeaisn with Laplacian (MAABL).
In order to verify the performance of BP estimation, the MD and the SD between the estimated BP and the auscultatory nurse measurements were calculated according to AAMI standard protocol recommended [15]. A blood pressure monitor could pass AAMI protocol, if its measurements error has a mean value of less than 5 mmHG with a SD of no more than 8 mmHG [15] Therefore, lower values of MD correspond to better overall performance. The MD of the proposed MAABG algorithm in SBP and DBP was compared to that of the MAA algorithm as in Table 5, confirming that the proposed MAABG has much effect on the error of the estimate. Tables 5 shows the MD as the average difference between the blood pressures measured through auscultation by the nurse, and the MAA and MAAB methods described in this paper. For example, the MD was found to be 6.80 and 5.39 (mmHG) for the SBP and DBP when comparing MAA and the reference ausculation method based on the result of the first measurement. The proposed method, MAABG showed lower MD compared to the MAA for both SBP and DBP consistently in all the five measurements, as shown in Table 5. In addition, the SD was used to describe a measure of error variability between the auscultatory nurse measurements and the estimates obtained using the proposed method. The SD between the proposed MAABG method and the auscultatory nurse measurements was found to be 2.99 mmHG for the SBP and 3.58 mmHG for the DBP, respectively, which were superior to those obtained from the auscultatory nurse measurements and the MAA method.
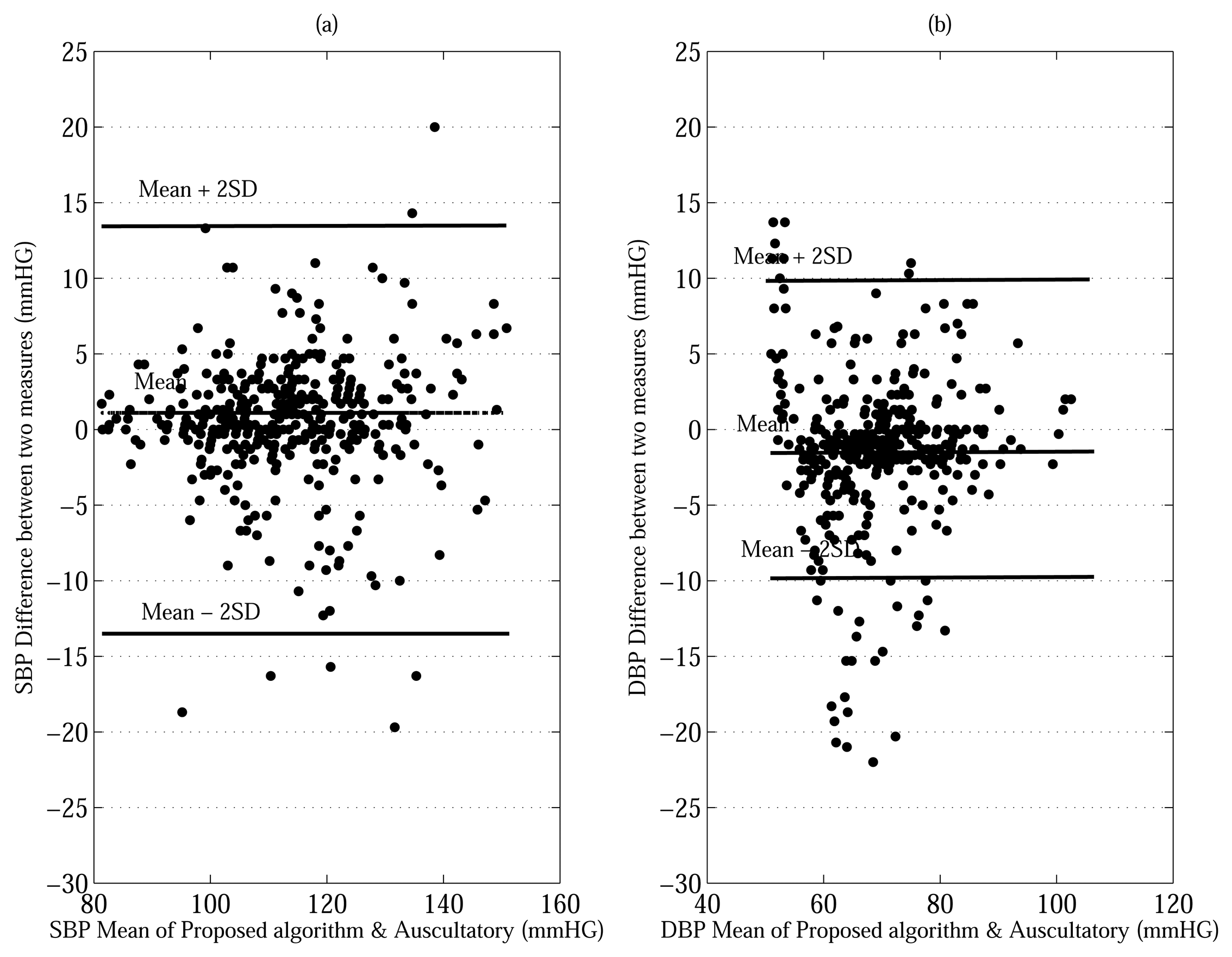
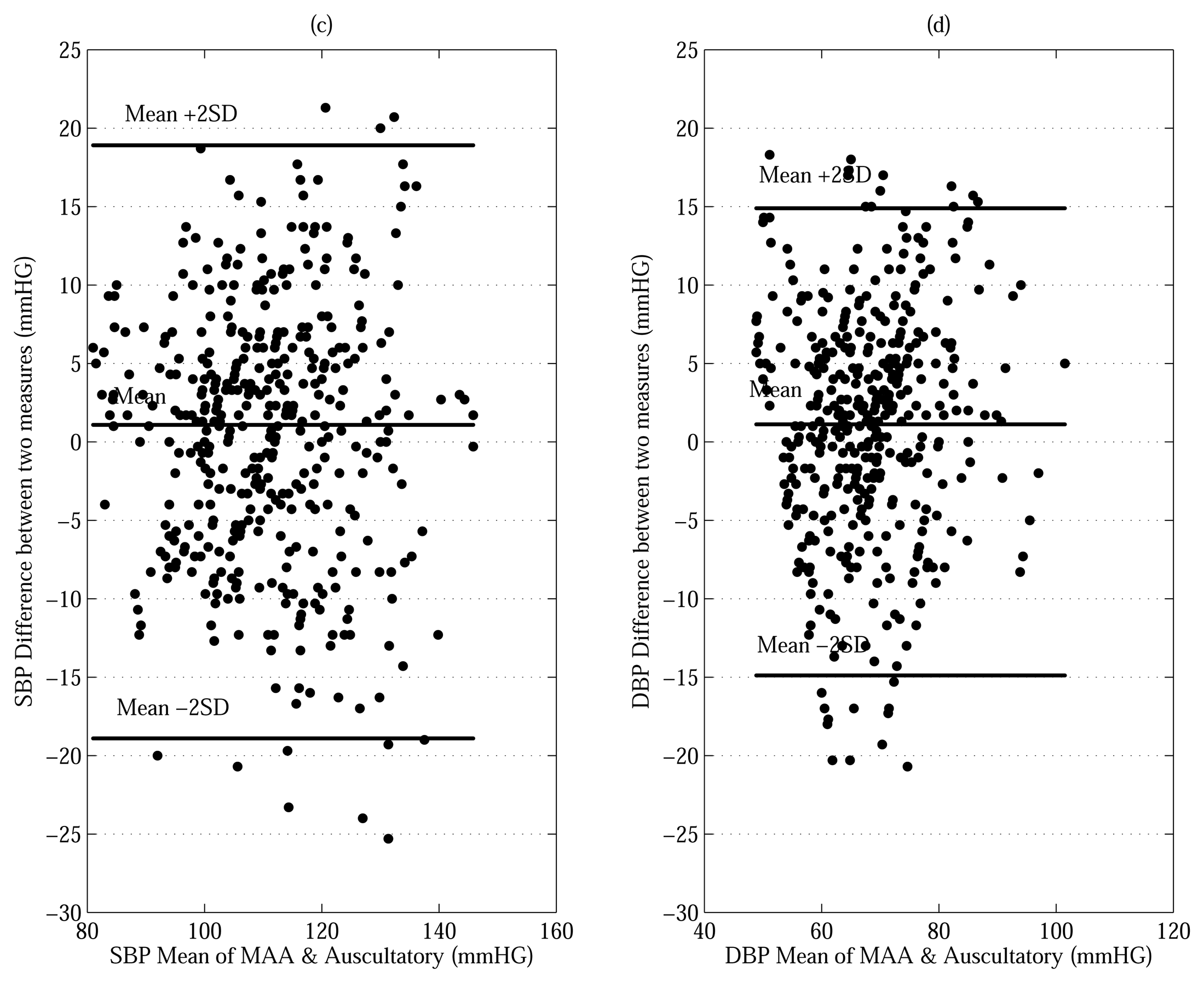
The work described in this paper is a systematic methodology with a theoretical basis using a Bayesian model for estimating the SBP and DBP. As seen from in the last row of Table 5, the proposed approaches, evaluated using both the MAABG and MAABL resulted in much lower MD's average for both SBP (MD = 6.25 and 6.25 mmHG) and the DBP (MD = 5.00 and 5.00 mmHG) compared to the conventional MAA. The difference in estimation error between the proposed methods and the conventional MAA for SBP and DBP is an MD of 0.78 and 0.95 mmHG. Figure 5 shows Bland-Altman plots comparing of the performance between the proposed MAABG algorithm and auscultatory nurse measurements (425 measurements) [22]. The performance between the conventional MAA and auscultatory nurse measurements (425 measurements) is compared by Bland-Altman plots as shown in Figure 6. The limits of agreement (see bold horizontal lines in Figures 5 and 6) that we use are (MD ± 2× SD) for all plots. For all plots in Figures 5 and 6, most of BP measurements' points within the limits of agreement. Moreover, the bias (see horizontal center lines) for all plots is negligible amount (< ±1.5 mmHG). This implies that the BP estimates made by the MAA and MAABG are in close agreement with those made by the auscultatory nurse measurement without being overly biased in any particular direction. We also note that the vertical spreads of the proposed MAABG algorithm for the SBP and DBP are smaller than those of the conventional MAA method as shown in Figures 5 and 6. That is, the proposed MAABG algorithm provides an improvement in oscillometric BP estimation.
In addition, the SD was utilized as a tool of error variable between the auscultatory nurse measurements and the estimates obtained using the proposed MAABG. The SD obtained with the proposed methods, which are the MAABG and MAABL, was found to be 3.32 and 3.32 mmHG for the SBP, respectively, and 3.34 and 3.34 mmHG for the DBP, respectively. This performance is superior to that obtained when the conventional MAA was compared with the auscultatory nurse measurements. The difference in SD between the proposed MAABG and the conventional MAA, for SBP and DBP is 2.99 and 1.13 mmHG. Such improvements could be very significant given that the AAMI protocol recommends for the automated BP monitors [15]. These results confirm that the proposed approaches which are based on the Bayeaian model acquires a high degree of accuracy in BP measurements. Note that, the proposed MAABG and MAABL shows the same results. This implies that the proposed approaches represent the robust characteristics despite using different likelihood function.
4. Conclusions
In conclusion, the MDs and SDs of the SBP and DBP obtained through the proposed MAABG and MAABL are smaller relative to the reference nurse values when compared to the conventional MAA method. This study has established that the proposed method has outperformed the conventional MAA method in estimating the SBP and DBP. Furthermore, a systematic methodology with a theoretical basis for calculating individualized SBPR and DBPR is demonstrated that can be used with conventional MAA algorithm.
Acknowledgments
The authors thank Biosign for providing equipment and data. The authors would like to thank Hilmi Dajani, Voicu Groza, Miodrag Bolic, and Sreeraman Rajan who are with the School of Electrical and Computer Science, University of Ottawa, Canada. This research was supported by NRF(2013R1A1A2012536). This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT and Future Planning(2013R1A1A1010797)
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Here, we add the basic concept of Bayes rule [18] in more detail for the individualized SBPR and DBPR which are already assumed in Section 2.2 as random variables Employing the definition of conditional probability with the product and sum rules produces Bayes rule such that
Based on Equation (18), we can see the parts in Equation (7). The prior distribution is given by the pps vector in Equation (5) which are assigned to equal candidate ratios due to the lack of any a priori information. We then observe the likelihood function This conditional probability function of given cr(l)s(i,j)), actually, the value that occurs and where cr(l)s(i,j)) is allowed to vary over its whole range for α1,…, αk. Thus, the posteriori probability distribution is given by the a POP evaluated at cr(l) for every l, l = 1, ⋯, K. This equation gives us a technique for revising our belief probabilities with respect to the possible values of cr(l) given that we obtained ) from the reference auscultatory measurement. Consequentially, we obtain the final ratios as given in Equation (15).
References
- Jilek, J.; Stork, M. Oscillometric Pressure Pulse Waveforms: Their Current and Prospective Applications in Biomedical Instrumentation. Proceedings of the 13th WSEAS International Conference on Systems, Rodos, Greece, 23–25 July 2009; pp. 133–138.
- Drzewiecki, G.; Hood, R.; Apple, H. Theory of the oscillometric maximum and the systolic and diastolic ratios. Ann. Biomed. Eng. 1994, 22, 88–96. [Google Scholar]
- Baker, P.D.; Westenskow, D.R. Theoretical analysis of non-invasive oscillometric maximum amplitude algorithm for estimating mean blood pressure. Med. Biol. Eng. Comput. 1997, 35, 271–278. [Google Scholar]
- Lee, S.; Bolic, M.; Groza, V.Z.; Dajani, H.R.; Rajan, S. Confidence interval estimation for oscillometric blood pressure measurements using bootstrap approaches. IEEE Trans. Instumen. Meas. 2011, 60, 3405–3415. [Google Scholar]
- Geddes, L.A.; Voelz, M.; Combs, C.; Reiner, D.; Babbs, C.F. Characterization of the oscillometric method for measuring indirect blood pressure. Ann. Biomed. Eng. 1982, 10, 271–280. [Google Scholar]
- Kayrak, M.; Ulgen, M.S.; Yazici, M.; Yilmaz, R.; Demir, K.; Dogan, Y.; Ozhan, H.; Alihanoglu, Y.; Koc, F.; Bodur, S. comparision of the blood pressure and pulse pressure values obtained by oscillometric and central measurements in hypertensive patients. Blood Pressure 2010, 19, 98–103. [Google Scholar]
- Hansen, S.; Staber, M. Oscillometric blood pressure measurement used for calibration of the arterial tonometry method contributes significantly to error. Eur. J. Anaesthesiol. 2006, 23, 781–787. [Google Scholar]
- Chen, S.; Groza, V.Z.; Bolic, M.; Dajani, H.R. Assessment of Algorithims for Oscillometric Blood Pressure Measurement. Proceedings of the International Conference IEEE Instrumentation and Measurement Technology, Singapore, 5–7 May 2009.
- Lin, C.T.; Liu, S.H.; Wang, J.J.; Wen, Z.C. Reduction of interference in oscillometric arterial blood pressure measurement using fuzzy logic. IEEE Trans. Biomed. Eng. 2003, 50, 432–441. [Google Scholar]
- Liu, J.; Hahn, J.-O.; Mukkamala, R. Error mechanisms of the oscillometric fixed-ratio blood pressure measurement method. Ann. Biomed. Eng. 2013, 41, 587–597. [Google Scholar]
- Moraes, J.; Cerulli, M.; Ng, P. A Strategy for Determination of Systolic, Mean And Diastolic Blood Pressures from Oscillometric Pulse Profiles. Proceedings of the International Conference IEEE Computers in Cardiology, Cambridge, MA, USA, 24–27 September 2000; pp. 211–214.
- Raamat, R.; Talts, J.; Jagomagi, K.; Kivastik, J. Errors of oscillometric blood pressure measurement as predicted by simulation. Blood Press. Monit. 2011, 16, 73–76. [Google Scholar]
- Soueidan, K.; Chen, S.; Dajani, H.; Bolic, M.; Groza, V. Augmented blood pressure measurement through the noninvasive estimation of physiological arterial pressure variability. Physiol. Meas. 2012, 33, 881–899. [Google Scholar]
- Arce, G.R. Nonlinear Signal Processing, A Statistical Approach; Wiley-Interscience: Hoboken, NY, USA, 2005; pp. 9–10. [Google Scholar]
- Manual, Electronic or Automated Sphygmonanometers, American National Standard ANSI/AAMI SP 10: 2002, 2003; Association for the Advancement of Medical Instrumentation: Arlington, VA, USA, 2003.
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence interval, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 54–77. [Google Scholar]
- Moore, D.S.; Mccabe, G.P. Introduction to the Practice of Statistics; W. H. Freeman and Company: New York, NY, USA, 2004; Appendix: Chapter 14; p. 13. [Google Scholar]
- Bolstad, W.M. Understanding Computational Bayesian Statistics; Wiley: New York, NY, USA, 2010; pp. 16–47. [Google Scholar]
- Cubic Spline Interpolation. Available online: http://online.redwoods.edu/instruct/darnold/laproj/Fall98/SkyMeg/Proj.PDF (accessed on 29 September 2013).
- Ahmad, S.; Bolic, M.; Dajani, H.; Groza, V.; Batkin, I.; Rajan, S. Measurement of heart rate variability using an oscillometric blood pressure monitor. IEEE Trans. Instumen. Meas. 2010, 59, 2575–2590. [Google Scholar]
- Chen, S.; Bolic, M.; Groza, V.; Dajani, H.; Batkin, I.; Rajan, S. Extraction of breathing signal and suppression of its effects in oscillometric blood pressure measurement. IEEE Trans. Instumen. Meas. 2011, 60, 1741–1750. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar]


| Method (n = 85) | Ratio (std) First | Ratio (std) Second | Ratio (std) Third | Ratio (std) Fourth | Ratio (std) Fifth |
|---|---|---|---|---|---|
| MAABG | 0.79 (0.11) | 0.79 (0.12) | 0.79 (0.12) | 0.80 (0.11) | 0.80 (0.11) |
| MAABL | 0.79 (0.11) | 0.79 (0.12) | 0.79 (0.12) | 0.80 (0.11) | 0.80 (0.11) |
| Method (n = 85) | Ratio (std) First | Ratio (std) Second | Ratio (std) Third | Ratio (std) Fourth | Ratio (std) Fifth |
|---|---|---|---|---|---|
| MAABG | 0.44 (0.11) | 0.43 (0.11) | 0.42 (0.11) | 0.41 (0.11) | 0.39 (0.11) |
| MAABL | 0.44 (0.11) | 0.43 (0.11) | 0.42 (0.11) | 0.41 (0.11) | 0.39 (0.11) |
| BP (mmHG) (N = 85) | SBP (std) First | SBP (std) Second | SBP (std) Third | SBP (std) Fourth | SBP (std) Fifth |
|---|---|---|---|---|---|
| Nurse | 108.9 (13.2) | 108.9 (13.5) | 109.8 (13.8) | 110.3 (13.5) | 112.2 (14.6) |
| MAA | 115.4 (14.0) | 115.5 (14.4) | 116.3 (14.5) | 118.1 (14.3) | 120.0 (15.4) |
| MAABG | 114.8 (13.2) | 114.6 (13.3) | 115.6 (13.1) | 116.7 (13.5) | 118.5 (14.6) |
| MAABL | 114.8 (13.2) | 114.6 (13.3) | 115.6 (13.1) | 116.7 (13.5) | 118.5 (14.6) |
| BP (mmHG) (N = 85) | DBP (std) First | DBP (std) Second | DBP (std) Third | DBP (std) Fourth | DBP (std) Fifth |
|---|---|---|---|---|---|
| Nurse | 67.6 (9.8) | 67.1 (9.6) | 67.2 (10.0) | 67.6 (9.8) | 67.5 (10.2) |
| MAA | 69.7 (10.5) | 69.8 (10.4) | 69.9 (10.3) | 72.0 (10.5) | 73.2 (10.8) |
| MAABG | 70.7 (10.3) | 70.4 (9.9) | 70.7 (9.9) | 72.0 (9.9) | 71.9 (9.9) |
| MAABL | 70.7 (10.3) | 70.4 (9.9) | 70.7 (9.9) | 72.0 (9.9) | 71.9 (9.9) |
| MAA (mmHG) Test | SBP MD (SD) | MAABG DBP MD (SD) | SBP MD (SD) | MAABL DBP MD (SD) | SBP MD (SD) | DBP MD (SD) |
|---|---|---|---|---|---|---|
| 1st mea. | 6.80 (6.70) | 5.39 (5.10) | 6.01 (2.99) | 4.92 (3.58) | 6.01 (2.99) | 4.92 (3.58) |
| 2nd mea. | 7.80 (6.22) | 5.60 (4.40) | 5.87 (3.27) | 4.56 (2.93) | 5.87 (3.27) | 4.56 (2.93) |
| 3rd mea. | 6.70 (5.80) | 5.70 (4.20) | 6.45 (3.73) | 4.88 (3.39) | 6.45 (3.73) | 4.88 (3.39) |
| 4th mea. | 6.30 (5.77) | 6.00 (4.09) | 6.14 (2.84) | 5.01 (3.32) | 6.14 (2.84) | 5.01 (3.32) |
| 5th mea. | 7.56 (7.07) | 7.08 (4.98) | 6.76 (3.79) | 5.63 (3.87) | 6.76 (3.79) | 5.63 (3.87) |
| avg. | 7.03 (6.31) | 5.95 (4.55) | 6.25 (3.32) | 5.00 (3.42) | 6.25 (3.32) | 5.00 (3.42) |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, S.; Jeon, G.; Lee, G. On Using Maximum a Posteriori Probability Based on a Bayesian Model for Oscillometric Blood Pressure Estimation. Sensors 2013, 13, 13609-13623. https://doi.org/10.3390/s131013609
Lee S, Jeon G, Lee G. On Using Maximum a Posteriori Probability Based on a Bayesian Model for Oscillometric Blood Pressure Estimation. Sensors. 2013; 13(10):13609-13623. https://doi.org/10.3390/s131013609
Chicago/Turabian StyleLee, Soojeong, Gwanggil Jeon, and Gangseong Lee. 2013. "On Using Maximum a Posteriori Probability Based on a Bayesian Model for Oscillometric Blood Pressure Estimation" Sensors 13, no. 10: 13609-13623. https://doi.org/10.3390/s131013609





