Fiber Loop Ringdown Sensor for Potential Real-Time Monitoring of Cracks in Concrete Structures: An Exploratory Study
Abstract
:1. Introduction
2. Sensor Design and Sensing Principle
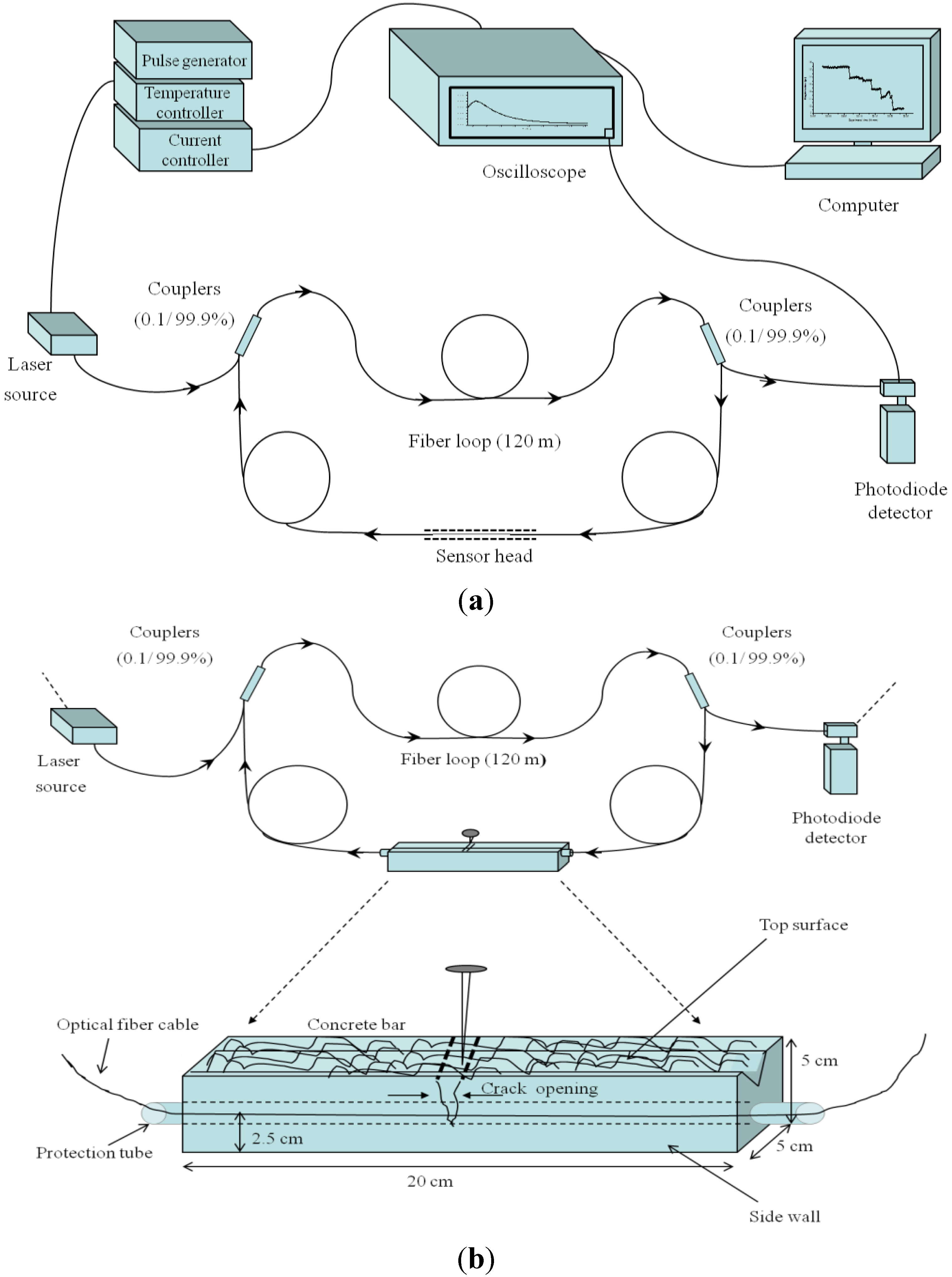
2.1. FLRD Sensors
2.2. FLRD Sensing Principle
2.3. Concrete Samples
2.4. A Sensor Unit
3. Results and Discussion
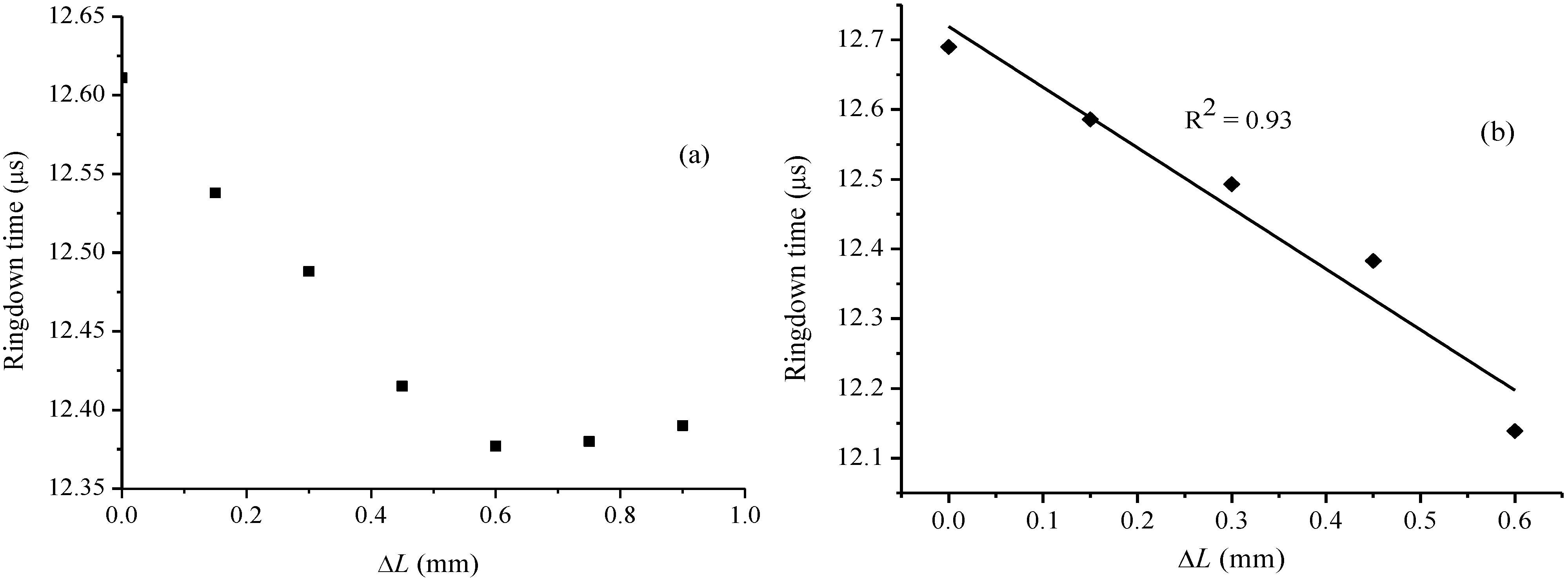
3.1. Response of FLRD Crack Sensors
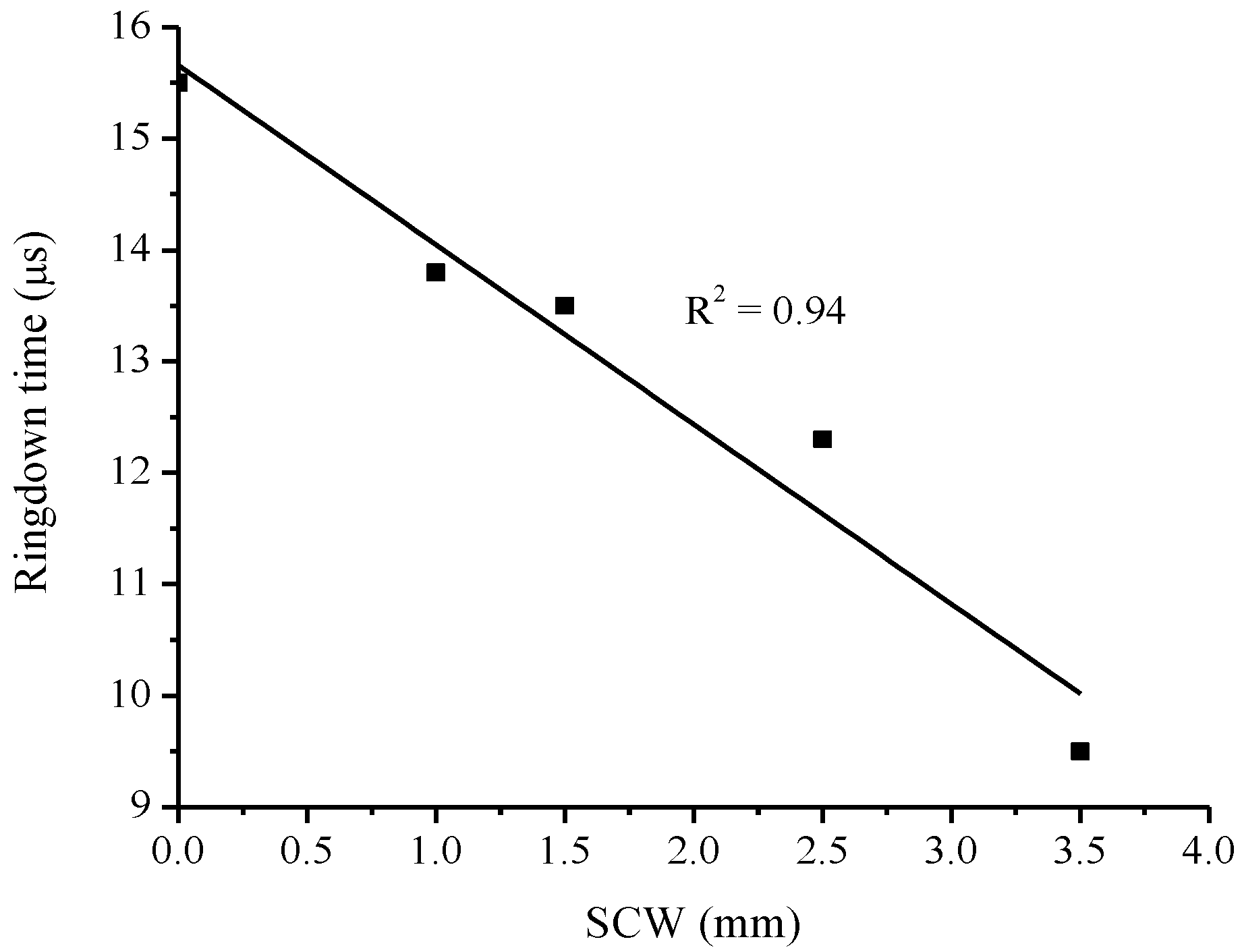
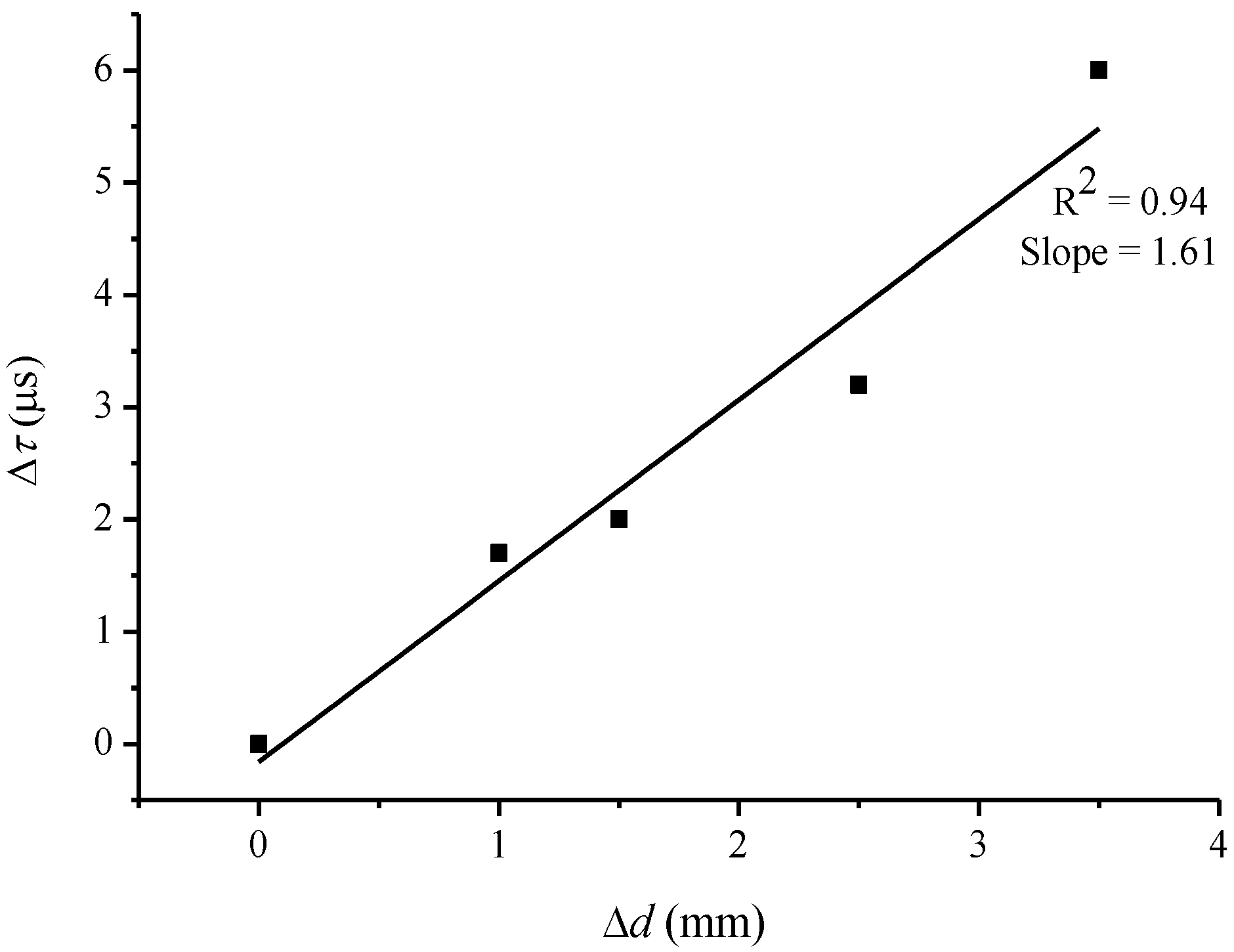
3.2. Detection Sensitivity of Surface Crack Width
3.3. Theoretical Detection Sensitivity of the Crack Sensor
3.4. Advantages and Limitations of the FLRD Crack Sensors
- Simplicity: The presented FLRD crack sensors offer simplicity in terms of construction and operation. A bare single mode fiber, without using any advanced fiber optic components or chemical coatings, is directly utilized as a sensor head for the purpose of sensing. Consequently, the use of SMF offers ease of construction as well as low cost of embedment in concrete structures, unlike other conventional sensors based on FBG, Brillouin scattering, or Fabry–Perot techniques, which involve complicated instrumentation procedures and special cares in the sensor embedment [23,49,52]. Furthermore, the FLRD crack sensor uses an inexpensive photodiode as the detector, significantly reducing costs in the terminal detection equipment.
- Temperature independence: The FLRD crack sensor is based on strain sensing mechanism. Due to the low thermal coefficient, 0.5 × 10−6 °C, of the silica fiber [40,53] and free of other optical components in the sensor head, the FLRD crack sensor is virtually independent of environmental temperature in the range of −169–800 °C [54]. This type of crack sensor is especially advantageous when temperature variations are an important factor, i.e., in combustion facility, reactors, etc.
- Near real-time response: Fast response of a sensor is always desirable. Near real-time response is another significant feature of the present sensor. The sharp decrease in the ringdown time in Figure 5 shows that the response time was 1.5 s. Taking the 100 measuring events into consideration, a single measuring time is only 15 milliseconds. In application in civil structure monitoring, this response time has significant socio-economic impact in structure damage mitigation, i.e., in the case of natural disasters.
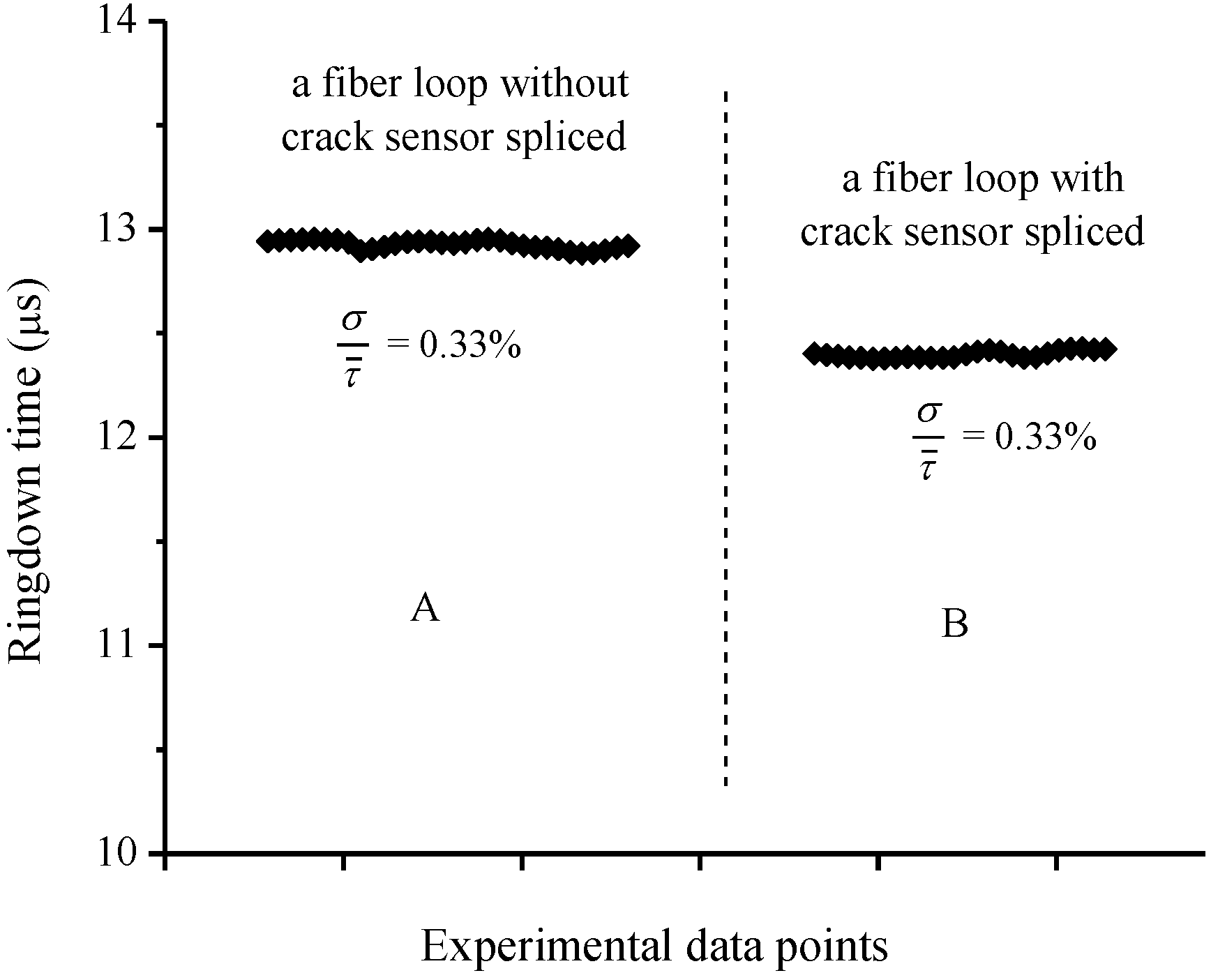
- High detection sensitivity and large dynamic range: Owing to the high baseline stability, ∼0.33%, this FLRD crack senor potentially has a crack detection sensitivity of tens of microns. As a typical example, the unit-3 has a detection sensitivity of 31 μm in terms of SCW. On the other hand, crack sensing was successfully carried out for SCW as large as 3.5 mm. Therefore, a large dynamic range of crack detection, from tens of microns to a few mm, can be expected from this sensor. Given the fact that the sensing is accomplished with a bare SMF with simplicity in the construction of sensor, this level of sensitivity and dynamic range for crack detection is still practically appreciable in some applications.
4. Conclusions
Acknowledgments
References
- Chong, K.P.; Carino, N.J.; Washer, G. Health monitoring of civil infrastructures. Smart Mater. Struct. 2003, 12, 483–493. [Google Scholar]
- Concrete Cracking. Available online: http://www.cfawalls.org/foundations/cracking.htm (accessed on 5 March 2012).
- Daniels, D.J. Surface-penetrating radar. Electron. Commun. Eng. 1996, 8, 165–182. [Google Scholar]
- Carino, N.J. The impact-echo method: an overview. Proceedings of Structures Congress & Exposition, Washington, DC, USA, 21–23 May 2001; pp. 1–18.
- Clark, M.; McCann, D.; Forde, M. Application of infrared thermography to the non-destructive testing of concrete and masonry bridges. NDT & E Int. 2003, 36, 265–275. [Google Scholar]
- Ohtsu, M. The history and development of acoustic emission in concrete engineering. Mag. Concrete Res. 1996, 48, 312–330. [Google Scholar]
- Song, G.; Mo, Y.L.; Otero, K.; Gu, H. Health monitoring and rehabilitation of a concrete structure using intelligent materials. Smart Mater. Struct. 2006, 15, 309–314. [Google Scholar]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.C.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959–968. [Google Scholar]
- Yan, S.; Sun, W.; Song, G.; Gu, H.; Huo, L.S.; Liu, B.; Zhang, Y.G. Health monitoring of reinforced concrete shear walls using smart aggregates. Smart Mater. Struct. 2009, 18, 047001:1–047001:6. [Google Scholar]
- Gu, H.; Moslehy, Y.; Sanders, D.; Song, G.; Mo, Y.L. Multi-functional smart aggregate-based structural health monitoring of circular reinforced concrete columns subjected to seismic excitations. Smart Mater. Struct. 2010, 19, 06506:1–06506:7. [Google Scholar]
- Chang, P.C.; Flatau, A.; Liu, S. Review paper: Health monitoring of civil infrastructure. Struc. Health Monit. 2003, 2, 257–267. [Google Scholar]
- Song, G.; Gu, H.C.; Mo, Y.L. Smart aggregates: multi-functional sensors for concrete structures: A tutorial and a review. Smart Mater. Struct. 2008, 17, 033001:1–033001:17. [Google Scholar]
- Mendez, A.; Morse, T.F.; Mendez, F. Applications of embedded optical fiber sensors in reinforced concrete buildings and structures. Proc. SPIE 1989, 1170, 60–69. [Google Scholar]
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A: Phys. 2000, 82, 40–61. [Google Scholar]
- Leung, C.K.Y. Fiber optic sensors in concrete: the future? NDT & E Int. 2001, 34, 85–94. [Google Scholar]
- Merzbacher, C.I.; Kersey, A.D.; Friebele, E.F. Fiber optic sensors in concrete structures: A review. Smart Mater. Struct. 1996, 5, 196–208. [Google Scholar]
- Zhou, G.; Sim, L.M. Damage detection and assessment in fibre-reinforced composite structures with embedded fibre optic sensors-review. Smart Mater. Struct. 2002, 5, 925–940. [Google Scholar]
- Ansari, F. Theory and Applications of Integrated Fiber Optic Sensors. In Intelligent Civil Engineering Materials and Structures; Ansari, F., Maji, A., Leung, C., Eds.; American Society of Civil Engineers: New York, NY, USA, 1997; pp. 2–28. [Google Scholar]
- Moyo, P.; Brownjohn, J.M.W.; Suresh, R.; Tjin, S.J. Development of fiber Bragg grating sensors for monitoring civil infrastructure. Eng. Struct. 2005, 27, 1828–1834. [Google Scholar]
- Li, H.N.; Li, D.S.; Song, G.B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar]
- Leng, J.; Asundi, A. Structural health monitoring of smart composite materials by using EFPI and FBG sensors. Sens. Actuators A: Phys. 2003, 103, 330–340. [Google Scholar]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D. Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A: Phys. 2008, 147, 150–164. [Google Scholar]
- Glišić, B.; Inaudi, D. Chapter 2: Fiber Optic Sensors. In Fibre Optic Methods for Structural Health Monitoring; John Wiley & Sons: New York, NY, USA, 2008; pp. 20–40. [Google Scholar]
- Gangopadhyay, T.K.; Majumder, M.; Chakraborty, A.K.; Dikshit, A.K.; Bhattacharya, D.K. Fibre Bragg grating strain sensor and study of its packaging material for use in critical analysis on steel structure. Sens. Actuators A: Phys. 2009, 150, 78–86. [Google Scholar]
- Villalba, S.; Casas, J.R. Application of optical fiber distributed sensing to health monitoring of concrete structures. Mech. Syst. Signal Process. 2012. [Google Scholar] [CrossRef]
- Rossi, P.; Le Maou, F. New method for detecting cracks in concrete using fibre optics. Mater. Struct. 1989, 22, 437–442. [Google Scholar]
- Ansari, F.; Navalurkar, R.K. Kinematics of crack formation in cementitious composites by fiber optics. Eng. Mech. 1993, 112, 1048–1061. [Google Scholar]
- Leung, C.K.Y.; Elvin, N.; Olson, N.; Morse, T.F.; He, Y.F. A novel distributed optical crack sensor for concrete structures. Eng. Fracture Mech. 2000, 65, 133–148. [Google Scholar]
- Habel, W.R.; Feddersen, I.; Fitschen, C. Embedded quasi-distributed fiber-optic sensors for the long-term monitoring of the grouting area of rock anchors in a large gravity dam. Intelligent Mater. Syst. Struct. 1999, 10, 330–339. [Google Scholar]
- Lee, D.; Lee, J.; Kwon, I.; Seo, D. Monitoring of fatigue damage of composite structures by using embedded intensity-based optical fiber sensors. Smart Mater. Struct. 2001, 10, 285–292. [Google Scholar]
- Annamdas, K.K.K.; Annamdas, V.G.M. Review on developments in fiber optical sensors and applications. Proc. SPIE 2010, 76770, 76770R:1–76770R:12. [Google Scholar]
- O'Keefe, A.; Deacon, D.A.G. Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources. Rev. Sci. Instrum. 1988, 59, 2544–2551. [Google Scholar]
- Cavity-Ringdown Spectroscopy: An Ultratrace-Absorption Measurement Technique; Busch, K.W.; Busch, M.A. (Eds.) American Chemical Society: Washington, DC, USA, 1999; Volume 720.
- Berden, G.; Peeters, R.; Meijer, G. Cavity ring-down spectroscopy: Experimental schemes and applications. Int. Rev. Phys. Chem. 2000, 19, 565–607. [Google Scholar]
- Stewart, G.; Atherton, K.; Yu, H.; Culshaw, B. An investigation of an optical fibre amplifier loop for intra-cavity and ring-down cavity loss measurements. Meas. Sci. Technol. 2001, 12, 843–849. [Google Scholar]
- Brown, R.S.; Kozin, I.; Tong, Z.; Oleschuk, R.D.; Loock, H.P. Fiber-loop ring-down spectroscopy. Chem. Phys. Lett. 2002, 117, 10444–10447. [Google Scholar]
- Tarsa, P.B.; Rabinowitz, P.; Lehmann, K.K. Evanescent field absorption in a passive optical fiber resonator using continuous-wave cavity ring-down spectroscopy. Chem. Phys. Lett. 2004, 383, 297–303. [Google Scholar]
- Wang, C.; Scherrer, S.T. Fiber ringdown pressure sensors. Opt. Lett. 2004, 29, 352–354. [Google Scholar]
- Wang, C.; Scherrer, S.T. Fiber Loop Ringdown for Physical Sensor Development: Pressure Sensor. Appl. Opt. 2004, 43, 6458–6464. [Google Scholar]
- Vallance, C. Innovations in cavity ringdown spectroscopy. New J. Chem. 2005, 29, 867–874. [Google Scholar]
- Wang, C. Fiber loop ringdown—A time-domain sensing technique for multi-function fiber optic sensor platforms: Current status and design perspectives. Sensors 2009, 9, 7595–7621. [Google Scholar]
- Waechter, H.; Litman, J.; Cheung, A.H.; Barnes, J.A.; Loock, H.P. Chemical sensing using fiber cavity ring-down spectroscopy. Sensors 2010, 10, 1716–1742. [Google Scholar]
- Qiu, H.; Qiu, Y.; Chen, Z.; Fu, B.; Chen, X.; Li, G. Multimode fiber ring-down presuure sensor. Microw. Opt. Techn. Let. 2007, 49, 1698–1700. [Google Scholar]
- Ni, N.; Chan, C.; Wong, W.; Shao, L.; Dong, X.; Shum, P. Cavity ring-down long period grating pressure sensor. Sens. Actuators A: Phys. 2010, 158, 207–211. [Google Scholar]
- Ni, N.; Chan, C.; Dong, X.; Sun, J.; Shum, P. Cavity ring-down long-period fibre grating strain sensor. Meas. Sci. Technol. 2007, 18, 3135–3138. [Google Scholar]
- Bo, L.; Jianhua, L.; Guiyun, K. Temperature and strain sensor based on weak LPG and fiber ring down. Microw. Opt. Techn. Lett. 2007, 50, 111–114. [Google Scholar]
- Qiu, H.; Qiu, Y.; Chen, Z.; Fu, B.; Li, G. Strain measurement by fiber-loop ring-down spectroscopy and fiber mode converter. IEEE Sens. J. 2008, 8, 1180–1183. [Google Scholar]
- Ravet, F.; Briffod, F.; Glisic, B.; Niklès, M.; Inaudi, D. Submillimeter crack detection with Brillouin-based fiber-optic sensors. Sensors 2009, 9, 1391–1396. [Google Scholar]
- Wang, C.; Herath, C. Fabrication and characterization of fiber loop ringdown evanescent field sensors. Meas. Sci. Technol. 2010, 21, 085205 1–8. [Google Scholar]
- Tarsa, P.B.; Brzozowski, D.M.; Rabinowitz, P.; Lehmann, K.K. Cavity ringdown strain gauge. Opt. Lett. 2004, 29, 1339–1341. [Google Scholar]
- Kesavan, K.; Ravisankar, K.; Parivallal, S.; Sreeshylam, P.; Sridhar, S. Experimental studies on fiber optic sensors embedded in concrete. Measurement 2010, 43, 157–163. [Google Scholar]
- Reid, M.B.; Ozcan, M. Temperature dependence of fiber optic Bragg gratings at low temperatures. Opt. Eng. 1998, 37, 237–240. [Google Scholar]
- Wang, C.; Mbi, A. An alternative method to develop fibre grating temperature sensors using the fibre loop ringdown scheme. Meas. Sci. Technol. 2006, 17, 1741–1751. [Google Scholar]


© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sahay, P.; Kaya, M.; Wang, C. Fiber Loop Ringdown Sensor for Potential Real-Time Monitoring of Cracks in Concrete Structures: An Exploratory Study. Sensors 2013, 13, 39-57. https://doi.org/10.3390/s130100039
Sahay P, Kaya M, Wang C. Fiber Loop Ringdown Sensor for Potential Real-Time Monitoring of Cracks in Concrete Structures: An Exploratory Study. Sensors. 2013; 13(1):39-57. https://doi.org/10.3390/s130100039
Chicago/Turabian StyleSahay, Peeyush, Malik Kaya, and Chuji Wang. 2013. "Fiber Loop Ringdown Sensor for Potential Real-Time Monitoring of Cracks in Concrete Structures: An Exploratory Study" Sensors 13, no. 1: 39-57. https://doi.org/10.3390/s130100039
APA StyleSahay, P., Kaya, M., & Wang, C. (2013). Fiber Loop Ringdown Sensor for Potential Real-Time Monitoring of Cracks in Concrete Structures: An Exploratory Study. Sensors, 13(1), 39-57. https://doi.org/10.3390/s130100039




