GPS-Supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments
Abstract
:1. Introduction
2. Monocular Ideal Sensor Model vs. Rigorous Sensor Model of a Panoramic Camera
2.1. Projection from Fish-Eye Lenses to Panoramic Camera
2.2. Ideal Panoramic Sensor Model
2.3. Rigid Panoramic Sensor Model
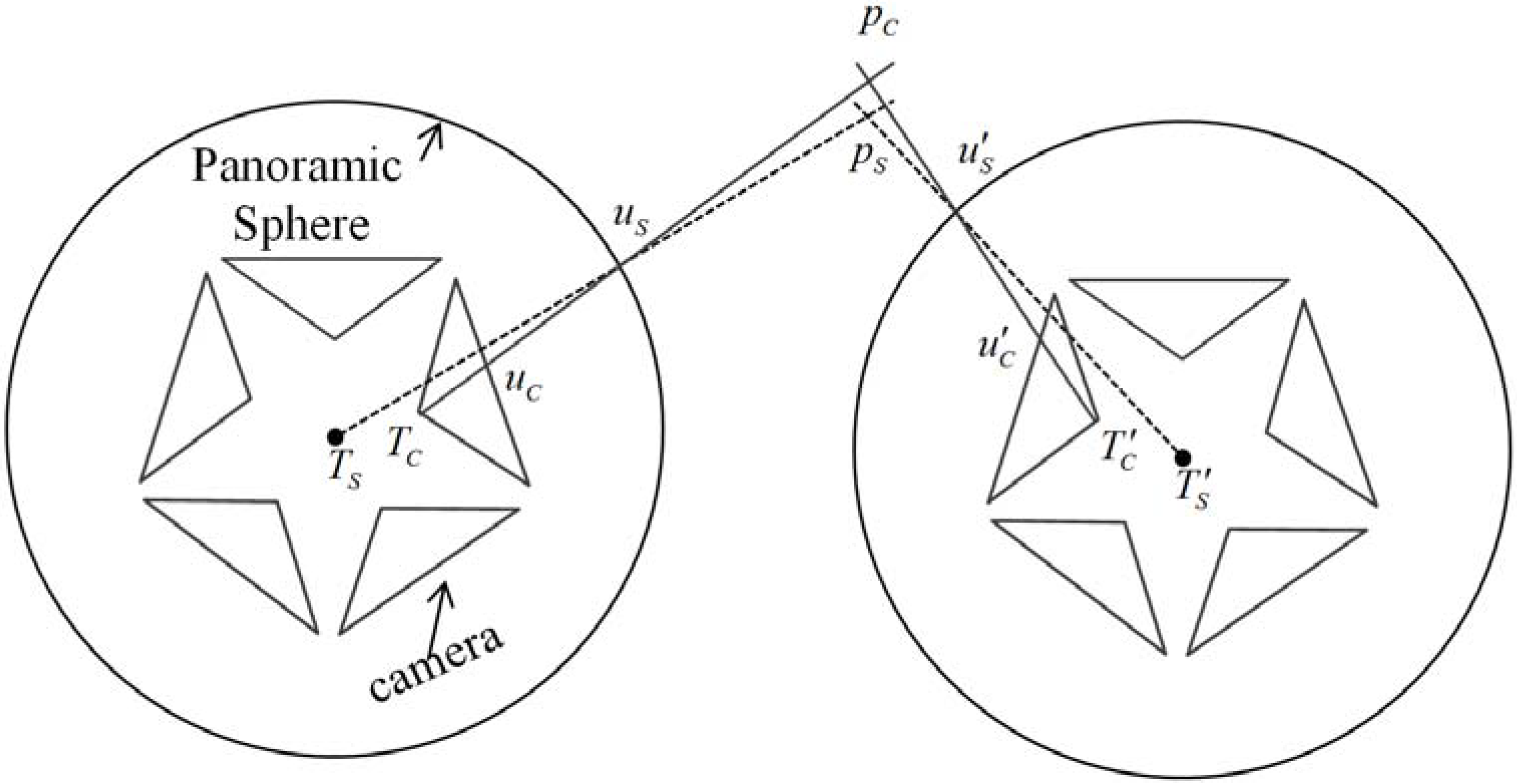
3. Ideal Co-Planarity vs. Rigorous Co-Planarity of a Panoramic Camera
3.1. Ideal Panoramic Co-Planarity
3.2. Rigorous Panoramic Co-Planarity
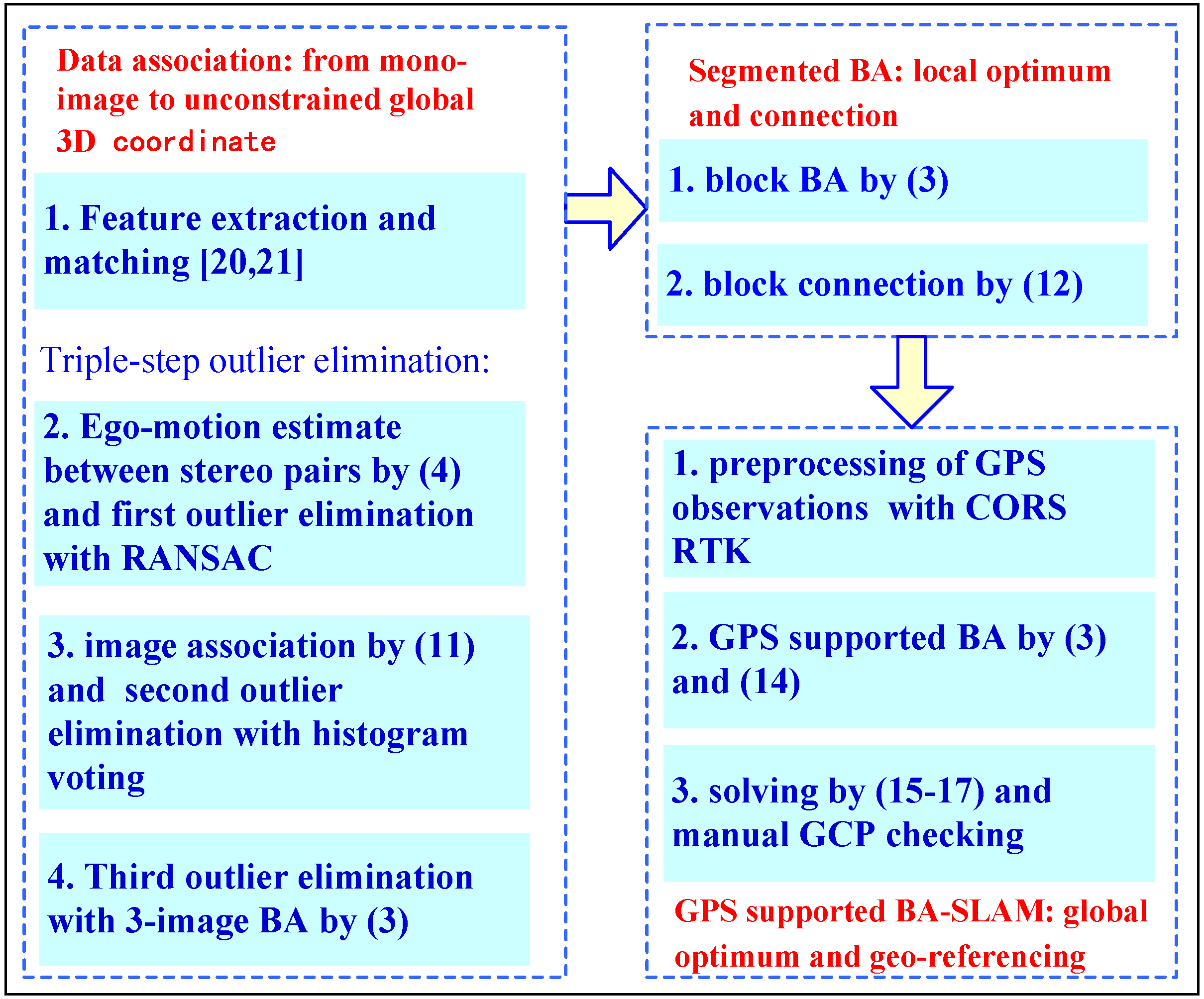
4. GPS-Supported Visual SLAM with the Rigorous Camera Model
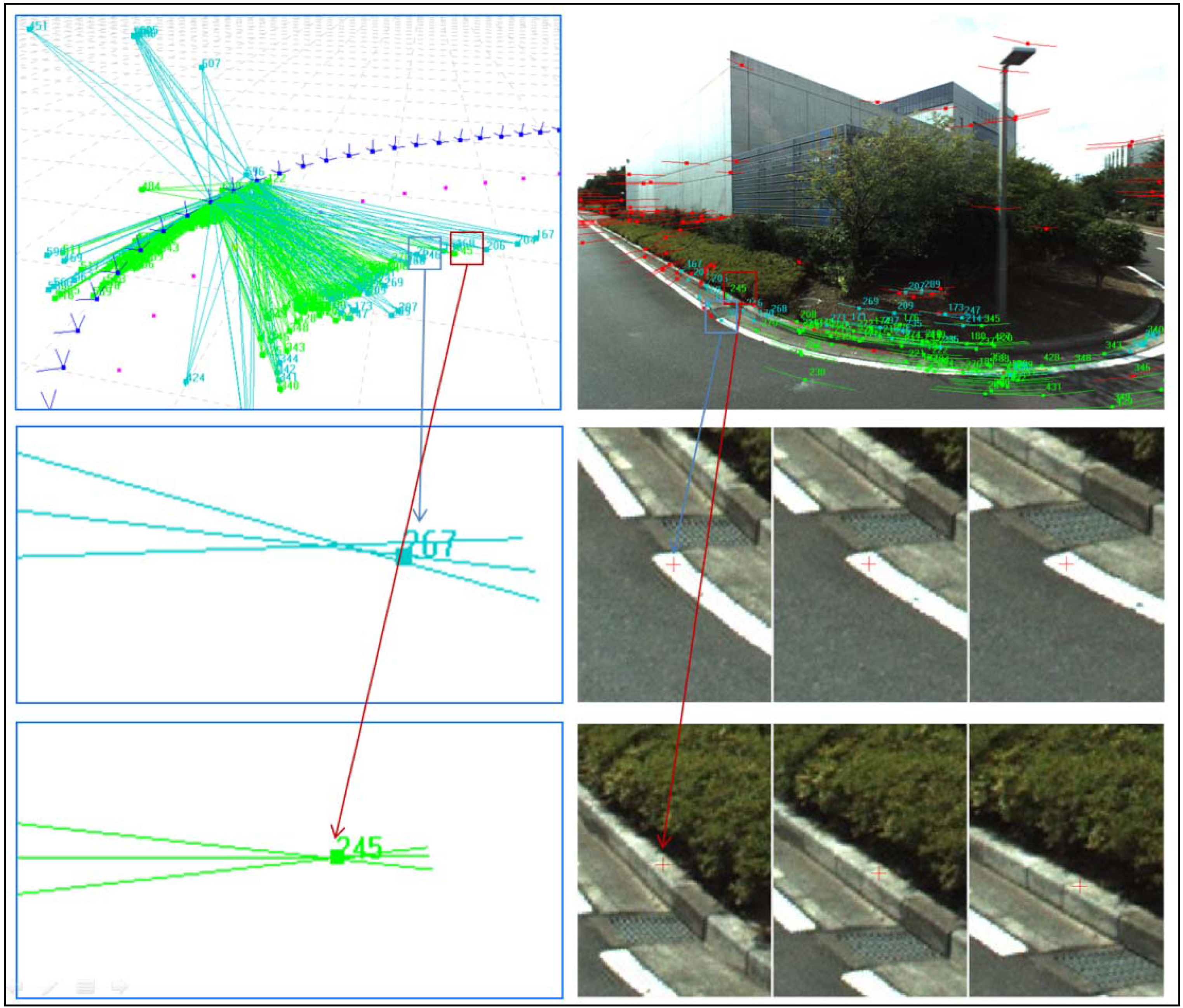
4.1. Data Association
4.2. Segmented BA-SLAM
4.3. GPS-Supported BA-SLAM
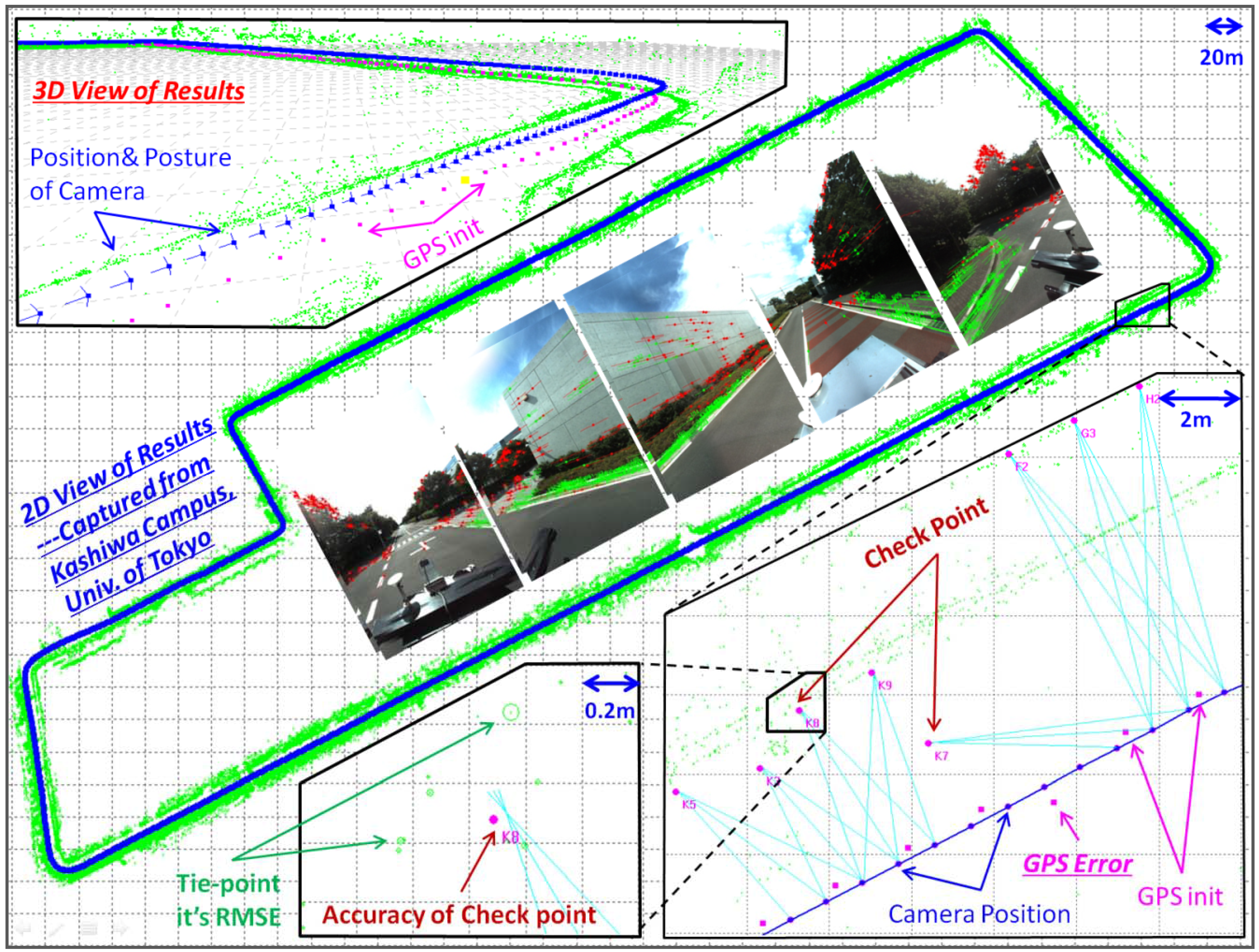
5. Experiments
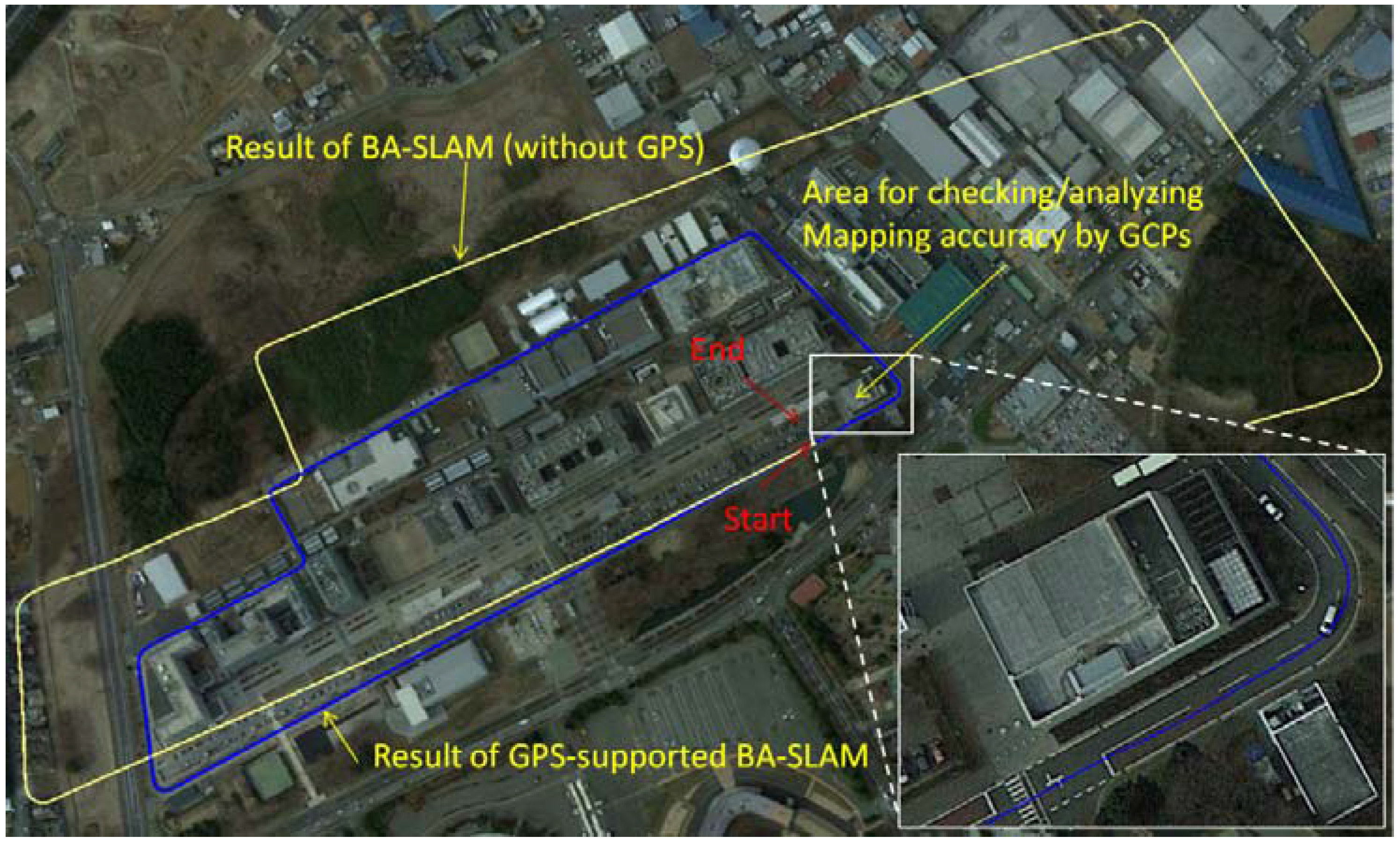
5.1. Test Design
5.2. BA Results without GPS
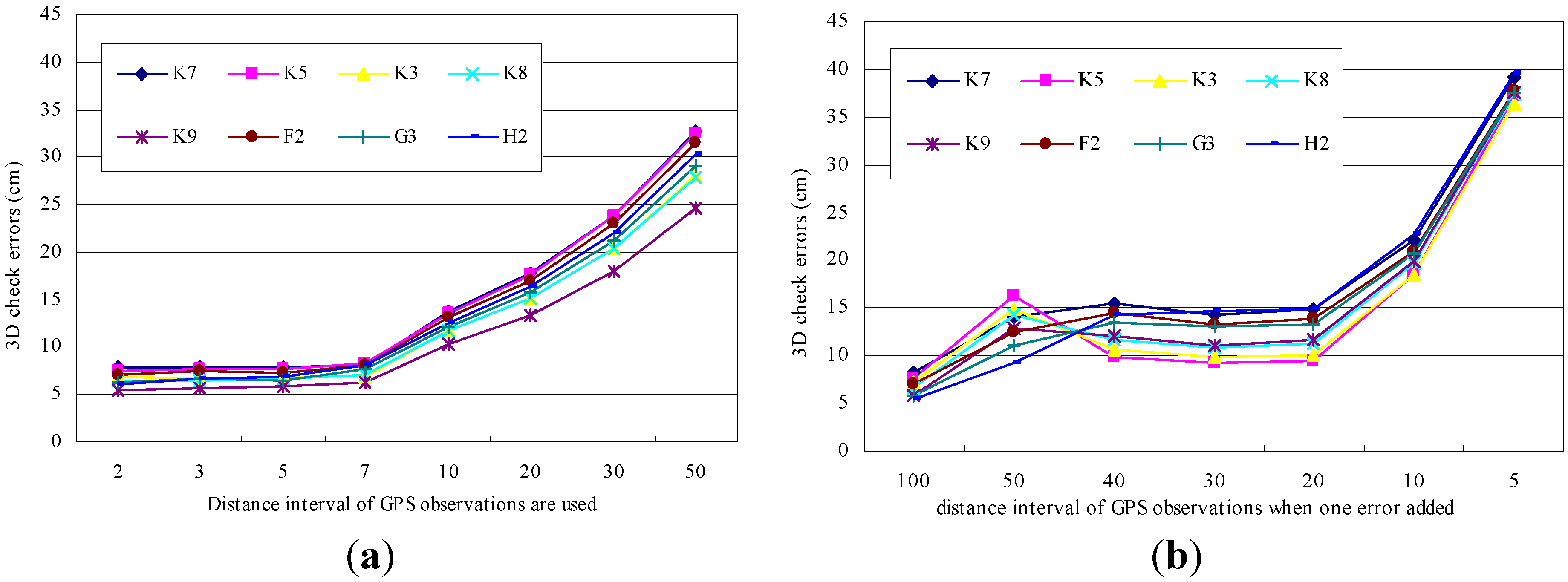
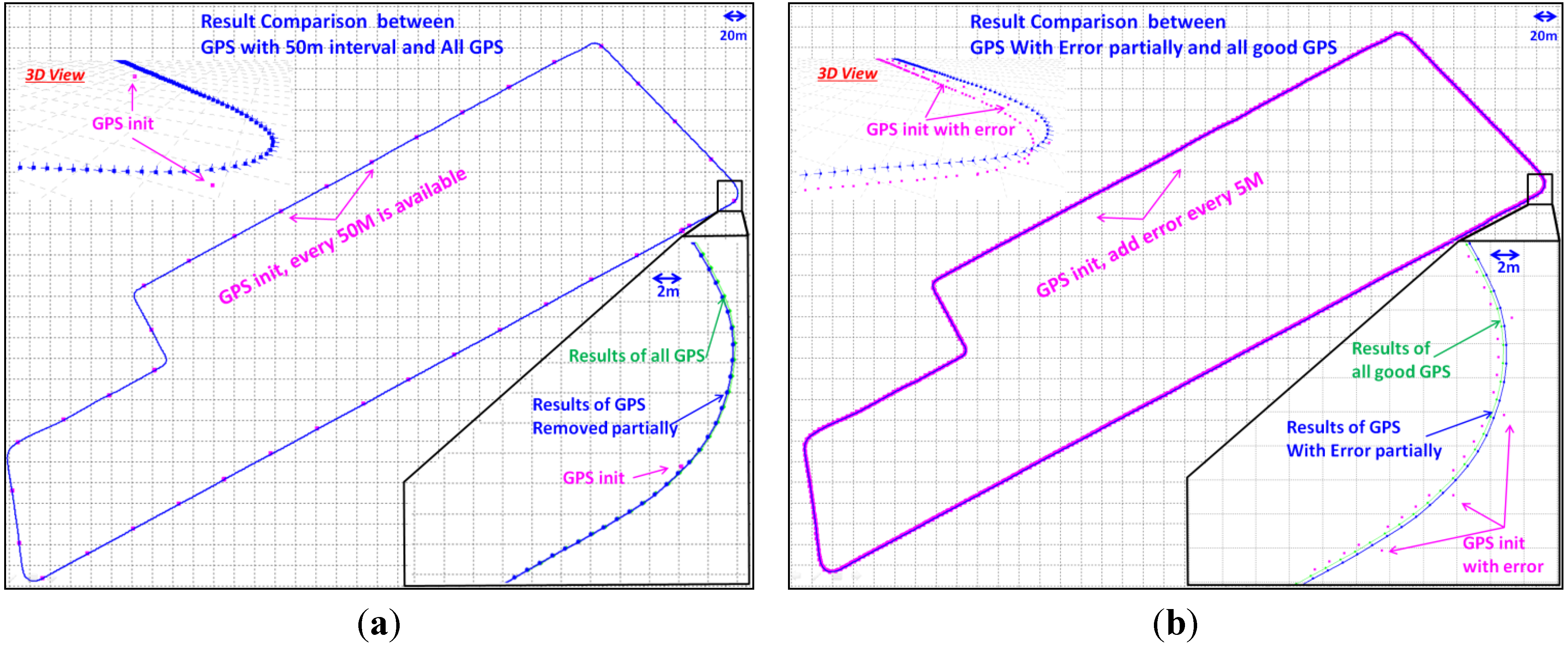
5.3. BA Results with GPS
6. Conclusions and Future Work
Acknowledgments
References
- Eade, E.; Fong, P.; Munich, M.E. Monocular graph SLAM with complexity reduction. Proceedings of 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18– 22 October 2010; pp. 3017–3024.
- Weiss, S.; Scaramuzza, D.; Siegwart, R. Monocular-SLAM-based navigation for autonomous micro helicopters in GPS-Denied environments. J. Field Robot. 2011, 28, 854–874. [Google Scholar]
- Senlet, T.; Elgammal, A. A framework for global vehicle localization using stereo images and satellite and road maps. Proceedings of 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 2034–2041.
- Lin, K.H.; Chang, C.H.; Dopfer, A.; Wang, C.C. Mapping and localization in 3D environments using a 2D Laser scanner and a stereo camera. J. Inf. Sci. Eng. 2012, 28, 131–144. [Google Scholar]
- Geyer, C.; Daniilidis, K. Catadioptric projective geometry. Int. J. Comp. Vis. 2001, 45, 223–243. [Google Scholar]
- Barreto, J.P.; Araujo, H. Geometric properties of central catadioptric line images and their application in calibration. IEEE Tran. Pattern Anal. Mach. Intel. 2005, 27, 1327–1333. [Google Scholar]
- Mei, C.; Benhimane, S.; Malis, E.; Rives, P. Efficient homography-based tracking and 3-D reconstruction for single-viewpoint sensors. IEEE Trans. Robot. 2008, 24, 1352–1364. [Google Scholar]
- Kaess, M.; Dellaert, F. Probabilistic structure matching for visual SLAM with a multi-camera rig. Comput. Vis. Image Underst. 2010, 114, 286–296. [Google Scholar]
- Paya, L; Fernandez, L; Gil, A.; Reinoso, O. Map building and Monte Carlo localization using global appearance of omnidirectional images. Sensors 2010, 10, 11468–11497. [Google Scholar]
- Gutierrez, D.; Rituerto, A.; Montiel, J.M.M.; Guerrero, J.J. Adapting a real-time monocular visual SLAM from conventional to omnidirectional cameras. Proceedings of the 11th OMNIVIS in IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 343–350.
- Strasdat, H.; Montiel, J.M.M.; Davison, A.J. Visual SLAM: Why filter? Image Vision Comput 2012, 30, 65–77. [Google Scholar]
- Artieda, J.; Sebastian, J.M.; Campoy, P.; Correa, J.F.; Mondragon, I.F.; Martinez, C.; Olivares, M. Visual 3-D SLAM from UAVs. J. Intell. Robot. Syst. 2009, 55, 299–321. [Google Scholar]
- Davison, J. Real-time simultaneous localization and mapping with a single camera. Proceedings of the International Conference on Computer Vision (ICCV), Nice, France, 13–16 October 2003; pp. 1403–1410.
- Zhang, X.; Rad, A.B.; Wong, Y.-K. Sensor fusion of monocular cameras and Laser rangefinders for line-based simultaneous localization and mapping (SLAM) tasks in autonomous mobile robots. Sensors 2012, 12, 429–452. [Google Scholar]
- Eade, E.; Drummond, T. Scalable monocular SLAM. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 17–22 June 2006; pp. 469–476.
- Sim, R.; Elinas, P.; Griffin, M.; Little, J.J. Vision-based SLAM using the Rao-Blackwellised particle filter. Proceedings of the IJCAI Workshop on Reasoning with Uncertainty in Robotics, Edinburgh, Scotland, 30 July 2005.
- Sibley, G.; Mei, C.; Reid, I.; Newman, P. Vast-scale outdoor navigation using adaptive relative bundle adjustment. Int. J. Robot. Res. 2010, 29, 958–980. [Google Scholar]
- Lim, J.; Pollefeys, M.; Frahm, J.M. Online environment mapping. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 20–25 June 2011; pp. 3489–3496.
- Miller, I.; Campbell, M.; Huttenlocher, D. Map-aided localization in sparse global positioning system environments using vision and particle filtering. J. Field Robot. 2011, 28, 619–643. [Google Scholar]
- Bergasa, L.M.; Ocana, M.; Barea, R.; Lopez, M.E. Real-time hierarchical outdoor SLAM based on stereovision and GPS fusion. IEEE Trans. Intell. Trans. Syst. 2009, 10, 440–452. [Google Scholar]
- Dusha, D.; Mejias, L. Error analysis and attitude observability of a monocular GPS/visual odometry integrated navigation filter. Int. J. Robot. Res. 2012, 31, 714–737. [Google Scholar]
- Berrabah, S.A.; Sahli, H.; Baudoin, Y. Visual-based simultaneous localization and mapping and global positioning system correction for geo-localization of a mobile robot. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
- Kannala, J. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Trans. PAMI 2006, 28, 1335–1340. [Google Scholar]
- Tardif, J.P.; Pavlidis, Y.; Daniilidis, K. Monocular visual odometry in urban environments using an omnidirectional camera. IEEE/RSJ Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 September 2008; pp. 2531–2538.
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar]
- Sinha, S.N.; Frahm, J.M.; Pollefeys, M.; Yakup Genc, Y. GPU-based video feature tracking and matching, EDGE 2006. Proceedings of Workshop on Edge Computing Using New Commodity Architectures, Chapel Hill, NC, USA, 23–24 May 2006.
- Fischler, M.A.; Bolles, R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. CACM 1981, 24, 381–395. [Google Scholar]
- Scaramuzza, D. 1-point-ransac structure from motion for vehicle-mounted cameras by exploiting non-holonomic constraints. Int. J. Comput. Vis. 2011, 95, 74–85. [Google Scholar]
- Pinies, P.; Tardos, J.D. Scalable SLAM building conditionally independent local maps. Proceedings of IEEE Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3466–3471.
- Eade, E.; Drummond, T. Unified loop closing and recovery for real time monocular SLAM. Proceedings of the British Machine Vision Conference, Leeds, UK, 1–4 September 2008.
- Snay, R.; Soler, T. Continuously operating reference station (CORS): History, applications, and future enhancements. J. Surv. Eng. 2008, 134, 95–104. [Google Scholar]
- Meguro, J.; Hashizume, T.; Takiguchi, J.; Kurosaki, R. Development of an autonomous mobile surveillance system using a network-based RTK-GPS. Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3096–3101.
- Kuemmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. g2o: A general framework for graph optimization. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3607–3613.
- LADYBUG. Available online: http://www.ptgrey.com/products/spherical.asp (accessed on 15 September 2012).

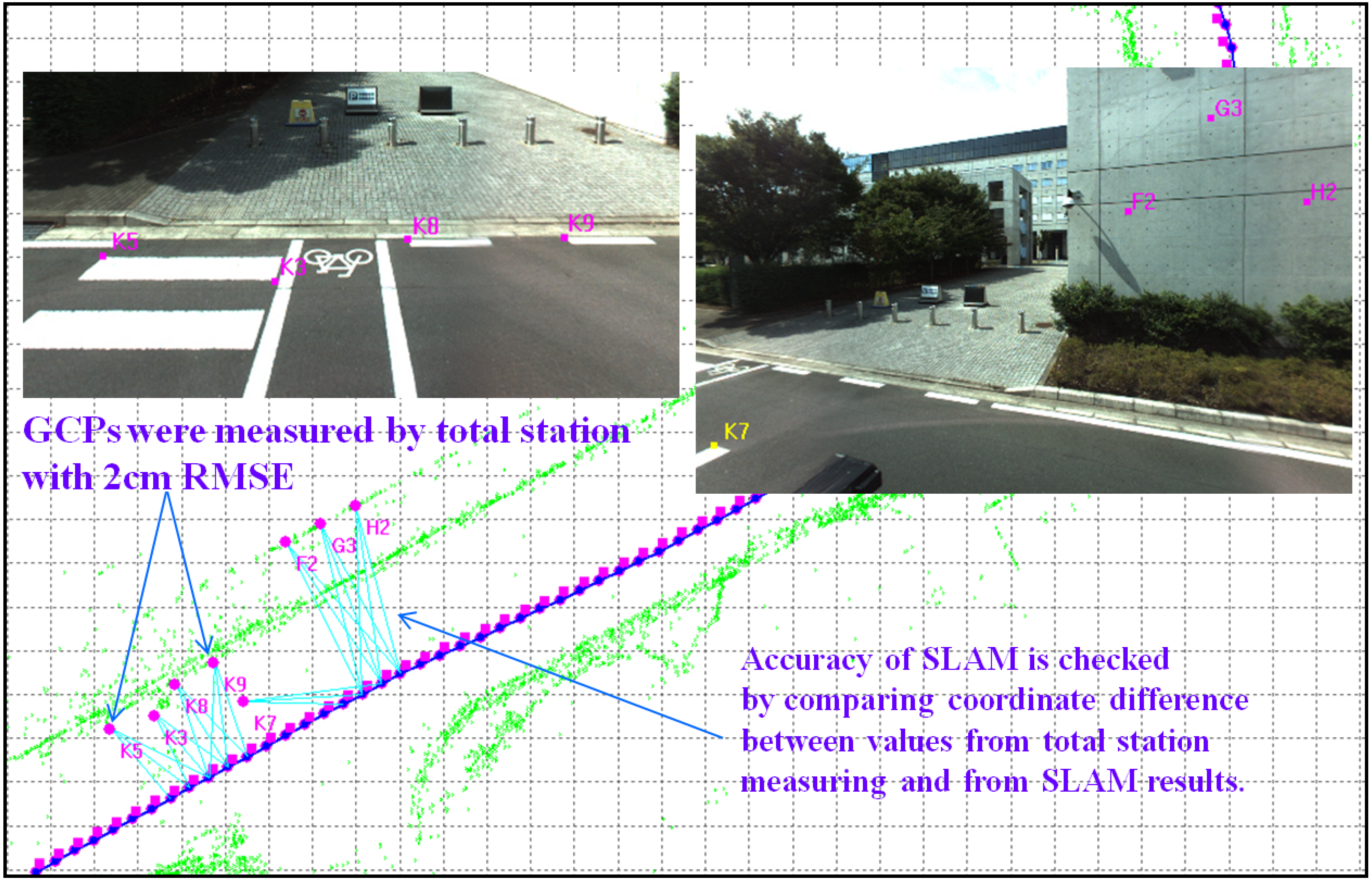
| ID | DX (cm) | DY (cm) | DZ (cm) | DXYZ (cm) |
|---|---|---|---|---|
| K7 | 3.6 | 6.6 | 3.1 | 8.1 |
| K5 | 3.8 | 6.0 | 1.7 | 7.3 |
| K3 | 4.0 | 4.6 | 3.5 | 7.0 |
| K8 | 4.4 | 4.2 | 2.3 | 6.5 |
| K9 | 3.3 | 4.2 | 1.8 | 5.6 |
| F2 | −1.7 | 6.9 | 0.5 | 7.1 |
| G3 | −1.2 | 6.0 | 0.2 | 6.1 |
| H2 | 2.4 | 5.2 | −0.6 | 5.7 |
| Average | 3.0 | 5.5 | 1.7 | 6.7 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shi, Y.; Ji, S.; Shi, Z.; Duan, Y.; Shibasaki, R. GPS-Supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments. Sensors 2013, 13, 119-136. https://doi.org/10.3390/s130100119
Shi Y, Ji S, Shi Z, Duan Y, Shibasaki R. GPS-Supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments. Sensors. 2013; 13(1):119-136. https://doi.org/10.3390/s130100119
Chicago/Turabian StyleShi, Yun, Shunping Ji, Zhongchao Shi, Yulin Duan, and Ryosuke Shibasaki. 2013. "GPS-Supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments" Sensors 13, no. 1: 119-136. https://doi.org/10.3390/s130100119





