Characterization of a New Heat Dissipation Matric Potential Sensor
Abstract
:1. Introduction
2. Experimental Section
2.1. Sensing Principle of the PlantCare Sensor
2.2. Experimental Setup
2.3. Two Point Calibration of the Sensor Signal
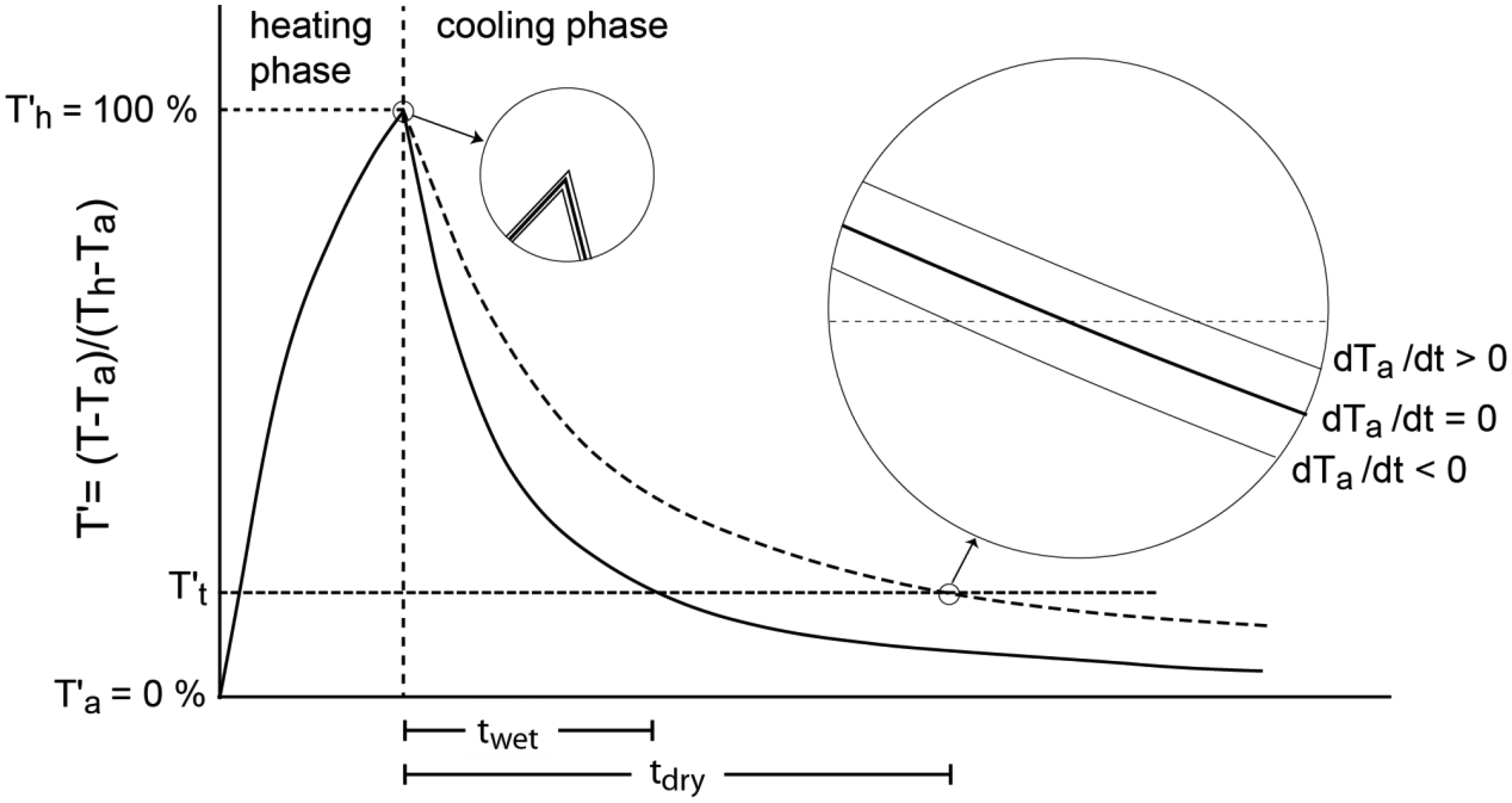
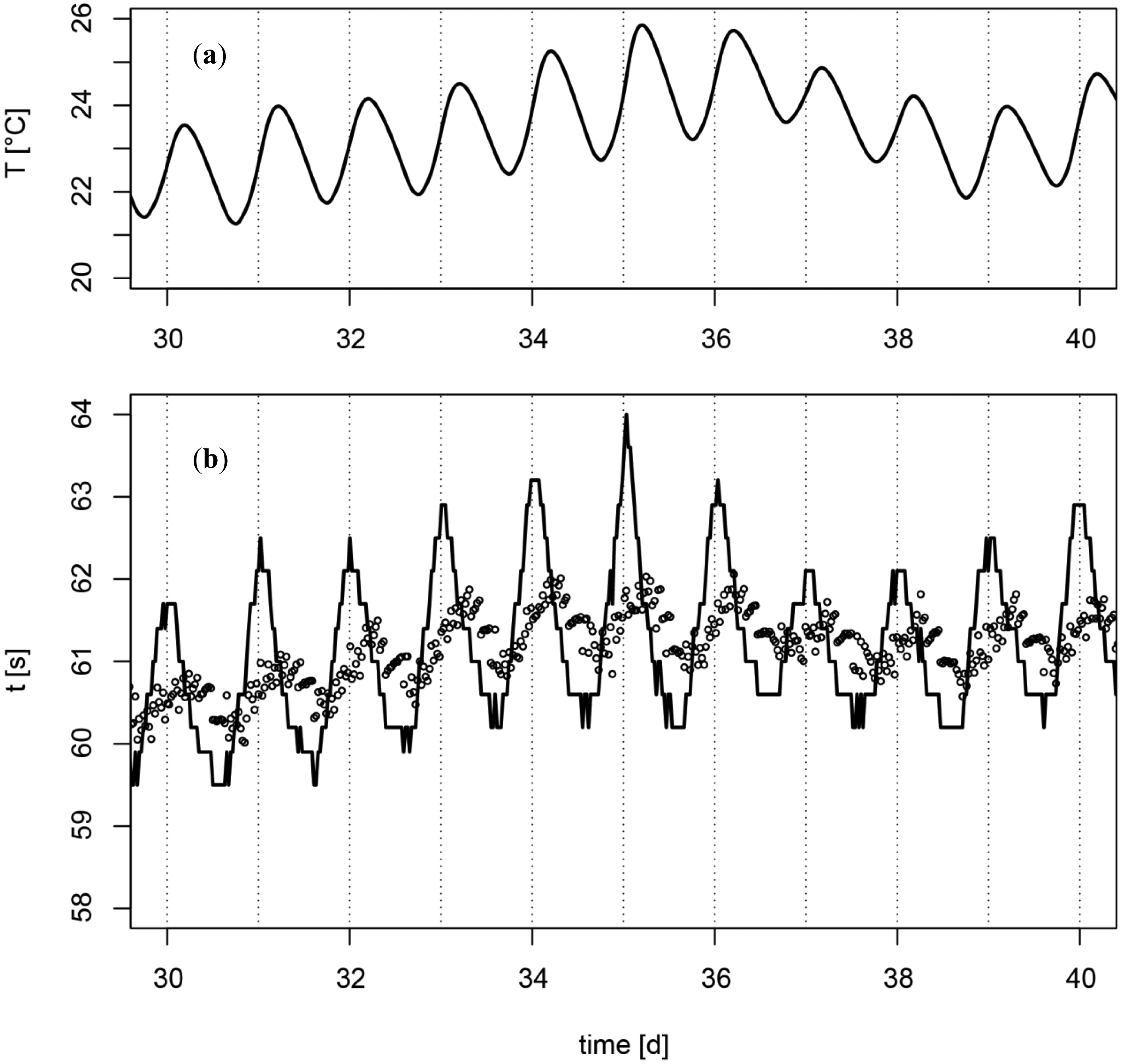
2.4. Correction of the Influence of the Temperature Change on the Sensor Signal
3. Results and Discussion
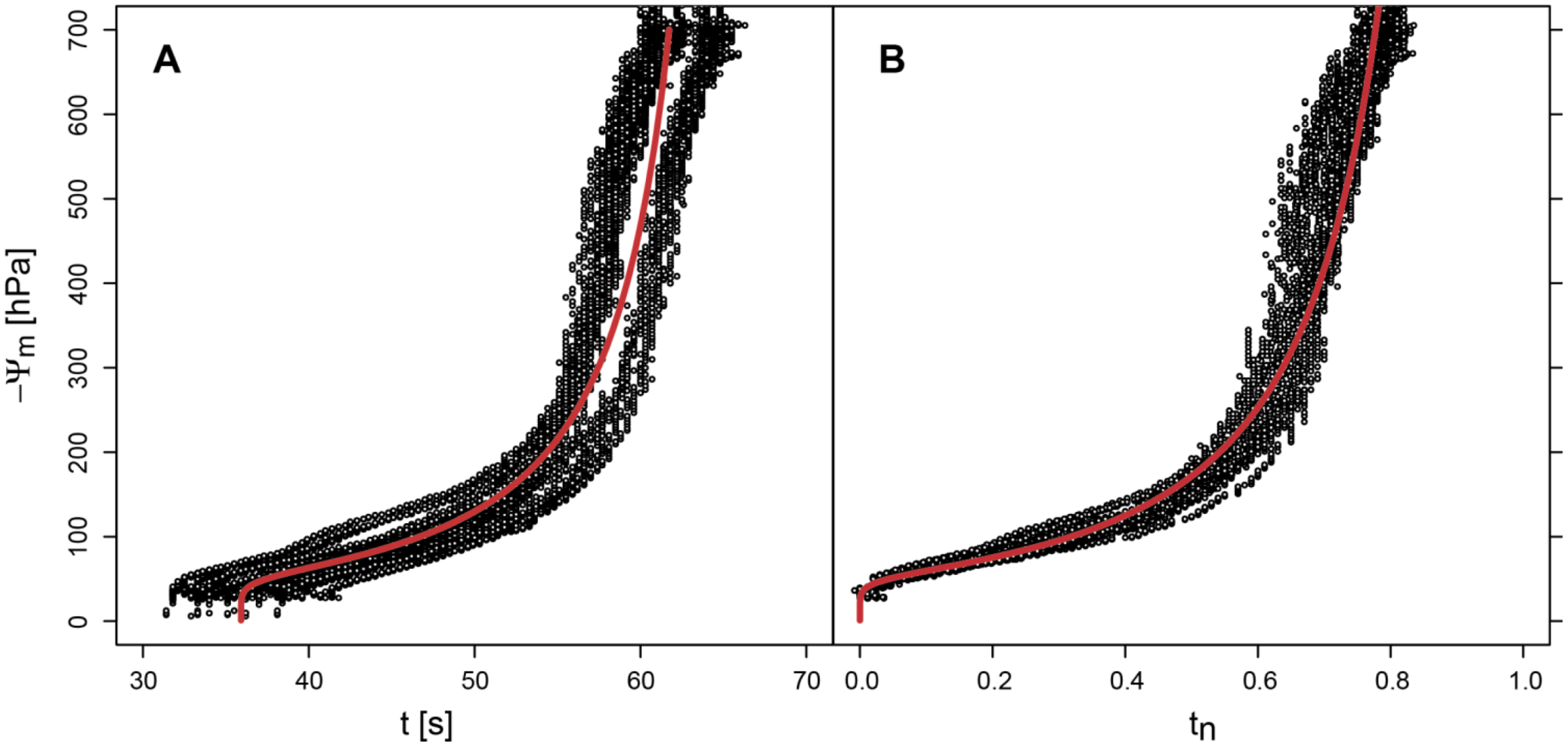
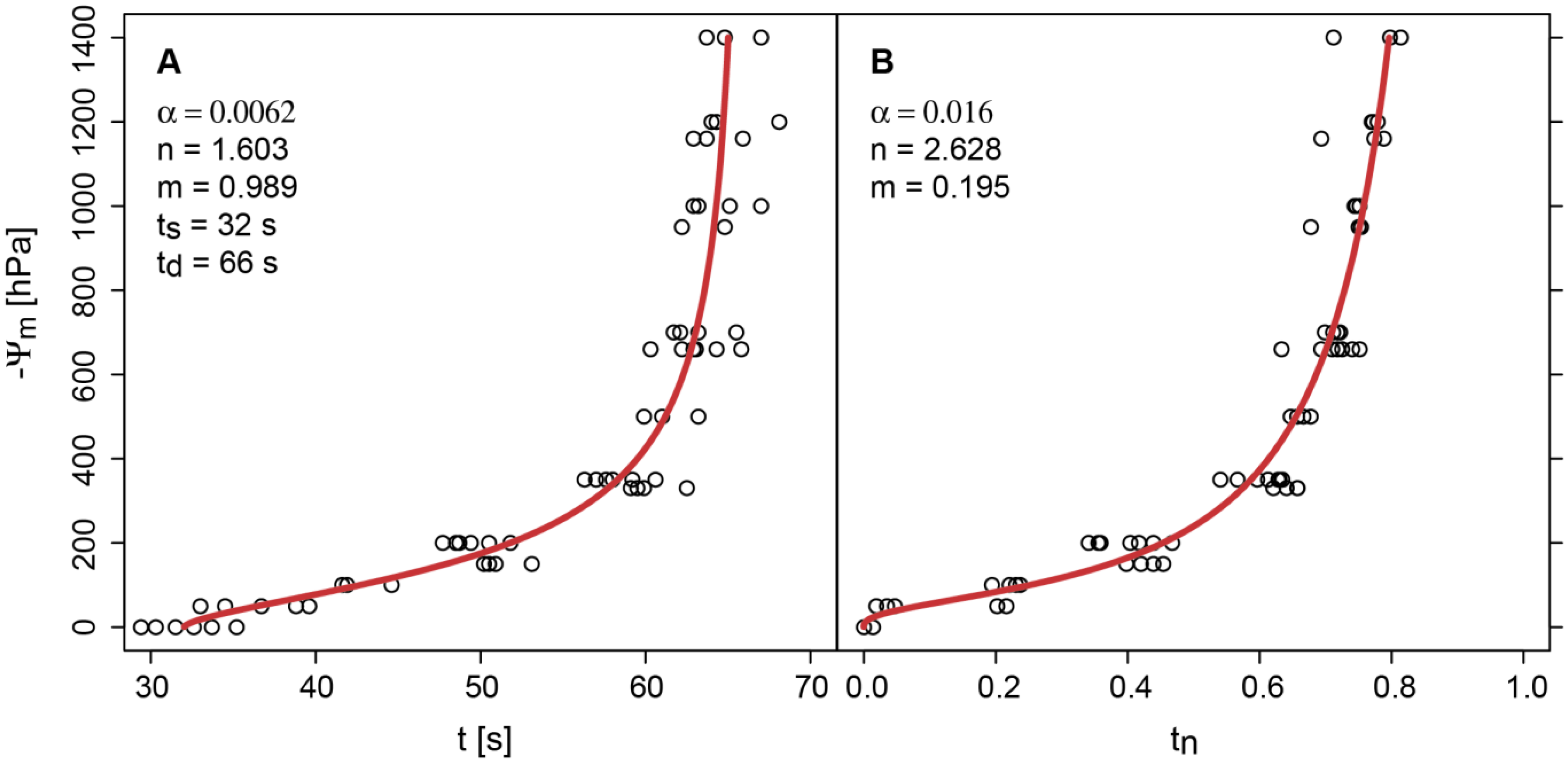
3.1. Calibration of the Sensor Signal
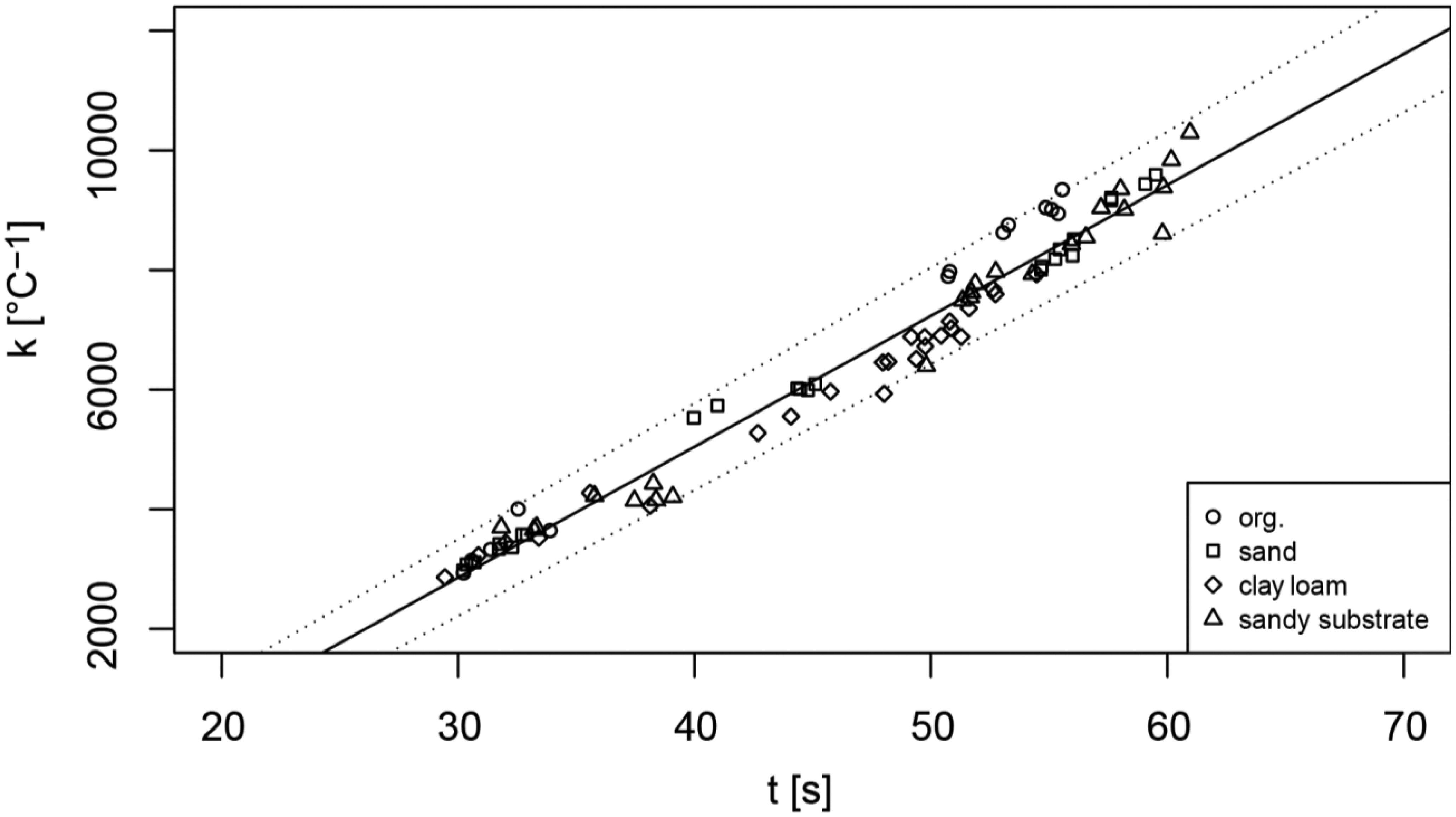
3.2. Correction of the Influence of the Temperature Change on the Sensor Signal
4. Conclusions/Outlook
Acknowledgments
References
- Crops and Drops: Making the Best Use of Water for Agriculture; FAO: Rome, Italy, 2002.
- Pardossi, A.; Incrocci, L.; Incrocci, G.; Malorgio, F.; Battista, P.; Bacci, L.; Rapi, B.; Marzialetti, P.; Hemming, J.; Balendonck, J. Root zone sensors for irrigation management in intensive agriculture. Sensors 2009, 9, 2809–2835. [Google Scholar]
- Young, M.H.; Sisson, J.B. Tensiometry. In Methods of Soil Analysis: Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 575–608. [Google Scholar]
- Scanlon, B.R.; Andraski, B.J. Miscellaneous methods for measuring matric or water potential. In Methods of Soil Analysis: Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 643–670. [Google Scholar]
- Durner, W.; Or, D. Soil Water Potential Measurement. In Encyclopedia of Hydrological Sciences; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar]
- Phene, C.J.; Hoffman, G.J.; Rawlins, S.L. Measuring soil matric potential in situ by sensing heat dissipation within a porous body. 1. Theory and sensor construction. Soil Sci. Soc. Am. J. 1971, 35, 27–33. [Google Scholar]
- Reece, C.F. Evaluation of a line heat dissipation sensor for measuring soil matric potential. Soil Sci. Soc. Am. J. 1996, 60, 1022–1028. [Google Scholar]
- Flint, A.L.; Campbell, G.S.; Ellett, K.M.; Calissendorff, C. Calibration and temperature correction of heat dissipation matric potential sensors. Soil Sci. Soc. Am. J. 2002, 66, 1439–1445. [Google Scholar]
- Abu-Hamdeh, N.H.; Reeder, R.C. Soil thermal conductivity: Effects of density, moisture, salt concentration, and organic matter. Soil Sci. Soc. Am. J. 2000, 64, 1285–1290. [Google Scholar]
- Blume, H.P.; Horn, R.; Kandeler, E.; Kretzschmar, R.; Stahr, K.; Wilke, B.M. Lehrbuch Der Bodenkunde; Spektrum-Akademischer Vlg: Heidelberg, Germany, 2009. [Google Scholar]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar]
- Malazian, A.; Hartsough, P.; Kamai, T.; Campbell, G.S.; Cobos, D.R.; Hopmans, J.W. Evaluation of MPS-1 soil water potential sensor. J. Hydrol. 2011, 402, 126–134. [Google Scholar]
- Hopmans, J.W.; Dane, J.H. Temperature-dependence of soil hydraulic-properties. Soil Sci. Soc. Am. J. 1986, 50, 4–9. [Google Scholar]
- Feng, M.; Fredlund, D.G.; Shuai, F.S. A laboratory study of the hysteresis of a thermal conductivity soil suction sensor. Geotech. Tes. J. 2002, 25, 303–314. [Google Scholar]

| Tt | a [s2/°C] | b [s/°C] | r2 |
|---|---|---|---|
| 15% | −6,233 | 296 | 0.95 |
| 18% | −3,709 | 219 | 0.97 |
| 25% | −1,798 | 141 | 0.98 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Matile, L.; Berger, R.; Wächter, D.; Krebs, R. Characterization of a New Heat Dissipation Matric Potential Sensor. Sensors 2013, 13, 1137-1145. https://doi.org/10.3390/s130101137
Matile L, Berger R, Wächter D, Krebs R. Characterization of a New Heat Dissipation Matric Potential Sensor. Sensors. 2013; 13(1):1137-1145. https://doi.org/10.3390/s130101137
Chicago/Turabian StyleMatile, Luzius, Roman Berger, Daniel Wächter, and Rolf Krebs. 2013. "Characterization of a New Heat Dissipation Matric Potential Sensor" Sensors 13, no. 1: 1137-1145. https://doi.org/10.3390/s130101137




