Abstract
We have successfully demonstrated video-rate CMOS single-photon avalanche diode (SPAD)-based cameras for fluorescence lifetime imaging microscopy (FLIM) by applying innovative FLIM algorithms. We also review and compare several time-domain techniques and solid-state FLIM systems, and adapt the proposed algorithms for massive CMOS SPAD-based arrays and hardware implementations. The theoretical error equations are derived and their performances are demonstrated on the data obtained from 0.13 μm CMOS SPAD arrays and the multiple-decay data obtained from scanning PMT systems. In vivo two photon fluorescence lifetime imaging data of FITC-albumin labeled vasculature of a P22 rat carcinosarcoma (BD9 rat window chamber) are used to test how different algorithms perform on bi-decay data. The proposed techniques are capable of producing lifetime images with enough contrast.1. Introduction
Fluorescence based imaging techniques have become essential tools for a large variety of disciplines, ranging from cell-biology, medical diagnosis, and pharmacological development to physical sciences. Fluorescence lifetime imaging microscopy (FLIM) yields images with each pixel sensing the exponential decay rate instead of the intensity of the fluorescence from a fluorophore. It has the advantages of insensitivity to variations in excitation illumination, photon scattering and probe concentration, and it allows the resolution of different fluorophores (with different lifetimes) fluorescing at the same wavelength. FLIM can be applied to acquire more quantitative information about physiological parameters such as pH, Ca2+, pO2, etc. or image intracellular functions with Förster resonance energy transfer (FRET) techniques [1–3].
Both time-domain and frequency-domain instrumentation systems are available to acquire FLIM data. Here, we will focus on the recently proposed time-domain approaches and discuss how they can be applied to the latest solid-state sensor arrays for FLIM applications. For detailed discussions in frequency-domain FLIM systems, please see [4–7]. In a typical time-resolved FLIM experiment, the samples with fluorescent markers are illuminated by a pulsed laser and the time-correlated photons emitted from the markers are collected by detectors. Commercially available FLIM systems usually use photomultiplier tubes (PMT) or multiple channel plate (MCP) PMTs plus time-correlated single-photon counting cards (TCSPC) [8] or gated intensified/electron-multiplying CCDs to measure the lifetimes. The latest multi-channel PMT systems can significantly increase the imaging speed, but they still require image-scanning. For example, to avoid local heating and photobleaching, the pixel dwell time is set to be 15.25 μs and the sample is scanned hundreds of times, say 200 times, to accumulate enough photon counts. It will take 256 × 256 × 200 × 15.25 μs/Np ∼ 200 s/Np (Np is the number of channels) to generate a 256 × 256 lifetime image. CCD based systems usually require coolers and/or high voltage supplies. Compared with CMOS compatible solutions, the above mentioned systems are expensive, bulky, and not user-friendly. Recent developments on CMOS-based FLIM systems can be found in [9–20]. Kawahito applies pin photodiodes whereas Shepard uses active pixel sensors, but both employed the 2-gate rapid lifetime determination (RLD) method [21] to calculate the lifetimes. Li et al. proposed several non-gating time-domain lifetime algorithms and demonstrated video-rate lifetime imaging [14,15] on single-photon avalanche diode (SPAD) plus in-pixel TCSPC arrays [22]. Unlike conventional CCD based sensors, a SPAD is a p-n junction reverse biased above the breakdown voltage to sustain the avalanche multiplication process triggered by photogenerated carriers. The transfer gain is so large that the output current from the SPAD can be easily converted into a digital signal without using complex front-end amplifiers deteriorating the signal-to-noise ratio (SNR). With such single photon sensitivity, SPADs are suitable for photon-starved applications such as single molecule detection [23,24], fluorescence lifetime measurements [13,20], optical range finding, optical fiber fault detection, and portable explosives sensing [25]. Recent developments of CMOS SPADs have shown significant improvements in the dead time [26], dark count [27], technology migration to advanced process [28] and pixel miniaturization [29], and quantum efficiency in the longer wavelength region [30]. It is expected high resolution CMOS SPAD arrays for ranging applications [31] will soon be applied to FLIM applications.
Another bottleneck for high-speed lifetime imaging is lifetime calculation. Common FLIM systems usually use iterative linear or non-linear least square methods (LSM), such as Marquardt-Levenberg algorithms, to extract the lifetimes. Although this approach is accurate and suitable for analyzing multi-exponential decays, it is computationally time consuming which makes it unsuitable for real-time applications. It is desirable, therefore, to develop non-iterative simple algorithms to speed up the lifetime calculations while maintaining enough imaging quality. Compared with the LSM, iterative-free gating methods only require two time bins for single-exponential decays [9,13,21], four bins for bi-exponential decays [32,33] or eight bins for multi-exponential decays [34]. The hardware complexity is greatly reduced and the speed is much higher. There are different acquisition schemes for the gating methods. Figure 1(a) shows the traditional sequential acquisition in a pixel, where at least two sub-images are recorded sequentially at different delayed windows with respect to the excited laser pulses to extract the lifetime. The block ‘counter’ can contain front-end circuits, analog-to-digital converters and accumulators in conventional imaging systems or simply inverters and digital buffers in the latest CMOS SPAD systems. Chang and Mycek applied four time-gates to analyze single-exponential decay data [35]. This approach is slow and sensitive to motion artifacts unless the samples are stationary, and the recorded sub-images are uncorrelated. If a full fluorescence emission histogram is needed for detailed examinations, it will take a significant amount of time to record a large number of sub-images with different delay times [36].
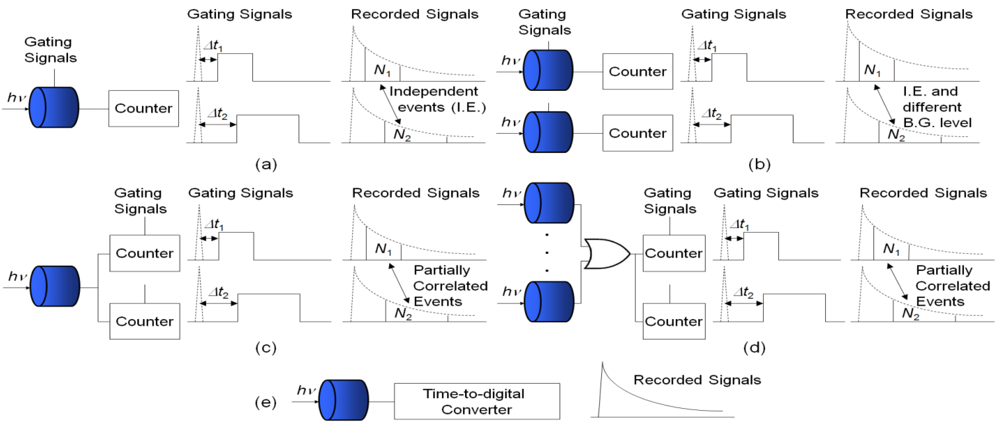
Unlike the sequential acquisition scheme, some researchers applied ‘single-shot’ acquisition methods by applying multi-channel segmented gated optical intensifiers (GOI) [37] or focusing optically delayed images on different sections of the detector [38,39] to collect sub-images simultaneously. Video-rate FLIM has been demonstrated in GOI FLIM systems. This trades off spatial resolution for imaging speed. Similar to the sequential acquisition scheme, the detectors enabled by the gating signals only work ‘part-time’. The background level for the two detectors could be different, and the two recorded events are independent (uncorrelated).
Figure 1(c) shows a different acquisition scheme from above. The detector works fully, but with several gated counters collecting photons in different timing windows. The gated counter accumulates only when the leading edge of the detector output is inside its enable period. The gating signals for controlling the counters can be non-overlapping [36–40] or overlapping [41]. Gerritsen et al. applied several non-overlapping gated counters to confocal scanning systems [40]. The system can deal with multiple-decay data. The overlapping gating acquisition, denoted as ORLD, was first proposed by Chan et al. [41] and it was proven to be efficient by running Monte Carlo simulations, but the authors only suggested splitting the PMT signal and sending to two gated counters without actually carrying out the experiments probably because of the complexity and the cost of reconfiguring the existing acquisition systems. Later, Elangovan et al. proposed an overlapping multi-gated algorithm to analyze double-exponential decays and applied Monte Carlo simulations to find suitable experiment settings [32]. For the latest developed CMOS SPAD arrays, however, the ORLD is a good option considering the system complexity and photon efficiency (the photon events collected in the gated counters are correlated if the overlapped proportion is significant). We will for the first time derive the theoretical error equations and test the ORLD methods on the data obtained from a 0.13 μm CMOS SPAD array.
Stoppa's research team combined the acquisition schemes (b) and (c) by binning 4 and 25 CMOS SPADs, respectively, in a ‘super’ pixel and using gated counters to collect the photon events [11,12] as in Figure 1(d). Similar to the second gating scheme, this technique trades the spatial resolution for imaging speed. It provides faster acquisition in some sensing applications such as high throughput screening. They used non-overlapping time gates to collect the photons and used nonlinear LSM to extract the lifetimes.
Figure 1(e) shows a pixel with time-correlated single-photon counting (TCSPC) circuitry. The detector works fully, with a time-to-digital converter (TDC) to record the time tag of each photon. Compared with the hardware for time-gating acquisition, the complexity of the TCSPC systems is much higher. The latest commercial multi-channel systems only contain several PMTs and still require scanning. Recently we have demonstrated a 1024-channel, a 20 k-channel and a 100 Mphoton/s multi-channel FLIM systems with 0.13 μm CMOS SPAD plus in-pixel TDC (10-bit TCSPC) arrays [14–16,20]. The parallelism of the proposed systems can be fully exploited by implementing lifetime calculations in hardware [42,43]. Similar to the above-mentioned ‘single-shot’ systems, the imaging speed of the proposed cameras can operate over 100 f/s.
2. Time-Domain FLIM Data Analysis
For simplicity, we consider a single-exponential decay with a negligible impulse response function (IRF). Such assumptions allow a proper comparison of various fitting algorithms. Moreover, a single-exponential decay model is still enough to contrast different types of fluorophores. We will discuss the accuracy of FLIM algorithms and compare the performance of various algorithms on bi-exponential decays. Assume that the fluorescence decay function f(t) = Aexp(−t/τ)u(t) with τ being the lifetime and u(t) the step function.
2.1. Gating Techniques
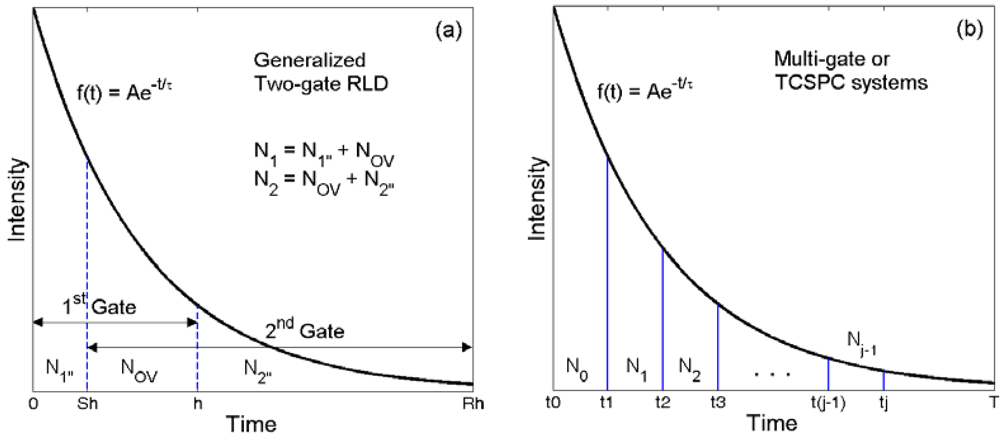
Gating algorithms have been widely used in real-time FLIM systems owing to their simplicity and compactness in hardware implementations. The simplest 2-gate RLD (RLD-2) only uses two time gates of the same width. We adopt the F value introduced in [44] to quantify the performance of a FLIM algorithm. The F value is defined as F = Nc1/2στ/τ, where στ is the standard deviation of repeated measurements of the lifetime value τ and Nc the total count in the measurement window from t = 0 to t = T, the average total count . The F value for the RLD-2 can be derived from [21] and [44] as:
Equation (2) allows us to determine an optimized setting without resorting to Monte Carlo simulations. Moreover, setting g(x) = 0 in Equation (A2), we can obtain:
Some researchers used mult-gate RLD (RLD-M) to calculate the lifetimes [35,36,42]:
2.2. Non-Iterative Algorithms Suitable for TCSPC Systems
Although the gating methods introduced above can provide fast lifetime preview and are easy to implement, scientists still prefer to keep the raw timing data for detailed examinations on what really happens in the samples. For gating methods, recording raw timing data is not easy. To obtain a full histogram, a large number of snap shots at different time delays are acquired sequentially. It is very inefficient. To increase the raw data collecting speed, the number of gated integrators can be increased as in [34], but at a cost of system complexity. To enhance the raw data collection rate, we incorporated on-chip high-resolution TDCs into the CMOS SPAD arrays and built 1024-channel and 20k-channel “miniaturized PMT+TCSPC” prototypes [16]. The prototypes can operate in the RAW MODE for collecting the raw data and in the COARSE MODE for high-speed lifetime imaging preview. Due to the slow speed of the widely used iterative based least square methods, several time-domain FLIM algorithms suitable for TCSPC systems (Figure 1(e)) have been proposed to improve the imaging speed [42,43]. We proposed an innovative background-insensitive algorithm suitable for our SPAD prototypes, called IEM. The calculated lifetimes are:
The analog version of Equation (7), denoted as analog mean-delay (AMD) hereafter, has been reported earlier using stand-alone components for lifetime sensing applications [47]. Recently, an AMD instrumentation considering the impact of IRFs and limited measurement window problems has been carried out almost at the same time with our digital CMM by Kim [48,49]. Their algorithms can work efficiently with low-cost single-channel PMTs, and it has been demonstrated in a confocal scanning microscope [50]. Padilla-Parra et al. also used Equation (7) to calculate the minimal fraction of interacting donor (MFD) in florescence resonance energy transfer (FRET) experiments [51,52]. The measurement window of the MFD, however, should be much larger than the largest lifetime component; otherwise the contrast capability would be lost, similar to the problems revealed in [15] and [49]. By automatically calibrating such problems, the MFD can be easily applied to our SPAD systems for FRET applications as well. Recently, a Bayesian FLIM analysis method was proposed, and it outperformed the commonly used MLE and LSM especially on noisy single-exponential data sets [53,54]. This algorithm is promising especially in single-cell cytometry. The Bayesian methods for multi-exponential decays are under development.
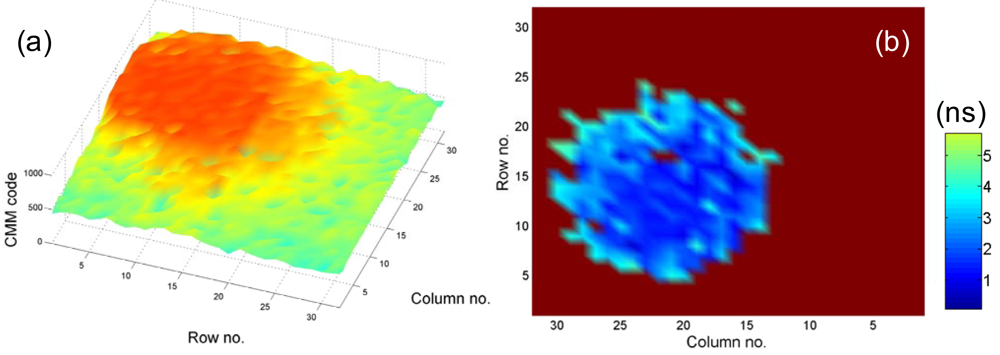
2.3. Error Performance of FLIM Algorithms on Data Collected by CMOS SPAD Arrays
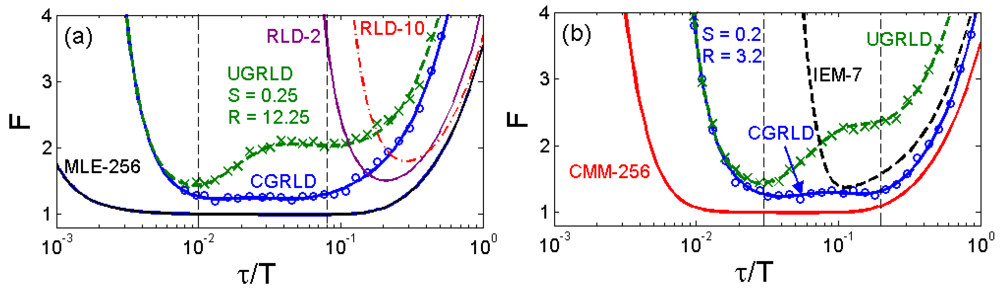
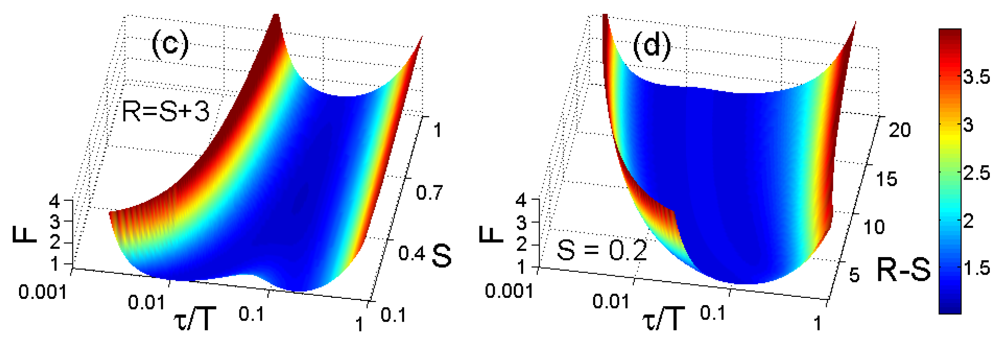
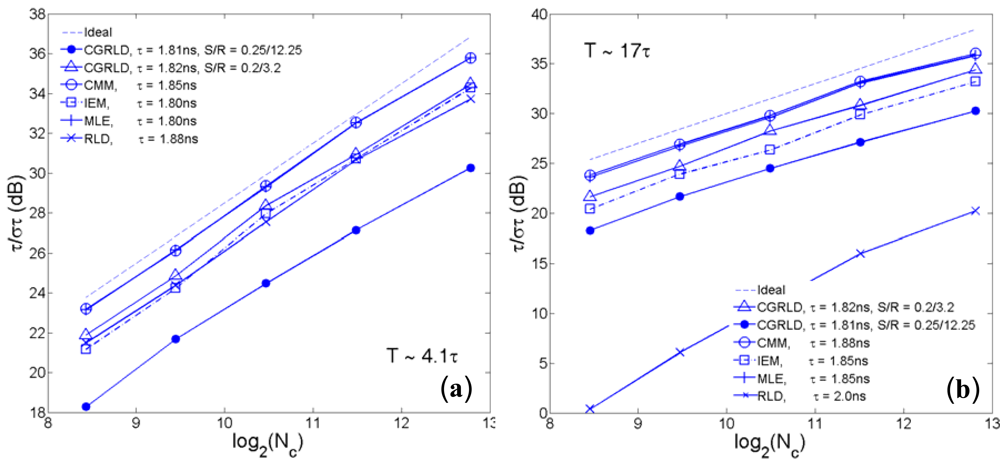
To compare the error performance of different FLIM algorithms, widefield lifetime images of a uniform aqueous solution of Rhodamine B were taken in different acquisition time. The imaging system was set up on a Nikon TE2000U inverted microscope. The excitation source was a PicoQuant pulsed diode laser with a wavelength of 470 nm coupled through the epi-fluorescence port of the microscope using a Nikon B-2A filter cube. The laser pulse rate is 20 MHz and the maximum power reaching the back focal plane of the objective is about 90 μW. The sample was imaged onto the 32 × 32 SPAD camera directly attached to one of the camera ports using a 20× objective (Nikon Plan Apo, 20×, NA 0.45). The TDC resolution is set to be 78 ps with the on-chip phase-locked loop enabled [22]. Two measurement windows of Mh ∼ 4.1τ and Mh ∼ 17τ were chosen to calculate lifetimes. Figure 5(a,b) show the precision curves in terms of photon counts for different algorithms. The ideal curve is the theoretical precision of MLE (or CMM) without considering system non-idealities. CMM and MLE behave almost the same in both plots, and they are about 0.5 ∼ 1.5 dB away from the ideal curve. The first window Mh/τ ∼ 4.1 is optimized for RLD-2, where RLD-2, IEM, and CGRLD (S/R = 0.2/3.2) work equally well. Figure 5(b) shows the reason why we need a fast FLIM algorithm other than RLD-2. The CGRLD with S/R = 0.25/12.25 still performs worse than the CGRLD with S/R = 0.2/3.2 making it inefficient in photon collecting due to low duty cycle operations (optimized window > 17τ). The conclusions drawn from Figure 5(a,b) are in good agreement with the theoretical Figure 3(a,d).
2.4. Contrast Capability of Algorithms on Bi-Exponential Decays
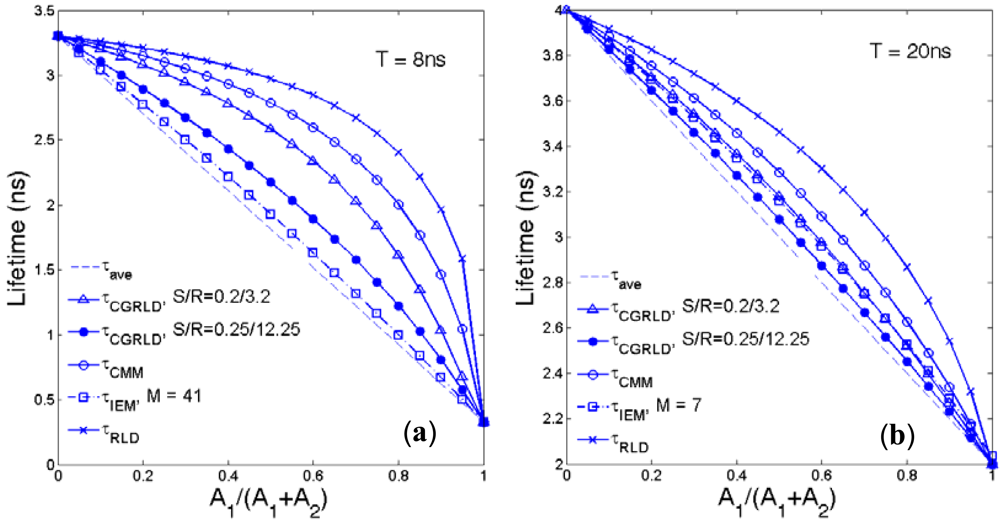
Assume a bi-exponential decay f(t) = A1exp(−t/τ1) + A2exp(−t/τ2) with τ1, τ2 being the lifetimes and A1, A2 being the pre-scalars. Although the above FLIM algorithms are for single-exponential data, it is worth comparing the average lifetimes produced for bi-decay data:
The average lifetimes defined by IEM [42], RLD-2 [21], CMM [15], and CGRLD are:
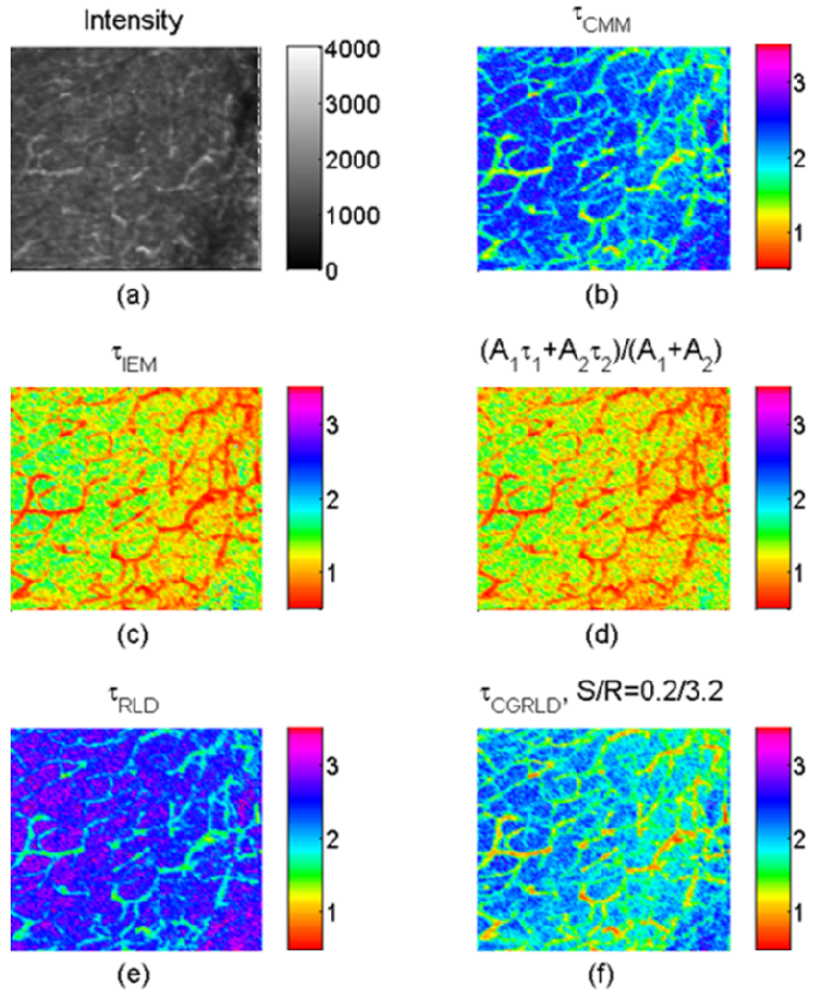
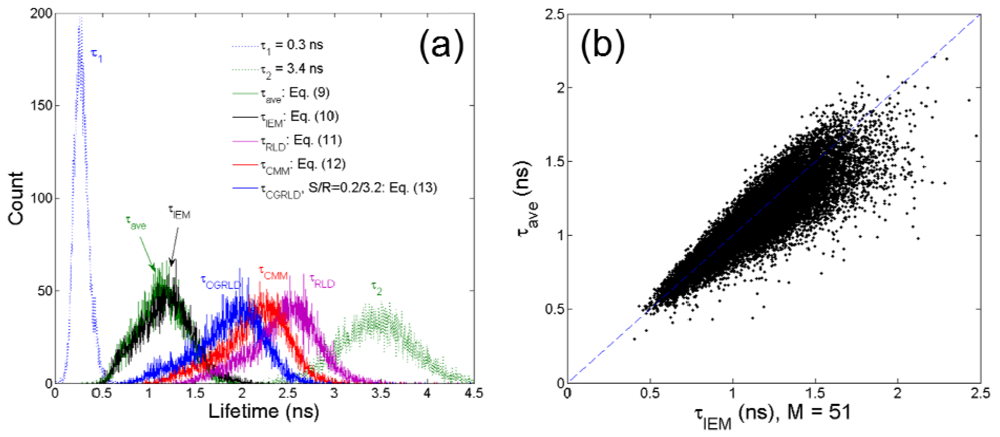
To demonstrate how the above-mentioned single-exponential FLIM algorithms perform on bi-exponential data, we apply them to lifetime imaging data obtained by multi-photon FLIM. The experimental procedure is given in full elsewhere [55]. Briefly, early generation transplants of the P22 rat carcinosarcoma were grown in transparent window chambers, surgically implanted into the fascial layer of a dorsal skin flap of male BD9 rats [56,57]. For imaging of the blood vessel architecture, the molecular probe FITC conjugated Bovine serum albumin was injected intravenously as a blood poolcontrast agent. After 100 minutes the FITC-BSA was observed to diffuse from the vasculature and the FLIM image taken. The intensity image in Figure 7(a) shows very little contrast between the vessels. and the tumor bulk. Compared with the intensity image, the lifetime images Figure 7(b–f) obtained by 150-bin CMM, 51-bin IEM, Equation (9), RLD-2, and CGRLD show much better contrast. The lifetimes in the vessels are smaller than those in the extra-vascular space. Figures 7(c,d) show very similar results except that there is a slightly larger variation in the IEM image shown in Figure 8(b). From Figures 6(a), 7(b) and 7(e), RLD and CMM generate larger lifetimes in the extra-vascular space due to, for example, the τ22 term in Equation (12). If A1 is small throughout the image, the RLD and CMM produce less contrast than the other algorithms. They favor a larger A1 distribution. The image data can also be analyzed with a bi-exponential fit algorithm throughout the image, and the lifetime components are τ1 = 0.3 ± 0.06 ns and τ2 = 3.4 ± 0.4 ns. The lifetime histograms for different algorithms are shown in Figure 8(a), and Table 1 shows the calculated lifetimes. Figure 8(b) shows that the lifetimes obtained by Equation (9) are highly correlated with those obtained by the 51-bin IEM. From Figure 8(b), the lifetime histogram showing a slightly larger variation in the IEM data reveals that the bi-exponential algorithms are crucial for examining most biological image data, but we are still benefitting from the high imaging speed and compactness single-exponential models can provide.

4. Conclusions
We have reviewed the latest developments on CMOS based FLIM systems and introduced several non-iterative high-speed time-domain algorithms suitable for massive sensor arrays. The theoretical error equations of the FLIM algorithms and their optimized operation conditions are discussed and compared. We have drawn from the theory several conclusions different from those in previously published literature and demonstrated the proposed gating schemes or FLIM algorithms on single-exponential data obtained from 0.13 μm CMOS SPAD arrays. The experimental results show good agreement with the theory. The contrast capabilities of the proposed algorithms on bi-exponential data are also discussed and demonstrated with an in vivo two photon fluorescence lifetime imaging data of FITC-albumin labeled vasculature of a P22 rat carcinosarcoma. With emerging CMOS imaging sensors, the proposed techniques capable of rapidly producing lifetime images with enough contrast show great potential in scientific and clinical applications.
Supplementary Material
sensors-12-05650-s001.movAcknowledgments
The authors acknowledge funding support from the EPSRC (D. R. Matthews EP/C546105/1; V. Visitkul and D. Tyndall EPSRC Studentships), Royal Society Paul Instrument Fund (S. M. Ameer-Beg) and an endowment from Dimbleby Cancer Care (S. M. Ameer-Beg). We gratefully acknowledge Gillian Tozer and Iain Wilson for their support. The SPAD chip was supported by the European Community within the Sixth Framework Programme of the Information Science Technologies, Future and Emerging Technologies Open MEGAFRAME project ( www.megaframe.eu).
Appendix
Similar to the analysis methods introduced in [45], we assume that the fluorescence decay function f(t) = Aexp(−t/τ)u(t), with τ being the lifetime and A the prescaler, but here h is the gate width of the “first” gate. Suppose , where x = e−h/τ then the expectation values for N1 and N2 in both categories can be obtained as:
We adopt the similar notation as in [45] for the recorded counts Nj, which are Poisson distributed with respective mean values ENj and standard deviations σNj = (ENj)1/2, j = 1, 2. From Equation (A1), EN1 and EN2 are related as EN1 (xS − xR) − EN2 (1 − x) = 0. We define:
Usually, the lifetime can be extracted from the recorded N1 and N2 in each pixel by solving g(xˆ) = 0 and τˆ = −h/ln(xˆ) and the prescaler Aˆ = A + σA can be obtained by solving Aˆ =Nc/[τˆ(1 − e−T/τˆ]. There is often no experimental interest in the parameter A [45], so we concentrate here on the derivation of σx. With the variations σNj in the recorded counts Nj (j = 1, 2), the calculated xˆ will contain a variation σx with respective to its mean value x accordingly, xˆ = x + σx. To express σx in terms of σNj for the UGRLD we substitute Nj = ENj + σNj (j = 1, 2) into Equation (A2) and g(x + σx) = 0, and we can obtain:
To derive the F-value for the CGRLD, we substitute N1 = N1″ + Nov = EN1″ + σ N1″ + ENov + σ Nov and N2 = N2″ + Nov = EN2″ + σ N2″ + ENov + σ Nov into Equation (A2) with EN1 = EN1″ + ENov and EN2 = EN2″ + ENov:
References
- Medintz, I.L.; Uyeda, H.T.; Goldman, E.R.; Mattoussi, H. Quantum dot bioconjugates for imaging, labelling and sensing. Nat. Mater. 2005, 4, 435–446. [Google Scholar]
- Carlin, L.M.; Evans, R.; Milewicz, H.; Matthews, D.R.; Fernandes, L.; Perani, M.; Levitt, J.; Keppler, M.; Monypenny, J.; Coolen, A.; et al. A targeted siRNA screen identifies regulators of Cdc42 activity at the Natural Killer cell immunological synapse. Sci. Signal. 2011. [Google Scholar] [CrossRef]
- Fruhwirth, G.O.; Fernandes, L.P.; Weitsman, G.; Patel, G.; Kelleher, M.; Lawler, K.; Brock, A.; Poland, S.P.; Mattews, D.R.; Keri, G.; et al. How föster resonance energy transfer imaging improves the understanding of protein interaction networks in cancer biology. Chem. Phys. Chem. 2011, 12, 442–461. [Google Scholar]
- Lakowicz, J.R.; Szmacinski, H.; Nowaczyk, K.; Johnson, M.L. Fluorescence lifetime imaging of calcium using Quin-2. Cell Calcium 1992, 13, 131–147. [Google Scholar]
- Spring, B.Q.; Clegg, R.M. Image analysis for denoising full-field frequency-domain fluorescence lifetime images. J. Microsc. 2009, 235, 221–237. [Google Scholar]
- Gratton, E.; Breusegem, S.; Sutin, J.; Ruan, Q.; Barry, N. Fluorescence lifetime imaging for the two-photon microscope: Time-domain and frequency-domain methods. J. Biomed. Opt. 2003, 8, 381. [Google Scholar]
- Clayton, A.H.A.; Hanley, Q.S.; Verveer, P.J. Graphical representation and multicomponent analysis of single-frequency fluorescence lifetime imaging microscopy data. J. Microsc. 2004, 213, 1–5. [Google Scholar]
- Becker, W. Advanced Time-Correlated Single Photon Counting Techniques; Springer: New York, NY, USA, 2005. [Google Scholar]
- Yoon, H.-J.; Itoh, S.; Kawahito, S. A CMOS image sensor with in-pixel two-stage charge transfer for fluorescence lifetime imaging. IEEE Trans. Electron. Devices 2009, 56, 214–221. [Google Scholar]
- Huang, T.-C.D.; Sorgenfrei, S.; Gong, P.; Levicky, R.; Shepard, K.L. A 0.18 μm CMOS array sensor for integrated time-resolved fluorescence detection. IEEE J. Solid-State Circuits 2009, 44, 1644–1654. [Google Scholar]
- Pancheri, L.; Stoppa, D. A SPAD-Based Pixel Linear Array for High-Speed Time-Gated Fluorescence Lifetime Imaging. Proceedings of the 34th IEEE European Solid-State Circuits Conference (ESSCIRC), Athens, Greece, 14–18 September 2009; pp. 428–431.
- Benetti, M.; Iori, D.; Pancheri, L.; Borghetti, F.; Pasquardini, L.; Lunelli, L.; Pederzolli, C.; Gonzo, L.; Betta, G.-F.D.; Stoppa, D. Highly parallel SPAD detector for time-resolved lab-on-chip. Proc. SPIE 2010, 7723, 77231Q. [Google Scholar]
- Rae, B.R.; Yang, J.B.; Mckendry, J.; Gong, Z.; Renshaw, D.; Gerkin, J.M.; Gu, E.; Dawson, M.D.; Henderson, R.K. A vertically integrated CMOS microsystem for time-resolved fluorescence analysis. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 437–444. [Google Scholar]
- Li, D.-U.; Arlt, J.; Richardson, J.; Walker, R.; Buts, A.; Stoppa, D.; Charbon, E.; Henderson, R. Real-time fluorescence lifetime imaging system with a 32 × 32 0.13 μm CMOS low dark-count single-photon avalanche diode array. Opt. Express 2010, 18, 10257–10269. [Google Scholar]
- Li, D.D.-U.; Arlt, J.; Tyndall, D.; Walker, R.; Richardson, J.; Stoppa, D.; Charbon, E.; Henderson, R.K. Video-rate fluorescence lifetime imaging camera with CMOS single-photon avalanche diode arrays and high-speed imaging algorithm. J. Biomed. Opt. 2011, 16, 096012. [Google Scholar]
- Veerappan, C.; Richardson, J.; Walker, R.; Li, D.-U.; Fishburn, M.W.; Maruyama, Y.; Stoppa, D.; Borghetti, F.; Gersbach, M.; Henderson, R.K.; et al. A 160 × 128 Single-Photon Image Sensor with on-pixel 55ps 10bit Time-to-Digital Converter. Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC) Dig. Tech. Papers, San Francisco, CA, USA, 20–24 February, 2011; pp. 312–314.
- Maruyama, Y.; Charbon, E. An All-Digital, Time-Gated 128 × 128 SPAD Array for On-Chip, Filter-Less Fluorescence Detection. Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference (Transducers), Beijing, China, 5–9 June 2011; pp. 1180–1183.
- Guo, J.; Sonkusale, S. A CMOS Imager with Digital Phase Readout for Fluorescence Lifetime Imaging. Proceedings of the 36th IEEE European Solid-State Circuits Conference (ESSCIRC), Helsinki, Finland, 12–16 September 2011; pp. 115–118.
- Yao, L.; Yung, K.Y.; Cheung, M.C.; Chodavarapu, V.P.; Bright, F.V. CMOS Direct Time Interval Measurement of Long-Lived Luminescence Lifetimes. Proceedings of the 33rd Annual International Conference of the IEEE EMBS, Boston, MA, USA, 30 August–3 September 2011; pp. 5–9.
- Tyndall, D.; Rae, B.; Li, D.; Richardson, J.; Arlt, J.; Henderson, R. A 100Mphoton/s Time-Resolved Mini-Silicon Photomultiplier with On-Chip Fluorescence Lifetime Estimation in 0.13 μm CMOS Imaging Technology. Proceedings of the IEEE Int. Solid-State Circuits Conference (ISSCC) Dig. Tech. Papers, San Francisco, CA, USA, 19–23 February 2012; pp. 122–123.
- Ballew, R.M.; Demas, J.N. An error analysis of the rapid lifetime determination method for the evaluation of single exponential decays. Anal. Chem. 1989, 61, 30–33. [Google Scholar]
- Richardson, J.; Walker, R.; Grant, L.; Stoppa, D.; Borghetti, F.; Charbon, E.; Gersbach, M.; Henderson, R. A 32 × 32 50ps Resolution 10bit Time to Digital Converter Array in 130 nm CMOS for Time Correlated Imaging. Proceedings of the IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 13–16 September 2009; pp. 77–80.
- Li, L.-Q.; Davis, L.M. Single photon avalanche diode for single molecule detection. Rev. Sci. Instrum. 1993, 64, 1524–1529. [Google Scholar]
- Colyer, R.A.; Scalia, G.; Villa, F.A.; Guerrieri, F.; Tisa, S.; Zappa, F.; Cova, S.; Weiss, S.; Michalet, X. Ultra high-throughput single molecule spectroscopy. Proc. SPIE 2011, 7905, 790503:1–790503:10. [Google Scholar]
- Wang, Y.; Rae, B.R.; Henderson, R.K.; Gong, Z.; Mckendry, J.; Gu, E.; Dawson, M.D.; Turnbull, G.A.; Samuel, I.D.W. Ultra-portable explosives sensor based on a CMOS fluorescence lifetime analysis micro-system. AIP Adv. 2011, 1, 032115. [Google Scholar]
- Niclass, C.; Soga, M. A Miniature Actively Recharged Single-Photon Detector Free of Afterpulsing Effects with 6 ns Dead Time in a 0.18 μm CMOS Technology. Proceedings of the IEEE International Electron Devices Meeting (IEDM) 2010, San Francisco, CA, USA, 6–8 December 2010; pp. 14.3:1–14.3:4.
- Richardson, J.A.; Grant, L.A.; Henderson, R.K. Low dark count single-photon avalanche diode structure compatible with standard nanometer scale CMOS technology. IEEE Photon. Tech. Lett. 2009, 21, 1020–1022. [Google Scholar]
- Henderson, R.K.; Webster, E.A.G.; Walker, R.; Richardson, J.A.; Grant, L.A. A 3 × 3, 5 μm Pitch, 3-Transistor Single Photon Avalanche Diode Array with Integrated 11 V Bias Generation in 90 nm CMOS Technology. Proceedings of the 2010 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 6–8 December 2010; pp. 14.2:1–14.2:4.
- Richardson, J.A.; Webster, E.A.G.; Grant, L.A.; Henderson, R.K. Scalable single-photon avalanche diode structure in nanometer CMOS technology. IEEE Trans. Electron Dev. 2011, 58, 2028–2035. [Google Scholar]
- Webster, E.A.G.; Richardson, J.A.; Grant, L.A.; Renshaw, D.; Henderson, R.K. A single-photon avalanche diode in 90-nm CMOS imaging technology with 44% photon detection efficiency at 690 nm. IEEE Electron. Dev. Lett. 2012, 33, 694–696. [Google Scholar]
- Niclass, C.; Soga, M.; Matsubara, H.; Kato, S. A 100 m-Range 10-Frame/s 340 × 96-Pixel Time-of-Flight Depth Sensor in 0.18 μm CMOS. Proceedings of the 36th IEEE European Solid-State Circuits Conference (ESSCIRC), Helsinki, Finland, 12–16 September 2011; pp. 107–110.
- Elangovan, M.; Day, R.N.; Periasamy, A. Nanosecond fluorescence resonance energy transfer-fluorescence lifetime imaging microscopy to localize the protein interactions in a single living cell. J. Microsc. 2002, 205, 3–14. [Google Scholar]
- Sharman, K.K.; Periasamy, A. Error analysis of the rapid lifetime determination method for double-exponential decays and new windowing schemes. Anal. Chem. 1999, 71, 947–952. [Google Scholar]
- Grauw, C.J.; Gerritsen, H.C. Multiple time-gate module for fluorescence lifetime imaging. Appl. Spectrosc. 2001, 55, 670–678. [Google Scholar]
- Chang, C.W.; Mycek, M.-A. Enhancing precision in time-domain fluorescence lifetime imaging. J. Biomed. Opt. 2010, 15, 056013. [Google Scholar]
- Rae, B.R.; Muir, K.R.; Gong, Z.; McKendry, J.; Girkin, J.M.; Gu, E.; Renshaw, D.; Dawson, M.D.; Henderson, R.K. A CMOS time-resolved fluorescence lifetime analysis micro-system. Sensors 2009, 9, 9255–9274. [Google Scholar]
- Elson, D.S.; Munro, I.; Requejo-Isidra, J.; McGinty, J.; Dunsby, C.; Galletly, N.; Stamp, G.W.; Neil, M.A.A.; Lever, M.J.; Kellett, P.A.; et al. Real-time time-domain fluorescence lifetime imaging including single-shot acquisition with a segmented optical image intensifier. New J. Phys. 2004, 6, 1–13. [Google Scholar]
- Agronskaia, A.V.; Tertoolen, L.; Gerritsen, H.C. High frame rate fluorescence lifetime imaging. J. Phys. D Appl. Phys. 2003, 36, 1655–1662. [Google Scholar]
- Agronskaia, A.V.; Tertoolen, L.; Gerritsen, H.C. Fast fluorescence lifetime imaging of calcium in living cells. J. Biomed. Opt. 2004, 9, 1230–1237. [Google Scholar]
- Gerritsen, H.C.; Asselbergs, M.A.H.; Agronskaia, A.V.; Vansark, J.H.M. Fluorescence lifetime imaging in scanning microscopes: acquisition speed, photon economy and lifetime resolution. J. Microsc. 2002, 206, 218–224. [Google Scholar]
- Chan, S.P.; Fuller, Z.J.; Demas, J.N.; DeGraff, B.A. Optimized gating scheme for rapid lifetime determinations of single-exponential luminescence lifetimes. Anal. Chem. 2001, 73, 4486–4490. [Google Scholar]
- Li, D.-U.; Bonnist Renshaw, D.; Henderson, R. On-chip time-correlated fluorescence lifetime extraction algorithms and error analysis. J. Opt. Soc. Am. A 2008, 25, 1190–1198. [Google Scholar]
- Li, D.-U.; Andrews, R.; Arlt, J.; Henderson, R. Hardware implementation algorithm and error analysis of high-speed fluorescence lifetime sensing systems using center-of-mass method. J. Biomed. Opt. 2010, 15, 017006. [Google Scholar]
- Draaijer, A.; Sanders, R.; Gerritsen, H.C. Fluorescence Lifetime Imaging, a New Tool in Confocal Microscopy. In Handbook of Biological Confocal Microscopy; Pawley, J., Ed.; Plenum Publishing: New York, NY, USA, 1995; pp. 491–505. [Google Scholar]
- Hall, P.; Selinger, B. Better estimates of exponential decay parameters. J. Phys. Chem. 1981, 85, 2941–2946. [Google Scholar]
- Li, D.-U.; Walker, R.; Richardson, J.; Rae, B.; Buts, A.; Renshaw, D.; Henderson, R. Hardware implementation and calibration of background noise for an integration-based fluorescence lifetime sensing algorithm. J. Opt. Soc. Am. 2009, 26, 804–814. [Google Scholar]
- Trabesinger, W.; Hübner, C.G.; Hecht, B.; Wild, T.P. Continuous real-time measurement of fluorescence lifetime. Rev. Sci. Instrum. 2002, 73, 3122–3124. [Google Scholar]
- Moon, S; Won, Y.J.; Kim, D.Y. Analog mean-delay method for high-speed fluorescence lifetime measurement. Opt. Express 2009, 17, 2834–2849. [Google Scholar]
- Wong, Y.J.; Han, W.-T.; Kim, D.Y. Precision and accuracy of the analog mean-delay method for high-speed fluorescence lifetime measurement. J. Opt. Soc. Am. A 2011, 28, 2026–2032. [Google Scholar]
- Won, Y.J.; Moon, S.; Yang, W.B.; Kim, D.G.; Han, W.-T.; Kim, D.Y. High-speed confocal fluorescence lifetime imaging microscopy (FLIM) with the analog mean delay (AMD) method. Opt. Express 2011, 19, 3396–3405. [Google Scholar]
- Padilla-Parra, S.; Auduge, N.; Coppey-Moisan, M.; Tramier, M. Quantitative FRET analysis by fast acquisition time domain FLIM at high spatial resolution in living cells. Biophys. J. 2008, 95, 2976–2988. [Google Scholar]
- Yamada, H.; Padilla-Parra, S.; Park, S.-J.; Itoh, T.; Chaineau, M.; Monaldi, I.; Cremona, O.; Benfenati, F.; Camilli, P.D.; Coppey-Moisan, M.; et al. Dynamic interaction of amphiphysin with N-WASP regulates actin assembly. J. Biol. Chem. 2009, 284, 34244–34256. [Google Scholar]
- Barber, P.R.; Ameer-Beg, S.M.; Pathmannanthan, S.; Rowly, M.; Collen, A.C.C. A Bayesian method for single molecule fluorescence burst analysis. Biomed. Opt. Express 2010, 1, 1148–1158. [Google Scholar]
- Rowley, M.I; Barber, P.R.; Coolen, A.C.C.; Vojnovic, B. Bayesian analysis of fluorescence lifetime imaging data. Proc. SPIE 2011, 7903, 790325:1–790325:9. [Google Scholar]
- Ameer-Big, S.M.; Barber, P.R.; Hodgkiss, R.J.; Locke, R.J.; Newman, R.G.; Tozer, G.M.; Vojnovic, B.; Wilson, J. Application of multiphoton steady state and lifetime imaging to mapping of tumour vascular architecture. in vivo. Proc. SPIE 2002, 4620, 85–95. [Google Scholar]
- Papenfuss, H.D.; Gross, J.F.; Intaglietta, M.; Treese, F.A. A transparent access chamber for the rat dorsal skin fold. Microvasc. Res. 1979, 18, 311–318. [Google Scholar]
- Dewhirst, M.W.; Gustafson, C.; Gross, J.F.; Tso, C.Y. Temporal effects of 5.0 Gy radiation in healing subcutaneous micro-vasculature of a dorsal flap window chamber. Rad. Res. 1987, 112, 581–591. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).