The mechanical strain energy of an infinitesimal beam element is: (2) dU m = σ 0 [ 1 2 ( dw dx ) 2 ] d ν + E [ 1 2 z 2 ( − d 2 w dx 2 ) 2 ] d ν

The total mechanical strain energy of the beam, as shown in Figure 1, can be expressed as: (3) U m = ∫ 0 L σ 0 [ 1 2 ( dw dx ) 2 ] hbdx + ∫ 0 L EI [ 1 2 ( − d 2 w dx 2 ) 2 ] dx = ∫ 0 L [ σ 0 bh 2 ( dw dx ) 2 + EI 2 ( d 2 w dx 2 ) 2 ] dxwhere b, E, h, I, L, and w represent the beam width, Young’s modulus, thickness, area inertia moment of beam cross section, beam length, and deflection, respectively. In the integrand of Equation (3), the first term is the strain energy induced by initial stress (σ₀) and the second term is the bending strain energy induced by external loads. The fringing fields are considerable and must be taken into account when modeling the electrostatic loads. For an infinitesimal beam element with length dx, the differential capacitance dC is given as [36]: (4) dC = ɛ [ ( b g − w ) − 1.06 + 3.31 ( h g − w ) 0.23 + 0.73 ( b h ) 0.23 ] dxwhere ε and g represent the permittivity of dielectric medium and the initial gap between test beam and ground plane, respectively. Hence, the total electrical potential energy U_e is given by: (5) U e = − ∫ 0 L 1 2 ɛ V 2 [ ( b g − w ) − 1.06 + 3.31 ( h g − w ) 0.23 + 0.73 ( b h ) 0.23 ] dxwhere V is the applied bias voltage. In Equation (5), the first term is ideal flat plate capacitance, the second term is a length-dependent adjustment parameter, and the third term is the fringing field capacitance due to beam thickness. Then, the total system energy U equals the sum of mechanical strain energy and electrical potential energy, i.e., (6) U = ∫ 0 L [ σ 0 bh 2 ( dw dx ) 2 + EI 2 ( d 2 w dx 2 ) 2 ] dx − ∫ 0 L 1 2 ɛ V 2 [ ( b g − w ) − 1.06 + 3.31 ( h g − w ) 0.23 + 0.73 ( b h ) 0.23 ] dx

It should be mentioned that nonlinearities are simplified with only in the electrostatic part of the model. Indeed, the beam structure is assumed linearly elastic, without any consideration of geometrical nonlinearity in virtue of large deformation. Expanding the electrostatic terms in Equation (6) by Taylor’s series with respect to the initial equilibrium position, i.e., w = 0, and truncate the fifth and higher order terms since (w/g)ⁿ << 1 for n≥5. Therefore, the total system potential energy U becomes: (7) U = ∫ 0 L σ 0 bh 2 ( dw dx ) 2 dx + ∫ 0 L EI 2 ( d 2 w dx 2 ) 2 dx − ∫ 0 L ɛ V 2 b 2 g ( 1 + ( w g ) + ( w g ) 2 + ( w g ) 3 + ( w g ) 4 ) dx + ∫ 0 L 1.06 ɛ V 2 2 dx − ∫ 0 L 3.31 ɛ V 2 h 0.23 2 g 0.23 ( 1 + 0.23 ( w g ) + 0.283 2 ( w g ) 2 + 0.631 6 ( w g ) 2 + 2.038 24 ( w g ) 4 ) dx − ∫ 0 L 0.73 ɛ V 2 2 ( b h ) 0.23 dx

The exact solution for the electrostatic-actuated beam is difficult to obtain since it is a nonlinear system with the nonlinear electrostatic force coupled with the structural deflection. Thus, such problem is often solved by the approximate analytical solution. Using the assumed mode method [38], the deflection function w(x) is expressed as: (8) w ( x ) = ∑ i = 1 n η i ϕ i ( x )where ϕ_i(x) is the ith mode and the coefficient η_i to be solved is the associated modal participation factors. Then substituting the assumed deflection function into the system energy expression, one can solve for the coefficient η_i. Since the natural mode is the exact solution to the free vibration of structures, it essentially satisfies the boundary conditions and the homogeneous part of the governing equation of a dynamic system. Thus, the natural modes form the foundation for forced response calculations in structural dynamics [38]. The first natural mode of a fixed-fixed beam is adopted since the electrostatic loads are attractive forces and the deflection is much similar to the first natural mode of fixed-fixed beam. The first natural mode of a fixed-fixed beam is [38]: (9) ϕ ( x ) = ( cosh λ x − cos λ x ) − ζ ( sinh λ x − sin λ x )where the coefficients ζ and λ satisfy the following equations: (10) ζ = cosh ( λ L ) − cos ( λ L ) sinh ( λ L ) − sin ( λ L ) ,     and     cos ( λ L ) ⋅ cosh ( λ L ) − 1 = 0

Substituting Equations (8) and (9) into Equation (7) yields: (11) U = ∫ 0 L σ 0 bh 2 ( η ϕ ′ ) 2 dx + ∫ 0 L EI 2 ( η ϕ ″ ) 2 dx − ∫ 0 L ɛ V 2 b 2 g ( 1 + ( η ϕ g ) + ( η ϕ g ) 2 + ( η ϕ g ) 3 + ( η ϕ g ) 4 ) dx + ∫ 0 L 1.06 ɛ V 2 2 dx − ∫ 0 L 3.31 ɛ V 2 h 0.23 2 g 0.23 ( 1 + 0.23 ( η ϕ g ) + 0.283 2 ( η ϕ g ) 2 + 0.631 6 ( η ϕ g ) 3 + 2.038 24 ( η ϕ g ) 4 ) dx − ∫ 0 L 0.73 ɛ V 2 2 ( b h ) 0.23 dx

The system is in static equilibrium when the first-order derivative of the total potential energy U with respect to the coefficient η equals zero, i.e., dU/dη = 0, then one have: (12) η [ σ 0 ∫ 0 L bh ( ϕ ′ ) 2 dx + E ∫ 0 L I ( ϕ ″ ) 2 dx ] = ɛ V 2 2 ( c 0 + c 1 η + c 2 η 2 + c 3 η 3 )Where c_j (j = 0–3) are shown as below: (13) { c 0 = ∫ 0 L ( b / g 2 + 0.76 h 0.23 / g 1.23 ) ϕ d x c 1 = ∫ 0 L ( 2 b / g 3 + 0.94 h 0.23 / g 2.23 ) ϕ 2 d x c 2 = ∫ 0 L ( 3 b / g 4 + 1.04 h 0.23 / g 3.23 ) ϕ 3 d x c 3 = ∫ 0 L ( 4 b / g 5 + 1.12 h 0.23 / g 4.23 ) ϕ 4 d x

The coefficients c_j depend only on the geometrical parameters of beam. Whether the equilibrium is stable or unstable is determined by the second-order derivative of the total potential energy with respect to η. At the transition from a stable to an unstable equilibrium, the second-order derivatives of the total potential energy with respect to η also equals zero, i.e., d²U/dη² = 0, then one has: (14) [ σ 0 ∫ 0 L bh ( ϕ ′ ) 2 dx + E ∫ 0 L I ( ϕ ″ ) 2 dx ] = ɛ V 2 2 ( c 1 + 2 c 2 η + 3 c 3 η 2 )

Substituting Equation (14) into Equation (12) gives: (15) 2 c 3 η 3 + c 2 η 2 − c 0 = 0

Equation (15) is a cubic equation of η and can be solved by Cardan solution[39]. The real number root of Equation (15) gives rise to the coefficient η_PI at pull-in as: (16) η PI = [ ( 1 4 c 0 c 3 ) − ( 1 6 c 2 c 3 ) 3 ] + [ ( 1 4 c 0 c 3 ) − ( 1 6 c 2 c 3 ) 3 ] 2 − 8 ( 1 6 c 2 c 3 ) 6 3 + [ ( 1 4 c 0 c 3 ) − ( 1 6 c 2 c 3 ) 3 ] − [ ( 1 4 c 0 c 3 ) − ( 1 6 c 2 c 3 ) 3 ] 2 − 8 ( 1 6 c 2 c 3 ) 6 3 − ( 1 6 c 2 c 3 )

Substituting Equation (16) into Equation (14) gives the approximate analytical solution to the pull-in voltage V_PI as: (17) V PI 2 = σ 0 ∫ 0 L 2 bh ( ϕ ′ ) 2 dx + E ∫ 0 L 2 I ( ϕ ″ ) 2 dx ɛ ( c 1 + 2 c 2 η PI + 3 c 3 η PI 2 )

As shown in Equation (17), the pull-in voltage contains two terms, the first one is dependent on initial residual stress, and the second one is dependent on beam flexibility. The pull-in voltage increases as the increasing of initial stress (σ₀) or Young’s modulus (E). A beam is considered as wide beam as b/h≥ 5. Wide beams exhibit plane strain conditions; therefore, the Young’s modulus (E) should be replaced by the equivalent Young’s modulus Ẽ = E/(1 –ν²) and the residual stress (σ₀) should be replaced by the equivalent residual stress σ̃₀= σ₀(1 –ν²). Therefore, Equation (17) yields: (18) V PI 2 = σ ˜ 0 ∫ 0 L 2 bh ( ϕ ′ ) 2 dx + E ˜ ∫ 0 L 2 I ( ϕ ″ ) 2 dx ɛ ( c 1 + 2 c 2 η PI + 3 c 3 η PI 2 )

The correlation between the pull-in voltage and the material parameters must be formulated quantitatively to realize the idea of extracting mechanical properties from pull-in voltage of the test beam. An equilibrium equation has been derived based on Euler-Bernoulli beam model and the fringing filed capacitance model. The equilibrium equation, Equation (18) yields: (19) S σ ˜ 0 + B E ˜ = V PI 2where the parameters S and B depend on the geometrical parameters of micro test beam and are given as: (20) S = ∫ 0 L 2 bh ( ϕ ′ ) 2 dx ɛ ( c 1 + 2 c 2 η PI + 3 c 3 η PI 2 ) (21) B = ∫ 0 L 2 I ( ϕ ″ ) 2 dx ɛ ( c 1 + 2 c 2 η PI + 3 c 3 η PI 2 )

For a given beam with the pull-in voltage V_PI, there are two unknowns in Equation (19), i.e., σ̃₀ and Ẽ. Therefore, one needs two test beams with different length to get the two unknowns. For the two test beams made of the same material, but with different length, they have the same Young’s modulus and mean stress but different pull-in voltages and different S and B parameters. Then, one has two equations: (22) { S 1 σ ˜ 0 + B 1 E ˜ = V PI 1 2 S 2 σ ˜ 0 + B 2 E ˜ = V PI 2 2

By rearranging Equation (22), the mean stress (σ̃₀) and Young’s modulus (Ẽ) are given as the following matrix operational form: (23) { σ ˜ 0 E ˜ } = [ S 1 B 1 S 2 B 2 ] − 1 { V PI 1 2 V PI 2 2 }

One can extract Young’s modulus (Ẽ) and mean stress (σ̃₀) easily by substituting the measured pull-in voltages of the two test beams with different length into Equation (23).

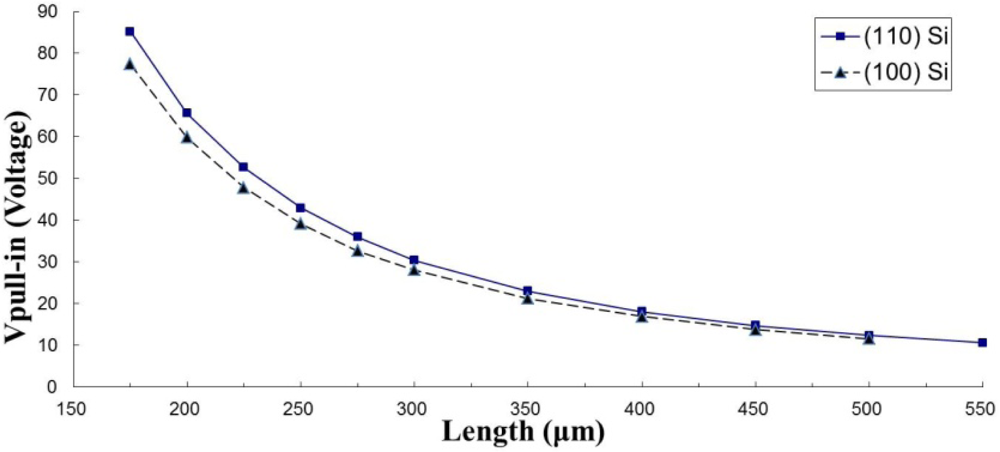
Osterberg [9] had measured pull-in voltages of numerous fixed-fixed beams with different lengths. The authors selected Osterberg’s measured data of two arbitrary test beams and substituted them into the algorithm to verify the validity of the present method. Table 2 lists the geometrical parameters and pull-in voltages of the selected fixed-fixed beams which are made of mono-crystalline silicon. There are two groups of fixed-fixed beams listed in Table 2; each group contains six beams of different lengths. The difference of the two groups is only the crystalline plane of cross section. The first group is in the (100) crystalline plane while the second one is in the (110) crystalline plane. The author selected two beams from each group and substituted the measured data and beam dimensions into Equation (23) to extract Young’s modulus (Ẽ) and mean stress (σ̃₀). Note that the cross-section of the beams of group 1 are in the (100) crystalline plane while that of the group 2 are in the (110) crystalline plane. The Young’s modulus of mono-crystalline silicon in (100) and (110) are 138 GPa and 168 GPa, respectively. The mean stresses of the two beam-samples are 10 MPa [9].

Tables 3 and 4 list the extracted Young’s modulus (Ẽ) and mean stress (σ̃₀) of mono-crystalline silicon in (100) and (110), respectively. It is shown that the extracted values of the present algorithm agree well with the average extracted value of Osterberg’s results [9], but with better convergence than Osterberg’s algorithm. The variety of standard deviation V_SD of the extracted Young’s modulus (Ẽ) are all within 1% which are almost tenth of the deviations of Osterberg’s results [9] for both mono-crystalline silicon in (100) and (110). Besides, the V_SD of the extracted mean stress (σ̃₀) are all within 2%, which are also almost tenth of the deviations of Osterberg’s results [9] for both mono-crystalline silicon in (100) and (110).

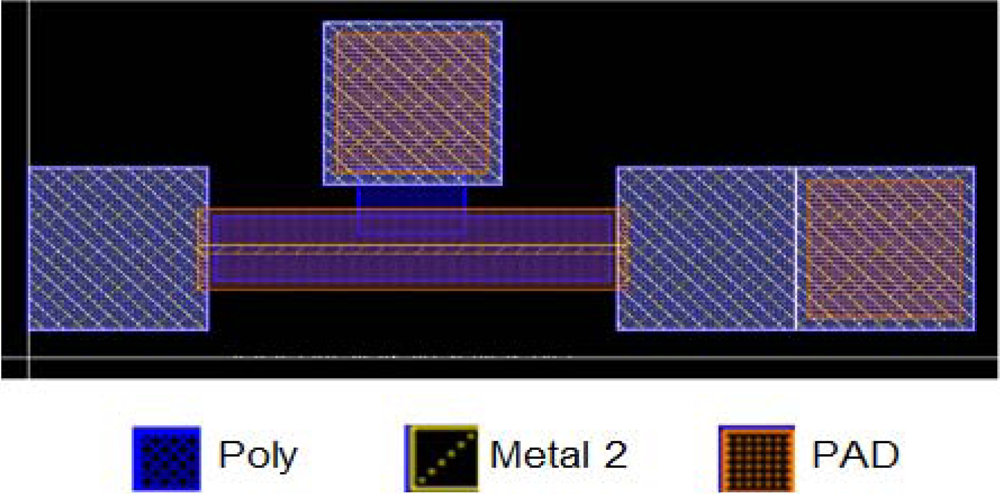
This paper takes bridge-type structures as test structures. The test structures are fabricated by a TSMC 0.18 μm 1P6M standard CMOS process. The upper electrode is metal 2, and the bottom electrode is a poly layer. The anchors are composed of metal and poly layers where viasconnect columns between each metal layer, and contact is the connecting column between metal 1 and the poly layer. When a driving voltage is applied between the test structure and ground plane, the test structure will deflect downward to the ground and this results in a capacitance variation. Figure 2 reveals the layout of the bridge-type test-key. There are two places which are defined as PAD layers-probing pad location and etching hole. The defined area of PAD layer at anchors is the probing pad location. It should be noticed that the probing location must maintain an appropriate distance away from the test structure to avoid measurement uncertainty. The other defined area of PAD layer between the neighboring passivation layers is the etching hole which makes the sacrificial layer etched by etching solution and then results in the structure release. Since the anchors are composed of metal layer, poly layers, via and contact columns, it can reduce the under-cut effect compared to the anchors composed of metal and poly layer without via and contact columns between that when the structures are soaked in etching solution.

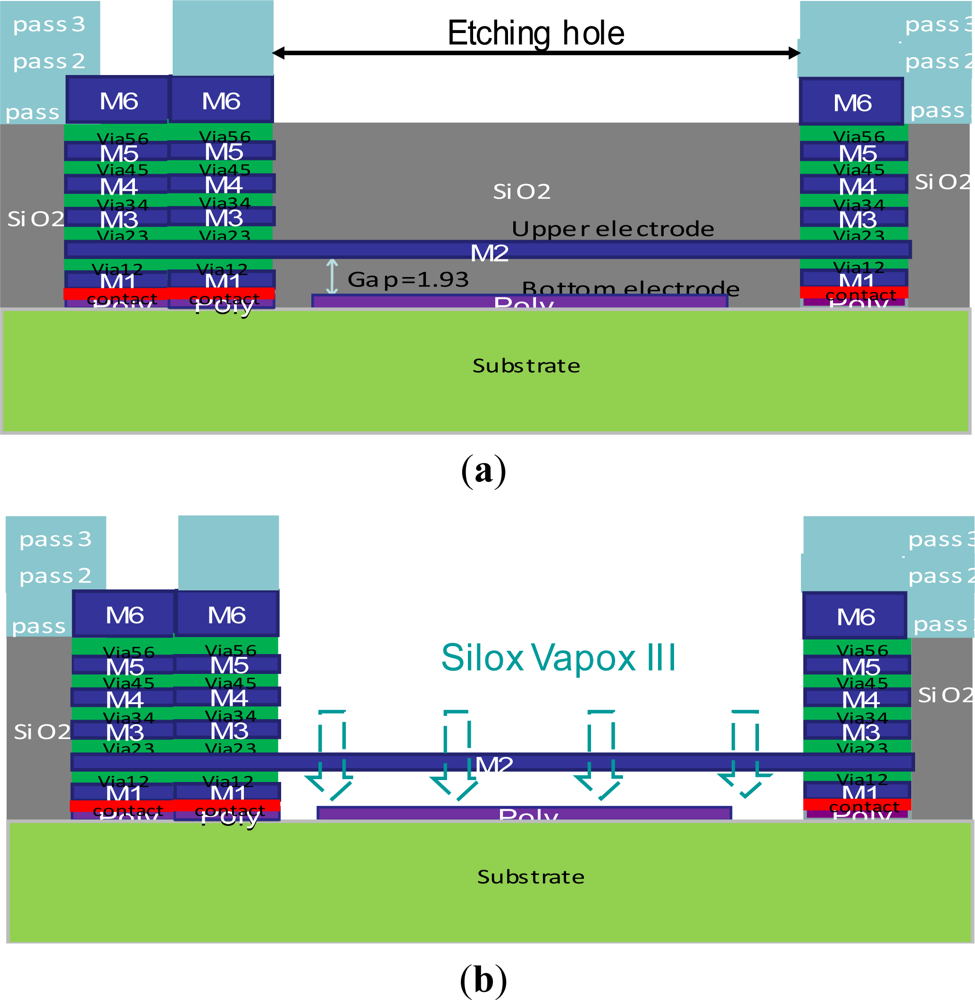
Figure 3 shows the schematic cross-section of the bridge-type test-key after the CMOS process and after post-process. A silicon dioxide layer between the upper electrode and the bottom electrode is a sacrificial layer (Figure 3(a)). Silox Vapox III is used as the etching solution since it has good etch rate selectivity between the metal and silicon dioxide layer. Soaking the bridge-type test-key after the CMOS process in Silox Vapox III, the etching solution will etch the silicon dioxide layer through the etching hole between the neighboring passivation layers, and form a gap between both electrodes (Figure 3(b)) during post-processing. Next, we utilize the critical point drying (CPD) method to dry the structures without collapsing to release the structures. It should be mentioned that the size of the etching hole affects the release time, and the appropriate design of the etching hole can make the release time shorter. Besides, setting a magnetic stirring rod below the etching solution tank can also shorten the release time, but one must make sure the structures have a protective pattern to prevent the damage caused during the stirring process. Excepting the probing pad location and etching hole, the other places are covered by passivation layers to avoid the damage caused by the etching solution.

Figure 4 shows SEM pictures of the bridge-type test-key after post-processing, and it is obvious that the test-key is released successfully by soaking in Silox Vapox III for 85 min.

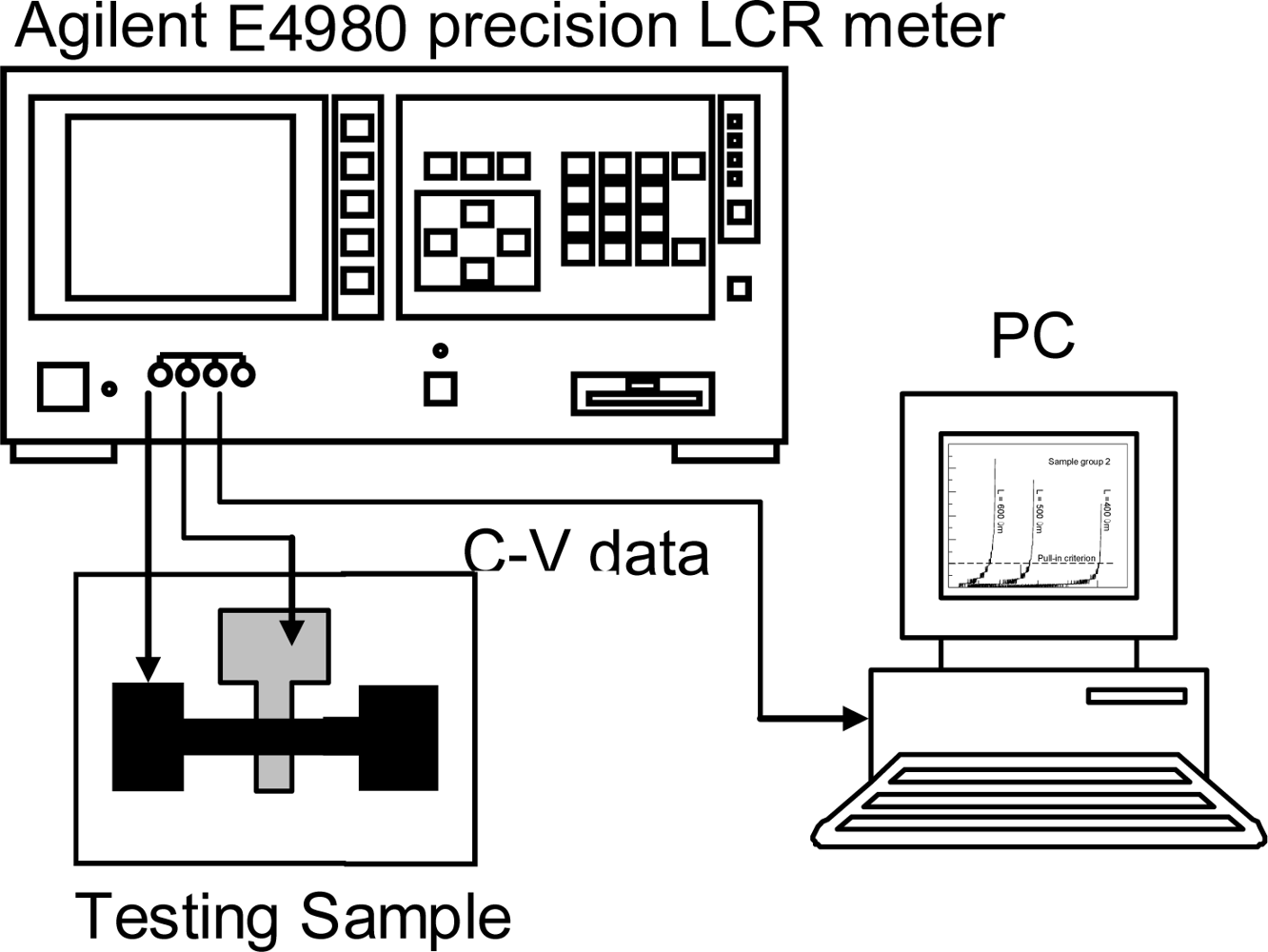
For a deflective microstructure subjected to electrostatic loads, as shown in Figure 1, the structural deflection causes a change in the gap between the upper and bottom electrodes and thus a change in the capacitance. Therefore, the variation of capacitances with the applied bias voltages is equivalent to the deformations to the external loads, and then one can detect the pull-in voltage by tracking the capacitance sensitivities with respect to applied bias voltages. Pull-in will occur when the capacitance shows a sharp increase. Through the capacitance-voltage measurement and the material property extraction algorithms mentioned above, one can obtain the material properties of the test microstructure. The principle of capacitance-voltage measurement is introduced as the following. The main idea is to measure the circuit capacitive reactance X_C to yield the capacitance C. The capacitive reactance is X_c = 1/(2π·f·C) where X_C, f, and C represent the circuit capacitive reactance, the testing signal frequency, and the capacitance, respectively. The input driving voltage is a small AC testing signal riding on a large DC bias voltage which induces the structural deflection. Then the capacitance can be calculated from the circuit capacitive reactance. It should be mentioned here that the frequency of the AC testing signal must avoid the resonance frequency of the test microstructure; otherwise the capacitance will show a large fluctuation. The Agilent E4980 precision LCR meter is used to measure the capacitance-voltage (C-V) variation of the test microstructure, as shown in Figure 5.

The frequency and level of the AC testing signal must be set properly since they will affect the accuracy of the capacitance measurement. The authors chose the root mean square value of the test AC signal level as 25 mV and the frequency 1 MHz. The integration time is set to medium (MED). The instrument parameters setting are listed in Table 5.

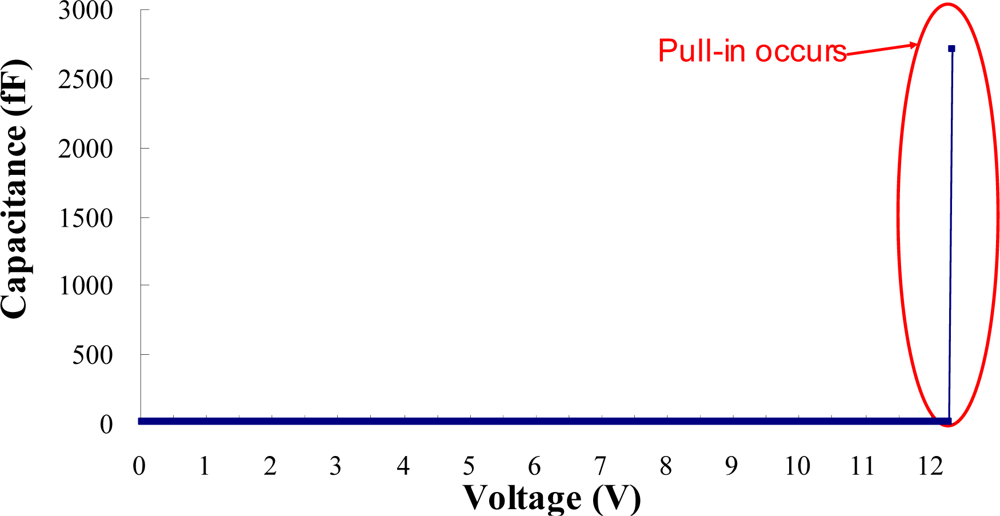
The pull-in voltage is detected by tracking the capacitance sensitivities with respect to the applied bias voltages. Two low noise probes touch the two probing pad of test beam, as shown in Figure 5. The probes are connected to the Agilent E4980 high precision LCR meter, which can supply a test signal of 25 mV/1 MHz riding on the bias voltages ranging from 0 to 40 V. Agilent E4980 exports the capacitance-voltage data to a personal computer and tracks the capacitance sensitivities to the applied bias voltage. Figure 6 shows the typical measured capacitance sensitivities results. Pull-in will occur when the capacitance is with sharp increase. Therefore, according to the results from capacitance-voltage measurement, one can obtain the pull-in voltage of the test beam exactly.

Table 6 lists the geometrical parameters of the bridge-type test beams which are fabricated by a TSMC 0.18 μm 1P6M standard CMOS process. The test beams have the same width, gap, and thickness, but different length. One knows that pull-in occurs when capacitance increases sharply. According to Figure 6, it is obvious that the capacitance will rise up to ten fold or even hundred fold compared to the original capacitance when pull-in occurs. Therefore, one can get the pull-in voltage of test beams, and the corresponding data is shown in Table 7, where V_PI-ave is the average value of measured pull-in voltage for five times of each test beam, and ΔV_PI is the corresponding standard deviation.