Combined Simulation of a Micro Permanent Magnetic Linear Contactless Displacement Sensor
Abstract
:1. Introduction
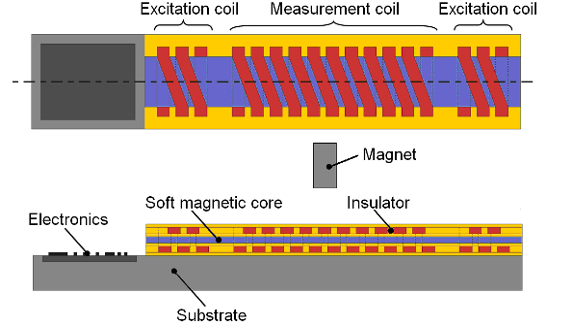
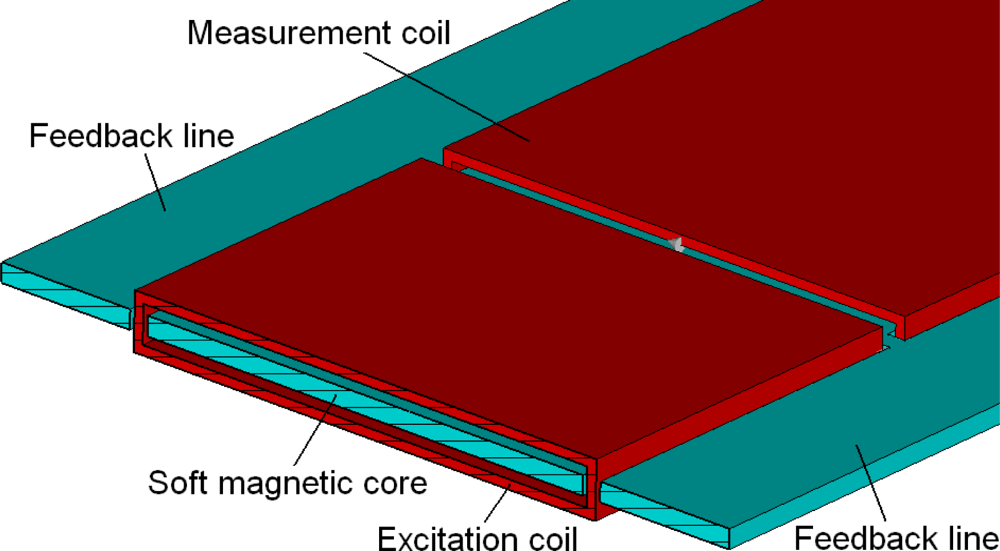
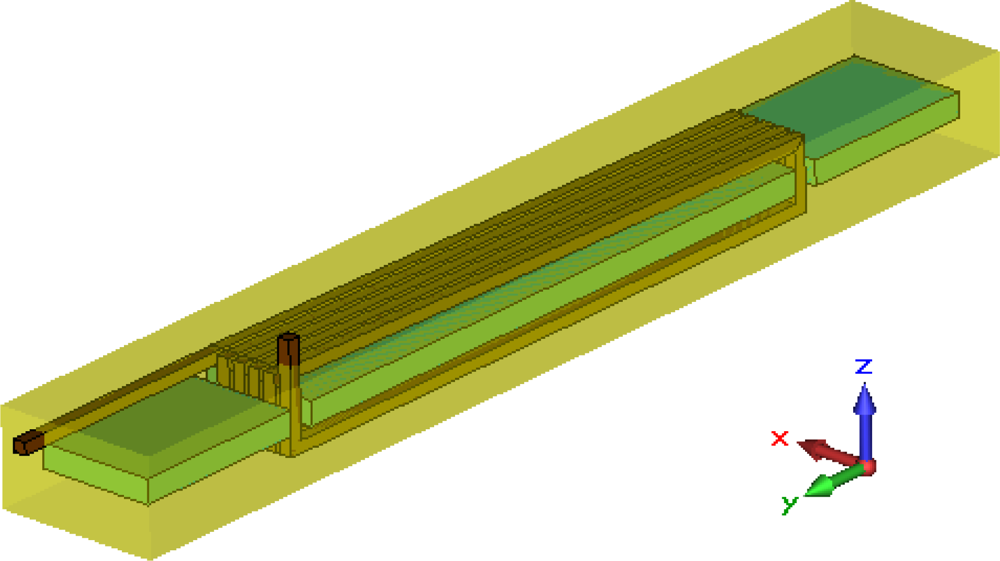
2. Modeling of the Micro-PLCD Sensor
3. Introduction to the Simulation Procedure
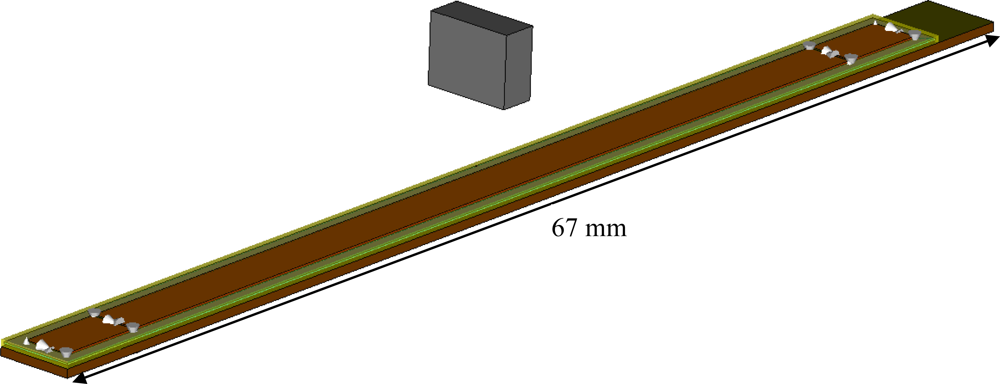
4. Magnetostatic Calculation
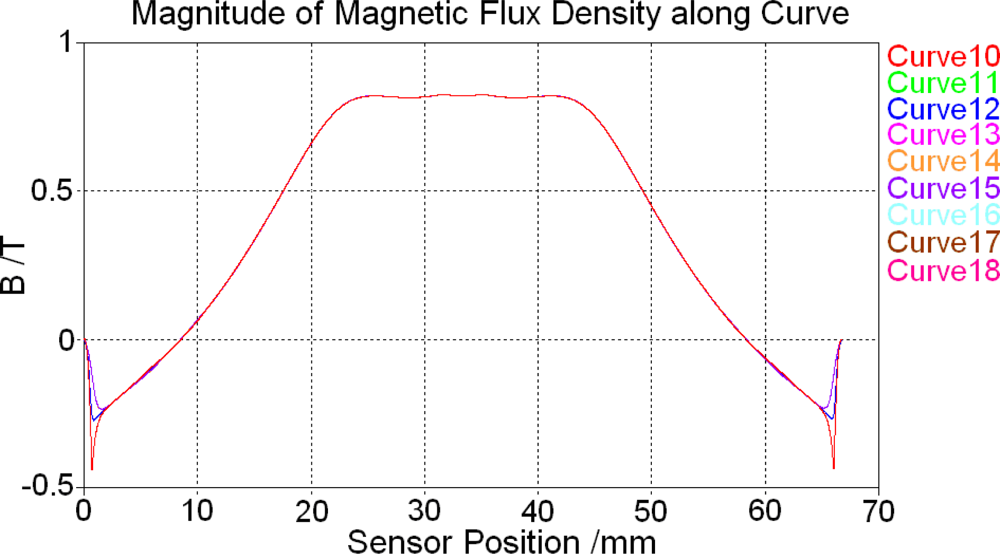
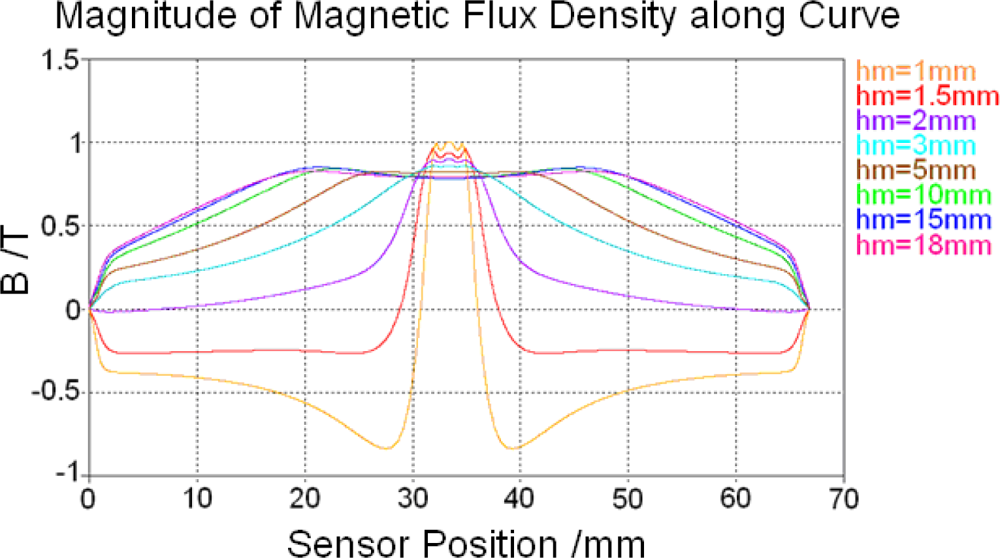
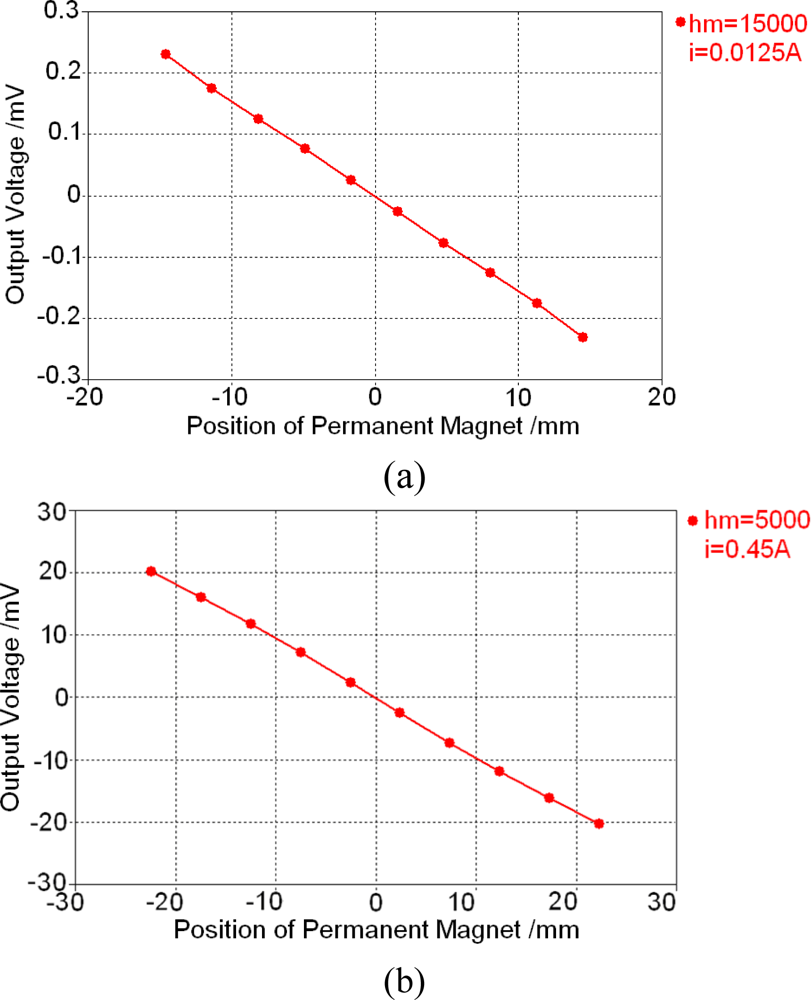
4.1. Magnetostatic calculation results
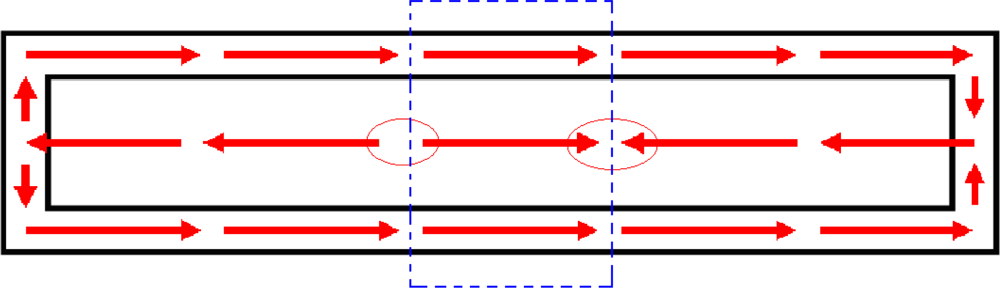
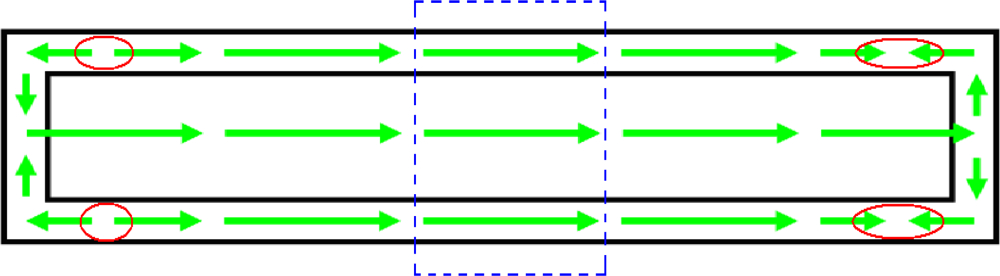
4.2. Magnetostatic field analysis
5. Low Frequency Calculation
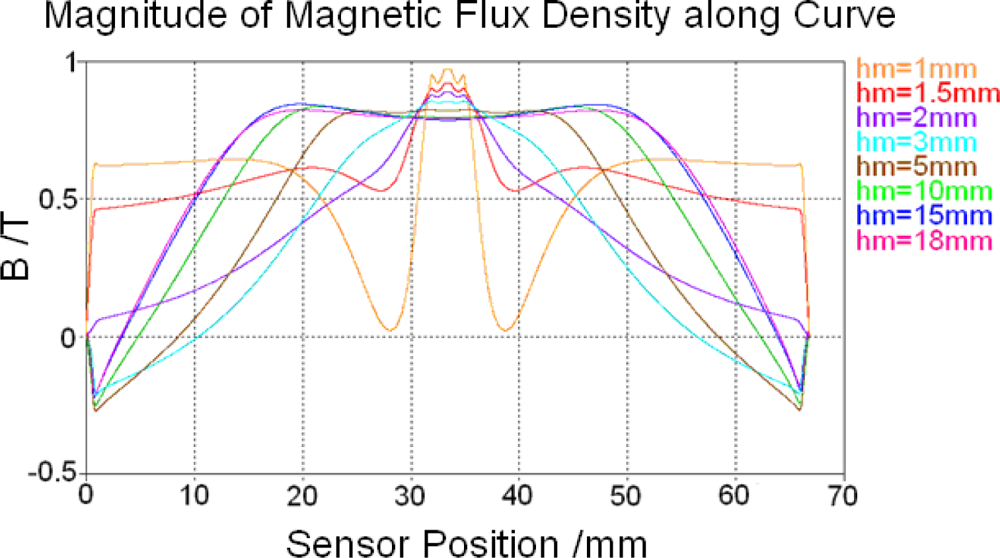
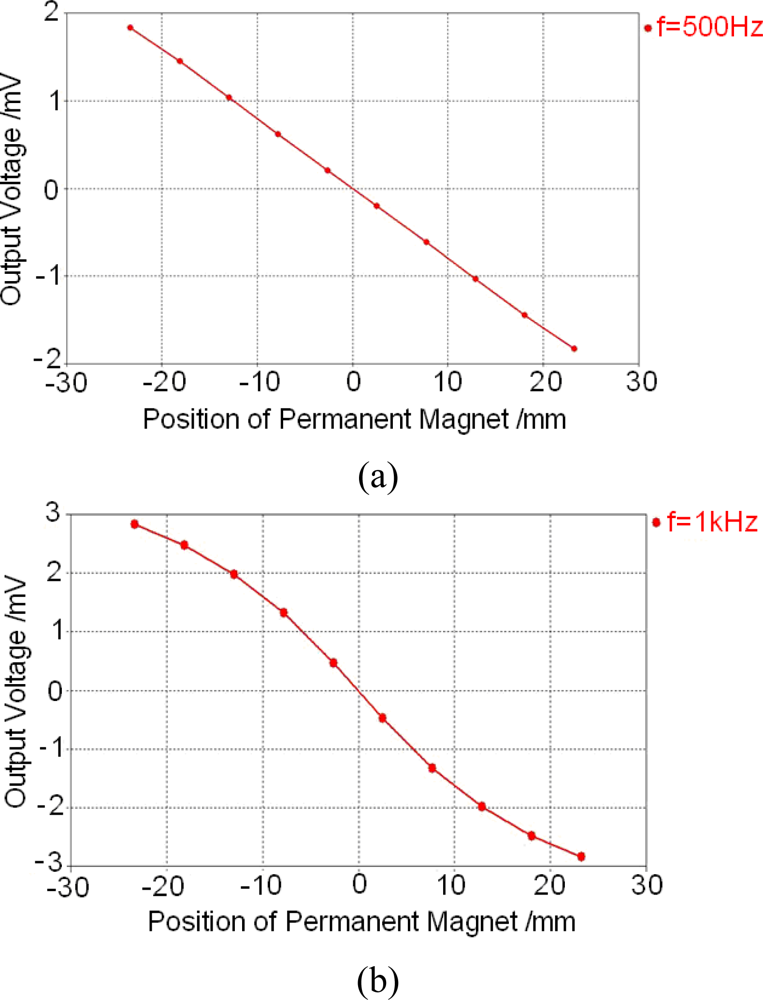
5.1. Low frequency calculation results
5.2. Influence of some parameters
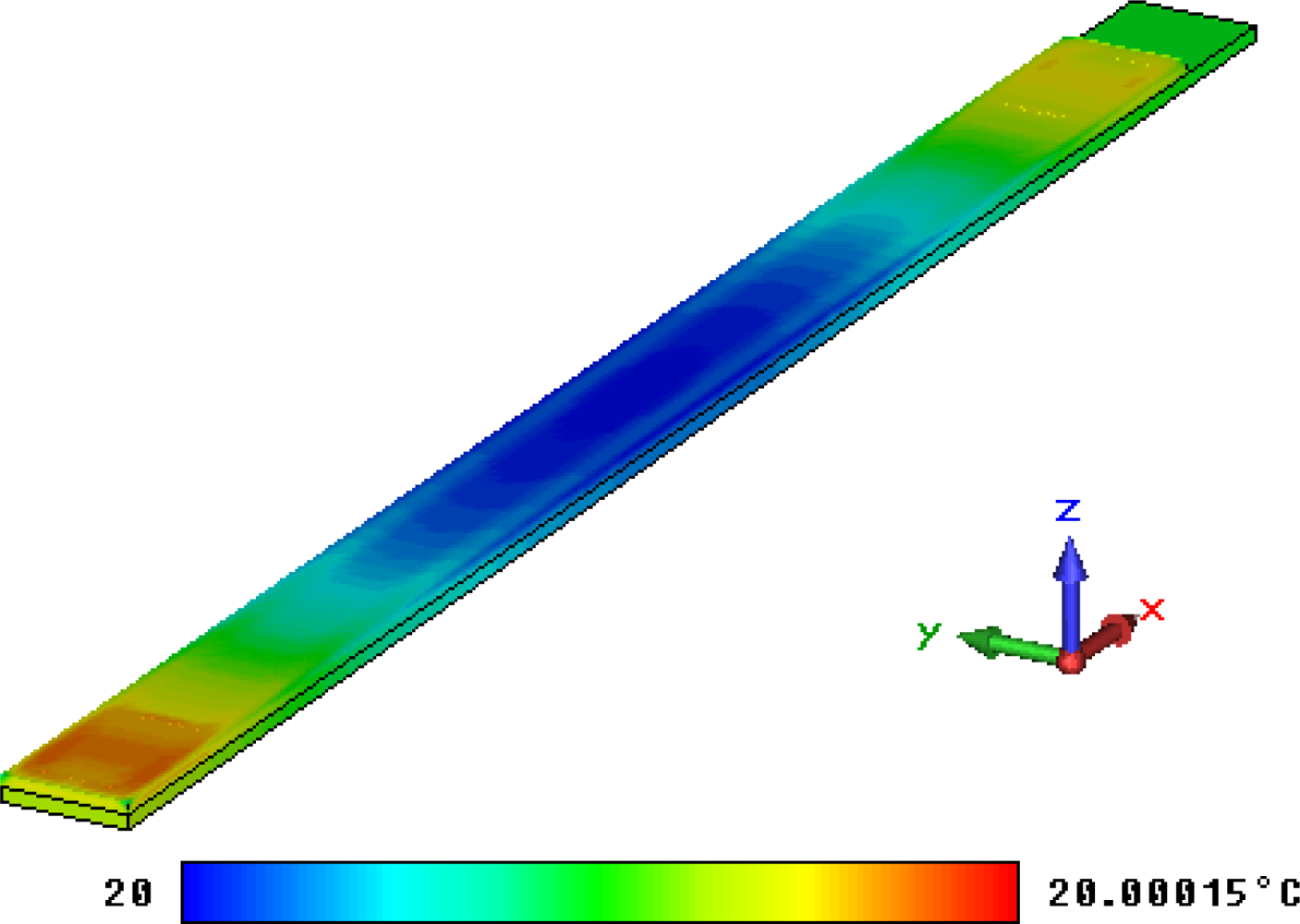
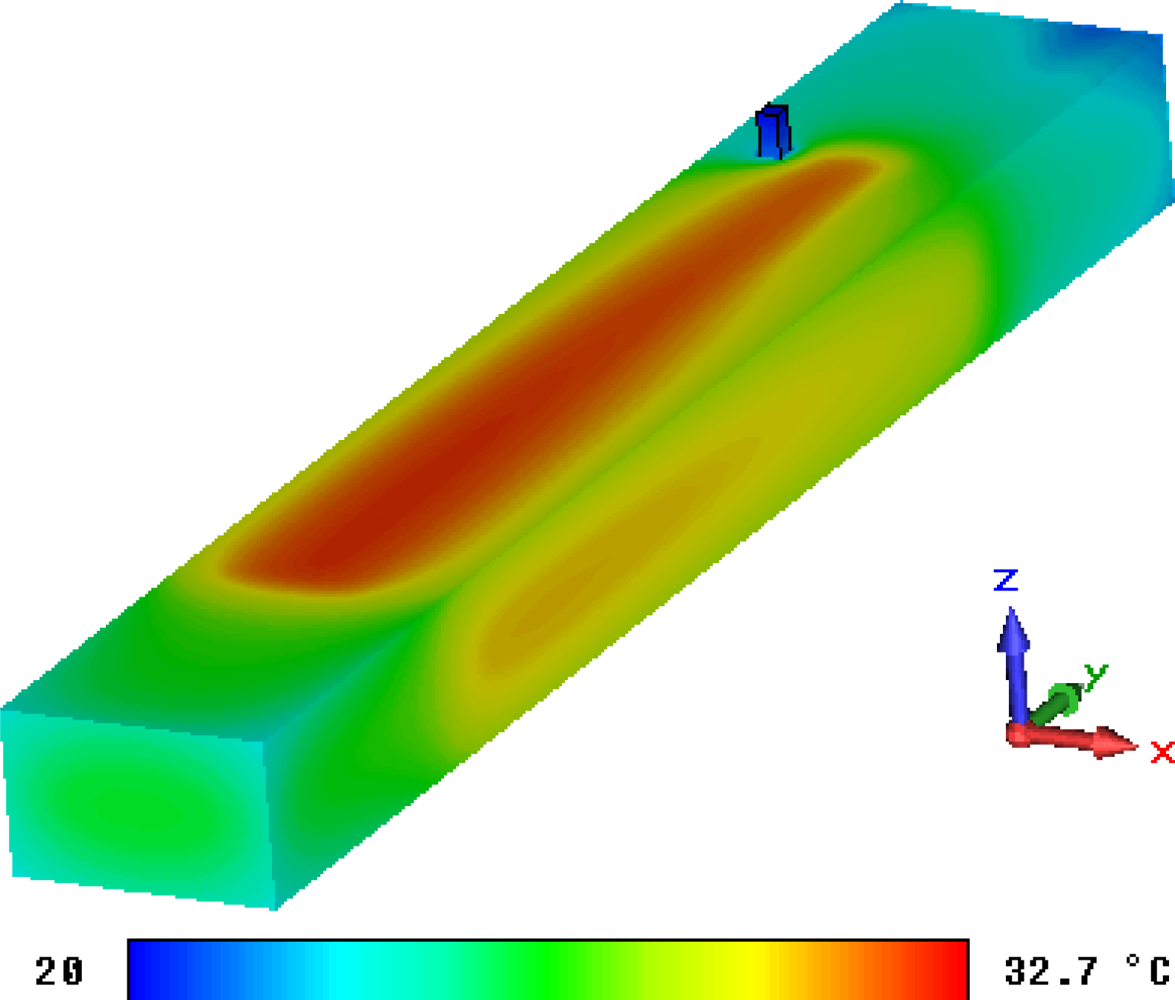
6. Thermal Calculation
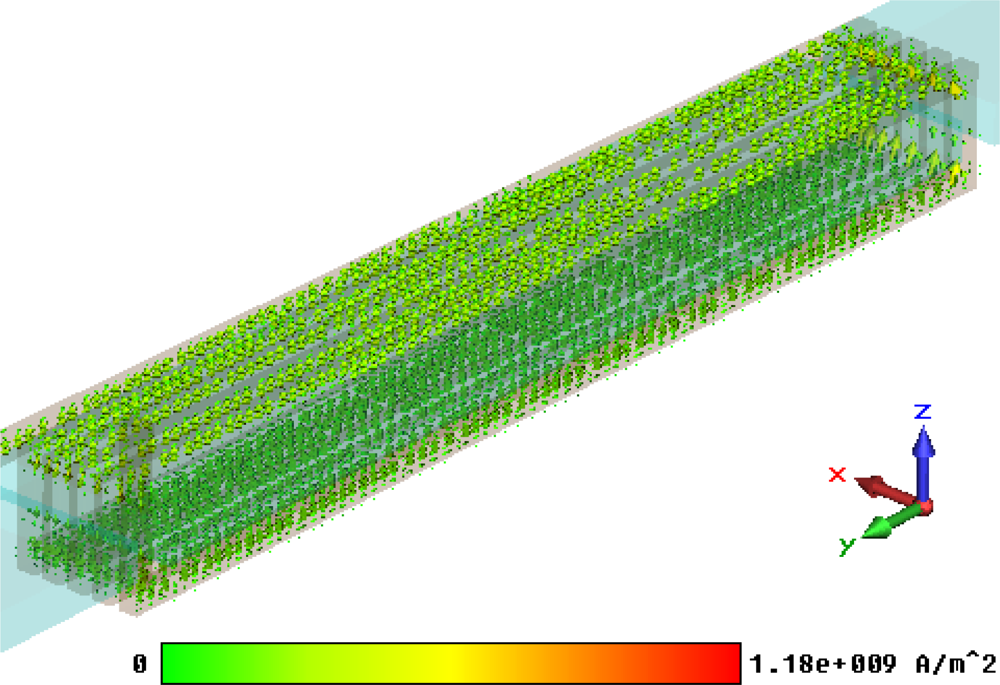
6.1. Steady current calculation results
6.2. Thermal calculation results
7. Conclusions and Outlook
Acknowledgments
References
- Tschulena, GR. Sensoren und ihre Anwendungsmöglichkeiten. Elektrotechnische Z 1986, 107, 215–217. [Google Scholar]
- Erb, O; Hinz, G; Preusse, N. PLCD, a novel magnetic displacement sensor. Sens. Actuator 1991, 26, 277–282. [Google Scholar]
- Eicher, D; Schlaak, HF. Elektrothermische Aktoren aus SU-8 für den Einsatz in miniaturisierten Schrittantrieben. Proceedings of the Mikrosystemtechnik-Kongress 2007, Dresden, Germany, 15–17 October 2007; pp. 195–198.
- Jungnickel, U; Eicher, D; Schlaak, HF. Novel micro-positioning system using parallel kinematics and inchworm actuator platform. Proceedings Actuator 2004, Bremen, Germany, 14–16 June 2004; pp. 14–16.
- Jungnickel, U; Eicher, D; Schlaak, HF. Miniaturised Micro-Positioning System for Large Displacements and Large Forces Based on an Inchworm Platform. Proceedings Actuator 2002, Bremen, Germany, 10–12 June 2002; pp. 684–687.
- Weiland, T. A discretization method for the solution of Maxwell’s equations for six-component fields. Arch. Elektron. Uebertragungstechnik 1977, 31, 116–120. [Google Scholar]
- Clemens, M; Weiland, T. Transient eddy current calculation with the FI-Method. IEEE Trans. Magn 1999, 35, 1163–1166. [Google Scholar]
- CST AG, Darmstadt, Germany. Available online: www.cst.com (accessed on 8 September 2010).
- VACUUMSCHMELZE GmbH & Co. KG, Hanau, Germany. Available online: www.vacuumschmelze.com (accessed on 8 September 2010).






| Element | Material | Permittivity | Conductivity S/m | Thermal conductivity W/m·K | Heat capacity J/g·K | Density Kg/m3 |
|---|---|---|---|---|---|---|
| Coils | Copper | 1 | 5.8 · 107 | 401 | 0.385 | 8,960 |
| Substrate | Silicon | 11.9 | 1.56 · 10−3 | 148 | 0.703 | 2,329 |
| Insulator | SU-8 | 3 | 1 · 10−10 | 0.25 | 1.3 | 1,200 |
| Magnet | NdFeB | 1 | 7.14 · 105 | 18 | 0.45 | 8,700 |
| Core | MUMETALL® | 1 | 1.82 · 106 | 18 | 0.45 | 8,700 |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, J.; Müller, W.F.O.; Greiner, F.; Eicher, D.; Weiland, T.; Schlaak, H.F. Combined Simulation of a Micro Permanent Magnetic Linear Contactless Displacement Sensor. Sensors 2010, 10, 8424-8436. https://doi.org/10.3390/s100908424
Gao J, Müller WFO, Greiner F, Eicher D, Weiland T, Schlaak HF. Combined Simulation of a Micro Permanent Magnetic Linear Contactless Displacement Sensor. Sensors. 2010; 10(9):8424-8436. https://doi.org/10.3390/s100908424
Chicago/Turabian StyleGao, Jing, Wolfgang F.O. Müller, Felix Greiner, Dirk Eicher, Thomas Weiland, and Helmut F. Schlaak. 2010. "Combined Simulation of a Micro Permanent Magnetic Linear Contactless Displacement Sensor" Sensors 10, no. 9: 8424-8436. https://doi.org/10.3390/s100908424