This paper was written as a continuation of [1]. In [1], there were two things left for further analysis. The first one was to test the piezoresistive accelerometer under test for the case in which the excitation acceleration had multiple frequency components; and the second one was to try to improve the convergence rate of the optimal adaptive filter by using another filter of the same family of LMS filters.

Testing the accelerometer for a multi-frequency acceleration excitation is very important because car manufacturers should know the dynamic response of the sensor systems they have embedded in the cars. Each specific application requires its specific kind of accelerometer. Some examples of applications are low frequency monitoring, vibration sensing, motion analysis, tilt, safety crash testing, shock testing, off-road testing, road testing, and so on.

Car manufactures should know the disturbance rejection of the sensor systems embedded in cars and how they respond to multi-frequency excitations, distinguishing two or more very close relevant signals from noise and/or interferences, because in real-life driving conditions we do not know the exact value of the frequency of interest, and the characteristics of disturbances and noise signals either.

So, if designers use fixed filters (i.e., Butterworth, Chebyshev, Bessel, etc.), which is what currently happens, they are bound to let noise pass through the sensor systems. Therefore, in today’s cars, in order to diminish this problem, designers use several parallel systems and auxiliary electronic circuits, which makes the system expensive, so that the filtering problem does not rely completely on only one filter.

Solving the above mentioned filtering problem can save lives in car accidents, because accelerometer are widely used in the airbag deployment system, in the anti-lock breaking system and in the active suspension system, among others.

Also, improving the convergence rate of the sensor systems embedded in cars, when filtering noise and interferences, is of paramount importance for drivers and passengers, because it means that such systems can respond very fast to unpredictable situations when driving under very difficult conditions that can cost human lives.

In the scientific literature on instrumentation and signal treatment for sensors, several research works on the application of classical and advanced filtering techniques aimed at improving the performance of sensor systems have been reported [1,2]. Authors have used robust algorithms [3,4], classical filters [5,6] and classical signal conditioning techniques [7,8].

Here, as in the first part of this research work [1], easy and inexpensive adaptive filtering techniques [9,10] have been used to improve the performance of the piezoresistive accelerometer 1201F of the manufacturer Measurement Specialties. The characteristics of the accelerometer were already mentioned in [1] and more general information about accelerometers can be found in [7,8,11].

This part of the research work was aimed at testing the above accelerometer for a multi-frequency acceleration excitation by using both the same LMS algorithm as in [1] and a fast LMS algorithm. Finally, based on the experimental results, a decision was made about what algorithm was best for solving the problem at hand.

The problem was to estimate a signal buried in a broad-band noise background, where we had little information of the signal and noise characteristics. Also, the relevant signal was a multi-frequency acceleration excitation and the noise reduction was treated as an unknown signal estimation problem, a condition that justified the fact that the use of fixed filters was discarded.

Therefore, in order to satisfactorily solve the previously outlined problem, it should be pointed out that the chosen adaptive filter should fulfil the following design requirements [10]:

It should not have a high computational burden.

However, as we demand more requirements, the designed filter has to be more complex. This fact led us to make a trade-off between the attributes that the filter should have and the final performance requirements.

According to the above statements, both the conventional and the fast LMS adaptive filters were chosen to carry out the filtering process in this research. The use of the LMS adaptive filter seemed to be one of the best solutions because of its robustness (its model-independent property) [9,10].

Also, due to its low round-off errors, stability characteristics and easy implementation, the LMS adaptive filter is well suited in applications where we have to design systems for continuous operation without any human intervention.

This filter was satisfactorily used in the first part of this research [1]. However, in order to improve the convergence rate and the signal-to-noise ratio (SNR) for a better performance of the accelerometer when placed in cars, it was necessary to test a fast LMS adaptive filter, which performs the adaptation of the filter parameters in the frequency domain.

In accordance with [10], there are two main reasons for seeking adaptation in the frequency domain:

Frequency-domain adaptive filters can deal with the requirement of long memory satisfactorily providing good solutions to the computational complexity problem.

Basically, the structure of the fast LMS adaptive filter is the one of a block-adaptive filter. The input signal is divided into several blocks of the same length by using a serial-to-parallel converter, and the resulting blocks of this conversion are filtered by a finite impulse response (FIR) filter, one block of data samples at a time. The adaptive process begins and continue on a block-by-block basis. In fact, the filter parameters are adapted in the frequency domain by using the fast Fourier transform (FFT) algorithm [12–15].

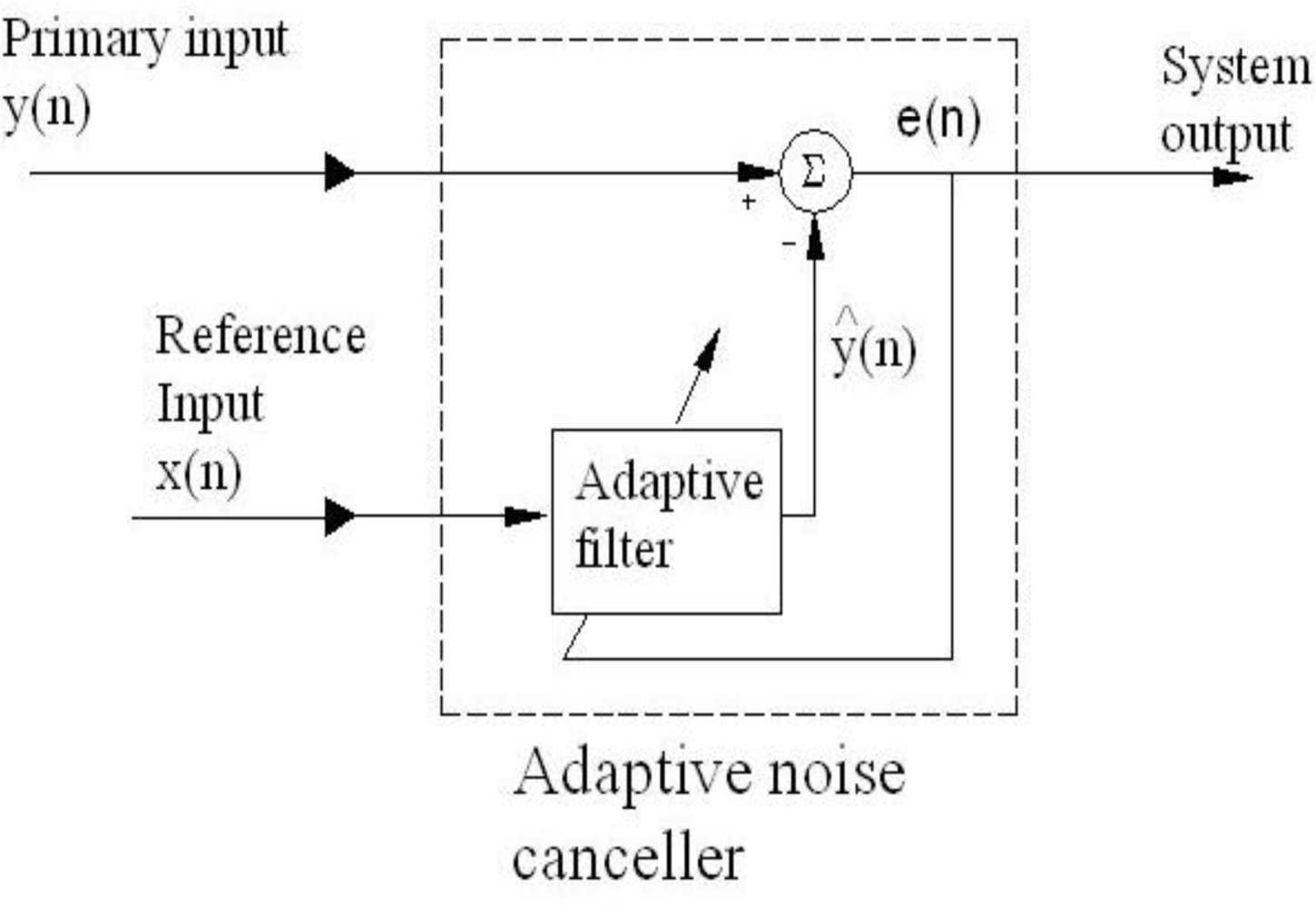
According to Haykin [10], it is known that the overlap-save method and the overlap-add method provide two efficient procedures for fast convolution – that is, the computation of linear convolution using the DFT. In this paper the fast LMS algorithm based on overlap-save sectioning (assuming real-valued data) [16] was used in an adaptive noise canceller (ANC) device [9,10]. Figure 1 shows the schematic diagram of such a device and a summary of this algorithm is given next.

A summary of the fast LMS adaptive filter. From Shynk [16] and Haykin [10]

Initialisation:

Ŵ(0) = 2M-by-1 null vector, where Ŵ is the frequency-domain tap-weight vector of the FIR filter for the kth block of input data and M is the length of the FIR filter.

Notations:

0 = M-by-1 null vector

Computation: For each new block of M input samples, compute

U(k) = diag{FFT[u(kM − M),..., u(kM − 1), u(kM),...,u(kM + M − 1)]^T}

As in [1], in the experiment, the accelerometer 1201F-1000-10-240X (Model 1201F, 1,000 g Full Scale Range, 10 VDC excitation, 240 inches cable, and no options), was tested under laboratory conditions by using the CS18 TF calibration system (SPEKTRA). This system can carry out calibrations of sensors with/without amplifiers in the frequency range 3 Hz to 5 kHz, with a repeatability of the calibration under identical conditions up to 5 kHz better than 0.5%. Here, the accelerometer 1201F-1000-10-240X was tested with a multi-frequency acceleration excitation of maximum amplitude 2 g and frequency components 200 Hz, 500 Hz and 1 kHz. The National Instruments Data Acquisition Card NI DAQCard-6062E was used for the laboratory experiments. In addition, for the multi-frequency acceleration excitation experiment the sampling frequency was 100 kHz. Figure 2 shows the National Instruments 68-pin shielded desktop connector block (NI SCB-68) DAQ device used in the laboratory experiment, Figure 3 shows the vibration exciter and Figure 4 shows the overall experimental setup.

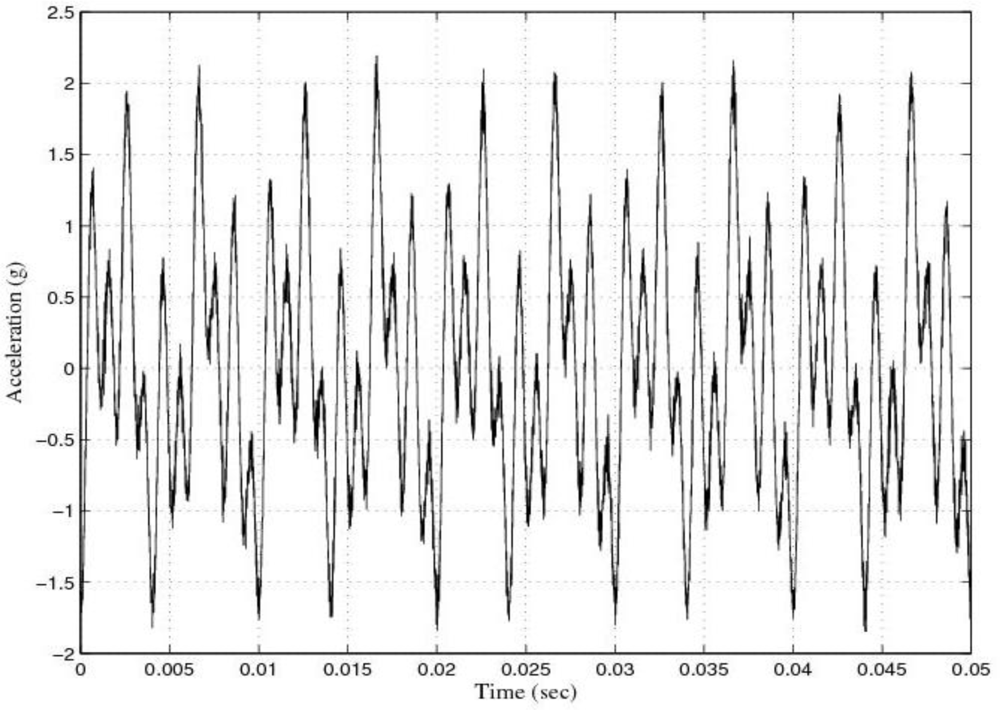
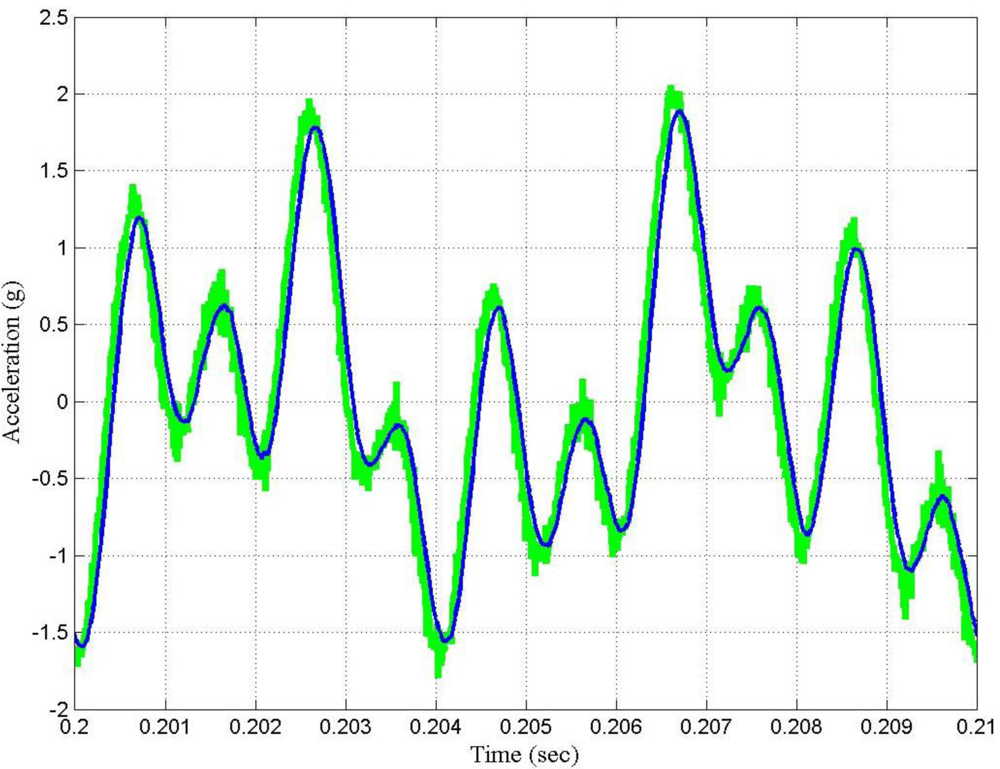
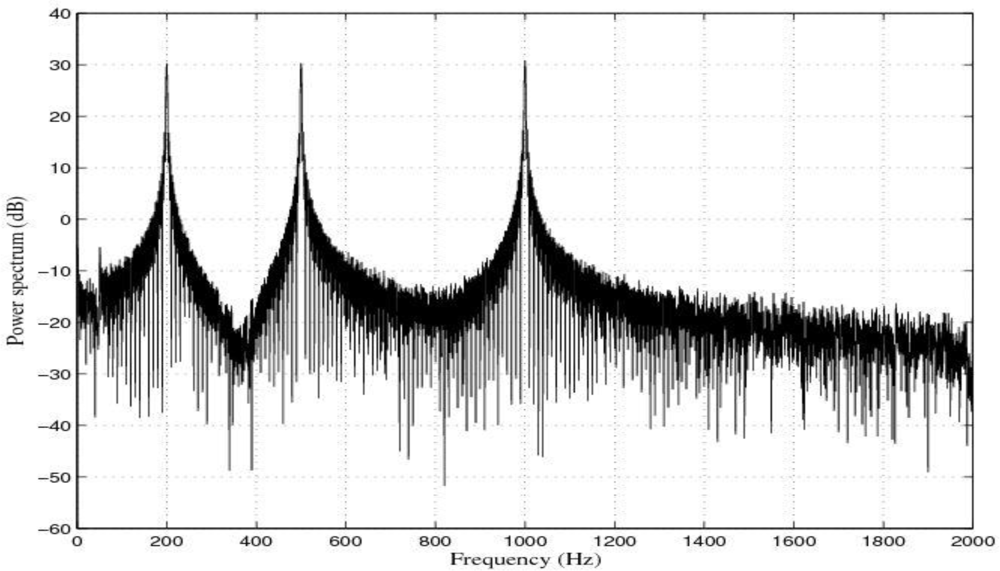
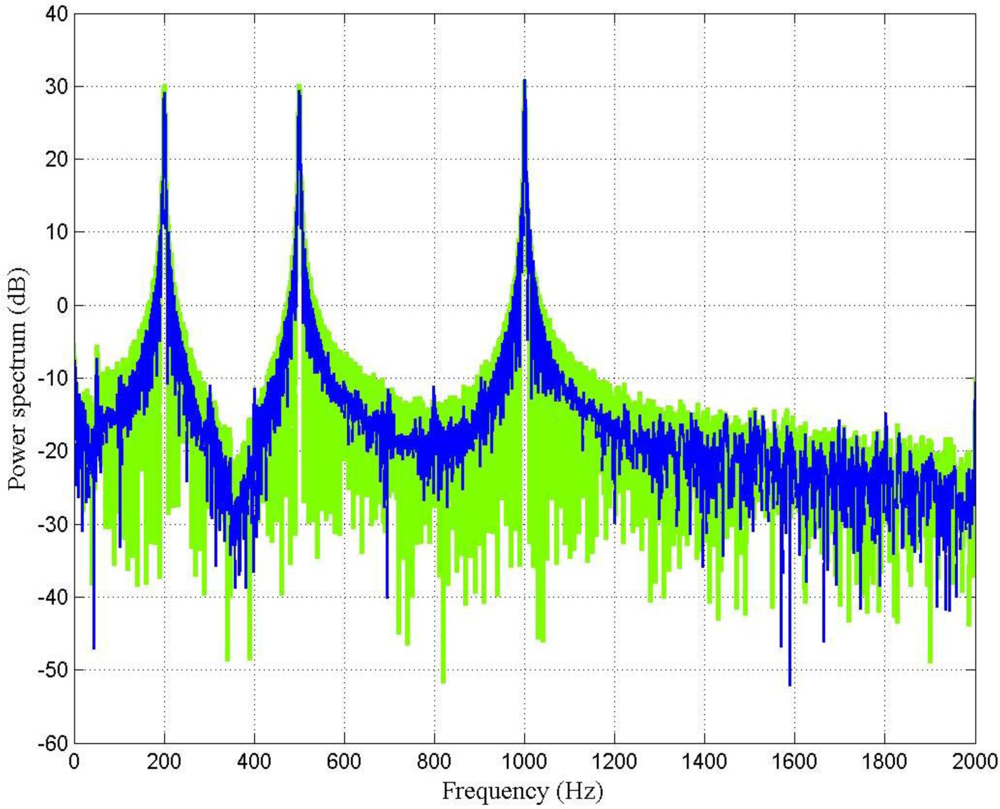
The response of the sensor before filtering for the experimental tests at 50 Hz, 100 Hz, 200 Hz, 500 Hz and 1 kHz was shown in [1]. Also in [1] the filtering process for the above tests was carried out by using 4-order band-pass digital Butterworth filters and a LMS adaptive filter. Figure 5 shows the response of the sensor for the multi-frequency acceleration excitation and Figure 6 shows the power spectrum of such a signal.

As in [1], the parameters of the LMS adaptive filter were the following: a tap-weight vector of length M equal to 100, and a step-size parameter μ equal to 1 over the maximum value of the power of the tap-input vector x(n) [10].

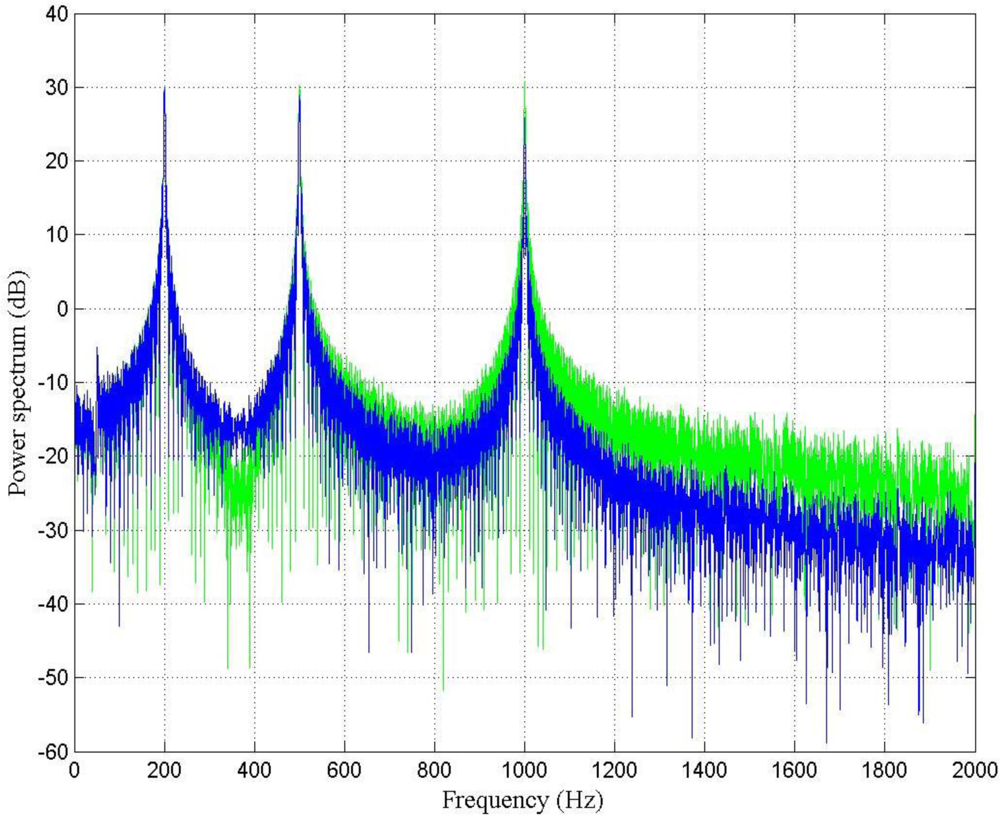
Figure 7 shows the power spectrum of the output signal before and after filtering by using the LMS adaptive filter. It is important to point out that at 200 Hz the LMS adaptive filter does not perform very well; however, the higher the frequency, the better the SNR.

Figure 8 shows the time waveform of the output signal before filtering and after filtering by using the LMS adaptive filter. From Figures 7 and 8, it can be said that in general the performance of the LMS adaptive filter was satisfactory.

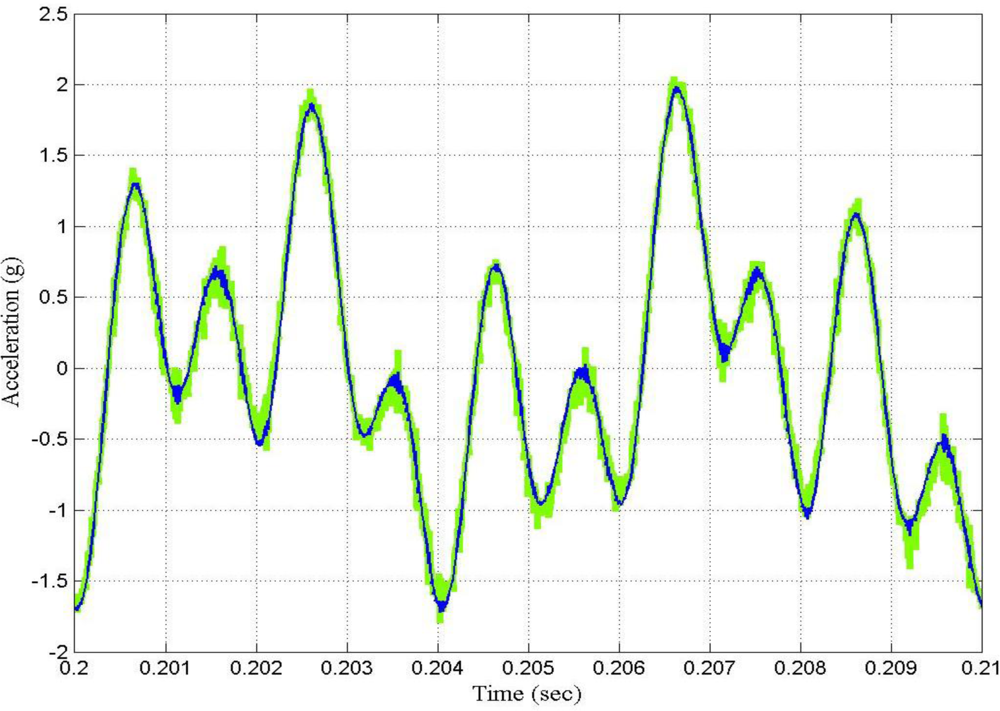
Figure 9 shows the power spectrum of the output signal before and after filtering by using the fast LMS adaptive filter with the following parameters: M = 100, α = 0.1, δ_i = 0.1, and γ = 0.999. From this figure it can be seen that the performance of the filter was satisfactory at every frequency of analysis.

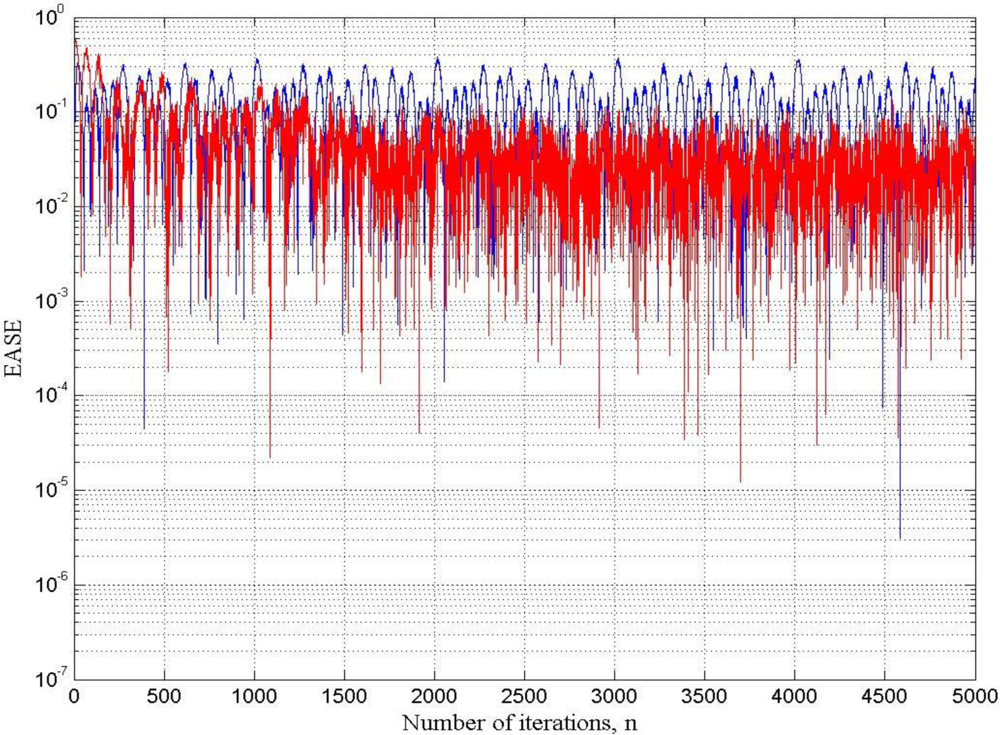
Figure 10 shows the time waveform of the output signal before filtering and after filtering by using the fast LMS adaptive filter, and Figure 11 shows the learning curves of both the conventional and the fast LMS adaptive filter.

From Figures 7, 9 and 11, it can be seen that the performance of the fast LMS adaptive filter was better than one of the conventional LMS adaptive filter. For the case under test, the conventional LMS adaptive filter behaved worst, it exhibited the worst SNR and the slowest rate of convergence.

In this paper, a real-life filtering problem of multi-frequency acceleration excitation to test an accelerometer for automotive applications has been solved by using both a conventional and a fast LMS adaptive filter. The results of the experiment were satisfactory for both filters and it has been shown that the best option to carry out the filtering problem discussed in this paper was to use the fast LMS adaptive filter.