Interaction between Dipolar Lipid Headgroups and Charged Nanoparticles Mediated by Water Dipoles and Ions
Abstract
:1. Introduction
2. Interaction between Lipid Headgroups and Charged Nanoparticle
2.1. Space Dependence of Relative Permittivity within the Modified Langevin-Poisson-Boltzmann (MLPB) Model
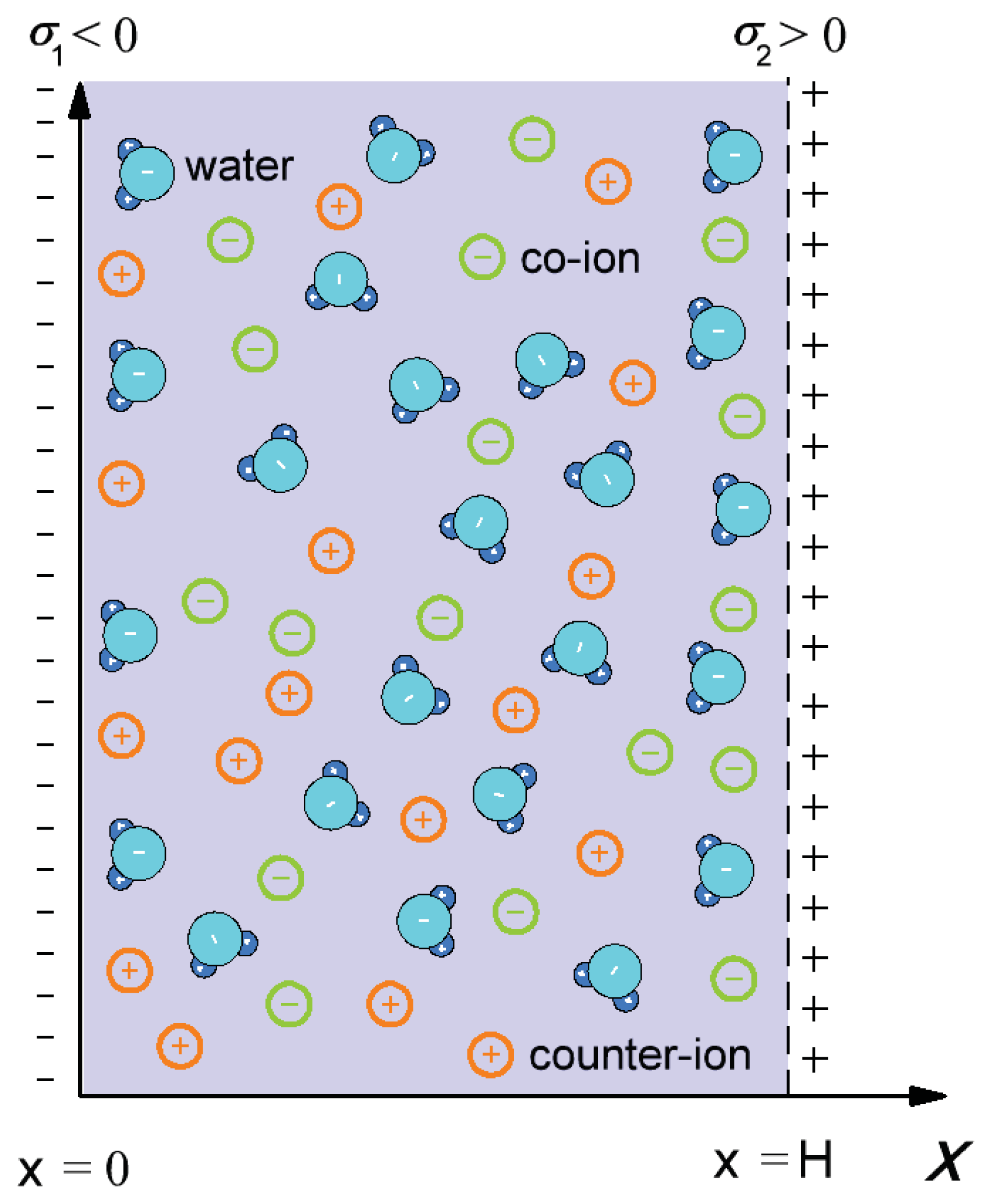
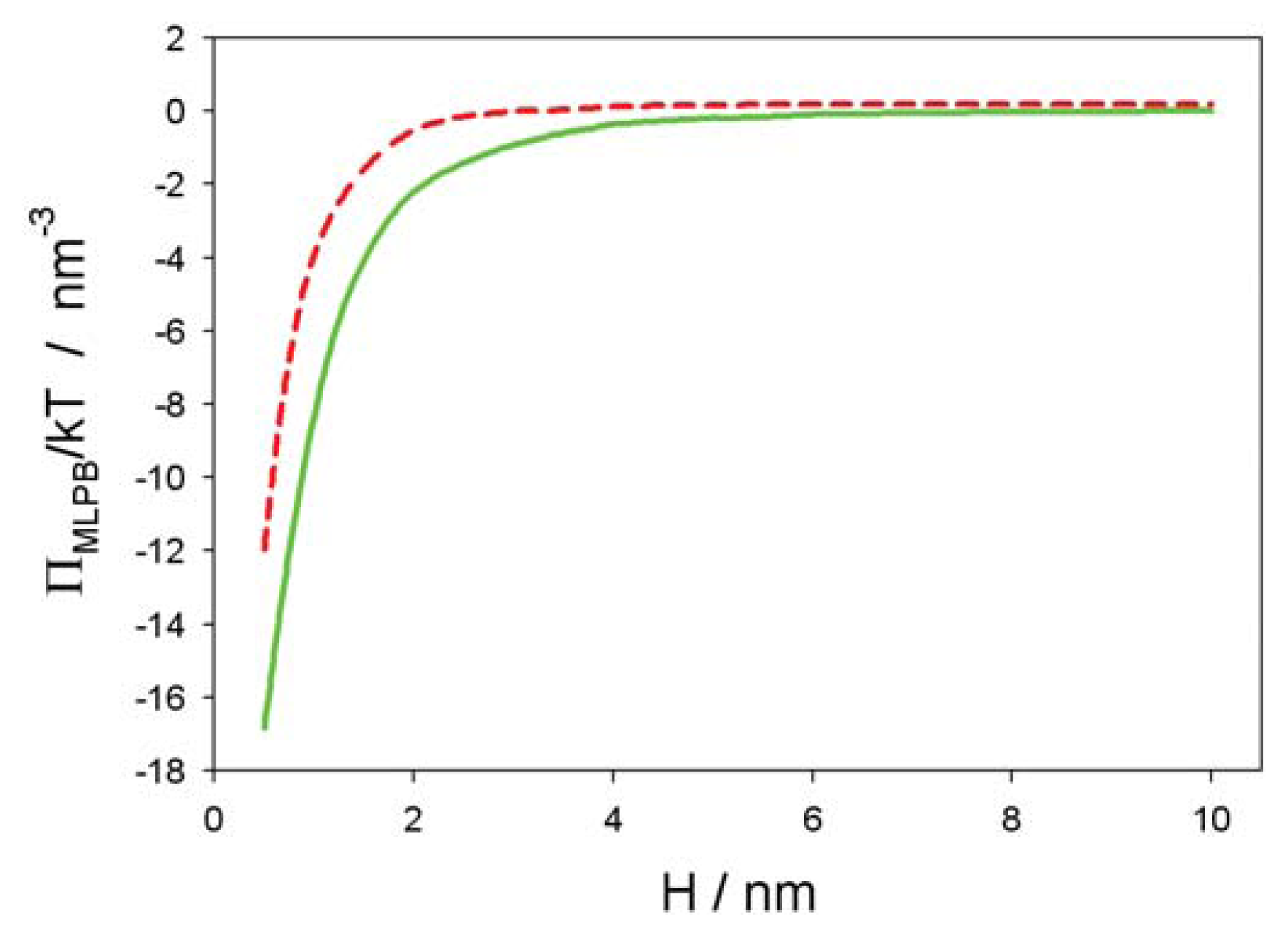
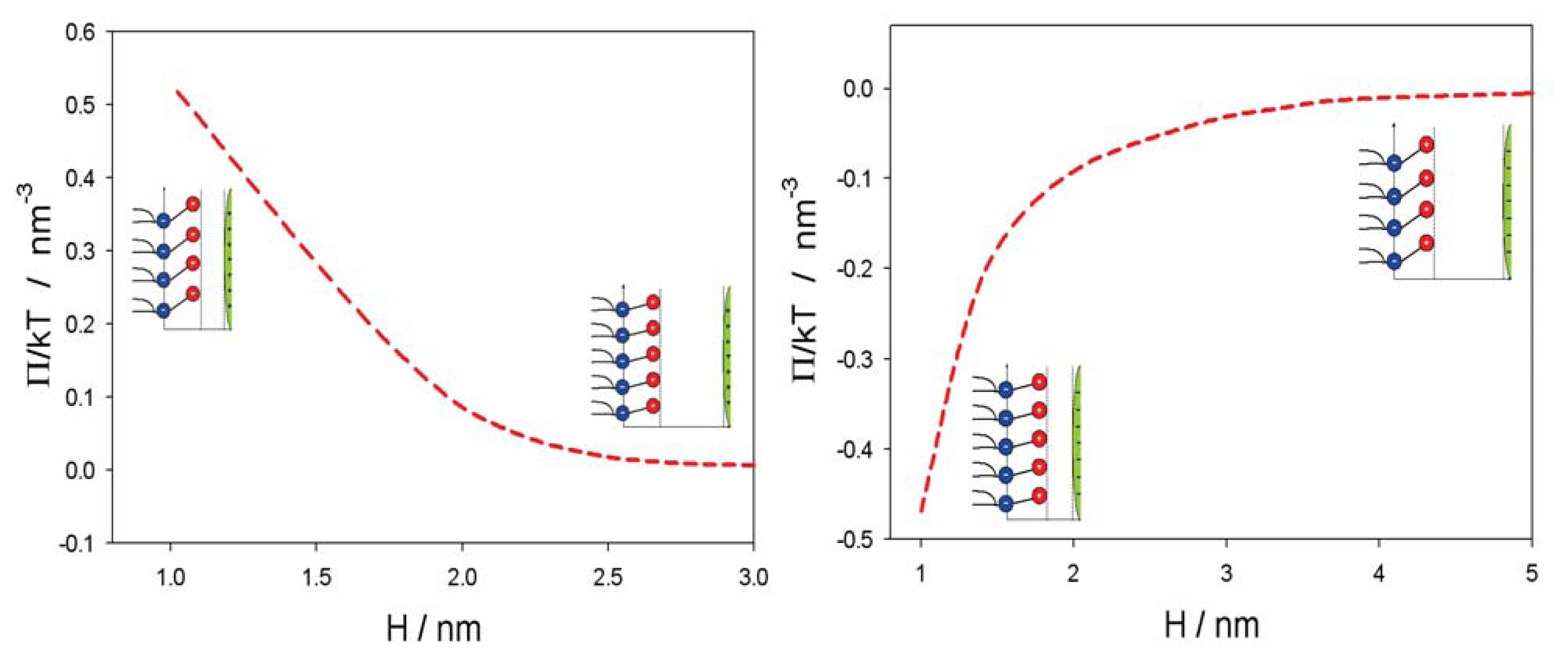
2.2. Osmotic Pressure between Two Planar Charged Surfaces
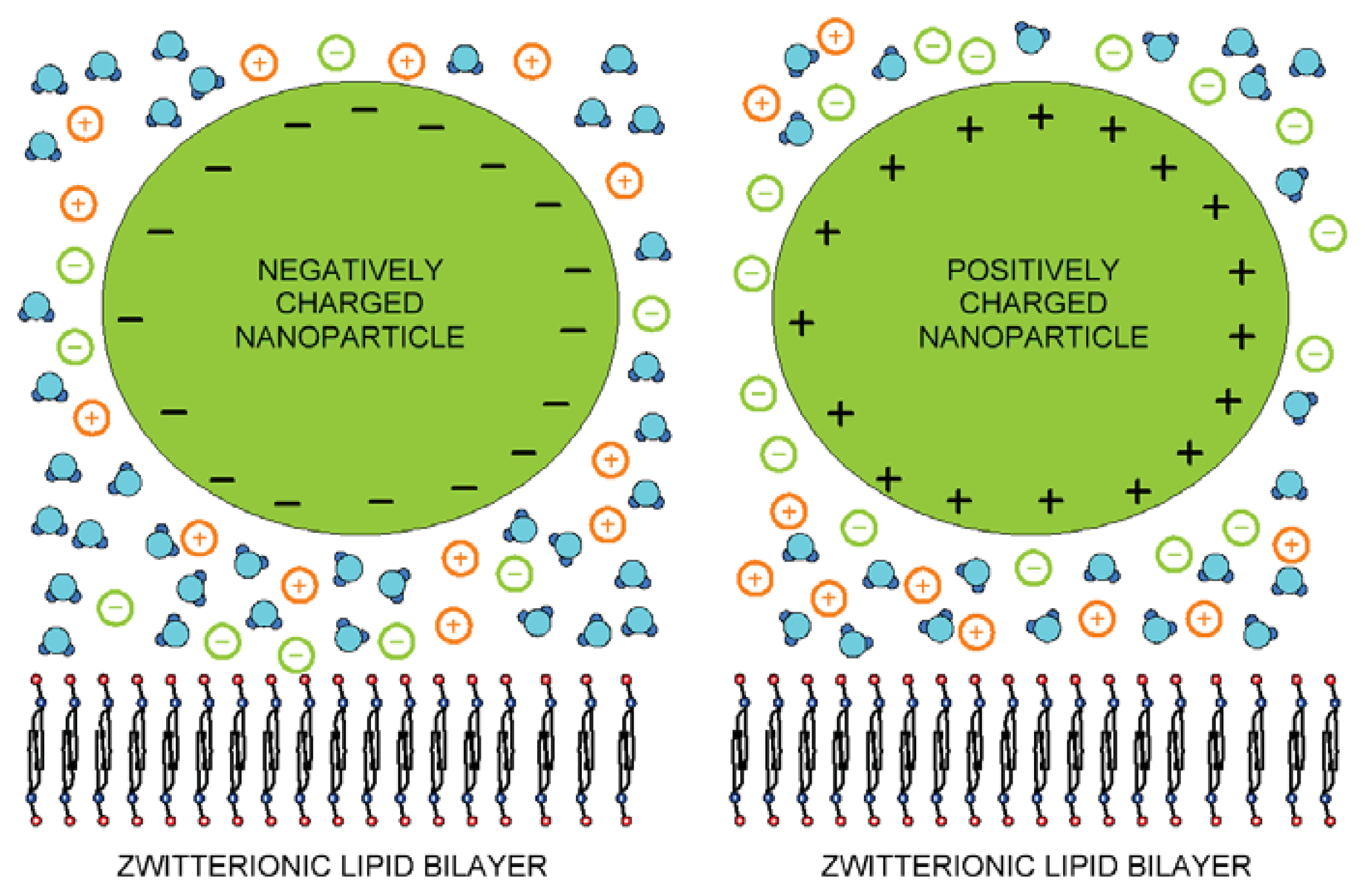
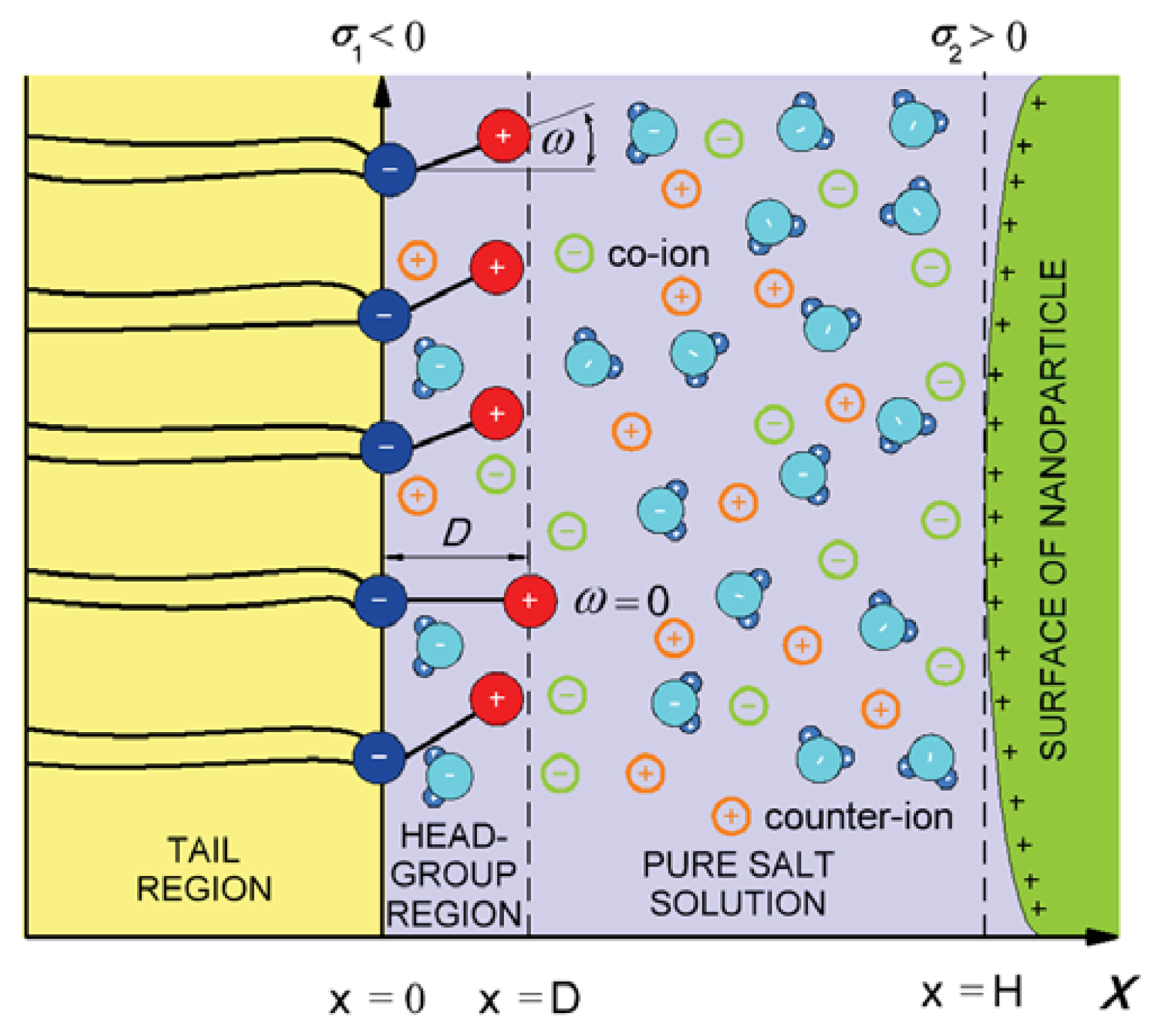
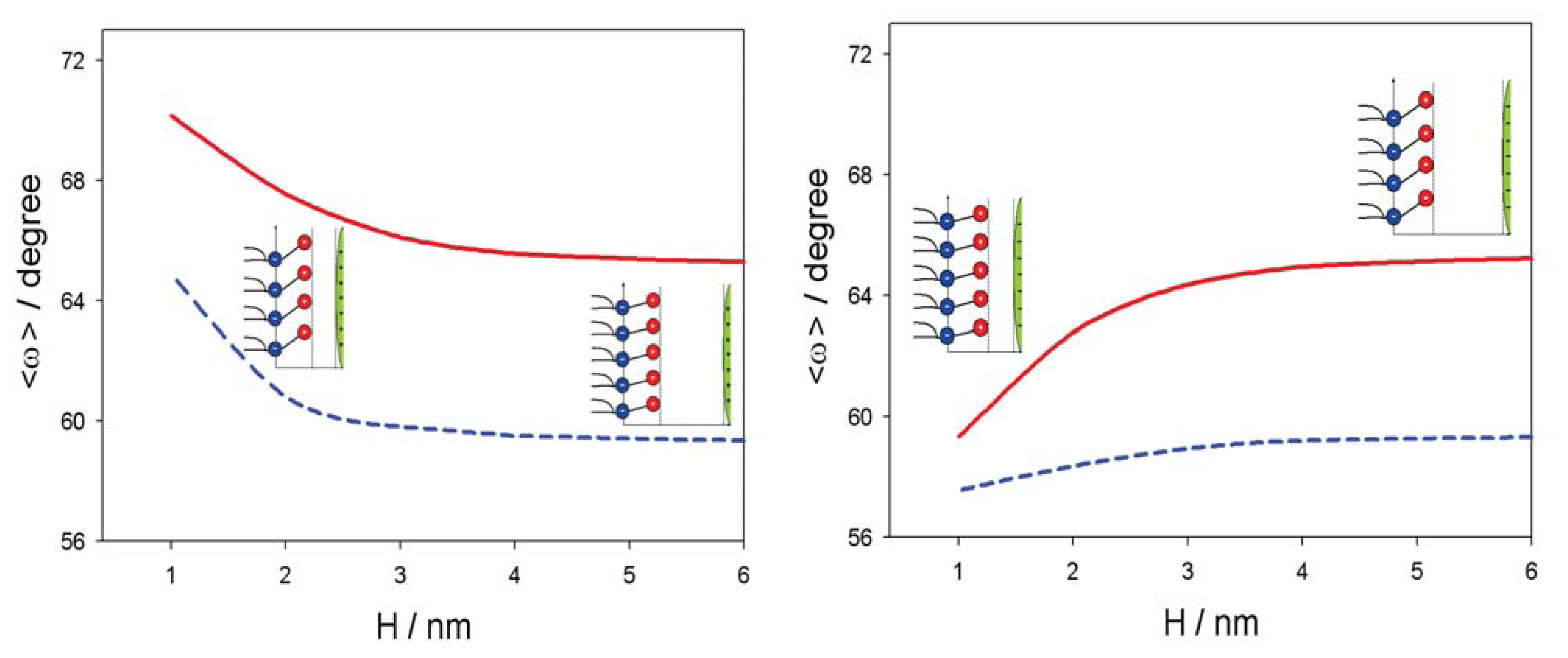
3. Interaction between Dipolar Zwitterionic Lipid Headgroups and Charged Nanoparticle
4. Experimental Results
4.1. Synthesis of Nanoparticles
4.2. Preparation of Liposome—Nanoparticle Conjugates
4.3. Fluorescence Anisotropy Measurements: Anisotropy and Fluidity
4.4. Influence of Nanoparticle-Membrane Interactions on Membrane Fluidity
5. Conclusions
Acknowledgments
Appendix
A. Derivation of Osmotic Pressure by Integration of the MLPB Equation
Conflict of Interest
References
- Sackmann, E. Biological Membranes Architecture and Function. In Structure and Dynamics of Membranes; Lipowsky, R., Sackmann, E., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; pp. 1–63. [Google Scholar]
- Rappolt, M.; Pabst, G. Flexibility and Struture of Fluid Bilyer Interfaces. In Structure and Dynamics of Membranous Interfaces; Nag, K., Ed.; John Wiley and Sons, Inc: Hoboken, NJ, USA, 2008; pp. 45–81. [Google Scholar]
- Yaghmur, A.; Rappolt, M. Structural characterization of lipidic systems under nonequilibrium conditions. Eur. Biophys. J 2012, 41, 831–840. [Google Scholar]
- Tien, H.T.; Ottova-Leitmannova, A. The Lipid Bilayer Concept: Experimental Realization and Current Application. In Planar Lipid Bilayers (BLMs) And Their Application; Tien, H.T., Ottova-Leitmannova, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; pp. 1–73. [Google Scholar]
- Luckey, M. Membrane Structural Biology, 1st ed; Cambridge University Press: New York, NY, USA, 2008; pp. 1–67. [Google Scholar]
- Bagatolli, L.A.; Ipsen, J.H.; Simonsen, A.C.; Mouritsen, O.G. An outlook on organization of lipids in membranes: Searching for a realistic connection with the organization of biological membranes. Prog. Lip. Res 2010, 49, 378–389. [Google Scholar]
- Rappolt, M.; Laggner, P.; Pabst, G. Structure and elasticity of phospholipid bilayers in the Lalpha phase: A comparison of phosphatidylcholine and phosphatidylethanolamine membranes. In Recent Research Developments in Biophysics, Part II; Pandalai, S.G., Ed.; Trivandrum - Transworld Research Network: Kerala, India, 2004; Volume 3, pp. 363–392. [Google Scholar]
- Cevc, G. Phospholipid Handbook, 1st ed; Marcel Dekker: New York, NY, USA; p. 1993.
- Bivas, I. Electrostatic and mechanical properties of a flat lipid bilayer containing ionic lipids. Coll. Surf. A 2006, 282–283, 423–434. [Google Scholar]
- Boulbitch, A.A. Deflection of a cell membrane under application of a local force. Phys. Rev. E 1998, 75, 2123–2128. [Google Scholar]
- Kulkarni, C.V. Lipid crystallization: From self-assembly to hierarchical and biological ordering. Nanoscale 2012, 4, 5779–5791. [Google Scholar]
- Hianik, T.; Passechnik, V.I. Bilayer Lipid Membranes: Structure and Mechanical Properties; Kluwer Academic Publishers: London, UK; p. 1995.
- McLaughlin, S. The Electrostatic properties of membranes. Ann. Rev. Biophys. Chem 1989, 18, 113–136. [Google Scholar]
- Cevc, G. Memrane electrostatics. Biochim. Biophys. Acta 1990, 1031, 311–382. [Google Scholar]
- Šuštar, V.; Bedina Zavec, A.; Štukelj, R.; Frank, M.; Bobojevič, G.; Janša, R.; Ogorevc, E.; Kruljc, P.; Mam, K.; Šimunič, B.; et al. Nanoparticles isolated from blood: A reflection of vesiculability of blood cells during the isolation process. Int. J. Nanomed 2011, 6, 2737–2748. [Google Scholar]
- Kralj-Iglič, V. Stability of membranous nanostructures: A possible key mechanism in cancer progression. Int. J. Nanomed 2012, 7, 3579–3596. [Google Scholar]
- Shlomovitz, R.; Gov, N.S. Pysical model of contractile ring initiation in dividing cells. Biophys. J 2008, 94, 1155–1168. [Google Scholar]
- Gouy, M.G. Sur la constitution de la charge electrique a la surface d’un electrolyte. J. Phys 1910, 9, 457–468. [Google Scholar]
- Chapman, D.L. A Contribution to the theory of electrocapillarity. Philos. Mag 1913, 25, 475–481. [Google Scholar]
- Kralj-Iglič, V.; Iglič, A. A simple statistical mechanical approach to the free energy of the electric double layer including the excluded volume effect. J. Phys. II 1996, 6, 477–491. [Google Scholar]
- Lamperski, S.; Outhwaite, C.W. Exclusion volume term in the inhomogeneous poisson-boltzmann theory for high surface charge. Langmuir 2002, 18, 3423–3424. [Google Scholar]
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces, 2nd ed; Wiley-VCH Verlag: Weinheim, Germany; p. 2003.
- Bazant, M.Z.; Kilic, M.S.; Storey, B.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solution. Adv. Colloid Interface Sci 2009, 152, 48–88. [Google Scholar]
- Gongadze, E.; Van Rienen, U.; Iglič, A. Generalized Stern models of an electric double layer considering the spatial variation of permittivity and finite size of ions in saturation regime. Cell. Mol. Biol. Lett 2011, 16, 576–594. [Google Scholar]
- Gongadze, E.; Van Rienen, U.; Kralj-Iglič, V.; Iglič, A. Spatial variation of permittivity of an electrolyte solution in contact with a charged metal surface: A mini review. Comput. Meth. Biomech. Biomed. Eng 2013, 16, 463–480. [Google Scholar]
- Velikonja, A.; Perutkova, Š.; Gongadze, E.; Kramar, P.; Polak, A.; Maček-Lebar, A.; Iglič, A. Monovalent ions and water dipoles in contact with dipolar zwitterionic lipid headroups theory and MD simulations. Int. J. Mol. Sci. 2013, 14, 2846–2861. [Google Scholar]
- Outhwaite, C.W. A treatment of solvent effects in the potential theory of electrolyte solutions. Mol. Phys 1976, 31, 1345–1357. [Google Scholar]
- Outhwaite, C.W. Towards a mean electrostatic potential treatment of an ion-dipole mixture or a dipolar system next to a plane wall. Mol. Phys 1983, 48, 599–614. [Google Scholar]
- Iglič, A.; Gongadze, E.; Bohinc, K. Excluded volume effect and orientational ordering near charged surface in solution of ions and Langevin dipoles. Bioelectrochemistry 2010, 79, 223–227. [Google Scholar]
- Gongadze, E.; Van Rienen, U.; Kralj-Iglič, V.; Iglič, A. Langevin Poisson-Boltzmannn equation: point-like ions and water dipoles near a charged surface. Gen. Physiol. Biophys 2011, 30, 130–137. [Google Scholar]
- Gongadze, E.; Iglič, A. Decrease of permittivity of an electrolyte solution near a charged surface due to saturation and excluded volume effects. Bioelectrochemistry 2012, 87, 199–203. [Google Scholar]
- Misra, R.P.; Das, S.; Mitra, S.K. Electric double layer force between charged surfaces: Effect of solvent polarization. J. Chem. Phys. 2013, 138, 114703. [Google Scholar]
- Torchilin, VP. Recent advances with liposomes as pharmaceutical carriers. Nat. Rev. Drug Discov. 2005, 4, 145–160. [Google Scholar]
- Bhandary, S.; Sultana, P.; Basu, R.; Das, S.; Nandy, P. A Study on the modulation of the phase behavior of lipid aggregates-effect of some metal nanoparticles. Adv. Sci. Eng. Med 2011, 3, 1–6. [Google Scholar]
- Roiter, Y.; Ornatska, M.; Rammohan, A.R.; Balakrishnan, J.; Heine, D.R.; Minko, S. Interaction of nanoparticles with lipid membrane. Nano Lett. 2008, 8, 941–944. [Google Scholar]
- Michel, R.; Gradzielski, M. Experimental aspect of colloidal interactions in mixed systems of liposome and inorganic nanoparticle and their applications. Int. J. Mol. Sci 2013, 13, 11610–11642. [Google Scholar]
- Zimmerberg, J.; Kozlov, M.M. How proteins produce cellular curvature. Nature Rew. Mol. Cell Biol 2006, 7, 9–19. [Google Scholar]
- Tian, A.; Baumgart, T. Sorting of lipids and proteins in membrane curvature gradients. Biophys. J 2009, 96, 2676–2688. [Google Scholar]
- Iglič, A.; Slivnik, T.; Kralj-Iglič, V. Elastic properties of biological membranes influenced by attached proteins. J. Biomech 2007, 40, 2492–2500. [Google Scholar]
- Powel, K. Ahead of the curve. Nature 2009, 460, 318–320. [Google Scholar]
- Bouma, B.; de Groot, P.G.; van den Elsen, J.M.H.; Ravelli, R.B.G.; Schouten, A.; Simmelink, J.A.; Derksen, M.J.A.; Kroon, J.; Gros, P. Adhesion mechanism of human β2-glycoprotein I to phospholipids based on its crystal structure. EMBO J 1999, 18, 5166–5174. [Google Scholar]
- Farsad, K.; De Camilli, P. Mechanisms of membrane deformation. Curr. Opin. Cell Biol 2003, 15, 372–381. [Google Scholar]
- Sorre, B.; Callan-Jones, A.; Manneville, J.B.; Nassoy, P.; Joanny, J.F.; Prost, J.; Goud, B.; Bassereau, P. Curvature-driven lipid sorting needs proximity to a demixing point and is aided by proteins. PNAS 2009, 106, 5622–5626. [Google Scholar]
- Fröhlich, H. Theory of Dielectrics, 1st ed; Clarendon Press: Oxford, UK; p. 1964.
- Booth, F. The dielectric constant of water and the saturation effect. J. Chem. Phys 1951, 19, 391–395. [Google Scholar]
- Evans, D.F.; Wennerström, H. The Colloidal Domain, 1st ed; Wiley-VCH: New York, NY, USA, 1999; pp. 223–238. [Google Scholar]
- Lee, A.G. How lipids affect the activities of integral membrane proteins. Biochim. Biophys. Acta 2004, 1666, 62–87. [Google Scholar]
- Casadei, M.A.; Manas, P.; Niven, G.; Needs, E.; Mackey, B.M. Role of membrane fluidity in pressure resistance of Escherichia coli NCTC 8164 Appl. Environ. Microbiol 2002, 68, 5965–5972. [Google Scholar]
- Gandhi, S.; Venkatesh, S.; Sharma, U.; Jagannathan, N.R.; Sethuramana, S.; Krishnan, U.M. Superparamagnetic nanosystems based on iron oxide nanoparticles & mesoporous silica: Synthesis & evaluation of their magnetic, relaxometric and biocompatability properties. J. Mater. Chem. 2011, 21, 15698. [Google Scholar]
- Wanten, G.J.; Naber, A.H. Human neutrophil membrane fluidity after exposure to structurally different lipid emulsions. JPEN J. Parenter. Enteral. Nutr 2001, 25, 352–355. [Google Scholar]
- Aricha, B.; Fishov, V.; Cohen, V.; Sikron, N.; Pesakhov, S.; Khozin-Goldberg, I.; Dagan, R.; Porat, N. Differences in membrane fluidity and fatty acid composition between phenotypic variants of streptococcus pneumoniae. J. Bacteriol. 2004, 186, 4638–4644. [Google Scholar]
- Gmajner, V.; Ota, A.; Šentjurc, M.; Poklar Ulrih, N. Stability of diether C25,25 liposomes from the hyperthermophilic archaeon Aeropyrum pernix K1. Chem. Phys. Lipids 2011, 164, 236–245. [Google Scholar]
- Pottel, H.; van der Meer, V.; Herreman, W. Correlation between the order parameter and the steady-state fluorescence anisotropy of 1,6-diphenyl-1,3,5-hexatriene and an evaluation of membrane fluidity. Biochim. Biophys. Acta 1983, 730, 181–186. [Google Scholar]
- Poklar Ulrih, N.; Gmajner, D.; Raspor, P. Structural and physicochemical properties of polar lipids from thermophilic archaea. Appl. Microbiol. Biotechnol 2009, 84, 249–260. [Google Scholar]
- Marczak, A. Fluorescence anisotropy of membrane fluidity probes in human erythrocytes incubated with anthracyclines and glutaraldehyde. Bioelectrochemistry 2009, 74, 236–239. [Google Scholar]
- Wrobel, D.; Kłys, A.; Ionov, M.; Vitovic, P.; Waczulikowa, I.; Hianik, T.; Gomez-Ramirez, R.; de la Mata, J.; Klajnert, B.; Bryszewska, M. Cationic carbosilane dendrimers-lipid membrane interactions. Chem. Phys. Lipids 2012, 165, 401–407. [Google Scholar]
- Michel, R.; Gradzielski, M. Experimental aspects of colloidal interactions in mixed systems of liposome and inorganic nanoparticle and their applications. Int. J. Mol. Sci 2012, 13, 11610–11642. [Google Scholar]
- Eleršič, K.; Pavlič, J.I.; Iglič, A.; Vesel, A.; Mozetič, M. Electric-field controlled liposome formation with embedded superparamagnetic iron oxide nanoparticles. Chem. Phys. Lipids 2012, 165, 120–124. [Google Scholar]
- Hayden, S.C.; Zhao, G.; Saha, K.; Phillips, R.L.; Li, X.; Miranda, O.R.; Rotello, V.M.; El-Sayed, M.A.; Schmidt-Krey, I.; Bunz, U.H.F. Aggregation and interaction of cationic nanoparticles on bacterial surfaces. J. Am. Chem. Soc 2012, 134, 6920–6923. [Google Scholar]
- Shlomovitz, R.; Gov, N.S. Membrane-mediated interactions drive the condensation and coalescence of FtsZ rings. Phys. Biol 2009, 6, 046017. [Google Scholar]
- Kabaso, D.; Gongadze, E.; Elter, P.; van Rienen, U.; Gimsa, J.; Kralj-Iglič, V.; Iglič, A. Attachment of rod-like (BAR) proteins and membrane shape. Mini Rev. Med. Chem 2011, 11, 272–282. [Google Scholar]
- Verma, A.; Stellacci, F. Effect of surface properties on nanoparticlecell interactions. Small 2010, 6, 12–21. [Google Scholar]
- Veksler, A.; Gov, N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J 2007, 93, 3798–3810. [Google Scholar]
- Bothun, G.D. Hydrophobic silver nanoparticles trapped in lipid bilayers: Size distribution, bilayer phase behavior, and optical properties. J. Nanobiotechnol 2008, 6, 13. [Google Scholar]
- Alexandre, H.; Mathieu, B.; Charpentier, C. Alteration in membrane fluidity and lipid composition, and modulation of H+-ATPase activity in Saccharomyces cerevisiae caused by decanoic acid. Microbiology 1996, 142, 469–475. [Google Scholar]
- Abrashkin, A.; Andelman, D.; Orland, H. Dipolar Poisson-Boltzmannn equation: Ions and dipoles close to charge interfaces. Phys. Rev. Lett 2007, 99, 077801. [Google Scholar]


© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Velikonja, A.; Santhosh, P.B.; Gongadze, E.; Kulkarni, M.; Eleršič, K.; Perutkova, Š.; Kralj-Iglič, V.; Ulrih, N.P.; Iglič, A. Interaction between Dipolar Lipid Headgroups and Charged Nanoparticles Mediated by Water Dipoles and Ions. Int. J. Mol. Sci. 2013, 14, 15312-15329. https://doi.org/10.3390/ijms140815312
Velikonja A, Santhosh PB, Gongadze E, Kulkarni M, Eleršič K, Perutkova Š, Kralj-Iglič V, Ulrih NP, Iglič A. Interaction between Dipolar Lipid Headgroups and Charged Nanoparticles Mediated by Water Dipoles and Ions. International Journal of Molecular Sciences. 2013; 14(8):15312-15329. https://doi.org/10.3390/ijms140815312
Chicago/Turabian StyleVelikonja, Aljaž, Poornima Budime Santhosh, Ekaterina Gongadze, Mukta Kulkarni, Kristina Eleršič, Šarka Perutkova, Veronika Kralj-Iglič, Nataša Poklar Ulrih, and Aleš Iglič. 2013. "Interaction between Dipolar Lipid Headgroups and Charged Nanoparticles Mediated by Water Dipoles and Ions" International Journal of Molecular Sciences 14, no. 8: 15312-15329. https://doi.org/10.3390/ijms140815312






