Dependence of Interaction Free Energy between Solutes on an External Electrostatic Field

Abstract

To explore the athermal effect of an external electrostatic field on the stabilities of protein conformations and the binding affinities of protein-protein/ligand interactions, the dependences of the polar and hydrophobic interactions on the external electrostatic field, −E^ext, were studied using molecular dynamics (MD) simulations. By decomposing E^ext into, along, and perpendicular to the direction formed by the two solutes, the effect of E^ext on the interactions between these two solutes can be estimated based on the effects from these two components. E^ext was applied along the direction of the electric dipole formed by two solutes with opposite charges. The attractive interaction free energy between these two solutes decreased for solutes treated as point charges. In contrast, the attractive interaction free energy between these two solutes increased, as observed by MD simulations, for E^ext = 40 or 60 MV/cm. E^ext was applied perpendicular to the direction of the electric dipole formed by these two solutes. The attractive interaction free energy was increased for E^ext = 100 MV/cm as a result of dielectric saturation. The force on the solutes along the direction of E^ext computed from MD simulations was greater than that estimated from a continuum solvent in which the solutes were treated as point charges. To explore the hydrophobic interactions, E^ext was applied to a water cluster containing two neutral solutes. The repulsive force between these solutes was decreased/increased for E^ext along/perpendicular to the direction of the electric dipole formed by these two solutes.

1. Introduction

Among the four fundamental interactions, the electrostatic force dominates non-covalent bond interactions between atoms in biomolecules such as proteins, DNA, and RNA. An external electrostatic field may alter the electrostatic interactions among atoms in proteins, and consequently change the stabilities of protein conformations or the binding affinities of protein-protein/ligand interactions. Changing the stability of the protein conformation may change the protein activity, and changing the binding affinities of the protein-protein/ligand interactions may change the regulation of the signal transduction network in cells or the expression of proteins. Although these effects may not cause diseases immediately, they may increase the possibility of diseases developing. Further, electromagnetic radiation is used to kill bacteria for food preservation. Potential problems have been studied [1,2] using protein experiments [3–7], cellular experiments [8–11], animal experiments [12], public health data [13], and computer simulations [14–16]. The results did not verify whether electromagnetic radiation is harmful to humans.

In most cases, the interactions in biomolecules or among biomolecules are regarded as the sum of the interactions among the atoms in the biomolecules. Understanding the interactions among atoms in biomolecules is therefore helpful in exploring problems such as the stability of protein conformations and the binding affinities of protein-protein/ligand interactions. In addition, understanding the effects of an external electrostatic field, −E^ext, on the interactions among atoms in biomolecules is helpful in exploring the effects of the external electric field on the stabilities of protein conformations or the binding affinities of protein-protein/ligand interactions. To explore the effects of E^ext on the mean force between two charged atoms in water, E^ext was decomposed into two components: one along the electric dipole formed by these two charged atoms, and the other perpendicular to this electric dipole. The effect of E^ext on the mean force between the two charged atoms in water was estimated by summing the effects on the mean force from these two components.

Most biomolecules exist in aqueous environments, and the interactions among atoms in water differ from those in vacuum. The solvent effect is significant for the stabilities of protein conformations [17–21] and the binding affinities of protein-protein/ligand interactions [22–25]. Numerous strategies have been developed for computing the solvation free energy [26–36]. By treating the charged atom as a point charge, the effect of E^ext on the interactions among charged atoms in water can be quickly estimated using Coulomb’s law. However, strategies using molecular dynamic (MD) simulations with explicit solvent models afford more accurate results.

For one or two charged atoms in a spherical water cluster, the dependence of the electric dipole of TIP3P water on the net electrostatic field at the oxygen atom of TIP3P water, and the dependence of the radial distribution function of TIP3P water on the mean force at the oxygen atom of TIP3P water, have been explored [33,37,38]. In this project, the source code of the Charmm package [39] was modified, and it was verified that it can be applied to an external electrostatic field. The external electrostatic field was applied to a simulation system containing one charged atom or two charged atoms in vacuum; the accelerations, velocities, and positions of atoms from MD simulations using the modified Charmm package were consistent with those obtained from analytical solutions (data not shown). The external electrostatic field along the x or y direction (E_X^ext, E_Y^ext) was applied to a pure water cluster, and the relation between the dipole moment of TIP3P water and the net electrostatic field at the oxygen atom of TIP3P water was consistent with the results obtained in previous works [37,38]. The external electrostatic field along the x or y direction (E_X^ext, E_Y^ext) was applied to a water cluster containing one or two charged atoms, and the dependences of the mean force and the potential of mean force (PMF) between the charged solutes on E^ext were studied using MD simulations [40]. The differences between the mean force estimated from a continuum solvent and that computed using MD simulations were discussed.

2. Results/Discussion

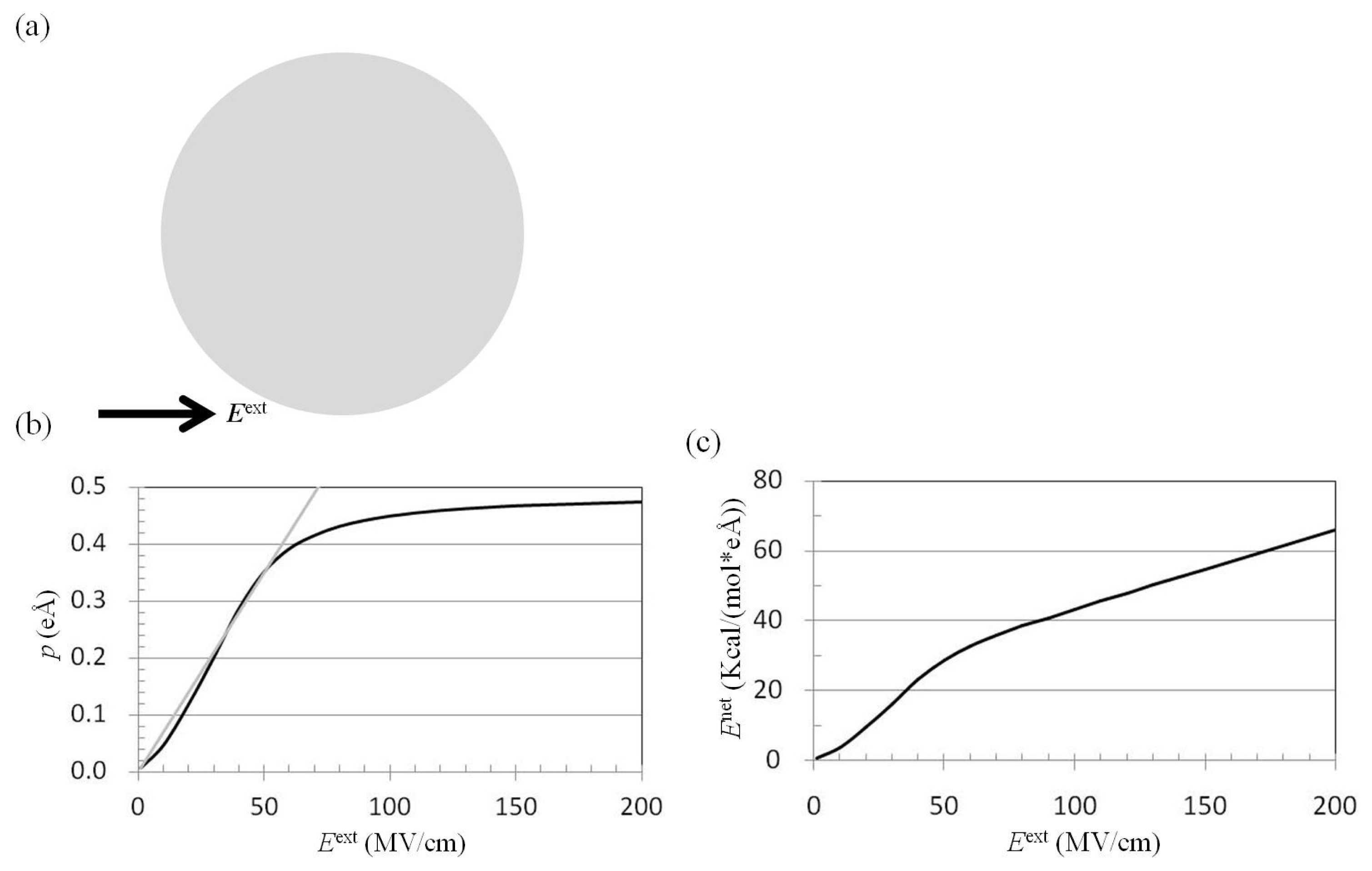
2.1. Dependence of p on E^ext

On applying E^ext to a water cluster containing solutes, the water molecules were polarized by the E^ext. The electric force on the atoms of the solute from E^ext could be shielded by the polarized water molecules. To explore the effect of the electric dipole per water molecule, −p, polarized by E^ext, E^ext was applied to the water cluster (Figure 1a), and p and the net electric field on the water molecule, −E^net were computed from the trajectories of MD simulations using (1) and (3), respectively. The results showed that p was proportional to E^ext in the region |E^ext| < 50 MV/cm. The ratio of p to E^ext was approximately 0.007 eÅ/(MV/cm), as p_E = 0.007 eÅ/(MV/cm) * E^ext (MV/cm). The p (black line) from MD simulations was compared with p_E (gray line) (Figure 1b). With regard to the relationship between E^net and E^ext, E^net was proportional to E^ext. The proportionality constant was larger in the region |E^ext| < 50 MV/cm than in the region |E^ext| > 50 MV/cm (Figure 1c). Based on these results, the external electrostatic field along the x direction, −E_X^ext = 40, 60, or 100 MV/cm, or the external electrostatic field along the y direction, −E_Y^ext = 50 or 100 MV/cm, was applied to a water cluster containing two solutes to compute the mean force and the PMF on the solute S₂.

The dependence of p on the charged solute and E^net has been extensively studied [37,38]. A solute with a charge of −4.0 e, −3.0 e, −2.0 e, −1.0 e, −0.8 e, −0.6 e, −0.4 e, −0.2 e, +0.2 e, +0.4 e, +0.6 e, +0.8 e, +1.0 e, +2.0 e, +3.0 e, or +4.0 e was at the center of a spherical water cluster (Figure 2a), and p and E^net were computed from the trajectories of MD simulations (Figure 2b). The solvent molecular polarizability ɛ₀γ_mol was defined as dp/dE^net. Δp was proportional to ΔE^net in the region |E^net| < 25 kcal/(mol·eÅ) (1 MV/cm = 0.231 kcal/(mol·eÅ)), and ɛ₀γ_mol = 0.0124 (mol·e²·Å²)/kcal (or γ_mol = 51.7 ų[37]). For E^net > 50 kcal/(mol·eÅ), the net dipole of TIP3P is towards the direction of E^net, and the value of p approaches +0.49 eÅ. For E^net < −100 kcal/(mol eÅ), one of the hydrogen atoms was toward the anion, and the value of p approaches −0.35 eÅ. In the region −100 kcal/(mol·eÅ) < E^net < −50 kcal/(mol·eÅ), the net dipole of TIP3P or one of the hydrogen atoms could be toward the anion, so the value of p depends not only on E^net, but also depends on the solute charge and position in calculating E^net. The values of p therefore varied between −0.49 eÅ and −0.35 eÅ.

The p from E^ext was compared with that from the charged solute. The p of water molecules polarized by E^ext (MV/cm) (Figure 1a) was compared with that polarized by a solute with charge Q(e) (Figure 2a). For example, when E^ext = 50 MV/cm was applied to a pure water cluster, p = 0.35 eÅ (Figure 1b), which is 70% of the permanent electric dipole moment of TIP3P water. For the solute with a charge of +1.0 e in water, and the same van der Waals (vdW) parameters as the oxygen atom of TIP3P water, p at the first peak of the radial distribution function, solute distance 2.8 Å, was 0.35 eÅ [37,38]. The subconclusion is that p polarized by E^ext = 50 MV/cm was similar to p at the first peak of the radial distribution function surrounding the solute with a charge of +1.0 e.

E^ext shifts the equilibrium position of the p − E^net curve of the water molecule, and could reduce the electric shielding effect between charged atoms in macromolecules. Consider a macromolecule such as a protein in water solvent; the solvent molecules are polarized by the charged atoms in the macromolecules, and the polarized molecules shield the electrostatic interactions between the charged atoms in the macromolecules. The solvent molecular polarizability, γ_mol, describes the electric shielding effect between charged particles in dielectrics. In the case of no applied E^ext, the equilibrium position is at position A (Figure 2b). The Δp is proportional to ΔE^net in the region |E^net| < 25 kcal/(mol eÅ), and ɛ₀γ_mol = 0.0124 (mol·e²·Å²)/kcal. Applying E^ext = 200 MV/cm to the water cluster leads to E^net = 66 kcal/(mol·eÅ). The equilibrium position is shifted to position B (Figure 2b). The ɛ₀γ_mol for computing the electric shielding effect between charged atoms in macromolecules is 0.0006 (mol·e²·Å²)/kcal. Applying E^ext = 50 MV/cm to the water cluster leads to E^net = 29 kcal/(mol·eÅ). The equilibrium position is shifted to position C (Figure 2b). The γ_mol was 0.0007/0.0022 (mol·e²·Å²)/kcal in the direction of increasing/decreasing p. The subconclusion is that the electric shielding effect of water for computing the electric interactions between charged atoms in macromolecules could be reduced by E^ext.

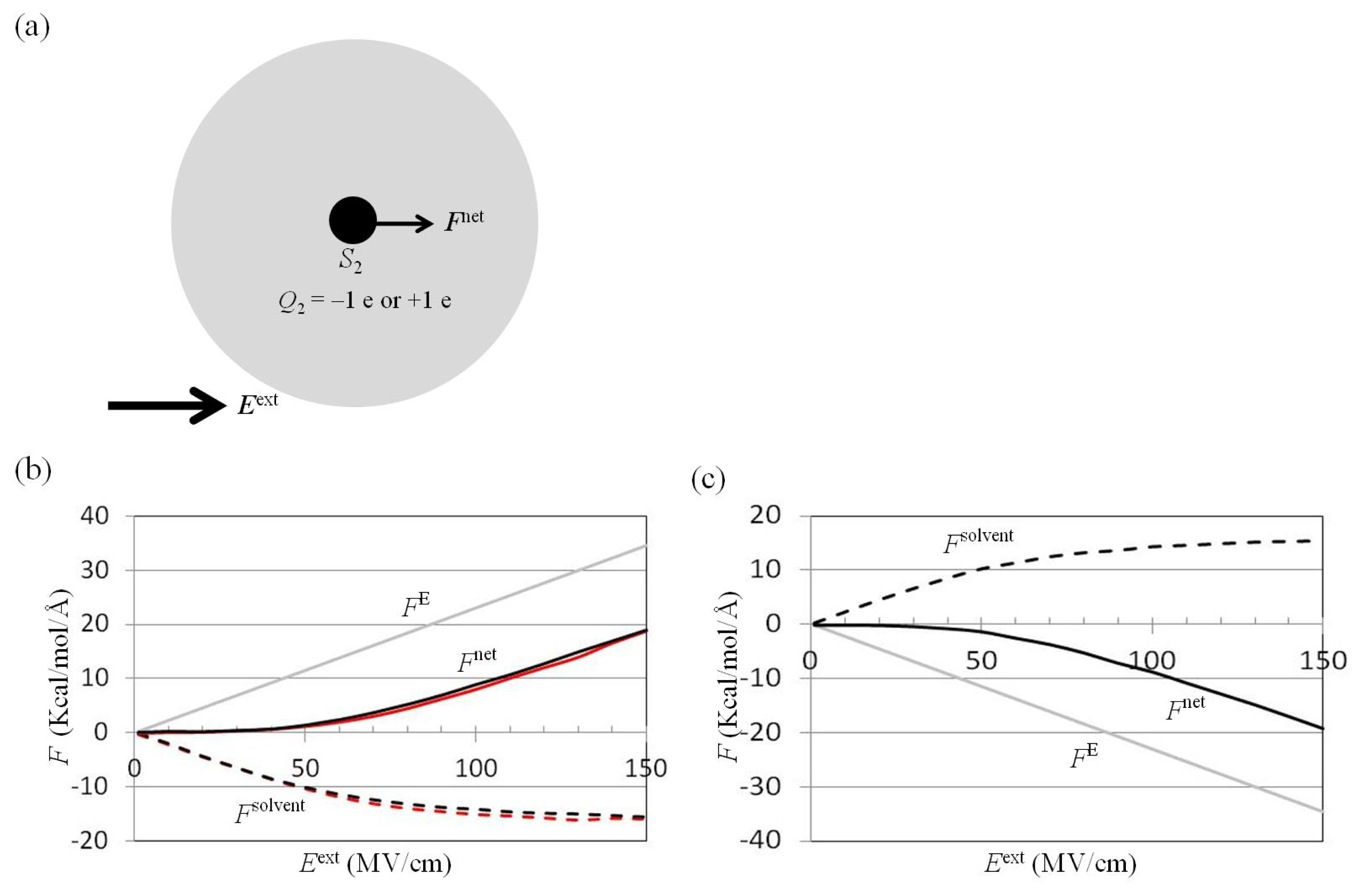
2.2. Dependence of F^net(One_Atom) on E^ext

To understand the effect of E^ext on the force on the charged solute, E^ext was applied to a water cluster of radius 20 Å, and the mean force on the solute S₂ was computed using the trajectories of the MD simulations (Figure 3a). The net mean force, −F^net, was contributed by the external electrostatic field −F^E and the polarized water molecules −F^solv, using (9) and (10) [38,42]. The results showed that |F^net| was small in the |E^ext| < 50 MV/cm region because the F^E force was almost balanced by the F^solv force (Figure 3b). For |E^ext| > 50 MV/cm, the dielectric water approached saturation, |F^solv| increased slowly as E^ext increaed, and d|F^net|/dE^ext approached a constant (Figure 3b). To understand the dependences of the F^net and F^solv forces on the radius of the water cluster, E^ext was applied to a water cluster of radius 25 Å containing one solute with a charge of +1.0 e. The results showed that the F^net and F^solv computed from the water cluster of radius of 25 Å were similar to those obtained using a radius of 20 Å (Figure 3b).

The TIP3P water molecule contained one oxygen and two hydrogen atoms. The vdW radius of the oxygen atom, R_min/2 = 1.7682 Å, was larger than that of the hydrogen atom, R_min/2 = 0.2245 Å. For the cation in water, the oxygen atom of water was closer to the cation. In contrast, for the anion in water, the hydrogen atom of water was closer to the anion. The radial distribution function of the oxygen or hydrogen atoms surrounding the cation therefore differed from that of those surrounding the anion [37]. However, the amplitude of F^net on the solute with a charge of +1 e was similar to that on the solute with a charge of −1 e (Figure 3c). This means that the F^net(one_atom; E^ext) was independent of the sign of the charged solute.

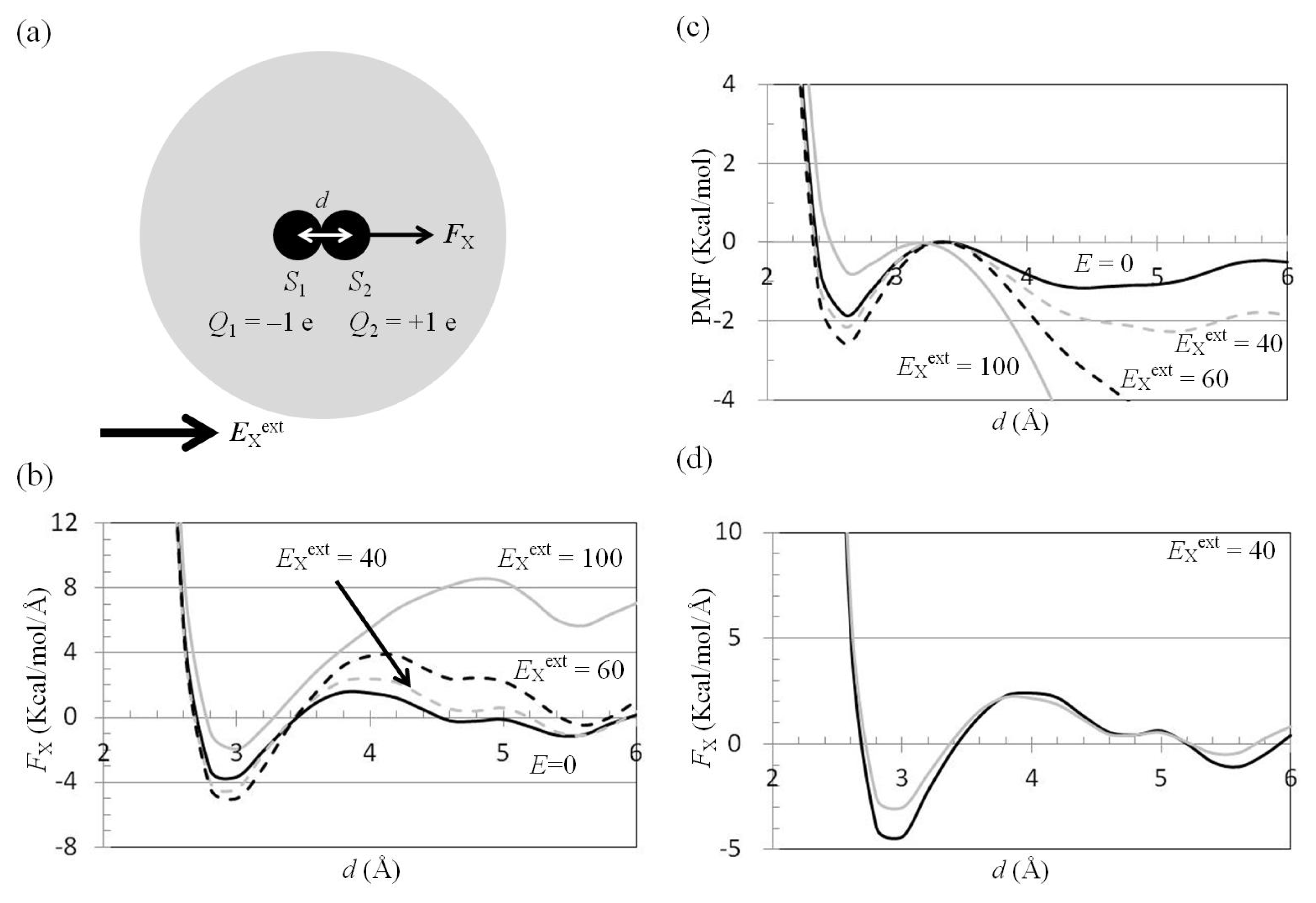
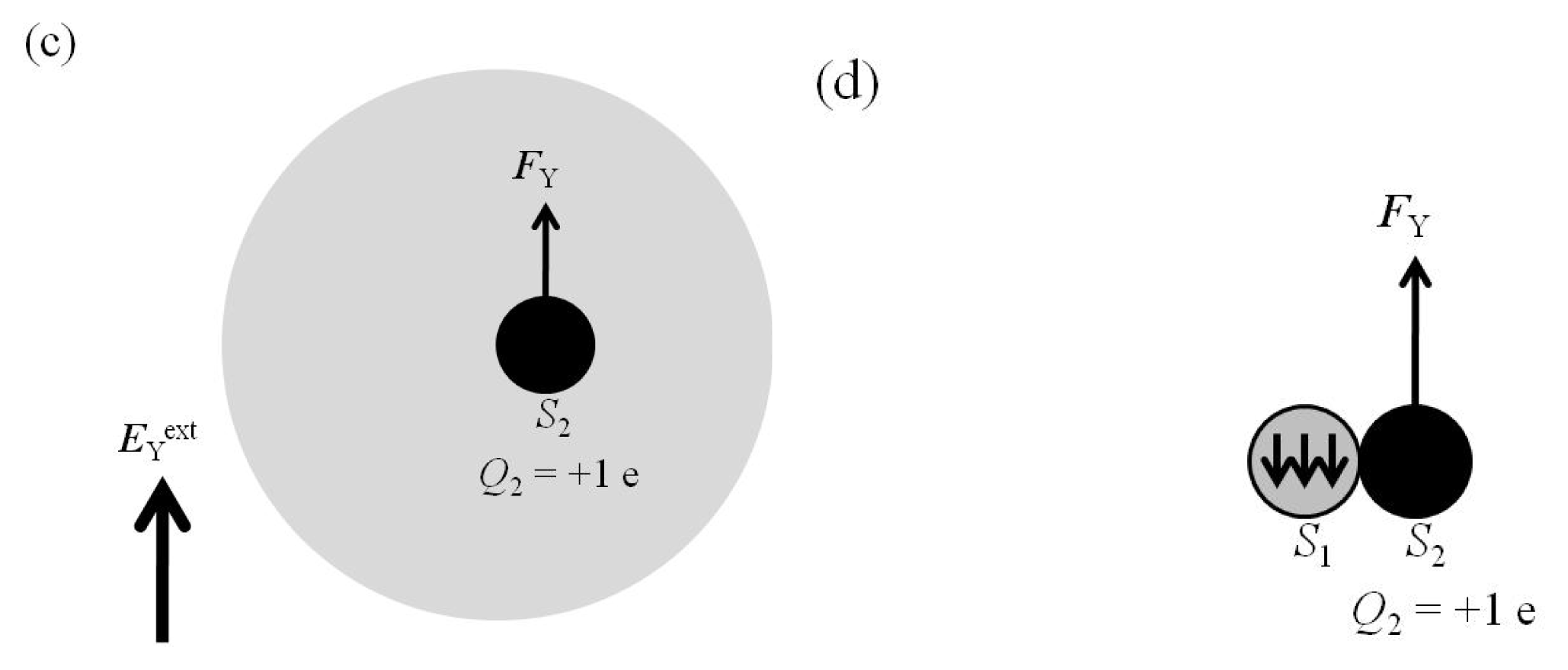
2.3. Attractive Force between S₁ and S₂ Could Not Be Decreased by Applying an External Electrostatic Field along the Direction of the Electric Dipole Formed by S₁ and S₂

Polar interactions, such as those between hydrogen bond donors and acceptors, play a significant role in stabilizing protein conformations and protein-protein/ligand complex structures. On applying E^ext to macromolecules containing polar interactions, the electric dipole formed by the two atoms with opposite charges, S₁ and the S₂, prefers to align in the direction of E^ext, to reduce the potential energy, and E^ext pulls S₁ and pushes S₂ along the direction of E^ext (Figure 4a). The attractive force and the attractive interaction free energy between S₁ and S₂ decreased if S₁ and S₂ were treated as point charges in continuum dielectrics.

For S₁ and S₂ exposed to water, the external electrostatic field along the x direction, −E_X^ext, was applied to the water cluster containing S₁ and S₂ solutes (Figure 4a). The mean force on S₂ along the x direction, −F_X(two_atoms; E_X^ext), was computed using the trajectories of the MD simulations. The results showed that F_X(two_atoms; E_X^ext = 0) was attractive (negative) in the 2.7 Å < d < 3.4 Å region, and the minimum value of F_X(two_atoms; E_X^ext = 0) was −3.7 kcal/(mol·Å) at the position d = 3.0 Å (Figure 4b). We also applied E_X^ext = 40 or 60 MV/cm to a water cluster containing one solute with a charge of +1 e, and the mean force F_X(one_atom; E_X^ext) on the solute with a charge of +1 e was positive (Figure 3a). Was the attractive force on the solute S₂ in Figure 4a decreased by application of the external electrostatic field? The results from the MD simulations showed that F_X(two_atoms; E_X^ext = 40 or 60 MV/cm) was more attractive than F_X(two_atoms; E_X^ext = 0) in the region 2.7 Å < d < 3.4 Å. The minimum values of F_X(two_atoms; E_X^ext) at position d = 3.0 Å were −4.4 and −5.0 kcal/(mol Å) for E_X^ext = 40 and 60 MV/cm, respectively (Figure 4b).

The PMF, −P_MF(two_atoms; E_X^ext = 40 or 60 MV/cm), was calculated by integration of the mean force F_X from infinity. For comparison of the energies needed to escape the first well of P_MF(two_atoms; E_X^ext = 40 or 60 MV/cm), the second peak of P_MF(two_atoms; E_X^ext), was set at zero. The results showed that the depth of the first well of P_MF(two_atoms; E_X^ext = 40 or 60 MV/cm) was deeper than that of P_MF(two_atoms; E_X^ext = 0) (Figure 4c).

Treating S₁ and S₂ as point charges, F_X(two_atoms; E_X^ext) was estimated by summation of F_X(two_atoms; E_X^ext = 0) (Figure 4b) and F_X^net(one_atom; E_X^ext) (Figure 3b). F_X^est(two_atoms; E_X^ext) was the sum of F_X(two_atoms; E_X^ext = 0) in Figure 4b and F_X^net(one_atom; E_X^ext) in Figure 3b. The results showed that F_X^est(two_atoms; E_X^ext) was larger than F_X(two_atoms; E_X^ext), especially in the d < 3.4, 3.8, and 4.4 Å regions for E_X = 40, 60, and 100 MV/cm, respectively (Figure 4d−f). This is because no water molecules can be polarized in the space occupied by S₁. If S₁ occupies the space, F_X(two_atoms; E_X^ext) should be estimated by summation of F^X(two_atoms; E_X^ext = 0) (Figure 4b), F_X^net(one_atom; E_X^ext) (Figure 4g), and F_X(excluded_solvent; E_X^ext) (Figure 4h), based on the superposition principle. F_X(excluded_solvent; E_X^ext) is the force on solute S₂ contributed by the water in the space occupied by S₁. The dielectric polarization in the space occupied by S₁ in Figure 4h was the reverse of the dielectric polarization in the space occupied by S₁ in Figure 4g. F_X(excluded_solvent; E_X^ext) was along the −x direction, therefore F_X^est(two_atoms; E_X^ext) was larger than F_X(two_atoms; E_X^ext).

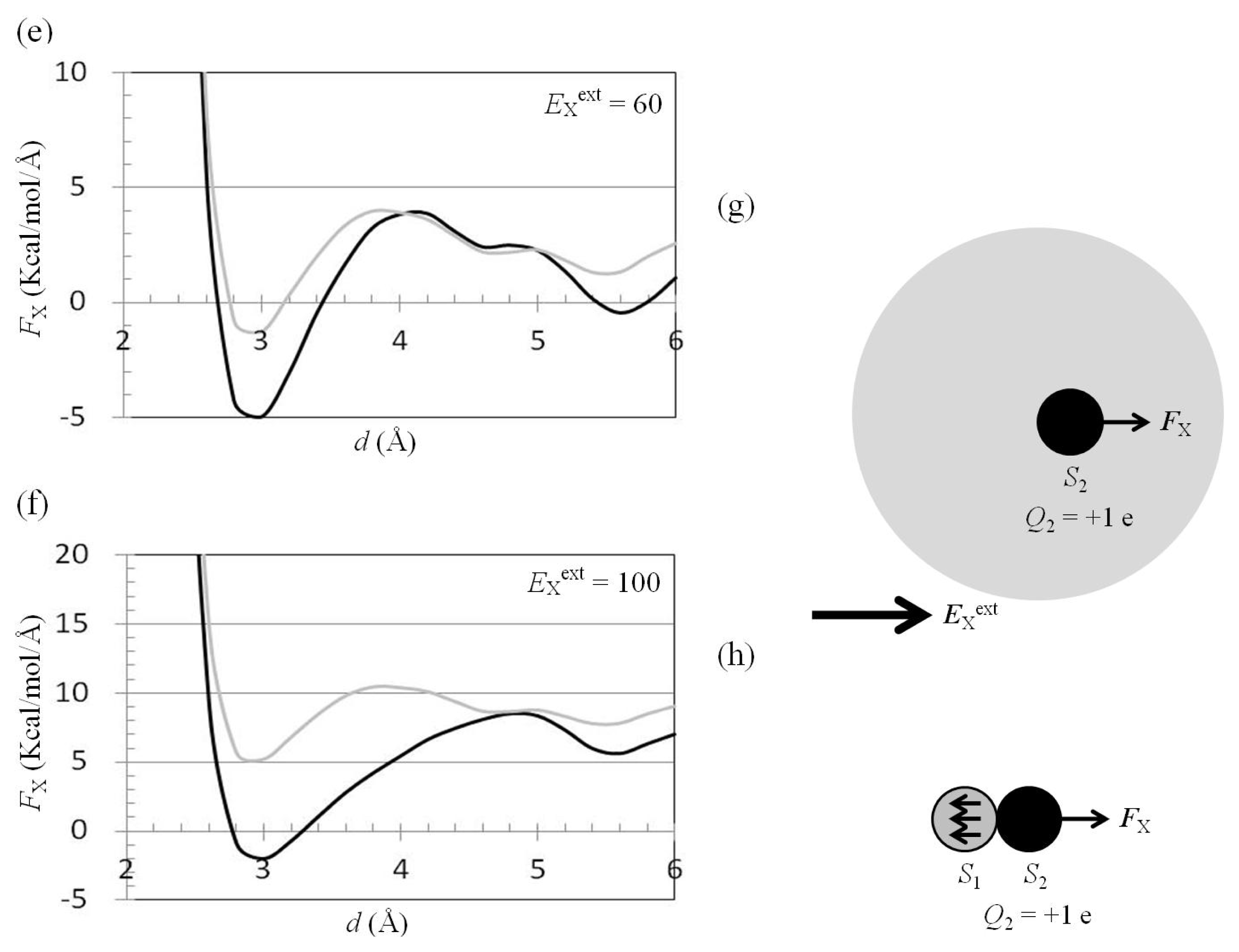
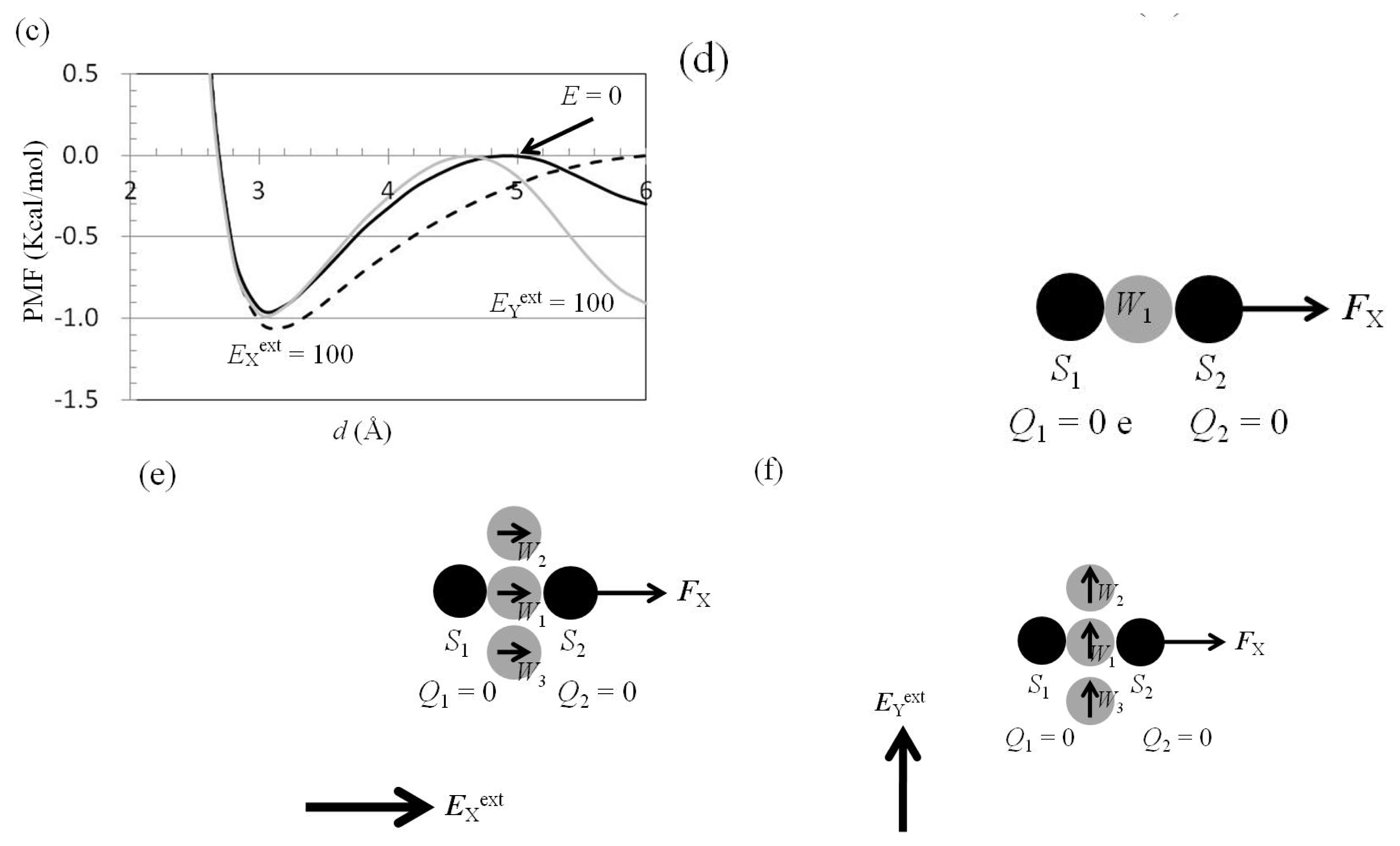
2.4. Attractive Force between S₁ and S₂ Was Unchanged and Increased by Applying E_Y^ext = 50 MV/cm and 100 MV/cm, Respectively

The external electrostatic field along the y direction, −E_Y^ext, was applied to a water cluster containing S₁ and S₂ solutes (Figure 5a). The mean force on S₂ along the x direction, −F_X(two_atoms; E_Y^ext), was computed using the trajectories of the MD simulations. The results showed that F_X(two_atoms; E_Y^ext = 50 MV/cm) was similar to F_X(two_atoms; E_ext = 0), but F_X(two_atoms; E_Y^ext = 100 MV/cm) was less than F_X(two_atoms; E_ext = 0) (Figure 5b). The difference between F_X(two_atoms; E_Y^ext = 50 MV/cm) and F_X(two_atoms; E_ext = 0) at the position of the first minimum of F_X(two_atoms; E_ext = 0) was 0.3 kcal/(mol Å), and the difference between F_X(two_atoms; E_Y^ext = 100 MV/cm) and F_X(two_atoms; E_ext = 0) at the position of the first minimum of F_X(two_atoms; E_ext = 0) was 2.2 kcal/(mol·Å) (Figure 5b).

E_ext was applied to the charged atom in the water cluster (Figure 2a), the force on the charged atom was along the direction of E_ext, and the force perpendicular to direction of E_ext was zero. S₁ and S₂ were treated as point charges. E_ext was applied perpendicular to the direction of the electric dipole formed by S₁ and S₂; the force on S₁ and S₂ from E_ext was along the direction of E_ext, and the attractive force and the interaction potential energy between S₁ and S₂ were unchanged. When E_ext = 100 MV/cm was applied perpendicular to the direction of the electric dipole formed by these two atoms (Figure 5a), the attractive force between S₁ and S₂ increased (Figure 5b), and the interaction free energy also increased, as observed from MD simulations. This is because polarization of the water molecules was saturated on application of E_Y^ext = 100 MV/cm. The saturated water molecule is hard to polarize further by S₁ and S₂. The dielectric shielding effect between S₁ and S₂ was therefore reduced.

2.5. F_Y(Two_Atoms; E_Y^ext) Was Greater than F_Y(one_atom; E_Y^ext), Especially When d Was Small

E_Y^ext was applied to a water cluster containing two charged solutes (Figure 6a); the mean force on S₂ along the y direction, −F_Y(two_atoms; E_Y^ext), was computed using the trajectories of the MD simulations. The results showed that F_Y(two_atoms; E_Y^ext = 50 or 100 MV/cm) was similar to F_Y(one_atom; E_Y^ext = 50 or 100 MV/cm), except in the region d < 3.0 Å (Figure 6b). The differences between F_Y(two_atoms; E_Y^ext) and F_Y(one_atom; E_Y^ext) at d = 6 Å were 0.2 and 0.3 kcal/(mol Å) for E_Y^ext = 50 and 100 MV/cm, respectively.

The force on S₂ from S₁ was along the −x direction. Treating S₁ and S₂ as point charges, F_Y(two_atoms; E_Y^ext) should be the same as F_Y(one_atom; E_Y^ext). However, the force on S₂ in the water cluster containing two solutes was greater than the force on the charged solute S₂ in the water cluster containing one solute (Figure 6b). This is because no water molecules in the space occupied by S₁ can be polarized. F_Y(two_atoms; E_Y^ext) should be estimated by summation of F_Y(one_atom; E_Y^ext) (Figure 6c) and F_Y(excluded_solvent; E_Y^ext) (Figure 6d), based on the superposition principle. F_Y(excluded_solvent; E_Y^ext) is the force on solute S₂ contributed by the water molecules in the region occupied by solute S₁. The dielectric polarization in the space occupied by S₁ in Figure 6d was the reverse of the dielectric polarization in the space occupied by S₁ in Figure 6c. F_Y(excluded_solvent; E_Y^ext) was along the +y direction (Figure 6d), therefore F_Y(one_atom; E_Y^ext) was less than F_Y(two_atoms; E_Y^ext).

2.6. Dependence of F_X(Two_Neutral_Atoms) on E_X^ext and E_Y^ext

Hydrophobic interactions play a significant role in the stabilities of protein conformations and the binding affinities of protein-protein/ligand interactions. The effect of an external electrostatic field on the mean force between two neutral solutes was explored. Consider two neutral solutes in a water cluster (Figure 7a). The mean force on S₂, −F_X(two_neutral_atoms; E^ext), was computed using the trajectories of the MD simulations. The results showed that F_X(two_neutral_atoms; E^ext = 0) was attractive in the region 3.2 Å < d < 5.0 Å, and repulsive in the region 5.0 Å < d < 6.0 Å (Figure 7a). The maximum attractive force was −0.8 kcal/(mol Å) at the d = 3.8 Å position, and the maximum repulsive force was 0.4 kcal/(mol Å) at the d = 5.6 Å position (Figure 7b).

E_X^ext = 100 MV/cm or E_Y^ext = 100 MV/cm was applied to a water cluster containing two neutral solutes (Figure 7a); the mean force on S₂, −F_X(two_neutral_atoms; E^ext), was computed using the trajectories of the MD simulations. The results showed that F_X(two_neutral_atoms; E_X^ext = 100 MV/cm) and F_X(two_neutral_atoms; E_Y^ext = 100 MV/cm) differed from F_X(two_neutral_atoms; E^ext = 0). F_X(two_neutral_atoms; E_X^ext = 100 MV/cm) was larger than F_X(two_neutral_atoms; E^ext = 0) in the region d < 4.4 Å, and less in the region 4.4 Å < d < 6.0 Å (Figure 7b). In contrast, F_X(two_neutral_atoms; E_Y^ext = 100 MV/cm) was similar to F_X(two_neutral_atoms; E^ext = 0) in the region d < 4.4 Å, and F_X(two_neutral_atoms; E_Y^ext = 100 MV/cm) was larger than F_X(two_neutral_atoms; E^ext = 0) in the region 4.4 Å < d < 6.0 Å (Figure 7b).

The PMF, −P_MF(two_neutral_atoms; E^ext), was calculated by integration of the mean force F_X(two_neutral_atoms; E^ext) from infinity. For comparison of the depths of the first wells of P_MF(two_neutral_atoms; E^ext) with E_X^ext = 100 MV/cm or E_Y^ext = 100 MV/cm, the second peak of P_MF was set to zero. The results showed that the depth of the first well of P_MF(two_neutral_atoms; E^ext = 0) was smaller than that of P_MF(two_neutral_atoms; E_X^ext = 100 MV/cm), and similar to that of P_MF(two_neutral_atoms; E_Y^ext = 100 MV/cm) (Figure 7c).

For solutes S₁ and S₂ separated by a distance greater than 5.4 Å, the space between S₁ and S₂ can accommodate a water molecule (Figure 7d). When one of the water molecules, e.g., W₁, stays at the position between solutes S₁ and S₂, W₁ will push S₂ along the +x direction. When E_X^ext = 100 MV/cm is applied to this water cluster, the water molecules will be polarized along the x direction. W₁ will be pushed by the neighboring water molecules, W₂ and W₃ (Figure 7e); the probability of one of the water molecules staying at the position of W₁ when E_X^ext = 100 MV/cm was applied was lower than that without application of an external electrostatic field. F_X(two_neutral_atoms; E_X^ext = 100 MV/cm) was therefore less than F_X(two_neutral_atoms; E^ext = 0) in the region 4.4 Å < d < 6.0 Å (Figure 7b). If E_Y^ext = 100 MV/cm is applied to this water cluster, the water molecules will be polarized along the y direction. W₁ will be attracted by the neighboring water molecules, W₂ and W₃ (Figure 7f); the probability of one of the water molecules staying at the position of W₁ under application of E_Y^ext = 100 MV/cm was larger than that without application of an external electrostatic field. F_X(two_neutral_atoms; E_Y^ext = 100 MV/cm) was therefore larger than F_X(two_neutral_atoms; E^ext = 0) in the region 4.4 Å < d < 6.0 Å (Figure 7b).

3. Method

3.1. MD Simulations

The simulations were performed in an NVE ensemble using the CHARMM package [39] and spherical boundary conditions. The ion-water and water-water interaction energies were calculated by summation of the electrostatic and vdW pairwise energies with a non-bond cutoff of 99 Å. For TIP3P water, the charge states of the oxygen and hydrogen atom were −0.834 e and +0.417 e, respectively, and the vdW parameters of the hydrogen atom were ɛ = −0.046 kcal/mol and R_min/2 = 0.2245 Å. The O–H bond length of TIP3P, 0.9572 Å, and the bond angle of H–O–H, 104.52°, were constrained during the simulations using the SHAKE algorithm [43]. The intrinsic electronic polarizability of the water molecule changed as a strong electric field [44] was not considered in this project. All atoms were propagated according to Newton’s equations using the leapfrog Verlet algorithm and a time-step of 2 fs at a mean temperature of 300 K. Each system was first minimized for 1000 steps, equilibrated for 200 ps, and subsequently subjected to 1 ns of production. The configurations were stored every 20 fs.

3.2. Application of E^ext to Pure Water Cluster and Calculation of p and E^net from Trajectories of MD Simulations

E^ext was applied to a pure water cluster (Figure 1a), and the electric dipole moment per water molecule, p, was calculated using the sum of the electric dipole moments of water molecules with an oxygen atom distance origin ≤ r_cut over N_C configurations/frames, divided by the number of water molecules N with an oxygen atom distance origin ≤ r_cut over N_C configurations/frames:

$$\mathit{p}=\frac{1}{N}\sum _{l=1}^{N_{\text{C}}}\sum _{m=1}^n\sum _{i=1}^3{q}_{\text{i}}{\mathit{r}}_{\text{i}}^{\text{lm}}u\left(r_{\text{cut}}-r_{\text{O}}^{\text{lm}}\right)$$

(1)

where q_i is the charge on water atom i, r_i^lm denotes the coordinates of atom i of water molecules m in configuration l, r_O^lm denotes the coordinates of the oxygen atom of water molecule m in configuration l, n is the number of solvent molecules in the simulation system, Nc is the number of configurations/frames collected in equilibrium state in the MD simulations, and u(r_cut − r_O^lm) is the Heaviside unit step function.

N was computed as the sum of the water molecules with oxygen atoms positioned at distance origin ≤ r_cut:

$$N=\sum _{l=1}^{N_{\text{C}}}\sum _{m=1}^{n}u\left(r_{\text{cut}}-r_{\text{O}}^{\text{lm}}\right)$$

(2)

where the first summation is over Nc configurations/frames, and the second summation is over the n solvent molecules in the simulation system.

The electrostatic field at the oxygen atom of TIP3P water, −E^net, was contributed by E^ext and water molecules with oxygen atom distance origins ≤ r_cut over N_C configurations/frames, divided by the number of water molecules N with oxygen atom distance origins ≤ r_cut over N_C configurations/frames as

$${\mathit{E}}^{\text{net}}={\mathit{E}}^{\text{ext}}+\frac{1}{N}\sum _{l=1}^{N_{\text{C}}}\sum _{m^{\prime }=1}^{n}u\left(r_{\text{cut}}-r_{\text{O}}^{\text{l}{\text{m}}^{\prime }}\right)\sum _{\begin{array}{l}m=1\\ m^{\prime }\ne m\end{array}}^n\sum _{i=1}^3\frac{q_{\text{i}}}{4\pi {\varepsilon }_0{\left(R_{\text{iO}}^{\text{lm}{\text{m}}^{\prime }}\right)}^3}{\mathit{R}}_{\text{iO}}^{\text{lm}{\text{m}}^{\prime }}$$

(3)

where ɛ₀ is the permittivity of free space, q_i is the charge on water atom i, R^lmm′_iO is the vector from atom i of water molecule m to the oxygen atom of water molecule m’ in configuration l.

3.3. For Charged Atom in Water Cluster, Calculation of p(r) and E^net(r) from Trajectories of MD Simulations

For one charged atom in a water cluster (Figure 2a), p(r) was calculated by summing the electric dipole moments of water molecules with oxygen atoms located between (r − Δr/2) and (r + Δr/2) over N_C configurations/frames, divided by the number of water molecules N(r), as

$$p(r)=\frac{1}{N(r)}{\int }_{r-\mathrm{\Delta }r/2}^{r+\mathrm{\Delta }r/2}\sum _{l=1}^{N_{\text{C}}}\sum _{m=1}^n\sum _{i=1}^3{q}_i\left({\mathit{r}}_{\text{i}}^{\text{lm}}\times \frac{{\mathit{r}}_{\text{O}}^{\text{lm}}}{r_{\text{O}}^{\text{lm}}}\right)\delta \left(r^{\prime }-r_{\text{O}}^{\text{lm}}\right)\hspace{0.17em}d{r}^{\prime }$$

(4)

N(r) in (4) was computed as the sum of the number of water molecules whose oxygen atoms were at a distance from the solute of between (r − Δr/2) and (r + Δr/2):

$$N(r)={\int }_{r-\mathrm{\Delta }r/2}^{r+\mathrm{\Delta }r/2}\sum _{l=1}^{N_{\text{C}}}\sum _{m=1}^n\delta \left(r^{\prime }-r_{\text{O}}^{\text{lm}}\right)\hspace{0.17em}d{r}^{\prime }$$

(5)

where the first summation is over Nc configurations/frames, the second summation is over the n solvent molecules in the simulation system, r_O^lm denotes the coordinates of the oxygen atom of water molecule m in configuration l, and Δr is set at 0.1 Å.

E^net(r) was calculated by summing the electrostatic fields of water with its oxygen atom located between (r − Δr/2) and (r + Δr/2) over N_C configurations/frames, divided by the number of water molecules N(r), as

$$E^{\text{net}}(r)=\frac{1}{N(r)}{\int }_{r-\mathrm{\Delta }r/2}^{r+\mathrm{\Delta }r/2}\sum _{l=1}^{N_{\text{C}}}\sum _{m^{\prime }=1}^n\delta \left(r^{\prime }-r_{\text{O}}^{\text{l}{\text{m}}^{\prime }}\right)\left[\frac{q_{\text{j}}}{4\pi {\varepsilon }_0{\left(R_{\text{jo}}^{\text{l}{\text{m}}^{\prime }}\right)}^2}+\sum _{\begin{array}{l}m=1\\ m^{\prime }\ne m\end{array}}^n\sum _{i=1}^3\frac{q_i}{4\pi {\varepsilon }_0{\left(R_{\text{iO}}^{\text{lm}{\text{m}}^{\prime }}\right)}^3}\left({\mathit{R}}_{\text{iO}}^{\text{lm}{\text{m}}^{\prime }}\times \frac{{\mathit{r}}_{\text{O}}^{\text{l}{\text{m}}^{\prime }}}{r_{\text{O}}^{\text{l}{\text{m}}^{\prime }}}\right)\right]d{r}^{\prime }$$

(6)

where ɛ₀ is the permittivity of free space, q_i is the charge on water atom i, q_j is the charge on the solute atom, R^lm′_jO is the distance between the oxygen atom of water molecule m’ in configuration l and solute j, R^lmm′_iO is the vector from atom i of water molecule m to the oxygen atom of water molecule m’ in configuration l.

3.4. Application of E^ext to Water Cluster Containing One or Two Solutes and Calculation of F^solv(r) and F^net(r) from Trajectories of MD Simulations

The net mean force on solute S₂ with charge Q₂, −F^net, was decomposed and contributed by the external electrostatic field −F^E, solute S₁ with charge Q₁, −F^S1, and the polarized solvent molecules, −F^solv. F^E was computed as F^E = Q₂E.

F^S1 was the force acting on solute S₂ at r₂ because of solute S₁ at r₁, and can be computed as the sum of the electrostatic and vdW forces as

$${\mathit{F}}_{\text{ele}}^{\text{S}1}=\frac{Q_1{Q}_2{\mathit{R}}_{12}}{4\pi {\varepsilon }_0{(R_{12})}^3}$$

(7)

$${\mathit{F}}_{\text{vdw}}^{\text{S}1}=\frac{12{\varepsilon }_{12}}{R_{12}}\left[{\left(\frac{R_{\text{min},12}}{R_{12}}\right)}^{12}-{\left(\frac{R_{\text{min},12}}{R_{12}}\right)}^6\right]\frac{{\mathit{R}}_{12}}{R_{12}}$$

(8)

where R₁₂ = r₂ − r₁, and the vdW parameters, ɛ₁₂ and R_min,12, were obtained using the standard combining rules.

F^solv was the force acting on solute S₂ at r₂ because of the solvent molecules, and can be computed as the sum of the electrostatic and vdW forces as

$${\mathit{F}}_{\text{ele}}^{\text{solvent}}=\frac{1}{N_{\text{C}}}\sum _{l=1}^{N_{\text{C}}}\sum _{m=1}^n\sum _{j=1}^3\frac{Q_2{q}_j}{4\pi {\varepsilon }_0{\left(R_{2\text{j}}^{\text{lm}}\right)}^3}{\mathit{R}}_{2\text{j}}^{\text{lm}}$$

(9)

$${\mathit{F}}_{\text{vdW}}^{\text{solvent}}=\frac{1}{N_{\text{C}}}\sum _{l=1}^{N_{\text{C}}}\sum _{m=1}^n\sum _{j=1}^3\frac{12{\varepsilon }_{2\text{j}}}{R_{2\text{j}}^{\text{lm}}}\left[{\left(\frac{R_{\text{min},2\text{j}}}{R_{2\text{j}}^{\text{lm}}}\right)}^{12}-{\left(\frac{R_{\text{min},2\text{j}}}{R_{2\text{j}}^{\text{lm}}}\right)}^6\right]\frac{{\mathit{R}}_{2\text{j}}^{\text{lm}}}{R_{2\text{j}}^{\text{lm}}}$$

(10)

where the first summation is over Nc configurations/frames, the second summation is over the n solvent molecules in the simulation system, q_j is the charge on water atom j, R^lm_2j is the vector from atom j of water molecule m to solute S₂ at r₂ in configuration l, and the vdW parameters, ɛ_2j and R_min,2j, were obtained using the standard combining rules.

4. Conclusions

To explore the athermal effect of E^ext on the stabilities of protein conformations and the binding affinities of protein-protein/ligand interactions, the dependence of the mean force between charged solutes or neutral solutes, S₁ and S₂, on E^ext was studied using MD simulations. The results showed that (1) E^ext shifts the equilibrium position of the p − E^net curve of the water molecule, and may reduce the dielectric shielding effect between charged atoms in macromolecules; (2) For E^ext along the direction of the electric dipole formed by S₁ and S₂, E^ext = 40 or 60 MV/cm enhances the polar interactions between the two charged solutes; (3) For E^ext perpendicular to the direction of the electric dipole formed by S₁ and S₂, E^ext = 100 MV/cm enhances the polar interactions between these two charged solutes; (4) The mean force and the PMF between two neutral solutes depend on E^ext.