Kinetic Model for Signal Binding to the Quorum Sensing Regulator LasR
Abstract
:1. Introduction
2. Results
3. Discussion
4. Methods
4.1. Kinetic Model
4.1.1. Driven Systems
4.1.2. Ligand Binding
4.1.3. Turnover of Dimer Variants
4.1.4. Regulator Formation
4.1.5. The Monitor
4.1.6. The Measured Response
4.1.7. Decay via the Monomer Channel
4.2. Materials
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Fuqua, C.; Winans, S.C.; Greenberg, E.P. Census and consensus in bacterial ecosystems: The LuxR-LuxI family of quorum-sensing transcriptional regulators. Ann. Rev. Microbiol 1996, 50, 727–753. [Google Scholar]
- Williams, P. Quorum sensing: An emerging target for antibacterial chemotherapy? Expert Opin. Ther. Targets 2000, 6, 257–274. [Google Scholar]
- Eberhard, A. Inhibition and activation of bacterial luciferase synthesis. J. Bacteriol 1972, 109, 1101–1105. [Google Scholar]
- Nealson, K.H.; Platt, T.; Hastings, J.W. Cellular control of the synthesis and activity of the bacterial luminescence system. J. Bacteriol 1970, 104, 313–322. [Google Scholar]
- Choi, S.H.; Greenberg, E.P. Genetic dissection of DNA binding and luminescence gene activation by the Vibrio fischeri LuxR protein. J. Bacteriol 1992, 174, 4064–4069. [Google Scholar]
- Hanzelka, B.L.; Greenberg, E.P. Evidence that the N-terminal region of the Vibrio fischeri LuxR protein constitutes an autoinducer-binding domain. J. Bacteriol 1995, 177, 815–817. [Google Scholar]
- Zhu, J.; Winans, S.C. Autoinducer binding by the quorum-sensing regulator TraR increases affinity for target promoters in vitro and decreases TraR turnover rates in whole cells. Proc. Natl. Acad. Sci. USA 1999, 96, 4832–4837. [Google Scholar]
- Welch, M.; Todd, D.E.; Whitehead, N.A.; McGowan, S.J.; Bycroft, B.W.; Salmond, G.P. N-acyl homoserine lactone binding to the CarR receptor determines quorum-sensing specificity in Erwinia. EMBO J 2000, 19, 631–641. [Google Scholar]
- Zhu, J.; Winans, S.C. The quorum-sensing transcriptional regulator TraR requires its cognate signaling ligand for protein folding, protease resistance, and dimerization. Proc. Natl. Acad. Sci. USA 2001, 98, 1507–1512. [Google Scholar]
- Ventre, I.; Ledgham, F.; Prima, V.; Lazdunski, A.; Foglino, M.; Sturgis, J.N. Dimerization of the quorum sensing regulator RhlR: Development of a method using EGFP fluorescence anisotropy. Mol. Microbiol 2003, 48, 187–198. [Google Scholar]
- Liu, H.B.; Koh, K.P.; Lee, J.H.; Kim, J.S.; Park, S. Characterization of LasR protein involved in bacterial quorum sensing mechanism of Pseudomonas aeruginosa. Biotechnol. Bioprocess Eng 2009, 14, 146–154. [Google Scholar]
- Gonzalez, J.E.; Keshavan, N.D. Messing with bacterial quorum sensing. Microbiol. Mol. Biol. Rev 2006, 70, 1. [Google Scholar]
- Yang, M.; Giel, J.L.; Cai, T.; Zhong, Z.; Zhu, J. The LuxR family quorum-sensing activator MrtR requires its cognate autoinducer for dimerization and activation but not for protein folding. J. Bacteriol 2009, 191, 434–438. [Google Scholar]
- Pinto, U.M.; Winans, S.C. Dimerization of the quorum-sensing transcription factor TraR enhances resistance to cytoplasmic proteolysis. Mol. Microbiol 2009, 73, 32–42. [Google Scholar]
- Schuster, M.; Urbanowski, M.L.; Greenberg, E.P. Promoter specificity in Pseudomonas aeruginosa quorum sensing revealed by DNA binding of purified LasR. Proc. Natl. Acad. Sci. USA 2004, 101, 15833–15839 a, nd 3373727.. [Google Scholar]
- Sappington, K.J.; Dandekar, A.A.; Oinuma, K.I.; Greenberg, E.P. Reversible signal binding by the Pseudomonas aeruginosa quorum-sensing signal receptor LasR. mBio 2011, 2, e00011–11. [Google Scholar]
- Hentzer, M.; Riedel, K.; Rasmussen, T.B.; Heydorn, A.; Andersen, J.B.; Parsek, M.R.; Rice, S.A.; Eberl, L.; Molin, S.; Hoiby, N.; et al. Inhibition of quorum sensing in Pseudomonas aeruginosa biofilm bacteria by a halogenated furanone compound. Microbiology 2002, 148, 87–102. [Google Scholar]
- Andersen, J.B.; Sternberg, C.; Poulsen, L.K.; Bjorn, S.P.; Givskov, M.; Molin, S. New unstable variants of green fluorescent protein for studies of transient gene expression in bacteria. Appl. Environ. Microbiol 1998, 64, 2240–2246. [Google Scholar]
- Lin-Chao, S.; Bremer, H. Effect of the bacterial growth rate on replication control of plasmid pBR322 in Escherichia coli. Mol. Gen. Genet. MGG 1986, 203, 143–149. [Google Scholar]
- Lin-Chao, S.; Chen, W.; Wong, T. High copy number of the pUC plasmid results from a Rom/Rop-suppressible point mutation in RNA-II. Mol. Microbiol 1992, 6, 3385–3393. [Google Scholar]
- Klumpp, S.; Zhang, Z.; Hwa, T. Growth rate-dependent global effects on gene expression in bacteria. Cell 2009, 139, 1366–1375. [Google Scholar]
- Atlung, T.; Christensen, B.B.; Hansen, F.G. Role of Rom protein in copy number control of plasmid pBR322 at different growth rates in Escherichia coli K-12. Plasmid 1999, 41, 110–119. [Google Scholar]
- Leveau, J.H.J.; Lindow, S.E. Predictive and interpretive simulation of green fluorescent protein expression in reporter bacteria. J. Bacteriol 2001, 183, 6752–6762. [Google Scholar]
- Bottomley, M.J.; Muraglia, E.; Bazzo, R.; Carfi, A. Molecular insights into quorum sensing in the human pathogen Pseudomonas aeruginosa from the structure of the virulence regulator LasR bound to its autoinducer. J. Biol. Chem 2007, 282, 13592–13600. [Google Scholar]
- Clark, D.J.; Maaløe, O. DNA Replication and the division cycle in Escherichia coli. J. Mol. Biol 1967, 23, 99–112. [Google Scholar]

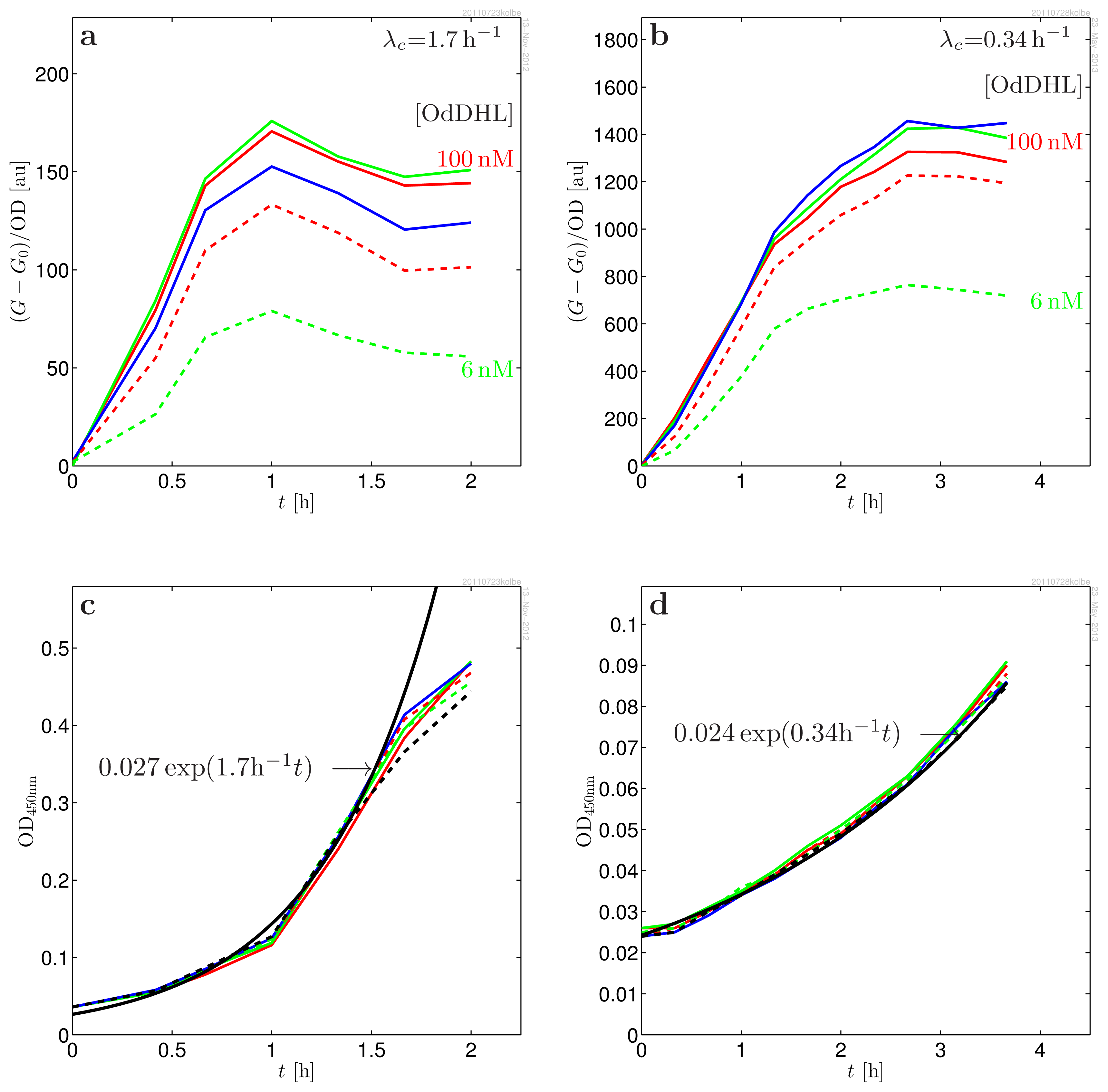

| Parameter | Value | |
|---|---|---|
| λn + kg | (2.1 ± 0.3) h−1 | degradation plus maturation (consistent with [18,23]) |
| λg, λn | (0.7 ± 0.3) h−1 | proteolytic decay for GFP (consistent with [18]) |
| Kd | (7 ± 2)nM | dissociation constant (agrees with [17]) |
| A | 2170 ± 200 [a.u.] | amplitude (Glucose, Casamino) |
| 1200 ± 200 [a.u.] | amplitude (Glycerol, l-leucine) | |
| md | 0.9 ± 0.2 | memory (Glucose, Casamino) |
| 0.3 ± 0.1 | memory (Glycerol, l-leucine) | |
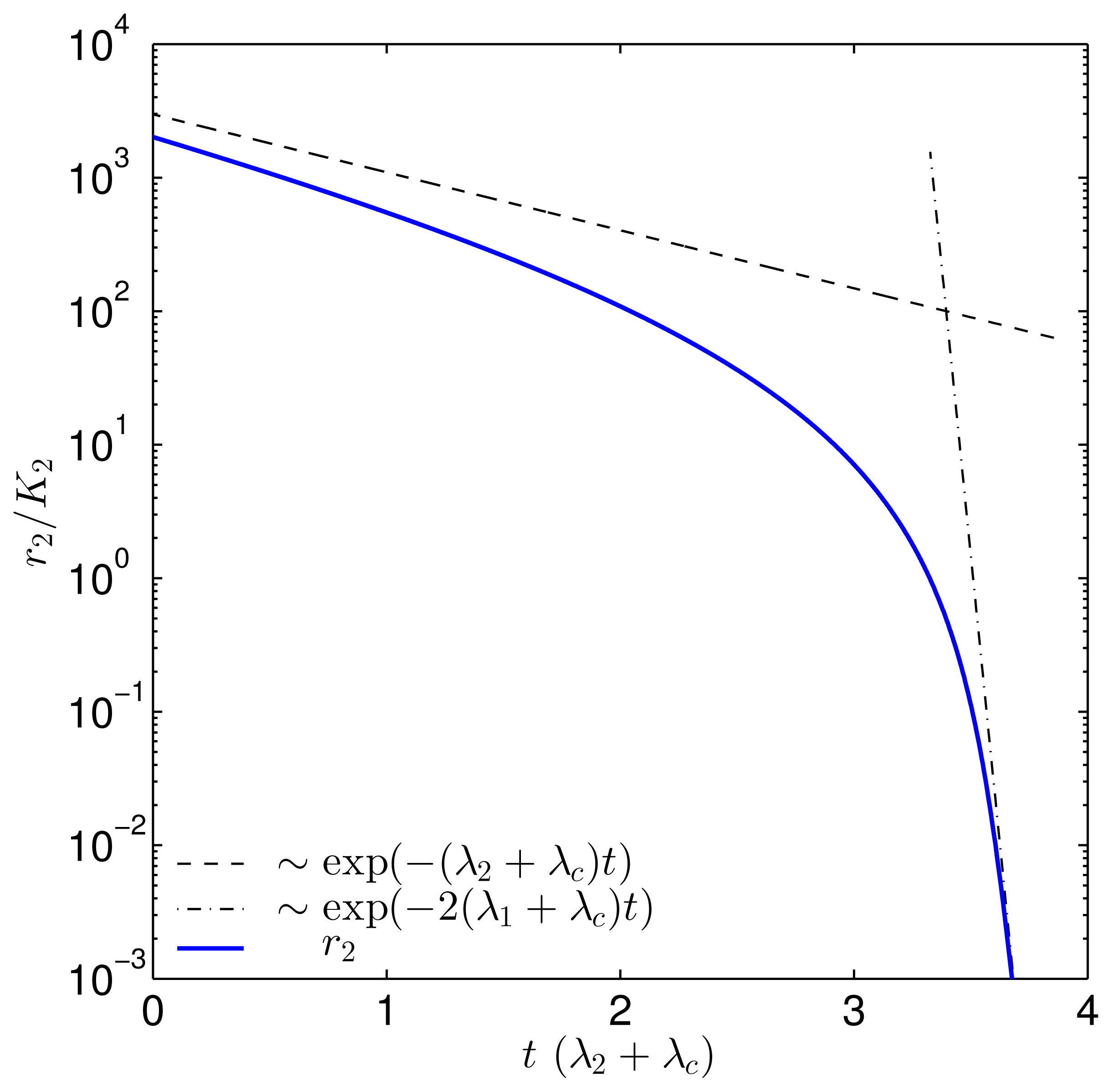
| λc | (1.69 ± 0.04) h−1 | growth rate (Glucose, Casamino) |
| (0.34 ± 0.03) h−1 | growth rate (Glycerol, l-leucine) | |
| g(t) | density normalized GFP response | |
| g0 | density normalized GFP response at s = 0 | |
| G(t) | measured fluorescence response | |
| G0(t) | measured fluorescence response at s = 0 | |
| OD(t) | optical density at 450nm | |
| hn(t), hg(t) | impulse response for GFP production and maturation | |
| on/off rates for dimer formation | ||
| on/off rates for ligand binding | ||
| K2 | dimer dissociation constant | |
| K3, K4 | ligand-dimer dissociation constants | |
| Kd | dissociation constant for cooperative ligand binding | |
| b1 | ~ 1000 h−1 | production rate of LasR per plasmid copy [21] |
| bn | background production of GFP(ASV) | |
| kn | ~ 1000 h−1 | induced production rate of GFP per plasmid copy |
| kg | ~ 1.5 h−1 | maturation rate of GFP [23] |
| λ1 | ~ 20 h−1 | R monomer degradation, [7] |
| λ2 | ~ 0 h−1 | R2 degradation (this study) |
| λ3 | R2S degradation, insensitive to this value | |
| λ4 | ~ 0 h−1 | degradation of R2S2[16] |
| λd | averaged dimer degradation rate | |
| Λn | kg + λn + λc | GFP parameter |
| Λg | λg + λc | GFP parameter |
| Rt | lac promoter density (plasmid density) | |
| St | lasB promoter density (plasmid density) | |
| Sa | active lasB promoter density (plasmid density) | |
| Sf | free lasB promoter density (plasmid density) | |
| r1, r2, r3, r4 | [R], [R2], [R2S], [R2S2] | LasR monomer and dimer concentrations |
| s | [S] | Signal molecule concentration |
| t | time since addition of signal molecules | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Claussen, A.; Jakobsen, T.H.; Bjarnsholt, T.; Givskov, M.; Welch, M.; Ferkinghoff-Borg, J.; Sams, T. Kinetic Model for Signal Binding to the Quorum Sensing Regulator LasR. Int. J. Mol. Sci. 2013, 14, 13360-13376. https://doi.org/10.3390/ijms140713360
Claussen A, Jakobsen TH, Bjarnsholt T, Givskov M, Welch M, Ferkinghoff-Borg J, Sams T. Kinetic Model for Signal Binding to the Quorum Sensing Regulator LasR. International Journal of Molecular Sciences. 2013; 14(7):13360-13376. https://doi.org/10.3390/ijms140713360
Chicago/Turabian StyleClaussen, Anetta, Tim Holm Jakobsen, Thomas Bjarnsholt, Michael Givskov, Martin Welch, Jesper Ferkinghoff-Borg, and Thomas Sams. 2013. "Kinetic Model for Signal Binding to the Quorum Sensing Regulator LasR" International Journal of Molecular Sciences 14, no. 7: 13360-13376. https://doi.org/10.3390/ijms140713360




