Optimization of the Culture Medium Composition to Improve the Production of Hyoscyamine in Elicited Datura stramonium L. Hairy Roots Using the Response Surface Methodology (RSM)
Abstract
:1. Introduction
- - First, to use the RSM method for the optimization of nutrients (nitrate, calcium and sucrose) in the culture medium B5 [Gamborg, 1968] to improve hyoscyamine production in elicited HRs;
- - Second, to show the value of the RSM method in the optimization of several responses in plant material cultures.
2. Materials and Methods
2.1. Plant Materials
2.2. Elicitation
2.3. Extraction and Hyoscyamine Analysis
2.4. Theory of RSM
2.5. Global Predicted Capacity, Analysis and Diagnostic of the Model
2.6. Determination of the Optimum
2.7. Application of the RSM for Optimization of the Culture Medium B5
- A factorial design with at least one experimental point located in the center of the experimental area;
- A star design whose axial points −α and +α are located on the axis of each factor. This design is particularly adapted to the progressive acquisition of results with a factorial design 2k.
3. Results and Discussion
3.1. Global Predictivity of the Model
3.2. Analysis of the Quadratic Model
3.3. Diagnostic of the Model
3.3.1. Diagnostic Plot
3.3.2. Influential Observations and Accommodation
3.5. Response Surface (RS) Analysis and Determination of Optimal Concentrations
3.6. Optimization Level
4. Conclusion
References
- Bourgaud, F; Bouque, V; Gontier, E; Guckert, A. Hairy root cultures for the production of secondary metabolites. AgBiotech News Inf 1997, 9, 205–208. [Google Scholar]
- Shanks, JV; Morgan, J. Plant ‘hairy root’ culture. Curr. Opin. Biotechnol 1999, 10, 151–155. [Google Scholar]
- Bourgaud, F; Gravot, A; Milesi, S; Gontier, E. Production of plant secondary metabolites: a historical perspective. Plant Sci 2001, 161, 839–851. [Google Scholar]
- Raoa, SR; Ravishankarb, GA. Plant cell cultures: Chemical factories of secondary metabolites. Biotechnol. Adv 2002, 20, 101–153. [Google Scholar]
- Gontier, E; Sangwan, BS; Barbotin, JN. Effects of calcium, alginate, and calcium-alginate immobilization on growth and tropane alkaloid levels of stable suspension cell line of Datura innoxia Mill. Plant Cell Rep 1994, 9, 533–536. [Google Scholar]
- Saenz-Carbonell, L; Loyola-Vargas, VM. Datura stramonium hairy roots tropane alkaloid content as a response to changes in Gamborg’s B5 medium. Appl. Biochem. Biotechnol 1996, 3, 321–337. [Google Scholar]
- Sikuli, NN; Demeyer, K. Influence of the ion-composition of the medium on alkaloid production by hairy roots of Datura stramonium. Plant Cell Tissue Organ Culture 1997, 47, 261–267. [Google Scholar]
- Nussbaumer, P; Kapétanidis, I; Christen, P. Hairy root of Datura candida × D. aurea: effect of culture medium composition on growth and biosynthesis. Plant Cell Rep 1998, 17, 405–409. [Google Scholar]
- Piñol, MT; Palazón, J; Cusidó, RM; Ribó, M. Influence of calcium ion-concentration in the medium on tropane alkaloid accumulation in Datura stramonium hairy roots. Plant Sci 1999, 141, 41–49. [Google Scholar]
- Boitel-Conti, M; Laberche, JC; Lanoue, A; Ducrocq, C; Sangwan-Norreel, BS. Influence of feeding precursors on tropane alkaloid production during an abiotic stress in Datura innoxia transformed roots. Plant Cell Tissue Organ Cultrue 2000, 60, 131–137. [Google Scholar]
- Lanoue, A; Boitel-Conti, M; Dechaux, C; Laberche, JC; Christen, P; Sangwan-Norreel, BS. Comparison of growth properties, alkaloid production and water uptake of two selected Datura hairy root lines. Acta Biol. Cracoviensia Serie Bot 2004, 46, 185–192. [Google Scholar]
- Amdoun, R; Khelifi, L; Khelifi-Slaoui, M; Amroune, S; Benyoussef, E-H; Thi, DV; Assaf-Ducrocq, C; Gontier, E. Influence of minerals and elicitation on Datura stramonium L. tropane alkaloid production: modelization of the in vitro biochemical response. Plant Sci 2009, 177, 81–87. [Google Scholar]
- Baş, D; Boyacı, IH. Modeling and optimization I: Usability of response surface methodology. J. Food Eng 2007, 78, 836–845. [Google Scholar]
- Bezerra, MA; Santelli, RE; Oliveira, EP; Villar, LS; Escaleira, LA. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar]
- Lundstedt, T; Seifert, E; Abramo, L; Thelin, B; Nyström, Å; Pettersen, J; Bergman, R. Experimental design and optimization. Chemom. Intell. Lab. Syst 1998, 42, 3–40. [Google Scholar]
- Box, GEP; Wilson, KB. On the experimental attainment of optimum conditions. J. R. Stat. Soc. B 1951, 13, 1–45. [Google Scholar]
- Calam, CT. Media for industrial fermentations. Process Biochem 1967, 2, 19–22. [Google Scholar]
- Saval, S; Pablos, L; Sanchez, S. Optimization of culture medium for streptomycin production using response surface methodology. Bioresour. Technol 1993, 43, 19–25. [Google Scholar]
- Maddox, IS; Richert, SH. Use of response surface methodology for the rapid optimization of microbiological media. J. Appl. Bacteriol 1977, 43, 197–204. [Google Scholar]
- Cheynier, V; Feinberg, M; Chararas, C; Ducauze, C. Application of Response Surface Methodology to Evaluation of Bioconversion Experimental Conditions. Appl. Environ. Microbiol 1983, 45, 634–639. [Google Scholar]
- Kartal, M; Kurucu, S; Altun, L; Ceyhan, T; Sayar, E; Cevheroğlu, S; Yetkin, Y. Quantitative Analysis of l-Hyoscyamine in Hyoscyamus reticulatus L. by GC-MS. Turk. J. Chem 2003, 27, 565–569. [Google Scholar]
- Teófilo, RF; Ferreira, MMC. Chemometrics II: spreadsheets for experimental design calculations, a tutorial. Quim. Nova 2006, 29, 338–350. [Google Scholar]
- Goupy, J; Creighton, L. Introduction aux Plans D’éxpériences; DUNOD: Paris, France, 2006. [Google Scholar]
- Myers, RH; Montgomery, DC. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons, Inc: New York, NY, USA, 2009. [Google Scholar]
- Dunlop, DS; Curtis, WR. Synergistic response of plant hairy-root cultures to phosphate limitation and fungal elicitation. Biotechnol. Prog 1991, 7, 434–438. [Google Scholar]
- Vasconsuelo, A; Boland, R. Molecular aspects of the early stages of elicitation of secondary metabolites in plants. Plant Sci 2007, 172, 861–875. [Google Scholar]
- Myers, RH. Response Surface Methodology; Allyn and Bacon Inc: Boston, MA, USA, 1971. [Google Scholar]
- Gamborg, OL; Miller, RA; Ojima, K. Nutrient requirements of suspension cultures of soybean root cells. Exp. Cell Res 1968, 50, 151–158. [Google Scholar]
- Dechaux, C; Boitel-Conti, M. A strategy for overaccumulation of scopolamine in Datura innoxia hairy root cultures. Acta Biol. Cracoviensia Serie Bot 2005, 47, 101–107. [Google Scholar]
- Haaland, PD. Experimental Design in Biotechnology; Marcel Dekker: New York, NY, USA, 1989; pp. 1–18. [Google Scholar]
- Chashmi, NA; Sharifi, M; Karimi, F; Rahnama, H. Enhanced production of tropane alkaloids by nitrate treatment in hairy root cultures of Atropa belladonna. J. Biotechnol 2008, 136, 22–71. [Google Scholar]
- Zhao, J; Davis, LC; Verpoorte, R. Elicitor signal transduction leading to production of plant secondary metabolites. Biotechnol. Adv 2005, 23, 283–333. [Google Scholar]
- Dodge, Y. Statistique: Dictionnaire Encyclopédique; DUNOD: Paris, France, 1993. [Google Scholar]
- Draper, NR; Smith, H. Applied Regression Analysis, 2nd ed; John Wiley & Sons Publication: New York, NY, USA, 1981. [Google Scholar]
- Montgomery, DC. Design and Analysis of Experiments; John Wiley & Sons, Inc: New York, NY, USA, 2008. [Google Scholar]
- Mason, RL; Gunst, RF; Hess, JL. Statistical Design and Analysis of Experiments with Applications to Engineering and Science, 2nd ed; John Wiley & Sons, Inc: New York, NY, USA, 2003. [Google Scholar]
- Cook, RD. Detection of influential observation in linear regression. Technometrics. 1977, 19, pp. 15–18. Available online: http://www.ime.usp.br/~abe/lista/pdfWiH1zqnMHo.pdf (accessed on 17 November 2010).
- Belsley, DA; Kuh, E; Welsch, RE. Regression Diagnostics—Identifying Influential Data and Sources of Collinearity; John Wiley & Sons, Inc: New York, NY, USA, 2004. [Google Scholar]
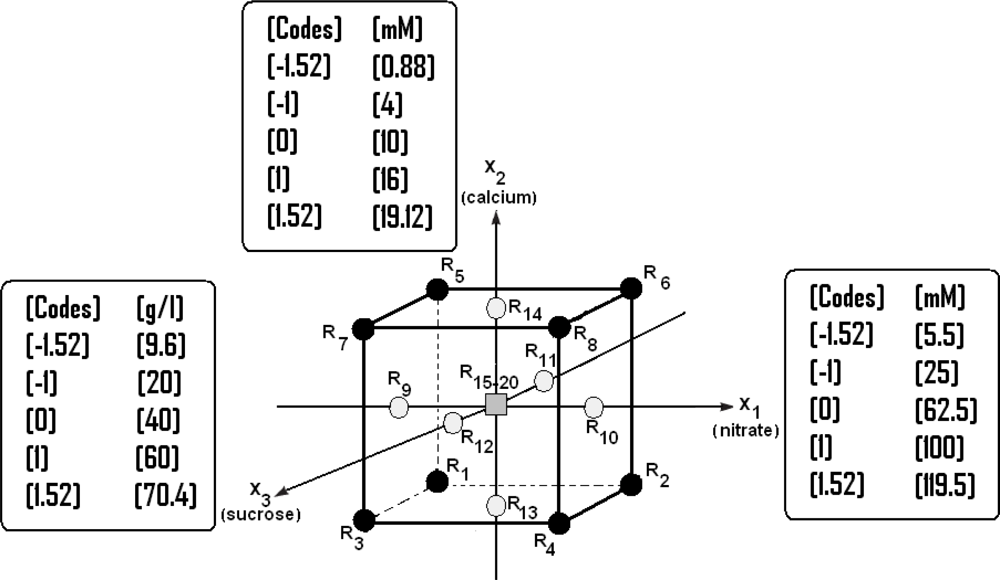
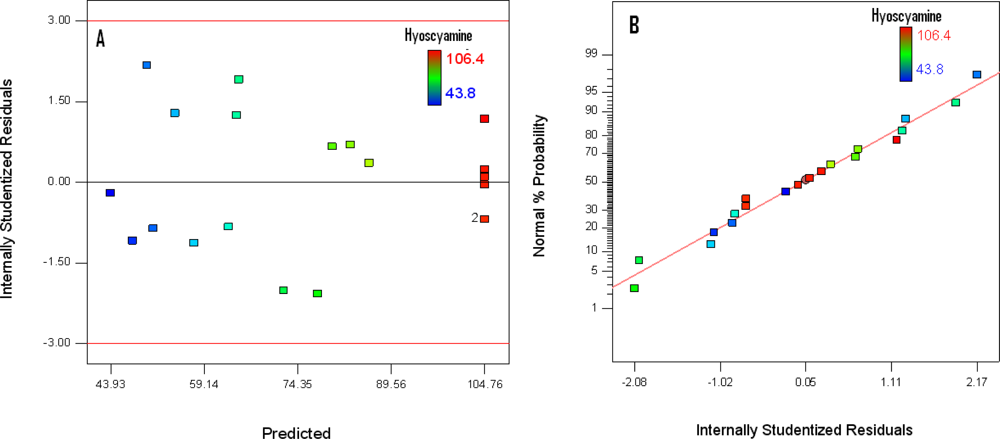
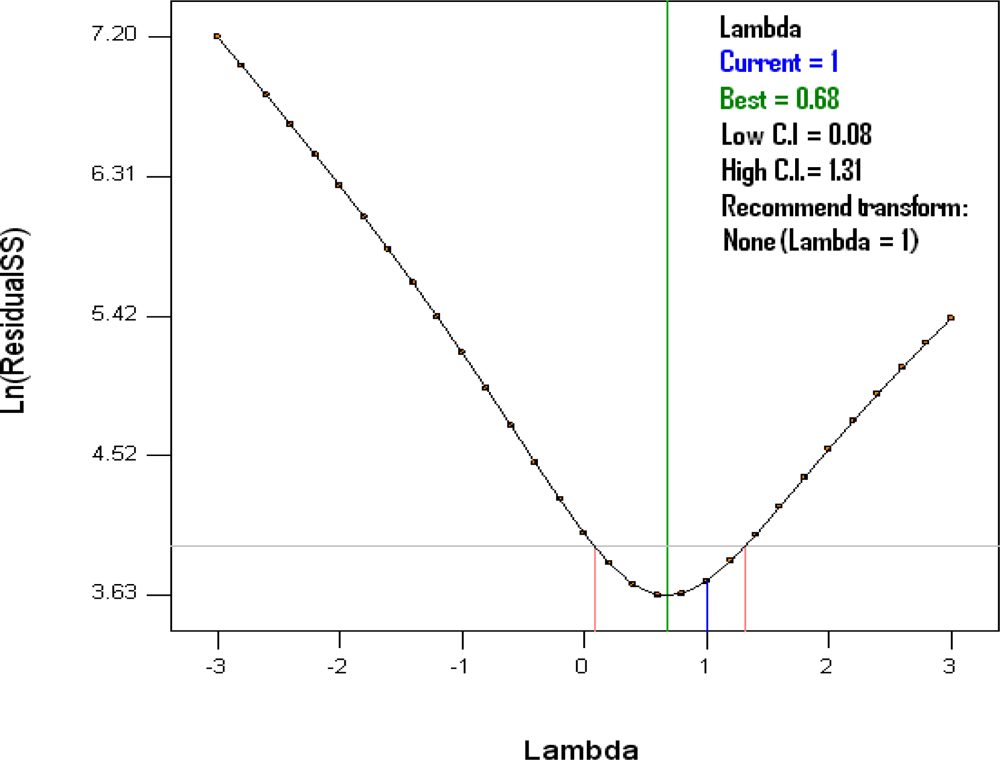
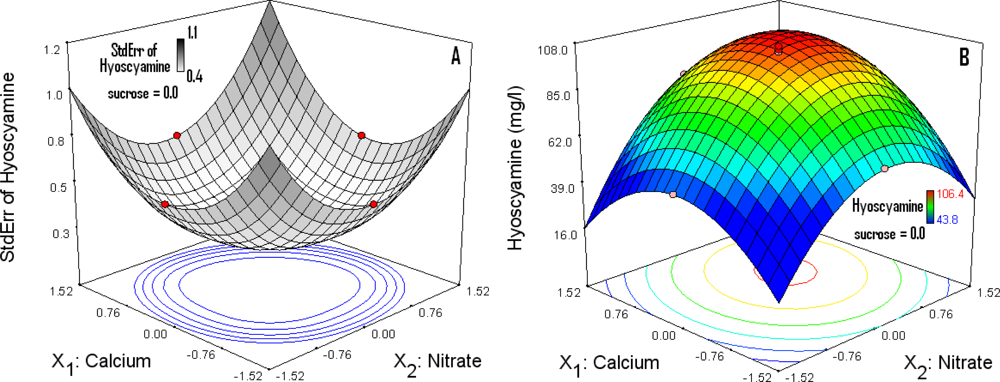
| Source | Sum of Squares | df | Mean Square | F-value | p-value |
|---|---|---|---|---|---|
| Model | 9537.1 | 10 | 953.7 | 414.1 | 0.0 |
| Residual | 20.7 | 9 | 2.3 | ||
| Lack of fit | 16.1 | 4 | 4.0 | 4.3 | 0.1 |
| Pure Error | 4.7 | 5 | 0.9 | ||
| Total | 9557.8 | 19 | |||
| Model Terms | Coefficient Estimate | t-statistic | p-value |
|---|---|---|---|
| Intercept | 104.8 | 172.2 | - |
| x1: nitrate | 10.5 | 24.6 | 0.0 |
| x2: calcium | 5.5 | 12.9 | 0.0 |
| x3: sucrose | 4.2 | 9.8 | 0.0 |
| x1x2 | 3.5 | 6.5 | 0.0 |
| x1x3 | 1.0 | 1.9 | 0.1 |
| x2x3 | 1.0 | 1.9 | 0.1 |
| x12 | −16.4 | −35.4 | 0.0 |
| x22 | −14.4 | −31.1 | 0.0 |
| x32 | −14.5 | −31.3 | 0.0 |
| x1x2x3 | 0.7 | 1.3 | 0.2 |
| Model with Full Terms | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Run Order (n) | Variable Code Levels | Measured | Predicted | Residual | hi Leverage | Cook’s Distance | DFFITS | ||
| x1 [NO3−] | x2 [Ca2+] | x3 [sucrose] | |||||||
| R1 | −1 | −1 | −1 | 43.8 | 43.9 | −0.1 | 0.8 | 0.0 | −0.4 |
| R2 | 1 | −1 | −1 | 56.8 | 57.5 | −0.7 | 0.8 | 0.5 | −2.5 |
| R3 | −1 | 1 | −1 | 46.8 | 47.5 | −0.7 | 0.8 | 0.5 | −2.4 |
| R4 | 1 | 1 | −1 | 70.8 | 72.0 | −1.3 | 0.8 | 1.7 | −5.6 |
| R5 | −1 | −1 | 1 | 51.2 | 49.8 | 1.4 | 0.8 | 2.0 | 6.5 |
| R6 | 1 | −1 | 1 | 65.2 | 64.4 | 0.8 | 0.8 | 0.7 | 2.8 |
| R7 | −1 | 1 | 1 | 55.2 | 54.4 | 0.8 | 0.8 | 0.7 | 2.9 |
| R8 | 1 | 1 | 1 | 86.2 | 86.0 | 0.2 | 0.8 | 0.1 | 0.7 |
| R9 | −1.52 | 0 | 0 | 50.0 | 50.9 | −0.9 | 0.6 | 0.1 | −1.0 |
| R10 | 1.52 | 0 | 0 | 83.6 | 83.0 | 0.7 | 0.6 | 0.1 | 0.8 |
| R11 | 0 | −1.52 | 0 | 62.3 | 63.1 | −0.8 | 0.6 | 0.1 | −0.9 |
| R12 | 0 | 1.52 | 0 | 80.6 | 79.9 | 0.7 | 0.6 | 0.1 | 0.7 |
| R13 | 0 | 0 | −1.52 | 66.7 | 64.8 | 1.8 | 0.6 | 0.4 | 2.7 |
| R14 | 0 | 0 | 1.52 | 75.5 | 77.5 | −2.0 | 0.6 | 0.5 | −3.1 |
| R15 | 0 | 0 | 0 | 103.8 | 104. 8 | −1.0 | 0.2 | 0.0 | −0.3 |
| R16 | 0 | 0 | 0 | 104.7 | 104.8 | −0.0 | 0.2 | 0.0 | 0.0 |
| R17 | 0 | 0 | 0 | 105.1 | 104.8 | 0.3 | 0.2 | 0.0 | 0.1 |
| R18 | 0 | 0 | 0 | 106.4 | 104.8 | 1.6 | 0.2 | 0.0 | 0.5 |
| R19 | 0 | 0 | 0 | 103.8 | 104.8 | −1.0 | 0.2 | 0.0 | −0.3 |
| R20 | 0 | 0 | 0 | 104.9 | 104.8 | 0.1 | 0.2 | 0.0 | 0.0 |
| Model with Only Significant Terms (Equation 5) | |||||||||
| R4 | 1 | 1 | −1 | 70.8 | 74.8 | −4.0 | 0.6 | 0.9 | −4.7 |
| R8 | 1 | 1 | 1 | 86.2 | 83.2 | 2.3 | 0.5 | 0.5 | 2.4 |
| R14 | 0 | 0 | 1.52 | 75.5 | 77.5 | −2.0 | 0.6 | 0.5 | −2.2 |
| Biomass (g DW/L) | Production of HS | |||||
|---|---|---|---|---|---|---|
| (mg/g DW) | (mg/L) | |||||
| Without Elicitation | With Elicitation | Without Elicitation | With Elicitation | |||
| B5 * | 8.4 ± 0.6 | 2.1 ± 0.1 | 4.2 ± 0.6 | 17.6 ± 1.6 | 35.3 ± 2.0 | |
| B5-OP ** | 12.7 ± 0.2 | 3.8 ± 0.1 | 8.5 ± 0.3 | 48.3 ± 2.3 | 110.3 ± 1.4 | |
| Optimization | 51.2% | 81% | 101.2% | 173.6% | 212.7% | |
| LSD test | differences | −4.3 | −1.7 | −4.3 | −30.6 | −75.0 |
| ±limits | 0.9 | 0.2 | 0.8 | 4.4 | 13.8 | |
| significance | significant | significant | significant | significant | significant | |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Amdoun, R.; Khelifi, L.; Khelifi-Slaoui, M.; Amroune, S.; Asch, M.; Assaf-Ducrocq, C.; Gontier, E. Optimization of the Culture Medium Composition to Improve the Production of Hyoscyamine in Elicited Datura stramonium L. Hairy Roots Using the Response Surface Methodology (RSM). Int. J. Mol. Sci. 2010, 11, 4726-4740. https://doi.org/10.3390/ijms11114726
Amdoun R, Khelifi L, Khelifi-Slaoui M, Amroune S, Asch M, Assaf-Ducrocq C, Gontier E. Optimization of the Culture Medium Composition to Improve the Production of Hyoscyamine in Elicited Datura stramonium L. Hairy Roots Using the Response Surface Methodology (RSM). International Journal of Molecular Sciences. 2010; 11(11):4726-4740. https://doi.org/10.3390/ijms11114726
Chicago/Turabian StyleAmdoun, Ryad, Lakhdar Khelifi, Majda Khelifi-Slaoui, Samia Amroune, Mark Asch, Corinne Assaf-Ducrocq, and Eric Gontier. 2010. "Optimization of the Culture Medium Composition to Improve the Production of Hyoscyamine in Elicited Datura stramonium L. Hairy Roots Using the Response Surface Methodology (RSM)" International Journal of Molecular Sciences 11, no. 11: 4726-4740. https://doi.org/10.3390/ijms11114726
APA StyleAmdoun, R., Khelifi, L., Khelifi-Slaoui, M., Amroune, S., Asch, M., Assaf-Ducrocq, C., & Gontier, E. (2010). Optimization of the Culture Medium Composition to Improve the Production of Hyoscyamine in Elicited Datura stramonium L. Hairy Roots Using the Response Surface Methodology (RSM). International Journal of Molecular Sciences, 11(11), 4726-4740. https://doi.org/10.3390/ijms11114726




