The Substituent Effect on the Radical Scavenging Activity of Apigenin
Abstract
:1. Introduction
2. Results
2.1. Frontier Orbitals Analysis
2.2. Donator Acceptor Map Analysis
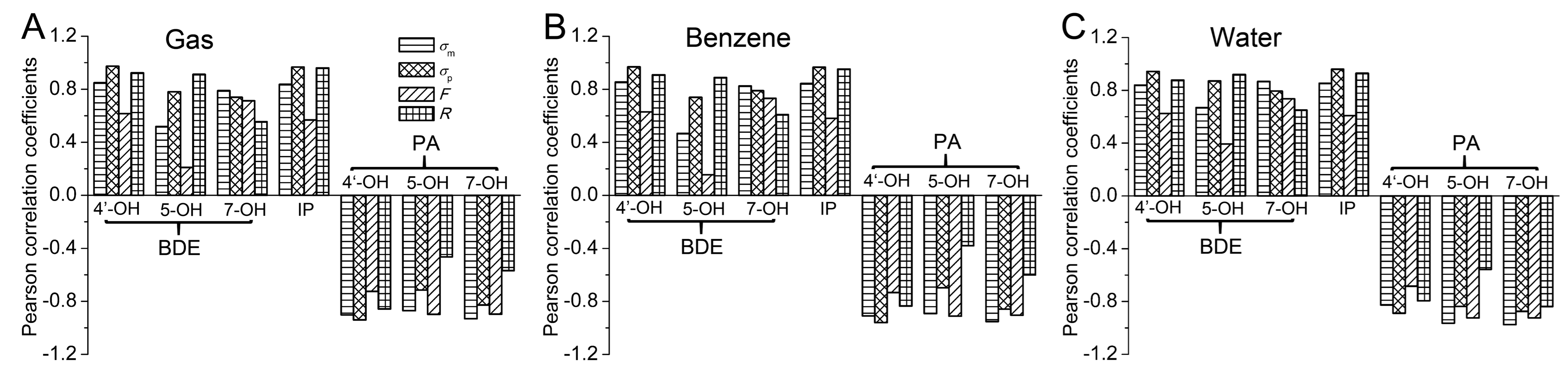
2.3. Bond Dissociation Enthalpy, Ionization Potential, and Proton Affinity Analysis
2.3.1. Bond Dissociation Enthalpy
2.3.2. Ionization Potential
2.3.3. Proton Affinity
3. Discussion
4. Materials and Methods
4.1. Computational Details
4.2. Statistics Analysis
5. Conclusions
- (1)
- The electronic effect of the substituent on the BDE and PA of 4′-OH and IP was mainly governed by the resonance effect, while that on the BDE and PA of 7-OH was mainly controlled by the field/inductive effect. For 5-OH, the BDE and PA were more influenced by the resonance effect and field/inductive effect, respectively.
- (2)
- The substituent effects on BDE and IP were very different from those on PA. The electron-withdrawing groups enhanced BDE and IP, while the electron-donating groups reduced the BDE and IP. The effect of the substituents on PA was to the contrary.
- (3)
- In the gas and benzene phases, the free radical scavenging progress of the investigated compounds underwent the HAT mechanism with the most possibility. In the water phase, SPLET was the most favorable mechanism. Therefore, in the gas and benzene phases, the electron-withdrawing groups at the C3 position reduced the antioxidative activity of apigenin while the electron-donating groups had the opposite effect. In the water phase, it was to the contrary. Furthermore, the NH2-substituted derivative was the strongest antioxidant in the gas and benzene phases, while the NO2-substituted derivative was the strongest antioxidant in the water phase.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DFT | density functional theory |
| HAT | hydrogen atom transfer |
| SPLET | sequential proton loss electron transfer |
| SET-PT | single electron transfer followed by proton transfer |
| ArOH | flavonoid |
| BDE | bond dissociation enthalpy |
| IP | ionization potential |
| PDE | proton dissociation enthalpy |
| PA | proton affinity |
| ETE | electron transfer enthalpy |
| ΔrG | Gibbs free energy |
| σ | Hammett sigma constants |
| F | field/inductive effect |
| R | resonance effect |
References
- Dizdaroglu, M.; Jaruga, P.; Birincioglu, M.; Rodriguez, H. Free radical-induced damage to DNA: Mechanisms and measurement. Free Radical Biol. Med. 2002, 32, 1102–1115. [Google Scholar] [CrossRef]
- Ross, J.A.; Kasum, C.M. Dietary flavonoids: Bioavailability, metabolic effects, and safety. Annu. Rev. Nutr. 2002, 22, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Treml, J.; Šmejkal, K. Flavonoids as potent scavengers of hydroxyl radicals. Compr. Rev. Food Sci. 2016, 15, 720–738. [Google Scholar] [CrossRef]
- Rhayem, Y.; Thérond, P.; Camont, L.; Couturier, M.; Beaudeux, J.L.; Legrand, A.; Jore, D.; Gardés-Albert, M.; Bonnefont-Rousselot, D. Chain-breaking activity of resveratrol and piceatannol in a linoleate micellar model. Chem. Phys. Lipids 2008, 155, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Procházková, D.; Boušová, I.; Wilhelmová, N. Antioxidant and prooxidant properties of flavonoids. Fitoterapia 2011, 82, 513–523. [Google Scholar] [CrossRef] [PubMed]
- Tapas, A.R.; Sakarkar, D.M.; Kakde, R.B. Flavonoids as nutraceuticals: A review. Trop. J. Pharm. Res. 2008, 7, 1089–1099. [Google Scholar] [CrossRef]
- Perron, N.R.; Brumaghim, J.L. A review of the antioxidant mechanisms of polyphenol compounds related to iron binding. Cell Biochem. Biophys. 2009, 53, 75–100. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zheng, J.; Li, Y.; Xu, D.P.; Li, S.; Chen, Y.M.; Li, H.B. Natural polyphenols for prevention and treatment of cancer. Nutrients 2016, 8, 515. [Google Scholar] [CrossRef] [PubMed]
- Bak, M.J.; Gupta, S.D.; Wahler, J.; Suh, N. Role of dietary bioactive natural products in estrogen receptor-positive breast cancer. Semin. Cancer Biol. 2016, 40–41, 170–191. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Afaq, F.; Mukhtar, H. Selective growth-inhibitory, cell-cycle deregulatory and apoptotic response of apigenin in normal versus human prostate carcinoma cells. Biochem. Bioph. Res. Commun. 2001, 287, 914–920. [Google Scholar] [CrossRef] [PubMed]
- Shukla, S.; Gupta, S. Apigenin: A promising molecule for cancer prevention. Pharm. Res. 2010, 27, 962–978. [Google Scholar] [CrossRef] [PubMed]
- Borges, R.S.; Batista, J.; Viana, R.B.; Baetas, A.C.; Orestes, E.; Andrade, M.A.; Honório, K.M.; da Silva, A.B.F. Understanding the molecular aspects of tetrahydrocannabinol and cannabidiol as antioxidants. Molecules 2013, 18, 12663–12674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nenadis, N.; Sigalas, M.P. A DFT study on the radical scavenging potential of selected natural 3′,4′-dihydroxy aurones. Food Res. Int. 2011, 44, 114–120. [Google Scholar] [CrossRef]
- Amić, A.; Lučić, B.; Stepanić, V.; Marković, Z.; Marković, S.; Marković, J.M.D.; Amić, D. Free radical scavenging potency of quercetin catecholic colonic metabolites: Thermodynamics of 2H+/2e− processes. Food Chem. 2017, 218, 144–151. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.Z.; Deng, G.; Chen, D.F.; Liang, Q.; Guo, R.; Fu, Z.M. Theoretical studies on the antioxidant activity of pinobanksin and its ester derivatives: Effects of the chain length and solvent. Food Chem. 2018, 240, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Anouar, E.H.; Shah, S.A.A.; Hassan, N.B.; Moussaoui, N.E.; Ahmad, R.; Zulkefeli, M.; Weber, J.F.F. Antioxidant activity of hispidin oligomers from medicinal fungi: A DFT study. Molecules 2014, 19, 3489–3507. [Google Scholar] [CrossRef] [PubMed]
- Gloria, C.; Jose, T.; Francisco, T. Classification of phenolic compounds by chemical structural indicators and its relation to antioxidant properties of Posidonia oceanica. Commun. Math. Comput. Chem. 2012, 67, 231–250. [Google Scholar]
- Vagánek, A.; Rimarčík, J.; Dropková, K.; Lengyel, J.; Klein, E. Reaction enthalpies of O−H bonds splitting-off in flavonoids: The role of non-polar and polar solvent. Comput. Theor. Chem. 2014, 1050, 31–38. [Google Scholar] [CrossRef]
- Bendary, E.; Francis, R.R.; Ali, H.M.G.; Sarwat, M.I.; El Hady, S. Antioxidant and structure–activity relationships (SARs) of some phenolic and anilines compounds. Ann. Agric. Sci. 2013, 58, 173–181. [Google Scholar] [CrossRef]
- Leopoldini, M.; Rondinelli, F.; Russo, N.; Toscano, M. Pyranoanthocyanins: A theoretical investigation on their antioxidant activity. J. Agric. Food Chem. 2010, 58, 8862–8871. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Zheng, Y.; An, L.; Dou, Y.; Liu, Y. Density functional theory study of the structure–antioxidant activity of polyphenolic deoxybenzoins. Food Chem. 2014, 151, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Xue, Y.; An, L.; Zheng, Y.; Dou, Y.; Zhang, L.; Liu, Y. Theoretical study on the structural and antioxidant properties of some recently synthesised 2, 4, 5-trimethoxy chalcones. Food Chem. 2015, 171, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Galano, A.; Mazzone, G.; Alvarez-Diduk, R.; Marino, T.; Alvarez-Idaboy, J.R.; Russo, N. Food antioxidants: Chemical insights at the molecular level. Annu. Rev. Food Sci. Technol. 2016, 7, 335–352. [Google Scholar] [CrossRef] [PubMed]
- Leopoldini, M.; Russo, N.; Toscano, M. The molecular basis of working mechanisms of natural polyphenolic antioxidants. Food Chem. 2011, 125, 288–306. [Google Scholar] [CrossRef]
- Stepanić, V.; Trošelj, K.G.; Lučić, B.; Marković, Z.; Amić, D. Bond dissociation free energy as a general parameter for flavonoid radical scavenging activity. Food Chem. 2013, 141, 1562–1570. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.S.; Johnson, E.R.; DiLabio, G.A. Predicting the activity of phenolic antioxidants: Theoretical method, analysis of substituent effects, and application to major families of antioxidants. J. Am. Chem. Soc. 2001, 123, 1173–1183. [Google Scholar] [CrossRef] [PubMed]
- Martínez, A.; Rodríguezgironés, M.A.; Barbosa, A.; Costas, M. Donator acceptor map for carotenoids, melatonin and vitamins. J. Phys. Chem. A 2008, 112, 9037–9042. [Google Scholar] [CrossRef] [PubMed]
- Martínez, A.; Vargas, R.; Galano, A. What is important to prevent oxidative stress? A theoretical study on electron-transfer reactions between carotenoids and free radicals. J. Phys. Chem. B 2009, 113, 12113–12120. [Google Scholar] [CrossRef] [PubMed]
- Martínez, A. Donator Acceptor map of psittacofulvins and anthocyanins: Are they good antioxidant substances? J. Phys. Chem. B 2009, 113, 4915–4921. [Google Scholar] [CrossRef] [PubMed]
- Genix, P.; Jullien, H.; Goas, R.L. Estimation of Hammett sigma constants from calculated atomic charges using partial least squares regression. J. Chemometr. 2015, 10, 631–636. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A.; Taft, R.W. A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Sun, Y.M.; Wang, X.L. Electronic effects on O−H proton dissociation energies of phenolic cation radicals: A DFT Study. J. Org. Chem. 2002, 67, 2709–2712. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.Y.; Sun, Y.M.; Chen, D.Z. O–H bond dissociation energies of phenolic compounds are determined by field/inductive effect or resonance effect? A DFT study and its implication. Mol. Inform. 2001, 20, 148–152. [Google Scholar] [CrossRef]
- Rimarčík, J.; Lukeš, V.; Klein, E.; Ilčin, M. Study of the solvent effect on the enthalpies of homolytic and heterolytic N-H bond cleavage in pphenylenediamine and tetracyano-p-phenylenediamine. J. Mol. Struct. Theochem 2010, 925, 25–30. [Google Scholar] [CrossRef]
- Bartmess, J.E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. [Google Scholar] [CrossRef]
- Parker, V.D. Homolytic bond (H–A) dissociation free energies in solution. Applications of the standard potential of the (H+/H.bul.) couple. J. Am. Chem. Soc. 1992, 114, 7458–7462. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N. Gaussian 03 (Revision C.02); Gaussian Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Rodriguez-Lujan, I.; Huerta, R.; Elkan, C.; Cruz, C.S. Quadratic programming feature selection. J. Mach. Learn. Res. 2010, 11, 1491–1516. [Google Scholar]
Sample Availability: Samples of the compounds are not available from the authors. |

| Gas | Benzene | Water | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 4′-OH | 5-OH | 7-OH | 4′-OH | 5-OH | 7-OH | 4′-OH | 5-OH | 7-OH | |
| H | 368.6 | 435.2 | 387.4 | 372.2 | 429.6 | 391.6 | 368.1 | 393.7 | 390.2 |
| NH2 | 357.4 | 424.7 | 384.4 | 359.4 | 419.3 | 386.5 | 351.0 | 383.6 | 379.1 |
| OMe | 366.2 | 430.7 | 387.3 | 370.0 | 425.9 | 391.2 | 367.4 | 391.9 | 389.2 |
| Me | 369.2 | 432.8 | 387.1 | 372.7 | 427.5 | 391.0 | 368.8 | 391.6 | 388.7 |
| OH | 360.5 | 422.8 | 386.9 | 363.7 | 417.6 | 390.2 | 357.9 | 384.9 | 385.5 |
| F | 369.8 | 431.2 | 389.4 | 373.9 | 425.2 | 393.8 | 370.6 | 390.6 | 392.1 |
| Cl | 372.3 | 432.6 | 389.9 | 376.6 | 426.8 | 394.7 | 373.8 | 392.4 | 393.4 |
| CHO | 374.0 | 435.5 | 391.2 | 377.1 | 430.2 | 395.8 | 373.1 | 396.5 | 395.0 |
| CF3 | 376.2 | 434.3 | 391.4 | 380.4 | 428.5 | 396.4 | 377.0 | 394.7 | 395.8 |
| CN | 378.5 | 435.9 | 392.2 | 382.9 | 429.8 | 397.4 | 379.3 | 395.9 | 397.1 |
| NO2 | 378.4 | 433.8 | 411.0 | 382.7 | 427.6 | 416.8 | 380.0 | 395.5 | 416.4 |
| Gas | Benzene | Water | |
|---|---|---|---|
| H | 792.9 | 684.0 | 589.1 |
| NH2 | 703.0 | 591.8 | 503.6 |
| OMe | 735.2 | 633.4 | 556.9 |
| Me | 779.8 | 671.8 | 586.2 |
| OH | 740.8 | 636.3 | 548.8 |
| F | 790.1 | 680.4 | 590.4 |
| Cl | 793.4 | 689.1 | 603.0 |
| CHO | 814.3 | 702.1 | 606.1 |
| CF3 | 815.0 | 703.2 | 604.6 |
| CN | 827.3 | 718.5 | 631.5 |
| NO2 | 833.0 | 724.8 | 636.8 |
| Gas | Benzene | Water | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 4′-OH | 5-OH | 7-OH | 4′-OH | 5-OH | 7-OH | 4′-OH | 5-OH | 7-OH | |
| H | 1354.8 | 1453.7 | 1378.4 | 402.0 | 476.4 | 411.7 | 146.9 | 162.5 | 139.1 |
| NH2 | 1371.2 | 1446.1 | 1377.8 | 412.6 | 471.2 | 414.7 | 155.4 | 164.9 | 144.2 |
| OMe | 1364.0 | 1445.2 | 1374.0 | 407.6 | 470.1 | 408.9 | 148.0 | 162.2 | 140.2 |
| Me | 1366.5 | 1456.4 | 1382.3 | 411.4 | 478.3 | 414.3 | 154.8 | 165.3 | 141.5 |
| OH | 1362.0 | 1423.5 | 1368.0 | 400.4 | 452.0 | 410.6 | 152.2 | 156.2 | 140.0 |
| F | 1353.0 | 1434.8 | 1364.7 | 399.1 | 459.6 | 400.8 | 147.0 | 155.9 | 136.8 |
| Cl | 1355.3 | 1436.1 | 1364.8 | 400.5 | 460.7 | 402.0 | 151.2 | 156.6 | 135.6 |
| CHO | 1340.1 | 1426.6 | 1353.9 | 389.4 | 456.1 | 394.1 | 141.2 | 155.7 | 133.9 |
| CF3 | 1341.9 | 1426.5 | 1355.4 | 391.5 | 453.5 | 393.7 | 146.8 | 153.2 | 133.1 |
| CN | 1329.2 | 1417.5 | 1345.7 | 381.5 | 447.2 | 387.3 | 141.4 | 151.9 | 131.8 |
| NO2 | 1330.4 | 1411.7 | 1343.0 | 382.3 | 442.7 | 385.7 | 137.8 | 149.0 | 130.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.-Z.; Chen, D.-F.; Deng, G.; Guo, R. The Substituent Effect on the Radical Scavenging Activity of Apigenin. Molecules 2018, 23, 1989. https://doi.org/10.3390/molecules23081989
Zheng Y-Z, Chen D-F, Deng G, Guo R. The Substituent Effect on the Radical Scavenging Activity of Apigenin. Molecules. 2018; 23(8):1989. https://doi.org/10.3390/molecules23081989
Chicago/Turabian StyleZheng, Yan-Zhen, Da-Fu Chen, Geng Deng, and Rui Guo. 2018. "The Substituent Effect on the Radical Scavenging Activity of Apigenin" Molecules 23, no. 8: 1989. https://doi.org/10.3390/molecules23081989




