A Polarizable Atomic Multipole-Based Force Field for Molecular Dynamics Simulations of Anionic Lipids
Abstract
:1. Introduction
Potential Energy Model
2. Results and Discussion
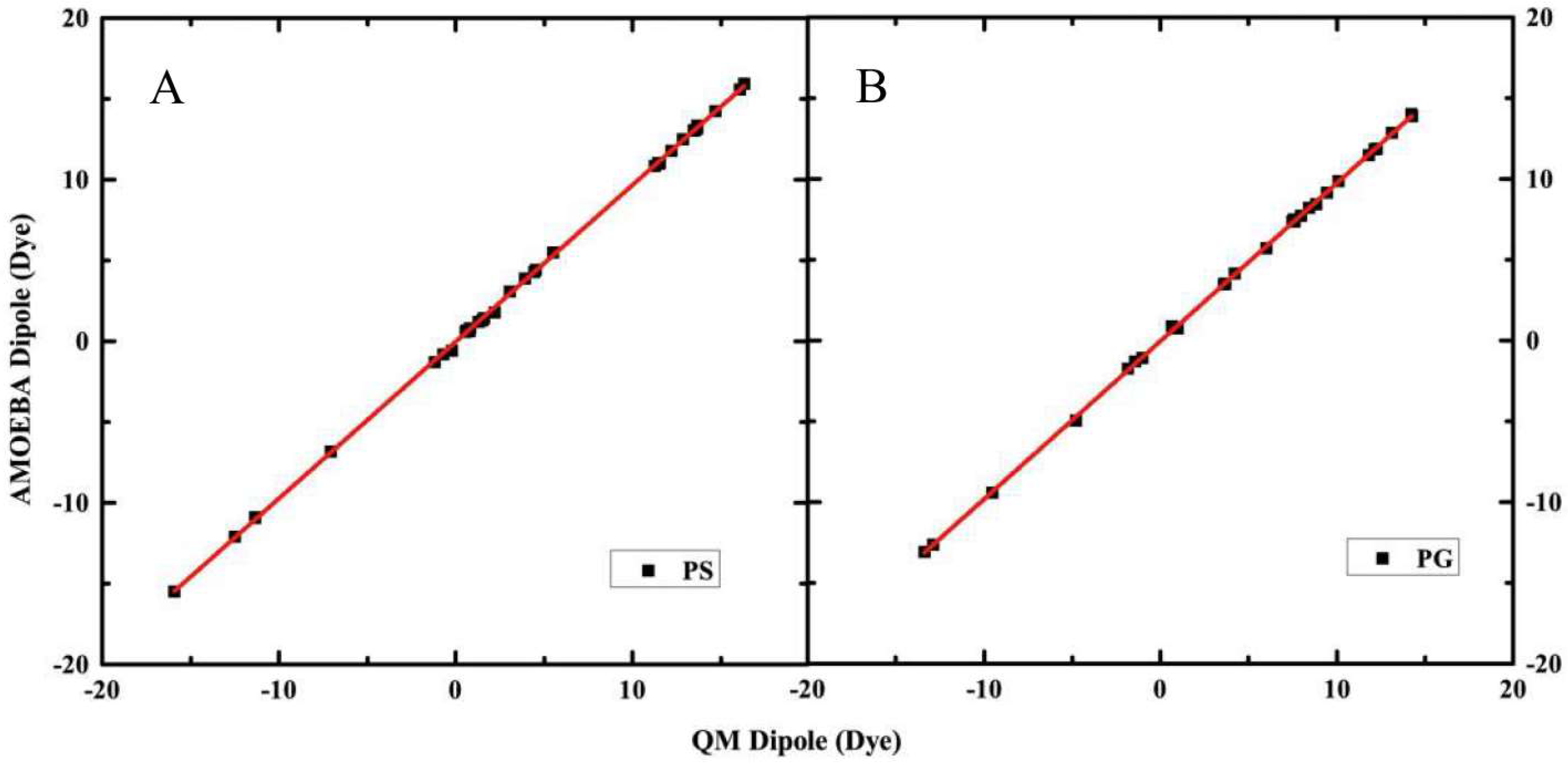
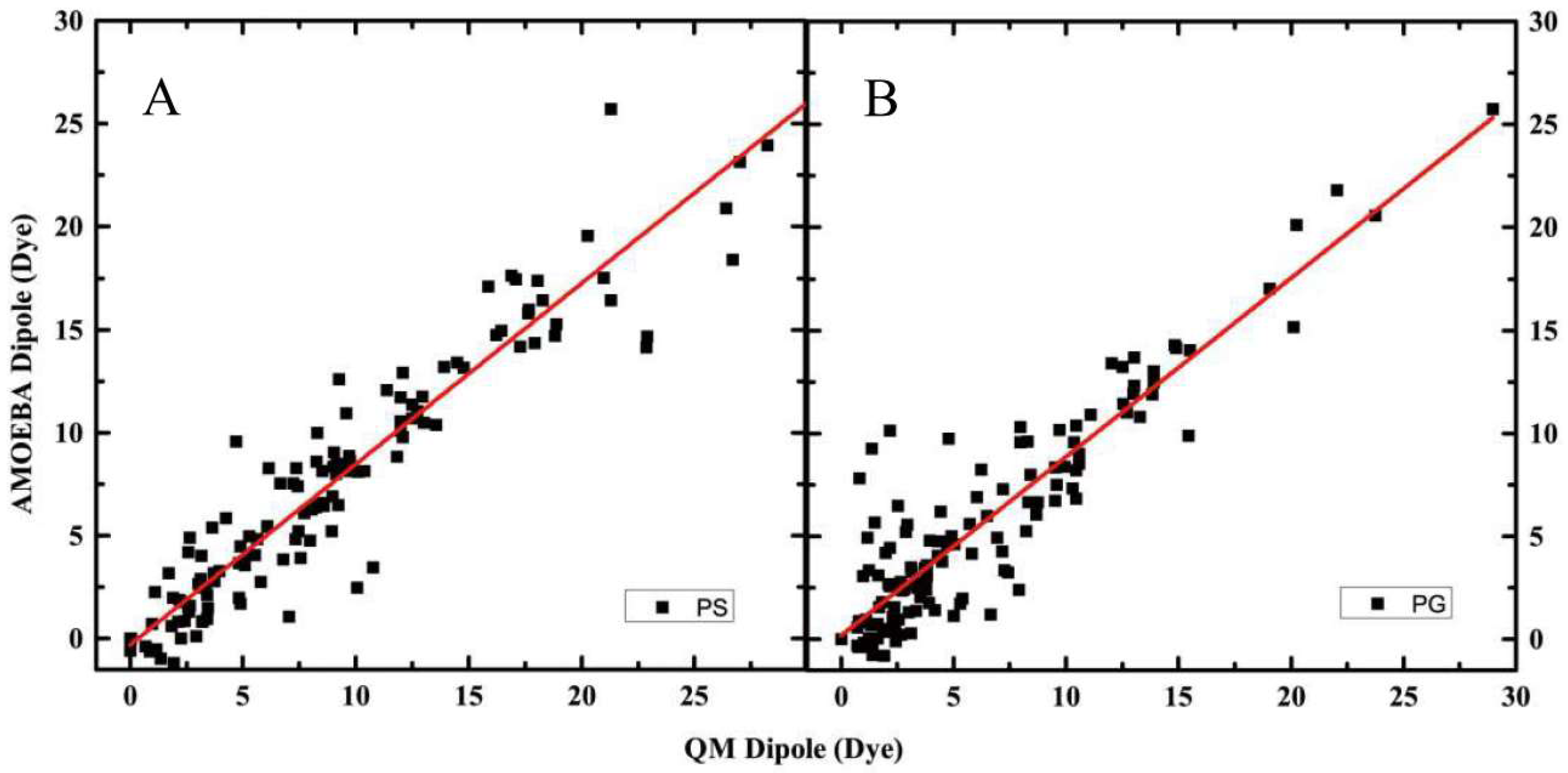
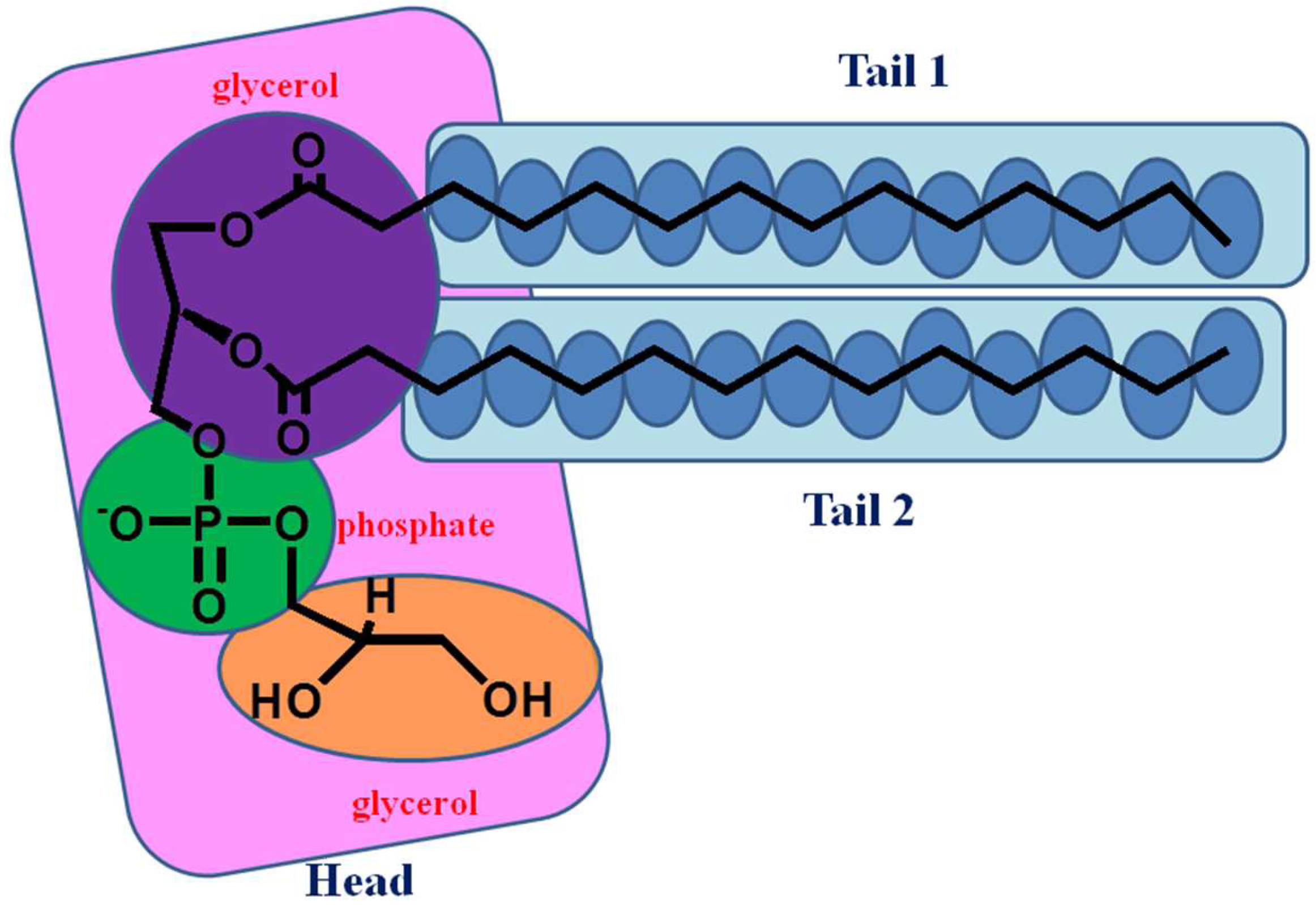
2.1. Electrostatic Properties of Headgroup
2.2. Modification of Torsion Parameters
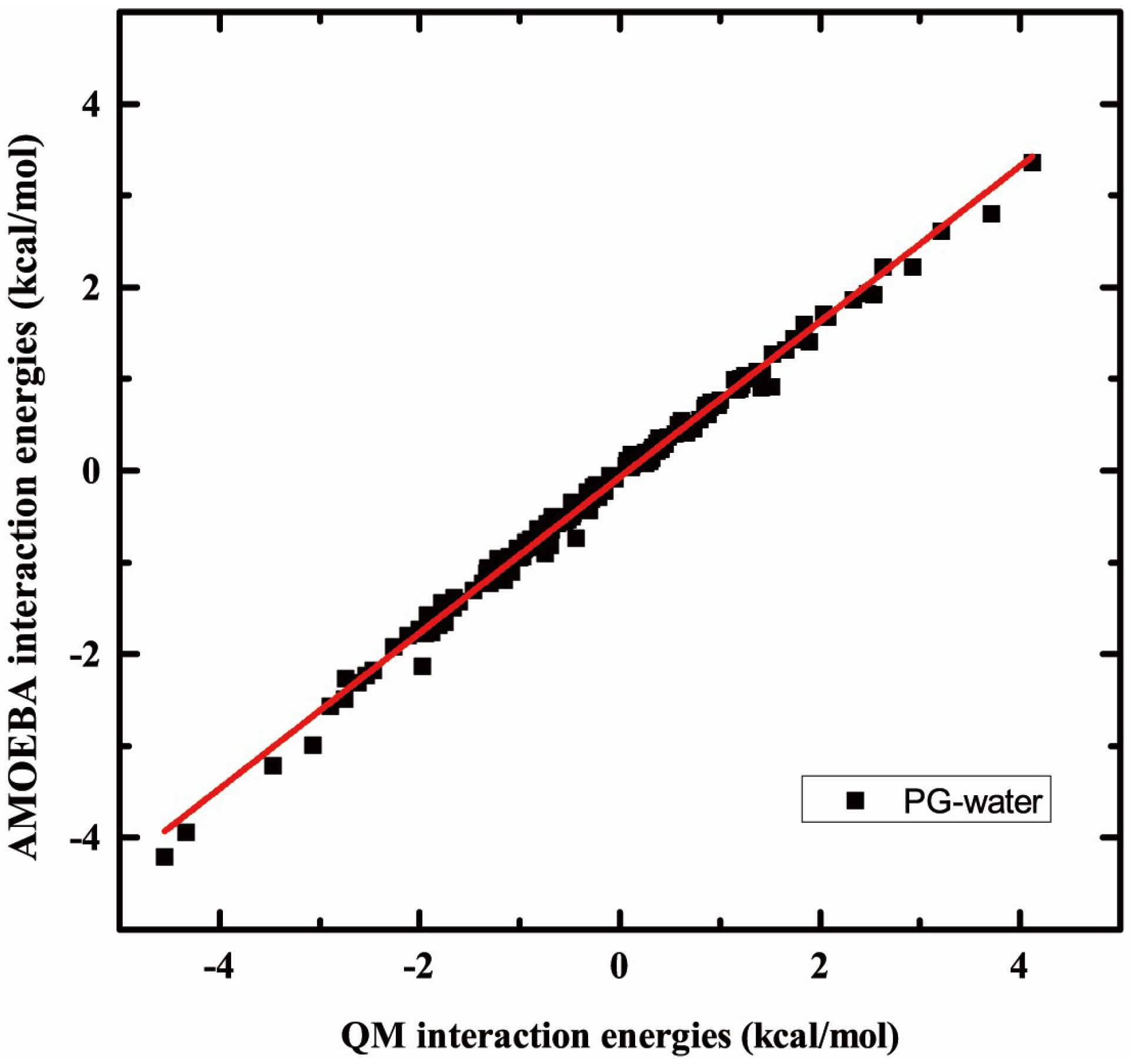
2.3. Validation of Interaction Headgroup with Small Molecules including Water and Ions
2.4. Simulation and Validation
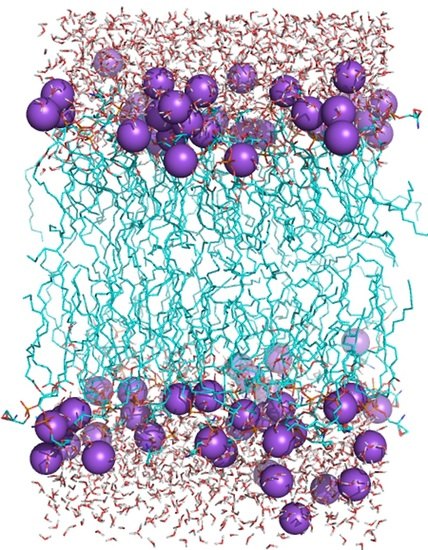
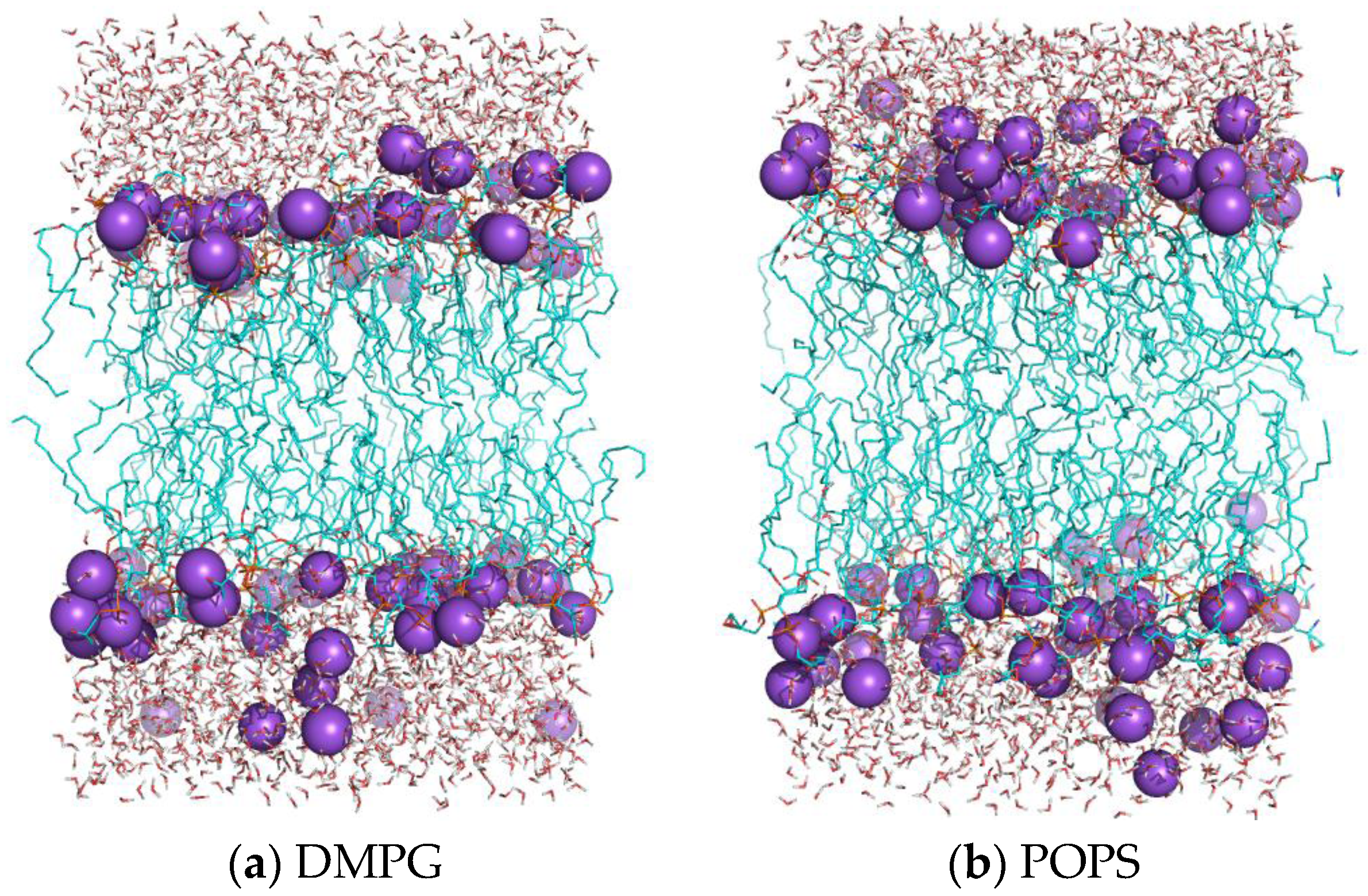
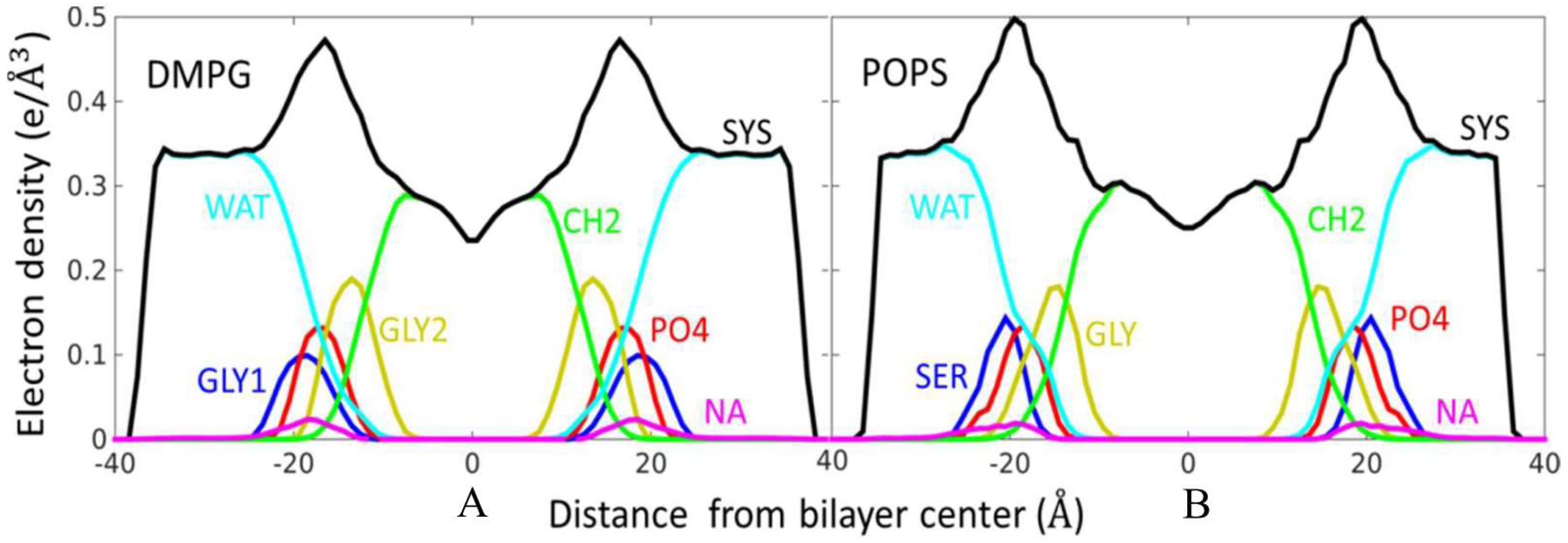
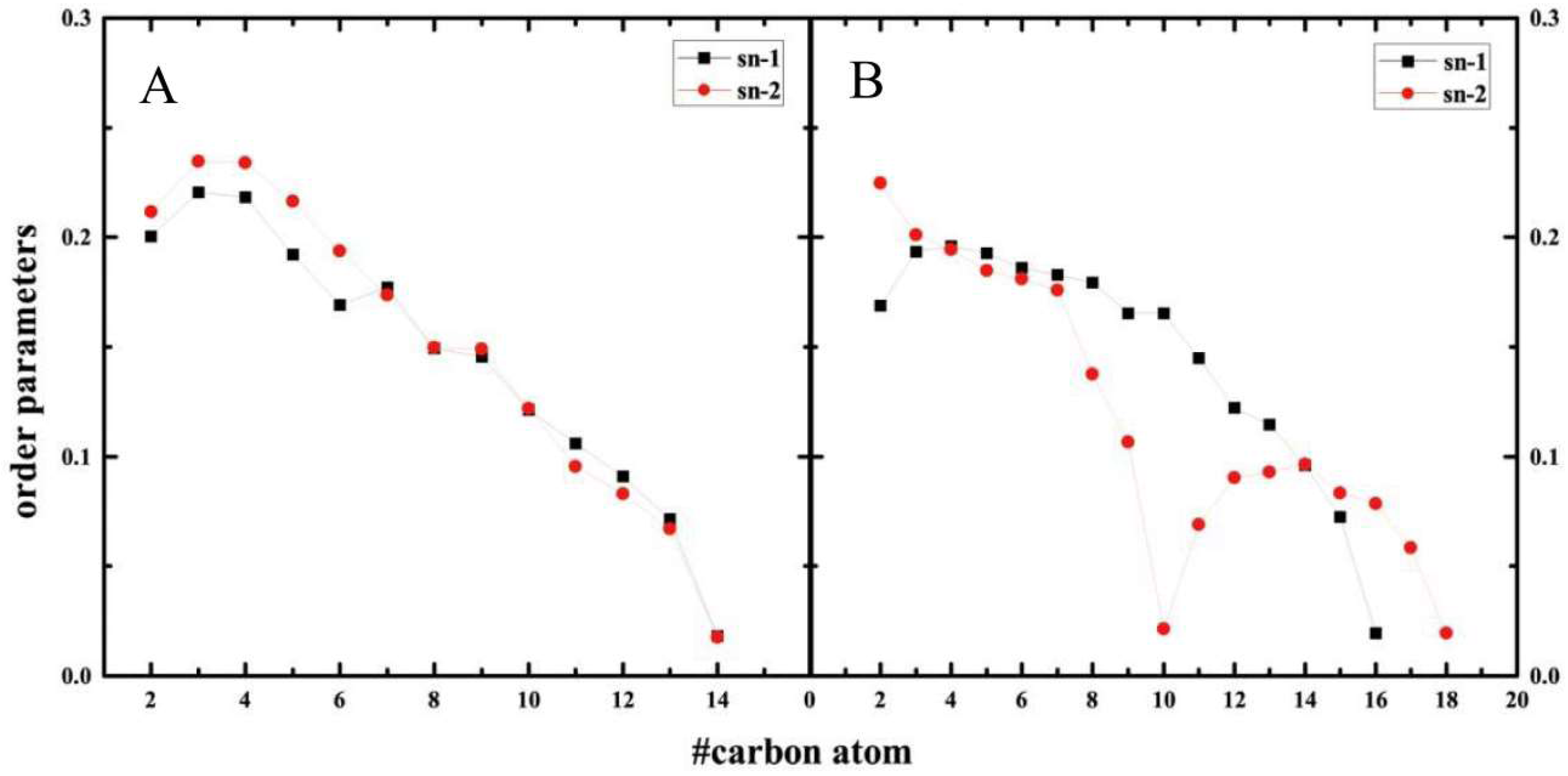
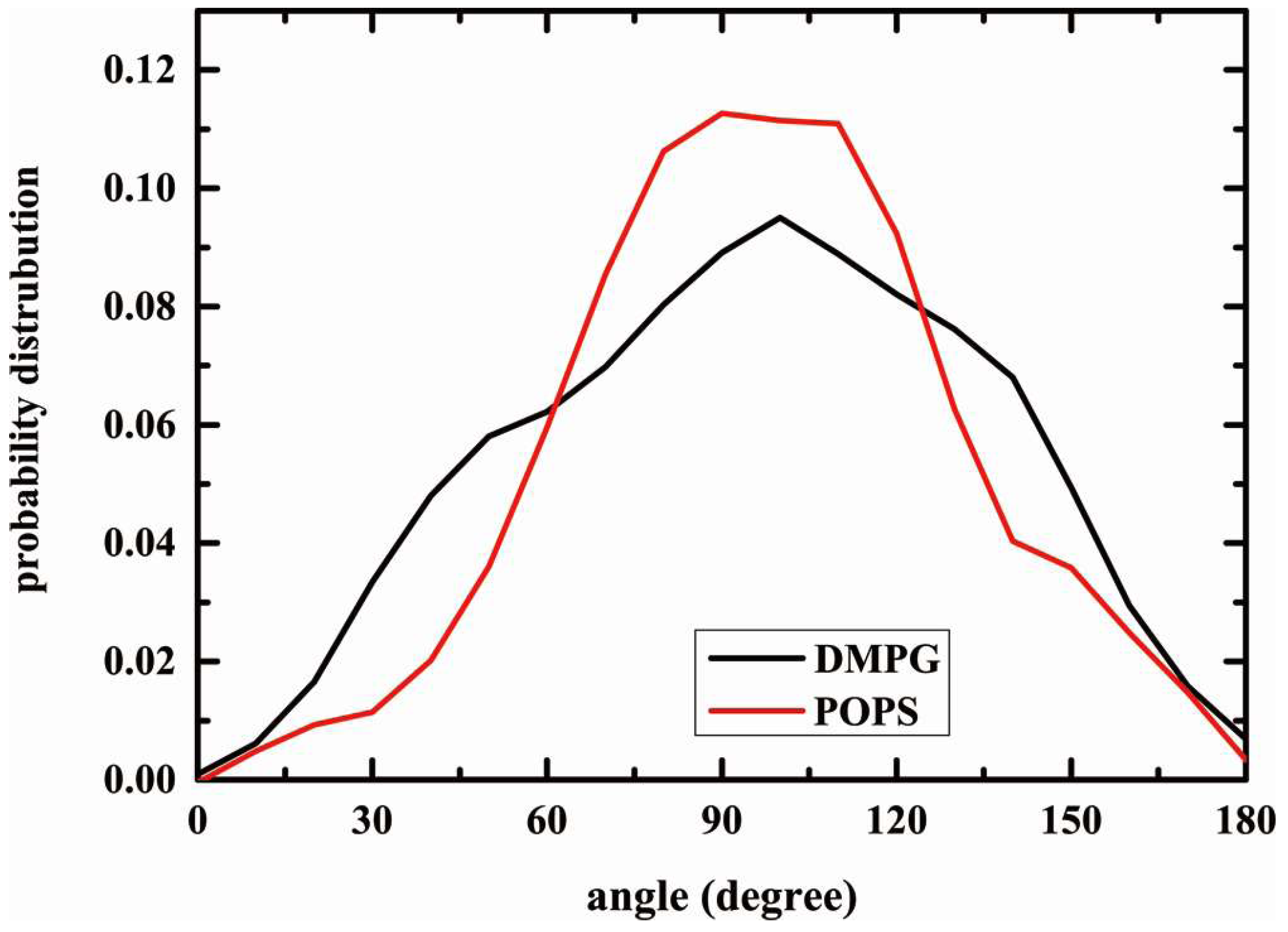
2.5. Structure of Lipid Bilayers
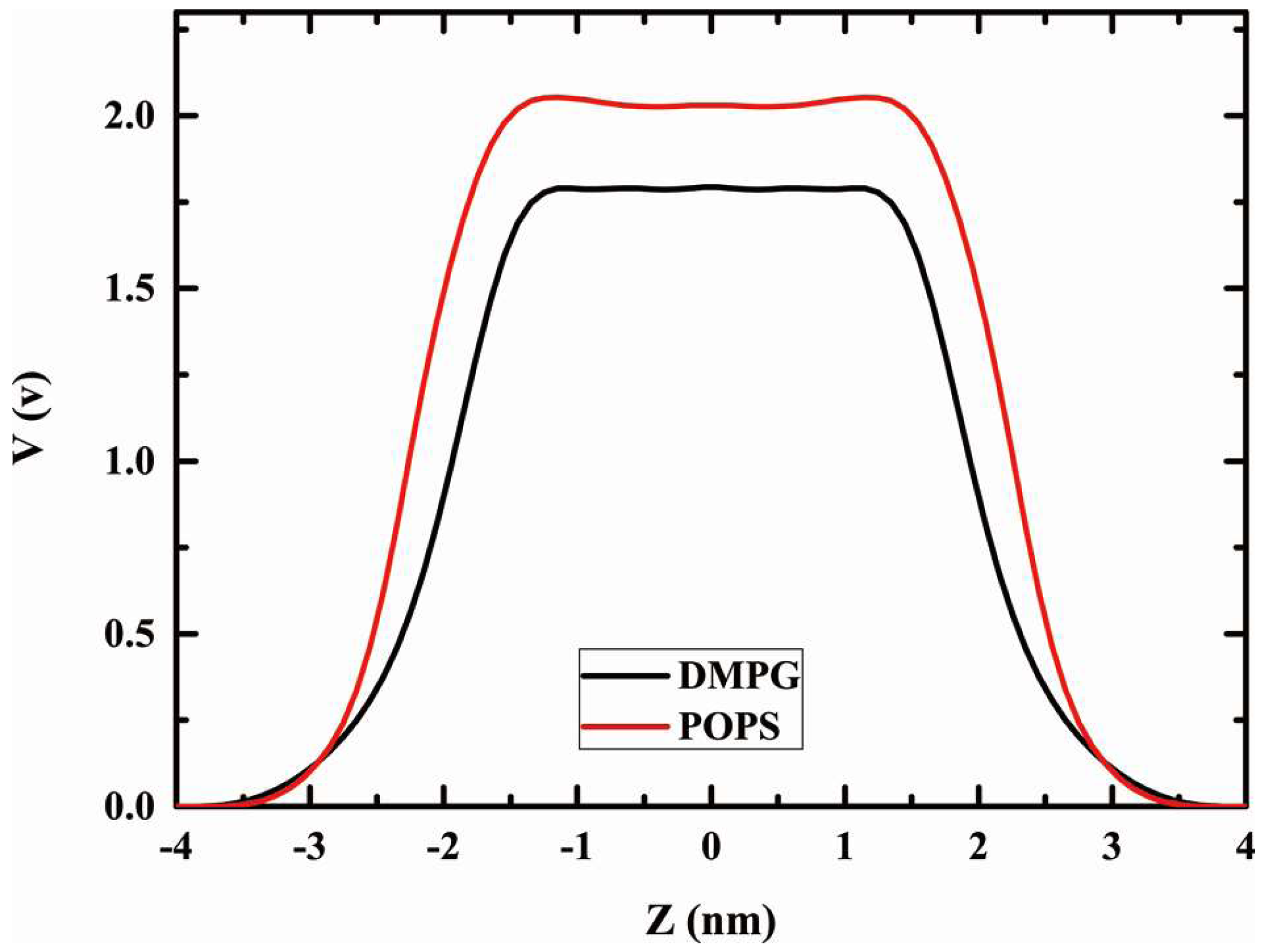
2.6. Dipole Potential
3. Computational Details
4. Conclusions
Supplementary Materials
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Nagle, J.F.; Tristram-Nagle, S. Structure of lipid bilayers. Biochim. Biophys. Acta Rev. Biomembr. 2000, 1469, 159–195. [Google Scholar] [CrossRef]
- Marrink, S.J.; Mark, A.E. Effect of undulations on surface tension in simulated bilayers. J. Phys. Chem. B 2001, 105, 6122–6127. [Google Scholar] [CrossRef]
- De Vries, A.H.; Mark, A.E.; Marrink, S.J. The binary mixing behavior of phospholipids in a bilayer: A molecular dynamics study. J. Phys. Chem. B 2004, 108, 2454–2463. [Google Scholar] [CrossRef]
- Pandit, S.A.; Bostick, D.; Berkowitz, M.L. Mixed bilayer containing dipalmitoylphosphatidylcholine and dipalmitoylphosphatidylserine: Lipid complexation, ion binding, and electrostatics. Biophys. J. 2003, 85, 3120–3131. [Google Scholar] [CrossRef]
- Choma, C.T.; Tieleman, D.P.; Cregut, D.; Serrano, L.; Berendsen, H.J.C. Towards the design and computational characterization of a membrane protein. J. Mol. Graph. Model. 2001, 20, 219–234. [Google Scholar] [CrossRef]
- Yu, C.H.; Pomes, R. Functional dynamics of ion channels: Modulation of proton movement by conformational switches. J. Am. Chem. Soc. 2003, 125, 13890–13894. [Google Scholar] [CrossRef] [PubMed]
- Lear, J.D. Proton conduction through the M2 protein of the influenza A virus; a quantitative, mechanistic analysis of experimental data. FEBS Lett. 2003, 552, 17–22. [Google Scholar] [CrossRef]
- Chowdhary, J.; Harder, E.; Lopes, P.E.M.; Huang, L.; MacKerell, A.D., Jr.; Roux, B. A Polarizable Force Field of Dipalmitoylphosphatidylcholine Based on the Classical Drude Model for Molecular Dynamics Simulations of Lipids. J. Phys. Chem. B 2013, 117, 9142–9160. [Google Scholar] [CrossRef] [PubMed]
- Vorobyov, I.V.; Anisimov, V.M.; MacKerell, A.D. Polarizable empirical force field for alkanes based on the classical drude oscillator model. J. Phys. Chem. B 2005, 109, 18988–18999. [Google Scholar] [CrossRef] [PubMed]
- Lamoureux, G.; MacKerell, A.D.; Roux, B. A simple polarizable model of water based on classical Drude oscillators. J. Chem. Phys. 2003, 119, 5185–5197. [Google Scholar] [CrossRef]
- Stern, H.A.; Feller, S.E. Calculation of the dielectric permittivity profile for a nonuniform system: Application to a lipid bilayer simulation. J. Chem. Phys. 2003, 118, 3401–3412. [Google Scholar] [CrossRef]
- Wang, L.G.; Bose, P.S.; Sigworth, F.J. Using cryo-EM to measure the dipole potential of a lipid membrane. Proc. Natl. Acad. Sci. USA 2006, 103, 18528–18533. [Google Scholar] [CrossRef] [PubMed]
- Roux, B.; Berneche, S.; Egwolf, B.; Lev, B.; Noskov, S.Y.; Rowley, C.N.; Yu, H. Ion selectivity in channels and transporters. J. Gen. Physiol. 2011, 137, 415–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Deng, Y.; Knight, J.L.; Wu, Y.; Kim, B.; Sherman, W.; Shelley, J.C.; Lin, T.; Abel, R. Modeling Local Structural Rearrangements Using FEP/REST: Application to Relative Binding Affinity Predictions of CDK2 Inhibitors. J. Chem. Theory Comput. 2013, 9, 1282–1293. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. The many roles of computation in drug discovery. Science 2004, 303, 1813–1818. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Davis, J.E.; Bauer, B.A. Exploring Ion Permeation Energetics in Gramicidin A Using Polarizable Charge Equilibration Force Fields. J. Am. Chem. Soc. 2009, 131, 13890–13891. [Google Scholar] [CrossRef] [PubMed]
- Bauer, B.A.; Lucas, T.R.; Meninger, D.J.; Patel, S. Water permeation through DMPC lipid bilayers using polarizable charge equilibration force fields. Chem. Phys. Lett. 2011, 508, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Allen, T.W.; Andersen, O.S.; Roux, B. Ion permeation through a narrow channel: Using gramicidin to ascertain all-atom molecular dynamics potential of mean force methodology and biomolecular force fields. Biophys. J. 2006, 90, 3447–3468. [Google Scholar] [CrossRef] [PubMed]
- Dorairaj, S.; Allen, T.W. On the thermodynamic stability of a charged arginine side chain in a transmembrane helix. Proc. Natl. Acad. Sci. USA 2007, 104, 4943–4948. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Chowdhary, J.; Huang, L.; He, X.; MacKerell, A.D.; Roux, B. Drude Polarizable Force Field for Molecular Dynamics Simulations of Saturated and Unsaturated Zwitterionic Lipids. J. Chem. Theory Comput. 2017, 13, 4535–4552. [Google Scholar] [CrossRef] [PubMed]
- Robinson, D. A Polarizable Force-Field for Cholesterol and Sphingomyelin. J. Chem. Theory Comput. 2013, 9, 2498–2503. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Ren, P.; Schnieders, M.; Piquemal, J.-P. Polarizable Force Fields for Biomolecular Modeling. In Reviews in Computational Chemistry; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; Volume 28, pp. 51–86. [Google Scholar]
- Applequist, J.; Carl, J.R.; Fung, K.K. Atom dipole interaction model for molecular polarizability—Application to polyatomic-molecules and determination of atom polarizabilities. J. Am. Chem. Soc. 1972, 94, 2952–2960. [Google Scholar] [CrossRef]
- Mu, X.; Wang, Q.; Wang, L.P.; Fried, S.D.; Piquemal, J.P.; Dalby, K.N.; Ren, P. Modeling organochlorine compounds and the sigma-hole effect using a polarizable multipole force field. J. Phys. Chem. B 2014, 118, 6456–6465. [Google Scholar] [CrossRef] [PubMed]
- Day, P.N.; Jensen, J.H.; Gordon, M.S.; Webb, S.P.; Stevens, W.J.; Krauss, M.; Garmer, D.; Basch, H.; Cohen, D. An effective fragment method for modeling solvent effects in quantum mechanical calculations. J. Chem. Phys. 1996, 105, 1968–1986. [Google Scholar] [CrossRef]
- Williams, D.E. Representation of the molecular electrostatic potential by atomic multipole and bond dipole models. J. Comput. Chem. 1988, 9, 745–763. [Google Scholar] [CrossRef]
- Shi, Y.; Xia, Z.; Zhang, J.; Best, R.; Wu, C.; Ponder, J.W.; Ren, P. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. [Google Scholar] [CrossRef] [PubMed]
- Jiao, D.; Golubkov, P.A.; Darden, T.A.; Ren, P. Calculation of protein-ligand binding free energy by using a polarizable potential. Proc. Natl. Acad. Sci. USA 2008, 105, 6290–6295. [Google Scholar] [CrossRef] [PubMed]
- Jiao, D.; Zhang, J.J.; Duke, R.E.; Li, G.H.; Schnieders, M.J.; Ren, P.Y. Trypsin-Ligand Binding Free Energies from Explicit and Implicit Solvent Simulations with Polarizable Potential. J. Comput. Chem. 2009, 30, 1701–1711, PMCID:PMC2752704. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhu, C.Z.; Martin, S.F.; Ren, P. Probing the Effect of Conformational Constraint on Phosphorylated Ligand Binding to an SH2 Domain Using Polarizable Force Field Simulations. J. Phys. Chem. B 2012, 116, 1716–1727, PMCID:PMC3277292. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Shi, Y.; Ren, P. Polarizable Force Fields for Scoring Protein–Ligand Interactions. In Protein-Ligand Interactions; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012; pp. 99–120. [Google Scholar]
- Zhang, J.; Yang, W.; Piquemal, J.P.; Ren, P. Modeling Structural Coordination and Ligand Binding in Zinc Proteins with a Polarizable Potential. J. Chem. Theory Comput. 2012, 8, 1314–1324, PMCID:PMC3383645. [Google Scholar] [CrossRef] [PubMed]
- Mooij, W.T.M.; Leusen, F.J.J. Multipoles versus charges in the 1999 crystal structure prediction test. Phys. Chem. Chem. Phys. 2001, 3, 5063–5066. [Google Scholar] [CrossRef]
- Lommerse, J.P.M.; Motherwell, W.D.S.; Ammon, H.L.; Dunitz, J.D.; Gavezzotti, A.; Hofmann, D.W.M.; Leusen, F.J.J.; Mooij, W.T.M.; Price, S.L.; Schweizer, B.; et al. A test of crystal structure prediction of small organic molecules. Acta Crystallogr. Sect. B Struct. Sci. 2000, 56, 697–714. [Google Scholar] [CrossRef]
- Schnieders, M.J.; Baltrusaitis, J.; Shi, Y.; Chattree, G.; Zheng, L.; Yang, W.; Ren, P. The Structure, Thermodynamics and Solubility of Organic Crystals from Simulation with a Polarizable Force Field. J. Chem. Theory Comput. 2012, 8, 1721–1736. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Zhang, Y.; Chu, H.; Li, Y.; Zhang, D.; Cao, L.; Li, G. Accurate Evaluation of Ion Conductivity of the Gramicidin A Channel Using a Polarizable Force Field without Any Corrections. J. Chem. Theory Comput. 2016, 12, 2973–2982, PMCID:PMC3348590. [Google Scholar] [CrossRef] [PubMed]
- Allen, T.W.; Bastug, T.; Kuyucak, S.; Chung, S.H. Gramicidin A channel as a test ground for molecular dynamics force fields. Biophys. J. 2003, 84, 2159–2168. [Google Scholar] [CrossRef]
- Allen, T.W.; Andersen, O.S.; Roux, B. Energetics of ion conduction through the gramicidin channel. Proc. Natl. Acad. Sci. USA 2004, 101, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Ingolfsson, H.I.; Li, Y.H.; Vostrikov, V.V.; Gu, H.; Hinton, J.F.; Koeppe, R.E.; Roux, B.; Andersen, O.S. Gramicidin A Backbone and Side Chain Dynamics Evaluated by Molecular Dynamics Simulations and Nuclear Magnetic Resonance Experiments. I: Molecular Dynamics Simulations. J. Phys. Chem. B 2011, 115, 7417–7426. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.O.; Jogini, V.; Eastwood, M.P.; Shaw, D.E. Atomic-level simulation of current-voltage relationships in single-file ion channels. J. Gen. Physiol. 2013, 141, 619–632. [Google Scholar] [CrossRef] [PubMed]
- Song, H.D.; Beck, T.L. Temperature Dependence of Gramicidin Channel Transport and Structure. J. Phys. Chem. C 2013, 117, 3701–3712. [Google Scholar] [CrossRef]
- Siu, S.W.I.; Bockmann, R.A. Low Free Energy Barrier for Ion Permeation through Double-Helical Gramicidin. J. Phys. Chem. B 2009, 113, 3195–3202. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.W.; Xu, Y.; Tang, P. Steered molecular dynamics simulations of Na+ permeation across the gramicidin a channel. J. Phys. Chem. B 2006, 110, 12789–12795. [Google Scholar] [CrossRef] [PubMed]
- De Fabritiis, G.; Coveney, P.V.; Villa-Freixa, J. Energetics of K(+) permeability through Gramicidin A by forward-reverse steered molecular dynamics. Proteins-Struct. Funct. Bioinform. 2008, 73, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Forney, M.W.; Janosi, L.; Kosztin, I. Calculating free-energy profiles in biomolecular systems from fast nonequilibrium processes. Phys. Rev. E 2008, 78, 051913. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, M.; Busath, D. The Gramicidin Channel Ion Permeation Free-Energy Profile: Direct and Indirect Effects of CHARMM Force Field Improvements. Interdiscip. Sci.-Comput. Life Sci. 2009, 1, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Vorobyov, I.; Bekker, B.; Allen, T.W. Electrostatics of Deformable Lipid Membranes. Biophys. J. 2010, 98, 2904–2913. [Google Scholar] [CrossRef] [PubMed]
- Giorgino, T.; De Fabritiis, G. A High-Throughput Steered Molecular Dynamics Study on the Free Energy Profile of Ion Permeation through Gramicidin A. J. Chem. Theory Comput. 2011, 7, 1943–1950. [Google Scholar] [CrossRef] [PubMed]
- Olah, G.A.; Huang, H.W.; Liu, W.H.; Wu, Y.L. Location of ion-binding sites in the gramicidin channel by X-ray-diffraction. J. Mol. Biol. 1991, 218, 847–858. [Google Scholar] [CrossRef]
- Roux, B.; Karplus, M. Ion-transport in a model gramicidin channel—Structure and thermodynamics. Biophys. J. 1991, 59, 961–981. [Google Scholar] [CrossRef]
- Stone, A.J. Distributed multipole analysis: Stability for large basis sets. J. Chem. Theory Comput. 2005, 1, 1128–1132. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.; Wu, C.; Ponder, J.W. Polarizable Atomic Multipole-based Molecular Mechanics for Organic Molecules. J. Chem. Theory Comput. 2011, 7, 3143–3161, PMCID:PMC3196664. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.Y.; Ponder, J.W. Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, C.; Ponder, J.W.; Ren, P. Multipole Electrostatics in Hydration Free Energy Calculations. J. Comput. Chem. 2011, 32, 967–977. [Google Scholar] [CrossRef] [PubMed]
- Halgren, T.A. Representation of vanderwaals (vdw) interactions in molecular mechanics force-fields—Potential form, combination rules, and vdw parameters. J. Am. Chem. Soc. 1992, 114, 7827–7843. [Google Scholar] [CrossRef]
- Chaudret, R.; Gresh, N.; Parisel, O.; Piquemal, J.-P. Many-Body Exchange-Repulsion in Polarizable Molecular Mechanics. I. Orbital-Based Approximations and Applications to Hydrated Metal Cation Complexes. J. Comput. Chem. 2011, 32, 2949–2957. [Google Scholar] [CrossRef] [PubMed]
- Thole, B.T. Molecular polarizabilities calculated with a modified dipole interaction. Chem. Phys. 1981, 59, 341–350. [Google Scholar] [CrossRef]
- Pan, J.; Marquardt, D.; Heberle, F.A.; Kučerka, N.; Katsaras, J. Revisiting the bilayer structures of fluid phase phosphatidylglycerol lipids: Accounting for exchangeable hydrogens. Biochim. Biophys. Acta (BBA) Biomembr. 2014, 1838, 2966–2969. [Google Scholar] [CrossRef] [PubMed]
- Jambeck, J.P.M.; Lyubartsev, A.P. Another Piece of the Membrane Puzzle: Extending Slipids Further. J. Chem. Theory Comput. 2013, 9, 774–784. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, P.; Monticelli, L.; Tieleman, D.P. Molecular dynamics simulation of a palmitoyl-oleoyl phosphatidylserine bilayer with Na+ counterions and NaCl. Biophys. J. 2004, 86, 1601–1609. [Google Scholar] [CrossRef]
- Siu, S.W.I.; Vacha, R.; Jungwirth, P.; Boeckmann, R.A. Biomolecular simulations of membranes: Physical properties from different force fields. J. Chem. Phys. 2008, 128, 03B620. [Google Scholar] [CrossRef] [PubMed]
- Chon, N.L.; Osterberg, J.R.; Henderson, J.; Khan, H.M.; Reuter, N.; Knight, J.D.; Lin, H. Membrane Docking of the Synaptotagmin 7 C2A Domain: Computation Reveals Interplay between Electrostatic and Hydrophobic Contributions. Biochemistry 2015, 54, 5696–5711. [Google Scholar] [CrossRef] [PubMed]
- Smaby, J.M.; Brockman, H.L. Surface dipole-moments of lipids at the argon-water interface—Similarities among glycerol-ester-based lipids. Biophys. J. 1990, 58, 195–204. [Google Scholar] [CrossRef]
- Zarzycki, P. Interfacial Water Screens the Protein-Induced Transmembrane Voltage. J. Phys. Chem. B 2015, 119, 1474–1482. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09. Revision D.1 Edn; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Ponder, J.W. TINKER: Software Tools for Molecular Design; v6.0Washington University: St. Louis, MO, USA, 2012; Available online: http://dasher.wustl.edu/tinker/ (accessed on 10 July 2017).
- Wu, J.C.; Chattree, G.; Ren, P. Automation of AMOEBA polarizable force field parameterization for small molecules. Theor. Chem. Acc. 2012, 131, 1138. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. Software news and updates—CHARNIM-GUI: A web-based grraphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
| Lipid System | Area Per Lipid AL(Å2) | Volume Per Lipid VL(Å3) | Peak Distance DHH (Å) |
|---|---|---|---|
| DMPG | |||
| 72 | 60.05 ± 0.73 | 1021.10 | 33.9 |
| Experiment | 62.5 (ref. [58]) | 33.8 (ref. [58]) | |
| POPS | |||
| 72 | 60.93 ± 0.55 | 1130.94 | 38.7 |
| Experiment |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, H.; Peng, X.; Li, Y.; Zhang, Y.; Li, G. A Polarizable Atomic Multipole-Based Force Field for Molecular Dynamics Simulations of Anionic Lipids. Molecules 2018, 23, 77. https://doi.org/10.3390/molecules23010077
Chu H, Peng X, Li Y, Zhang Y, Li G. A Polarizable Atomic Multipole-Based Force Field for Molecular Dynamics Simulations of Anionic Lipids. Molecules. 2018; 23(1):77. https://doi.org/10.3390/molecules23010077
Chicago/Turabian StyleChu, Huiying, Xiangda Peng, Yan Li, Yuebin Zhang, and Guohui Li. 2018. "A Polarizable Atomic Multipole-Based Force Field for Molecular Dynamics Simulations of Anionic Lipids" Molecules 23, no. 1: 77. https://doi.org/10.3390/molecules23010077