Systematic Identification of Machine-Learning Models Aimed to Classify Critical Residues for Protein Function from Protein Structure
Abstract
:1. Introduction
2. Results
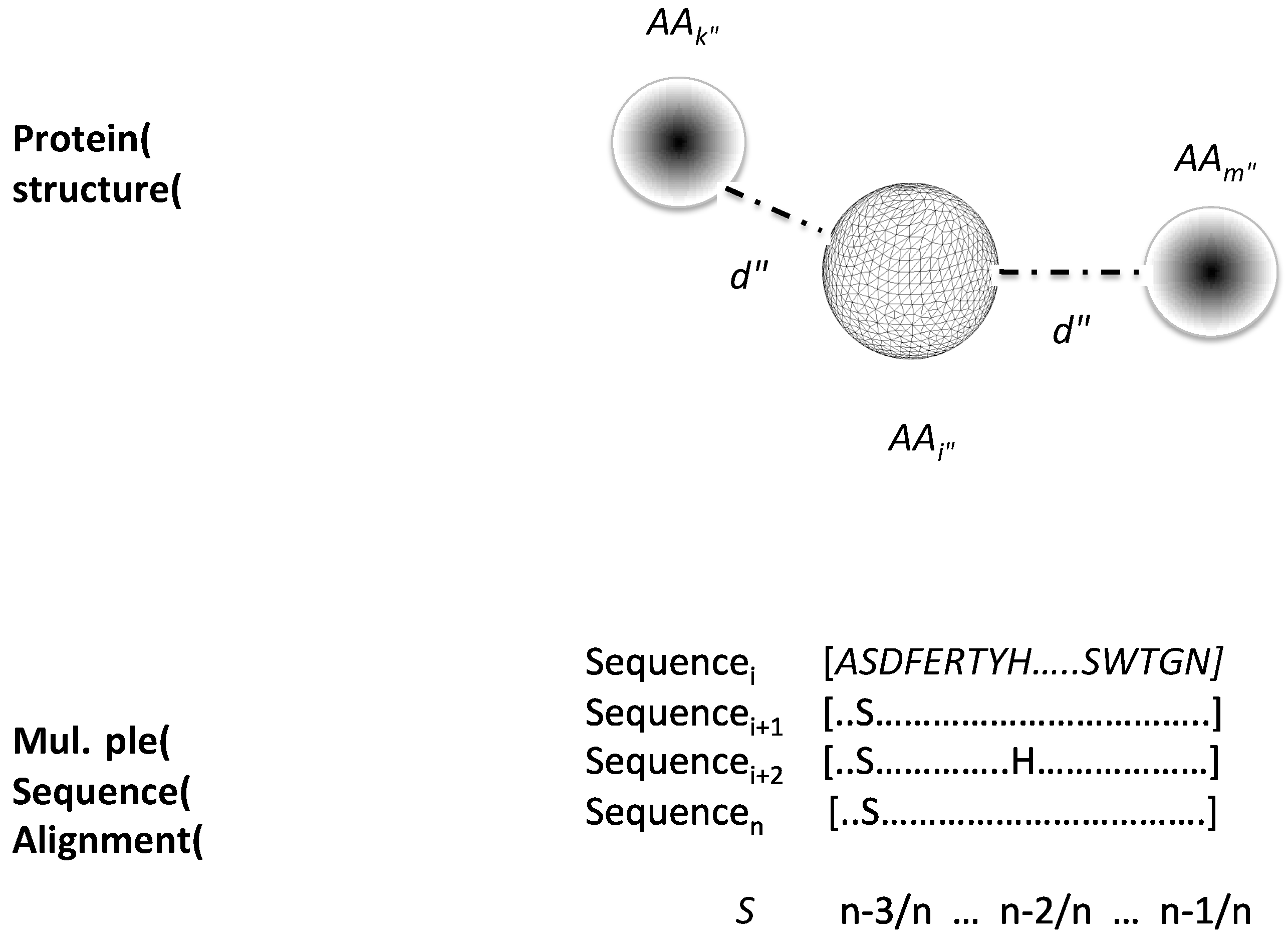
2.1. Data Sets and Protein Structure Descriptors Used to Train Machine-Learning Models to Classify Critical Residues for Protein Function
2.2. Testing Protein Structure Descriptors to Classify Critical Residues for Protein Function
2.3. Are Critical Residues for Protein Function Best Classified Using a Unique and Quantitative Formalism?
2.4. Are Critical Residues for Protein Function Best Modeled by a Binary Classification?
2.5. Are Critical Residues Best Classified by a Single Model?
3. Discussion
4. Materials and Methods
4.1. Set of Proteins
4.2. Protein Structure Descriptors
4.3. Correlated Mutation Index of Contacting Residues
4.4. Function Criticality Index from Site-Directed Mutagenesis Experiments
4.5. Selection of Protein Structure Descriptors
4.6. Combined Selection and Parameter Optimization Using AutoWEKA
4.7. Comparison of Critical Residue Classification among Different Models
4.8. A Filter-Wrapper Method for Selecting Descriptors in the Critical Residues Classification Problem
4.8.1. Filter Method
4.8.2. Wrapper Method
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moretti, R.; Fleishman, S.J.; Agius, R.; Torchala, M.; Bates, P.A.; Kastritis, P.L.; Rodrigues, J.P.G.L.M.; Trellet, M.; Bonvin, A.M.J.J.; Cui, M.; et al. Community-wide evaluation of methods for predicting the effect of mutations on protein-protein interactions. Proteins Struct. Funct. Bioinform. 2013, 81, 1980–1987. [Google Scholar]
- Hopf, T.A.; Ingraham, J.B.; Poelwijk, F.J.; Schärfe, C.P.I.; Springer, M.; Sander, C.; Marks, D.S. Mutation effects predicted from sequence co-variation. Nat. Biotechnol. 2017, 35, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.; Biswas, D.; Jayaram, B. AADS-An Automated Active Site Identification, Docking, and Scoring Protocol for Protein Targets Based on Physicochemical Descriptors. J. Chem. Inf. Model. 2011, 51, 2515–2527. [Google Scholar] [CrossRef] [PubMed]
- Fajardo, J.E.; Fiser, A. Protein structure based prediction of catalytic residues. BMC Bioinform. 2013, 14, 63. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Xu, S. Improving the performance of the PLB index for ligand-binding site prediction using dihedral angles and the solvent-accessible surface area. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Vamparys, L.; Laurent, B.; Carbone, A.; Sacquin-Mora, S. Great interactions: How binding incorrect partners can teach us about protein recognition and function. Proteins Struct. Funct. Bioinform. 2016, 84, 1408–1421. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-P.; Chen, L. Prediction and dissection of protein-RNA Interactions by molecular descriptors. Curr. Top. Med. Chem. 2016, 16, 604–615. [Google Scholar] [CrossRef] [PubMed]
- Si, J.; Zhao, R.; Wu, R. An overview of the prediction of protein DNA-binding sites. Int. J. Mol. Sci. 2015, 16, 5194–5215. [Google Scholar] [CrossRef] [PubMed]
- Lise, S.; Buchan, D.; Pontil, M.; Jones, D.T. Predictions of hot spot residues at protein-protein interfaces using support vector machines. PLoS ONE 2011, 6, e16774. [Google Scholar] [CrossRef] [PubMed]
- Pires, D.E.V.; Ascher, D.B.; Blundell, T.L. DUET: A server for predicting effects of mutations on protein stability using an integrated computational approach. Nucleic Acids Res. 2014, 42, W314–W319. [Google Scholar] [CrossRef] [PubMed]
- Bloom, J.D.; Silberg, J.J.; Wilke, C.O.; Drummond, D.A.; Adami, C.; Arnold, F.H. Thermodynamic prediction of protein neutrality. Proc. Natl. Acad. Sci. USA 2005, 102, 606–611. [Google Scholar] [CrossRef] [PubMed]
- Worth, C.L.; Preissner, R.; Blundell, T.L. SDM—A server for predicting effects of mutations on protein stability and malfunction. Nucleic Acids Res. 2011, 39, W215–W222. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Randall, A.; Baldi, P. Prediction of protein stability changes for single-site mutations using support vector machines. Proteins Struct. Funct. Bioinform. 2005, 62, 1125–1132. [Google Scholar] [CrossRef] [PubMed]
- Amitai, G.; Shemesh, A.; Sitbon, E.; Shklar, M.; Netanely, D.; Venger, I.; Pietrokovski, S. Network Analysis of Protein Structures Identifies Functional Residues. J. Mol. Biol. 2004, 344, 1135–1146. [Google Scholar] [CrossRef] [PubMed]
- Thibert, B.; Bredesen, D.E.; del Rio, G. Improved prediction of critical residues for protein function based on network and phylogenetic analyses. BMC Bioinform. 2005, 6, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cusack, M.P.; Thibert, B.; Bredesen, D.E.; del Rio, G. Efficient Identification of Critical Residues Based Only on Protein Structure by Network Analysis. PLoS ONE 2007, 2, e421. [Google Scholar] [CrossRef] [PubMed]
- Ambriz-Rivas, M.; Pastor, N.; del Rio, G. Relating Protein Structure and Function Through a Bijection and Its Implications on Protein Structure Prediction, 1st ed.; Cai, J., Wang, R.E., Eds.; Protein Interactions; InTech: University Campus, Rijeka, Croatia, 2012; pp. 349–368. ISBN 978-953-51-0244-1. [Google Scholar]
- Ruiz-Blanco, Y.B.; Paz, W.; Green, J.; Marrero-Ponce, Y. ProtDCal: A program to compute general-purpose-numerical descriptors for sequences and 3D-structures of proteins. BMC Bioinform. 2015, 16, 162. [Google Scholar] [CrossRef] [PubMed]
- Sverchkov, Y.; Craven, M. A review of active learning approaches to experimental design for uncovering biological networks. PLOS Comput. Biol. 2017, 13, e1005466. [Google Scholar] [CrossRef] [PubMed]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined Selection and Hyperparameter Optimization of Classification Algorithms. Comput. Sci. 2013, 847–855. [Google Scholar] [CrossRef]
- Haspel, N.; Jagodzinski, F. Methods for Detecting Critical Residues in Proteins. Method Mol. Biol. 2017, 1498, 227–242. [Google Scholar]
- Ortiz, M.T.L.; Rosario, P.B.L.; Luna-Nevarez, P.; Gamez, A.S.; Martínez-del Campo, A.; del Rio, G. Quality Control Test for Sequence-Phenotype Assignments. PLoS ONE 2015, 10, e0118288. [Google Scholar] [CrossRef] [PubMed]
- Yates, C.M.; Filippis, I.; Kelley, L.A.; Sternberg, M.J.E. SuSPect: Enhanced Prediction of Single Amino Acid Variant (SAV) Phenotype Using Network Features. J. Mol. Biol. 2014, 426, 2692–2701. [Google Scholar] [CrossRef] [PubMed]
- Hecht, M.; Bromberg, Y.; Rost, B. Better prediction of functional effects for sequence variants. BMC Genom. 2015, 16, S1. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, A.; Gupta, K.; Khare, S.; Jain, P.C.; Patel, S.; Kumar, P.; Pulianmackal, A.J.; Aghera, N.; Varadarajan, R. Molecular Determinants of Mutant Phenotypes, Inferred from Saturation Mutagenesis Data. Mol. Biol. Evol. 2016, 33, 2960–2975. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Li, D.; Zeng, X.; Wu, Y.; Guo, L.; Zou, Q. nDNA-Prot: Identification of DNA-binding proteins based on unbalanced classification. BMC Bioinform. 2014, 15, 298. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Wan, S.; Ju, Y.; Tang, J.; Zeng, X. Pretata: Predicting TATA binding proteins with novel features and dimensionality reduction strategy. BMC Syst. Biol. 2016, 10, 114. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Xing, P.; Tang, J.; Zou, Q. PhosPred-RF: A novel sequence-based predictor for phosphorylation sites using sequential information only. IEEE Trans. Nanobiosci. 2017, 16, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Tang, J.; Zou, Q. Local-DPP: An improved DNA-binding protein prediction method by exploring local evolutionary information. Inf. Sci. 2016, 384, 135–144. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Petrosino, J.; Hirsch, M.; Shenkin, P.S.; Palzkill, T. Amino Acid Sequence Determinants of β-Lactamase Structure and Activity. J. Mol. Biol. 1996, 258, 688–703. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.H.; Choe, J.; Loeb, L.A. Protein tolerance to random amino acid change. Proc. Natl. Acad. Sci. USA 2004, 101, 9205–9210. [Google Scholar] [CrossRef] [PubMed]
- Terwilliger, T.C.; Zabin, H.B.; Horvath, M.P.; Sandberg, W.S.; Schlunk, P.M. In Vivo Characterization of Mutants of the Bacteriophage f1 Gene V Protein Isolated by Saturation Mutagenesis. J. Mol. Biol. 1994, 236, 556–571. [Google Scholar] [CrossRef] [PubMed]
- Loeb, D.D.; Swanstrom, R.; Everitt, L.; Manchester, M.; Stamper, S.E.; Hutchison, C.A. Complete mutagenesis of the HIV-1 protease. Nature 1989, 340, 397–400. [Google Scholar] [CrossRef] [PubMed]
- Daber, R.; Stayrook, S.; Rosenberg, A.; Lewis, M. Structural analysis of Lac repressor bound to allosteric effectors. J. Mol. Biol. 2007, 370, 609–619. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Cho, Y.; Choe, D.; Jeong, Y.; Cho, S.; Kim, S.C.; Cho, B.-K. Exploring the functional residues in a flavin-binding fluorescent protein using deep mutational scanning. PLoS ONE 2014, 9, e97817. [Google Scholar] [CrossRef] [PubMed]
- Das, K.; Bauman, J.D.; Clark, A.D.; Frenkel, Y.V.; Lewi, P.J.; Shatkin, A.J.; Hughes, S.H.; Arnold, E. High-resolution structures of HIV-1 reverse transcriptase/TMC278 complexes: Strategic flexibility explains potency against resistance mutations. Proc. Natl. Acad. Sci. USA 2008, 105, 1466–1471. [Google Scholar] [CrossRef] [PubMed]
- Rennell, D.; Bouvier, S.E.; Hardy, L.W.; Poteete, A.R. Systematic mutation of bacteriophage T4 lysozyme. J. Mol. Biol. 1991, 222, 67–88. [Google Scholar] [CrossRef]
- Wen, J.; Chen, X.; Bowie, J.U. Exploring the allowed sequence space of a membrane protein. Nat. Struct. Biol. 1996, 3, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Joosten, RP.; te Beek, T.A.H.; Krieger, E.; Hekkelman, M.L.; Hooft, R.W.W.; Schneider, R.; Sander, C.; Vriend, G. A series of PDB related databases for everyday needs. Nucleic Acids Res. 2011, 39, D411–D419. [Google Scholar] [CrossRef] [PubMed]
- Kosciolek, T.; Jones, D.T. De novo structure prediction of globular proteins aided by sequence variation-derived contacts. PLoS ONE 2014, 9, e92197. [Google Scholar] [CrossRef] [PubMed]
- Tusnády, G.E.; Kalmár, L.; Simon, I. TOPDB: Topology data bank of transmembrane proteins. Nucleic Acids Res. 2008, 36, D234–D239. [Google Scholar] [CrossRef] [PubMed]
- Atchley, W.R.; Zhao, J.; Fernandes, A.D.; Druke, T. Solving the protein sequence metric problem. Proc. Natl. Acad. Sci. USA 2005, 102, 6395–6400. [Google Scholar] [CrossRef] [PubMed]
- Jinjie, H.; Yunze, C.; Xiaoming, X. A hybrid genetic algorithm for feature selection wrapper based on mutual information. Pattern Recogn. Lett. 2007, 28, 1825–1844. [Google Scholar]
- Emmanouilidis, C.; Hunter, A.; MacIntyre, J. A multiobjective evolutionary setting for feature selection and a commonality-based crossover operator. In Evolutionary Computation, Proceedings of the 2000 Congress on Evolutionary Computation (Vol. 1, pp. 309–316), La Jolla, CA, USA, 16–19 July 2000; IEEE Service Center: Piscataway, NJ, USA, 2000. [Google Scholar]
Sample Availability: Samples of the compounds described in this work are available. |

| Descriptors | Algorithm | Parameters | Relative Absolute Error (%) |
|---|---|---|---|
| Centralities 1 | Multilayer Perceptron | [-L, 0.5571819547734898, -M, 0.23520521436874284, -B, -H, o, -C, -D, -S, 1] Attribute search: GreedyStepwise [-C, -B, -R] Attribute evaluation: CfsSubsetEval [-L] | 77.2 |
| Centralities 2 | LWL | [-A, weka.core.neighboursearch.LinearNNSearch, -W, weka.classifiers.functions.MultilayerPerceptron, --, -L, 0.3899191912662868, -M, 0.4683563849238558, -H, o, -C, -R, -D, -S, 1] | 78.2 |
| ProtDCal 1 | Logistic | [-R, 0.057140274761388915] Attribute search: BestFirst [-D, 1, -N, 4] Attribute evaluation: CfsSubsetEval [-L] | 67.9 |
| ProtDCal 2 | Logistic | [-R, 0.057140274761388915] Attribute search: BestFirst [-D, 1, -N, 4] Attribute evaluation: CfsSubsetEval [-L] | 67.9 |
| Union 1 | SMO | [-C, 0.7127949742291734, -N, 0, -M, -K, weka.classifiers.functions.supportVector.PolyKernel -E 1.1133446901320447 -L] Attribute search: GreedyStepwise [-C, -N, 898] Attribute evaluation: CfsSubsetEval [-L] | 68.6 |
| Union 2 | SMO | [-C, 0.7127949742291734, -N, 0, -M, -K, weka.classifiers.functions.supportVector.PolyKernel -E 1.1133446901320447 -L] Attribute search: GreedyStepwise [-C, -N, 898] Attribute evaluation: CfsSubsetEval [-L] | 68.6 |
| Attribute Set | TP Rate | FP Rate | Precision | Recall | MCC | ROC Area |
|---|---|---|---|---|---|---|
| Centralities 1 | 0.83 | 0.53 | 0.81 | 0.83 | 0.37 | 0.77 |
| Centralities 2 | 0.83 | 0.51 | 0.81 | 0.83 | 0.37 | 0.79 |
| ProtDCal 1, 2 | 0.84 | 0.52 | 0.82 | 0.84 | 0.39 | 0.81 |
| Union 1, 2 | 0.84 | 0.53 | 0.82 | 0.84 | 0.38 | 0.81 |
| SVM-Centralities | 0.79 | 0.33 | 0.82 | 0.79 | 0.41 | 0.73 |
| SVM-ProtDCal | 0.81 | 0.27 | 0.84 | 0.81 | 0.48 | 0.81 |
| SVM-Union | 0.82 | 0.25 | 0.85 | 0.82 | 0.49 | 0.78 |
| Attribute Set | TP Rate | FP Rate | Precision | Recall | MCC | ROC Area |
|---|---|---|---|---|---|---|
| Centralities 1 | 0.61 | 0.67 | 0.55 | 0.61 | −0.07 | 0.42 |
| ProtDCal 1 | 0.58 | 0.60 | 0.54 | 0.58 | −0.02 | 0.45 |
| Union 1 | 0.58 | 0.61 | 0.74 | 0.58 | −0.02 | 0.40 |
| Descriptors | Algorithm | Parameters | Relative Absolute Error (%) |
|---|---|---|---|
| Centralities 1 | Linear Regression | [-S, 2, -R, 7.855468822045874E-7], Attribute search: GreedyStepwise [-C, -B, -N, 172], Attribute evaluation: CfsSubsetEval [] | 82.8 |
| Centralities 2 | LWL | [-A, weka.core.neighboursearch.LinearNNSearch, -W, weka.classifiers.functions.LinearRegression, --, -S, 0, -R, 0.20912016083576357], Attribute search: GreedyStepwise [-C, -N, 213], Attribute evaluation: CfsSubsetEval [-L] | 82.4 |
| ProtDCal 1 | M5P | [-M, 1, -R] | 80.1 |
| ProtDCal 2 | M5P | [-M, 1, -R] | 80.1 |
| Union 1 | Bagging | [-P, 74, -I, 8, -S, 1, -W, weka.classifiers.trees.DecisionStump, --] | 88.5 |
| Union 2 | Bagging | [-P, 74, -I, 8, -S, 1, -W, weka.classifiers.trees.DecisionStump, --] | 88.5 |
| Attribute Set | Correlation Coefficient | Relative Absolute Error (%) |
|---|---|---|
| Centralities 1 | 0.54 | 83.2 |
| Centralities 2 | 0.55 | 83.0 |
| ProtDCal 1, 2 | 0.64 | 74.5 |
| Union 1, 2 | 0.52 | 83.7 |
| Descriptors | Algorithm | Parameters | Relative Absolute Error (%) |
|---|---|---|---|
| Centralities 1 | IBk | [-K, 13] | 82.3 |
| Centralities 2 | AdaBoostM1 | [-P, 79, -I, 108, -Q, -S, 1, -W, WEKA.classifiers.functions. MultilayerPerceptron, -L, 0.7665662779502016, -M, 0.21535709618934423, -B, -H, i, -C, -R, -D, -S, 1] | 99.8 |
| ProtDCal 1 | Naïve Bayes | [-D] Attribute search: GreedyStepwise [-C, -N, 161], Attribute evaluation: CfsSubsetEval [-L] | 61.5 |
| ProtDCal 2 | J48 | [-J, -A, -S, -M, 18, -C, 0.3184313887632543] Attribute search: BestFirst [-D, 1, -N, 7] Attribute evaluation: CfsSubsetEval [-M] | 67.5 |
| Union 1 | Simple Logistic | [-W, 0] | 100 |
| Union 2 | J48 | [-J, -A, -S, -M, 18, -C, 0.3184313887632543] Attribute search: BestFirst [-D, 1, -N, 7] Attribute evaluation: CfsSubsetEval [-M] | 67.5 |
| Attribute Set | TP Rate | FP Rate | Precision | Recall | MCC | ROC Area |
|---|---|---|---|---|---|---|
| Centralities 1 | 0.76 | 0.50 | 0.75 | 0.76 | 0.34 | 0.76 |
| ProtDCal 1 | 0.83 | 0.61 | 0.80 | 0.83 | 0.31 | 0.79 |
| ProtDCal 2 | 0.82 | 0.55 | 0.80 | 0.82 | 0.32 | 0.68 |
| Union 1 | 0.84 | 0.55 | 0.82 | 0.84 | 0.37 | 0.81 |
| Union 2 | 0.84 | 0.49 | 0.82 | 0.84 | 0.41 | 0.73 |
| SVM-Centralities | 0.72 | 0.26 | 0.77 | 0.72 | 0.42 | 0.72 |
| SVM-ProtDCal | 0.74 | 0.29 | 0.76 | 0.74 | 0.42 | 0.72 |
| SVM-Union | 0.74 | 0.19 | 0.81 | 0.74 | 0.50 | 0.77 |
| Attribute Set | TP Rate | FP Rate | Precision | Recall | MCC | ROC Area |
|---|---|---|---|---|---|---|
| Centralities 1 | 0.54 | 0.78 | 0.63 | 0.54 | −0.2 | 0.30 |
| ProtDCal 2 | 0.72 | 0.76 | 0.68 | 0.72 | −0.04 | 0.53 |
| Union 2 | 0.72 | 0.76 | 0.68 | 0.72 | −0.04 | 0.53 |
| Training Set | Centralities 1 | Centralities 2 | ProtDCal 1, 2 | Union 1, 2 | Average | |
|---|---|---|---|---|---|---|
| Centralities 1 | 1 | 100 | 78 | 0 | 62 | 60 |
| Centralities 2 | 1 | 92 | 100 | 0 | 63 | 63 |
| ProtDCal 1, 2 | 1 | 0 | 0 | 100 | 0 | 25 |
| Union 1, 2 | 1 | 66 | 56 | 0 | 100 | 55 |
| Centralities 1 | 3 | 100 | 47 | 50 | 65 | 65 |
| ProtDCal 1 | 3 | 35 | 100 | 100 | 84 | 79 |
| ProtDCal 2 | 3 | 28 | 75 | 100 | 69 | 68 |
| Union 2 | 3 | 37 | 63 | 69 | 100 | 67 |
| Centrality | Description |
|---|---|
| Excentricity | This is defined as the longest shortest distance of a node. The shortest distance was computed using the Dijkstra’s algorithm. |
| Excentricity inverted | 1/Excentricity |
| Degree | This is defined as the number of contacts for any residue in the graph. |
| Sphere degree | For any given i-residue, identify its neighbors and count the number of contacts. This is the degree at a second level of i-node. |
| Sphere degree accumulated (SNN) | Is derived as the sphere degree, but the counts include the number of neighbors of i-residue. |
| Mean distance | This is the sum of the shortest distances recorded from i-residue to any other residue divided by the number of neighbors for i-residue. |
| Closeness centrality | Is derived from the calculation of the shortest distances, according to the Dijkstra’s algorithm, between i-residue and the other residues in the protein. Closeness is the inverse of the sum of all these distances and is equivalent to 1/mean distance. |
| Clustering coefficient | Is obtained by dividing the observed number of neighbors between the neighbors of i-residue (o) by the expected number of neighbors (n): o/(n*(n − 1)). |
| Clustering coefficient inverted | 1/Clustering coefficient |
| Traversity | This index measures the number of times a residue is traversed while connecting every pair of residues in the contact map using the shortest path from the Dijkstra’s algorithm. Two version of this centrality are produced: One that follows the order of residues in the protein sequence (Traversity A) and another that does not (Traversity B). |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corral-Corral, R.; Beltrán, J.A.; Brizuela, C.A.; Del Rio, G. Systematic Identification of Machine-Learning Models Aimed to Classify Critical Residues for Protein Function from Protein Structure. Molecules 2017, 22, 1673. https://doi.org/10.3390/molecules22101673
Corral-Corral R, Beltrán JA, Brizuela CA, Del Rio G. Systematic Identification of Machine-Learning Models Aimed to Classify Critical Residues for Protein Function from Protein Structure. Molecules. 2017; 22(10):1673. https://doi.org/10.3390/molecules22101673
Chicago/Turabian StyleCorral-Corral, Ricardo, Jesús A. Beltrán, Carlos A. Brizuela, and Gabriel Del Rio. 2017. "Systematic Identification of Machine-Learning Models Aimed to Classify Critical Residues for Protein Function from Protein Structure" Molecules 22, no. 10: 1673. https://doi.org/10.3390/molecules22101673






