Urban Heat Island Intensification during Hot Spells—The Case of Paris during the Summer of 2003
Abstract
:1. Introduction
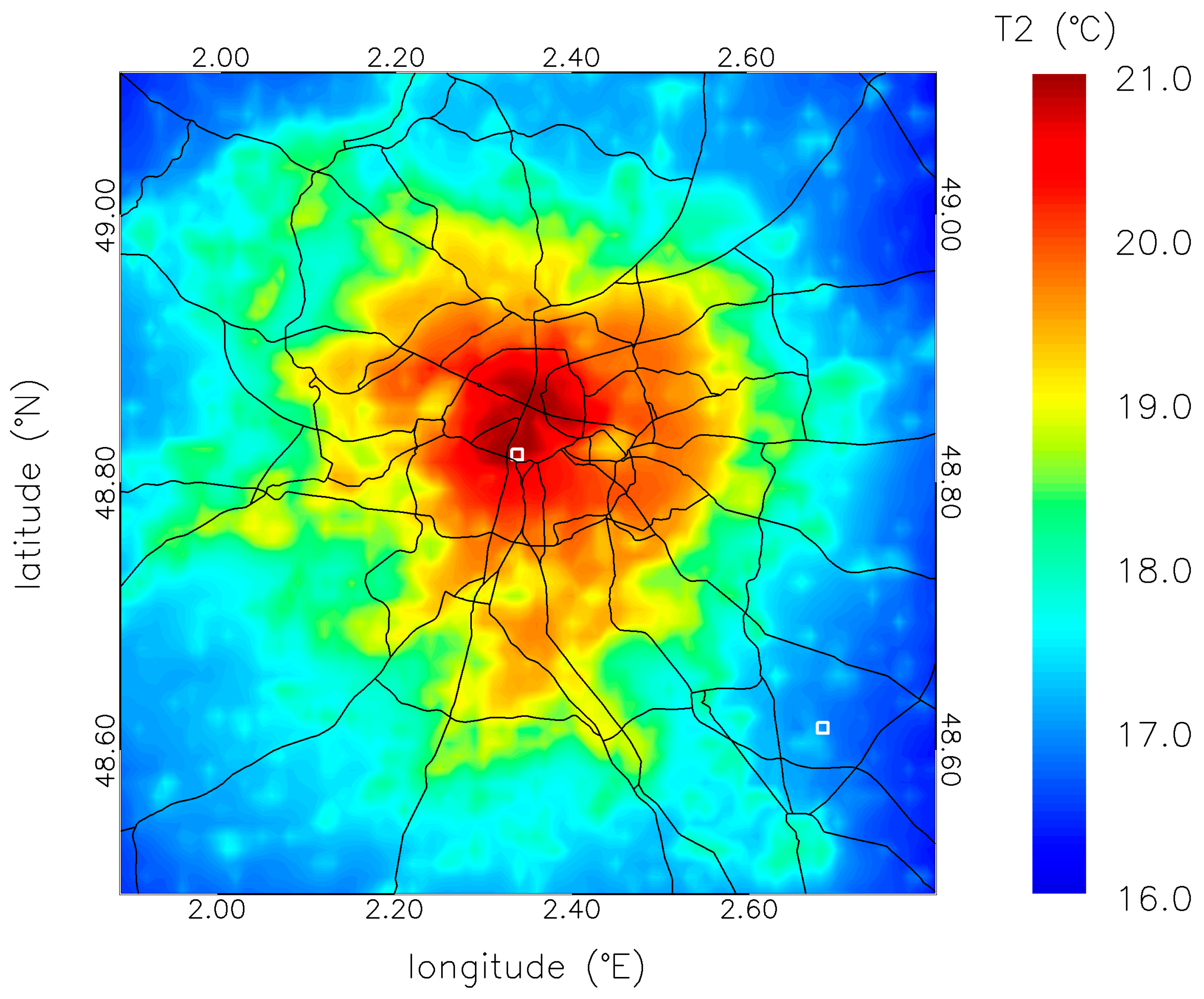
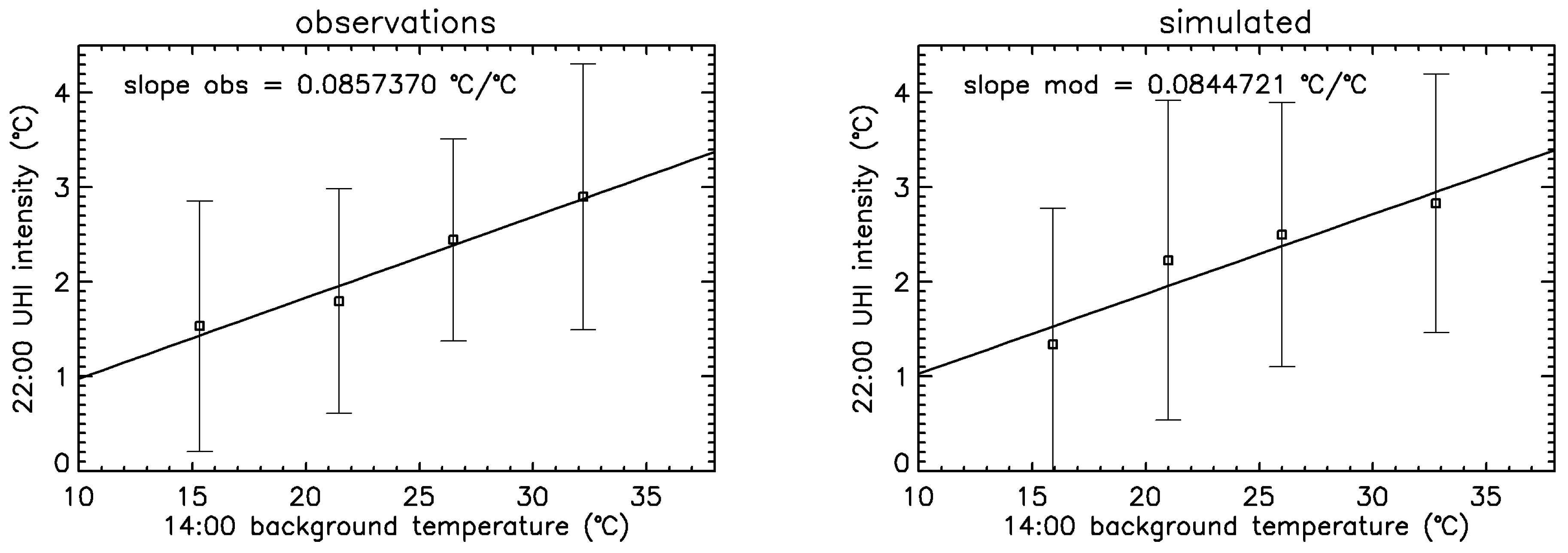
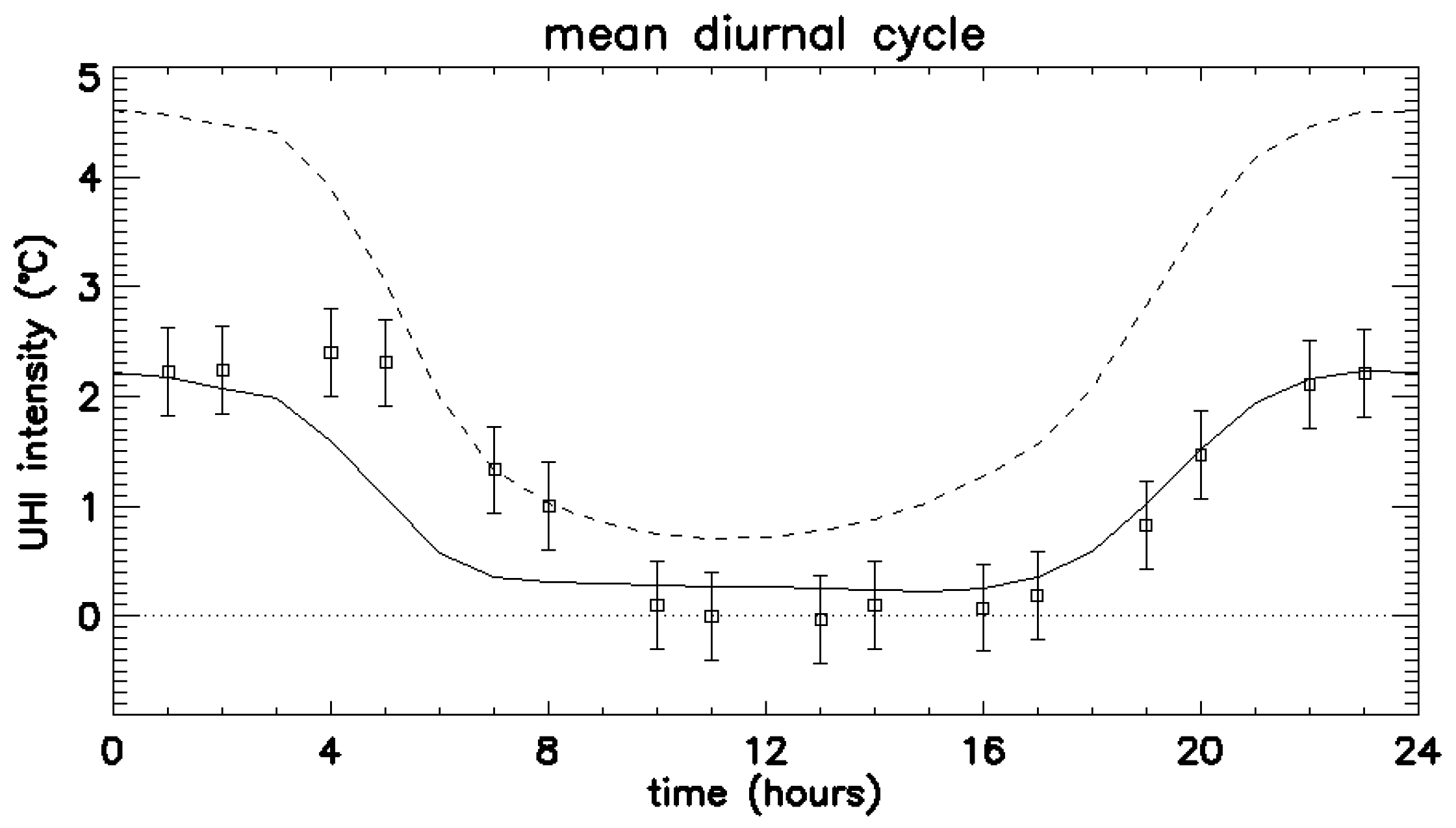
2. Observations
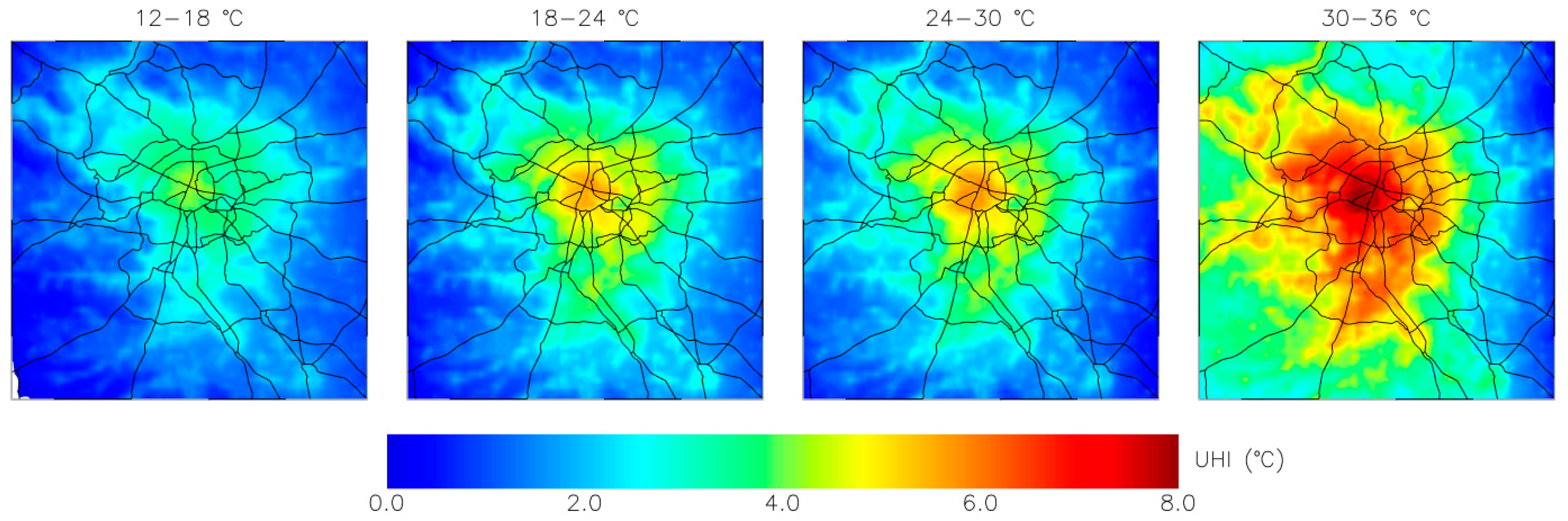
3. Simulation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meehl, G.A.; Tebaldi, C. More intense, more frequent and longer lasting heat waves in the 21st century. Nature 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Diffenbaugh, N.S.; Giorgi, F. Climate change hotspots in the CMIP5 global climate model ensemble. Clim. Chang. 2012, 114, 813–822. [Google Scholar] [CrossRef] [PubMed]
- Schär, C.; Vidale, P.L.; Luthi, D.; Frei, C.; Haberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European Summer heat waves. Nature 2004, 427, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Borden, K.A.; Cutter, S.L. Spatial patterns of natural hazards mortality in the United States. Int. J. Health Geograph. 2008, 7, 64. [Google Scholar] [CrossRef] [PubMed]
- Beven, J.L., II; Avila, L.A.; Blake, E.S.; Brown, D.P.; Franklin, J.L.; Knabb, R.D.; Pasch, R.J.; Rhome, J.R.; Stewart, S.R. Atlantic Hurricane Season of 2005. Mon. Weather Rev. 2008, 136, 1109–1173. [Google Scholar] [CrossRef]
- Robine, J.-M.; Cheung, S.L.K.; le Roy, S.; van Oyen, H.; Griffiths, C.; Michel, J.-P.; Herrmann, F.R. Death toll exceeded 70,000 in Europe during the summer of 2003. Comptes Rendus Biol. 2008, 331, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Saha, M.V.; Davis, R.E.; Hondula, D.M. Mortality displacement as a function of heat event strength in 7 US cities. Am. J. Epidemiol. 2014, 179, 467–744. [Google Scholar] [CrossRef] [PubMed]
- Toulemon, L.; Barbieri, M. The mortality impact of the August 2003 heat wave in France: Investigating the “harvesting” effect and other long-term consequences. Popul. Stud. 2008, 62, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Keller, R.C. Fatal isolation: The Devastating Paris Heat Wave of 2003; University of Chicago Press: Chicago, IL, USA, 2015; p. 240. [Google Scholar]
- Gabriel, K.M.A.; Endlicher, W.R. Urban and rural mortality rates during heat waves in Berlin and Brandenburg, Germany. Environ. Poll. 2011, 159, 2044–2050. [Google Scholar] [CrossRef] [PubMed]
- Dousset, B.; Gourmelon, F.; Laaidi, K.; Zeghnoun, A.; Giraudet, E.; Bretin, P.; Maurid, E.; Vandentorren, S. Satellite monitoring of summer heat waves in the Paris metropolitan area. Int. J. Climatol. 2011, 31, 313–323. [Google Scholar] [CrossRef]
- Vandentorren, S.; Suzan, F.; Medina, S.; Pascal, M.; Maulpoix, A.; Cohen, J.-C.; Ledrans, M. Mortality in 13 French cities during the August 2003 heatwave. Am. J. Public Health 2004, 94, 1518–1520. [Google Scholar] [CrossRef] [PubMed]
- Ho, H.C.; Knudby, A.; Walker, B.B.; Henderson, S.B. Delineation of Spatial Variability in the Temperature-Mortality Relationship on Extremely Hot Days in Greater Vancouver, Canada. Environ. Health Perspect. 2016. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Barnett, A.G.; Tong, S. Spatiotemporal model or time series model for assessing city-wide temperature effects on mortality? Environ. Res. 2013, 120, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Hattis, D.; Ogneva-Himmelberger, Y.; Ratick, S. The spatial variability of heat-related mortality in Massachusetts. Appl. Geogr. 2012, 33, 45–52. [Google Scholar] [CrossRef]
- Hondula, D.M.; Davis, R.E. The predictability of high-risk zones for heat-related mortality in seven US cities. Nat. Hazards 2014, 74, 771–788. [Google Scholar] [CrossRef]
- Hondula, D.M.; Davis, R.E.; Leisten, M.J.; Saha, M.V.; Veazey, L.M.; Wegner, C.R. Fine-scale spatial variability of heat-related mortality in Philadelphia County, USA, from 1983–2008: A case-series analysis. Environ. Health 2012, 11, 16. [Google Scholar] [PubMed]
- Vaneckova, P.; Beggs, P.J.; Jacobson, C.R. Spatial analysis of heat-related mortality among the elderly between 1993 and 2004 in Sydney, Australia. Soc. Sci. Med. 2010, 70, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Vargo, J.; Stone, B.; Habeeb, D.; Liu, P.; Russell, A. The social and spatial distribution of temperature-related health impacts from urban heat island reduction policies. Environ. Sci. Policy 2016, 66, 366–374. [Google Scholar]
- Zhu, Q.; Liu, T.; Lin, H.; Xiao, J.; Luo, Y.; Zeng, W.; Zeng, S.; Wei, Y.; Chu, C.; Baum, S.; et al. The spatial distribution of health vulnerability to heat waves in Guangdong Province, China. Glob. Health Action 2014, 7, 25051. [Google Scholar] [CrossRef] [PubMed]
- Stone, B. The City and the Coming Climate. Climate Change in the Places We Live; Cambridge University Press: Cambridge, UK, 2012; p. 206. [Google Scholar]
- Li, D.; Bou-Zeid, E. synergistic interactions between urban heat islands and heat waves: The impact in cities is larger than the sum of its parts. J. Appl. Meteorol. Climatol. 2013, 52, 2051–2064. [Google Scholar]
- Li, D.; Sun, T.; Liu, M.; Yong, L.; Wang, L.; Gao, Z. Contrasting responses of urban and rural surface energy budgets to heat waves explain synergies between urban heat islands and heat waves. Environ. Res. Lett. 2015, 10, 054009. [Google Scholar]
- Schatz, J.; Kucharik, C.J. Urban climate effects on extreme temperatures in Madison, Wisconsin, USA. Environ. Res. Lett. 2015, 10, 094024. [Google Scholar] [CrossRef]
- Maiheu, B.; de Ridder, K.; Dousset, B.; Manunta, P.; Ceriola, G.; Viel, M.; Daglis, I.; Keramitsoglou, I.; Ginannaros, T.; Melas, D.; et al. Modelling air temperature via assimilation of satellite derived surface temperature within the Urban Heat Island project. In Proceedings of the Joint SIG Workshop, European Association of Remote Sensing Laboratories (EARSeL), Ghent, Belgium, 22–24 September 2010; pp. 162–181.
- Doucet, A.; de Freitas, N.; Gordon, N.J. (Eds.) Sequential Monte Carlo Methods in Practice; Springer: New York, NY, USA, 2001; p. 582.
- Bechtel, B.; Wiesner, S.; Zakšek, K. Estimation of dense time series of urban air temperatures from multitemporal geostationary satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4129–4137. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Qin, F. A statistical method based on remote sensing for the estimation of air temperature in China. Int. J. Climatol. 2015, 35, 2131–2143. [Google Scholar] [CrossRef]
- Cristóbal, J.; Ninyerola, M.; Pons, X. Modeling air temperature through a combination of remote sensing and GIS data. J. Geophys. Res. Atmosp. 2008, 113. [Google Scholar] [CrossRef]
- Emamifar, S.; Rahimikhoob, A.; Noroozi, A.A. Daily mean air temperature estimation from MODIS land surface temperature products based on M5 model tree. Int. J. Climatol. 2013, 33, 3174–3181. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, Y.; Cheng, M.; Jiang, H. Near-surface air temperature retrieval from Chinese Geostationary FengYun Meteorological Satellite (FY-2C) data. Int. J. Remote Sens. 2014, 35, 3892–3914. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Sirovyak, P.; Xu, Y.; Hodul, M.; Henderson, S.B. Mapping maximum urban air temperature on hot summer days. Remote Sens. Environ. 2014, 154, 38–45. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Xu, Y.; Hodul, M.; Aminipouri, M. A comparison of urban heat islands mapped using skin temperature, air temperature, and apparent temperature (Humidex), for the greater Vancouver area. Sci. Total Environ. 2016, 544, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Holden, Z.A.; Abatzoglou, J.T.; Luce, C.H.; Baggett, L.S. Empirical downscaling of daily minimum air temperature at very fine resolutions in complex terrain. Agric. Forest Meteorol. 2011, 151, 1066–1073. [Google Scholar] [CrossRef]
- Hou, P.; Chen, Y.; Qiao, W.; Cao, G.; Jiang, W.; Li, J. Near-surface air temperature retrieval from satellite images and influence by wetlands in urban region. Theor. Appl. Climatol. 2013, 111, 109–118. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, C.; Huang, J.; Zhu, D.; Wang, L.; Liu, J. Mapping of daily mean air temperature in agricultural regions using daytime and nighttime land surface temperatures derived from Terra and Aqua MODIS data. Remote Sens. 2015, 7, 8728–8756. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2016. [Google Scholar] [CrossRef]
- Kloog, I.; Chudnovsky, A.; Koutrakis, P.; Schwartz, J. Temporal and spatial assessments of minimum air temperature using satellite surface temperature measurements in Massachusetts, USA. Sci. Total Environ. 2012, 432, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Lin, S.; Moore, N.J.; Messina, J.P.; DeVisser, M.H.; Wu, J. Evaluation of estimating daily maximum and minimum air temperature with MODIS data in east Africa. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 128–140. [Google Scholar] [CrossRef]
- Mao, K.B.; Tang, H.J.; Wang, X.F.; Zhou, Q.B.; Wang, D.L. Near-surface air temperature estimation from ASTER data based on neural network algorithm. Int. J. Remote Sens. 2008, 29, 6021–6028. [Google Scholar] [CrossRef]
- Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical estimation of daily maximum and minimum air temperatures from MODIS LST data over the state of Mississippi. GISci. Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef]
- Nichol, J.E.; Fung, W.Y.; Lam, K.S.; Wong, M.S. Urban heat island diagnosis using ASTER satellite images and “in situ” air temperature. Atmos. Res. 2009, 94, 276–284. [Google Scholar] [CrossRef]
- Nichol, J.E.; Wong, M.S. Spatial variability of air temperature and appropriate resolution for satellite-derived air temperature estimation. Int. J. Remote Sens. 2008, 29, 7213–7223. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Şahin, M. Modelling of air temperature using remote sensing and artificial neural network in Turkey. Adv. Space Res. 2012, 50, 973–985. [Google Scholar] [CrossRef]
- Shen, S.; Leptoukh, G.G. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature. Environ. Res. Lett. 2011, 6, 045206. [Google Scholar] [CrossRef]
- Shi, L.; Liu, P.; Kloog, I.; Lee, M.; Kosheleva, A.; Schwartz, J. Estimating daily air temperature across the Southeastern United States using high-resolution satellite data: A statistical modeling study. Environ. Res. 2016, 146, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Sun, H.; Chen, Y.; Gong, A.; Zhao, X.; Zhan, W.; Wang, M. Estimating mean air temperature using MODIS day and night land surface temperatures. Theor. Appl. Climatol. 2014, 118, 81–92. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Ho, H.C. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y. Monitoring the Near-surface Urban Heat Island in Beijing, China by Satellite Remote Sensing. Geogr. Res. 2015, 53, 16–25. [Google Scholar] [CrossRef]
- Xu, Y.; Qin, Z.; Shen, Y. Study on the estimation of near-surface air temperature from MODIS data by statistical methods. Int. J. Remote Sens. 2012, 33, 7629–7643. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, J.; Hou, Y.; He, Y. Estimation of air temperature from MODIS data in east China. Int. J. Remote Sens. 2009, 30, 6261–6275. [Google Scholar] [CrossRef]
- Yang, G.; Pu, R.; Huang, W.; Wang, J.; Zhao, C. A novel method to estimate subpixel temperature by fusing solar-reflective and thermal-infrared remote-sensing data with an artificial neural network. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2170–2178. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B. MODIS-based estimation of air temperature of the Tibetan Plateau. J. Geogr. Sci. 2013, 23, 627–640. [Google Scholar] [CrossRef]
- Zakšek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
- Zhu, W.; Lu, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Daglis, I.A.; Amiridis, V.; Chrysoulakis, N.; Ceriola, G.; Manunta, P.; Maiheu, B.; de Ridder, K.; Lauwaet, D.; Paganini, M. Evaluation of satellite-derived products for the characterization of the urban thermal environment. J. Appl. Remote Sens. 2012, 6, 061704. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Kiranoudis, C.T.; Maiheu, B.; de Ridder, K.; Daglis, I.A.; Manunta, P.; Paganini, M. Heat wave hazard classification and risk assessment using artificial intelligence fuzzy logic. Environ. Monit. Assess. 2013. [Google Scholar] [CrossRef] [PubMed]
- Brandsma, T.; van der Meulen, J.P. Thermometer screen intercomparison in De Bilt (The Netherlands)—Part II: Description and modeling of mean temperature differences and extremes. Int. J. Climatol. 2008, 28, 389–400. [Google Scholar] [CrossRef]
- De Ridder, K.; Lauwaet, D.; Maiheu, B. UrbClim—A fast urban boundary layer climate model. Urban Clim. 2015, 12, 21–48. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Ridder, K.; Maiheu, B.; Lauwaet, D.; Daglis, I.A.; Keramitsoglou, I.; Kourtidis, K.; Manunta, P.; Paganini, M. Urban Heat Island Intensification during Hot Spells—The Case of Paris during the Summer of 2003. Urban Sci. 2017, 1, 3. https://doi.org/10.3390/urbansci1010003
De Ridder K, Maiheu B, Lauwaet D, Daglis IA, Keramitsoglou I, Kourtidis K, Manunta P, Paganini M. Urban Heat Island Intensification during Hot Spells—The Case of Paris during the Summer of 2003. Urban Science. 2017; 1(1):3. https://doi.org/10.3390/urbansci1010003
Chicago/Turabian StyleDe Ridder, Koen, Bino Maiheu, Dirk Lauwaet, Ioannis A. Daglis, Iphigenia Keramitsoglou, Kostas Kourtidis, Paolo Manunta, and Marc Paganini. 2017. "Urban Heat Island Intensification during Hot Spells—The Case of Paris during the Summer of 2003" Urban Science 1, no. 1: 3. https://doi.org/10.3390/urbansci1010003





