Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing
Abstract
:1. Introduction
2. Materials and Methods
3. Results
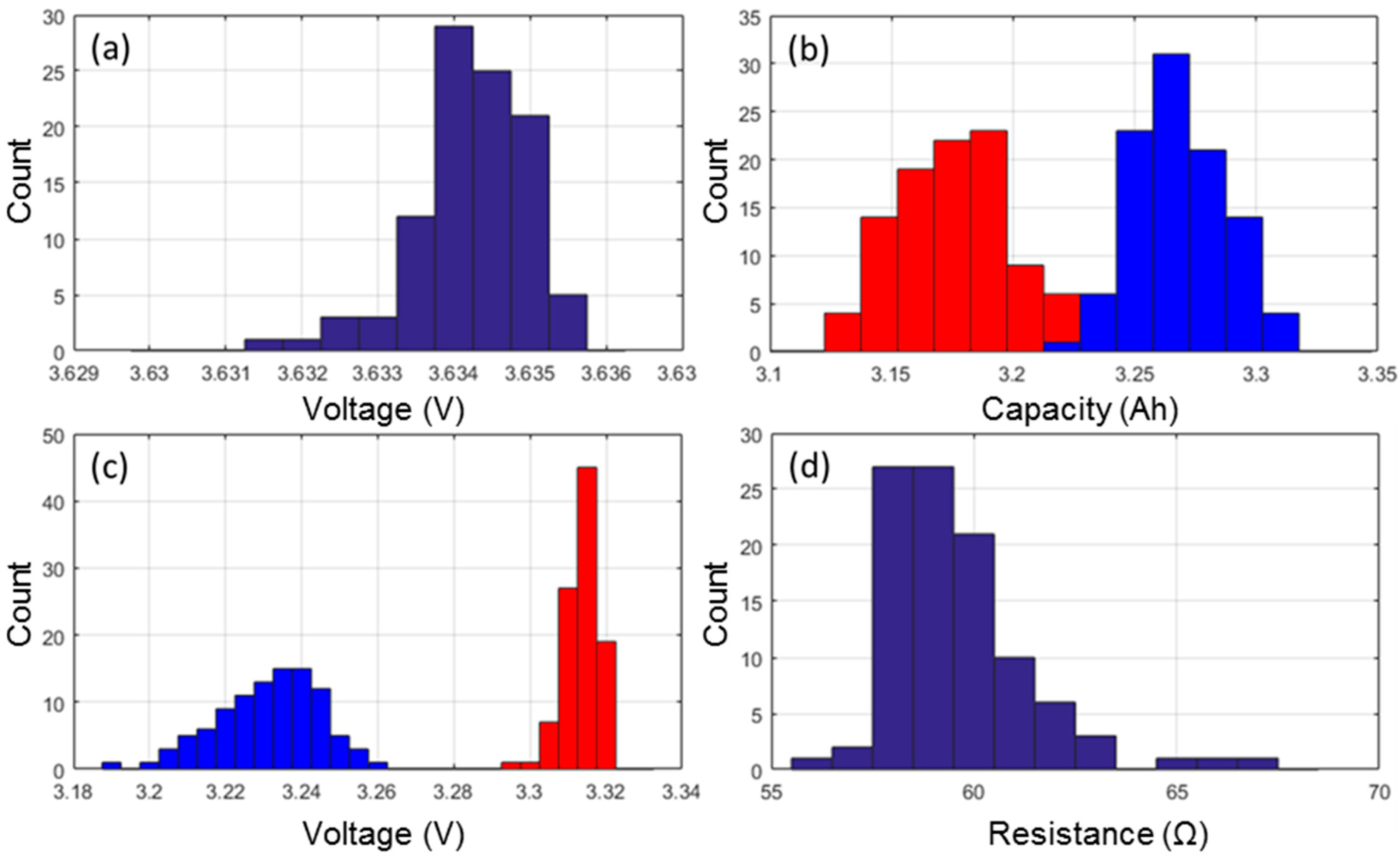
3.1. Formation Cycles Testing
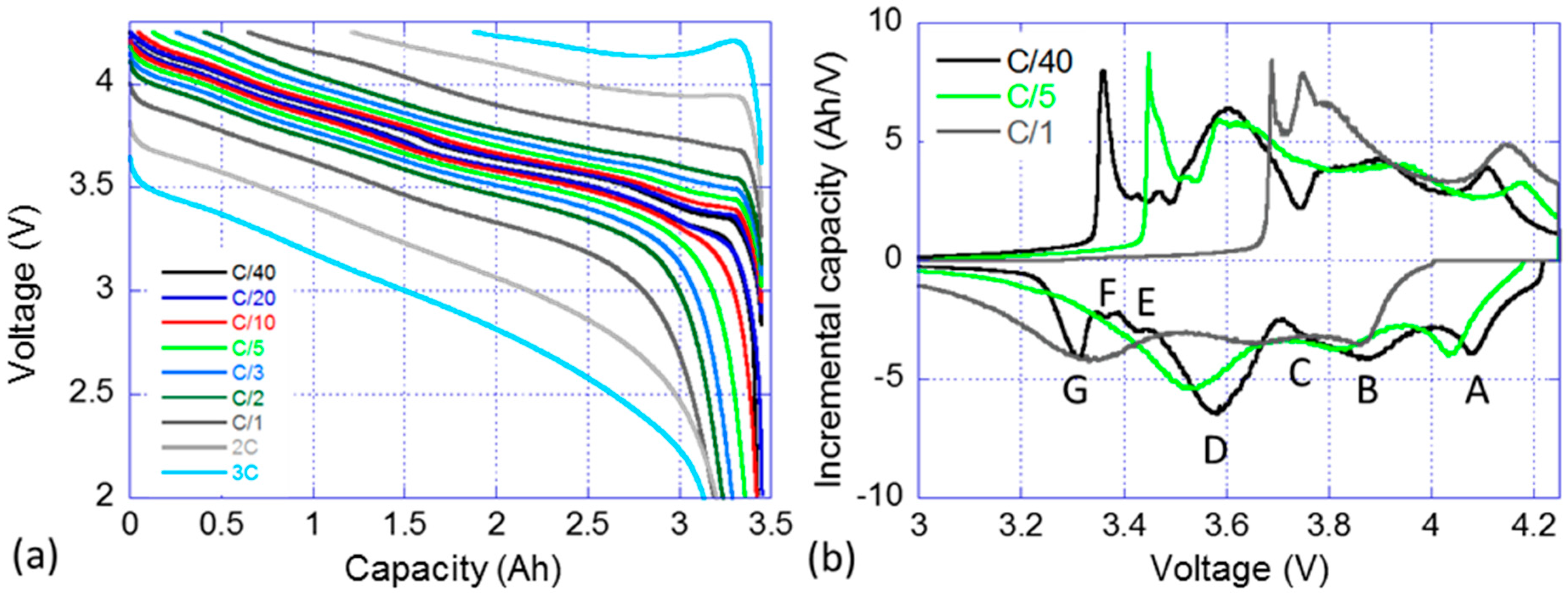
3.2. Nominal Sample Cell Reference Performance Testing
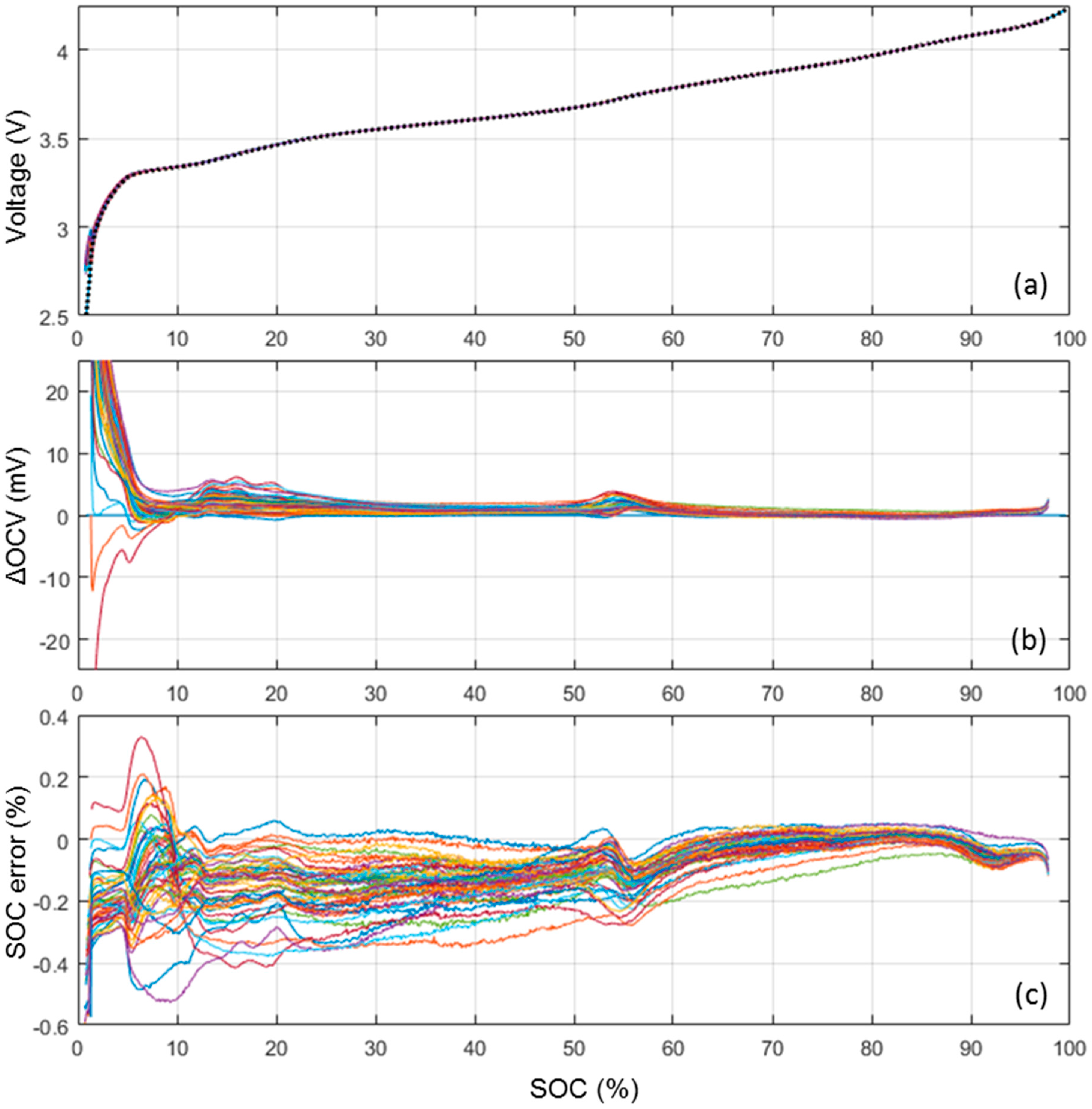
3.3. ps-OCV = f(SOC) Curve Cell-to-Cell Variations
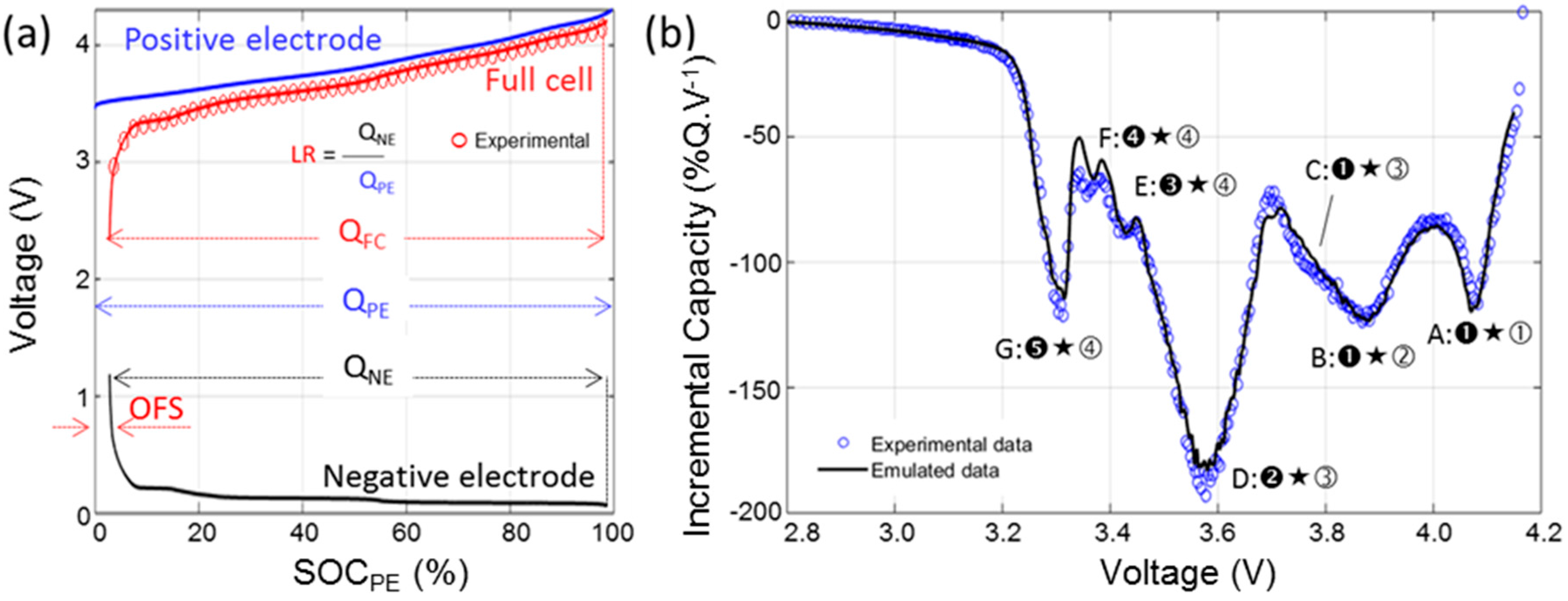
3.4. Half-Cell Testing
4. Discussion
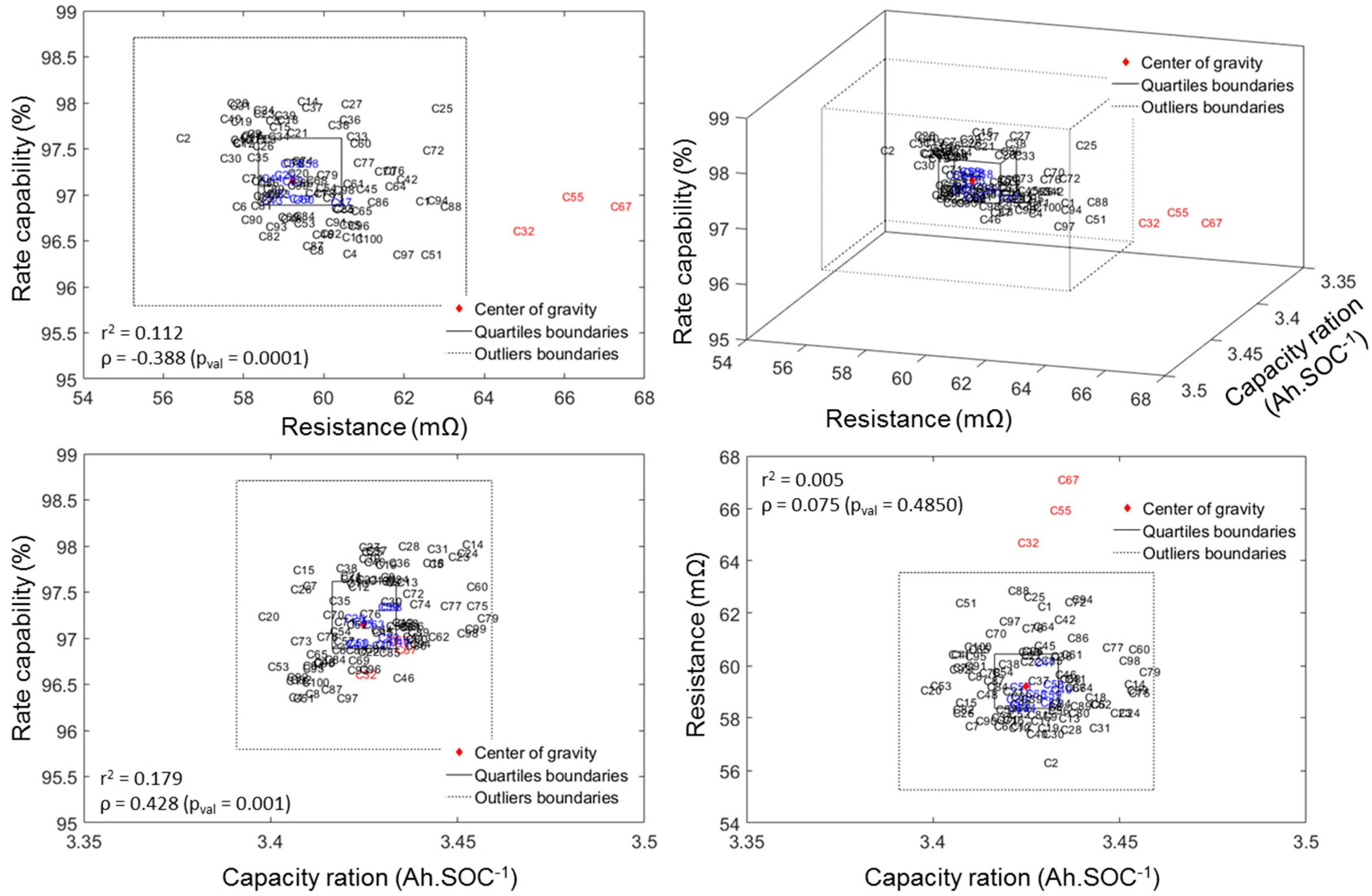
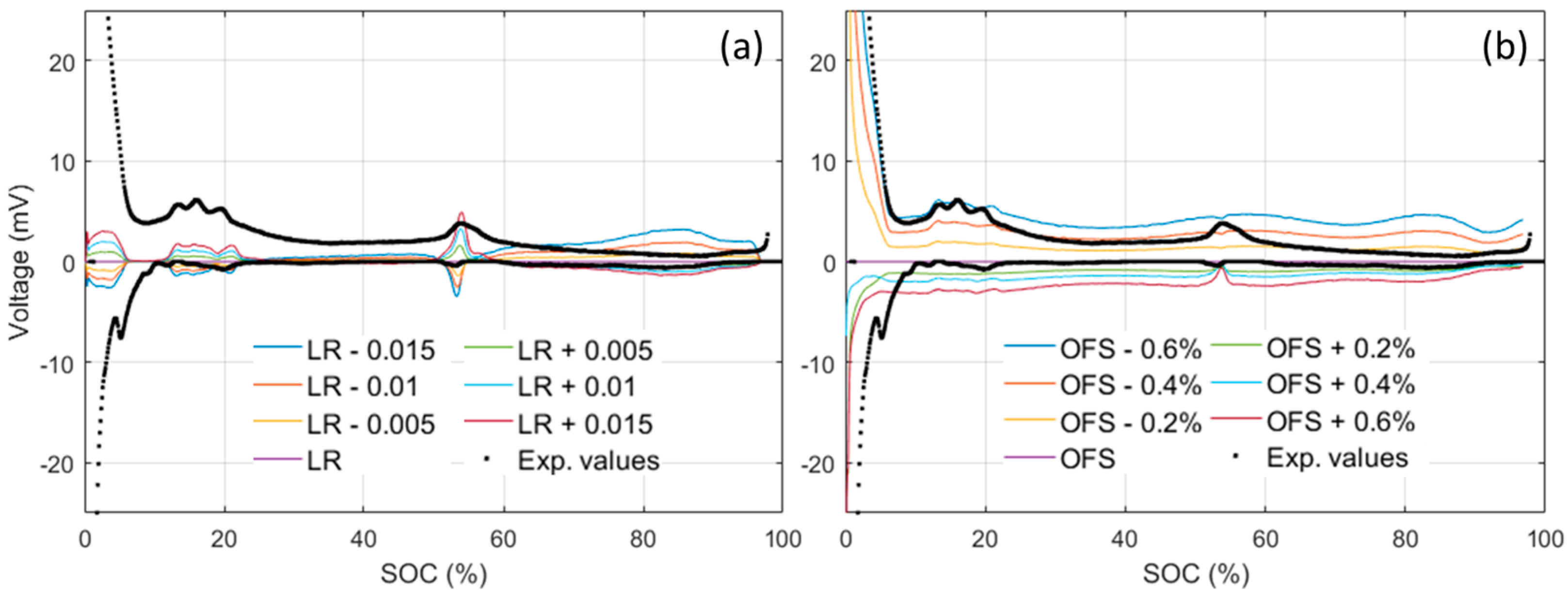
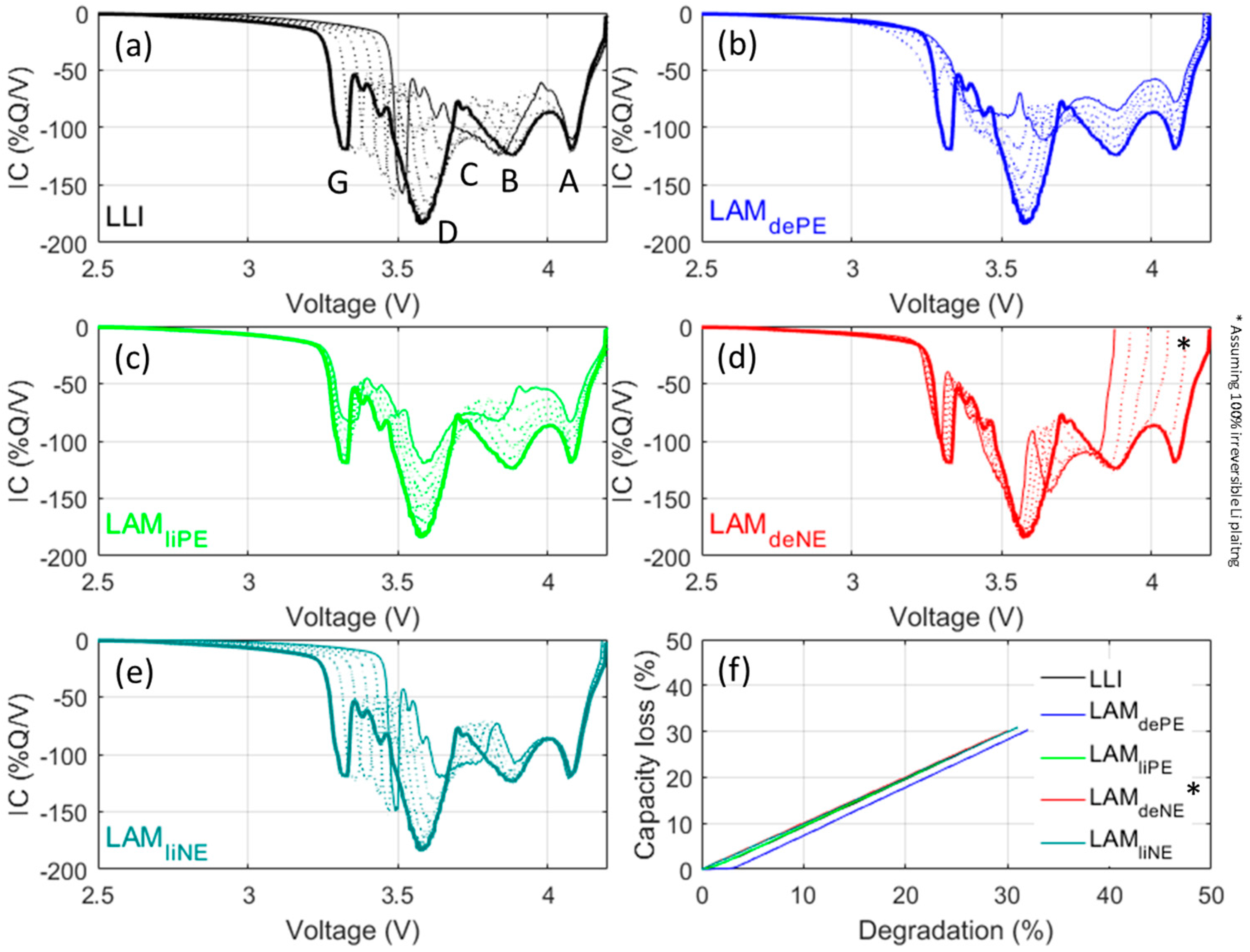
4.1. Cell-to-Cell Variations
4.2. Cell Emulation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mwasilu, F.; Justo, J.J.; Kim, E.-K.; Do, T.D.; Jung, J.-W. Electric vehicles and smart grid interaction: A review on vehicle to grid and renewable energy sources integration. Renew. Sustain. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Habib, S.; Kamran, M.; Rashid, U. Impact analysis of vehicle-to-grid technology and charging strategies of electric vehicles on distribution networks—A review. J. Power Sources 2015, 277, 205–214. [Google Scholar] [CrossRef]
- Babrowski, S.; Heinrichs, H.; Jochem, P.; Fichtner, W. Load shift potential of electric vehicles in Europe. J. Power Sources 2014, 255, 283–293. [Google Scholar] [CrossRef]
- Honarmand, M.; Zakariazadeh, A.; Jadid, S. Optimal scheduling of electric vehicles in an intelligent parking lot considering vehicle-to-grid concept and battery condition. Energy 2014, 65, 572–579. [Google Scholar] [CrossRef]
- Aziz, M.; Oda, T.; Mitani, T.; Watanabe, Y.; Kashiwagi, T. Utilization of Electric vehicles and their used batteries for peak-load shifting. Energies 2015, 8, 3720–3738. [Google Scholar] [CrossRef]
- Zhang, L.; Jabbari, F.; Brown, T.; Samuelsen, S. Coordinating plug-in electric vehicle charging with electric grid: Valley filling and target load following. J. Power Sources 2014, 267, 584–597. [Google Scholar] [CrossRef]
- Talebizadeh, E.; Rashidinejad, M.; Abdollahi, A. Evaluation of plug-in electric vehicles impact on cost-based unit commitment. J. Power Sources 2014, 248, 545–552. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, Q.; Pu, Y. The reserve trading model considering V2G Reverse. Energy 2013, 59, 50–55. [Google Scholar]
- Zhou, C. Modeling of the cost of EV battery wear due to V2G application in power systems. IEEE Trans. Energy Convers. 2011, 26, 1043–1050. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Multi-objective scheduling of electric vehicles in smart distribution system. Energy Convers. Manag. 2014, 79, 43–53. [Google Scholar] [CrossRef]
- Soares, J.; Ghazvini, M.A.F.; Silva, M.; Vale, Z. Multi-dimensional signaling method for population-based metaheuristics: Solving the large-scale scheduling problem in smart grids. Swarm Evolut. Comput. 2016, 29, 13–32. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, T.; Wan, S.; Zhang, S.; Li, K. Optimal charging scheduling for large-scale EV (electric vehicle) deployment based on the interaction of the smart-grid and intelligent-transport systems. Energy 2016, 97, 359–368. [Google Scholar] [CrossRef]
- White, C.D.; Zhang, K.M. Using vehicle-to-grid technology for frequency regulation and peak-load reduction. J. Power Sources 2011, 196, 3972–3980. [Google Scholar] [CrossRef]
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- Bishop, J.D.K.; Axon, C.J.; Bonilla, D.; Tran, M.; Banister, D.; McCulloch, M.D. Evaluating the impact of V2G services on the degradation of batteries in PHEV and EV. Appl. Energy 2013, 111, 206–218. [Google Scholar] [CrossRef]
- Fernández, I.J.; Calvillo, C.F.; Sánchez-Miralles, A.; Boal, J. Capacity fade and aging models for electric batteries and optimal charging strategy for electric vehicles. Energy 2013, 60, 35–43. [Google Scholar] [CrossRef]
- Guenther, C.; Schott, B.; Hennings, W.; Waldowski, P.; Danzer, M.A. Model-based investigation of electric vehicle battery aging by means of vehicle-to-grid scenario simulations. J. Power Sources 2013, 239, 604–610. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Aki, H. A practical battery wear model for electric vehicle charging applications. Appl. Energy 2014, 113, 1100–1108. [Google Scholar] [CrossRef]
- Marongiu, A.; Roscher, M.; Sauer, D.U. Influence of the vehicle-to-grid strategy on the aging behavior of lithium battery electric vehicles. Appl. Energy 2015, 137, 899–912. [Google Scholar] [CrossRef]
- Peterson, S.B.; Apt, J.; Whitacre, J.F. Lithium-ion battery cell degradation resulting from realistic vehicle and vehicle-to-grid utilization. J. Power Sources 2010, 195, 2385–2392. [Google Scholar] [CrossRef]
- Wood, E.; Alexander, M.; Bradley, T.H. Investigation of battery end-of-life conditions for plug-in hybrid electric vehicles. J. Power Sources 2011, 196, 5147–5154. [Google Scholar] [CrossRef]
- Schuster, S.F.; Brand, M.J.; Berg, P.; Gleissenberger, M.; Jossen, A. Lithium-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 2015, 297, 242–251. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Quantifying cell-to-cell variations in lithium ion batteries. Int. J. Electrochem. 2012, 2012. [Google Scholar] [CrossRef]
- Prochazka, W.; Pregartner, G.; Cifrain, M. Design-of-experiment and statistical modeling of a large scale aging experiment for two popular lithium ion cell chemistries. J. Electrochem. Soc. 2013, 160, A1039–A1051. [Google Scholar] [CrossRef]
- Kenney, B.; Darcovich, K.; MacNeil, D.D.; Davidson, I.J. Modelling the impact of variations in electrode manufacturing on lithium-ion battery modules. J. Power Sources 2012, 213, 391–401. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. Origins and accommodation of cell variations in Li-ion battery pack modeling. Int. J. Energy Res. 2010, 34, 216–231. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Cugnet, M.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part I: Initial characterizations. J. Power Sources 2011, 196, 10328–10335. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From single cell model to battery pack simulation for Li-ion batteries. J. Power Sources 2009, 186, 500–507. [Google Scholar] [CrossRef]
- Balewski, L.; Brenet, J.P. A new method for the study of the electrochemical reactivity of manganese dioxide. Electrochem. Technol. 1967, 5, 527–531. [Google Scholar]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries. Electrochem. Solid-State Lett. 2006, 9, A454–A457. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y. Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Sources 2009, 194, 541–549. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Elon Musk, Code Conference 2016. Start Time: 32m37s. Available online: https://youtu.be/wsixsRI-Sz4?t=32m37s (accessed on 6 September 2016).
- EV and More. Let’s talk about the Panasonic NCR18650B. Available online: http://blog.evandmore.com/lets-talk-about-the-panasonic-ncr18650b/ (accessed on 6 September 2016).
- 'Alawa Central. Available online: https://www.soest.hawaii.edu/HNEI/alawa/ (accessed on 15 May 2016).
- Kassem, M.; Delacourt, C. Postmortem analysis of calendar-aged graphite/LiFePO4 cells. J. Power Sources 2013, 235, 159–171. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Tran, H.Y.; Richter, J.; Ivers-Tiffée, E.; Wohlfahrt-Mehrens, M. Analysis and prediction of the open circuit potential of lithium-ion cells. J. Power Sources 2013, 239, 696–704. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Devie, A.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle (PHEV) applications. IV. Over-discharge phenomena. J. Electrochem. Soc. 2015, 162, A1787–A1792. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M.; Liaw, B.Y. Overcharge study in Li4Ti5O12 based lithium-ion pouch cell, I. Quantitative diagnosis of degradation modes. J. Electrochem. Soc. 2015, 162, A1033–A1040. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Cell degradation in commercial LiFePO4 cells with high-power and high-energy designs. J. Power Sources 2014, 258, 408–419. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Liaw, B.Y. The value of battery diagnostics and prognostics. J. Energy Power Sources 2014, 1, 242–249. [Google Scholar]
- Zenodo. Panasonic NCR18650B Formation, RPT and Half Cell Data Set. Available online: http://dx.doi.org/10.5281/zenodo.60232 (accessed on 6 September 2016).
- Dahn, J. Phase-diagram of LixC6. Phys. Rev. B 1991, 44, 9170–9177. [Google Scholar] [CrossRef]
- Aurbach, D.; Markovsky, B.; Weissman, I.; Levi, E.; Ein-Eli, Y. On the correlation between surface chemistry and performance of graphite negative electrodes for Li ion batteries. Electrochem. Acta 1999, 45, 67–86. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Boston, MA, USA, 1977. [Google Scholar]
- Dubarry, M.; Devie, A. Initial Conditioning Characterization Test and Other Preliminary Testing; EVTC Report HNEI-06-15; Electric Vehicle Transportation Center (EVTC): Cocoa, FL, USA, 2015; pp. 1–25. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devie, A.; Dubarry, M. Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing. Batteries 2016, 2, 28. https://doi.org/10.3390/batteries2030028
Devie A, Dubarry M. Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing. Batteries. 2016; 2(3):28. https://doi.org/10.3390/batteries2030028
Chicago/Turabian StyleDevie, Arnaud, and Matthieu Dubarry. 2016. "Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing" Batteries 2, no. 3: 28. https://doi.org/10.3390/batteries2030028
APA StyleDevie, A., & Dubarry, M. (2016). Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing. Batteries, 2(3), 28. https://doi.org/10.3390/batteries2030028





