Interaction between Graphene Nanoribbon and an Array of QDs: Introducing Nano Grating
Abstract
:1. Introduction
2. Mathematical Formalism
2.1. Induced Polarization in Graphene and Quantum Dots
2.2. Interaction between Graphene Nanoribbon and Quantum Dots
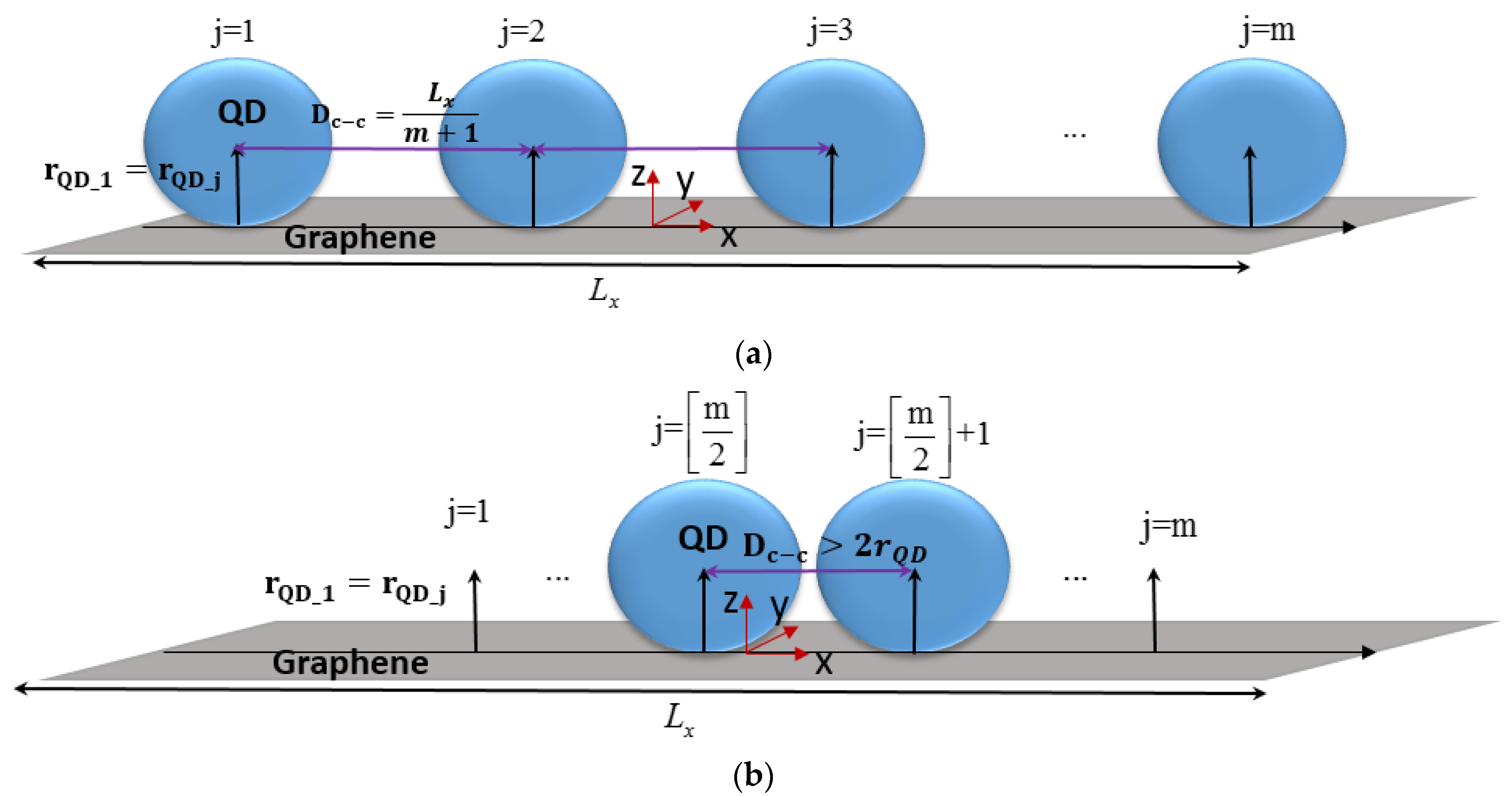
2.3. Interaction between Quantum Dots in an Array
2.3.1. Array of Quantum Dots with the Same Radii
2.3.2. Array of Quantum Dots with the Same Radii
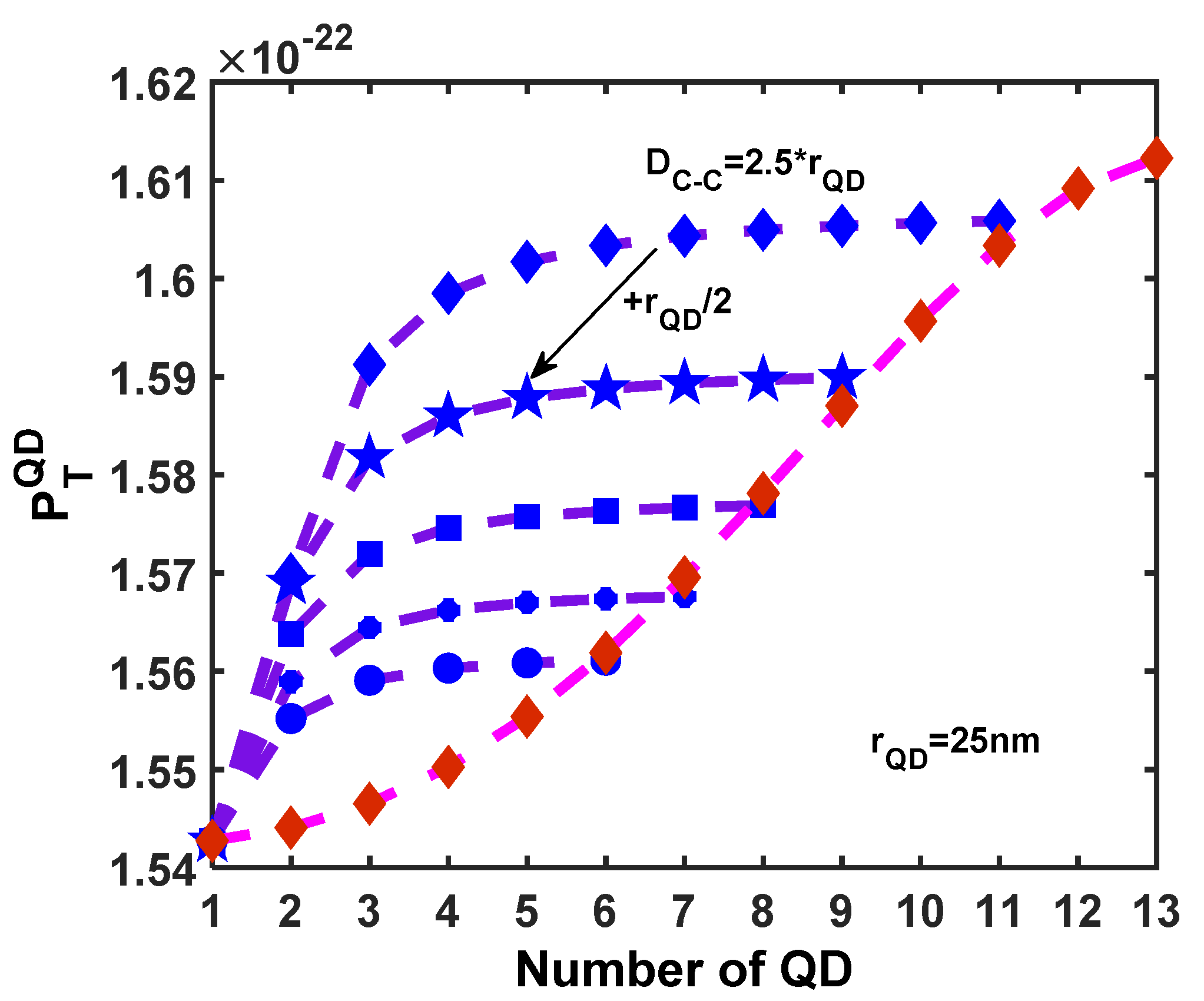
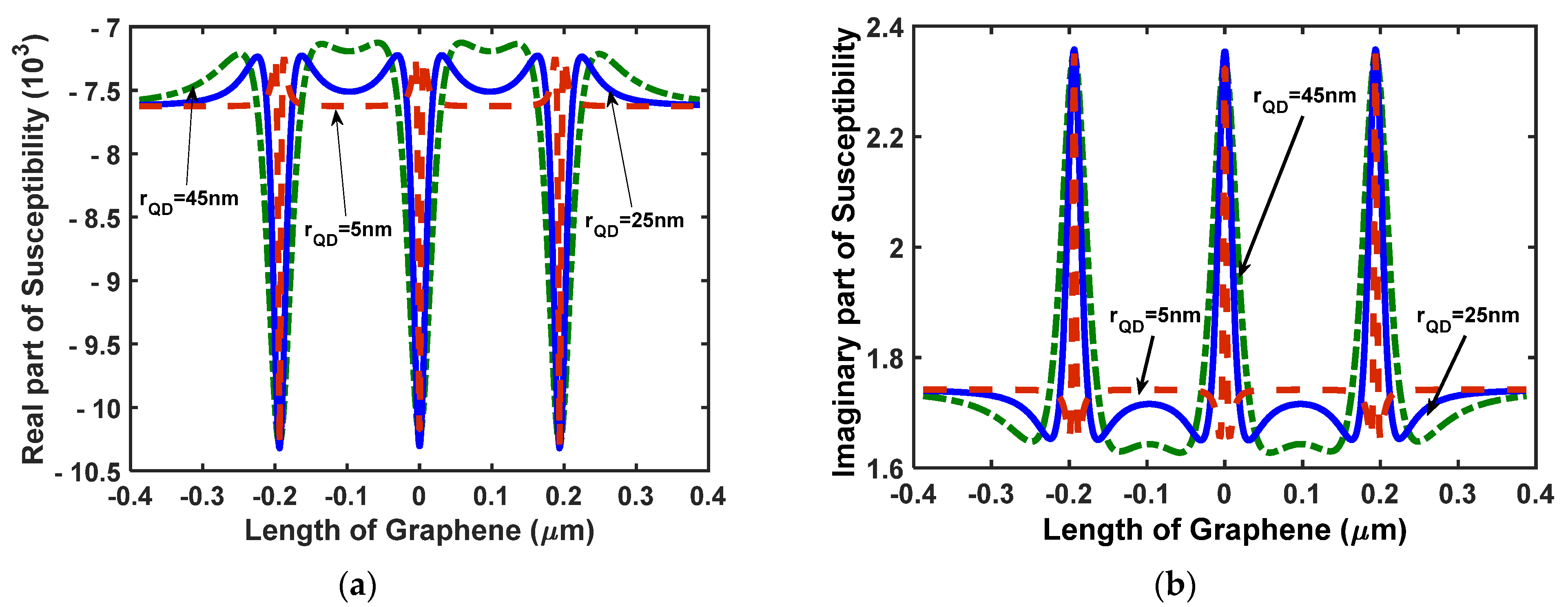
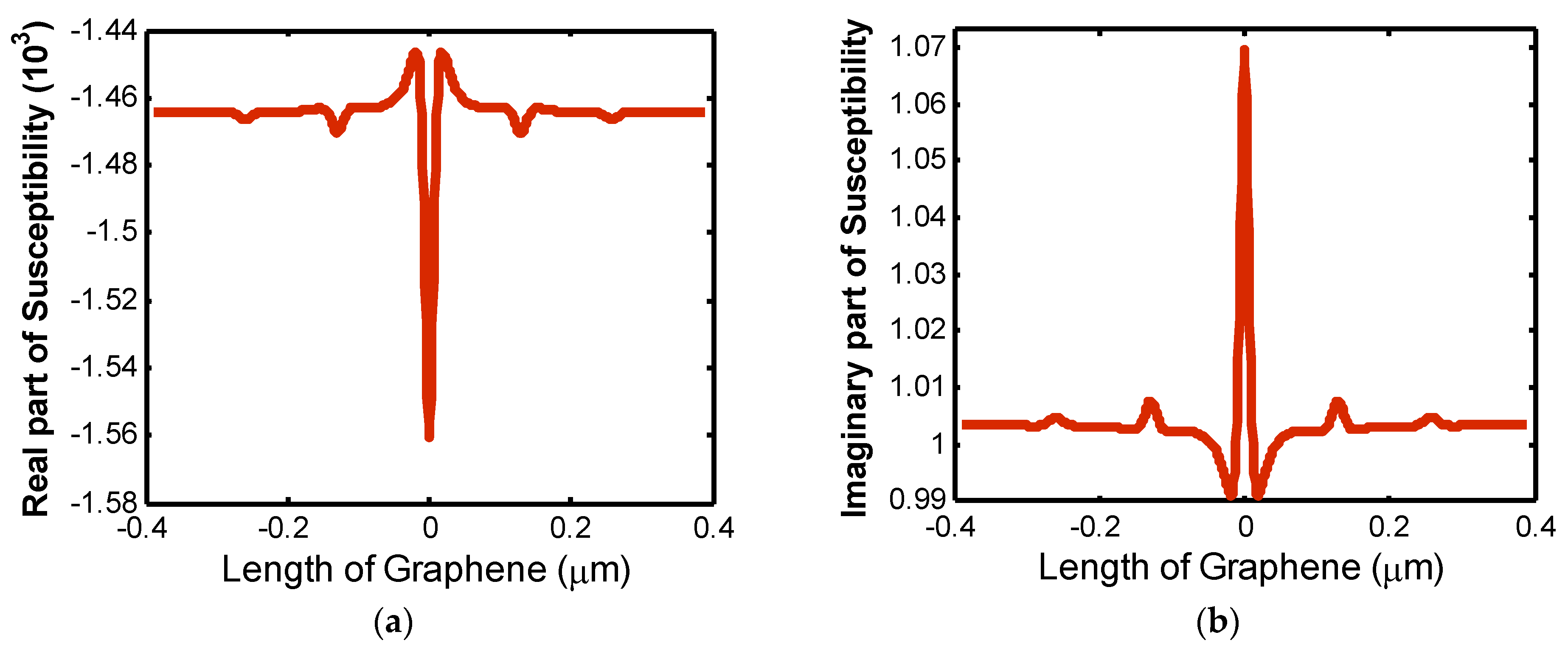
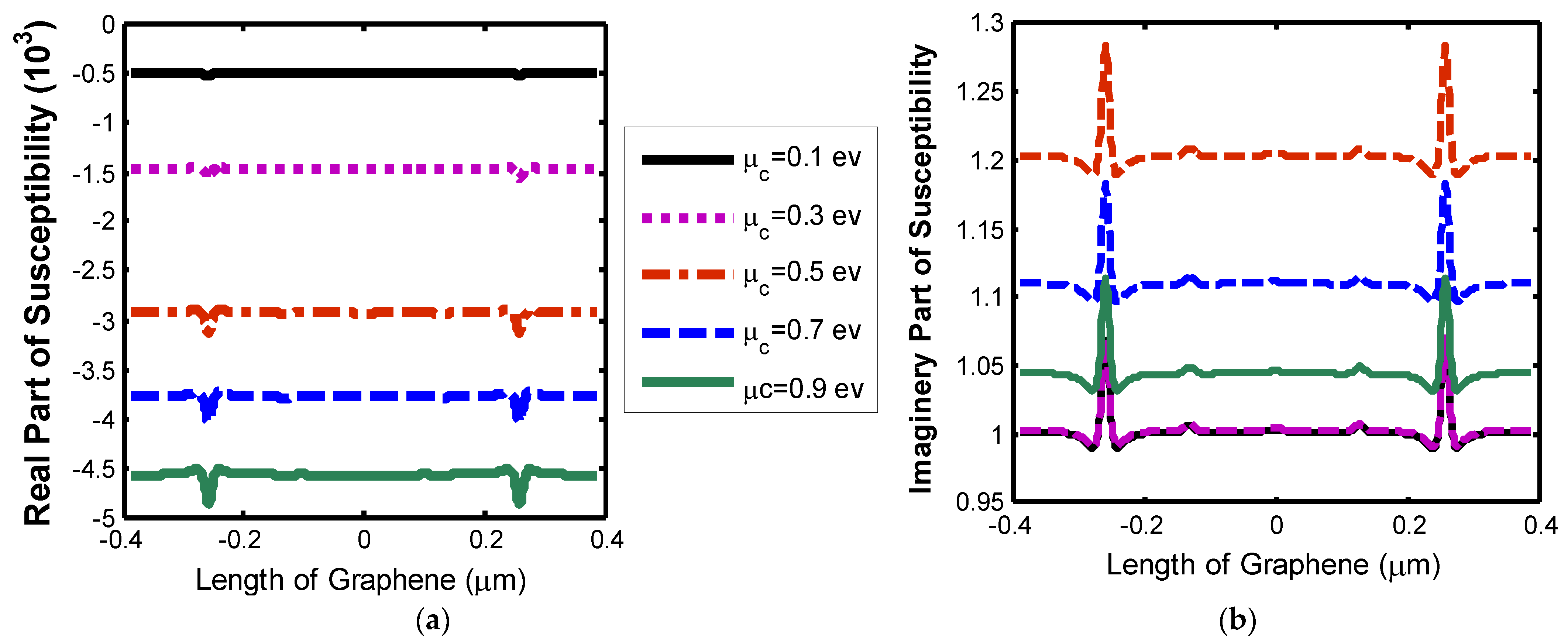
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tran, M.A.; Huang, D.; Komljenovic, T.; Peters, J.; Malik, A.; Bowers, J.E. Ultra-low-loss silicon waveguides for heterogeneously integrated silicon/III-V photonics. Appl. Sci. 2018, 8, 1139. [Google Scholar] [CrossRef] [Green Version]
- Barnes, W.L. Surface plasmon–polariton length scales: A route to sub-wavelength optics. J. Opt. A Pure Appl. Opt. 2006, 8, S87. [Google Scholar] [CrossRef]
- Ono, M.; Taniyama, H.; Kuramochi, E.; Nozaki, K.; Notomi, M. Toward application of plasmonic waveguides to optical devices. NTT Tech. Rev. 2018, 16, 14–19. [Google Scholar]
- Huang, X.; Chen, G.; Zhou, W.; Huang, X. Cm-level photonic-crystal-like subwavelength waveguide platform with high integration density. Appl. Sci. 2019, 9, 3410. [Google Scholar] [CrossRef] [Green Version]
- Veronis, G.; Fan, S. Bends and splitters in metal-dielectric-metal subwavelength plasmonic waveguides. Appl. Phys. Lett. 2005, 87, 131102. [Google Scholar] [CrossRef]
- Berini, P. Long-range surface plasmon polaritons. Adv. Opt. Photonics 2009, 1, 484–588. [Google Scholar] [CrossRef]
- Hao, R.; Li, E.; Wei, X. Two-dimensional light confinement in cross-index-modulation plasmonic waveguides. Opt. Lett. 2012, 37, 2934–2936. [Google Scholar] [CrossRef] [PubMed]
- Briggs, R.M.; Grandidier, J.; Burgos, S.P.; Feigenbaum, E.; Atwater, H.A. Efficient coupling between dielectric-loaded plasmonic and silicon photonic waveguides. Nano Lett. 2010, 10, 4851–4857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pacifici, D.; Lezec, H.J.; Atwater, H.A. All-optical modulation by plasmonic excitation of CdSe quantum dots. Nat. Photonics 2007, 1, 402–406. [Google Scholar] [CrossRef]
- Gubin, M.Y.; Prokhorov, A.V.; Volkov, V.S.; Evlyukhin, A.B. Controllable Excitation of Surface Plasmon Polaritons in Graphene-Based Semiconductor Quantum Dot Waveguides. Ann. der Phys. 2021, 533, 2100139. [Google Scholar] [CrossRef]
- Aliofkhazraei, M.; Ali, N.; Milne, W.I.; Ozkan, C.S.; Mitura, S.; Gervasoni, J.L. (Eds.) Graphene Science Handbook: Electrical and Optical Properties; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Hosseininejad, S.E.; Komjani, N.; Noghani, M.T. A comparison of graphene and noble metals as conductors for plasmonic one-dimensional waveguides. IEEE Trans. Nanotechnol. 2015, 14, 829–836. [Google Scholar] [CrossRef]
- Armaghani, S.; Khani, S.; Danaei, M. Design of all-optical graphene switches based on a Mach-Zehnder interferometer employing optical Kerr effect. Superlattices Microstruct. 2019, 135, 106244. [Google Scholar] [CrossRef]
- Sun, Z.; Martinez, A.; Wang, F. Optical modulators with 2D layered materials. Nat. Photonics 2016, 10, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Zheng, K.; Yuan, Y.; Zhao, L.; Chen, Y.; Zhang, F.; Song, J.; Qu, J. Ultra-compact, low-loss terahertz waveguide based on graphene plasmonic technology. 2D Mater. 2019, 7, 015016. [Google Scholar] [CrossRef]
- Wu, J.; Gong, M.; Schmitz, R.C.; Liu, B. Quantum Dot/Graphene Heterostructure Nanohybrid Photodetectors, in Quantum Dot Photodetectors; Springer: Berlin/Heidelberg, Germany, 2021; pp. 215–248. [Google Scholar]
- Gubin, M.Y.; Leksin, A.Y.; Shesterikov, A.V.; Volkov, V.S.; Prokhorov, A.V. Nonlinear plasmonic switching in graphene-based stub nanoresonator loaded with core-shell nanowire. Appl. Surf. Sci. 2020, 506, 144814. [Google Scholar] [CrossRef]
- Xing, G.; Liu, X.; Hao, S.; Li, X.; Fan, L.; Li, Y. Diameter-and length-controlled synthesis of ultrathin ZnS nanowires and their size-dependent UV absorption properties, photocatalytic activities, and band-edge energy levels. Nanomaterials 2019, 9, 220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007; Volume 1. [Google Scholar]
- Engheta, N.; Ziolkowski, R.W. Metamaterials: Physics and Engineering Explorations; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Cox, J.D.; Singh, M.R.; Gumbs, G.; Anton, M.A.; Carreno, F. Dipole-dipole interaction between a quantum dot and a graphene nanodisk. Phys. Rev. B 2012, 86, 125452. [Google Scholar] [CrossRef] [Green Version]
- Armaghani, S.; Rostami, A.; Mirtaheri, P. Analysis and Simulation of the Optical Properties of a Quantum Dot on a Graphene Nanoribbon System. Photonics 2022, 9, 220. [Google Scholar] [CrossRef]

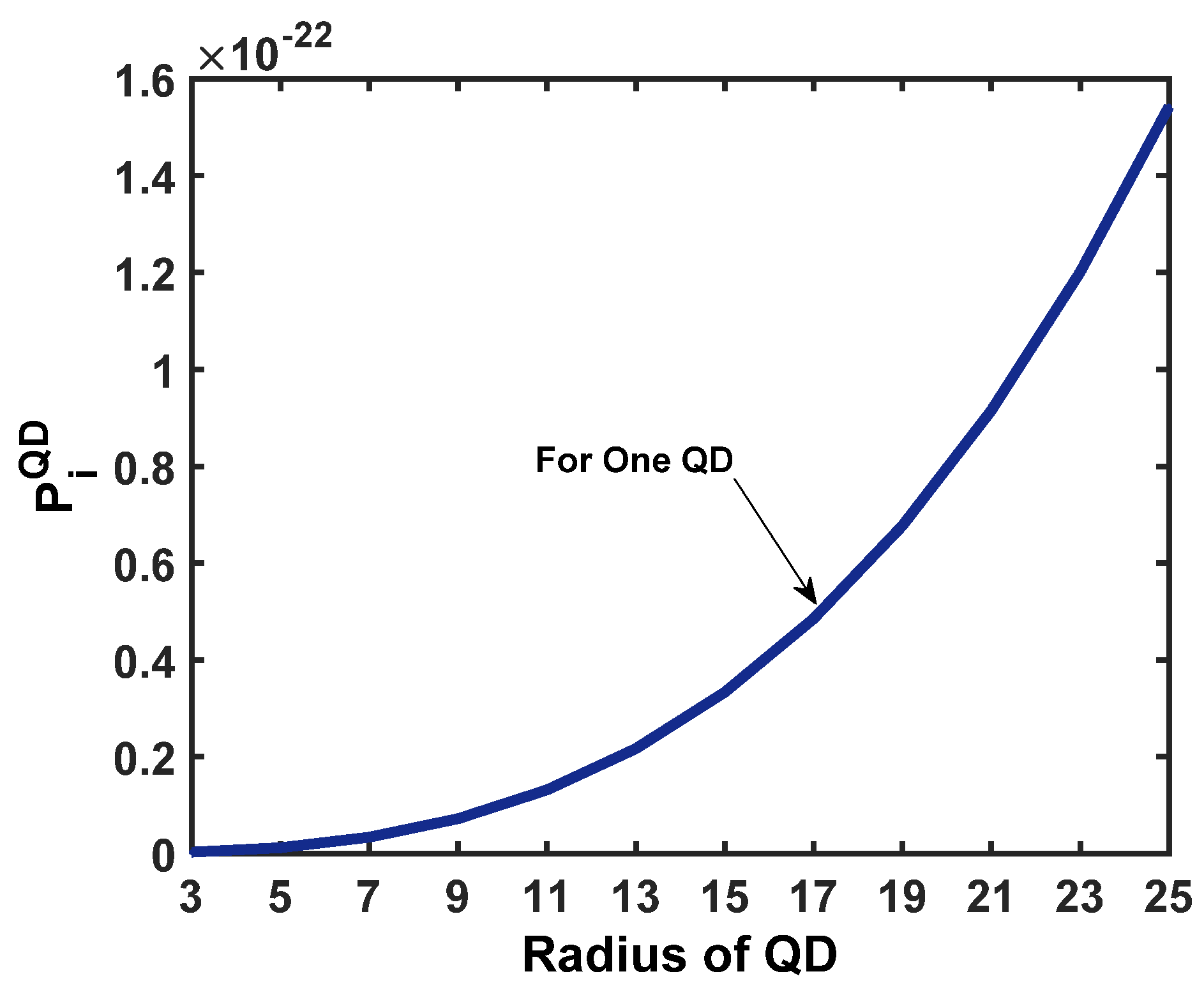



| The Radius of QD (nm) | |
|---|---|
| 10 | 0.0099 |
| 15 | 0.033 |
| 20 | 0.079 |
| 25 | 0.1543 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armaghani, S.; Rostami, A.; Mirtaheri, P. Interaction between Graphene Nanoribbon and an Array of QDs: Introducing Nano Grating. Photonics 2022, 9, 348. https://doi.org/10.3390/photonics9050348
Armaghani S, Rostami A, Mirtaheri P. Interaction between Graphene Nanoribbon and an Array of QDs: Introducing Nano Grating. Photonics. 2022; 9(5):348. https://doi.org/10.3390/photonics9050348
Chicago/Turabian StyleArmaghani, Sahar, Ali Rostami, and Peyman Mirtaheri. 2022. "Interaction between Graphene Nanoribbon and an Array of QDs: Introducing Nano Grating" Photonics 9, no. 5: 348. https://doi.org/10.3390/photonics9050348





