Semiconductor Three-Dimensional Photonic Crystals with Novel Layer-by-Layer Structures
Abstract
:1. Introduction
2. Nanocavity Formed in <110>-Layered Diamond 3D PhCs
2.1. <110>-Layered Diamond Structure and Numerical Analysis
2.2. Fabrication and Optical Characterization of PhC Nanocavity <110>-Layered Diamond Structure
3. Artificial Optical Activity in Semiconductor Chiral Photonic Crystals
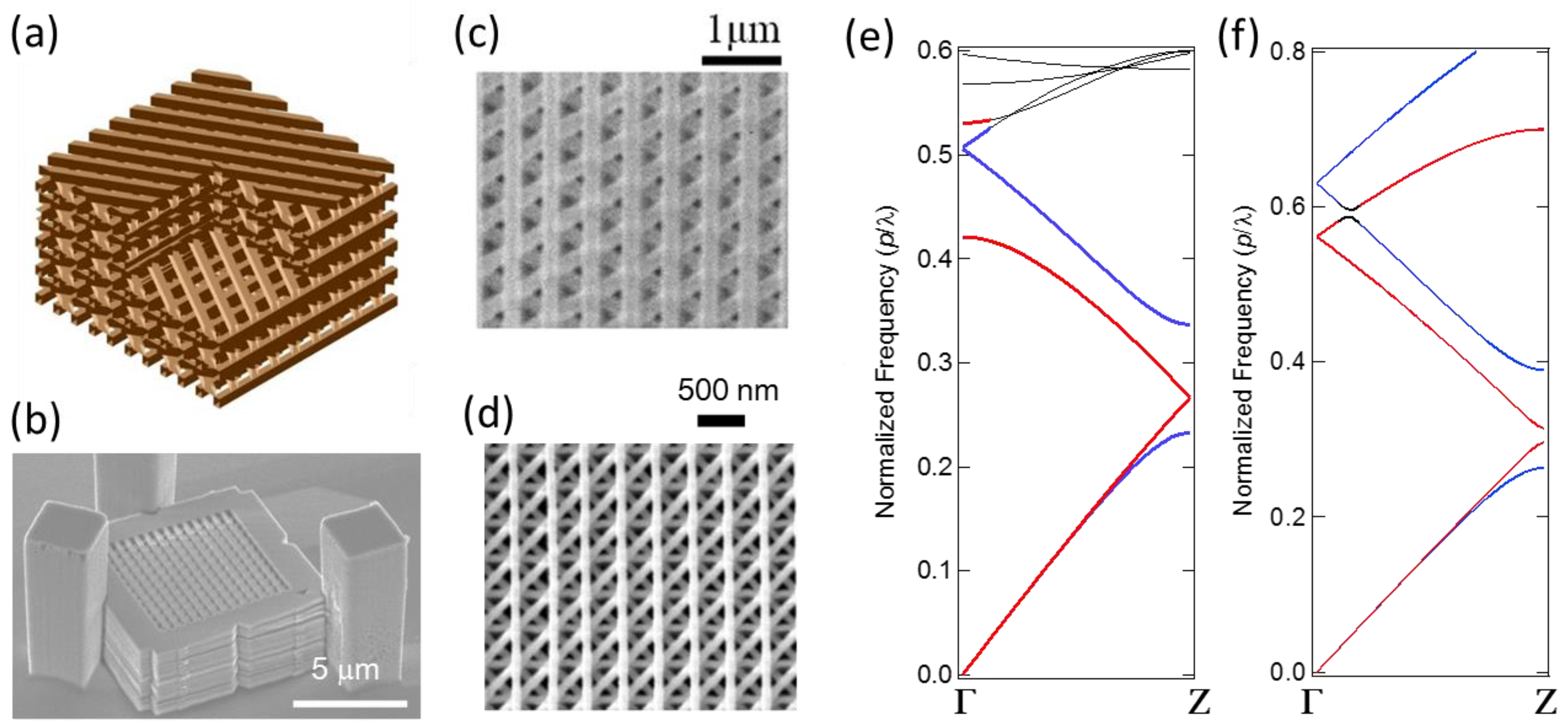
3.1. Semiconductor Chiral 3D PhCs
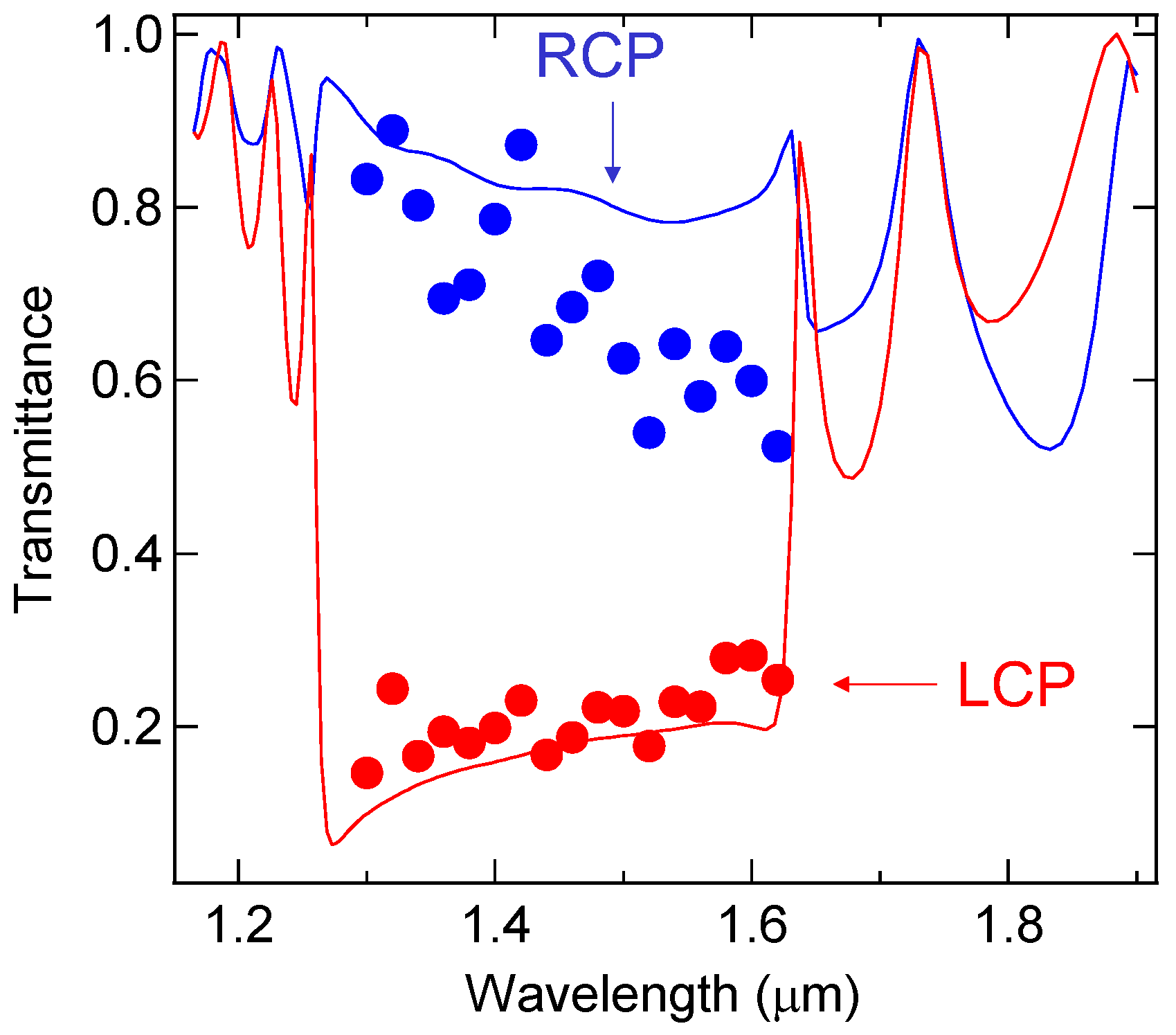
3.2. Broadband Circular Dichroism in Semiconductor Chiral 3D PhC
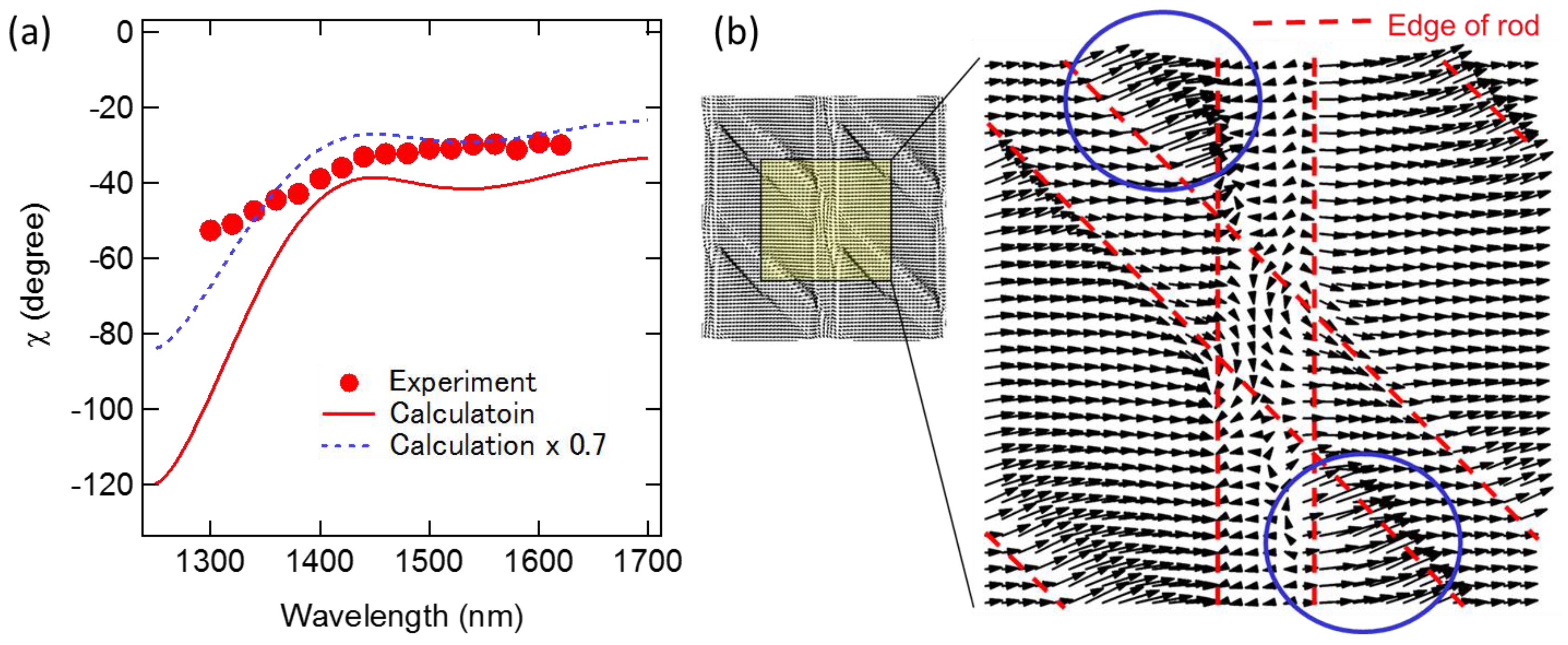
3.3. Enahnced Opical Rotationin a Semcionductor Chiral 3D PhC
4. Summary
Acknowledgments
Conflicts of Interest
Abbreviations
| PhC | photonic crystal |
| 3D | there-dimensional |
| 2D | two-dimensional |
| QD | quantum dot |
| CQED | cavity quantum electrodynamics |
| PBG | photonic bandgap |
| cPBG | complete photonic bandgap |
| CP | circularly polarized |
| RCP | right-handed circularly polarized |
| LCP | left-handed circularly polarized |
| LP | linearly polarized |
| PL | photoluminescence |
| FDTD | finite-difference time domain method |
References
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.R. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Sekoguchi, H.; Takahashi, Y.; Asano, T.; Noda, S. Photonic crystal nanocavity with a Q-factor of ~9 million. Opt. Express 2014, 22, 916–924. [Google Scholar] [CrossRef] [PubMed]
- Strauf, S.; Hennessy, K.; Rakher, M.T.; Choi, Y.-S.; Badolato, A.; Andreani, L.C.; Hu, E.L.; Petroff, P.M.; Bouwmeester, D. Self-Tuned Quantum Dot Gain in Photonic Crystal Lasers. Phys. Rev. Lett. 2006, 96, 127404. [Google Scholar] [CrossRef] [PubMed]
- Nomura, M.; Iwamoto, S.; Watanabe, K.; Kumagai, N.; Nakata, Y.; Ishida, S.; Arakawa, Y. Room temperature continuous-wave lasing in photonic crystal nanocavity. Opt. Express 2006, 14, 6308–6315. [Google Scholar] [CrossRef] [PubMed]
- Ellis, B.; Mayer, M.A.; Shambat, G.; Sarmiento, T.; Harris, J.; Haller, E.E.; Vučković, J. Ultralow-threshold electrically pumped quantum-dot photonic-crystal nanocavity laser. Nat. Photonics 2011, 5, 297–300. [Google Scholar] [CrossRef]
- Jeong, K.-J.; No, Y.-S.; Hwang, Y.; Kim, K.S.; Seo, M.-K.; Park, H.-G.; Lee, Y.-H. Electrically driven nanobeam laser. Nat. Commun. 2013, 4, 2822. [Google Scholar] [CrossRef]
- Prieto, I.; Llorens, J.M.; Muñoz-Camúñez, L.E.; Taboada, A.G.; Canet-Ferrer, J.; Ripalda, J.M.; Robles, C.; Muñoz-Matutano, G.J.; Martínez-Pastor, P.; Postigo, P.A. Near thresholdless laser operation at room temperature. Optica 2015, 2, 66–69. [Google Scholar] [CrossRef]
- Takiguchi, M.; Taniyama, H.; Sumikura, H.; Birowosuto, M.D.; Kuramochi, E.; Shinya, A.; Sato, T.; Takeda, K.; Matsuo, S.; Notomi, M. Systematic study of thresholdless oscillation in high-β buried multiple-quantum-well photonic crystal nanocavity lasers. Opt. Express 2016, 24, 3441–3450. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, Y.; Iwamoto, S.; Nomura, M.; Tandaechanurat, A.; Ota, Y. Cavity Quantum Electrodynamics and Lasing Oscillation in Single Quantum Dot-Photonic Crystal Nanocavity Coupled Systems. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 1818–1829. [Google Scholar] [CrossRef]
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.M.; Rupper, G.; Ell, C.; Shchekin, O.B.; Deppe, D.G. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Hennessy, K.; Badolato, A.; Winger, M.; Gerace, D.; Atatüre, M.; Gulde, S.; Fält, S.; Hu, E.L.; Imamoğlu, A. Quantum nature of a strongly coupled single quantum dot-cavity system. Nature 2007, 445, 896–899. [Google Scholar] [CrossRef] [PubMed]
- Englund, D.; Faraon, A.; Fushman, I.; Stoltz, N.; Petroff, P.; Vučković, J. Controlling cavity reflectivity with a single quantum dot. Nature 2007, 450, 857–861. [Google Scholar] [CrossRef] [PubMed]
- Ota, Y.; Ohta, R.; Kumagai, N.; Iwamoto, S.; Arakawa, Y. Vacuum Rabi Spectra of a Single Quantum Emitter. Phys. Rev. Lett. 2015, 114, 143603. [Google Scholar] [CrossRef] [PubMed]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347. [Google Scholar] [CrossRef]
- Vos, W.L.; Woldering, L.A. Cavity quantum electrodynamics with three-dimensional photonic bandgap crystals. In Light Localisation and Lasing: Random and Quasi-random Photonic Structures, 1st ed.; Ghulinyan, M., Pavesi, L., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 180–214. [Google Scholar]
- Yablonovitch, E.; Gmitter, T.J.; Leung, K.M. Photonic band structure: The face-centered-cubic case employing nonspherical atoms. Phys. Rev. Lett. 1991, 67, 2295–2298. [Google Scholar] [CrossRef] [PubMed]
- Wijnhoven, J.E.G.J.; Vos, W.L. Preparation of Photonic Crystals Made of Air Spheres in Titania. Science 1998, 281, 802–804. [Google Scholar] [CrossRef]
- Míguez, H.; Meseguer, F.; López, C.; Blanco, Á.; Moya, J.S.; Requena, J.; Mifsud, A.; Fornés, V. Control of the Photonic Crystal Properties of fcc-Packed Submicrometer SiO2 Spheres by Sintering. Adv. Mater. 1999, 10, 480–483. [Google Scholar] [CrossRef]
- Schilling, J.; White, J.; Scherer, A.; Stupian, G.; Hillebrand, R.; Gösele, U. Three-dimensional macroporous silicon photonic crystal with large photonic band gap. Appl. Phys. Lett. 2005, 86, 011101. [Google Scholar] [CrossRef]
- Takahashi, S.; Suzuki, K.; Okano, M.; Imada, M.; Nakamori, T.; Ota, Y.; Ishizaki, K.; Noda, S. Direct creation of three-dimensional photonic crystals by a top-down approach. Nat. Mat. 2009, 8, 721–725. [Google Scholar] [CrossRef] [PubMed]
- Grishina, D.A.; Harteveld, C.A.M.; Woldering, L.A.; Vos, W.L. Method for making a single-step etch mask for 3D monolithic nanostructures. Nanotechnology 2015, 26, 505302. [Google Scholar] [CrossRef] [PubMed]
- Deubel, M.; von Freymann, G.; Wegener, M.; Pereira, S.; Busch, K.; Soukoulis, C.M. Direct laser writing of three-dimensional photonic-crystal templates for telecommunications. Nat. Mat. 2004, 3, 444–447. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, N.; Noda, S.; Chutinan, A. Development of One Period of a Three-Dimensional Photonic Crystal in the 5–10 μm Wavelength Region by Wafer Fusion and Laser Beam Diffraction Pattern Observation Techniques. Jpn. J. Appl. Phys. 1998, 37, L1052–L1054. [Google Scholar] [CrossRef]
- Noda, S.; Tomoda, K.; Yamamoto, N.; Chutinan, A. Full Three-Dimensional Photonic Bandgap Crystals at Near-Infrared Wavelengths. Science 2000, 289, 604–606. [Google Scholar] [CrossRef] [PubMed]
- Aoki, K.; Miyazaki, H.T.; Hirayama, H.; Inoshita, K.; Baba, T.; Sakoda, K.; Shinya, N.; Aoyagi, Y. Microassembly of semiconductor three-dimensional photonic crystals. Nat. Mater. 2003, 2, 117–121. [Google Scholar] [CrossRef] [PubMed]
- Aoki, K.; Guimard, D.; Nishioka, M.; Nomura, M.; Iwamoto, S.; Arakawa, Y. Coupling of quantum-dot light emission with a three-dimensional photonic-crystal nanocavity. Nat. Photonics 2008, 2, 688–692. [Google Scholar] [CrossRef]
- Kawakami, S. Fabrication of submicrometre 3D periodic structures composed of Si/SiO2. Electron. Lett. 1997, 33, 1260–1261. [Google Scholar] [CrossRef]
- Fleming, J.G.; Lin, S.-Y. Three-dimensional photonic crystal with a stop band from 1.35 to 1.95 μm. Opt. Lett. 1999, 24, 49–51. [Google Scholar] [CrossRef] [PubMed]
- Lourtioz, J.-M.; Benisty, H.; Berger, V.; Gerard, J.-M.; Maystre, D.; Tchelnokov, A. Three-Dimensional Structures in Optics. In Photonic Crystals towards Nanoscale Photonic Devices, 2nd ed.; Springer: Berlin, Germany, 2008; pp. 393–412. [Google Scholar]
- Imada, M.; Lee, L.H.; Okano, M.; Kawashima, S.; Noda, S. Development of three-dimensional photonic-crystal waveguides at optical-communication wavelengths. Appl. Phys. Lett. 2006, 88, 171107. [Google Scholar] [CrossRef]
- Qi, M.; Lidorikis, E.; Rakich, P.T.; Johnson, S.G.; Joannopoulos, J.D.; Ippen, E.P.; Smith, H.I. A three-dimensional optical photonic crystal with designed point defects. Nature 2004, 429, 538–542. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Imada, M.; Yoshimoto, S.; Okano, M.; Noda, S. Control of Light Emission by 3D Photonic Crystals. Science 2004, 305, 227–229. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, K.; Koumura, M.; Suzuki, K.; Gondaira, K.; Noda, S. Realization of three-dimensional guiding of photons in photonic crystals. Nat. Photonics 2013, 7, 133–137. [Google Scholar] [CrossRef]
- Tandaechanura, A.; Ishida, S.; Guimard, D.; Nomura, M.; Iwamoto, S.; Arakawa, Y. Lasing oscillation in a three-dimensional photonic crystal nanocavity with a complete bandgap. Nat. Photonics 2010, 5, 91–94. [Google Scholar] [CrossRef]
- Ishizaki, K.; Noda, S. Manipulation of photons at the surface of three-dimensional photonic crystals. Nature 2009, 460, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, K.; Gondaira, K.; Ota, Y.; Suzuki, K.; Noda, S. Nanocavities at the surface of three-dimensional photonic crystals. Opt. Express 2013, 21, 10590–10596. [Google Scholar] [CrossRef] [PubMed]
- Cao, D.; Tangaechanurat, A.; Nakayama, S.; Ishida, S.; Iwamoto, S.; Arakawa, Y. Silicon-based three-dimensional photonic crystal nanocavity laser with InAs quantum-dot gain. Appl. Phys. Lett. 2012, 101, 191107. [Google Scholar] [CrossRef]
- Tandaechanurat, A.; Ota, Y.; Kumagai, N.; Ishida, S.; Iwamoto, S.; Arakawa, Y. Observation of Purcell effect in a 3D photonic crystal nanocavity with a single quantum dot. In Proceeding of the IQEC/CLEO Pacific Rim Conference, Sydney, Australia, 28 August–1 September 2011.
- Ho, K.M.; Chan, C.T.; Soukoulis, C.M.; Biswas, R.; Sigalas, M. Photonic band gaps in three dimensions: New layer-by-layer periodic structures. Solid State Commun. 1994, 89, 413–416. [Google Scholar] [CrossRef]
- Hillebrand, R.; Hergert, W. Scaling properties of a tetragonal photonic crystal design having a large complete bandgap. Photonics Nanostruc. Fundam. Appl. 2004, 2, 33–39. [Google Scholar] [CrossRef]
- Fan, S.; Villeneuve, P.R.; Meade, R.D.; Joannopoulos, J.D. Design of three-dimensional photonic crystals at submicron lengthscales. Appl. Phys. Lett. 1994, 65, 1466–1468. [Google Scholar] [CrossRef]
- Maldovan, M. Layer-by-layer photonic crystal with a repeating two-layer sequence. Appl. Phys. Lett. 2004, 85, 911–913. [Google Scholar] [CrossRef]
- Maldovan, M.; Thomas, E.L. Diamond-structured photonic crystals. Nat. Matter. 2004, 3, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Men, K.; Lee, K.Y.K.; Freund, R.M.; Peraire, J.; Johnson, S.G. Robust topology optimization of three-dimensional photonic-crystal band-gap structures. Opt. Express 2014, 22, 22632–22648. [Google Scholar] [CrossRef] [PubMed]
- Tajiri, T.; Takahashi, S.; Tandaechanurat, A.; Iwamoto, S.; Arakawa, Y. Design of ta three-dimensional photonic crystal nanocavity based on a <110>-layered diamond structure. Jpn. J. Appl. Phys. 2014, 53, 04EG08. [Google Scholar] [CrossRef]
- Tajiri, T.; Takahashi, S.; Ota, Y.; Tatebayashi, J.; Iwamoto, S.; Arakawa, Y. Demonstration of a three-dimensional photonic crystal nanocavity in a <110>-layered diamond structure. Appl. Phys. Lett. 2015, 107, 071102. [Google Scholar] [CrossRef]
- Gywat, O.; Krenner, H.J.; Berezovsky, J. Experimental Methods for Optical Initialization, Readout, and Manipulation. In Spins in Optically Active Quantum Dots; Wiley-VCH: Weinheim, Germany, 2010; pp. 111–165. [Google Scholar]
- Kuwata-Gonikami, M.; Saito, N.; Ino, Y.; Kauranen, M.; Jefimovs, K.; Vallius, T.; Turunen, J.; Svirko, Y.P. Giant optical activity in quasi-two-dimensional planar nanostructures. Phys. Rev. Lett. 2005, 95, 227401. [Google Scholar] [CrossRef] [PubMed]
- Konishi, K.; Sugimoto, T.; Bai, B.; Svirko, Y.; Kuwata-Gonokami, M. Effect of surface plasmon resonance on the optical activity of chiral metal nanogratings. Opt. Express 2007, 15, 9575–9583. [Google Scholar] [CrossRef] [PubMed]
- Konishi, K.; Bai, B.; Meng, X.; Karvinen, P.; Turunen, J.; Svirko, Y.P.; Kuwata-Gonokami, M. Observation of extraordinary optical activity in planer chiral photonic crystals. Opt. Express 2008, 16, 7189–7196. [Google Scholar] [CrossRef] [PubMed]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, J.G.; Mark, A.G.; Eslami, S.; Fischer, P. Plasmonic nanohelix metamaterials with tailorable giant circular dichroism. Appl. Phys. Lett. 2013, 103, 213101. [Google Scholar] [CrossRef]
- Decker, M.; Zhao, R.; Soukoulis, C.M.; Linden, S.; Wegener, M. Twisted split-ring-resonator photonic metamaterial with huge optical activity. Opt. Lett. 2010, 35, 1593–1595. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Belkin, M.A.; Alu, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 2012, 3, 870. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.C.W.; Chan, C.T. Circularly polarized thermal radiation from layer-by-layer photonic crystal structures. Appl. Phys. Lett. 2007, 90, 051912. [Google Scholar] [CrossRef]
- Kopp, V.I.; Zhang, Z.-Q.; Genack, A.Z. Lasing in chiral photonic structures. Prog. Quantum Electron. 2003, 27, 369–416. [Google Scholar] [CrossRef]
- Coles, H.; Morris, S. Liquid-crystal lasers. Nat. Photonics 2010, 4, 676–685. [Google Scholar] [CrossRef]
- Thiel, M.; von Freymann, G.; Wegener, M. Layer-by-layer three dimensional chiral photonic crystal. Opt. Lett. 2007, 32, 2547–2549. [Google Scholar] [CrossRef] [PubMed]
- Thiel, M.; Decker, M.; Deubel, M.; Wegener, M.; Linden, S.; von Freymann, G. Polarization stop bands in chiral polymeric three-dimensional photonic crystals. Adv. Mater. 2007, 19, 207–210. [Google Scholar] [CrossRef]
- Turner, M.D.; Saba, M.; Zhang, Q.; Cumming, B.P.; Schoeder-Turk, G.E.; Gu, M. Miniature chiral beam splitter based on gyroid photonic crystals. Nat. Photonics 2013, 7, 801–805. [Google Scholar] [CrossRef]
- Kroutvar, M.; Ducommun, Y.; Heiss, D.; Bichler, M.; Schuh, D.; Abstreiter, G.; Finley, J.J. Optically programmable electron spin memory using semiconductor quantum dots. Nature 2004, 432, 81–84. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.B.; Fallahi, P.; Togan, E.; Sanchez, J.M.; Imamoglu, A. Observation of entanglement between a quantum dot spin and a single photon. Nature 2012, 491, 426–429. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Tajiri, T.; Ota, Y.; Tatebayashi, J.; Iwamoto, S.; Arakawa, Y. Circular dichroism in a three-dimensional semiconductor chiral photonic crystal. Appl. Phys. Lett. 2014, 105, 051107. [Google Scholar] [CrossRef]
- Takahashi, S.; Tandaechanurat, A.; Igusa, R.; Ota, Y.; Tatebayashi, J.; Iwamoto, S.; Arakawa, Y. Giant optical rotation in a three-dimensional semiconductor chiral photonic crystal. Opt. Express 2013, 21, 29905–29913. [Google Scholar] [CrossRef] [PubMed]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwamoto, S.; Takahashi, S.; Tajiri, T.; Arakawa, Y. Semiconductor Three-Dimensional Photonic Crystals with Novel Layer-by-Layer Structures. Photonics 2016, 3, 34. https://doi.org/10.3390/photonics3020034
Iwamoto S, Takahashi S, Tajiri T, Arakawa Y. Semiconductor Three-Dimensional Photonic Crystals with Novel Layer-by-Layer Structures. Photonics. 2016; 3(2):34. https://doi.org/10.3390/photonics3020034
Chicago/Turabian StyleIwamoto, Satoshi, Shun Takahashi, Takeyoshi Tajiri, and Yasuhiko Arakawa. 2016. "Semiconductor Three-Dimensional Photonic Crystals with Novel Layer-by-Layer Structures" Photonics 3, no. 2: 34. https://doi.org/10.3390/photonics3020034



