Soret & Dufour and Triple Stratification Effect on MHD Flow with Velocity Slip towards a Stretching Cylinder
Abstract
:1. Introduction
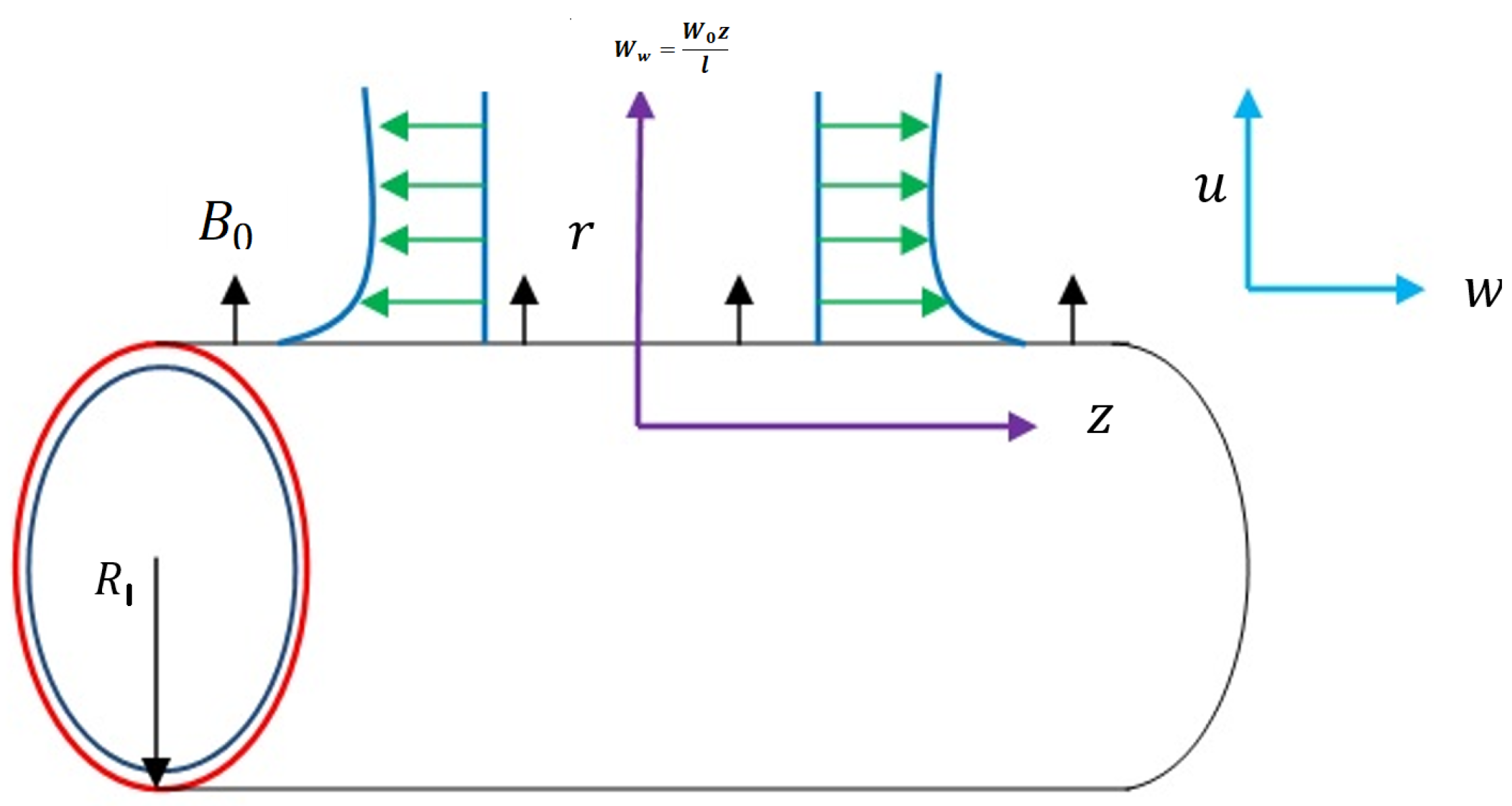
2. Mathematical Formulation
- The flow is steady, laminar and -dimensional.
- The fluid is incompressible.
- The uniform external magnetic field is applied. The induced magnetic field is neglected.
- The cylinder is stretching with uniform velocity along z-direction.
- The stratification effect for temperature, nanoparticle volume fraction and concentration is considered.
3. Convergence of the Solution
4. Computational Results and Discussion
5. Conclusions
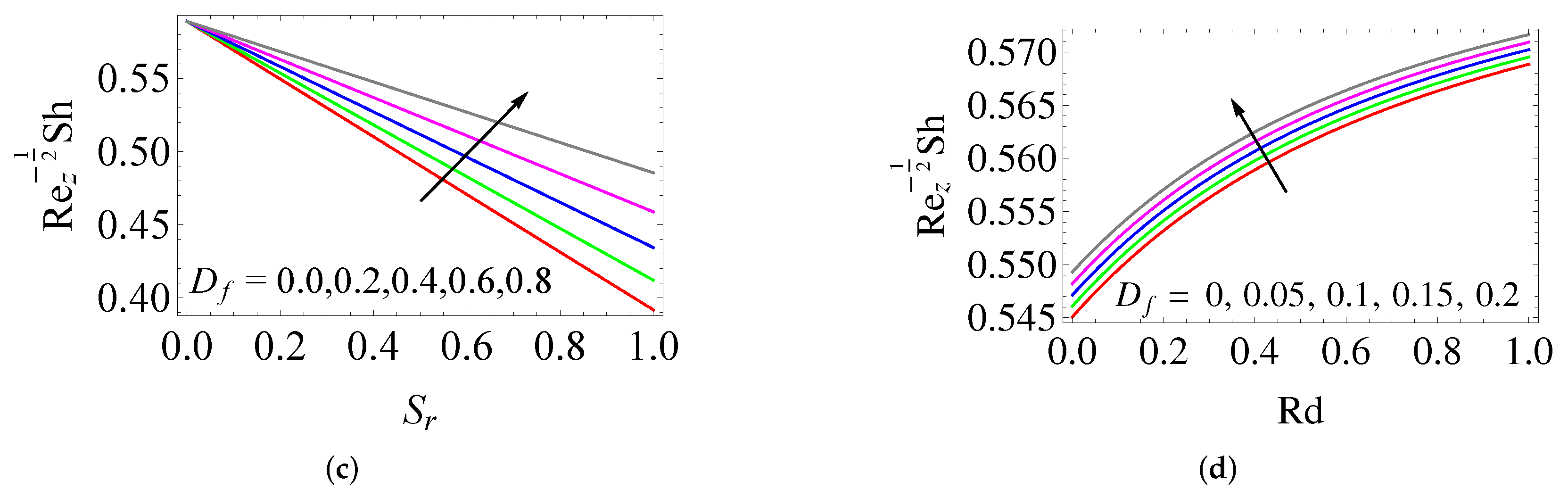
- While increasing the concentration slip, the solutal concentration boundary layer thickness shrinks, which results in a reduction in the rate of mass transfer.
- When the NLTR parameter value is increased, the local heat transfer rate reduces, whereas the local mass transfer rate increases.
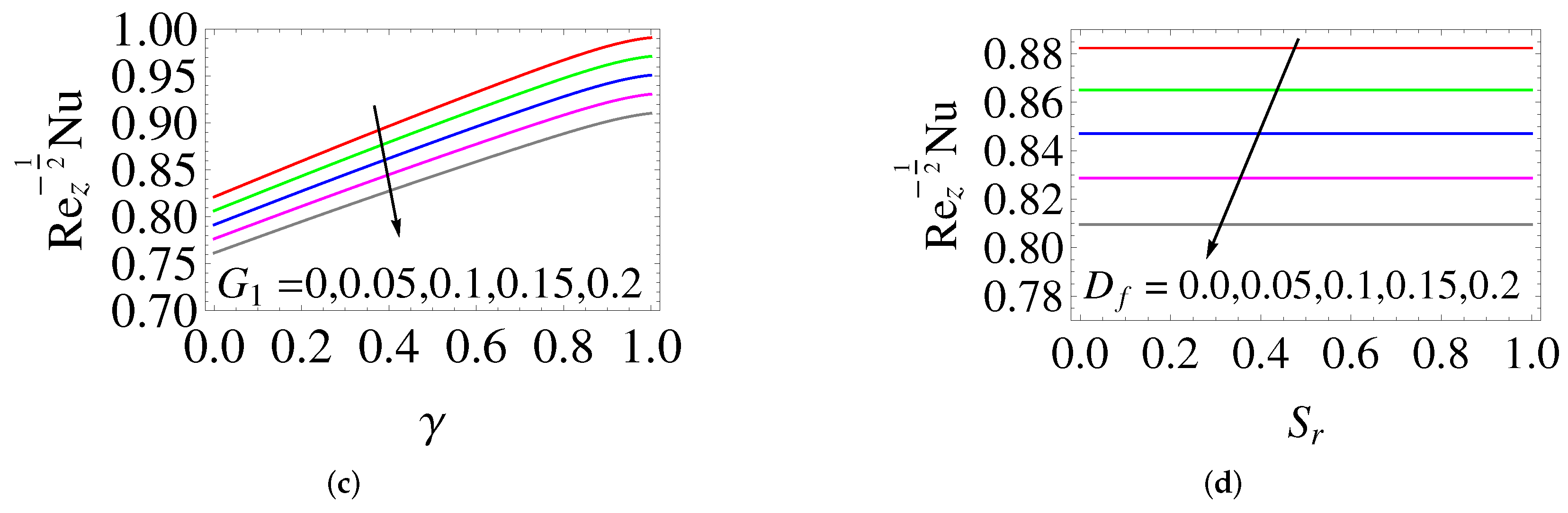
- The thermal (concentration) boundary layer is thickened by increasing the Dufour (Soret) number.
- While raising thermal radiation, the thermal boundary layer thickness enhances.
- When the thermal energy, nanoparticle volume fraction and solutal stratification are increased, the thickness of thermal and solutal concentration boundary layers diminishes.
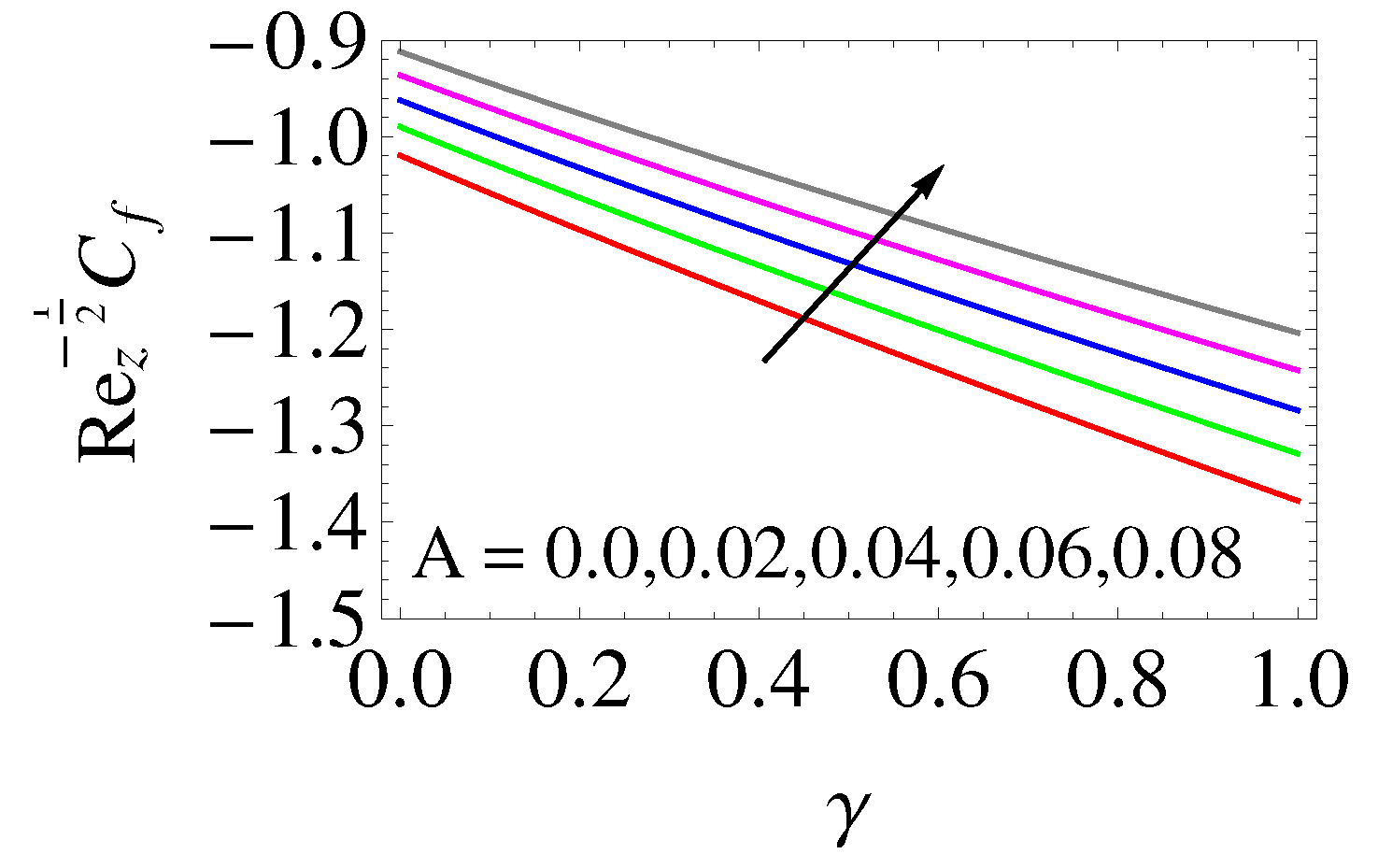
- The thermal and concentration boundary layer thickness and skin friction raise when the velocity slip is increased, whereas the momentum boundary layer thickness, heat and mass transfer rate diminish.
- The present results are very useful to the thermal science community to improve the cooling processes in heat transfer systems.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NLTR | Nonlinear thermal radiation |
| TSF | Triple stratification |
| MHD | Magneto-hydrodynamics |
| HAM | Homotopy analysis method |
| Nomenclature | |
| specific heat (J·kg) | |
| concentration susceptibility | |
| thermal diffusion ratio | |
| chemical reaction | |
| l | reference length (m) |
| heat flux (kg·m·s) | |
| r- and z-axis velocity components (m·s) | |
| A | velocity slip parameter |
| strength of magnetic field (m·A) | |
| thermal slip parameter | |
| nanoparticles volume fraction slip parameter | |
| concentration slip parameter | |
| nanoparticles volume fraction | |
| chemical reaction parameter | |
| reference nanoparticles volume fraction | |
| Brownian motion | |
| Dufour (diffusion-thermo) number | |
| mass diffusivity (m·s) | |
| thermophoresis coefficient | |
| thermal stratification parameter | |
| nanoparticle volume fraction stratification parameter | |
| concentration stratification parameter | |
| thermal slip factor | |
| nanoparticle volume fraction slip factor | |
| concentration slip factor | |
| L | magnetic parameter |
| Brownian motion parameter | |
| thermophoresis parameter | |
| Prandtl number | |
| thermal radiation parameter | |
| local Reynolds number | |
| S | concentration |
| Schmidt number | |
| nanofluid Schmidt number | |
| (thermal-diffusion) Soret number | |
| reference concentration (m·mol) | |
| temperature (K) | |
| mean fluid temperature | |
| reference temperature | |
| uniform velocity of the plate | |
| Greek Symbols | |
| thermal diffusivity (m·s) | |
| curvature parameter | |
| kinematic viscosity of the fluid (m·s) | |
| density of the fluid (kg·m) | |
| ratio between the effective nanoparticles materials and fluid heat capacity | |
| temperature ratio parameter | |
| electrical conductivity (S·m) | |
References
- Rahman, M.M.; Aziz, A. Heat transfer in water based nanofluids (TiO2–H2O, Al2O3–H2O and Cu–H2O) over a stretching cylinder. Int. J. Heat Mass Transf. 2012, 30, 31–42. [Google Scholar] [CrossRef]
- Rasekh, A.; Ganji, D.D.; Tavakoli, S. Numerical Solutions for a Nanofluid Past over a Stretching Circular Cylinder with Non-Uniform Heat Source. Front. Heat Mass Transf. 2012, 3, 043003. [Google Scholar] [CrossRef] [Green Version]
- Pandey, A.K.; Kumar, M. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alex. Eng. J. 2017, 56, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Das, M.; Mahatha, B.K.; Nandkeolyar, R. Mixed Convection and Nonlinear Radiation in the Stagnation Point Nanofluid flow towards a Stretching Sheet with Homogenous-Heterogeneous Reactions effects. Procedia Eng. 2015, 127, 1018–1025. [Google Scholar] [CrossRef] [Green Version]
- Raju, C.S.K.; Sandeep, N.; Gnaneswara Reddy, M. Effect of Nonlinear Thermal Radiation on 3D Jeffrey Fluid Flow in the Presence of Homogeneous–Heterogeneous Reactions. Int. J. Eng. Res. Afr. 2015, 21, 52–68. [Google Scholar] [CrossRef]
- Abbas, Z.; Perveen, R.; Sheikh, M.; Pop, I. Thermophoretic diffusion and nonlinear radiative heat transfer due to a contracting cylinder in a nanofluid with generalized slip condition. Results Phys. 2016, 6, 1080–1087. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.J.; Rana, P.; Anwar Bég, O.; Ismail, A.I.M. Finite element simulation of magnetohydrodynamic convective nanofluid slip flow in porous media with nonlinear radiation. Alex. Eng. J. 2016, 55, 1305–1319. [Google Scholar] [CrossRef]
- Kumar, M.S.; Sandeep, N.; Kumar, B.R.; Prakash, J. Effect of Cattaneo–Christov Heat Flux on Nonlinear Radiative Mhd Flow of Casson Fluid Induced by a Semi-Infinte Stretching Surface. Front. Heat Mass Transf. 2017, 8, 8. [Google Scholar]
- Veera Krishna, M.; Chamkha, A.J. Hall and ion slip effects on Unsteady MHD Convective Rotating flow of Nanofluids—Application in Biomedical Engineering. J. Egypt. Math. Soc. 2020, 28, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Veera Krishna, M. Hall and ion slip effects on radiative MHD rotating flow of Jeffreys fluid past an infinite vertical flat porous surface with ramped wall velocity and temperature. Int. Commun. Heat Mass Transf. 2021, 126, 105399. [Google Scholar] [CrossRef]
- Veera Krishna, M.; Chamkha, A.J. Hall and ion slip effects on MHD Rotating Boundary layer flow of Nanofluid past an infinite vertical plate Embedded in a Porous medium. Results Phys. 2019, 15, 102652. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Ibraheem, R.O.; Mahanthesh, B.; Babatunde, H.A. A meta-analysis on the effects of haphazard motion of tiny/nano-sized particles on the dynamics and other physical properties of some fluids. Chin. J. Phys. 2019, 60, 676–687. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abd El-Aziz, M.M.; Ahmed, S.E. Effects of thermal stratification on flow and heat transfer due to a stretching cylinder with uniform suction/injection. Int. J. Energy Technol. 2010, 2, 1–7. [Google Scholar]
- Mukhopadhyay, S.; Ishak, A. Mixed Convection Flow along a Stretching Cylinder in a Thermally Stratified Medium. J. Appl. Math. 2012, 2012, 491695. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Bhuvaneswari, M.; Sivasankaran, S.; Rajan, S. Soret and Dufour effects on MHD mixed convection heat and mass transfer of a stagnation point flow towards a vertical plate in a porous medium with chemical reaction, radiation and heat generation. J. Appl. Fluid Mech. 2016, 9, 1447–1455. [Google Scholar] [CrossRef]
- Eswaramoorthi, S.; Bhuvaneswari, M.; Sivasankaran, S.; Rajan, S. Soret and Dufour effects on viscoelastic boundary layer flow over a stretching surface with convective boundary condition with radiation and chemical reaction. Sci. Iran. B 2016, 23, 2575–2586. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Nassem, A.; Khan, M.J.; Farooq, M.; Al-Saedi, A. Magnetohydrodynamic (MHD) flow of nanofluid with double stratification and slip conditions. Phys. Chem. Liq. 2018, 56, 189–208. [Google Scholar] [CrossRef]
- Faraz, F.; Imran, S.M.; Ali, B.; Haider, S. Thermo-Diffusion and Multi-Slip Effect on an Axisymmetric Casson Flow over a Unsteady Radially Stretching Sheet in the Presence of Chemical Reaction. Processes 2019, 7, 851. [Google Scholar] [CrossRef] [Green Version]
- Ali, B.; Naqvi, R.A.; Haider, A.; Hussain, D.; Hussain, S. Finite Element Study of MHD Impacts on the Rotating Flow of Casson Nanofluid with the Double Diffusion Cattaneo–Christov Heat Flux Model. Mathematics 2020, 8, 1555. [Google Scholar] [CrossRef]
- Abdal, S.; Mariam, A.; Ali, B.; Younas, S.; Ali, L.; Habib, D. Implications of bioconvection and activation energy on Reiner–Rivlin nanofluid transportation over a disk in rotation with partial slip. Chin. J. Phys. 2021, 73, 672–683. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Abbasbandy, S.; Hashim, I. Heat flux performance in a porous medium embedded Maxwell fluid flow over a vertically stretched plate due to heat absorption. J. Nonlinear Sci. Appl. 2016, 9, 2986–3001. [Google Scholar] [CrossRef] [Green Version]
- Noor, N.F.M.; Hashim, I. Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2010, 53, 2044–2051. [Google Scholar] [CrossRef]
- Andersson, H. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Chemical reaction and variable viscosity effects on flow and mass transfer of a non-Newtonian visco-elastic fluid past a stretching surface embedded in a porous medium. Meccanica 2010, 45, 835–846. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Waheed, S.E. MHD flow and heat transfer of a micropolar fluid over a stretching surface with heat generation (absorption) and slip velocity. J. Egypt Math Soc. 2012, 20, 20–27. [Google Scholar] [CrossRef] [Green Version]
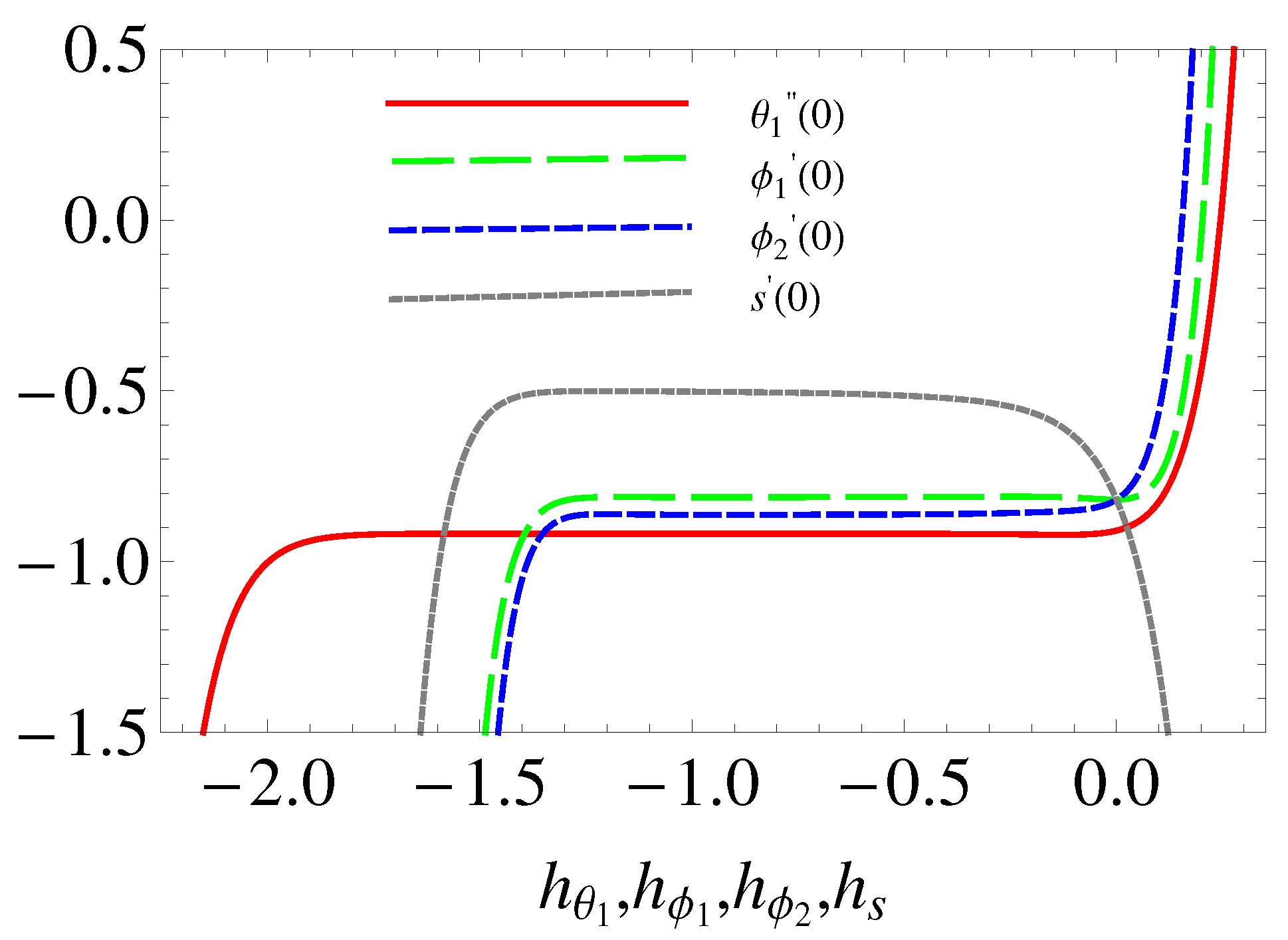
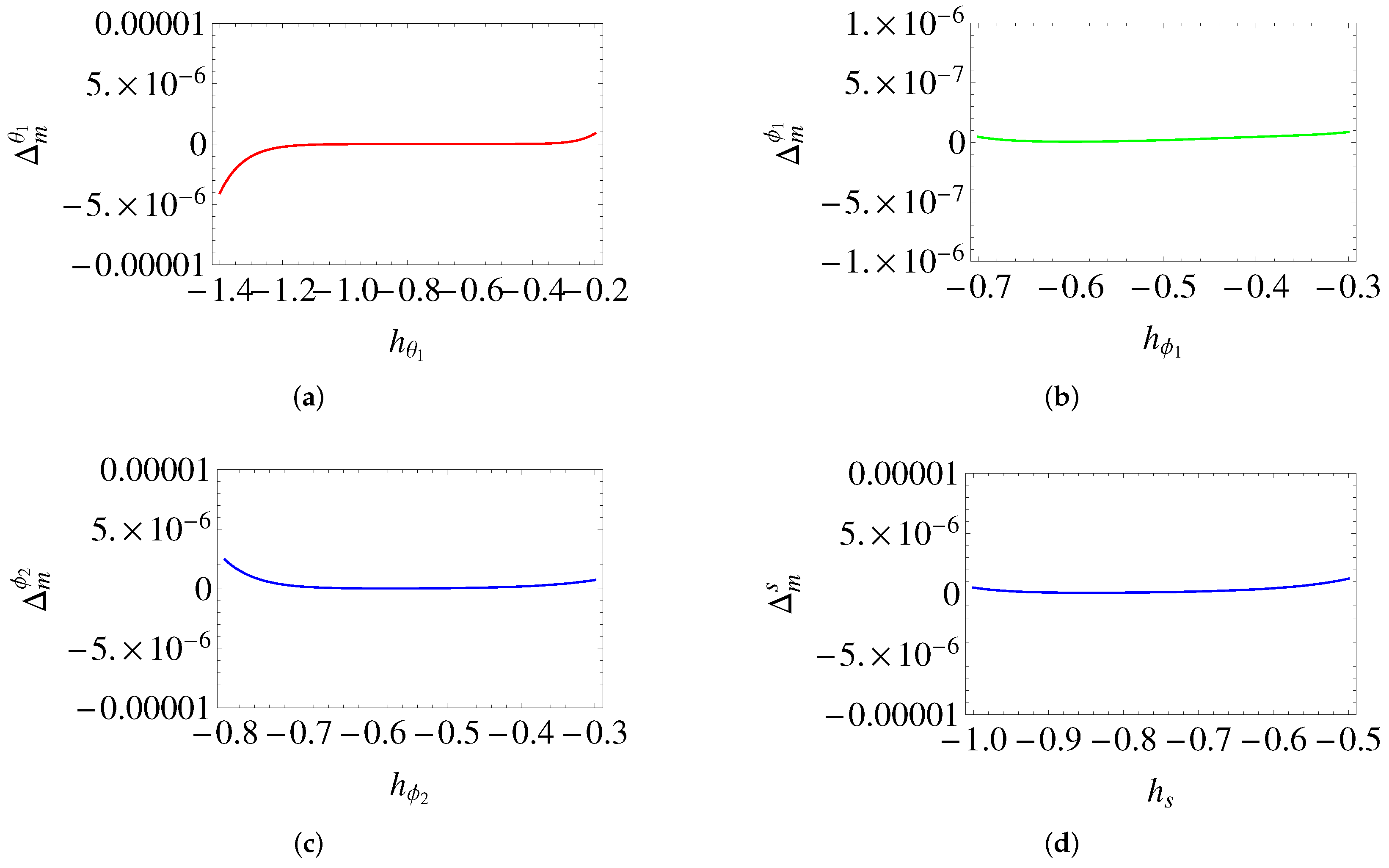
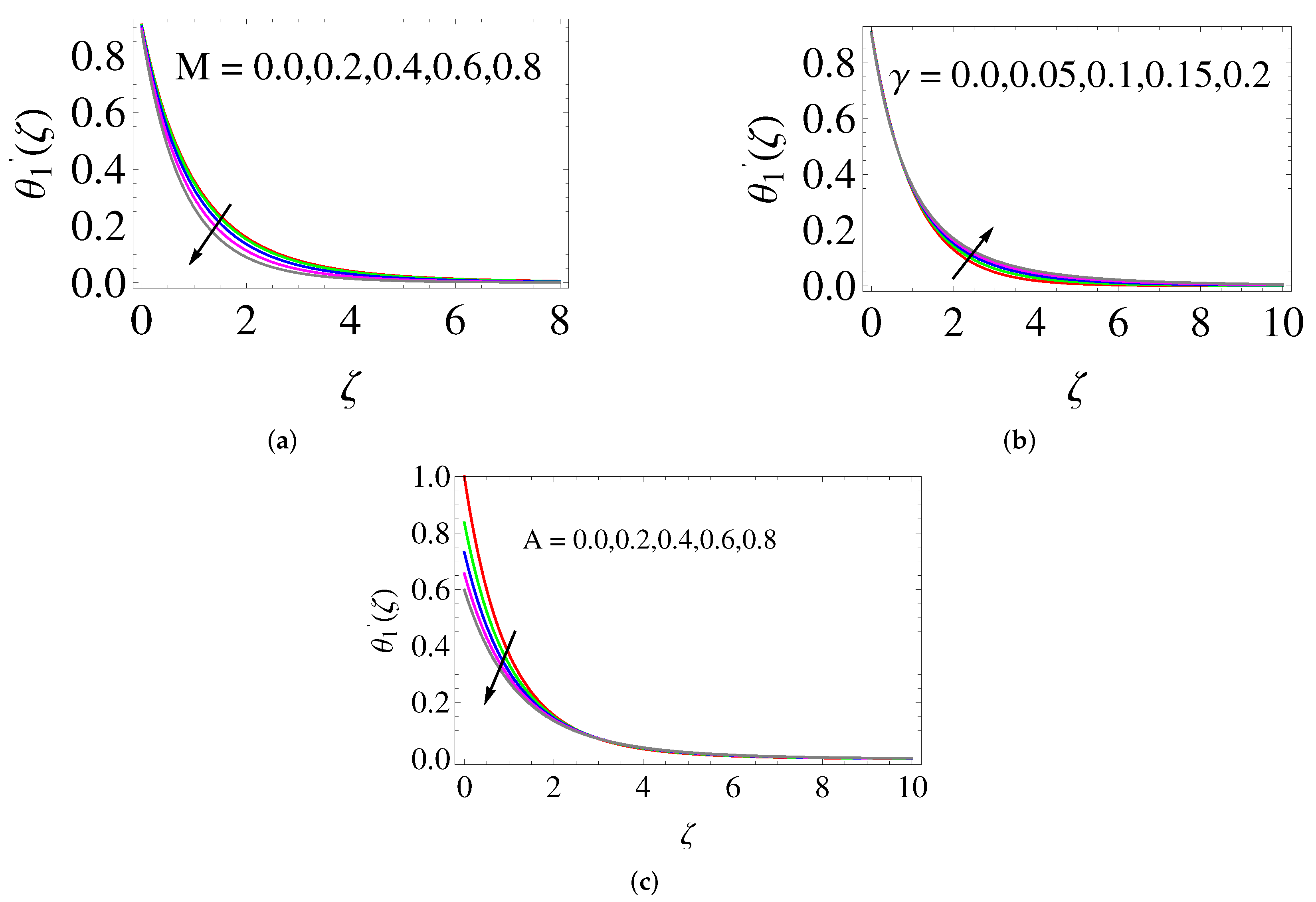
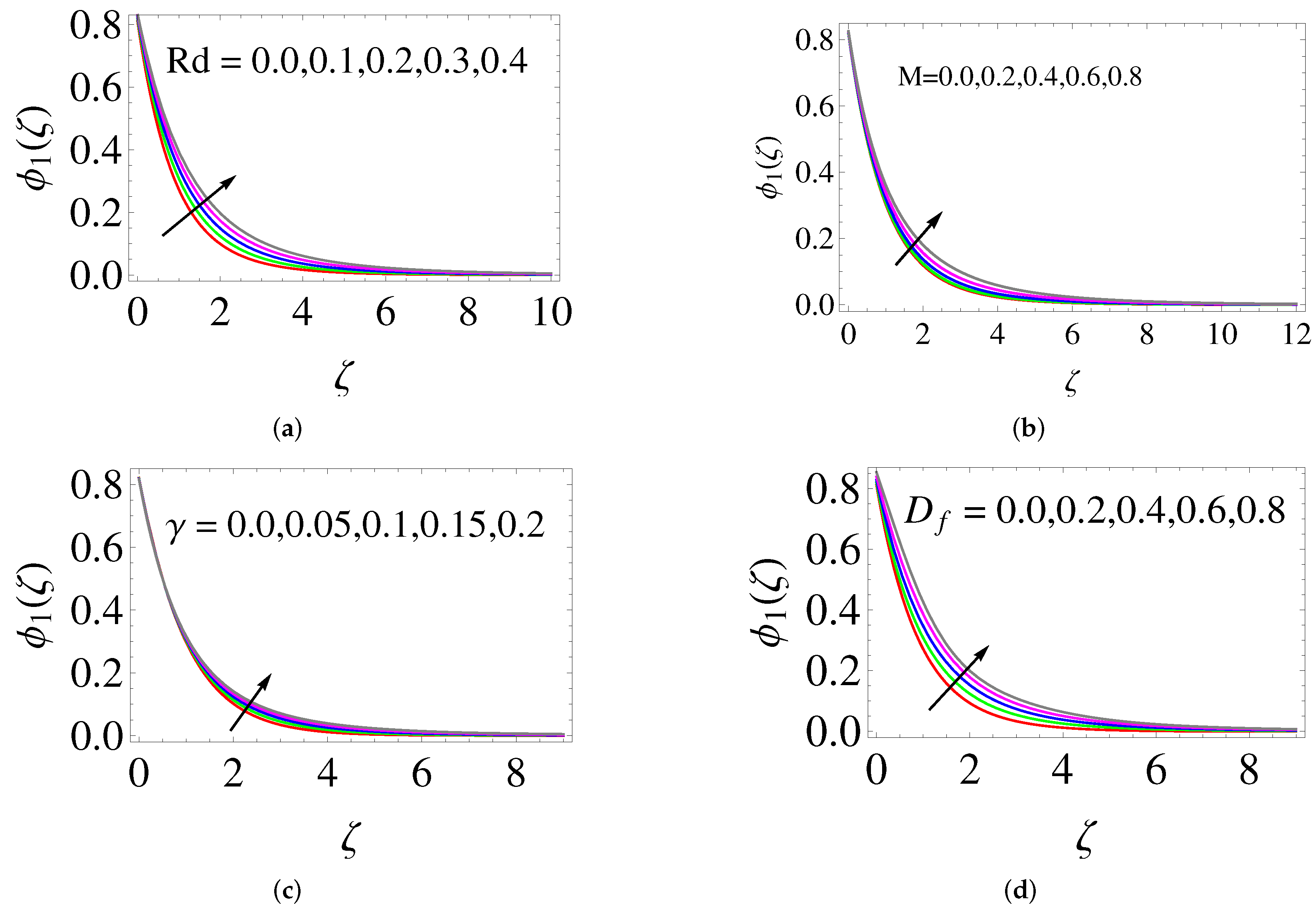
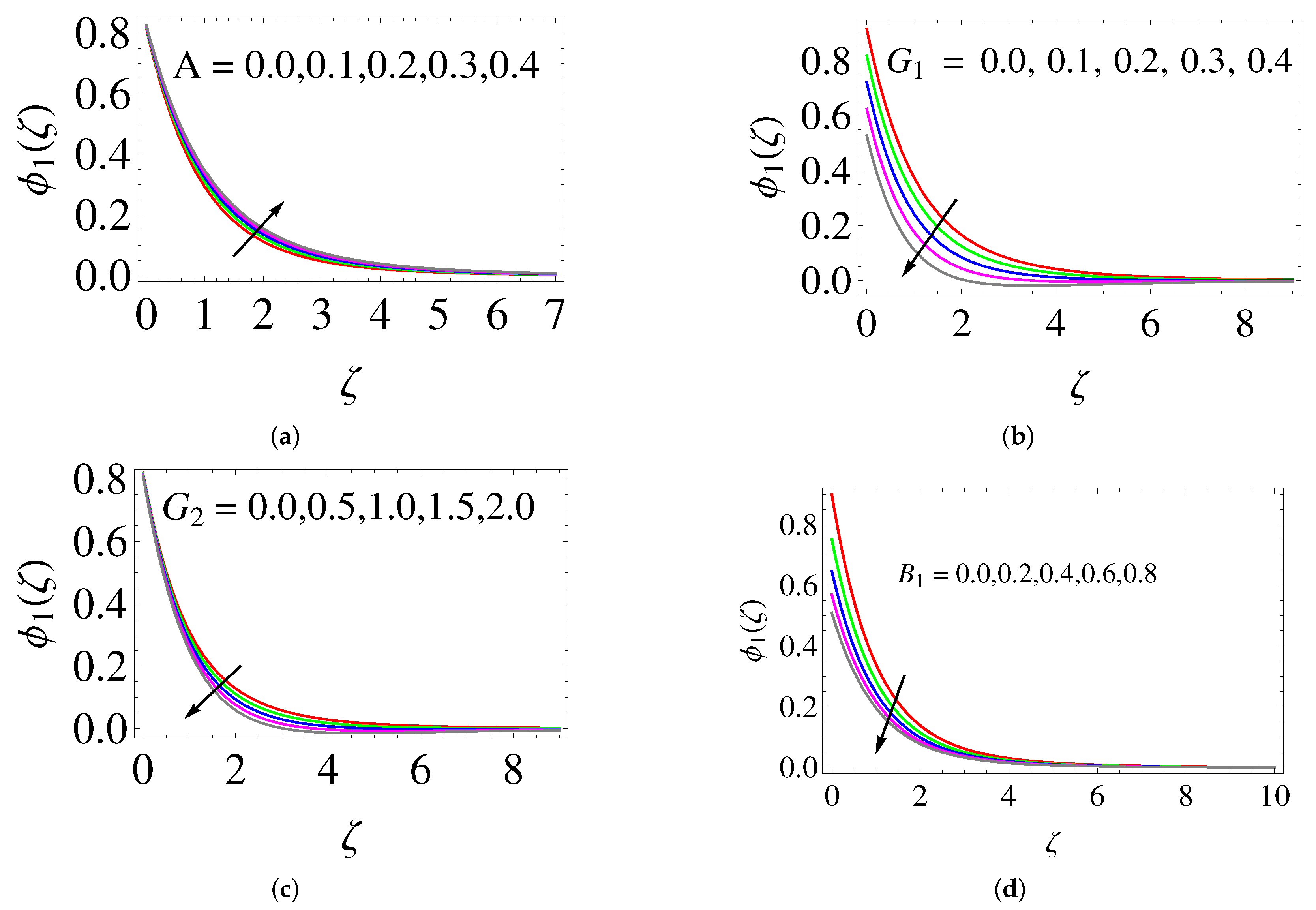


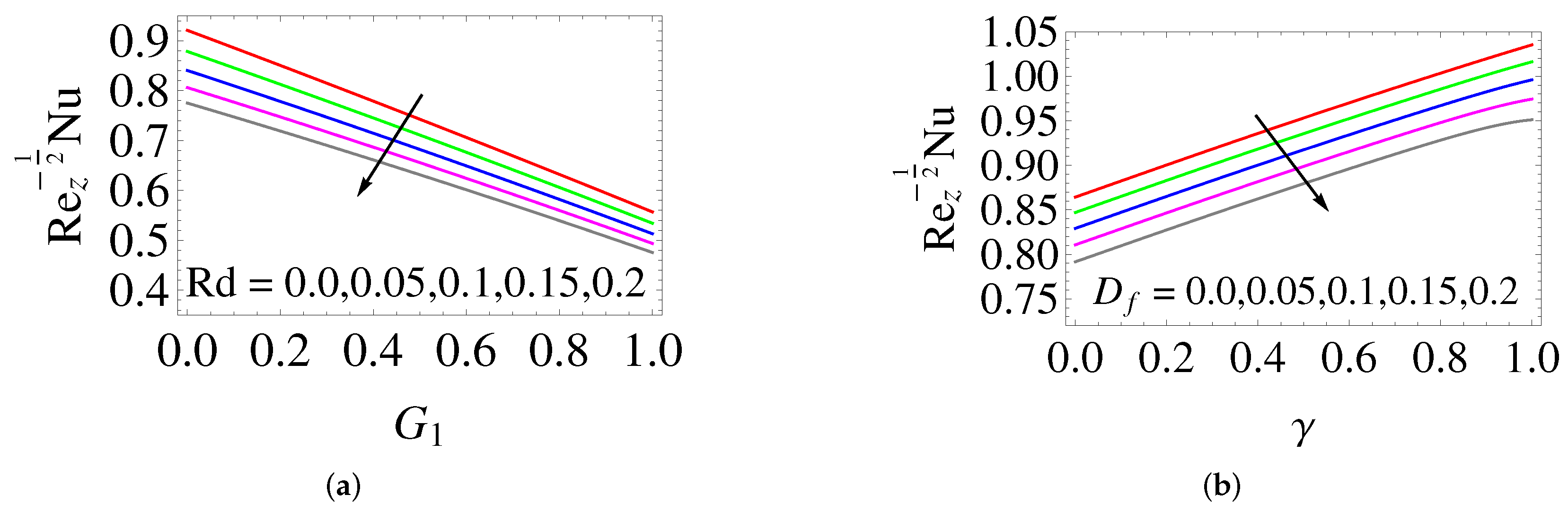


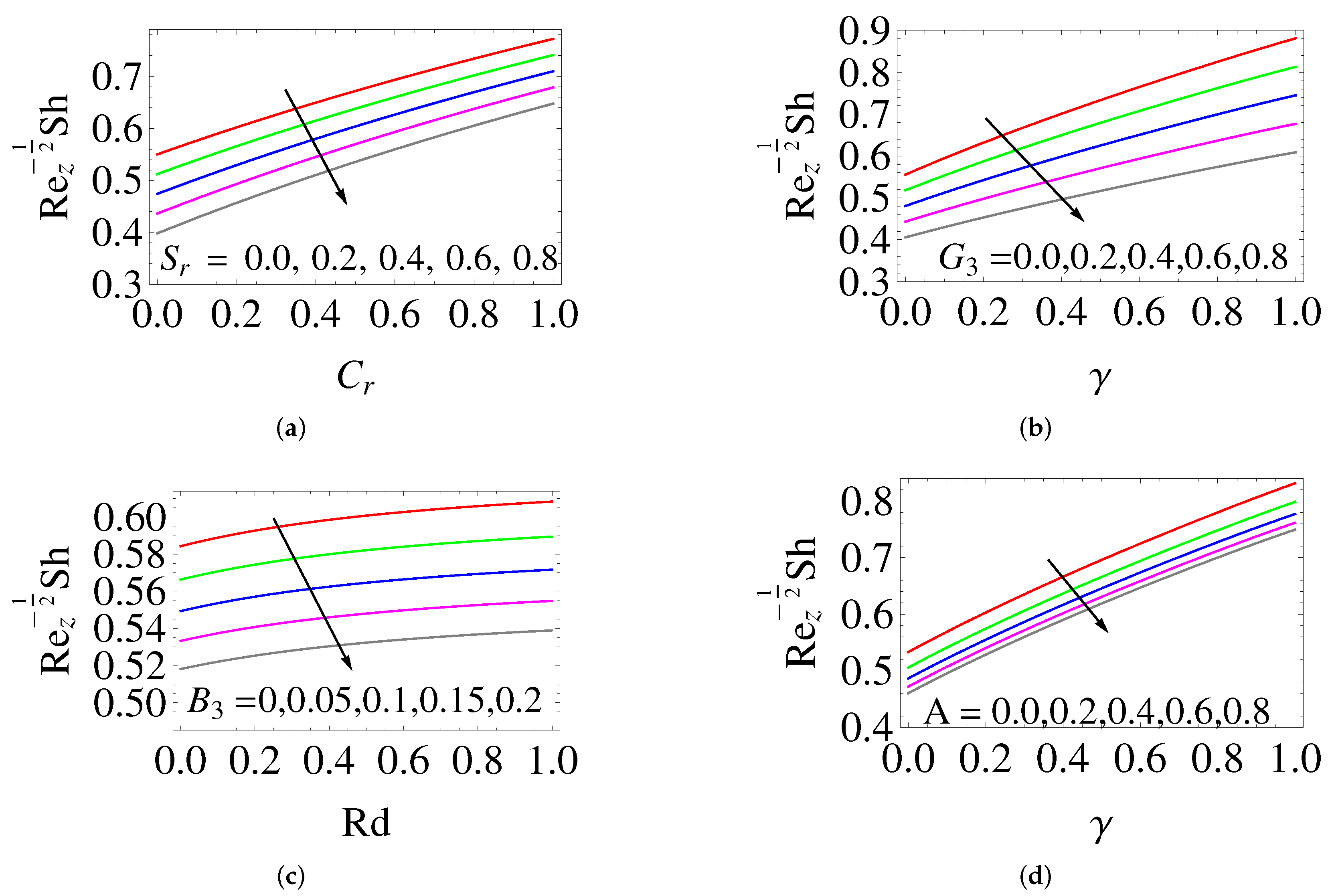
| m-th Order Approximation | ||||
|---|---|---|---|---|
| 1 | ||||
| 4 | ||||
| 8 | ||||
| 12 | ||||
| 16 | ||||
| 18 | ||||
| 19 | ||||
| 20 |
| A | Andersson [23] | Mahmoud [24] | Mahmoud & Waheed [25] | Hayat et al. [17] | Present |
|---|---|---|---|---|---|
| 0 | |||||
| A | Andersson [23] | Mahmoud [24] | Mahmoud & Waheed [25] | Hayat et al. [17] | Present |
|---|---|---|---|---|---|
| 0 | |||||
| M | A | Hayat et al. [17] | Present | |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jagan, K.; Sivasankaran, S. Soret & Dufour and Triple Stratification Effect on MHD Flow with Velocity Slip towards a Stretching Cylinder. Math. Comput. Appl. 2022, 27, 25. https://doi.org/10.3390/mca27020025
Jagan K, Sivasankaran S. Soret & Dufour and Triple Stratification Effect on MHD Flow with Velocity Slip towards a Stretching Cylinder. Mathematical and Computational Applications. 2022; 27(2):25. https://doi.org/10.3390/mca27020025
Chicago/Turabian StyleJagan, Kandasamy, and Sivanandam Sivasankaran. 2022. "Soret & Dufour and Triple Stratification Effect on MHD Flow with Velocity Slip towards a Stretching Cylinder" Mathematical and Computational Applications 27, no. 2: 25. https://doi.org/10.3390/mca27020025





