New Analytic Solutions for the (N + 1)-Dimensional Generalized Boussinesq Equation
Abstract
:1. Introduction
2. Summary of the Generalized Jacobi Elliptic Functions Expansion Method
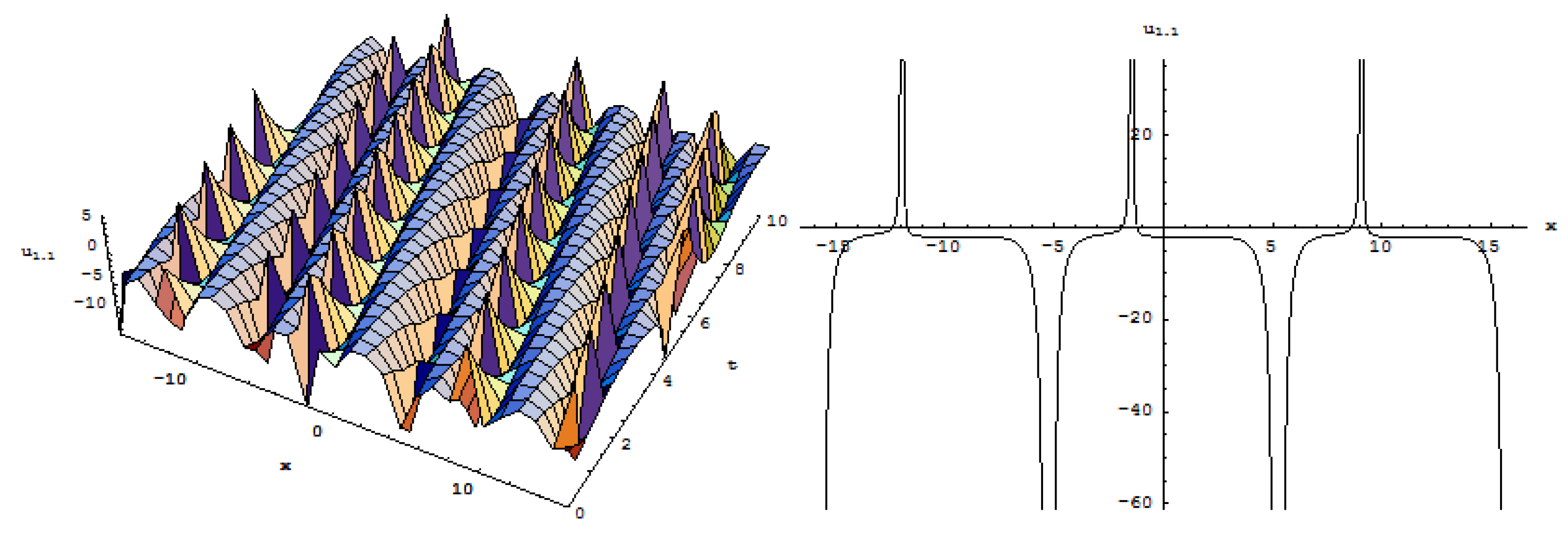
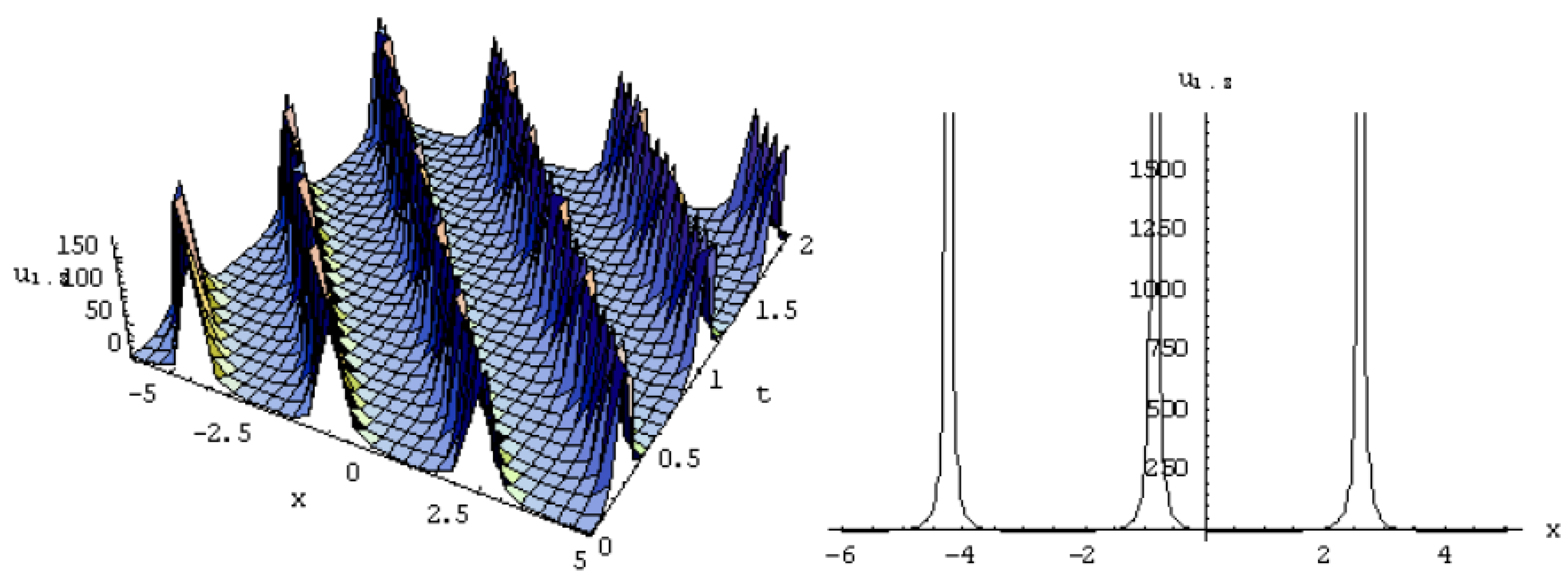
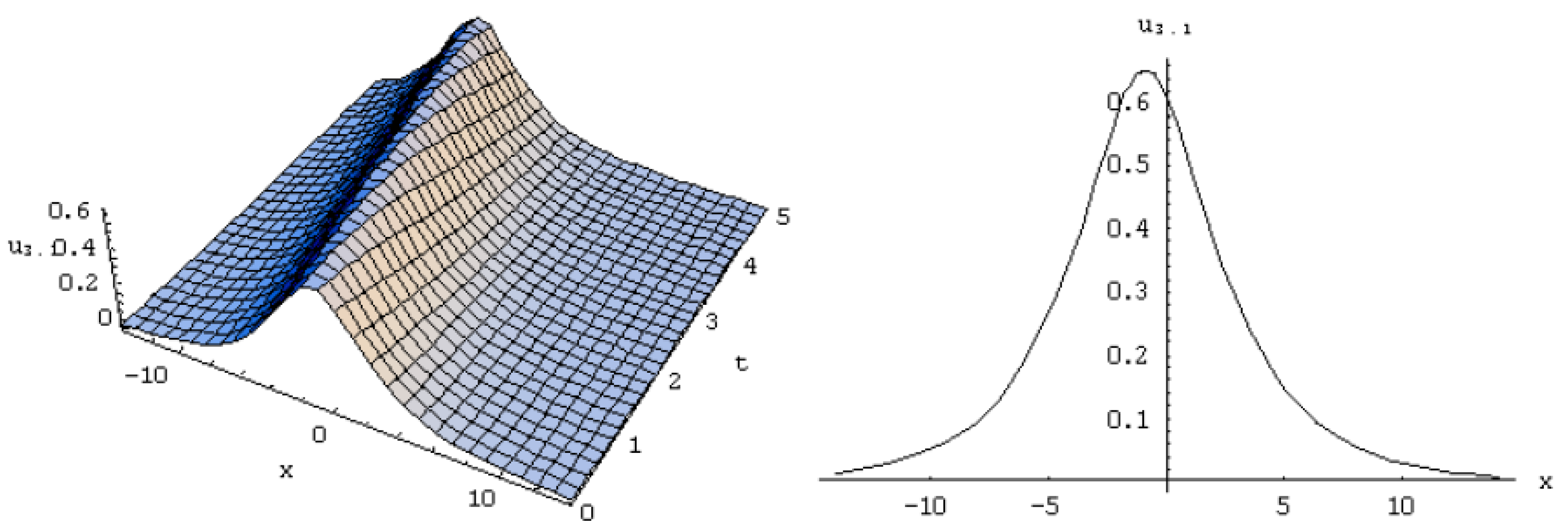
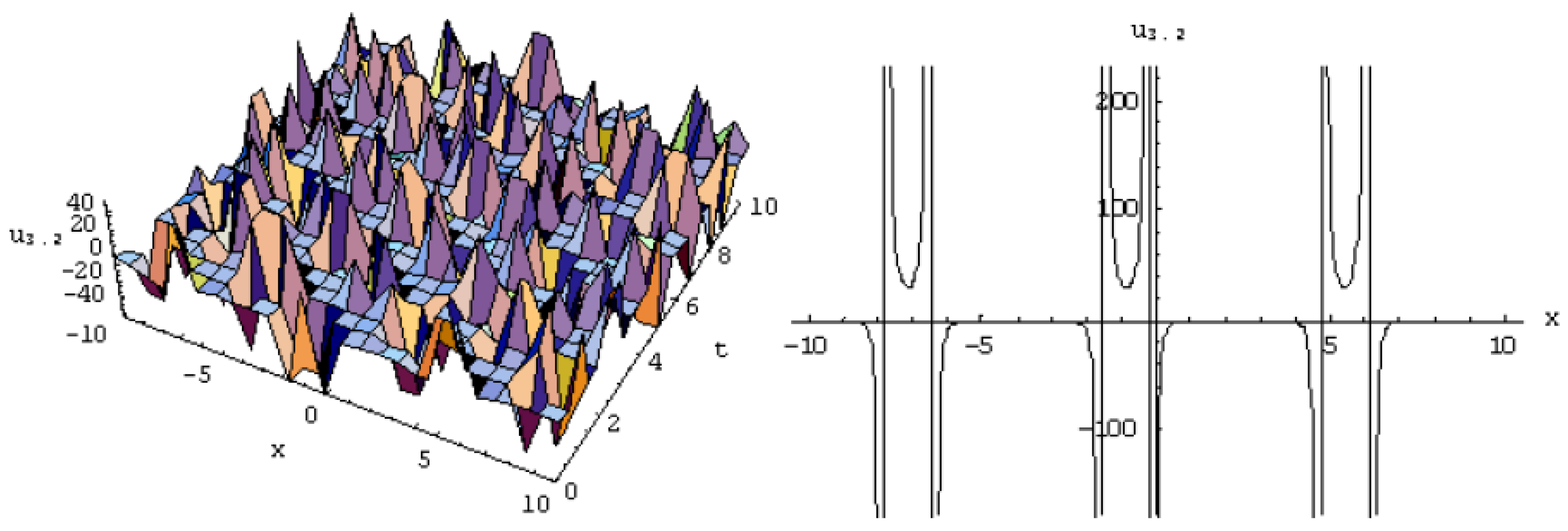
3. Exact Solutions of the Equation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ablowitz, M.J.; Clarkson, P.A. Soliton, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Matveev, V.A.; Salle, M.A. Darboux Transformations and Solitons; Springer-Verlag: Berlin, Heidelberg, Germany, 1991. [Google Scholar]
- Hong, B.J. New Jacobi elliptic functions solutions for the variable-coefficient mKdV equation. Appl. Math. Comput. 2009, 215, 2908–2913. [Google Scholar] [CrossRef]
- Yan, Z.Y. Similarity transformations and exact solutions for a family of higher-dimensional generalized Boussninesq equations. Phys. Lett. A 2007, 361, 223–230. [Google Scholar]
- Guo, Y.X.; Lai, S.Y. New exact solutions for an (N+1)-dimensional generalized Boussinesq equation. Nonlinear Anal. Theor. Methods Appl. 2010, 72, 2863–2873. [Google Scholar] [CrossRef]
- Boussinesq, J. Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. Journal de Mathématiques Pures et Appliquées, Deuxième Série 1872, 17, 55–108. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Dodd, R.K.; Eilbeck, J.C.; Gibbon, J.D.; Morries, H.C. Soliton and Nonlinear Waves; Academic Press: London, UK, 1982. [Google Scholar]
- Yan, Z.Y.; Xie, F.D.; Zhang, H.Q. Symmetry Reductions, Integrability and Solitary Wave Solutions to High-Order Modified Boussinesq Equations with Damping Term. Commun. Theor. Phys. 2001, 36, 1–6. [Google Scholar]
- Chen, Y.; Yan, Z.Y.; Zhang, H.Q. New explicit solitary wave solutions for (2+1)-dimensionalBoussinesq equation and (3+1)-dimensional KP equation. Phys. Lett. A 2003, 307, 107–113. [Google Scholar] [CrossRef]
- Allen, M.A.; Rowlands, G. On the transverse instabilities of solitary waves. Phys. Lett. A 1997, 235, 145–146. [Google Scholar] [CrossRef]
- El-Sayed, S.M.; Kaya, D. The decomposition method for solving (2 + 1)-dimensional Boussinesq equation and (3 + 1)-dimensional KP equation. Appl. Math. Comput. 2004, 157, 523–534. [Google Scholar] [CrossRef]
- Matsukawa, M.; Watanabe, S. N-Soliton solution of two dimensional modified boussinesq equation. J. Phys. Soc. Jpn. 1988, 57, 2936–2940. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Construction of soliton solutions and periodic solutions of the Boussinesq equation by the modified decomposition method. Chaos Solitons Fract. 2001, 12, 1549–1556. [Google Scholar] [CrossRef]
- Feng, D.H.; Li, J.B.; Lue, J.L.; He, T.L. The improved Fan sub-equation method and its application to the Boussinseq wave equation. Appl. Math. Comput. 2007, 194, 309–320. [Google Scholar] [CrossRef]
- Wang, D.; Sun, W.W.; Kong, C.C.; Zhang, H.Q. New extended rational expansion method and exact solutions of Boussinesq equation and Jimbo-Miwa equations. Appl. Math. Comput. 2007, 189, 878–886. [Google Scholar] [CrossRef]
- Lai, S.Y. Different physical structures of solutions for a generalized Boussinesqwave equation. J. Comput. Appl. Math. 2009, 231, 311–318. [Google Scholar] [CrossRef]
- Abd-el-Malek, M.B.; Badran, N.A.; Hassan, H.S.; Abbas, H.H. New solutions for solving Boussinesq equation via potential symmetries method. Appl. Math. Comput. 2015, 251, 225–232. [Google Scholar] [CrossRef]
- Hubert, M.B.; Betchewe, G.; Doka, S.Y.; Crepin, K.T. Soliton wave solutions for the nonlinear transmission line using the Kudryashov method and the (G’/G)-expansion method. Appl. Math. Comput. 2014, 239, 299–309. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, W.; Tong, J.L. The improved sub-ODE method for a generalized KdV-mKdVequation with nonlinear terms of any order. Phys. Lett. A 2008, 372, 3808–3813. [Google Scholar] [CrossRef]
- Zhang, Y.; Lai, S.Y.; Yin, J.; Wu, Y.H. The application of the auxiliary equation technique to ageneralized mKdV equation with variable coefficients. J. Comput. Appl. Math. 2009, 223, 75–85. [Google Scholar] [CrossRef]
- Hong, B.J. New exact Jacobi elliptic functions solutions for the generalized coupled Hirota-Satsuma KdV system. Appl. Math. Comput. 2010, 217, 472–479. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, B.; Lu, D. New Analytic Solutions for the (N + 1)-Dimensional Generalized Boussinesq Equation. Math. Comput. Appl. 2016, 21, 8. https://doi.org/10.3390/mca21020008
Hong B, Lu D. New Analytic Solutions for the (N + 1)-Dimensional Generalized Boussinesq Equation. Mathematical and Computational Applications. 2016; 21(2):8. https://doi.org/10.3390/mca21020008
Chicago/Turabian StyleHong, Baojian, and Dianchen Lu. 2016. "New Analytic Solutions for the (N + 1)-Dimensional Generalized Boussinesq Equation" Mathematical and Computational Applications 21, no. 2: 8. https://doi.org/10.3390/mca21020008





