Estimating Variances in Weighted Least-Squares Estimation of Distributional Parameters
Abstract
:1. Introduction
2. LSE Method for Log-Logistic and Weibull Distributions
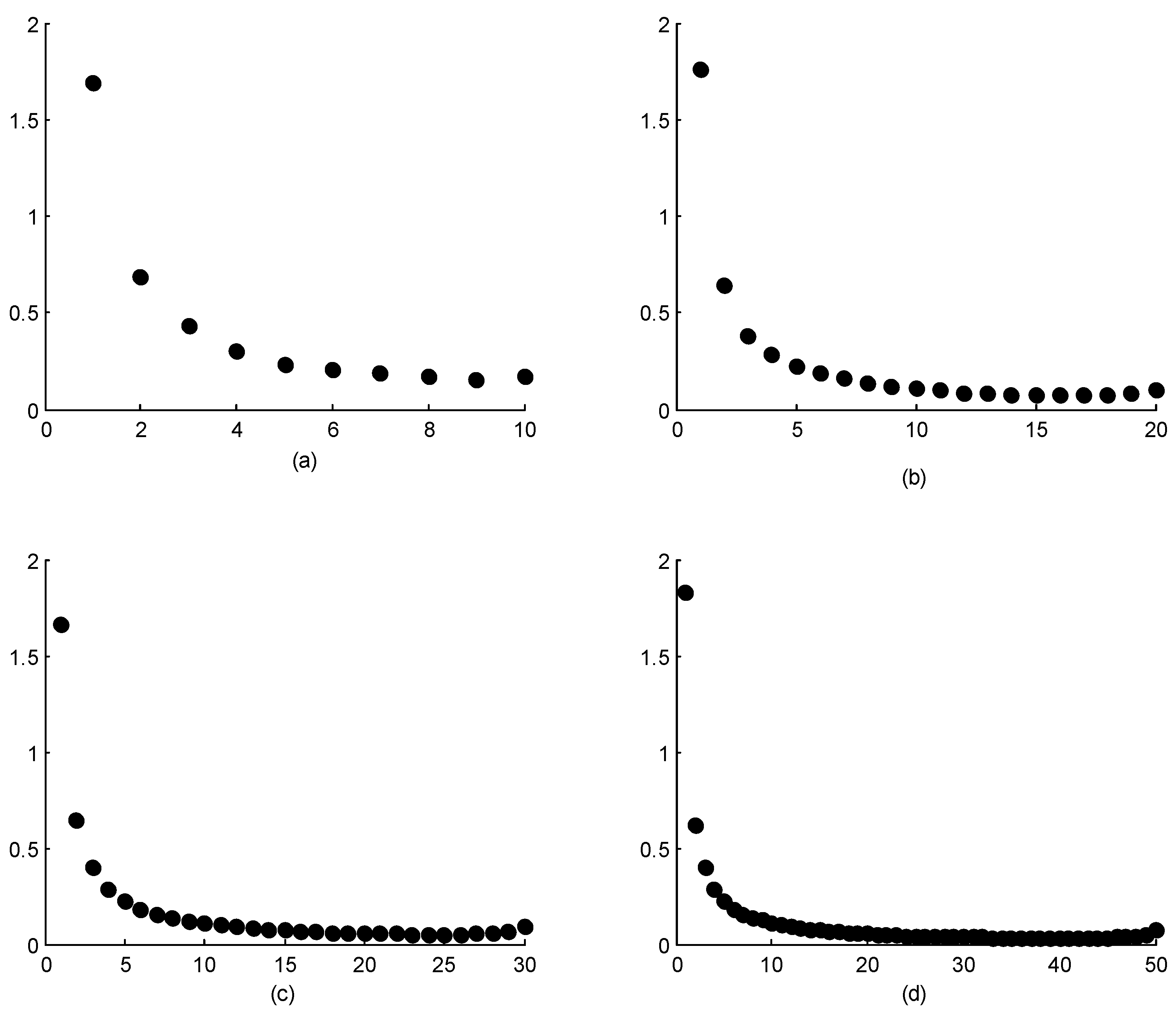
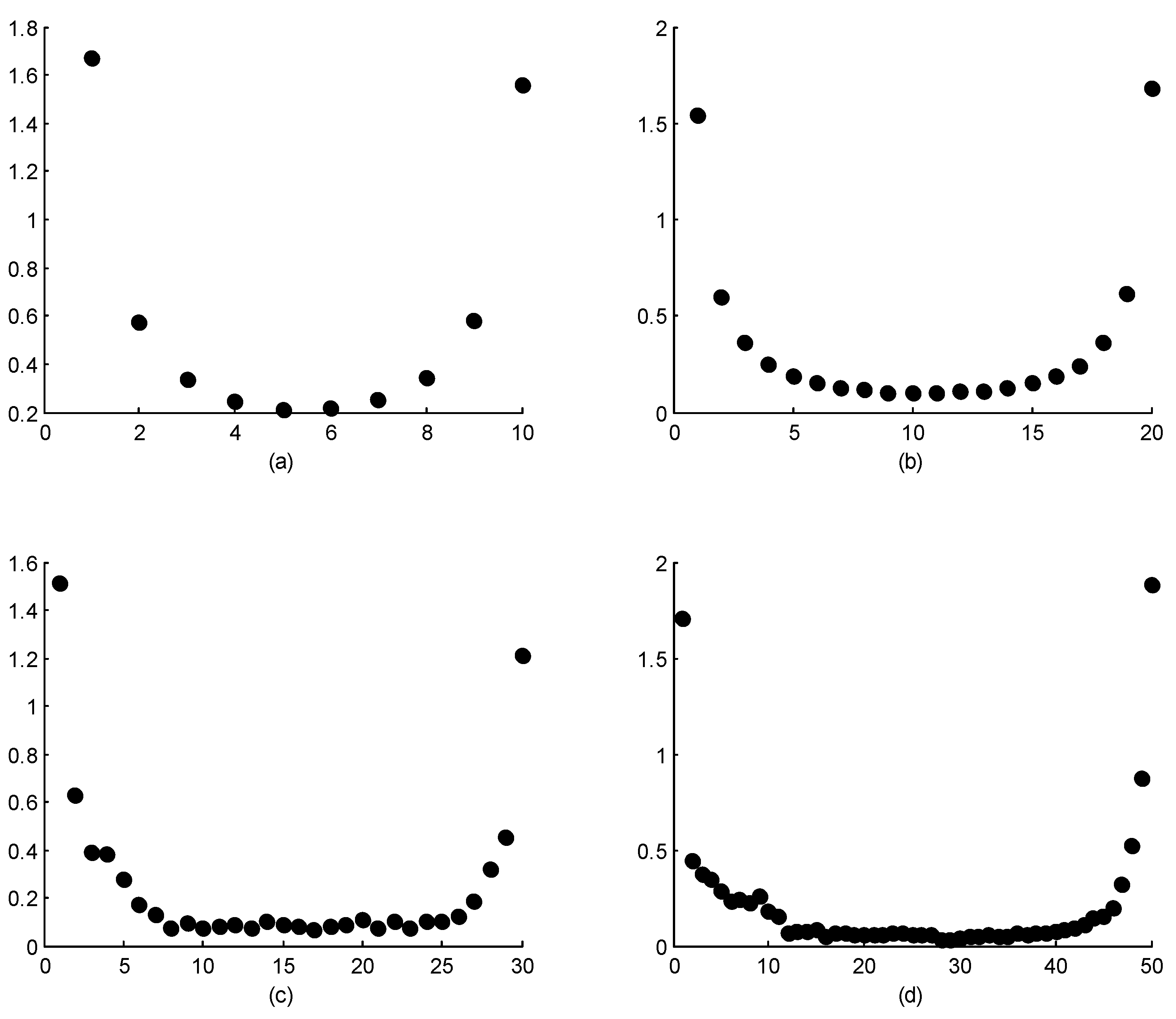
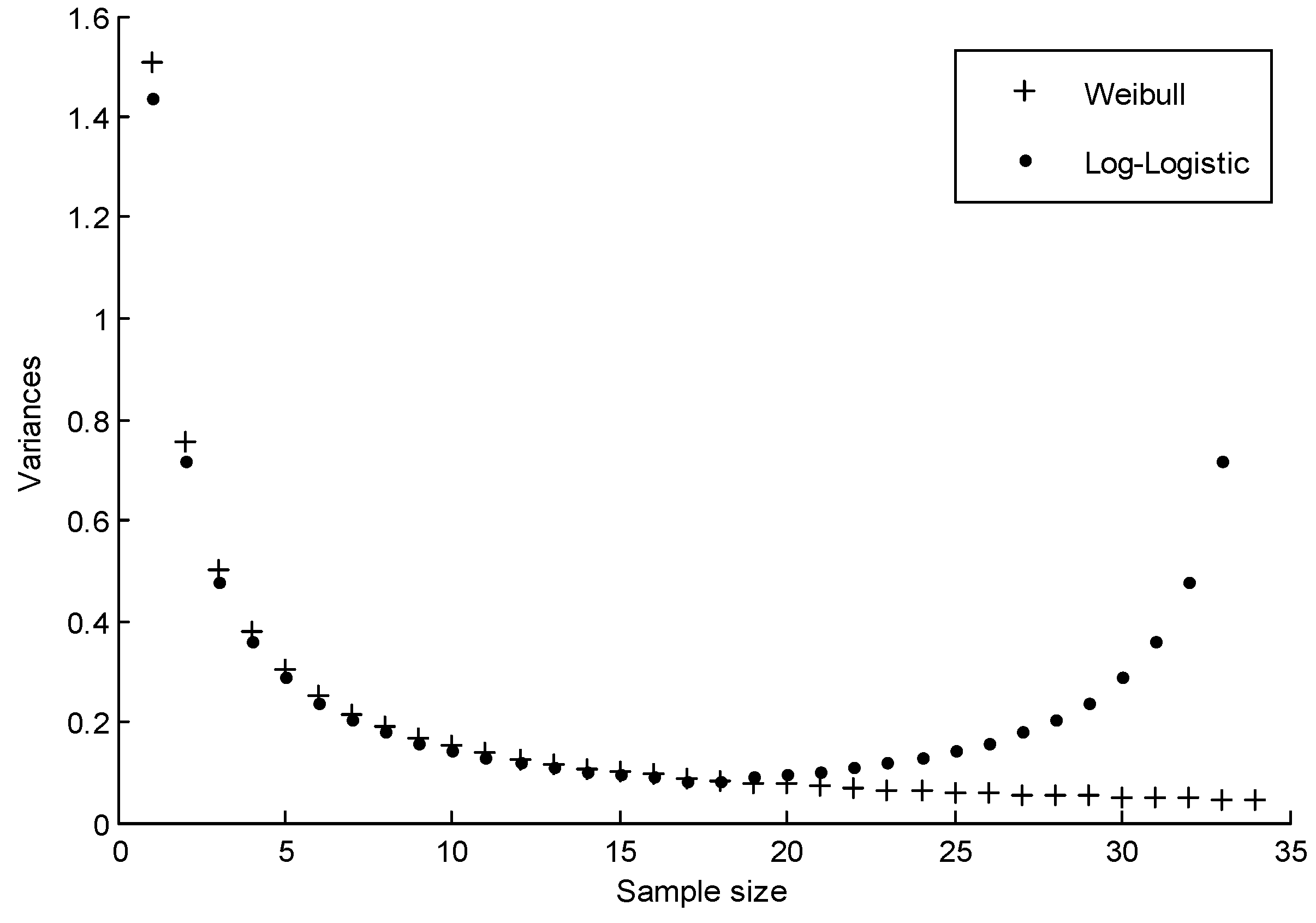
3. Estimating Weights in the Weighted Least-Squares Estimation for Parameters of the Log-Logistic and Weibull Distributions
4. Monte Carlo Simulation
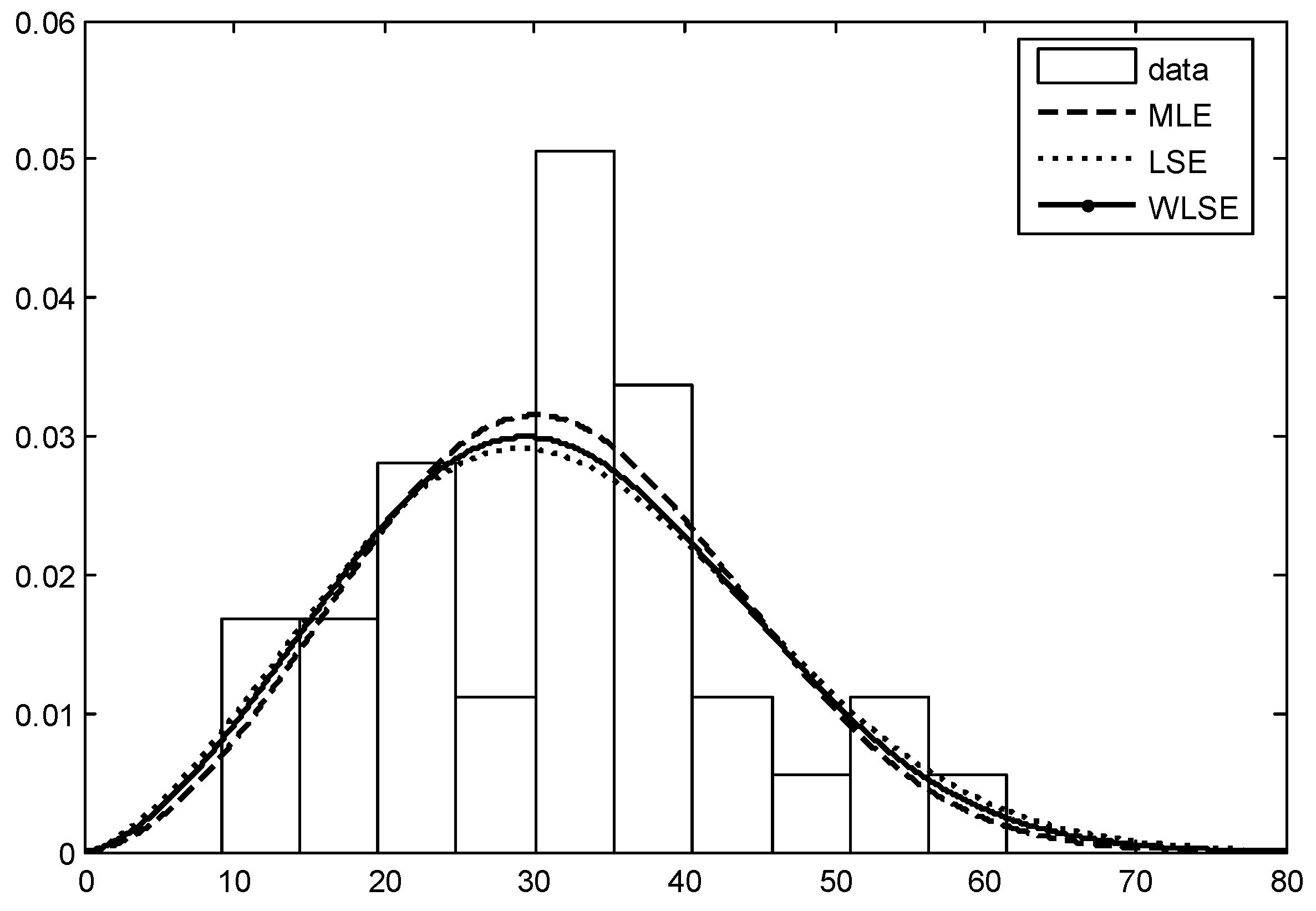
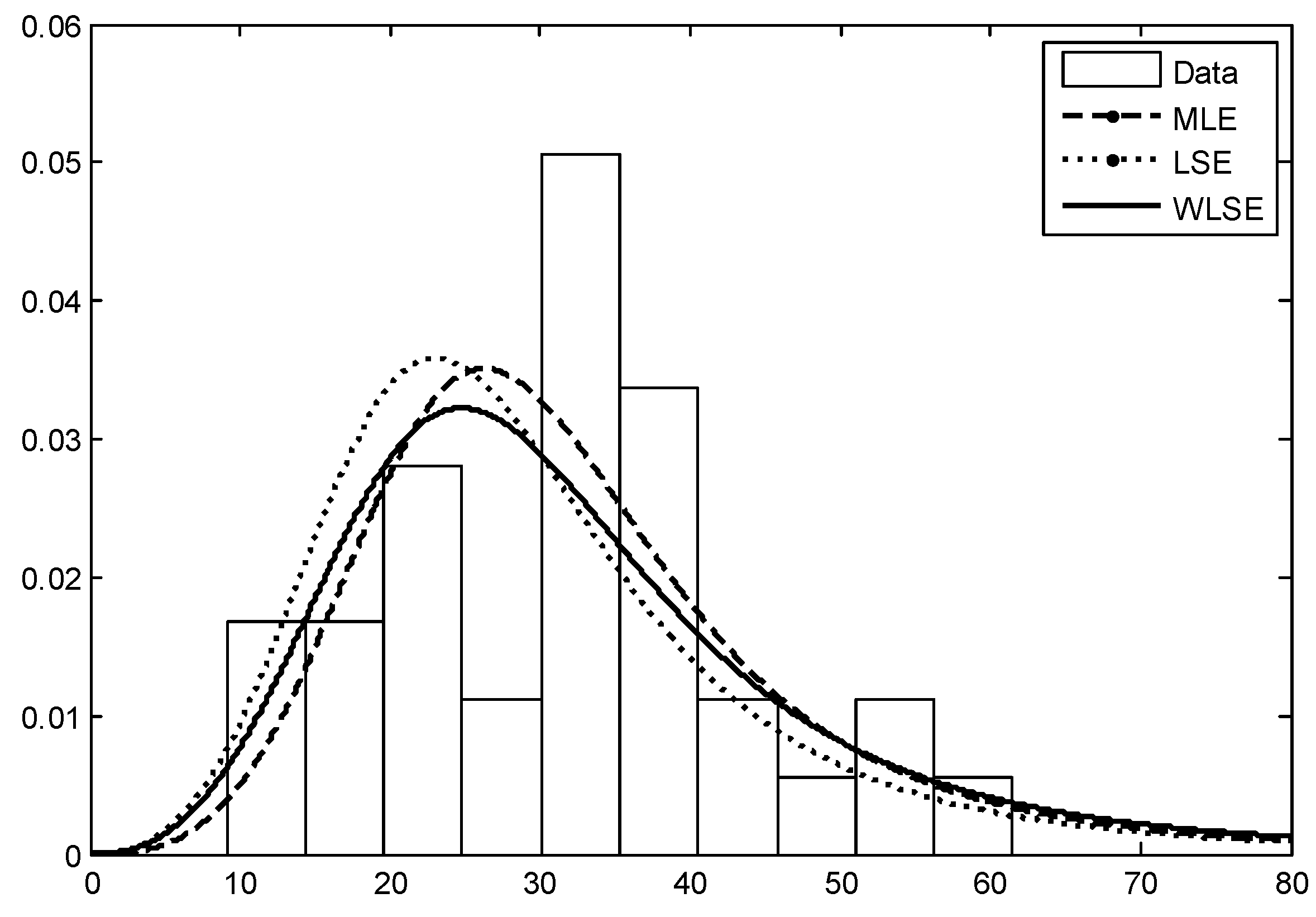
5. Real-Life Application from Hydrology
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Kantar, Y.M.; Şenoğlu, B. A comparative study for the location and scale parameters of the Weibull distribution with a given shape parameter. Comput. Geosci. 2008, 34, 1900–1909. [Google Scholar] [CrossRef]
- Marks, N.B. Estimation of Weibull parameters from common percentiles. J. Appl. Statist. 2005, 1, 17–24. [Google Scholar] [CrossRef]
- Altun, A. Estimation of the shape parameter of the Weibull distribution using linear regression methods: Non-censored samples. Qual. Reliab. Eng. Int. 2012, 29, 1207–1219. [Google Scholar]
- Tiryakioglu, M.; Hudak, D. On estimating Weibull modulus by the linear regression method. Mater. Sci. 2007, 42, 10173–10179. [Google Scholar] [CrossRef]
- Zhang, L.F.; Xie, M.; Tang, L.C. A study of two estimation approaches for parameters of Weibull distribution based on WPP. Reliab. Eng. Syst. Saf. 2007, 92, 360–368. [Google Scholar] [CrossRef]
- Genschel, U.; Meeker, W.Q. A Comparison of maximum likelihood and median-rank regression for Weibull estimation. Qual. Eng. 2010, 22, 236–255. [Google Scholar] [CrossRef]
- Hossain, A.; Howlader, H.A. Unweighted least squares estimation of Weibull parameters. J. Statist. Comput. Sim. 1996, 54, 265–271. [Google Scholar] [CrossRef]
- Kantar, Y.M.; Arik, I. M-estimation of log-logistic distribution parameters with outliers. Int. J. Agric. Stat. Sci. 2014, 10, 7–16. [Google Scholar]
- Boudt, K.; Caliskan, D.; Croux, C. Robust explicit estimators of Weibull parameters. Metrika 2011, 73, 187–209. [Google Scholar] [CrossRef]
- Bergman, B. Estimation of Weibull parameters using a weight function. J. Mater. Sci. 1986, 5, 611–614. [Google Scholar] [CrossRef]
- Hung, W.L. Weighted least squares estimation of the shape parameter of the Weibull distribution. Qual. Reliab. Eng. Int. 2001, 17, 467–469. [Google Scholar] [CrossRef]
- Lu, H.L.; Chen, C.H.; Wu, J.W. A Note on weighted least-squares estimation of the shape parameter of the Weibull distribution. Qual. Reliab. Eng. Int. 2004, 20, 579–586. [Google Scholar] [CrossRef]
- Zhang, L.F.; Xie, M.; Tang, L.C. On weighted least squares estimation for the parameters of Weibull distribution. In Recent Advances in Reliability and Quality in Design, 1st ed.; Pham, H., Ed.; Springer Series in Reliability Engineering: London, UK, 2008; pp. 57–84. [Google Scholar]
- Lu, H.L.; Tao, S.H. The Estimation of Pareto distribution by a weighted least square method. Qual. Quant. 2007, 41, 913–926. [Google Scholar] [CrossRef]
- Zyl, J.M.V. A median regression model to estimate the parameters of the three-parameter generalized Pareto distribution. Commun. Stat.-Simul. 2012, 41, 544–553. [Google Scholar]
- Zyl, J.M.V.; Schall, R. Parameter Estimation through weighted least-squares rank regression with specific reference to the Weibull and Gumbel distributions. Commun. Stat. Simul. 2012, 41, 1654–1666. [Google Scholar]
- Kantar, Y.M.; Arik, A. The use of the data transformation techniques in estimating the shape parameter of the Weibull distribution. IJEOE 2014, 3, 20–33. [Google Scholar] [CrossRef]
- Kantar, Y.M.; Arik, A.; Yenilmez, İ.; Usta, İ. Comparison of some estimation methods of the two parameter Weibull distribution for unusual wind speed data cases. Int. J. Inform. Technol. 2016, in press. [Google Scholar]
- Engeman, R.M.; Keefe, T.J. On generalized least squares estimation of the Weibull distribution. Commun. Stat. Theory Methods 1982, 19, 2181–2193. [Google Scholar] [CrossRef]
- Kantar, Y.M. Generalized least squares and weighted least squares estimation methods for distributional parameters. REVSTAT—Stat. J. 2015, 13, 263–282. [Google Scholar]
- Zhang, L.F.; Xie, M.; Tang, L.C. Robust regression using probability plots for estimating the Weibull shape parameter. Qual. Reliab. Eng. Int. 2006, 22, 905–917. [Google Scholar] [CrossRef]
- Kantar, Y.M.; Usta, I. Analysis of wind speed distributions: Wind distribution function derived from minimum cross entropy principles as better alternative to Weibull function. Energy Convers. Manag. 2008, 49, 962–973. [Google Scholar] [CrossRef]
- Acıtaş, Ş.; Kasap, P.; Şenoğlu, B.; Arslan, O. Robust estimation with the skew 2t distribution. Pak. J. Stat. 2013, 29, 409–430. [Google Scholar]
- Arik, I.; Kantar, Y.M.; Yenilmez, I. The evaluation of robust and efficient estimators for log-logistic distribution for censored data with/without outliers. JSRAD 2015, 2, 24–32. [Google Scholar]
- Kantar, Y.M.; Usta, I.; Acitas, S. A Monte Carlo Simulation Study on Partially Adaptive Estimators of linear Regression Models. J. Appl. Stat. 2011, 38, 1681–1699. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Ruskeepa, H.; Singh, V.P.; Sivakumar, B. Flood frequency analysis using mathematica. Turk. J. Eng. Environ. Sci. 2010, 34, 171–188. [Google Scholar]
| 0.98 | 0.98 | 0.99 | 0.95 |
| 0.98 | 0.98 | 0.99 | 0.95 |
| Shape Parameter | 1 | 2 | 3 | 6 | ||||
|---|---|---|---|---|---|---|---|---|
| n = 10 | ||||||||
| Methods | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias |
| MLE | 0.15170 | −0.15212 | 0.61690 | −0.31629 | 1.37293 | −0.44112 | 5.67004 | −0.98941 |
| LSE | 0.11440 | −0.09667 | 0.54134 | −0.20337 | 1.10040 | −0.28495 | 3.99536 | −0.64275 |
| WLSE(Zyl and Schall) | 0.19999 | −0.21543 | 0.81328 | −0.44568 | 1.78391 | −0.62753 | 7.43891 | −1.37432 |
| Proposed WLSE | 0.10839 | −0.02486 | 0.43330 | −0.06128 | 1.00824 | −0.06953 | 3.98816 | −0.21838 |
| n = 20 | ||||||||
| MLE | 0.05213 | −0.06977 | 0.20253 | −0.13622 | 0.45077 | −0.20854 | 1.79207 | −0.40466 |
| LSE | 0.05036 | −0.03032 | 0.19174 | −0.05249 | 0.42394 | −0.08664 | 1.68610 | −0.17020 |
| WLSE(Zyl and Schall) | 0.07190 | −0.11669 | 0.28007 | −0.22935 | 0.63664 | −0.35112 | 2.46200 | −0.68556 |
| Proposed WLSE | 0.04278 | 0.02031 | 0.16383 | 0.04718 | 0.36171 | 0.06327 | 1.45807 | 0.14500 |
| n = 30 | ||||||||
| MLE | 0.02778 | −0.04194 | 0.11692 | −0.09339 | 0.26793 | −0.12972 | 1.15141 | −0.29157 |
| LSE | 0.02773 | −0.00947 | 0.11498 | −0.02627 | 0.26564 | −0.03313 | 1.12986 | −0.09620 |
| WLSE(Zyl and Schall) | 0.03941 | −0.07720 | 0.16531 | −0.15971 | 0.37430 | −0.23364 | 1.59306 | −0.50179 |
| Proposed WLSE | 0.02509 | 0.02770 | 0.10194 | 0.04546 | 0.23752 | 0.08039 | 0.99113 | 0.12622 |
| n = 50 | ||||||||
| MLE | 0.01566 | −0.02583 | 0.03070 | −0.02512 | 0.14066 | −0.07853 | 0.57653 | −0.13840 |
| LSE | 0.01633 | 0.00006 | 0.03428 | 0.01186 | 0.14630 | 0.00037 | 0.60268 | 0.01698 |
| WLSE(Zyl and Schall) | 0.02169 | −0.04636 | 0.04053 | −0.04015 | 0.19377 | −0.13955 | 0.79926 | −0.27090 |
| Proposed WLSE | 0.01521 | 0.02195 | 0.03136 | 0.02328 | 0.13589 | 0.06200 | 0.56752 | 0.13359 |
| n = 100 | ||||||||
| MLE | 0.00737 | −0.01237 | 0.02925 | −0.02169 | 0.06983 | −0.04588 | 0.26815 | −0.07447 |
| LSE | 0.00819 | 0.00447 | 0.03224 | 0.01293 | 0.07529 | 0.00617 | 0.29422 | 0.02979 |
| WLSE(Zyl and Schall) | 0.00993 | −0.02040 | 0.03966 | −0.03845 | 0.09062 | −0.07264 | 0.34757 | −0.12550 |
| Proposed WLSE | 0.00749 | 0.01454 | 0.03025 | 0.03137 | 0.07067 | 0.03276 | 0.27823 | 0.08239 |
| n = 250 | ||||||||
| MLE | 0.00288 | −0.00549 | 0.01132 | −0.00937 | 0.02607 | −0.01758 | 0.10527 | −0.02345 |
| LSE | 0.00325 | 0.00419 | 0.01289 | 0.01079 | 0.02891 | 0.01211 | 0.12167 | 0.03412 |
| WLSE(Zyl and Schall) | 0.00375 | −0.00810 | 0.01484 | −0.01423 | 0.03342 | −0.02428 | 0.13741 | −0.03586 |
| Proposed WLSE | 0.00312 | 0.00624 | 0.01228 | 0.01308 | 0.02845 | 0.01610 | 0.11304 | 0.04641 |
| Shape Parameter | 1 | 2 | 3 | 6 | ||||
|---|---|---|---|---|---|---|---|---|
| n = 10 | ||||||||
| Methods | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias |
| MLE | 0.53291 | −0.16983 | 0.08620 | −0.03690 | 0.03530 | −0.01621 | 0.0086 | −0.00188 |
| LSE | 0.28823 | 0.28573 | 0.09542 | 0.19277 | 0.04874 | 0.14074 | 0.01472 | 0.07957 |
| WLSE(Zyl and Schall) | 0.27738 | 0.20752 | 0.08143 | 0.14670 | 0.04022 | 0.10846 | 0.01173 | 0.06139 |
| Proposed WLSE | 0.27505 | 0.19492 | 0.07949 | 0.13951 | 0.03900 | 0.10382 | 0.01127 | 0.05852 |
| n = 20 | ||||||||
| MLE | 0.20817 | −0.08162 | 0.04173 | −0.02409 | 0.01733 | −0.00745 | 0.00442 | −0.00346 |
| LSE | 0.16078 | 0.19233 | 0.04737 | 0.11886 | 0.02340 | 0.08807 | 0.00654 | 0.04575 |
| WLSE(Zyl and Schall) | 0.14875 | 0.11459 | 0.03943 | 0.07457 | 0.01863 | 0.05758 | 0.00509 | 0.02970 |
| Proposed WLSE | 0.14925 | 0.10117 | 0.03864 | 0.06670 | 0.01819 | 0.05303 | 0.00491 | 0.02705 |
| n = 30 | ||||||||
| MLE | 0.11511 | −0.04886 | 0.02753 | −0.01467 | 0.01128 | −0.00538 | 0.00276 | −0.00181 |
| LSE | 0.10550 | 0.15271 | 0.03210 | 0.08778 | 0.01482 | 0.06448 | 0.00399 | 0.03366 |
| WLSE(Zyl and Schall) | 0.09359 | 0.08221 | 0.02668 | 0.05080 | 0.01187 | 0.03837 | 0.00308 | 0.02013 |
| Proposed WLSE | 0.09378 | 0.07111 | 0.02630 | 0.04494 | 0.01161 | 0.03451 | 0.00299 | 0.01821 |
| n = 50 | ||||||||
| MLE | 0.06937 | −0.03995 | 0.00766 | −0.00371 | 0.00696 | −0.00388 | 0.00173 | −0.00055 |
| LSE | 0.06566 | 0.09608 | 0.00896 | 0.03468 | 0.00870 | 0.04251 | 0.00234 | 0.02330 |
| WLSE(Zyl and Schall) | 0.05982 | 0.03974 | 0.00765 | 0.01630 | 0.00714 | 0.02252 | 0.00185 | 0.01269 |
| Proposed WLSE | 0.05973 | 0.03129 | 0.00745 | 0.01355 | 0.00702 | 0.01960 | 0.00182 | 0.01126 |
| n = 100 | ||||||||
| MLE | 0.03096 | −0.01622 | 0.00757 | −0.00265 | 0.00327 | −0.00273 | 0.00085 | −0.00016 |
| LSE | 0.03227 | 0.05936 | 0.00890 | 0.03609 | 0.00395 | 0.02353 | 0.00107 | 0.01298 |
| WLSE(Zyl and Schall) | 0.02912 | 0.02344 | 0.00763 | 0.01716 | 0.00332 | 0.01043 | 0.00088 | 0.00646 |
| Proposed WLSE | 0.02901 | 0.01845 | 0.00750 | 0.01454 | 0.00328 | 0.00867 | 0.00088 | 0.00559 |
| n = 250 | ||||||||
| MLE | 0.01215 | −0.00633 | 0.00296 | −0.00003 | 0.00137 | −0.00053 | 0.00034 | 0.00010 |
| LSE | 0.01320 | 0.02975 | 0.00345 | 0.01802 | 0.00156 | 0.01156 | 0.00041 | 0.00610 |
| WLSE(Zyl and Schall) | 0.01181 | 0.00944 | 0.00300 | 0.00800 | 0.00138 | 0.00477 | 0.00035 | 0.00277 |
| Proposed WLSE | 0.01175 | 0.00720 | 0.00298 | 0.00667 | 0.00138 | 0.00399 | 0.00035 | 0.00236 |
| Shape parameter | 1 | 2 | 3 | 6 | ||||
|---|---|---|---|---|---|---|---|---|
| n = 10 | ||||||||
| Methods | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias |
| MLE | 0.16290 | −0.17684 | 0.61002 | −0.34672 | 1.39320 | −0.48813 | 5.30808 | −1.00735 |
| LSE | 0.10553 | 0.02617 | 0.40657 | 0.05791 | 0.92350 | 0.10020 | 3.63395 | 0.18918 |
| WLSE(Zyl and Schall) | 0.09019 | 0.04832 | 0.33633 | 0.10347 | 0.80193 | 0.17179 | 3.01066 | 0.32833 |
| Proposed WLSE | 0.08970 | 0.04528 | 0.33353 | 0.09746 | 0.79808 | 0.16480 | 2.98083 | 0.31209 |
| n = 20 | ||||||||
| MLE | 0.05051 | −0.07862 | 0.20273 | −0.15801 | 0.43237 | −0.22142 | 1.76956 | −0.44148 |
| LSE | 0.05122 | 0.03667 | 0.20062 | 0.07636 | 0.45081 | 0.12566 | 1.81754 | 0.24342 |
| WLSE(Zyl and Schall) | 0.03805 | 0.04307 | 0.15174 | 0.08599 | 0.33618 | 0.13991 | 1.38091 | 0.28552 |
| Proposed WLSE | 0.03713 | 0.04112 | 0.14802 | 0.08202 | 0.32646 | 0.13488 | 1.34091 | 0.27419 |
| n = 30 | ||||||||
| MLE | 0.02709 | −0.04567 | 0.10771 | −0.09483 | 0.23843 | −0.14551 | 0.96885 | −0.30166 |
| LSE | 0.03418 | 0.04049 | 0.13882 | 0.07656 | 0.29428 | 0.11197 | 1.23346 | 0.22298 |
| WLSE(Zyl and Schall) | 0.02383 | 0.03874 | 0.09409 | 0.07331 | 0.20710 | 0.10699 | 0.83766 | 0.20695 |
| Proposed WLSE | 0.02288 | 0.03733 | 0.08996 | 0.07127 | 0.19936 | 0.10311 | 0.79907 | 0.19891 |
| n = 50 | ||||||||
| MLE | 0.01465 | −0.0233 | 0.06141 | −0.0627 | 0.13222 | −0.0875 | 0.52323 | −0.1647 |
| LSE | 0.02333 | 0.06806 | 0.09433 | 0.14283 | 0.21502 | 0.21366 | 0.86411 | 0.42794 |
| WLSE(Zyl and Schall) | 0.01490 | 0.04802 | 0.05899 | 0.08928 | 0.13479 | 0.14028 | 0.55811 | 0.28503 |
| Proposed WLSE | 0.01440 | 0.04733 | 0.05896 | 0.08917 | 0.13236 | 0.10311 | 0.5300 | 0.28891 |
| n = 100 | ||||||||
| MLE | 0.00677 | −0.01440 | 0.02660 | −0.03043 | 0.05868 | −0.04105 | 0.24495 | −0.09501 |
| LSE | 0.01114 | 0.02299 | 0.04404 | 0.04507 | 0.09679 | 0.07418 | 0.38372 | 0.13333 |
| WLSE(Zyl and Schall) | 0.00711 | 0.01278 | 0.02742 | 0.02316 | 0.06246 | 0.04011 | 0.24995 | 0.06395 |
| Proposed WLSE | 0.00663 | 0.01205 | 0.02589 | 0.02420 | 0.05872 | 0.04100 | 0.24438 | 0.06505 |
| n = 250 | ||||||||
| MLE | 0.00242 | −0.00611 | 0.00982 | −0.01081 | 0.02268 | −0.02154 | 0.08933 | −0.02439 |
| LSE | 0.00434 | 0.01466 | 0.01728 | 0.03187 | 0.03825 | 0.03658 | 0.16016 | 0.09904 |
| WLSE(Zyl and Schall) | 0.00270 | 0.00405 | 0.01112 | 0.01105 | 0.02511 | 0.00906 | 0.10153 | 0.04266 |
| Proposed WLSE | 0.00249 | 0.00404 | 0.01024 | 0.01169 | 0.02329 | 0.01205 | 0.09355 | 0.04241 |
| Shape Parameter | 1 | 2 | 3 | 6 | ||||
|---|---|---|---|---|---|---|---|---|
| n = 10 | ||||||||
| Methods | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias |
| MLE | 0.11141 | −0.01587 | 0.02711 | 0.00626 | 0.01246 | 0.00561 | 0.00312 | 0.00412 |
| LSE | 0.15382 | −0.04226 | 0.03203 | −0.00566 | 0.01343 | 0.00074 | 0.00326 | 0.00258 |
| WLSE(Zyl and Schall) | 0.17017 | −0.08331 | 0.03342 | −0.02544 | 0.01375 | −0.01216 | 0.00328 | −0.00398 |
| Proposed WLSE | 0.17033 | −0.08574 | 0.03400 | −0.03128 | 0.01372 | −0.01586 | 0.00328 | −0.00590 |
| n = 20 | ||||||||
| MLE | 0.05694 | −0.00975 | 0.01438 | 0.00157 | 0.00613 | 0.00245 | 0.00162 | 0.00248 |
| LSE | 0.06613 | −0.00934 | 0.01561 | 0.00333 | 0.00660 | 0.00446 | 0.00168 | 0.00229 |
| WLSE(Zyl and Schall) | 0.07133 | −0.03953 | 0.01603 | −0.01178 | 0.00661 | −0.00566 | 0.00168 | −0.00258 |
| Proposed WLSE | 0.07289 | −0.04828 | 0.01619 | −0.01601 | 0.00661 | −0.00840 | 0.00168 | −0.00297 |
| n = 30 | ||||||||
| MLE | 0.03774 | −0.00943 | 0.00924 | 0.00119 | 0.00415 | 0.00154 | 0.00103 | 0.00096 |
| LSE | 0.04201 | 0.00142 | 0.01003 | 0.00484 | 0.00440 | 0.00435 | 0.00110 | 0.00328 |
| WLSE(Zyl and Schall) | 0.04407 | −0.02275 | 0.01004 | −0.00763 | 0.00438 | −0.00371 | 0.00107 | −0.00091 |
| Proposed WLSE | 0.04455 | −0.02932 | 0.01003 | −0.01076 | 0.00437 | −0.00478 | 0.00106 | −0.00119 |
| n = 50 | ||||||||
| MLE | 0.02187 | −0.00347 | 0.00558 | 0.00231 | 0.00248 | 0.00129 | 0.00062 | 0.00103 |
| LSE | 0.02378 | 0.00483 | 0.00599 | 0.00366 | 0.00264 | 0.00385 | 0.00067 | 0.00229 |
| WLSE(Zyl and Schall) | 0.02425 | −0.01454 | 0.00597 | −0.00594 | 0.00261 | −0.00256 | 0.00064 | −0.00097 |
| Proposed WLSE | 0.02423 | −0.01881 | 0.00597 | −0.00813 | 0.00259 | −0.00302 | 0.00064 | −0.00108 |
| n = 100 | ||||||||
| MLE | 0.01100 | −0.00012 | 0.00276 | 0.00007 | 0.00122 | 0.00199 | 0.00031 | 0.00101 |
| LSE | 0.01167 | 0.00325 | 0.00297 | 0.00447 | 0.00132 | 0.00169 | 0.00033 | 0.00112 |
| WLSE(Zyl and Schall) | 0.01168 | −0.00876 | 0.00291 | −0.00193 | 0.00129 | −0.00251 | 0.00033 | −0.00102 |
| Proposed WLSE | 0.01162 | −0.01009 | 0.00287 | −0.00300 | 0.00127 | −0.00307 | 0.00032 | −0.00112 |
| n = 250 | ||||||||
| MLE | 0.00432 | 0.00057 | 0.00107 | 0.00078 | 0.00048 | 0.00056 | 0.00012 | 0.00050 |
| LSE | 0.00457 | 0.00327 | 0.00113 | 0.00227 | 0.00052 | 0.00153 | 0.00013 | 0.00072 |
| WLSE(Zyl and Schall) | 0.00454 | −0.00396 | 0.00112 | −0.00122 | 0.00051 | −0.00083 | 0.00012 | −0.00042 |
| Proposed WLSE | 0.00436 | −0.00379 | 0.00110 | −0.00112 | 0.00050 | −0.00109 | 0.00012 | −0.00043 |
| Log-logistic Distribution | |||||||
|---|---|---|---|---|---|---|---|
| Parameters | MLE | LSE | WLSE (Zyl and Schall) | Proposed WLSE | LAD | WLSE (Hung) | WLSE (Lu et al.) |
| Scale | 30.0184 | 27.0712 | 28.8336 | 29.4025 | 28.5428 | - | - |
| Shape | 3.94881 | 3.58588 | 4.47555 | 3.48969 | 3.82828 | - | - |
| Weibull Distribution | |||||||
| Scale | 35.21229 | 35.5353 | 35.3532 | 35.2858 | 35.3344 | 35.0005 | 35.3607 |
| Shape | 2.80503 | 2.548301 | 2.634572 | 2.638023 | 2.659215 | 2.738903 | 2.63333 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mert Kantar, Y. Estimating Variances in Weighted Least-Squares Estimation of Distributional Parameters. Math. Comput. Appl. 2016, 21, 7. https://doi.org/10.3390/mca21020007
Mert Kantar Y. Estimating Variances in Weighted Least-Squares Estimation of Distributional Parameters. Mathematical and Computational Applications. 2016; 21(2):7. https://doi.org/10.3390/mca21020007
Chicago/Turabian StyleMert Kantar, Yeliz. 2016. "Estimating Variances in Weighted Least-Squares Estimation of Distributional Parameters" Mathematical and Computational Applications 21, no. 2: 7. https://doi.org/10.3390/mca21020007





