New Complex Hyperbolic Function Solutions for the (2+1)-Dimensional Dispersive Long Water–Wave System
Abstract
:1. Introduction
2. Fundamental Properties of Methods
2.1.The Modified Exp(−Ω(ξ))-Expansion Function Method
2.2. Improved Bernoulli Sub-Equation Function Method (IBSEFM)
3. The Implementations of Techniques
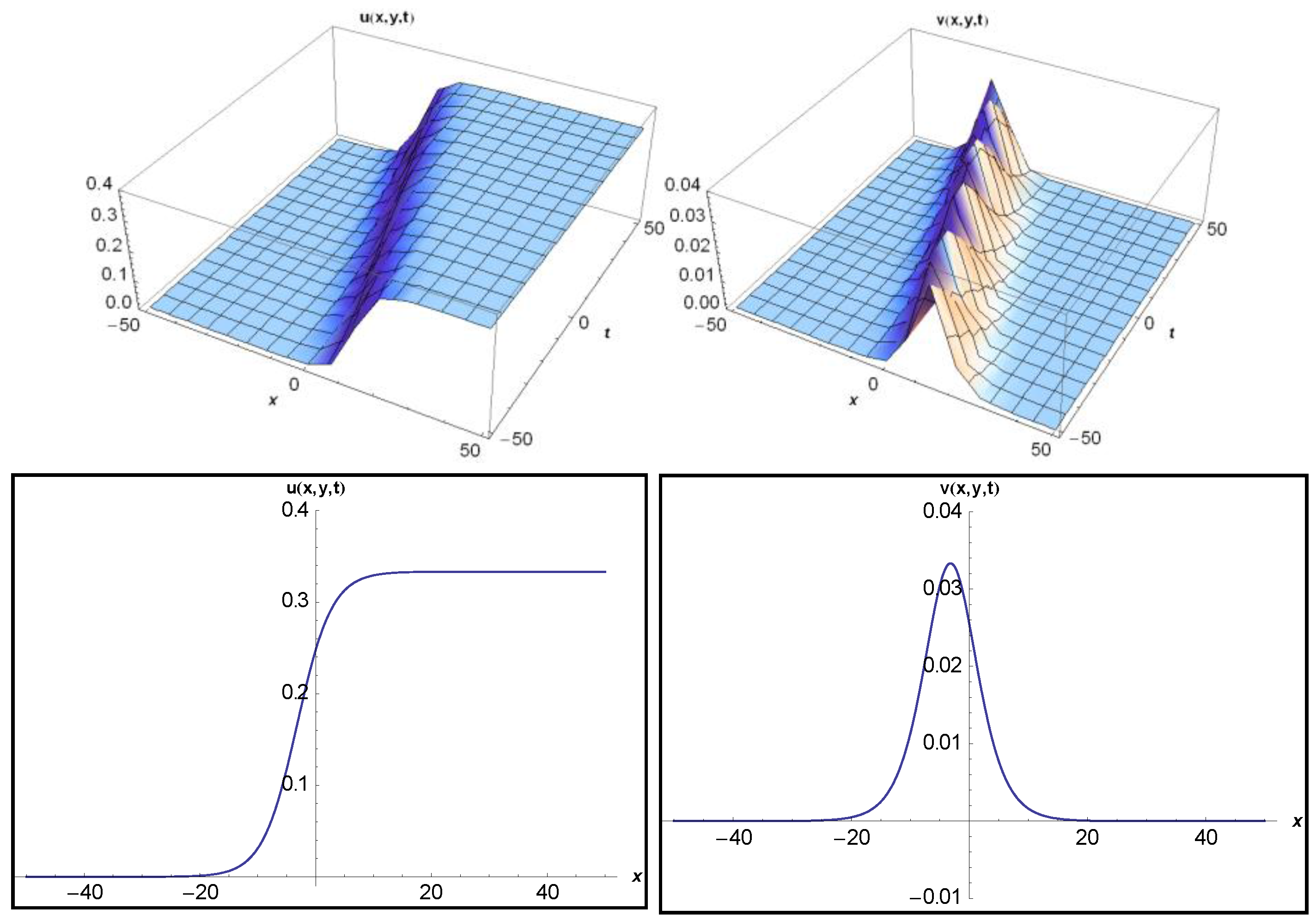
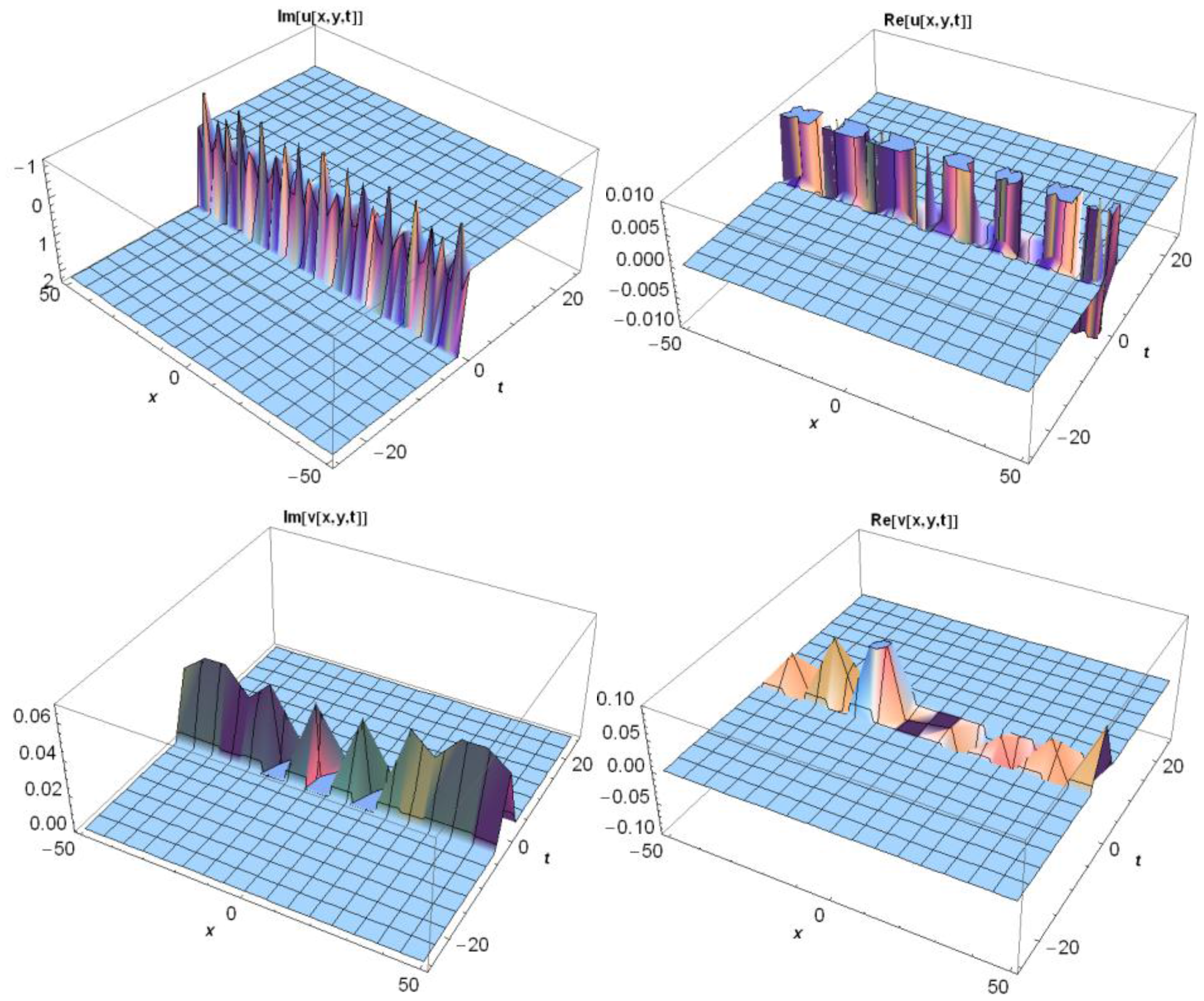
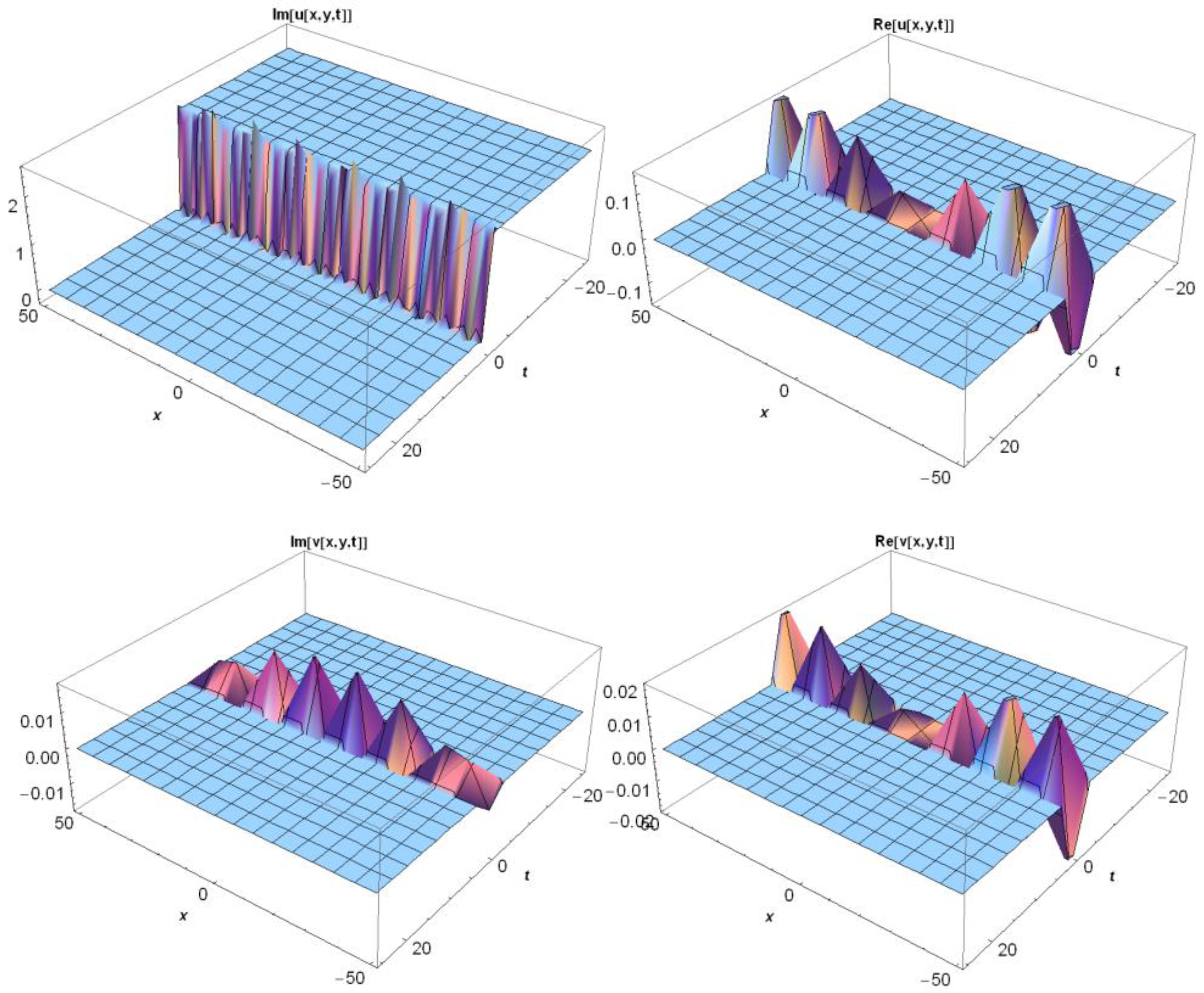
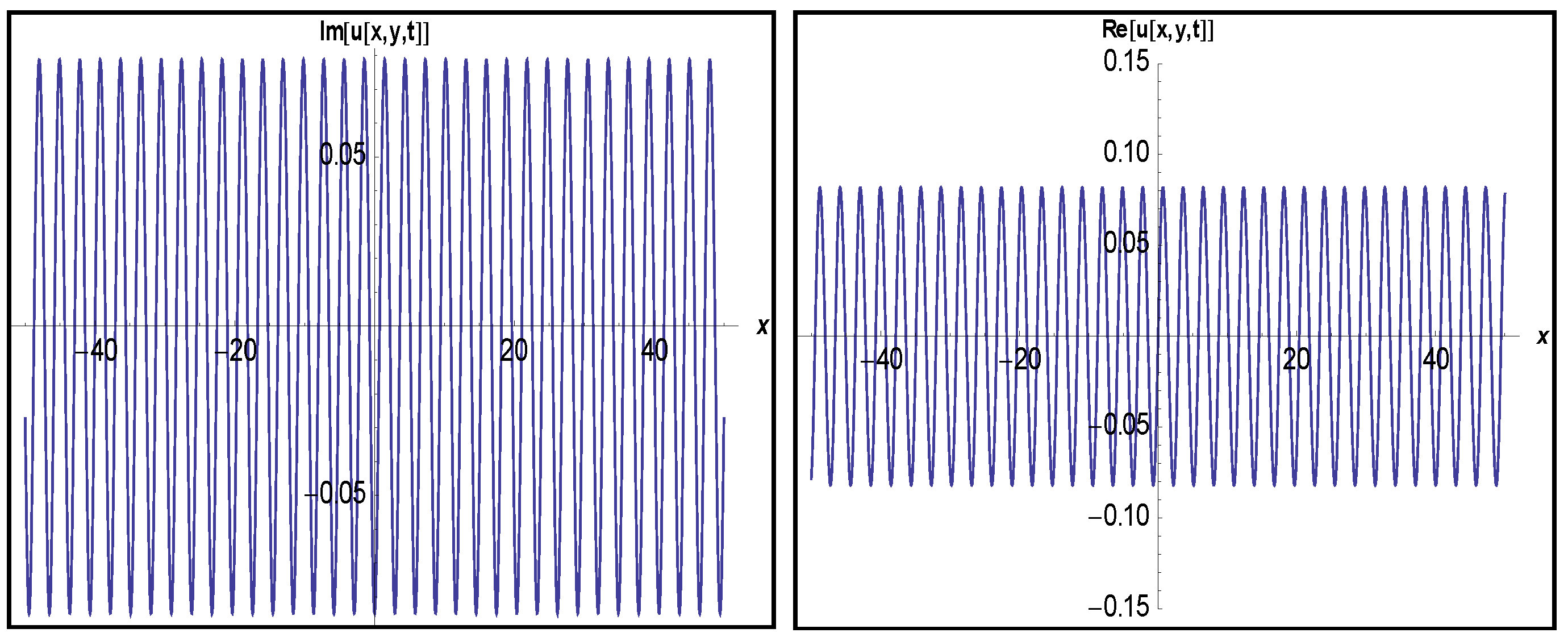
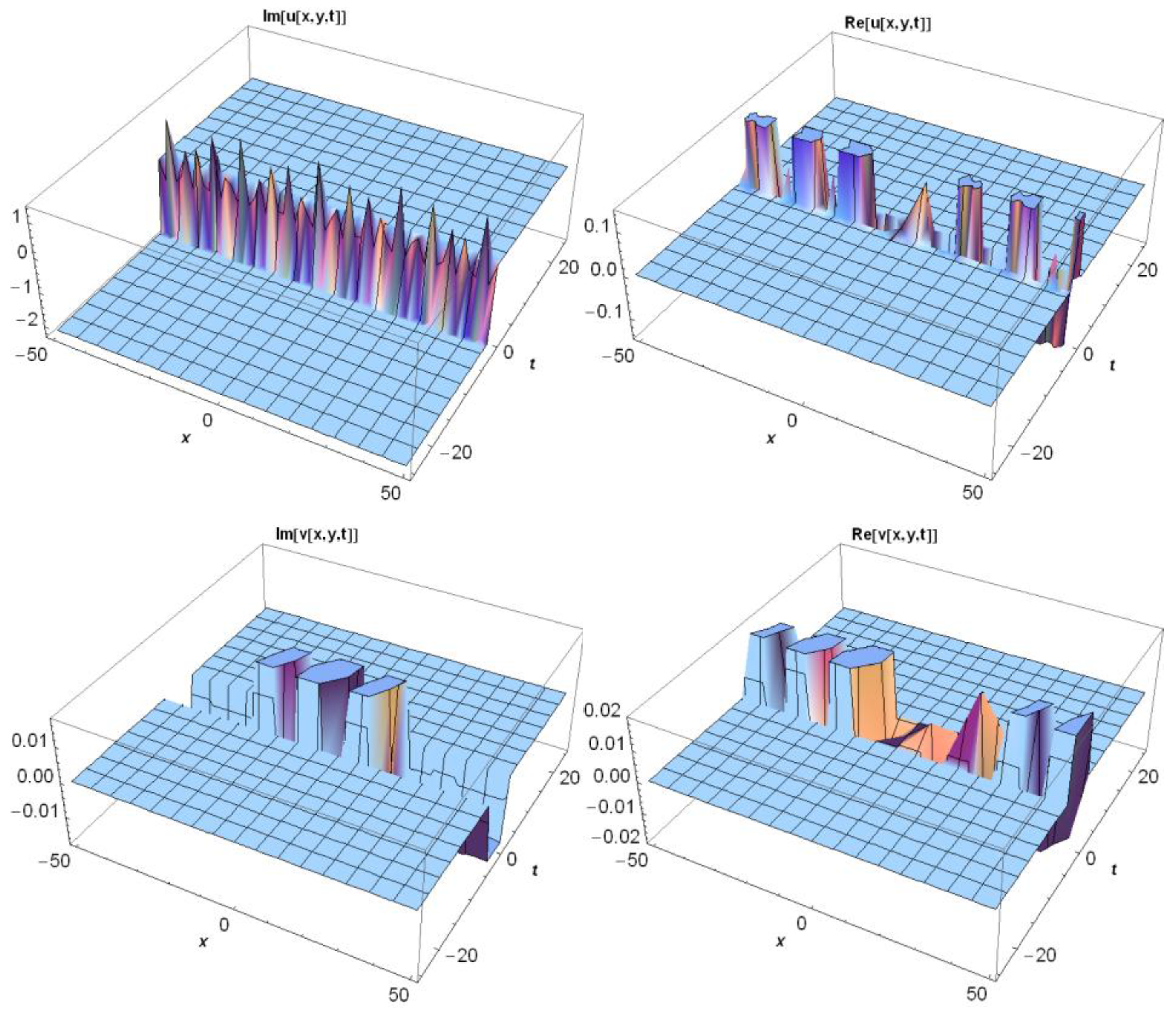
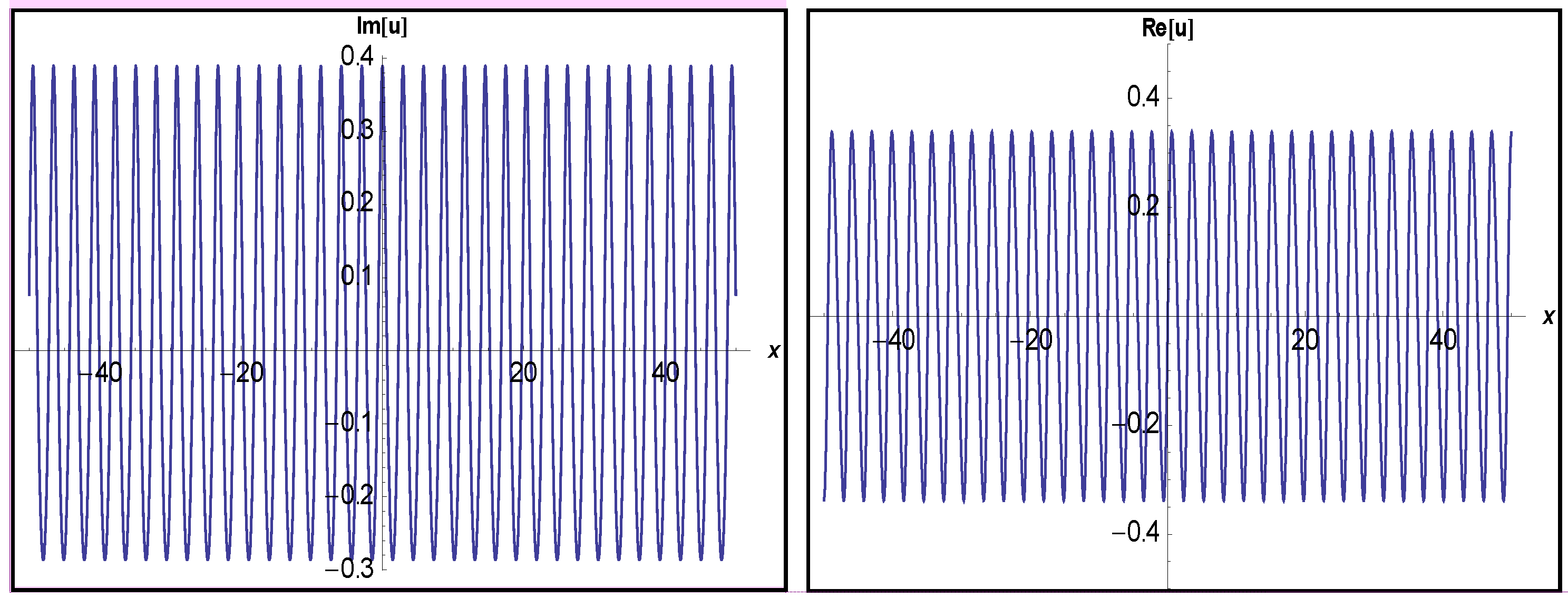
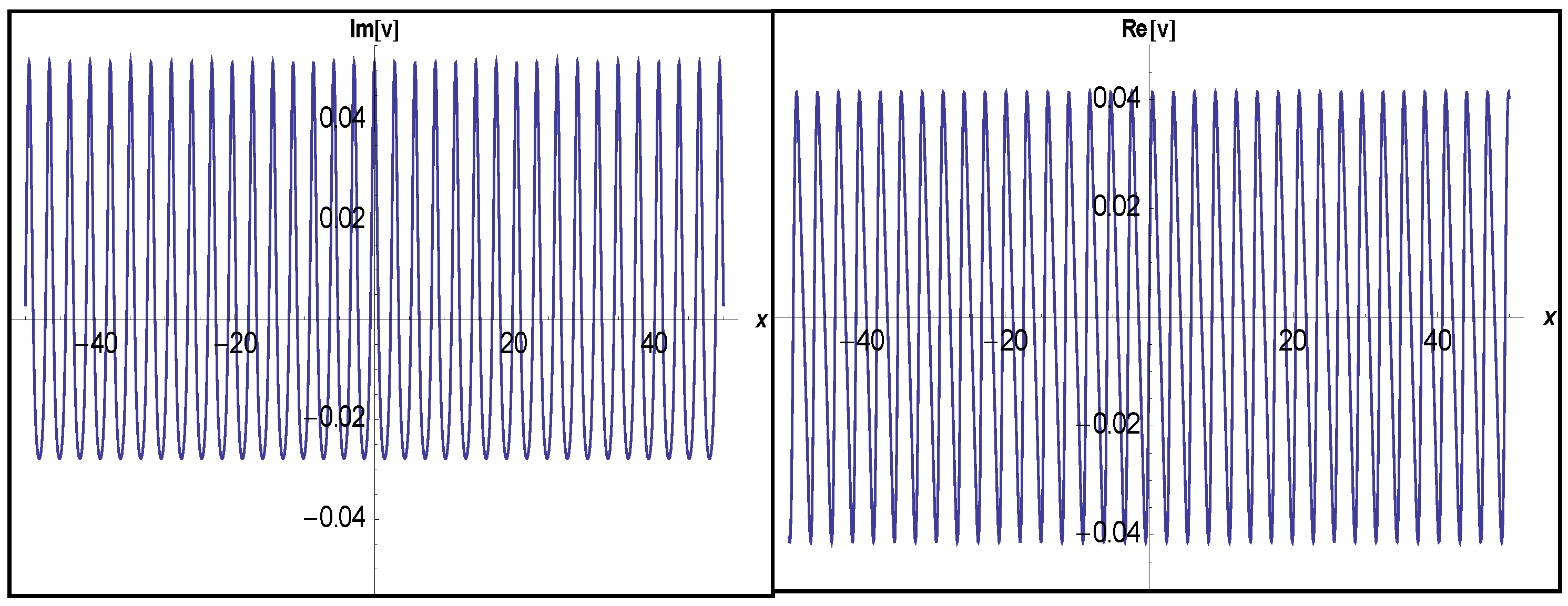
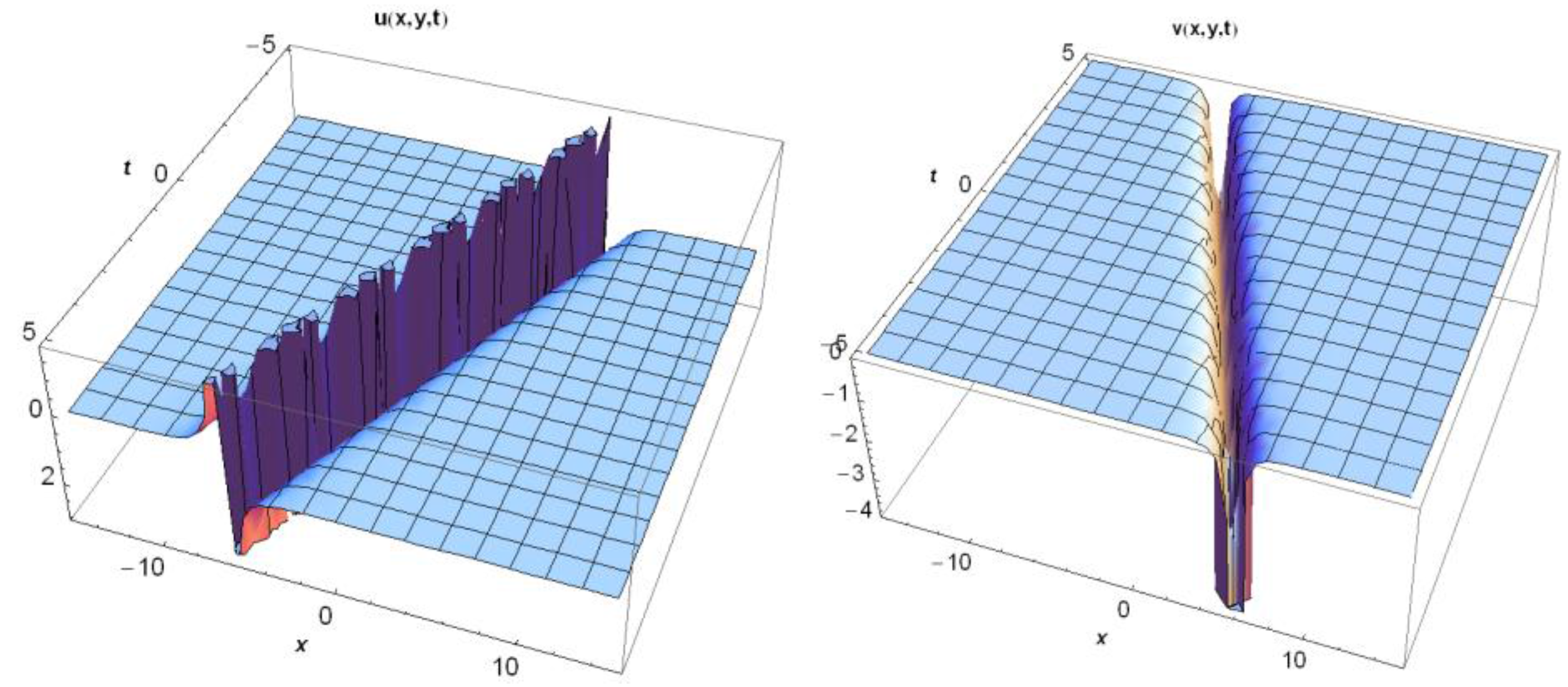
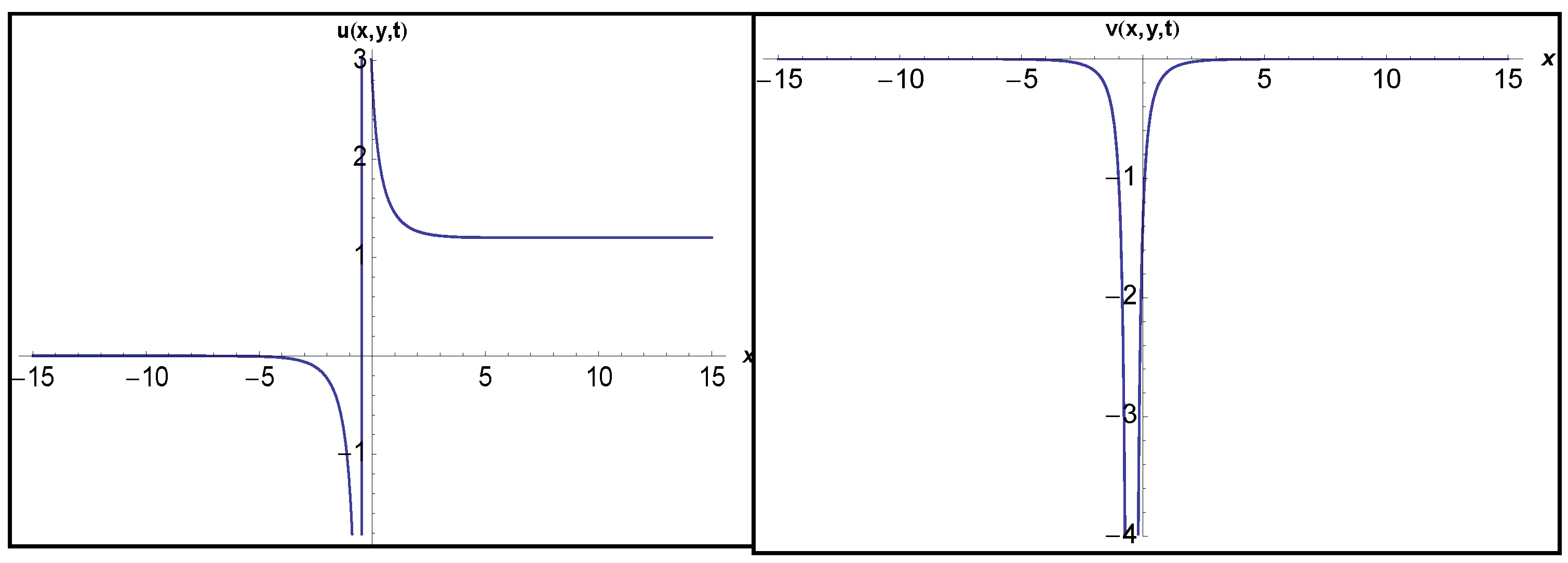
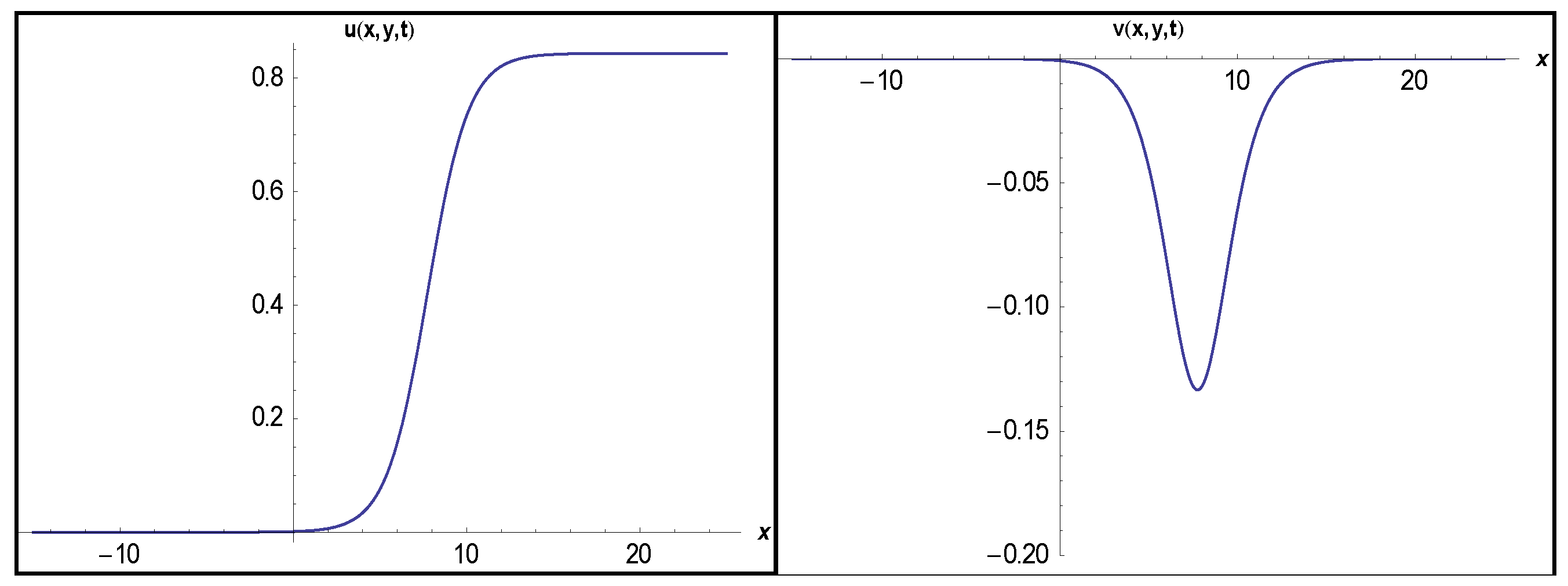
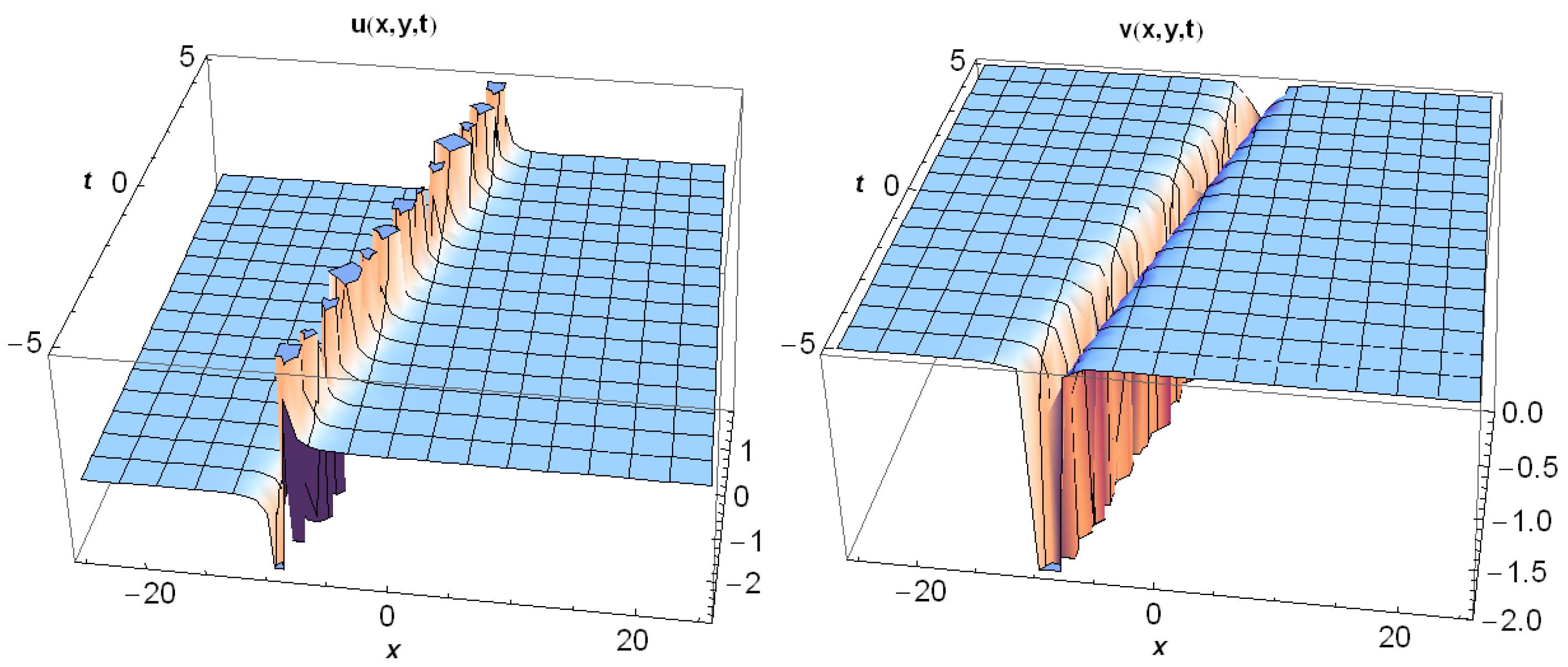
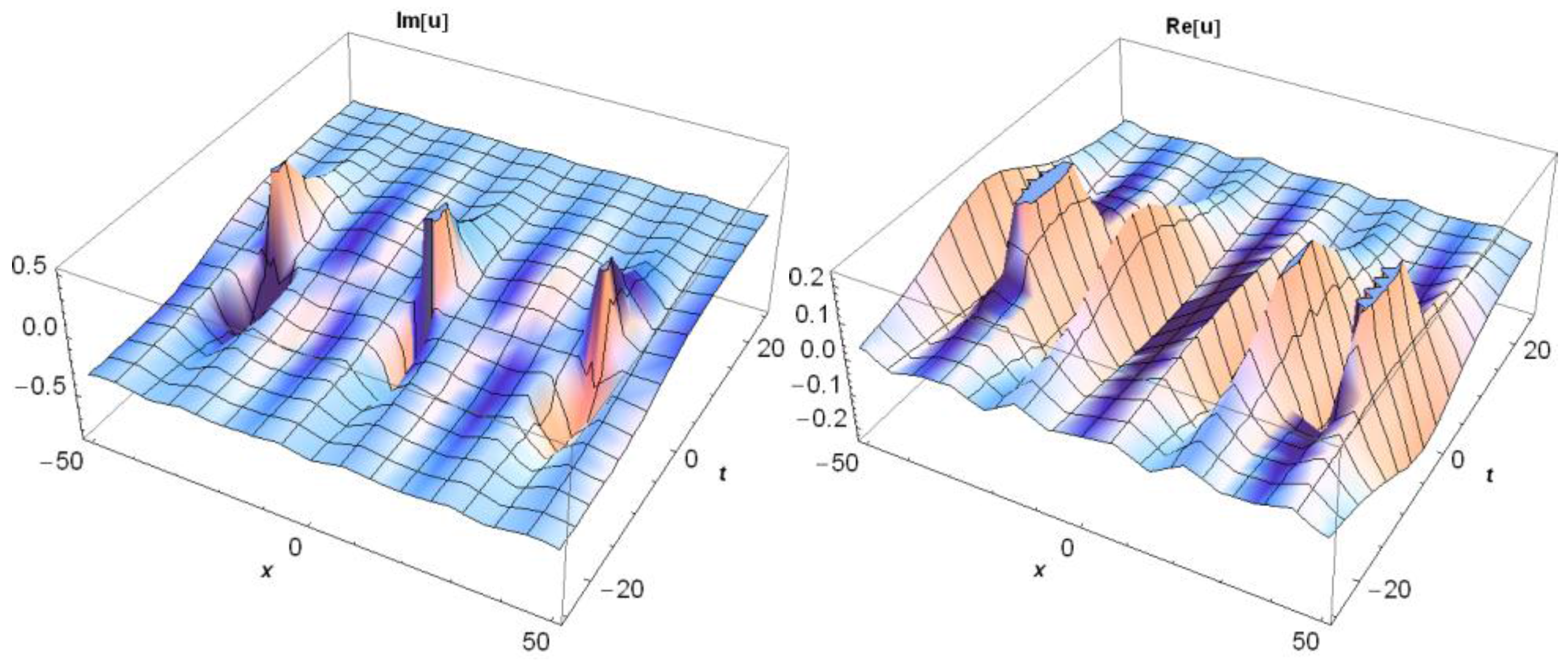
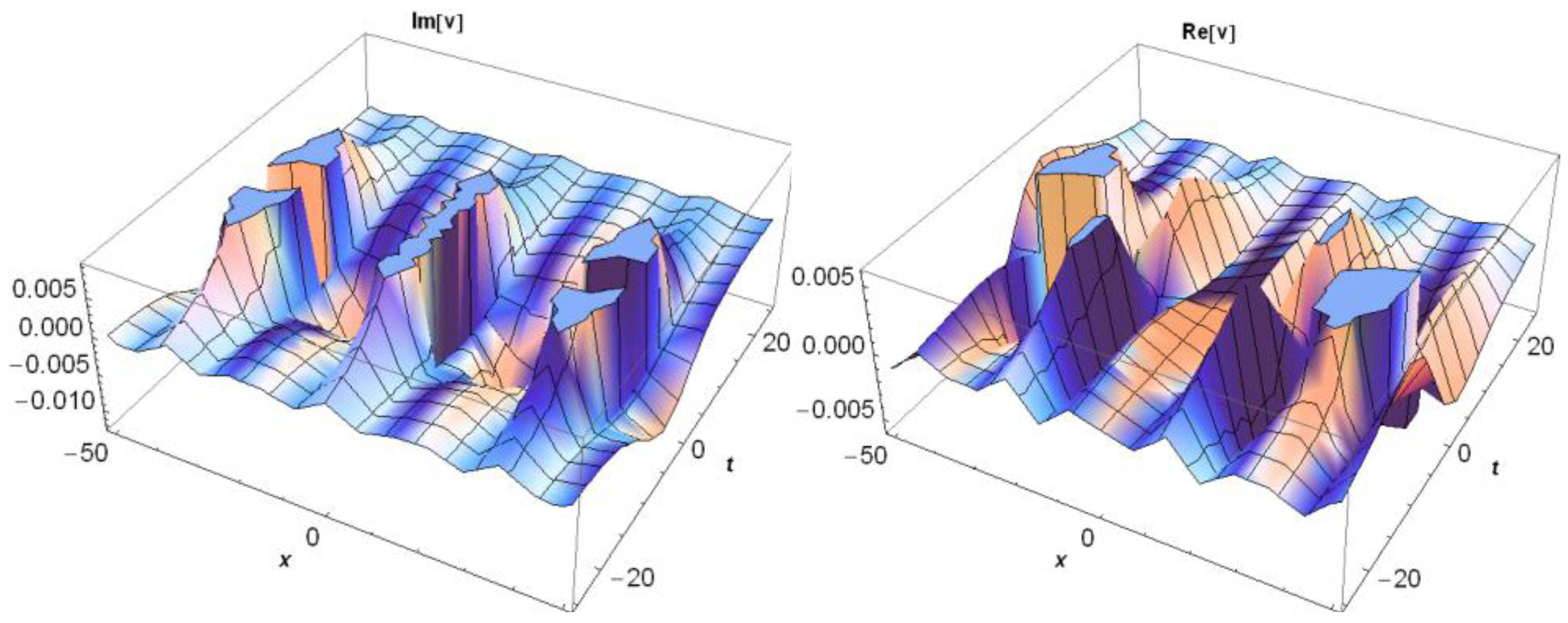
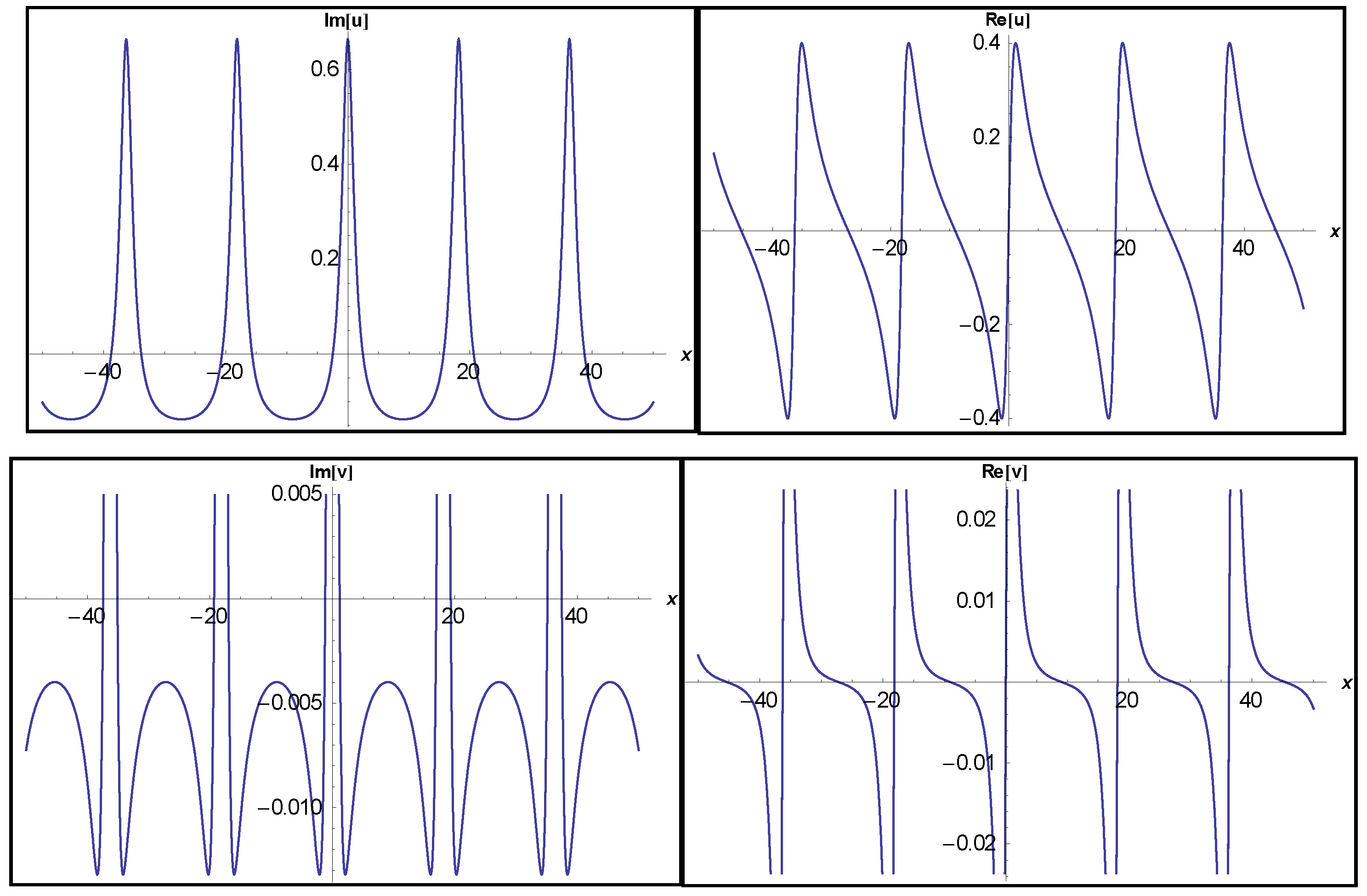
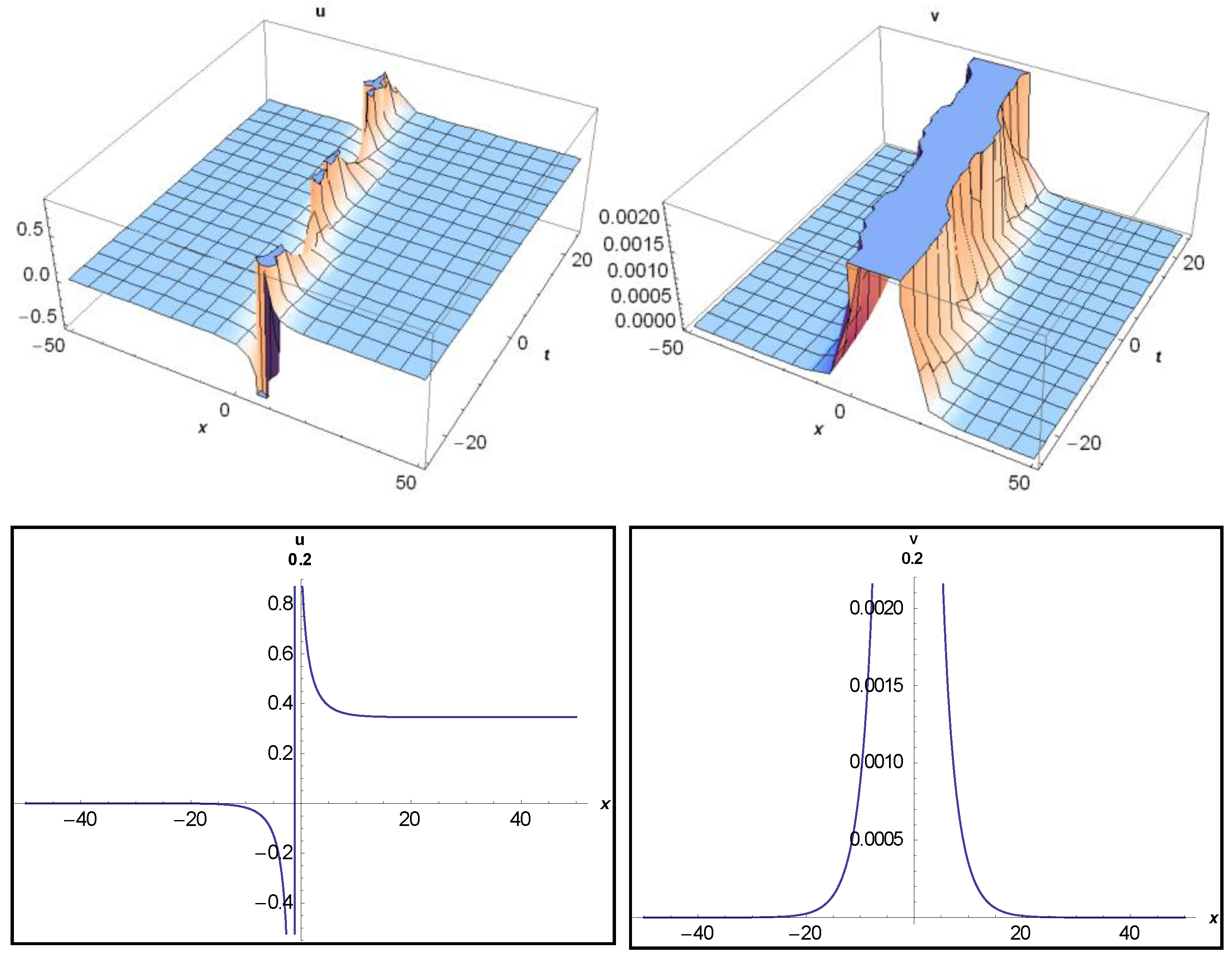
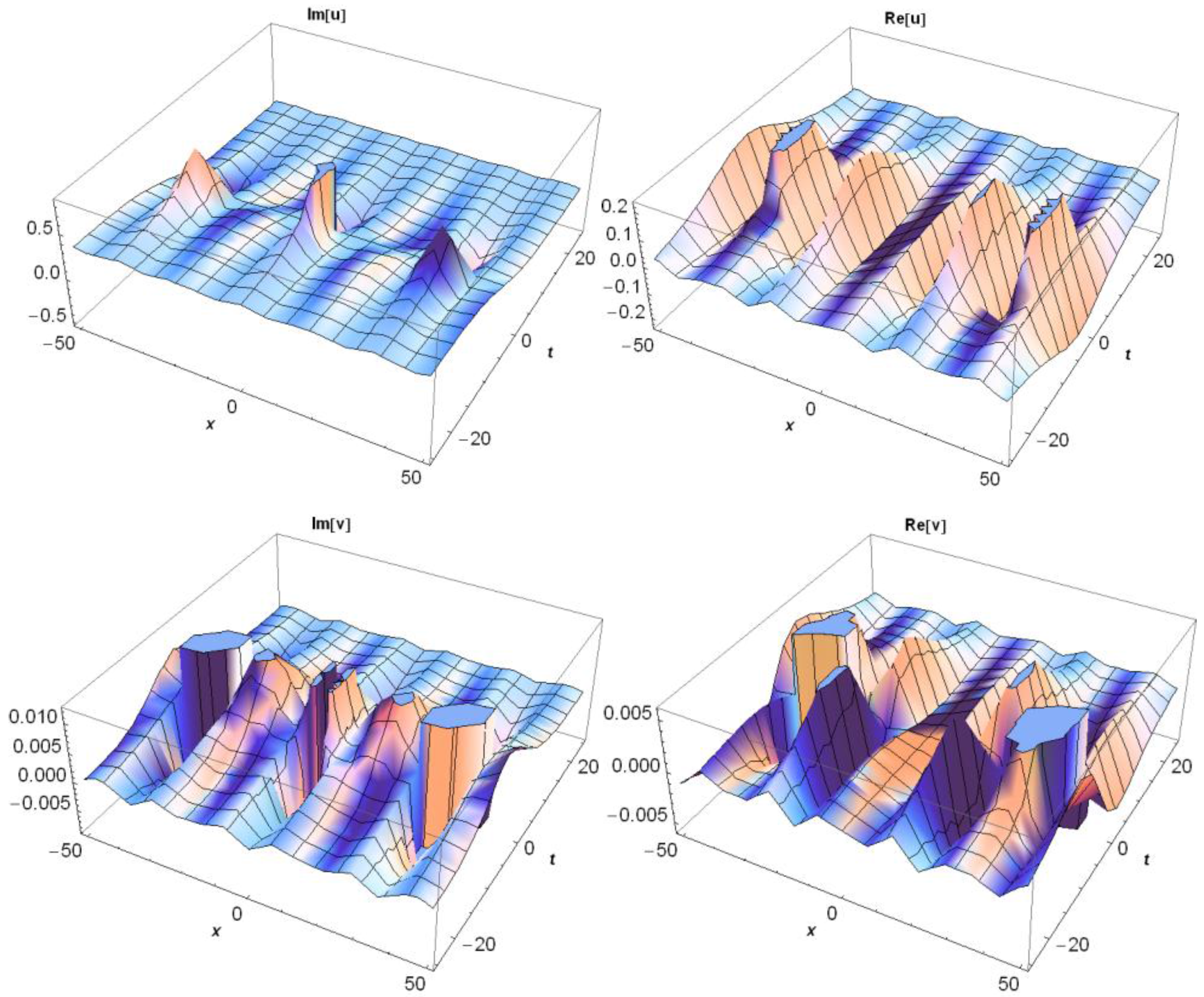
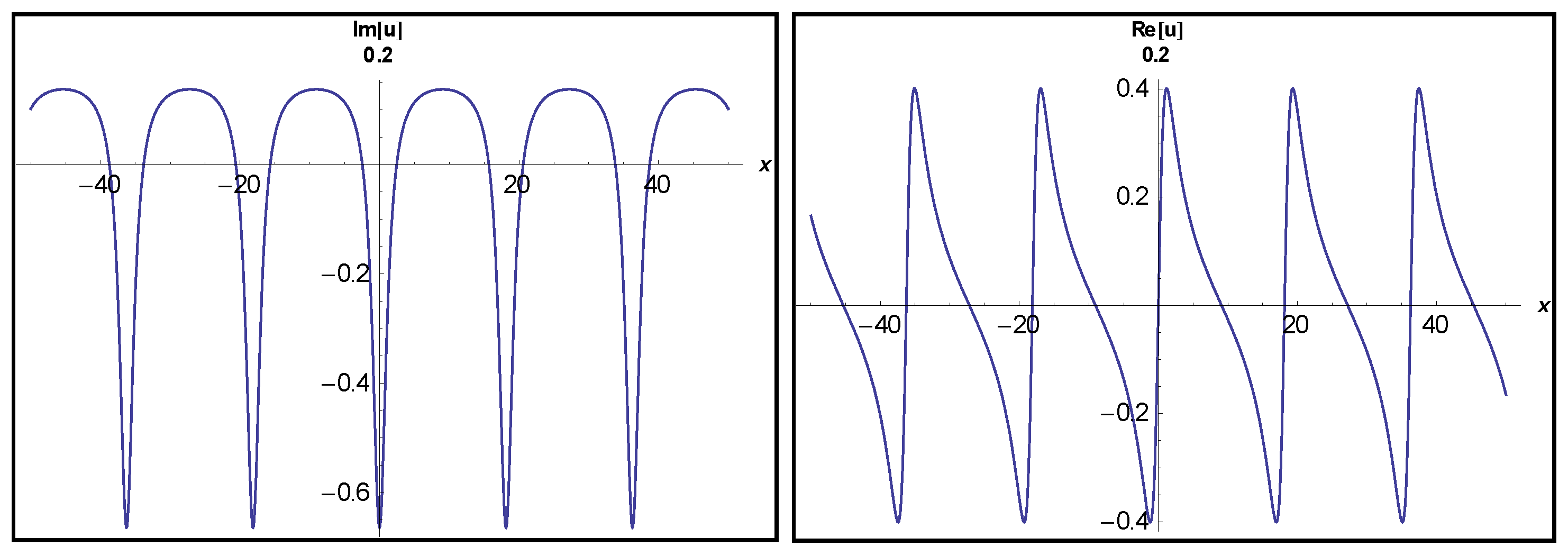
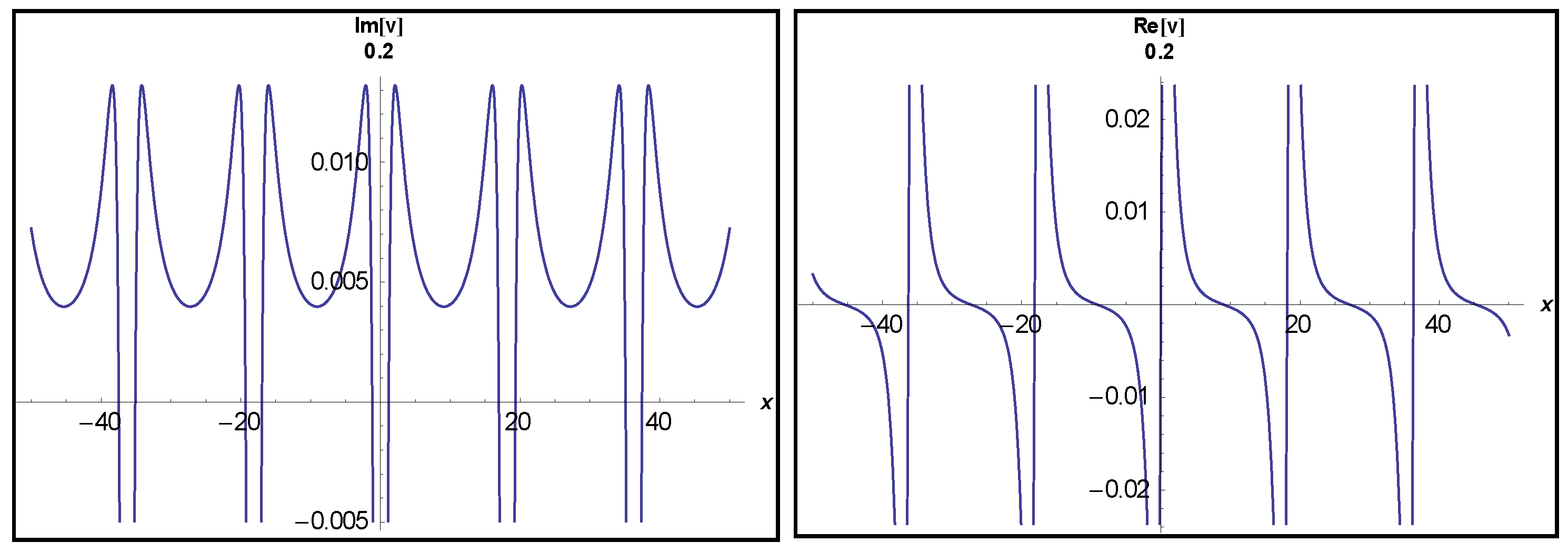
3.1. Application of MEFM
3.2. Application of IBSEFM
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cho, Y.-S.; Sohn, D.-H.; Oh Lee, S. Practical modified scheme of linear shallow-water equations for distant propagation of tsunamis. Ocean Eng. 2007, 34, 1769–1777. [Google Scholar] [CrossRef]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Dynamics of Dengue epidemics when using optimal control. Math. Comput. Model. 2010, 52, 1667–1673. [Google Scholar] [CrossRef] [Green Version]
- Silva, C.J.; Torres, D.F.M. Modeling TB-HIV syndemic and treatment. J. Appl. Math. 2014. [Google Scholar] [CrossRef]
- Mul, O.V.; Torres, D.F.M.; Kravchenko, V.P. Dynamics of controlled hybrid systems of aerial cable-ways. Nonlinear Anal. Hybrid Syst. 2008, 2, 431–440. [Google Scholar] [CrossRef]
- Qiu, Z. Dynamical behavior of a vector-host epidemic model with demographic structure. Comput. Math. Appl. 2008, 56, 3118–3129. [Google Scholar] [CrossRef]
- Zhang, T.; Gou, Q. Traveling Wave Solutions for Epidemic Cholera Model with Disease-Related Death. Sci. World J. 2014. [CrossRef] [PubMed]
- Mari, L.; Bertuzzo, E.; Righetto, L.; Casagrandi, R.; Gatto, M.; Rodriguez-Iturbe, I.; Rinaldo, A. Modelling cholera epidemics: The role of waterways, human mobility and sanitation. J. R. Soc. Interface 2012, 9, 376–388. [Google Scholar] [CrossRef] [PubMed]
- Bekir, A.; Güner, Ö.; Bilgil, H. Optical soliton solutions for the variable coefficient modified Kawahara equation. OptikInt. J. Light Electron Opt. 2015. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. On some new analytical solutions for the (2+1)-dimensional burgers equation and the special type of dodd-bullough- mikhailov equation. J. Appl. Anal. Comput. 2015, 5, 613–625. [Google Scholar]
- Baskonus, H.M.; Bulut, H. new hyperbolic function solutions for some nonlinear partial differential equation arising in mathematical physics. Entropy 2015, 17, 4255–4270. [Google Scholar] [CrossRef]
- Sakkaravarth, K.; Kanna, T.; Vijayajayanthi, M.; Lakshmanan, M. Multi component long-wave and short-wave resonance interaction system: Bright solitons, energy-sharing collisions, and resonant solitons. Phys. Rev. E 2014, 90. Article ID 052912. [Google Scholar]
- Zabolotskii, A.A. Inverse scattering transform for the Yajima-Oikawa equations with nonvanishing boundary conditions. Phys. Rev. A 2009, 80. [Google Scholar] [CrossRef]
- Khater, A.H.; Hassan, M.M.; Callebaut, D.K. Travelling wave solutions to some important equations of mathematical physics. Rep. Math. Phys. 2010, 66, 1–19. [Google Scholar] [CrossRef]
- Roshid, H.O.; Kabir, M.R.; Bhowmik, R.C.; Datta, B.K. Investigation of Solitary wave solutions for Vakhnenko-Parkes equation via exp-function and Exp-expansion method. SpringerPlus 2014. [Google Scholar] [CrossRef]
- Roshid, H.O.; Rahman, N.; Akbar, M.A. Traveling waves solutions of nonlinear Klein Gordon equation by extended-expasion method. Ann. Pure Appl. Math. 2013, 3, 10–16. [Google Scholar]
- Wazwaz, A.-M. Multiple soliton solutions and rational solutions for the (2+1)-dimensional dispersive long water–wave system. Ocean Eng. 2013, 60, 95–98. [Google Scholar] [CrossRef]
- Paquin, G.; Winternitz, P. Group theoretical analysis of dispersive long wave equations in two space dimensions. Physica D 1990, 46, 122–138. [Google Scholar] [CrossRef]
- Chun-Long, Z.; Jian-Ping, F.; Li-Qun, C. Localized excitations with and without propagating properties in (2+1)-dimensions obtained by a mapping approach. Chin. Phys. 2005, 14, 676–682. [Google Scholar] [CrossRef]
- Fei, J.-X.; Zheng, C.-L. Localized excitations in a dispersive long water–wave system via an extended projective approach. Z. Naturforschung A 2007, 62, 140–146. [Google Scholar] [CrossRef]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Travelling wave solutions for some important coupled nonlinear physical models via the coupled Higgs equation and the Maccari system. J. King Saud Univ. Sci. 2015, 27, 105–112. [Google Scholar] [CrossRef]
- Uddin, S.; Alam, N.; Hossain, S.M.S.; Samiu, H.; Akbar, M.A. Some new exact traveling wave solutions to the (3+1)-dimensional zakharov-kuznetsov equation and the burgers equations via exp -expansion method. Front. Math. Appl. 2014, 1, 1–8. [Google Scholar]
- Roshid, H.O.; Rahman, M.A. The exp(−Φ(η))-expansion method with application in the (1+1)-dimensional classical Boussinesq equations. Results Phys. 2014, 4, 150–155. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Zahran, E.H.M.; Khater, M.M.A. The exp(−ϕ(ξ))-Expansion Method and Its Application for Solving Nonlinear Evolution Equations Mahmoud. Int. J. Mod. Nonlinear Theory Appl. 2015, 4, 37–47. [Google Scholar] [CrossRef]
- Hafez, M.G.; Alam, M.N.; Akbar, M.A. Application of the exp(−Φ(η))-expansion Method to Find Exact Solutions for the Solitary Wave Equation in an Unmagnatized Dusty Plasma. World Appl. Sci. J. 2014, 32, 2150–2155. [Google Scholar]
- Zheng, B. Application of a generalized Bernoulli sub-ODE method for finding traveling solutions of some nonlinear equations. WSEAS Trans. Math. 2012, 7, 618–626. [Google Scholar]




© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulut, H.; Baskonus, H.M. New Complex Hyperbolic Function Solutions for the (2+1)-Dimensional Dispersive Long Water–Wave System. Math. Comput. Appl. 2016, 21, 6. https://doi.org/10.3390/mca21020006
Bulut H, Baskonus HM. New Complex Hyperbolic Function Solutions for the (2+1)-Dimensional Dispersive Long Water–Wave System. Mathematical and Computational Applications. 2016; 21(2):6. https://doi.org/10.3390/mca21020006
Chicago/Turabian StyleBulut, Hasan, and Haci Mehmet Baskonus. 2016. "New Complex Hyperbolic Function Solutions for the (2+1)-Dimensional Dispersive Long Water–Wave System" Mathematical and Computational Applications 21, no. 2: 6. https://doi.org/10.3390/mca21020006





