Nonlinear Vibration of a Nanobeam on a Pasternak Elastic Foundation Based on Non-Local Euler-Bernoulli Beam Theory
Abstract
:1. Introduction
2. Governing Equations
2.1. Non-Local Effects
2.2. Nonlocal Euler-Bernoulli Beam
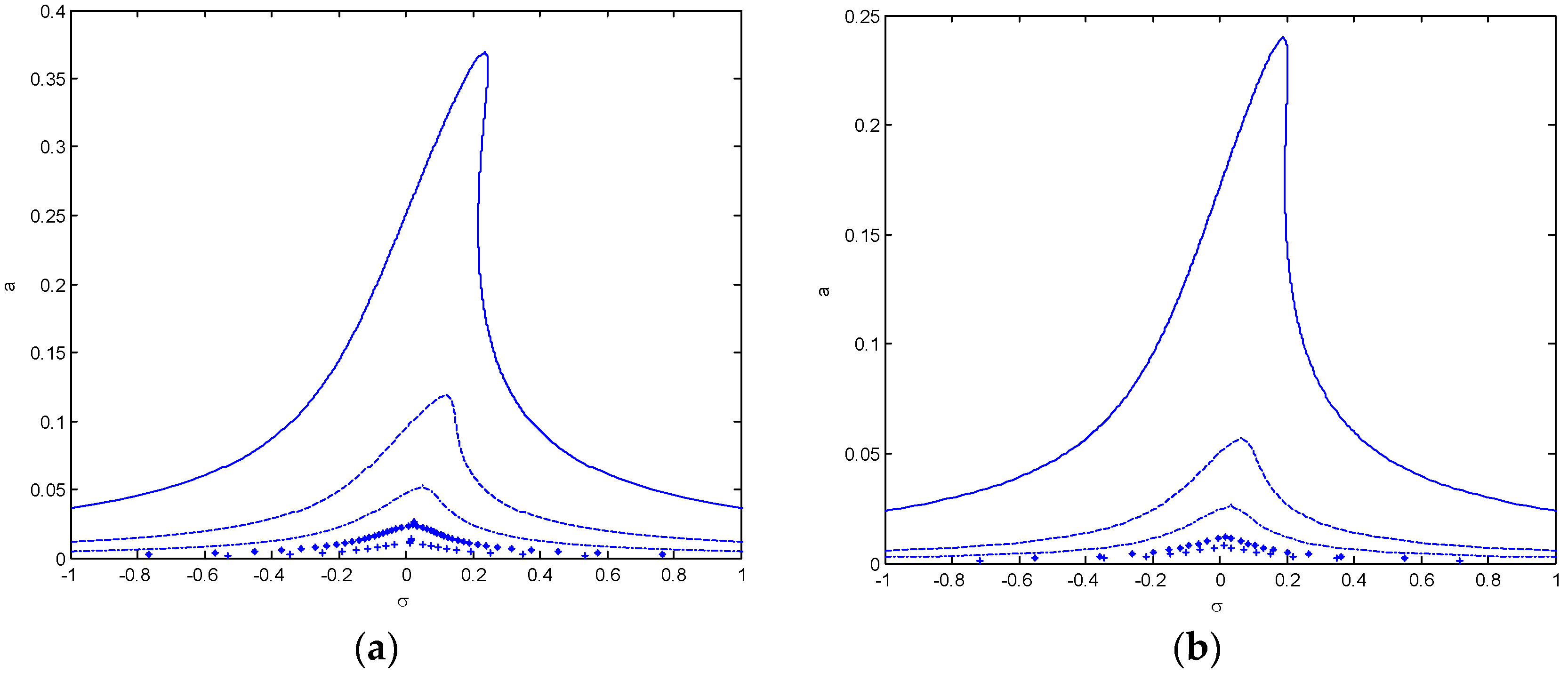
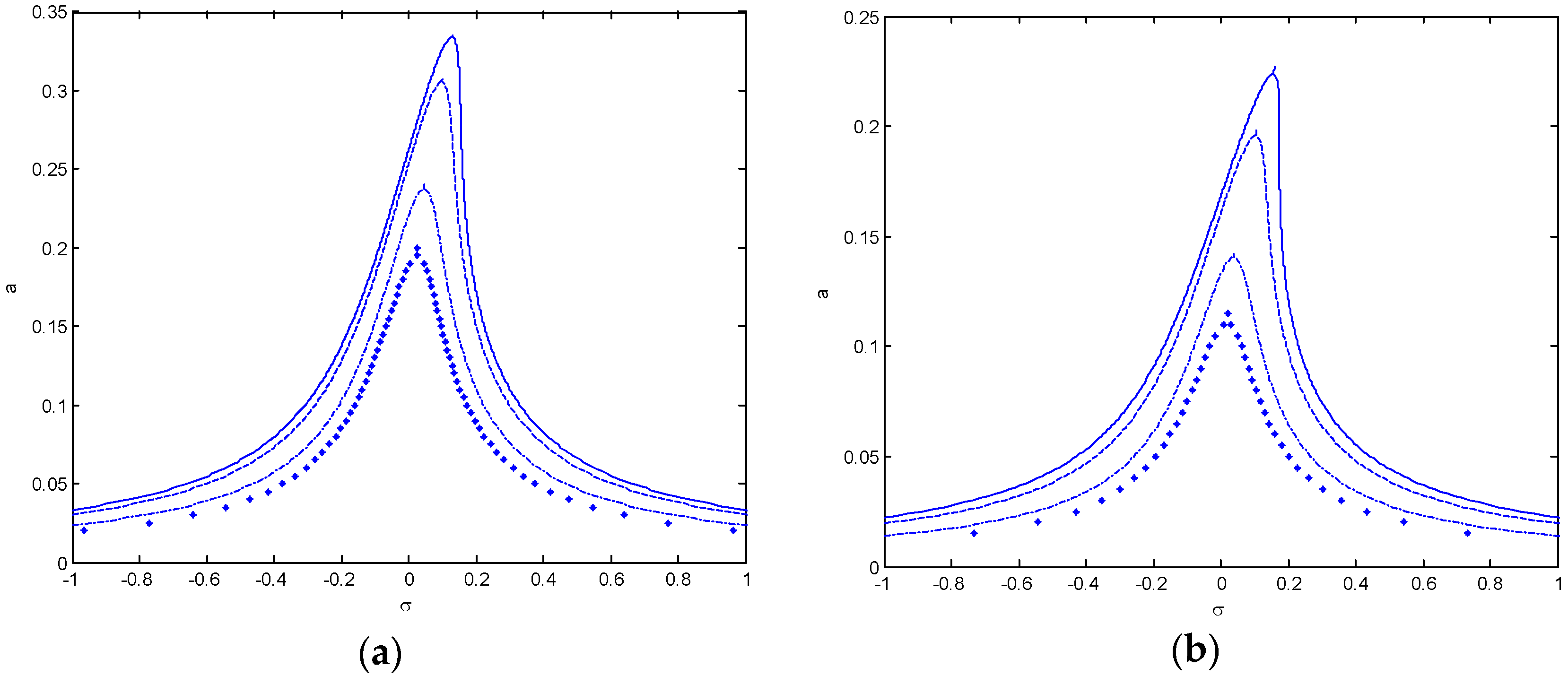
3. Numerical Results
4. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| CNT | Carbon Nanotube |
| SWCNT | Single walled carbon nanotube |
| DWCNT | Double walled carbon nanotube |
| MWCNT | Multi walled carbon nanotube |
References
- Eringen, A.C. On differential-equations of nonlocal elasticity and solutions of screw dislocation and surface-waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Niknam, H.; Aghdam, M.M. A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation. Compos. Struct. 2015, 119, 452–462. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. Eur. J. Mech. A Solids 2011, 30, 571–583. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Compos. B Eng. 2012, 43, 1523–1530. [Google Scholar] [CrossRef]
- Kanani, A.S.; Niknam, H.; Ohadi, A.R.; Aghdam, M.M. Effect of nonlinear elastic foundation on large amplitude free and forced vibration of functionally graded beam. Compos. Struct. 2014, 115, 60–68. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlinear static and free vibration analysis of microbeams based based on the nonlinear elastic foundation using modified couple stress theory and He’s variational method. Compos. Struct. 2014, 112, 264–272. [Google Scholar] [CrossRef]
- Mustapha, K.B.; Zhong, Z.W. Free transverse vibration of an axially loaded non-prismatic single-walled carbon nanotube embedded in a two-parameter elastic medium. Comput. Mater. Sci. 2010, 50, 742–751. [Google Scholar] [CrossRef]
- Mehdipour, I.; Barari, A.; Kimiaeifar, A.; Domairry, G. Vibrational analysis of curved single-walled carbon nanotube on a Pasternak elastic foundation. Adv. Eng. Softw. 2012, 48, 1–5. [Google Scholar] [CrossRef]
- Shen, H.S.; Zhang, C.L. Nonlocal beam model for nonlinear analysis of carbon nanotubes on elastomeric substrates. Comput. Mater. Sci. 2011, 50, 1022–1029. [Google Scholar] [CrossRef]
- Arani, A.G.; Atabakhshian, V.; Loghman, A.; Shajari, A.R.; Amir, S. Nonlinear vibration of embedded SWBNNTs based on nonlocal Timoshenko beam theory using DQ method. Physica B 2012, 407, 2549–2555. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Physica E 2009, 41, 1232–1239. [Google Scholar] [CrossRef]
- Yas, M.H.; Samadi, N. Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation. Int. J. Press. Vessels Pip. 2012, 98, 119–128. [Google Scholar] [CrossRef]
- Kazemi-Lari, M.A.; Fazelzadeh, S.A.; Ghavanloo, E. Non-conservative instability of cantilever carbon nanotubes resting on viscoelastic foundation. Physica E 2012, 44, 1623–1630. [Google Scholar] [CrossRef]
- Ghanvanloo, E.; Daneshmand, F.; Rafiei, M. Vibration and instability analysis of carbon nanotubes conveying fluid and resting on a linear viscoelastic Winkler foundation. Physica E 2010, 42, 2218–2224. [Google Scholar] [CrossRef]
- Rafiei, M.; Mohebpour, S.R.; Daneshmand, F. Small-scale effect on the vibration of non-uniform carbon nanotubes conveying fluid and embedded in viscoelastic medium. Physica E 2012, 44, 1372–1379. [Google Scholar] [CrossRef]
- Arani, A.G.; Amir, S. Electro-thermal vibration of visco-elastically coupled BNNT systems conveying fluid embedded on elastic foundation via strain gradient theory. Physica B 2013, 419, 1–6. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Li, F.M. Nonlinear free vibration of nanotube with small scale effects embedded in viscous matrix. Mech. Res. Commun. 2014, 60, 45–51. [Google Scholar] [CrossRef]
- Mahdavi, M.H.; Jiang, L.Y.; Sun, X. Nonlinear vibration of a double-walled carbon nanotube embedded in a polymer matrix. Physica E 2011, 43, 1813–1819. [Google Scholar] [CrossRef]
- Lee, H.L.; Chang, W.J. Vibration analysis of a viscous-fluid-conveying single-walled carbon nanotube embedded in an elastic medium. Physica E 2009, 41, 529–532. [Google Scholar] [CrossRef]
- Kiani, K. Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subject to axial load using nonlocal shear deformable beam theories. Int. J. Mech. Sci. 2013, 68, 16–34. [Google Scholar] [CrossRef]
- Aydogdu, M. Axial vibration analysis of nanorods (carbon nanotubes) embedded in an elastic medium using nonlocal elasticity. Mech. Res. Commun. 2012, 43, 34–40. [Google Scholar] [CrossRef]
- Wang, B.L.; Wang, K.F. Vibration analysis of embedded nanotubes using nonlocal continuum theory. Compos. B Eng. 2013, 47, 96–101. [Google Scholar] [CrossRef]
- Ke, L.L.; Xiang, Y.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comput. Mater. Sci. 2009, 47, 409–417. [Google Scholar] [CrossRef]
- Fang, B.; Zhen, Y.X.; Zhang, C.P.; Tang, Y. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Appl. Math. Model. 2013, 37, 1096–1107. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlocal effects in the forced vibration of an elastically connected double-carbon nanotube system under a moving nanoparticle. Comput. Mater. Sci. 2011, 50, 2112–2123. [Google Scholar] [CrossRef]
- Ansari, R.; Ramezannezhad, H. Nonlocal Timoshenko beam model for the large-amplitude vibrations of embedded multiwalled carbon nanotubes including thermal effects. Physica E 2011, 43, 1171–1178. [Google Scholar] [CrossRef]
- Ansari, R.; Ramezannezhad, H.; Gholami, R. Nonlocal beam theory for nonlinear vibrations of embedded multiwalled carbon nanotubes in thermal environment. Nonlinear Dyn. 2012, 67, 2241–2254. [Google Scholar] [CrossRef]
- Kiani, K. A meshless approach for free transverse vibration of embedded single walled nanotubes with arbitrary boundary conditions accounting for nonlocal effect. Int. J. Mech. Sci. 2010, 52, 1343–1356. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Thermo-mechanical vibration of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Comput. Mater. Sci. 2009, 46, 854–859. [Google Scholar] [CrossRef]
- Chang, T.P. Thermal–mechanical vibration and instability of a fluid-conveying single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Appl. Math. Model. 2012, 36, 1964–1973. [Google Scholar] [CrossRef]
- Rahmati, A.H.; Mohammadimehr, M. Vibration analysis of non-uniform and non-homogeneous boron nitride nanorods embedded in elastic medium under combined loadings using DQM. Physica B 2014, 440, 88–98. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Reddy, G.K. Buckling analysis of single walled carbon nanotube on Winkler foundation using on nonlocal elasticity theory and DTM. Comput. Mater. Sci. 2011, 50, 1052–1056. [Google Scholar] [CrossRef]
- Narender, S.; Gopalakrishnan, S. Critical buckling temperature of single walled carbon nanotubes embedded in a one-parameter elastic medium based on nonlocal continuum mechanics. Physica E 2011, 43, 1185–1191. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Thermal effects on the stability of embedded carbon nanotubes. Comput. Mater. Sci. 2010, 47, 721–726. [Google Scholar] [CrossRef]
- Arani, A.G.; Amir, S.; Shajari, A.R.; Mozdianfard, M.R.; Maraghi, Z.K.; Mohammadimehr, M. Electro-thermal nonlocal vibration analysis of embedded DWBNNTs. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2011, 224, 745–756. [Google Scholar] [CrossRef]
- Mikhasev, G. On localized modes of free vibrations of single walled carbon nanotubes embedded in nonhomogeneous elastic medium. ZAMM 2014, 94, 130–141. [Google Scholar] [CrossRef]
- Fu, Y.M.; Hong, J.W.; Wang, X.Q. Analysis of nonlinear vibration for embedded carbon nanotubes. J. Sound Vib. 2006, 296, 746–756. [Google Scholar] [CrossRef]
- Komijani, M.; Esfahani, S.E.; Reddy, J.N.; Liu, Y.P.; Eslami, M.R. Nonlinear thermal stability and vibration of pre/post-buckled temperature and microstructure dependent functionally graded beams resting on elastic foundation. Compos. Struct. 2014, 112, 292–307. [Google Scholar] [CrossRef]
- Ozturk, B.; Coskun, S.B.; Koc, M.Z.; Atay, M.T. Homotopy perturbation method for free vibration analysis of beams on elastic foundation. IOP Conf. Ser. Mater. Sci. Eng. 2010, 10, 012158. [Google Scholar] [CrossRef]
- Öz, H.R.; Pakdemirli, M.; Özkaya, E.; Yılmaz, M. Nonlinear vibrations of a slightly curved beam resting on a nonlinear elastic foundation. J. Sound Vib. 1998, 212, 295–309. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, W.; Zhang, L. Applied multiscale method to analysis of nonlinear vibration for double walled carbon nanotubes. Appl. Math. Model. 2011, 35, 2279–2289. [Google Scholar] [CrossRef]
- Bağdatlı, S.M. Non-linear vibration of nanobeams with various boundary condition based on nonlocal elasticity theory. Compos. B Eng. 2015, 80, 43–52. [Google Scholar] [CrossRef]
- Bağdatlı, S.M. Non-linear transverse vibrations of tensioned nanobeams using nonlocal beam theory. Struct. Eng. Mech. 2015, 55, 281–298. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Techniques; John Wiley: New York, NY, USA, 1981. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Yokoyama, T. Vibrations and transient responses of Timoshenko beams resting on elastic foundations. Arch. Appl. Mech. 1987, 57, 81–90. [Google Scholar] [CrossRef]
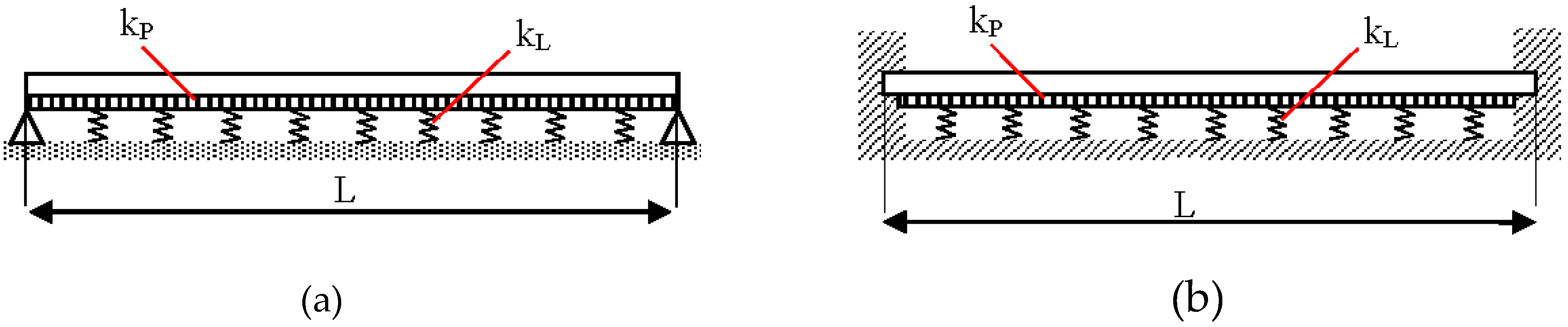

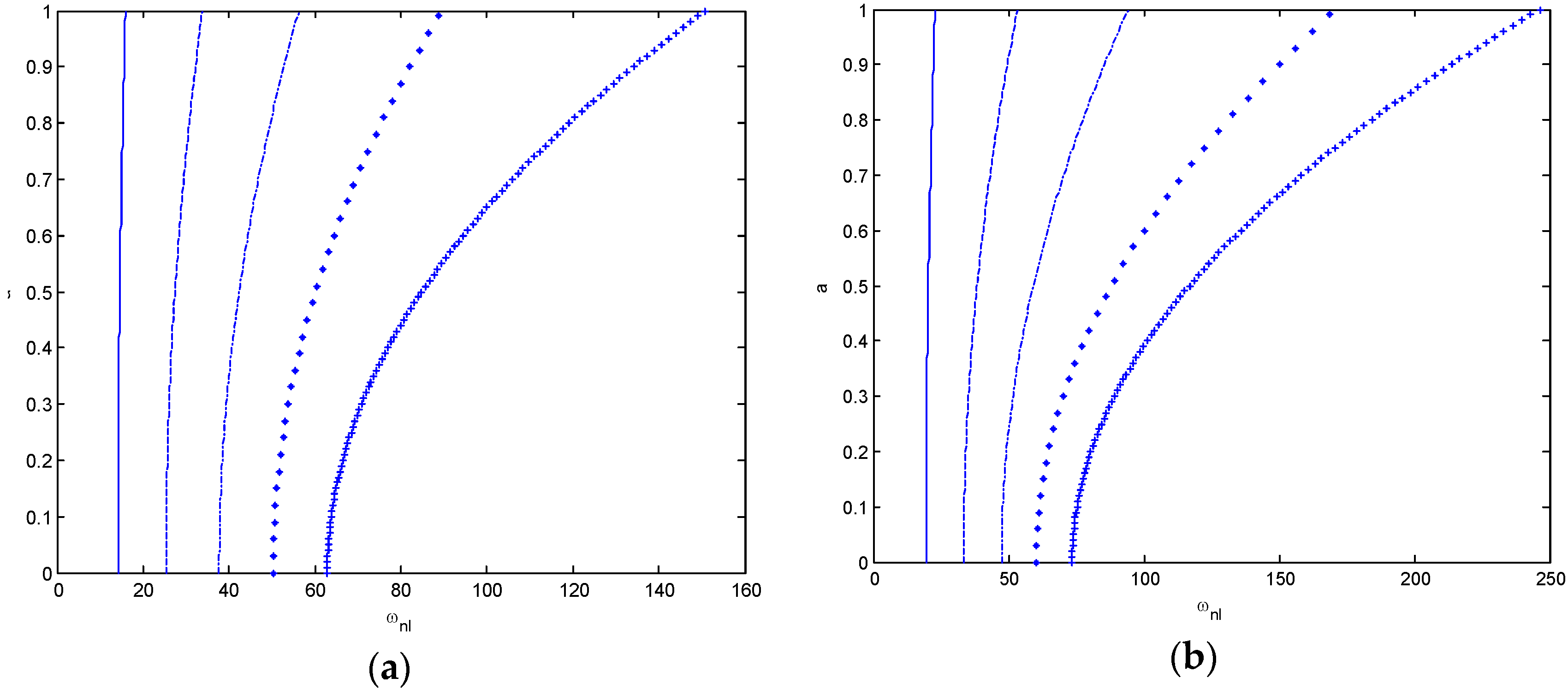
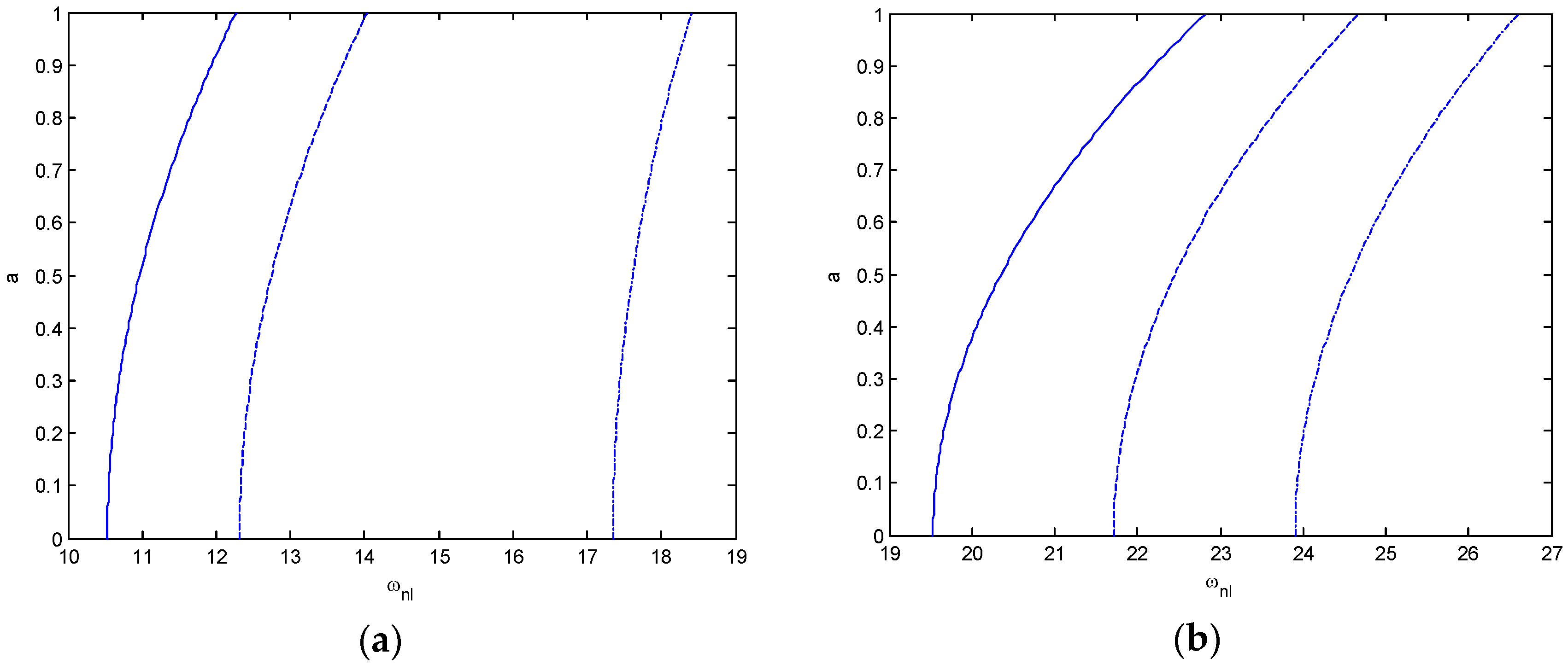
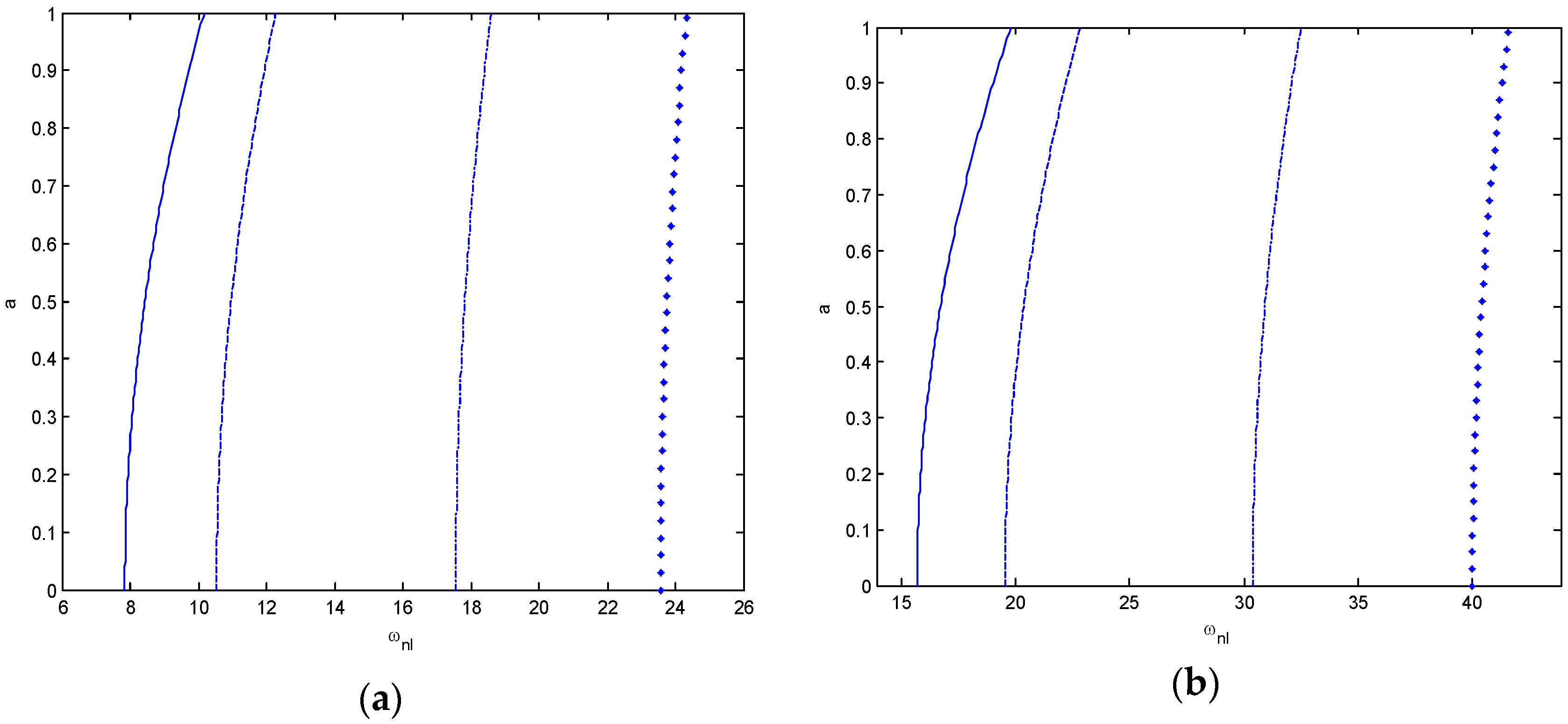



| KL | KP | γ | ω1 | ω2 | ω3 | ω4 | ω5 | λ |
|---|---|---|---|---|---|---|---|---|
| 10 | 0 | 0 | 10.3638 | 39.6049 | 88.8827 | 157.945 | 246.76 | 1.76231 |
| 0.1 | 9.93271 | 33.5769 | 64.7187 | 98.38 | 132.544 | 1.83879 | ||
| 0.2 | 8.93522 | 24.7849 | 41.7484 | 58.4659 | 74.9066 | 2.04407 | ||
| 0.3 | 7.84771 | 18.7699 | 29.7864 | 40.611 | 51.3169 | 2.32733 | ||
| 0.4 | 6.91145 | 14.9337 | 22.9928 | 30.9739 | 38.9105 | 2.6426 | ||
| 0.5 | 6.17194 | 12.3849 | 18.7082 | 25.021 | 31.3244 | 2.95923 | ||
| 5 | 0 | 12.5203 | 42.0231 | 91.347 | 160.425 | 249.248 | 1.45877 | |
| 0.1 | 12.1658 | 36.3978 | 68.0635 | 102.314 | 137.119 | 1.50127 | ||
| 0.2 | 11.366 | 28.49 | 46.7661 | 64.8678 | 82.7327 | 1.60692 | ||
| 0.3 | 10.5325 | 23.4457 | 36.4878 | 49.3844 | 62.1862 | 1.73408 | ||
| 0.4 | 9.85475 | 20.5039 | 31.1898 | 41.8205 | 52.4188 | 1.85334 | ||
| 0.5 | 9.35098 | 18.7291 | 28.1803 | 37.6247 | 47.0629 | 1.95319 | ||
| 25 | 0 | 18.8189 | 50.552 | 100.602 | 169.984 | 258.958 | 0.97052 | |
| 0.1 | 18.5849 | 45.9823 | 80.0573 | 116.732 | 154.067 | 0.98274 | ||
| 0.2 | 18.0715 | 40.0156 | 62.9571 | 85.826 | 108.533 | 1.01066 | ||
| 0.3 | 17.5592 | 36.596 | 55.7485 | 74.8137 | 93.8186 | 1.04015 | ||
| 0.4 | 17.1612 | 34.7847 | 52.4341 | 70.0516 | 87.65 | 1.06427 | ||
| 0.5 | 16.877 | 33.769 | 50.7016 | 67.6306 | 84.556 | 1.08219 | ||
| 50 | 0 | 24.513 | 59.5186 | 111.092 | 181.225 | 270.606 | 0.74508 | |
| 0.1 | 24.3339 | 55.6896 | 92.8969 | 132.568 | 172.931 | 0.75057 | ||
| 0.2 | 23.9441 | 50.8745 | 78.64 | 106.367 | 133.97 | 0.76279 | ||
| 0.3 | 23.5599 | 48.231 | 72.9969 | 97.6982 | 122.354 | 0.77522 | ||
| 0.4 | 23.2647 | 46.8715 | 70.4982 | 94.1014 | 117.69 | 0.78506 | ||
| 0.5 | 23.0559 | 46.1227 | 69.2193 | 92.3132 | 115.405 | 0.79217 | ||
| 100 | 0 | 0 | 14.0502 | 40.7252 | 89.3876 | 158.23 | 246.943 | 1.29992 |
| 0.1 | 13.7353 | 34.8914 | 65.4103 | 98.8364 | 132.883 | 1.32973 | ||
| 0.2 | 13.0322 | 26.5385 | 42.8127 | 59.2306 | 75.505 | 1.40147 | ||
| 0.3 | 12.312 | 21.0311 | 31.2607 | 41.7044 | 52.1864 | 1.48345 | ||
| 0.4 | 11.7375 | 17.6923 | 24.8731 | 32.3942 | 40.0503 | 1.55606 | ||
| 0.5 | 11.3178 | 15.6008 | 20.9761 | 26.7591 | 38.7995 | 1.61376 | ||
| 5 | 0 | 15.7085 | 43.0806 | 91.8383 | 160.706 | 249.428 | 1.1627 | |
| 0.1 | 15.4275 | 37.6139 | 68.7215 | 102.753 | 137.447 | 1.18387 | ||
| 0.2 | 14.8049 | 30.028 | 47.7186 | 65.5579 | 83.2749 | 1.23366 | ||
| 0.3 | 14.1751 | 25.2923 | 37.701 | 50.2874 | 62.9056 | 1.28847 | ||
| 0.4 | 13.679 | 22.5922 | 32.6007 | 42.883 | 53.2703 | 1.3352 | ||
| 0.5 | 13.3207 | 20.9947 | 29.7343 | 38.8023 | 48.0095 | 1.37111 | ||
| 25 | 0 | 21.0748 | 51.4345 | 101.048 | 170.249 | 259.132 | 0.86664 | |
| 0.1 | 20.8662 | 46.9507 | 80.6175 | 117.117 | 154.358 | 0.8753 | ||
| 0.2 | 20.4102 | 41.1248 | 63.6678 | 86.3487 | 108.947 | 0.89486 | ||
| 0.3 | 19.9581 | 37.8057 | 56.5499 | 75.4128 | 94.297 | 0.91513 | ||
| 0.4 | 19.6089 | 36.0552 | 53.2854 | 70.6911 | 88.162 | 0.93142 | ||
| 0.5 | 19.3606 | 35.0763 | 51.5815 | 68.2927 | 85.0865 | 0.94337 | ||
| 50 | 0 | 26.2848 | 60.2699 | 111.496 | 181.473 | 270.772 | 0.69486 | |
| 0.1 | 26.1178 | 56.4919 | 93.3801 | 132.907 | 173.191 | 0.6993 | ||
| 0.2 | 25.755 | 51.7514 | 79.2102 | 106.789 | 134.306 | 0.70915 | ||
| 0.3 | 25.3982 | 49.1551 | 73.6108 | 98.1577 | 122.721 | 0.71911 | ||
| 0.4 | 25.1247 | 47.8219 | 71.1336 | 94.5784 | 118.072 | 0.72694 | ||
| 0.5 | 24.9314 | 47.0883 | 69.8664 | 92.7994 | 115.794 | 0.73258 | ||
| 200 | 0 | 0 | 17.2456 | 41.935 | 89.9452 | 158.546 | 247.145 | 1.05906 |
| 0.1 | 16.99 | 36.2961 | 66.1703 | 99.341 | 133.259 | 1.075 | ||
| 0.2 | 16.4267 | 28.36 | 43.9651 | 60.0688 | 76.1643 | 1.11186 | ||
| 0.3 | 15.8615 | 23.2875 | 32.8212 | 42.8865 | 53.1359 | 1.15148 | ||
| 0.4 | 15.4197 | 20.3228 | 26.808 | 33.9026 | 41.2799 | 1.18447 | ||
| 0.5 | 15.1027 | 18.5307 | 23.2378 | 28.5666 | 34.223 | 1.20933 | ||
| 5 | 0 | 18.6214 | 44.226 | 92.3811 | 161.016 | 249.628 | 0.98082 | |
| 0.1 | 18.385 | 38.9205 | 69.4453 | 103.239 | 137.81 | 0.99343 | ||
| 0.2 | 17.8658 | 31.6494 | 48.7551 | 66.3162 | 83.8731 | 1.0223 | ||
| 0.3 | 17.3475 | 27.1974 | 39.0046 | 51.2721 | 63.6955 | 1.05284 | ||
| 0.4 | 16.9445 | 24.7064 | 34.0999 | 44.0335 | 54.2008 | 1.07788 | ||
| 0.5 | 16.6566 | 23.2546 | 31.3708 | 40.0702 | 49.0399 | 1.09651 | ||
| 25 | 0 | 23.327 | 52.3976 | 101.542 | 170.542 | 259.324 | 0.78296 | |
| 0.1 | 23.1387 | 48.0039 | 81.2353 | 117.544 | 154.682 | 0.78934 | ||
| 0.2 | 22.7284 | 42.3232 | 64.4484 | 86.9259 | 109.405 | 0.80359 | ||
| 0.3 | 22.3232 | 39.1059 | 57.4273 | 76.073 | 94.8257 | 0.81817 | ||
| 0.4 | 22.0115 | 37.4163 | 54.2156 | 71.3949 | 88.7273 | 0.82976 | ||
| 0.5 | 21.7907 | 36.4739 | 52.5419 | 69.021 | 85.6722 | 0.83817 | ||
| 50 | 0 | 28.1228 | 61.0939 | 111.944 | 181.748 | 270.957 | 0.64944 | |
| 0.1 | 27.9667 | 57.3701 | 93.914 | 133.283 | 173.479 | 0.65307 | ||
| 0.2 | 27.6282 | 52.7087 | 79.8389 | 107.256 | 134.677 | 0.66107 | ||
| 0.3 | 27.2959 | 50.162 | 74.287 | 98.6658 | 123.128 | 0.66912 | ||
| 0.4 | 27.0416 | 48.8563 | 71.8331 | 95.1056 | 118.495 | 0.67541 | ||
| 0.5 | 26.8621 | 48.1384 | 70.5784 | 93.3367 | 116.225 | 0.67992 |
| KL | KP | γ | ω1 | ω2 | ω3 | ω4 | ω5 | λ |
|---|---|---|---|---|---|---|---|---|
| 10 | 0 | 0 | 22.5957 | 61.7538 | 120.945 | 199.884 | 298.572 | 1.87211 |
| 0.1 | 21.3446 | 51.0811 | 85.7747 | 121.389 | 156.772 | 2.05167 | ||
| 0.2 | 18.5608 | 36.5609 | 54.6156 | 71.6824 | 88.5434 | 2.42999 | ||
| 0.3 | 15.6759 | 27.1862 | 38.9625 | 49.7775 | 60.8526 | 2.90516 | ||
| 0.4 | 13.2865 | 21.375 | 30.1288 | 37.9597 | 46.2584 | 3.87926 | ||
| 0.5 | 11.4372 | 17.5601 | 24.537 | 30.6482 | 37.2987 | 6.69827 | ||
| 5 | 0 | 23.9143 | 63.5888 | 122.972 | 202.019 | 300.775 | 1.65438 | |
| 0.1 | 23.0822 | 53.8346 | 89.2907 | 125.642 | 161.759 | 1.82242 | ||
| 0.2 | 21.2855 | 41.035 | 60.6274 | 79.1969 | 97.5636 | 2.17425 | ||
| 0.3 | 19.5297 | 33.3506 | 47.3877 | 60.3333 | 73.6037 | 2.51772 | ||
| 0.4 | 18.1866 | 29.0183 | 40.6783 | 51.1438 | 62.2405 | 2.80017 | ||
| 0.5 | 17.2362 | 26.4531 | 36.892 | 46.048 | 56.0107 | 3.02728 | ||
| 25 | 0 | 28.5299 | 70.4196 | 130.757 | 210.337 | 309.426 | 1.18673 | |
| 0.1 | 28.9764 | 63.6572 | 102.155 | 141.384 | 180.334 | 1.34457 | ||
| 0.2 | 29.7794 | 55.4292 | 80.2951 | 103.958 | 127.411 | 1.66884 | ||
| 0.3 | 30.3974 | 51.0386 | 71.8034 | 91.0459 | 110.794 | 1.96823 | ||
| 0.4 | 30.7834 | 48.8132 | 68.137 | 85.5259 | 103.971 | 2.18714 | ||
| 0.5 | 31.0191 | 47.5964 | 66.3087 | 82.7336 | 100.604 | 2.33713 | ||
| 50 | 0 | 33.3266 | 78.0638 | 139.862 | 220.285 | 319.907 | 0.92027 | |
| 0.1 | 34.9378 | 74.1135 | 116.255 | 158.885 | 201.157 | 1.0774 | ||
| 0.2 | 37.7969 | 69.3394 | 99.5596 | 128.361 | 156.931 | 1.37241 | ||
| 0.3 | 40.0275 | 66.8639 | 93.7733 | 118.747 | 144.388 | 1.62261 | ||
| 0.4 | 41.4571 | 65.6397 | 91.529 | 114.841 | 139.572 | 1.79539 | ||
| 0.5 | 42.3505 | 64.9805 | 90.5076 | 112.918 | 137.3 | 1.90954 | ||
| 100 | 0 | 0 | 24.5064 | 62.4783 | 121.316 | 200.109 | 298.723 | 1.50573 |
| 0.1 | 23.3579 | 51.9546 | 86.2978 | 121.759 | 157.059 | 1.63646 | ||
| 0.2 | 20.8447 | 37.7717 | 55.4334 | 72.3074 | 89.0502 | 1.91101 | ||
| 0.3 | 18.323 | 28.7939 | 40.1008 | 50.6734 | 61.5876 | 2.3019 | ||
| 0.4 | 16.3258 | 23.3857 | 31.5871 | 39.1272 | 47.2212 | 3.26741 | ||
| 0.5 | 14.8597 | 19.9588 | 26.3071 | 32.0829 | 38.4863 | 6.27336 | ||
| 5 | 0 | 25.7273 | 64.2926 | 123.337 | 202.242 | 300.924 | 1.37867 | |
| 0.1 | 24.9557 | 54.6641 | 89.7933 | 126 | 162.037 | 1.50948 | ||
| 0.2 | 23.304 | 42.1173 | 61.3651 | 79.763 | 98.0238 | 1.7793 | ||
| 0.3 | 21.712 | 34.6737 | 48.328 | 61.0746 | 74.2126 | 2.04099 | ||
| 0.4 | 20.5123 | 30.5297 | 41.7699 | 52.0162 | 62.9594 | 2.26079 | ||
| 0.5 | 19.6745 | 28.1028 | 38.0923 | 47.0151 | 56.8084 | 2.44452 | ||
| 25 | 0 | 30.0659 | 71.0558 | 131.101 | 210.551 | 309.571 | 1.06129 | |
| 0.1 | 30.4898 | 64.3603 | 102.595 | 141.702 | 180.583 | 1.1989 | ||
| 0.2 | 31.254 | 56.2352 | 80.8536 | 104.39 | 127.764 | 1.48043 | ||
| 0.3 | 31.8434 | 51.9128 | 72.4274 | 91.5388 | 111.2 | 1.73861 | ||
| 0.4 | 32.2121 | 49.7265 | 68.7942 | 86.0504 | 104.403 | 1.92589 | ||
| 0.5 | 32.4374 | 48.5326 | 66.9839 | 83.2758 | 101.05 | 2.05326 | ||
| 50 | 0 | 34.6506 | 78.6381 | 140.183 | 220.489 | 320.047 | 0.85284 | |
| 0.1 | 36.2029 | 74.7182 | 116.641 | 159.168 | 201.381 | 0.99659 | ||
| 0.2 | 38.9693 | 69.9854 | 100.011 | 128.711 | 157.218 | 1.26757 | ||
| 0.3 | 41.1364 | 67.5336 | 94.252 | 119.126 | 144.699 | 1.49748 | ||
| 0.4 | 42.5288 | 66.3217 | 92.0193 | 115.232 | 139.894 | 1.65584 | ||
| 0.5 | 43.4 | 65.6694 | 91.0034 | 113.315 | 137.627 | 1.76014 | ||
| 200 | 0 | 0 | 26.4682 | 63.2735 | 121.728 | 200.359 | 298.89 | 1.76017 |
| 0.1 | 25.4085 | 52.9083 | 86.8752 | 122.169 | 157.377 | 1.97028 | ||
| 0.2 | 23.1193 | 39.073 | 56.3282 | 72.9956 | 89.6099 | 2.41183 | ||
| 0.3 | 20.8742 | 30.481 | 41.3289 | 51.6507 | 62.3942 | 2.83125 | ||
| 0.4 | 19.145 | 25.4341 | 33.1323 | 40.3849 | 48.2685 | 3.14686 | ||
| 0.5 | 17.9112 | 22.3239 | 28.1437 | 33.6052 | 39.7643 | 3.36847 | ||
| 5 | 0 | 27.6024 | 65.0657 | 123.742 | 202.489 | 301.09 | 1.59829 | |
| 0.1 | 26.8847 | 55.5713 | 90.3484 | 126.396 | 162.345 | 1.79521 | ||
| 0.2 | 25.3589 | 43.2882 | 62.1746 | 80.3875 | 98.5325 | 2.20304 | ||
| 0.3 | 23.9042 | 36.0869 | 49.3517 | 61.8879 | 74.8833 | 2.58175 | ||
| 0.4 | 22.82 | 32.1257 | 42.9502 | 52.9687 | 63.7486 | 2.86038 | ||
| 0.5 | 22.07 | 29.829 | 39.383 | 48.0668 | 57.6819 | 3.05255 | ||
| 25 | 0 | 31.6853 | 71.756 | 131.482 | 210.788 | 309.732 | 1.19923 | |
| 0.1 | 32.0879 | 65.1325 | 103.081 | 142.054 | 180.86 | 1.37629 | ||
| 0.2 | 32.8149 | 57.1174 | 81.4697 | 104.868 | 128.155 | 1.71325 | ||
| 0.3 | 33.3767 | 52.8672 | 73.1145 | 92.0834 | 111.649 | 2.0006 | ||
| 0.4 | 33.7286 | 50.7221 | 69.5172 | 86.6295 | 104.881 | 2.20012 | ||
| 0.5 | 33.9439 | 49.5521 | 67.7262 | 83.874 | 101.544 | 2.33272 | ||
| 50 | 0 | 36.0647 | 79.2714 | 140.539 | 220.716 | 320.203 | 0.94342 | |
| 0.1 | 37.5586 | 75.3844 | 117.069 | 159.482 | 201.629 | 1.11319 | ||
| 0.2 | 40.2319 | 70.6962 | 100.509 | 129.099 | 157.536 | 1.40332 | ||
| 0.3 | 42.3344 | 68.2699 | 94.781 | 119.545 | 145.044 | 1.63477 | ||
| 0.4 | 43.6886 | 67.0713 | 92.5611 | 115.665 | 140.251 | 1.79052 | ||
| 0.5 | 44.5372 | 66.4264 | 91.5512 | 113.756 | 137.99 | 1.89222 |
| Mode | Non-Dimensional Natural Frequencies | |||||
|---|---|---|---|---|---|---|
| KL = 25 and Kp = 25 | KL = 36 and Kp = 36 | |||||
| Present | Ref. [9] | Ref. [48] | Present | Ref. [9] | Ref. [48] | |
| 1 | 19.2133 | 19.2178 | 19.21 | 22.1069 | 22.1112 | ------ |
| 2 | 50.7002 | 50.7804 | 50.71 | 54.916 | 55.1873 | ------ |
| 3 | 100.677 | ------ | ------ | 105.47 | ------ | ------ |
| 4 | 170.028 | ------ | ------ | 175.093 | ------ | ------ |
| 5 | 258.987 | ------ | ------ | 264.196 | ------ | ------ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Togun, N.; Bağdatlı, S.M. Nonlinear Vibration of a Nanobeam on a Pasternak Elastic Foundation Based on Non-Local Euler-Bernoulli Beam Theory. Math. Comput. Appl. 2016, 21, 3. https://doi.org/10.3390/mca21010003
Togun N, Bağdatlı SM. Nonlinear Vibration of a Nanobeam on a Pasternak Elastic Foundation Based on Non-Local Euler-Bernoulli Beam Theory. Mathematical and Computational Applications. 2016; 21(1):3. https://doi.org/10.3390/mca21010003
Chicago/Turabian StyleTogun, Necla, and Süleyman Murat Bağdatlı. 2016. "Nonlinear Vibration of a Nanobeam on a Pasternak Elastic Foundation Based on Non-Local Euler-Bernoulli Beam Theory" Mathematical and Computational Applications 21, no. 1: 3. https://doi.org/10.3390/mca21010003






