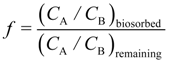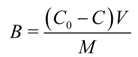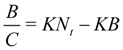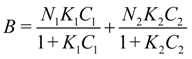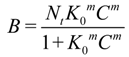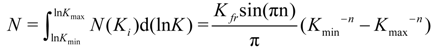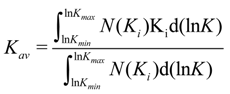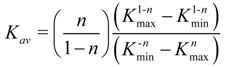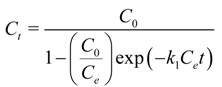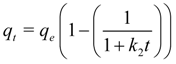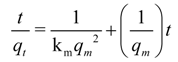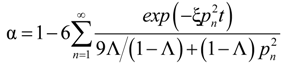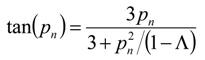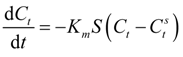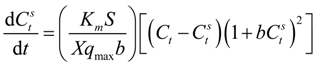1. Introduction
Worldwide environmental problems are becoming more and more acute. It is known, for example, that many specific industrial wastewater streams with large flows contain toxic metals in concentrations up to 500 mg/L, which have to be removed prior to water recycling, indirect discharge into the sewage system or direct discharge into surface waters [
1]. When discharged directly into rivers, polluted wastewater poses a great risk to the aquatic ecosystem, whilst discharge into the sewage system negatively affects bio-sludge activity and leads to contamination of the excess sludge to be disposed of. As a result of the standards specified in the Water Resources Act, industry takes precautions against these risks by treating dangerous components in a partial stream,
i.e., before being mixed with other types of wastewater. For centuries, water has been a manufacturing tool that industry has taken for granted, because it is inexpensive and plentiful. However, population growth, globalization, and climate change are shepherding in a new water-constrained era. Good, clean water just cannot be replaced and it is becoming harder to come by [
2].
Therefore, research was focused, among other things, on the development of highly selective bonding agents, including the biosorbents, with fast reaction kinetics for the removal of toxic substances. The latter may led to a better use of the capacity of the bonding agents, resulting in smaller units and low residual concentration of pollutants in the treated water streams, to comply with individual standards for water re-use or discharge. The ability of microorganisms to remove metal ions is a well-known phenomenon; biosorption was called the process that makes use of dead biomass (in comparison to bioaccumulation), a separation technique usually applied to fermentation wastes or byproducts. This process has been recently reviewed in depth [
3]. Several biomass types were investigated, such as bacteria (
Streptomyces clavuligerus or
Actinomycetes AK61/JL322), yeast (
Saccharomyces cerevisiae or
carlsbergensis) fungi (
Penicillium Chrysogenum), as well as biomass from a biological wastewater treatment plant after anaerobic digestion and grape stalks (a by-product of the winery industry).
As an example, the use of
Aeromonas caviae biomass is given in the following (
i.e., in the kinetics study) for the removal of cadmium and/or chromate ions; this microorganism is a Gram-negative bacterium, isolated from raw water wells near Thessaloniki [
4,
5]. An advantage of the proposed operation is that its basic unit processes are rather conventional and widely applied in the field [
6]. Biosorbents can be regenerated for multiple reuse, offering in addition and meanwhile the metal recovery possibility from concentrated wash solutions,
i.e., by electrochemical methods. Non-living biomass showed generally greater metal binding capacities than the respective living bacterium. From a comparison between biosorption and other metal separation methods, as filtration, centrifugation,
etc., it was found that in terms of the removal efficiency and applicability at lower (acidic) pH values, the former was favored [
2,
7]. In the latter, biosorption was studied for a mixture of copper, zinc and nickel.
A common feature in biotechnology is of course the presence of suspended particles, living or disrupted microorganisms (generally, having low density), which are difficult or time-consuming to remove by filtration and on the other hand, centrifugation is apparently more expensive. The possibility of applying downstream biomass flotation has been extensively reviewed in this volume; observed recoveries were reaching almost 100% [
8]. The efficiency of combined “biosorptive flotation” process has been proved for the treatment of toxic metals’ mixture, even when applying a multi-cycle biosorption-flotation operation [
2]. A flowsheet of the proposed (two-stage countercurrent) biosorptive flotation process was presented [
9].
The microbial biosorption of metals has attracted the interest of scientists as a treatment method, especially during the last two decades. Although the biological treatments are a removal process for some organic compounds, their products of biodegradation may also be hazardous [
10].
2. Selectivity
Generally, metal recovery or removal from solution may involve the following pathways: (i) The binding of metal cations to cell surfaces, or within the cell wall, where microprecipitation may enhance uptake; (ii) Translocation of the metal into the cell, possibly by active (metabolic energy dependent) transport; the active uptake or concentration of metal by living microbial cells; (iii) The formation of metal-containing precipitates, by reaction with extracellular polymers or microbially produced anions such as sulfide or phosphate (“bioprecipitation”); (iv) The volatilization of the metal by biotransformation—see Hughes and Poole [
11]. The metal binding properties of Gram-positive bacteria, including the actinomycetes, according to Hancock [
12] are largely due to specific anionic polymers in the cell wall structure.
Equilibrium and kinetic analyses classically lead to the appropriate rate expressions, characteristic of the possible reaction mechanism(s). The results of titration experiments suggested the presence of carboxylic and phosphate groups on the bacterial cell wall. These types of acidic sites can remove metallic ions, usually cations (cadmium), from aqueous solutions through the application of different mechanisms, such as cell surface sorption (complexation, surface precipitation
etc.), as well as by extracellular and intracellular accumulation [
13].
As for the removal of hexavalent chromium oxyanions (by
Aeromonas caviae) at low pH values may be attributed to their attraction/affinity toward positively charged surface groups of biomass or reduction of Cr(VI) to Cr(III), followed by its bonding to the negatively charged biosorbent. The characterization of our biomass,
Aeromonas caviae, including zeta-potential measurements, supports clearly this argument [
5]. Thousand tons of residual biomass are produced each year from fermentation industries and also from biological wastewater treatment plants; hence, it could be considered as suitable biosorbents, perhaps with certain modification or treatment [
14].
A selectivity factor “f” was defined [
15], when considering two metals, A and B, as:
in order to describe the effectiveness of biosorption as a separation process, similar to the one used in ion exchange or solvent extraction processes. For the system Zn/Cd, where some selective separation was apparent, the value off reached around 40 in the pH range 8 to 9. Selectivity is of interest specifically if recovery of metals is sought from a mixture of metal ions, which most of the practical cases of wastes are. Selectivity was said to be a problem generally with biosorption systems, but this may be minimized depending on the relative concentrations of the various metals present [
16].
As also discussed by Zouboulis
et al. [
7], the biosorption results for copper did worth mentioning, showing a selectivity of the process for copper; it is further noted that this selective separation was obtained in only one stage operation. A good explanation for that can be found in the literature [
17].
A two cycles operation was attempted with alternative addition of dodecylamine surfactant; both the metals (copper, nickel, zinc) removal due to biosorption on (zetag-modified)
Streptomyces rimosus industrial biomass, and also flotation behavior of the system, was investigated as a function of solution pH. Again a pronounced indication for possible selective recovery of copper (at a pH value of around 6.5) was observed [
18].
The selective removal of Cu(II), Cr(III) and Ni(II) by strains of exopolysaccharide-producing cyanobacteria was assessed and the interaction of sorption in solutions with multiple-metals was investigated [
19]. Experimental results elsewhere indicated that the uptake capacity and biosorption yield of one metal ion were reduced by the presence of the other metal ion; the selectivity order of Pb
2+ > Cu
2+ > Zn
2+ was found [
20]. Although biosorption for reclaiming single precious metal was frequently reported, the actual subsistent adsorptive competition among different metal ions sometimes shows diverging reinforcement or prohibition for different species. Another study tried to screen bacteria that are able to absorb certain precious metals with high selectivity under competitive conditions. For binary metal system, the adsorption parameters of extended-Langmuir model were modified by introducing a selectivity factor of the solute [
21].
A mass action law was able to predict the ion exchange equilibrium with Na-loaded algae, considering a ternary system Na
+/H
+/Cd
2+ or Na
+/H
+/Pb
2+ [
22]. The selectivity coefficients of the Na-loaded algae increases in the following order: Na
+ < H
+ < Cd
2+ < Pb
2+, which indicates that carboxylic and sulfonic groups have a higher preference (affinity) to Pb
2+, followed by Cd
2+, H
+ and Na
+. The higher affinity of lead ion to sulfonic groups was attributed to the hard and soft acid and base theory. A mass transfer model, considering that the ion exchange limiting step is the intraparticle ion diffusion, was then able to fit the concentration profile of all ionic species at the liquid and solid phases.
Adsorption behaviors of non-conventional and cost-effective adsorbent prepared from orange waste has been investigated for various metal ions [
23]. Separation factors for Fe(III) and Zr(IV) over Zn(II) at around pH 2, derived from individual adsorption isotherm by fitting a linear curve, suggested that there was an excellent selectivity for transition metals over alkaline/alkaline earths. The selectivity of a bio-based dithiocarbamate modified chitosan, using Pb(II) as imprinted ions and the non-imprinted beads for lead ions over other metal ions were evaluated from the selectivity coefficient, defined as the ratio of the distribution ratios of the Pb(II) ions and other coexistent metal ions [
24]. Cross-linked imprinted chitosan polymer has been recently prepared from chitosan, using citric acid-cadmium complex as template and glutaraldehyde as the cross-linker [
25]. Therefore, this may explain the following attempt and proposal.
2.1. MIPs as Alternative Biosorbent Candidates
One of the hot topics of recent research is the reuse of some compounds existed as pollutants in environment. These compounds (molecules, ions, complexes,
etc.) are of high-added value and it will be ideal to selectively bind them with any environmental application and reuse them in their initial or modified form. The latter could be achieved using selective biosorbents with a special technique, which is called molecular recognition. Molecular recognition is realized with molecular imprinting which is an emerging technique to create high affinity polymeric matrices (MIPs) for target molecules. Many papers in literature refer monomers (or their derivatives) used in molecular imprinting. Detailed studies (as that of Mayes and Whitcombe) presents especially those used in non-covalent technique [
26]. Some of the widely used monomers are: (i) methacrylic acid or acrylic acid; (ii) 4-vynilpyridine; (iii) diethylaminoethyl methacrylate; (iv) acrylamides; (v) 2-hydroxyethyl methacrylate; (vi) acrylamide,
etc. The other crucial reagent in MIP preparation is the cross-linker which samely presents variety. There are the acrylated-based cross-linkers (ethyleneglycol dimethacrylate, trimethylolpropane trimethacrylate,
etc.), those which are structurally based on styrene and its derivatives (
i.e., divinylbenzene), and those which are soluble in water (ethylenebisacrylamide).
Molecular recognition is a process occurred everywhere. We can call that molecular recognition exists when two molecules has the spatially same geometry but each molecule can selectively interact with only one functional site [
27]. Therefore, a specific technology has been bloomed and re-designed in the last 40 years, called molecular imprinting (MI). The whole process is based on adsorption technology, which is already one of the most successful techniques for pollutants removal [
28,
29,
30,
31,
32,
33,
34].
MI is not a recent science. The first track of imprinting was recorded in 1930 from Polyakov [
35]. His target was to prepare silica gels (not only one but a series of those). Finally, he understood that the silica prepared showed selective capacity (binding) for a particular solvent in which the synthesis has been done. In 1955, a senior student of Linus Pauling, Frank Dickey, observed that after the removal of “patterning” dye the silica would re-bind the same dye in preference to the others [
36]. However, in 1972, a step change in molecular imprinting occurred when the group of Wulff reported that they had successfully prepared a molecularly imprinting organic polymer (MIP) [
37], using what is now termed a “covalent approach”, to prepare an organic molecularly imprinted polymer capable of discriminating between the enantiomers of glyceric acid. The technique, which is widely used for MIP preparation, is based on reactions of condensation that can be characterized as reversible. Characteristic examples are the use of (i) boronate ester [
38]; (ii) ketal/acetal [
39]; (iii) formation of Schiff’s base [
40], in order to synthesize different combinations between templates and monomers. In more recent decades (1970s and 1980s), the research group of Wulff used this technique/approach with different templates and prepared numerous specialized MIPs.
The second major breakthrough in organic polymer imprinting occurred in 1981 when Arshady and Mosbach reported that they had prepared an organic MIP using non-covalent interactions only [
41]. This approach was termed the “non-covalent approach”, as opposed to the covalent approach favored by Wulff, and it was this, with its simple, seemingly trivial methodology that triggered the explosion in molecular imprinting, occurring during the 1990s. Contrarily, the non-covalent technique is based on some attractive bonds among the molecules (hydrogen bonding, ion-pairs, forces of dipole-dipole, van der Waals bonds). All the aforementioned forces produce and stabilize the template molecule and the monomer (after selection) in the solution (solvent). The basic difference between covalent and non-covalent technique is that in latter the additives are not stable during the imprinting process. To this day, the non-covalent
versus covalent debate continues with both sides being championed. However, it is generally accepted that there are pros and cons to both approaches. Therefore, in 1995, Whitcombe reported an intermediate approach that combine the advantages of both [
42]. Importantly, in order to improve subsequent non-covalent binding geometry, Whitcombe’s approach incorporated a sacrificial spacer group that was designed to be lost during template removal. The non-covalent approach however is still by far the most widely used approach in MIP synthesis. Several of its drawbacks can be overcome by the use of stoichiometrically associating monomer-template systems [
43]. This has resulted in a range of receptors exhibiting high capacity and effective recognition properties in aqueous media.
It is interesting to prepare/design materials, which only selectively remove carcinogenic pollutants from wastewaters, as ions, phenols and drugs/pharmaceuticals. Nowadays, MIPs are designed in such way in order to be stable in extreme conditions (pH
etc.). Therefore, a high cross-linking is required. Another interesting point is the turn of researchers on the more environmental-based application. To achieve this, a high selectivity is required to bind only the templates, employed in separation processes of environmental pollutants (chromatography, solid-phase extraction, membrane separations, adsorption), artificial antibodies and sensors recognition elements [
40]. Many examples of template molecules have been reported; mention can be given in environmental targets as dyes (see
Figure 1), ions, metals, drugs, phenols,
etc.
Figure 1.
Example for the synthesis of Molecular Imprinted Polymers (MIPs) for capturing/binding dye molecules.
Figure 1.
Example for the synthesis of Molecular Imprinted Polymers (MIPs) for capturing/binding dye molecules.
The simplicity of use, the relatively low cost and the broad range of possible guest molecules (small organic molecules, ions but also biological macro-molecules) have since led to the important development of this technique, as illustrated by the increasing numbers of publications over recent years. This review aims to gather and report the bioengineering insights regarding the rebinding (adsorption) using MIPs along with discussion for the importance of the models for fitting.
2.2. Limitations
The engineering part is based on the selection of the suitable model for fitting of rebinding experiments either of equilibrium (isotherms) or kinetics. However, similarly as in the case of all biosorbents, each system of MIP (adsorbent) and target molecule (adsorbate) is unique. Modifying the conditions in polymer “cookery” (synthesis/polymerization, cross-linking, template extraction), the product will be completely different. The latter can be confirmed with scanning electron micrographs (SEM) of the prepared MIPs. For example, a recent study investigated the synthesis for selectively binding dyes, but having obvious surface changes due to the different solvent used (organic or aqueous) (
Figure 2).
Figure 2.
SEM micrographs of dye-MIPs using (
a) aqueous and (
b) organic solvent. Reproduced with permission from George Z. Kyzas [
44], published by Elsevier, 2009.
Figure 2.
SEM micrographs of dye-MIPs using (
a) aqueous and (
b) organic solvent. Reproduced with permission from George Z. Kyzas [
44], published by Elsevier, 2009.
An important parameter regarding the possible porosity of MIPs is the solvent [
45]. The type of solvent (or else “porogen”) demonstrates some morphological properties of porosity and surface area. There are two possible cases: (i) the use of solvents with low solubility phase, which can be rapidly separated and give adequate large pores, but MIPs with lower surface areas; (ii) the use of solvents with high solubility phase, which can be separated later and give smaller pore size distributions, but MIPs with higher surface area. It does not appear, however, that binding and selectivity in MIPs is dependent on a particular porosity. In fact, optimum results are often obtained when chloroform is used. In this case, the polymers prepared did not present adequate porosity or surface area (BET measurements), they were highly solvated and MIPs made without any porogen did not exhibit any selectivity, because substrate could not access the polymer. Thus, diffusion of substrates through the MIP appears to be fast enough through the chloroform solvated polymers without requiring porosity. Therefore, there is no big chance to repeat the data of literature. Researchers have understood the latter and studied uniquely each system of MIPs and for this reason, they have tested many isotherm models to predict the affinity or theoretical capacity of MIPs.
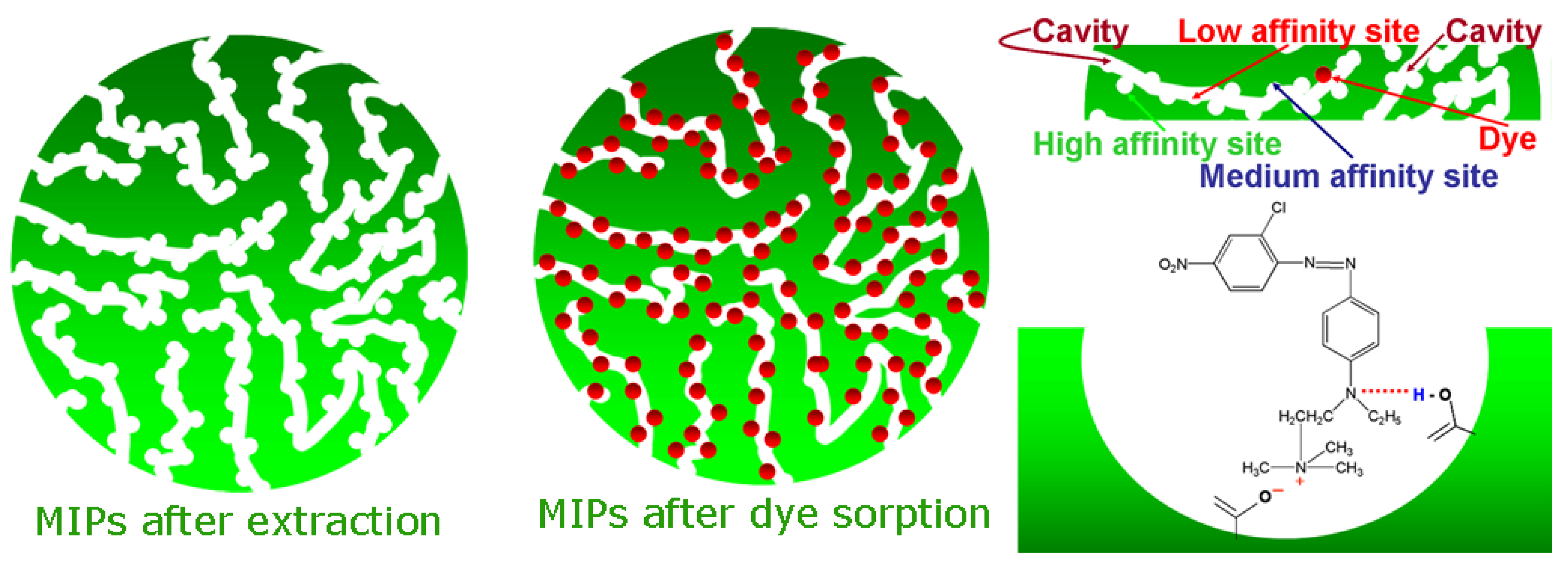
Apart from the synthesis limitations, as described above, another crucial factor which influences the engineering behavior of MIPs is the limitations during extraction of template molecules from the polymeric matrix, after synthesis. A 100% removal of the template was not achievable despite sequential attempts, using mainly Soxhlet apparatus. The latter is presented because some regions of MIP are highly cross-linked and therefore, the insertion/accessibility to them is limited. Another possible scenario is that in many cases, the template molecule does not present enough solubility in the porogen and therefore, cannot participate in interactions with the cavity of MIP [
46,
47]. The results from the above are not simple: (i) the most possible is a reduction of the total number of cavities suitable for rebinding (
Figure 3); (ii) the template can be “escaped” during the last step of elution mainly in MIPs used in columns for solid phase extraction [
48] or during analysis [
49].
Figure 3.
Example for the synthesis of MIP for capturing/binding dye molecules. Reproduced with permission from Rosa A. Lorenzo [
50], published by MDPI AG, 2011.
Figure 3.
Example for the synthesis of MIP for capturing/binding dye molecules. Reproduced with permission from Rosa A. Lorenzo [
50], published by MDPI AG, 2011.
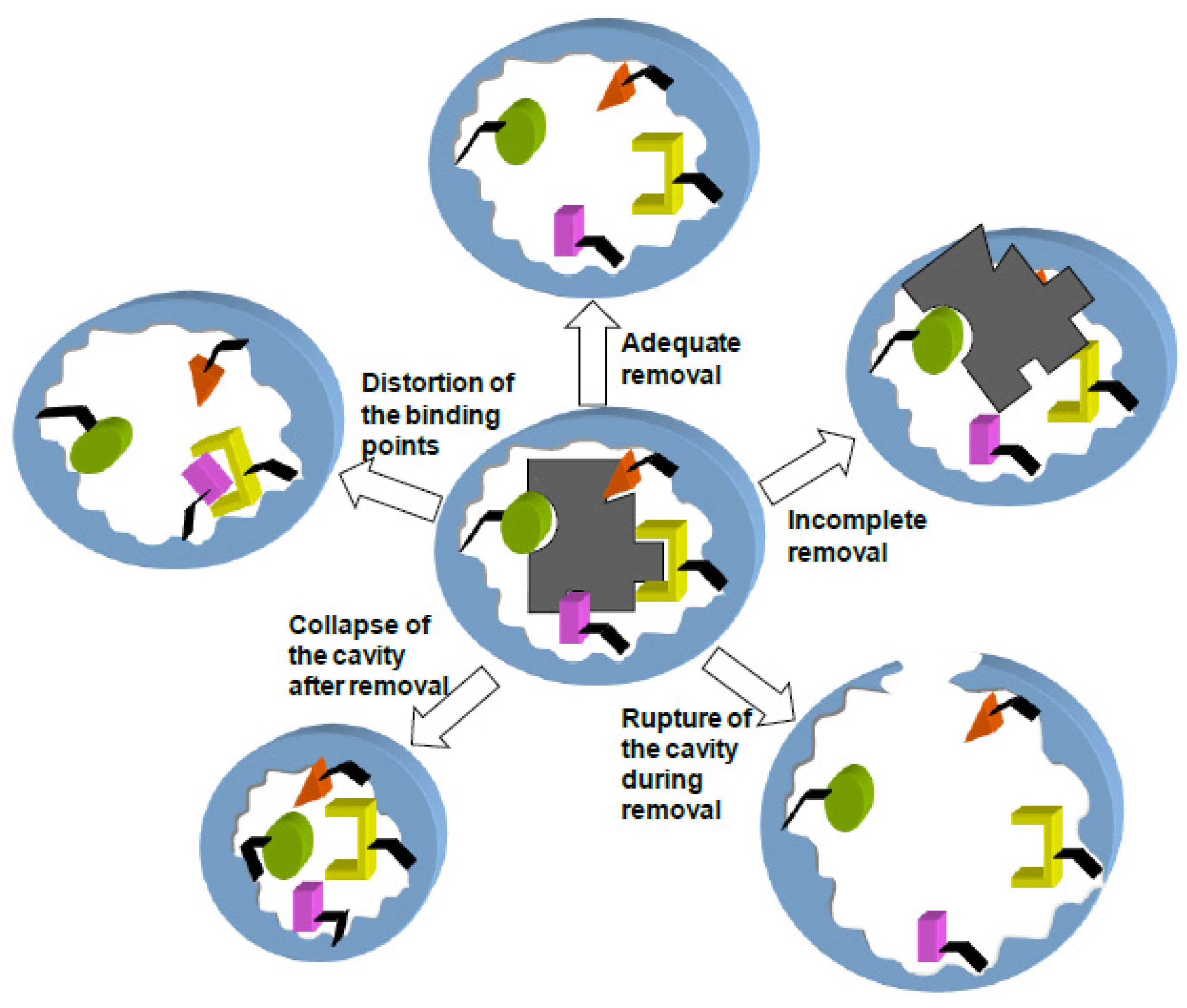
Even in the case of MIPs prepared with non-covalent or self-assembly technique, the binding of the template to the components of the imprinted cavity can be so strong that extraction under drastic conditions is required [
51]. Extreme pH or temperature applied for a long time can lead to distortion and even rupture of the cavity during removal, resulting in MIPs of poor selectivity and recovery [
46]. Furthermore, changes in the degree of swelling of the MIP network during extraction and subsequent desiccation can result in the collapse of the cavity, sterically hindering the entrance of target molecule, or in a distortion of the binding points or the strength of interactions [
52,
53].
One of the key assumptions in the analysis of binding data is that these are gathered after equilibrium between the template and the imprinted polymer is reached. Usually, this is accomplished by serial incubation of a known amount of imprinted polymer with different concentrations of the template during a specified period of time, necessary to reach equilibrium. The incubation time for most assays is the time required for 90% of the template to bind.
3. Isotherm Models
Studies of biosorbents contain mainly factors such as: (i) the isotherm models and (ii) the affinity distribution analysis (selectivity). An adsorption isotherm is a measure of the relationship between the equilibrium concentrations of bound and free guest over a certain concentration range and is readily generated from equilibrium batch rebinding studies or chromatographic frontal-zone analysis. Binding properties can be calculated from the binding isotherm by fitting the adsorption. It is a fact that the main theories are the same compared to the commonly-used biosorbents. However, some changes in the symbols and the physical meanings differentiate the models and give other potential to the whole engineering part. Models are used everywhere for simulating any possible process [
54,
55,
56,
57,
58,
59,
60,
61,
62,
63,
64,
65,
66]. The main models, which will be discussed in following, are the Freundlich, Langmuir, and Langmuir-Freundlich (L-F) equations. In general, the model chosen to explain the particular performance of a biosorbent is the simplest and most statistically significant. For example, if the data fit a model with three different binding sites better than a model with one or two kind of binding sites, the three-binding site model is often chosen, unless other independent data suggest using a different model (tetra-modal, exponential,
etc.). Before accepting a given n-site fit it is advisable to test whether the improvement is statistically significant.
The Freundlich isotherm is an empirical power function for non-ideal sorption on heterogeneous surfaces as well as for multilayer sorption and is expressed by the equation:
where
B is the amount of adsorbed pollutant at equilibrium;
a is the Freundlich adsorption coefficient (related with the adsorption capacity (
Nt) and the average affinity(
K0));
m is the Freundlich constant which represents the heterogeneity index and varies from zero to one (values approaching to zero indicate increasingly heterogeneity and one being homogeneous);
C is the equilibrium concentration of template. The term
B in Equation (2) was calculated from the simple mass balance equation as follows:
where
C0 is the initial pollutant concentration,
C is the pollutant concentration at equilibrium,
V is the volume of and
M is the mass of biosorbent. The linearized form of Equation (2) was obtained by taking log on both sides:
therefore, the plot of log(
B)
versus log(
C) was employed to generate the intercept value of a and the slope of
m. The Freundlich equation has been derived by assuming an exponentially decaying adsorption site energy distribution.
The data given by this model can be explained, in most cases, taking into account that the Freundlich model is a generalization of the Langmuir model applied to a heterogeneous surface with an energy distribution corresponding to an exponential decrease. Although the Freundlich model predicts that there is an indefinite increase of the adsorbed solute increasing its concentration in solution, this empirical equation is suitable for highly heterogeneous surfaces [
67,
68,
69,
70] and often represents typical adsorption data over a restricted range of concentration. In spite that the Freundlich isotherm is suitable to describe the dependence between the coverage degree (
θ) and the adsorption energy, it does not follow the fundamental thermodynamic basis since it does not reduce to Henry’s law at lower concentrations nor predicts the monolayer saturation at higher concentrations. Even so, several methods have been developed in order to estimate the exponential distribution of the isotherm.
On the other hand, the Langmuir sorption isotherm assumes that adsorption takes place at specific homogeneous sites within the material. The isotherm equation is derived from simple mass action kinetics, assuming chemisorption. Also, it assumes that once a template occupies a site, no further adsorption can take place at that site, all sites are energetically equivalent and there is no interaction between molecules adsorbed on neighboring sites. A saturation value should be reached beyond which no further sorption can take place.
While the Langmuir model assumes that there is only a single class of binding sites, the bi-Langmuir model assumes that there are two classes of sites within the imprinted material. It is straightforward to implement the Langmuir and bi-Langmuir models using Scatchard plots to determine the binding parameters, the binding affinity (
K) and the number of binding sites (
Nt), using the general expression:
where
B is the amount of adsorbed pollutant at equilibrium;
Nt is the total number of accessible adsorption sites;
C is the equilibrium concentration of template;
K is the Langmuir isotherm equilibrium constant.
In homogeneous systems with only one type of binding sites, by plotting
B/
C against
B, it is possible to obtain the value of
N from the x-intercept and the value of
K from the slope. In heterogeneous systems, Scatchard plots are not linear and the simplest model in this case is a material with two different kinds of adsorption sites. Langmuir equation is then extended to an equation with two Langmuir terms (bi-Langmuir equation):
Thus, the plot B/C versus B is composed of two straight lines, from which two sets of binding parameters (K1, N1 and K2, N2) for the two classes of binding sites within the imprinted polymer can be obtained. The steeper line corresponds to the high-affinity sites while the flatter line measured the low-affinity ones.
Furthermore, another isotherm model can be used which is the combination of Langmuir and Freundlich equations namely Langmuir-Freundlich (L-F) isotherm. This model, first described by Sips [
71,
72] was introduced for the biosorbents by the groups of Shimizu
et al. [
69,
70,
73] and Guiochon
et al. [
74,
75,
76]. The model describes an equilibrium relationship between the concentration of a bound template (
B) and the equilibrium template concentration in solution (
C) such that (where
Nt is the total number of binding sites and
K0 is the median binding affinity):
The variable
a is related to
K0 via
K0 =
a1/m. The fitting parameter “
m” is identical to the heterogeneity index of site energies from the Freundlich isotherm. The difference between the L-F model and the Freundlich one is evident at high adsorbate concentrations, for which the L-F model is able to represent the saturation behavior. At low adsorbate concentrations, the L-F equation reduces to the classical Freundlich equation. On the other hand, as m approaches unity, indicative of a completely homogeneous adsorbent surface (
i.e., energetic equivalence of all binding sites) the L-F equation reduces to the classical Langmuir equation. Thus, the hybridised L-F isotherm is able to model adsorption of solutes at high and low concentrations onto homogeneous and heterogeneous biosorbents. Although a linear analysis is not possible for a three-parameter isotherm, the L-F isotherm can be fitted to the experimental data following the method of Shimizu
et al. [
4,
5] in which a solver function may be used to maximize the coefficient of determination (
R2) by iteratively varying the three fitting parameters
Nt,
a and
m.
R2 is calculated from the sum of residuals (
i.e., the difference between the experimental model and model-predicted bound concentrations).
Linear regression is frequently used to determine the most fitted isotherm for two-parameter isotherms. The idea is to transform the data to create a linear graph and use the method of least squares to find the parameters of the isotherm. Examples include Scatchard plots of binding data [
70,
77,
78] and linearized forms of Freundlich and Langmuir equations [
69,
75,
79,
80]. It is very common to express the isotherm models in linear form. A drawback resulting from linearization (
y = a + b
x) is that some assumptions of linear regression are violated. In particular, the analysis of linear regression shows that the experimental data/points located around the fitting line has a Gaussian trend regarding their distribution. Furthermore, for each value of
x, the analysis with standard deviation is the same. Also, in some transformations, the relationship between
x and
y are altered. For example, when a Scatchard plot is created, the measured value of bound template winds up on both the
x-axis (which plots bound) and the
y-axis (which plots bound/free). In spite of these drawbacks, linearizing methods are a good starting point for generating initial values for non-linear regression.
3.1. Examples
Some characteristic examples of literature will be given below. It is interesting that in many cases the adsorption results were fitted in two or more models comparing the fitting parameters. Tsai and Syu [
81] studied the preparation of MIP-poly(4-vinylpyridine-co-divinylbenzene) (poly(4-VP-co-DVB)) as the specific receptor of creatinine by heated polymerization. The monomer used in that case was 4-Vinylpyridine. The other reagents for synthesis were creatinine (template) and divinylbenzene (cross-linker). The equilibrium rebinding data were fitted using Langmuir equation and gave 11.95 mg/g maximum theoretical capacity.
Milojkovic
et al. [
82] developed a novel synthesis procedure for MIPs. The polymerization was initiated by γ-radiation, but using as template molecule (±)-menthol. The evaluation of the adsorption results were done comparing the isotherms camphor (model molecule for testing) and menthol from
n-hexane. The results isotherms seemed to be as those of Langmuir.
Hsu
et al. [
83] prepared a molecularly imprinted polymer of morphine was prepared through thermal radical copolymerization of methacrylic acid and ethylene glycol dimethacrylate. A MIP assay was also synthesized (using mainly colorimetric reporter) was in order to observe and record the adsorption isotherm of morphine imprinted polymer binding. The adsorption isotherms fitted to Langmuir equation.
Baggiani and co-workers [
84] investigated the adsorption isotherms of polymers prepared by imprinting them with 2,4,5-trichlorophenoxyacetic acid (2,4,5-T). The polymers were prepared by thermoinduced polymerization of template mixtures, 4-vinylpyridine and ethylene dimethacrylate. The experimental adsorption isotherms were fitted by using several isotherm models, and the L-F model was found to give the best fitting.
Sajonz
et al. [
75] studied the adsorption isotherms of d- and l-phenylalanine anilide (PA) on an l-phenylalanine anilide imprinted stationary phase have been determined using staircase frontal analysis. It was found that the adsorption data fit well to both the Freundlich and the Bi-Langmuir isotherm models. Examination of the best values of the numerical coefficients of the Bi-Langmuir model shows that the site class representing the binding sites with the highest binding energy exhibits a very low saturation capacity for the non-imprinted enantiomer, indicating a high selectivity for the imprinted l-enantiomer.
Hwang and Lee [
85] synthesized cholesterol-imprinted polymers in bulk polymerization by the methods of covalent and non-covalent imprinting. For the covalent imprinting, the combination of template/monomer was cholesteryl (4-vinyl)phenyl carbonate, while for the non-covalent imprinting the respective combination was methacrylic acid or 4-vinylpyridine. The equilibrium data were successfully fitted to L-F model.
Lehmann
et al. [
86] investigated the binding of l-Boc-phenylalanine anilide (BFA) and l-Boc-phenylalanine (phe) to molecularly imprinted and non-imprinted polymer nanoparticles consisting of poly[(ethylene glycol dimethacrylate)-co-(methacrylic acid)] by adsorption experiments and mathematical modeling. The isotherms have been fitted using the Freundlich, L-F, bi-Langmuir, Langmuir and extended Langmuir model.
4. Affinity Distribution Analysis
A property of sorbents that has limited their wider applicability is their heterogeneity. The drawback, for instance, of the MIP technique is its low fidelity, which increases the distribution of association constants [
87]. Therefore, a first target the improvement of heterogeneity and change the so-called distribution in higher affinity sites. The majority of papers face the MIPs with homogeneity. Their surfaces are homogeneous where all functional sites can be estimated as one (Langmuir model) or two (bi-Langmuir model) general classes [
88,
89]. Therefore, we cannot base on these models in order to compare the possible changes of distributions. A possible solution for the latter is the analysis of limiting slopes according to scatchard plots, which can be characterized as type of bi-Langmuir equation [
90]. Hence, the comparison of binding properties of different or even of the same MIP by homogeneous models is difficult [
78].
Umpleby and co-workers [
69] beginning from the Freundlich equation (Equation (2)), express the affinity distribution, calculating the total number of binding sites (
N) (Equation (8)):
To find the number average binding constant (for a specified range of
Kmin −
Kmax), the sum of all sites
Ni multiplied by the corresponding affinity constant,
Ki, is divided by the sum of
Ni, which is the total number of sites
N Equation (9):
The term Σ
NiKi of the Equation (8) can be shifted using the integration of the number of binding sites with its corresponding association constant each time. When this is divided by the number of binding sites
N from Equation (10), the number average association constant (
Kav) is obtained.
After substitution and followed by integration, we get the following solution for the number average association constant (Equation (11)):
From Equation (11), the number average association constant can be calculated using a binding isotherm that is modeled by the Freundlich equation (Equation (2)).
5. Kinetics
The process is describing, by definition, the attachment of charged species (like the toxic metal ions) from a solution to a coexisting biosolid surface. Kinetics may be controlled by several independent processes that can act in series or in parallel. These sorption (a general term) processes fall in one of the following general categories: (i) bulk diffusion; (ii) external mass transfer (film diffusion); (iii) chemical reaction (chemisorption) and (iv) intraparticle diffusion. Kinetic analyses not only allow estimation of sorption rates but also lead to suitable rate expressions characteristic of possible reaction mechanisms [
91].
Many studies engaged so far to examine sorption phenomena involved analysis of batch experiments where data were sampled at even time intervals over the entire course of the process. As a result, fast changing kinetic data characteristic of the phenomena just after the onset of sorption could not be accurately depicted in an adequately short time scale. The model selection criteria proposed by Ho
et al. concerning sorption of pollutants in aqueous systems were used herein, as a guideline [
92].
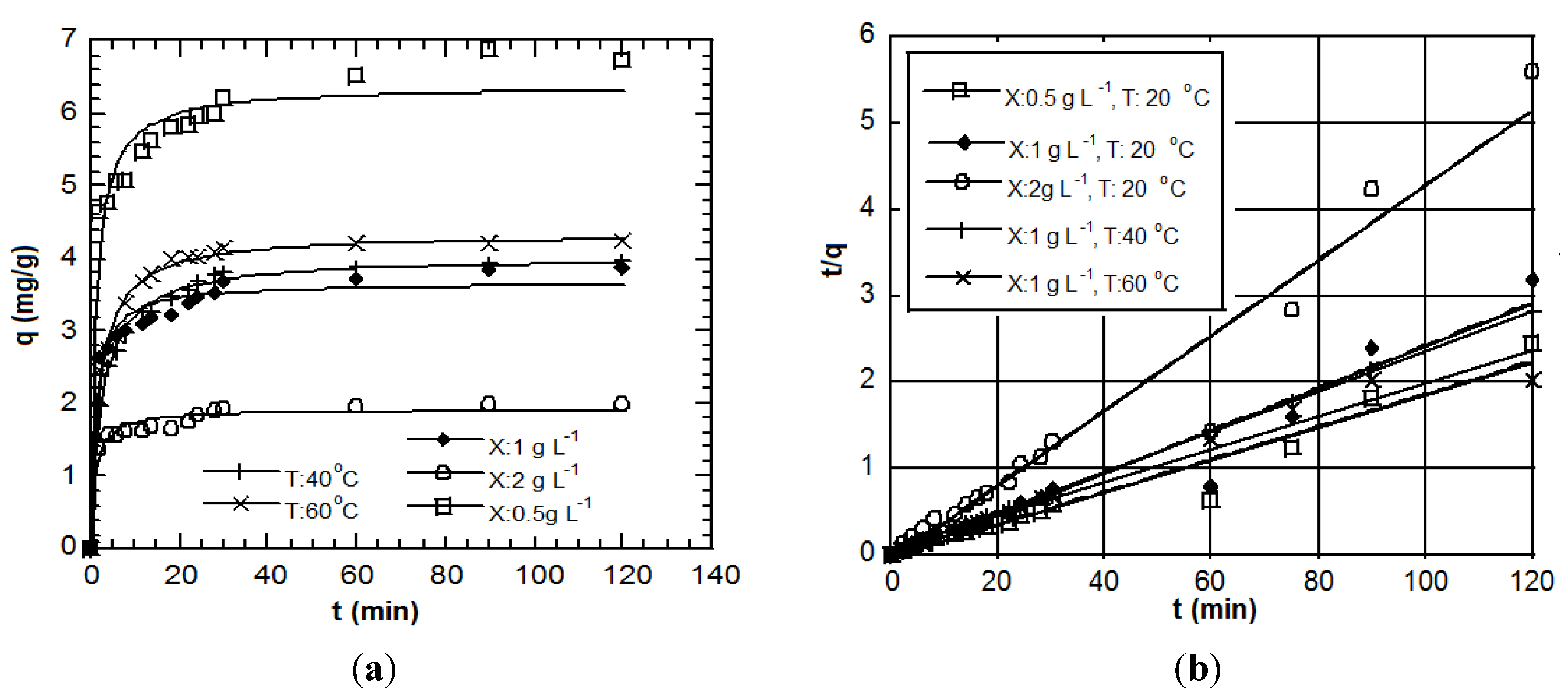
For equilibrium and kinetic modeling, usually an overall mass balance of the sorbate across the biosorbent surface is initially written. The used example below deals with an investigation of the removal and depletion of cadmium and chromates from aqueous solutions by biosorption on
Aeromonas cavia; this microorganism is often present in groundwater and general in aquatic environments. From the data, evidence was provided that the examined system was a complex process. More than one sorption models were often reported to describe correctly a case study [
93].
From the chemical reaction category (chemisorption), the best fit for the data sets of this study is achieved by 2nd order-type chemical reactions [
94]. The solution of the standard 2nd order reaction based on a constant stoichiometry of one metal ion per binding site is:
where
k1 is the reaction rate constant [L × (mg
−1 of metal) × min
−1];
C is the metal bulk concentration (mg·L
−1). Subscripts 0 and
t denote conditions at the beginning and any other instant (time,
t) of the process, respectively; and the subscript
e denotes equilibrium conditions.
This adsorption model has been very effective in describing the kinetics of adsorption of gases on solids. Nevertheless, when the data were plotted as a figure, it was shown that Equation (12) clearly fails to capture the steep concentration gradient of the early removal stage. This was a direct indication that adsorption on solids from a liquid phase is a different process than adsorption from a gas phase where traditionally the remaining bulk concentration dictates the kinetics.
If the rate of sorption depends not on bulk concentration but on uptake by the sorbent this can be described by the so-called Ritchie 2nd order equation according to which one metal ion occupies two binding sites [
95]:
where
q is the specific metal uptake (mg of metal per g of sorbent) and
k2 is the reaction rate constant (min
−1). When in the above treatment it is not necessarily
qe to dictate the sorbate uptake then a pseudo 2nd order rate expression is more appropriate:
where
km is the reaction rate constant [g of sorbent × (mg
−1 of metal) × min
−1] and
qm is a numerically determined parameter which under ideal 2nd order rate control corresponds to
qe. It is noted that in the literature [
92] various other kinetic equations have been attempted: zero, first (forward or reversible) order, Langmuir-Hinshelwood, Elovich-type,
etc.
Figure 4.
Comparison of experimental removal curves against theoretical predictions based: (
a) on the Ritchie 2nd order equation (at initial cadmium concentration of 5 mg·L
−1) and (
b) on the pseudo 2nd order equation (at initial cadmium concentration of 50 mg·L
−1). Reprinted with permission from reference [
94]; copyright (2005) Taylor & Francis.
Figure 4.
Comparison of experimental removal curves against theoretical predictions based: (
a) on the Ritchie 2nd order equation (at initial cadmium concentration of 5 mg·L
−1) and (
b) on the pseudo 2nd order equation (at initial cadmium concentration of 50 mg·L
−1). Reprinted with permission from reference [
94]; copyright (2005) Taylor & Francis.
Equations (13) and (14) provided a quite suitable description of data for advancing time (see
Figure 4). It is noteworthy that both models adequately capture the rapid rate of adsorption during the first minutes of the experiments. This already implies that the metal uptake by the sorbent is a satisfactory rate-controlling parameter under a 2nd order reaction mechanism.
For intraparticle diffusion, Crank [
96] proposed a model, which takes into account the continuously decreasing bulk concentration due to sorbate removal. This gives rise to a time dependent boundary condition for the concentration at the surface of the sorbent particle. The solution of the diffusion equation for such a boundary condition and a concentration independent diffusivity is:
where
pn is given by the non-zero roots of
and Λ ≡ (
C0 −
C∞)/
C0 is the fraction of metal ultimately adsorbed by the sorbent.
Equation (15) can be solved numerically to determine ξ, the effective diffusional time constant, which for the case of particle (also called micropore) diffusion control equals to Dc/ Rc2, Dc and Rc being the intraparticle diffusion coefficient (m2·s−1) and mean particle radius (m), respectively. The same expression is the solution of the diffusion equation for a (macro) pore diffusion control but only in cases where the equilibrium isotherm is linear for the concentration range under investigation.
External mass transfer has been customary analyzed in literature by adopting a pseudo first-order reaction model [
97]. This approach tacitly assumes that the sorbate concentration at the sorbent surface is zero at all times. However, this is not true particularly in cases where a significant quantity of sorbate is adsorpted rapidly at the beginning of the process. A more realistic model should consider instead a rapid equilibrium being established between the sorbate at the interface and that present on the sorbent surface [
98] and this concept has been adopted.
If one combines the mass balance across the sorbent surface, the Langmuir adsorption isotherm and the rate equation of change in the bulk concentration one ends up after some algebra with:
where
Km is the external mass transfer coefficient (m·s
−1),
S is the specific surface area of the sorbent particles per unit volume of the reactor (m
2·m
−3) and
X is the sorbent feeding per unit volume of solution (g·L
−1); dimensionless variables could be also used. The conversion a system of two first-order ordinary differential equations that must be solved simultaneously [
99]. The values of Λ, ξ and the computed values of
Dc (being the intraparticle diffusion coefficient, m
2·s
−1) were displayed in the form of a table.
Equations (15)–(16) and (17)–(18) were solved numerically to determine ξ and
KmS, respectively. The non-linear numerical regression to fit experimental data to those equations is performed by the Levenberg-Marquardt method, which gradually shifts the search for the minimum of the sum of the errors squared, from steepest descent to quadratic minimization—
i.e., Gauss-Newton [
100].
Figure 5a presents the results of fitting Equation (15) to biosorption data obtained with different initial concentrations, solids loads and temperatures. It is apparent that despite some scatter in measurements the finite volume diffusion model can describe fairly well the entire range of data, including also the steep concentration gradient at short times. Such behavior has been customary met as a consequence of the decreasing slope of a non-linear equilibrium curve, e.g., Langmuir isotherm, which causes the diffusivity to increase rapidly with increasing concentration [
93].
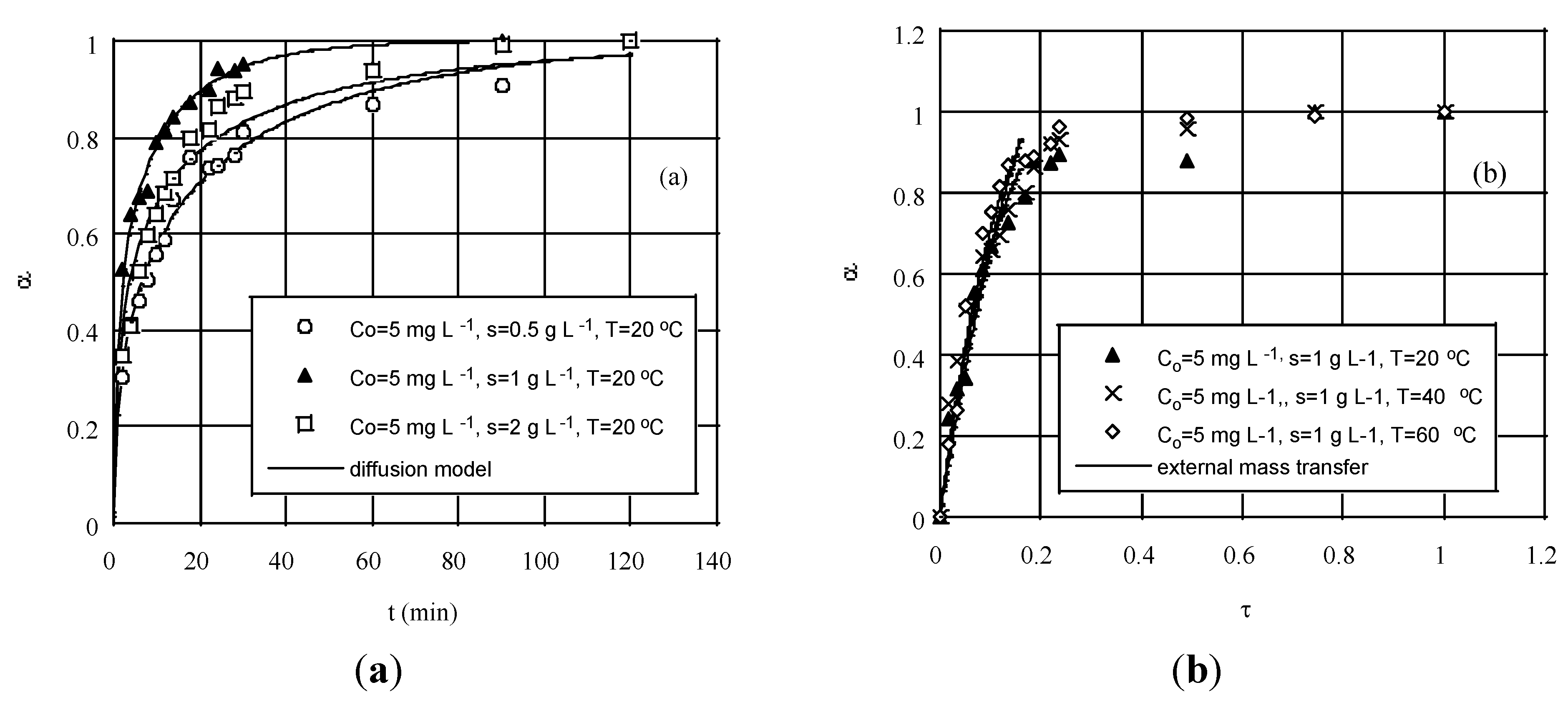
Figure 5.
Experimental degree of conversion, α, against predictions based on the solution of the: (
a) diffusion equation, for various adsorbent loads and (
b) mass transfer equation, for various temperatures (both at initial chromium concentration of 5 mg·L
−1). Reprinted with permission from Ref. [
99]; copyright (2004) American Chemical Society.
Figure 5.
Experimental degree of conversion, α, against predictions based on the solution of the: (
a) diffusion equation, for various adsorbent loads and (
b) mass transfer equation, for various temperatures (both at initial chromium concentration of 5 mg·L
−1). Reprinted with permission from Ref. [
99]; copyright (2004) American Chemical Society.
A way to check further on the possibility of a pore diffusion-controlled mechanism is to perform desorption kinetic tests with adsorbent previously used for sorption. For the case of a non-porous sorbent particle, transport of solute inside the particle may be neglected and it can be assumed that biosorption occurs mainly at the particle surface. This idea can be effectively extended to cases of relatively large macropores, where the metal ions may have a ready access to react with internal surface sites.
It was argued that at the beginning of the process that chromium is sorbed according to a quite fast and highly favorable chemical mechanism, such as ion-exchange, but soon external film diffusion comes into play. By this account, if one ignores the very first minute of sorption, the remaining curves were fitted pretty well by the model Equations (17) and (18).
Figure 5b displays these results. Near the end of sorption a much slower process, e.g., intraparticle diffusion, becomes gradually the rate-controlling step. Yet, this is a regime of no practical significance [
91,
101]. Rather contradictory indications on the subject were pointed out [
3].