Performance Comparison and Optimization of 16V265H Diesel Engine Fueled with Biodiesel Based on Miller Cycle
Abstract
:1. Introduction
2. Numerical Approaches
2.1. Theory of Diesel Engine Working Process
- (1)
- The gas in the cylinder is ideal, and there is no leakage during the sealing process. The characteristic values such as specific enthalpy h, specific internal energy u, and specific heat capacity C are only related to the gas temperature T and gas composition;
- (2)
- The state of the working medium in the cylinder of the diesel engine is the same everywhere (i.e., the pressure, temperature, and concentration of the working medium), and the gas left in the previous cycle should be fully mixed with the fresh air charge in the cylinder at the boundary of the intake stroke of this cycle;
- (3)
- The kinetic energy of the fresh working medium during the cycle stroke, the temperature and pressure changes in the fresh working medium during the intake process are ignored, and the flow process of the fresh working medium is quasi-stable.
- (1)
- Energy conservation equation [48]:
- U—System internal energy, kJ;
- WQ—Heat energy generated by fuel combustion inside the cylinder, kJ;
- WR—Heat energy exchanged by modules of cylinder system, kJ;
- hs—Common mass-specific enthalpy of the inlet valve;
- he—Common mass-specific enthalpy of the exhaust valve.
- (2)
- Mass conservation equation:
- m—Internal working medium quality of cylinder;
- me—Cylinder outflow waste mass;
- mB—Mass of fuel burned in the cylinder.
- (3)
- Equation of state of an ideal gas:
- m—Mass of working medium in the cylinder, kg;
- V—The working volume of a cylinder, m3;
- p—Working medium pressure in the cylinder, Pa;
- T—Temperature of working medium in the cylinder, K;
- R—Gas constant.
2.2. Theoretical Basis of Diesel Engine Application Optimization Method
- (1)
- x* is the local optimal solution of the above problem, and the effective set is I* = {i|ci (x*) = 0, i = 1, 2,…, m};
- (2)
- f(x), ci(x) (1≤ I≤ M is differentiable at point x*);
- (3)
- For i ∈ I*, is linearly independent. Then there is vector .
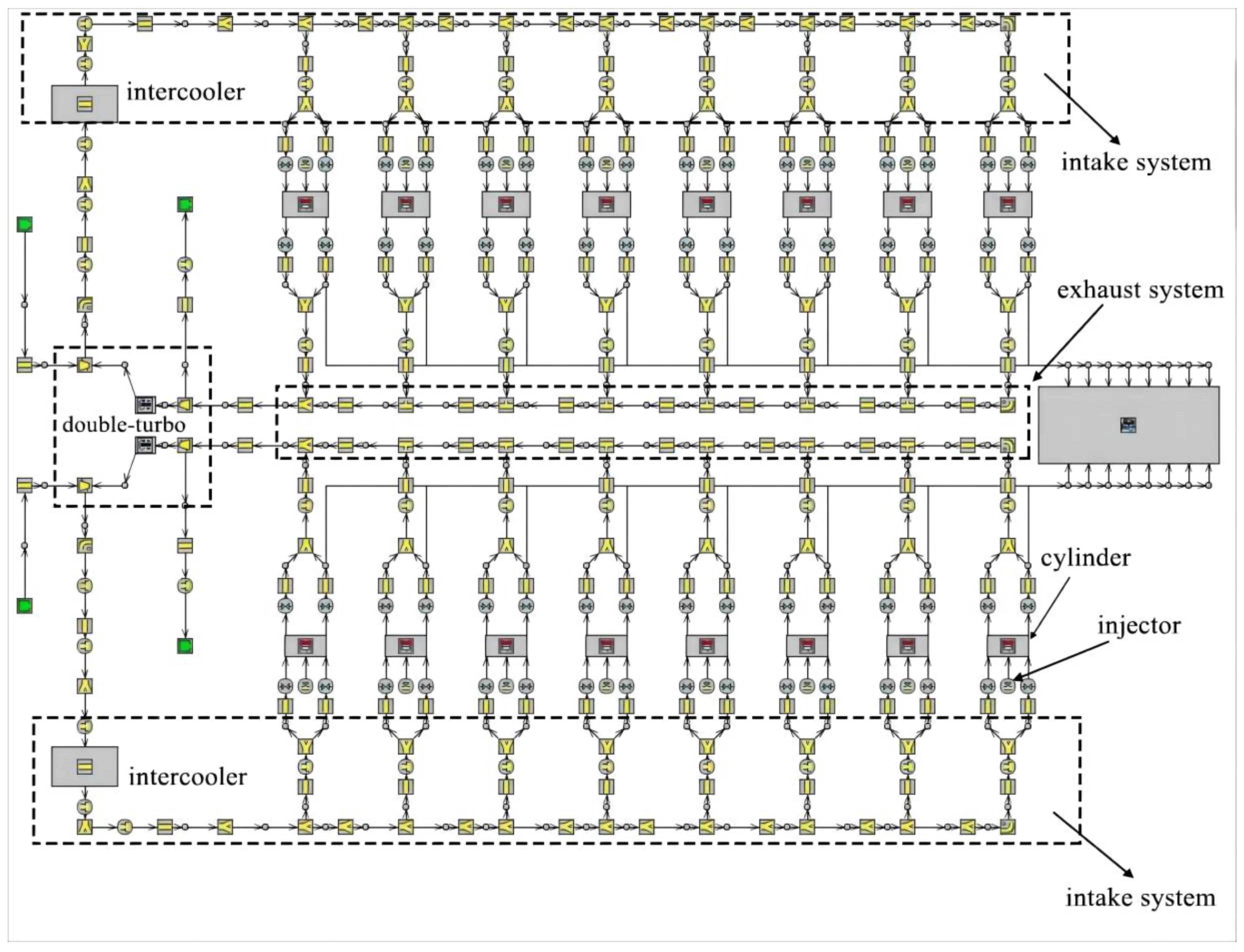
2.3. Overall Simulation Model
3. Results and Discussion
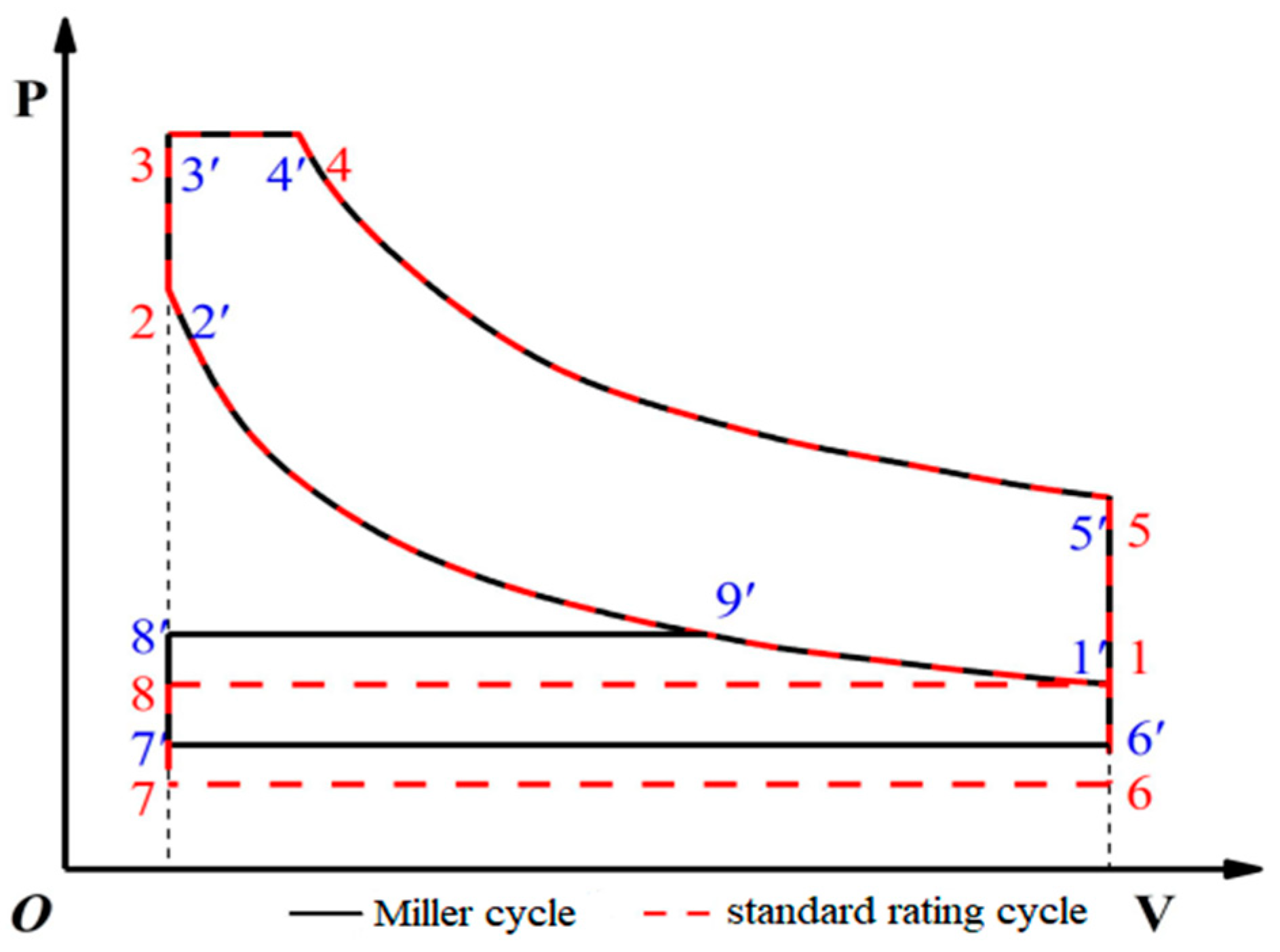
3.1. Two Miller Cycle Principles
3.2. Performance Comparison of B20 Biodiesel in Two Miller Cycle Modes
3.2.1. Comparative Analysis of Two Miller Cycle Power of B20 Biodiesel under Different Loads
3.2.2. Comparative Analysis of Fuel Consumption of Two Miller Cycles of B20 Biodiesel under Different Loads
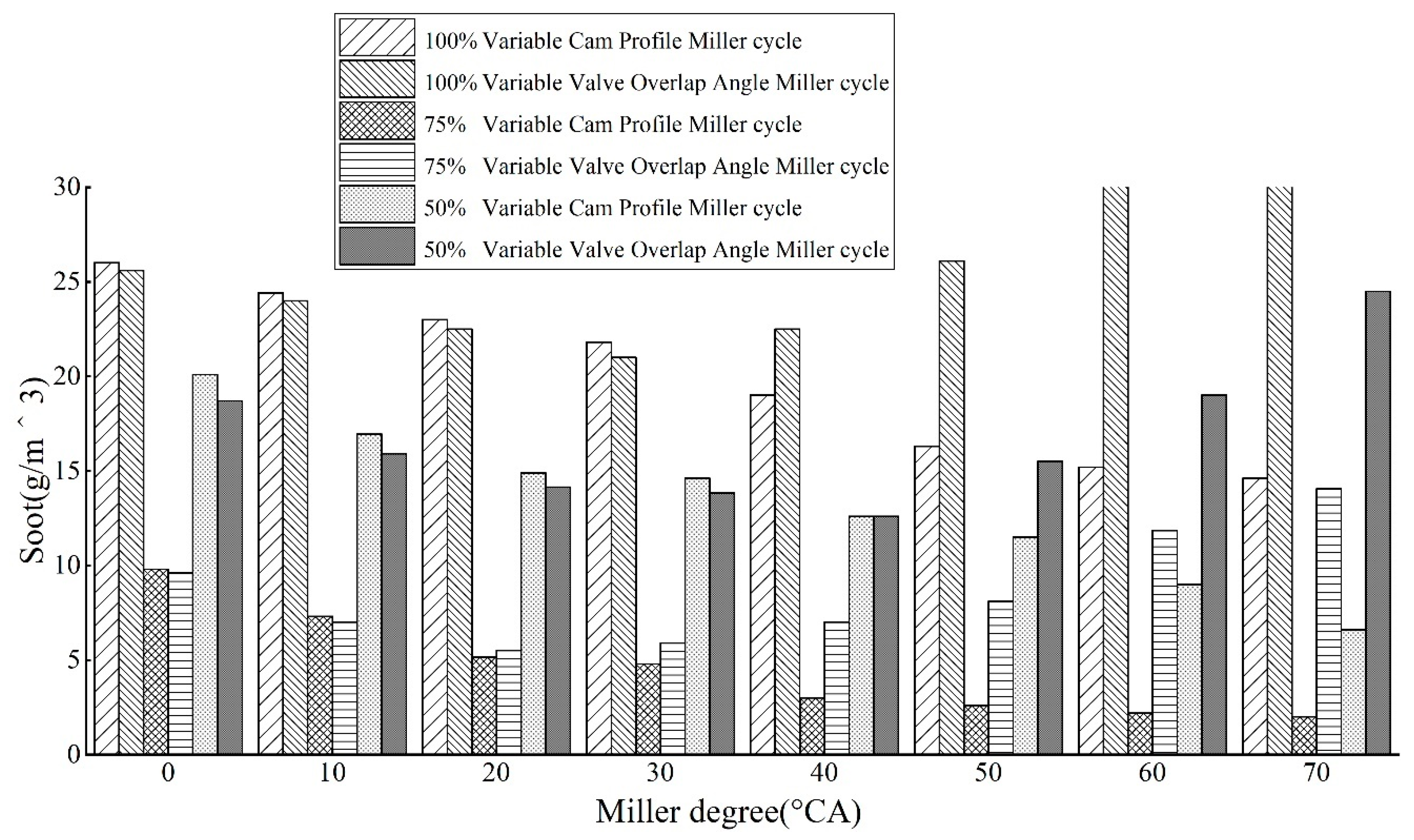
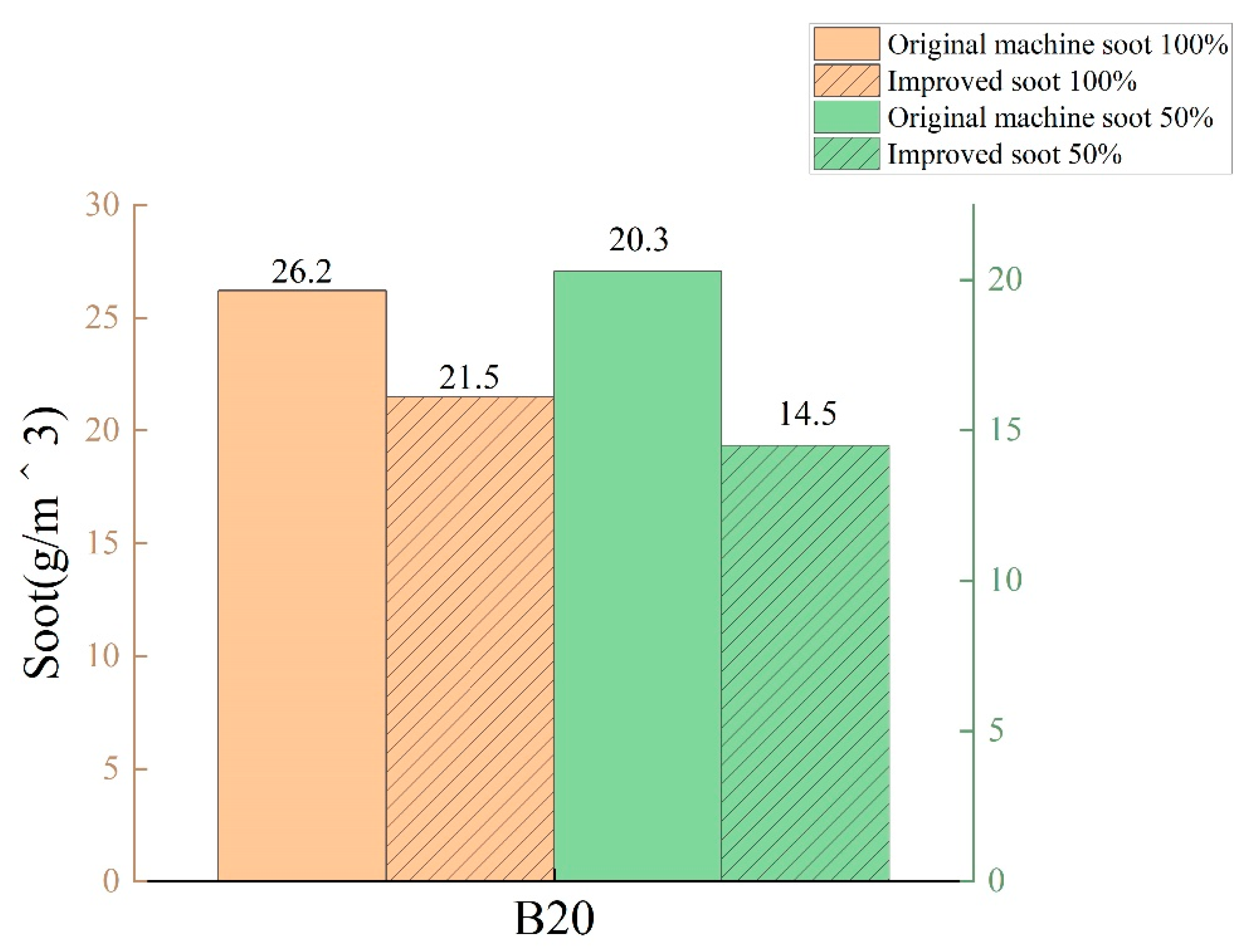
3.2.3. Comparative Analysis of Soot Emission from Two Miller Cycles of B20 Biodiesel under Different Loads
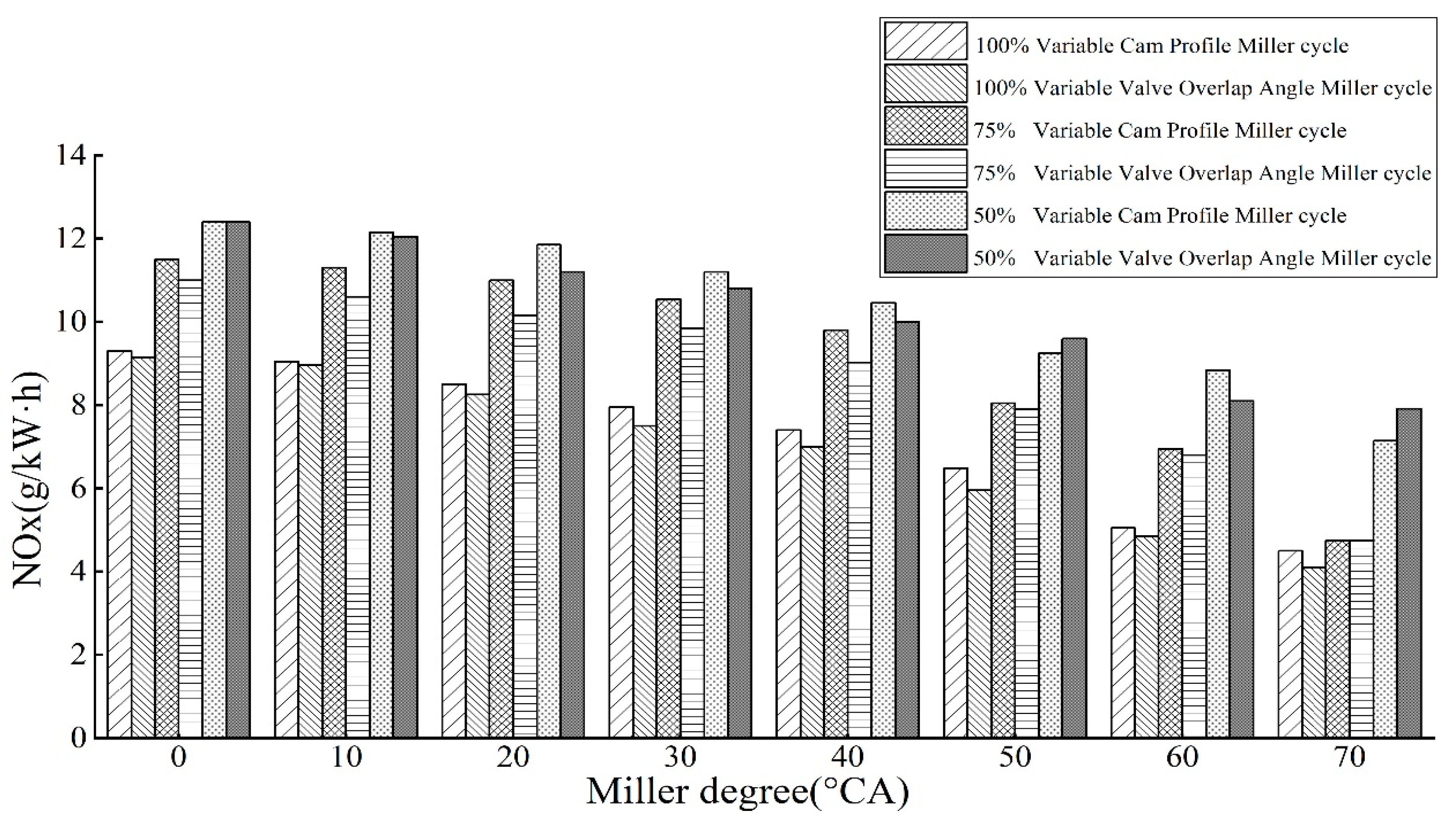
3.2.4. Comparative Analysis of NOX Emission of B20 Biodiesel in Two Miller Cycles under Different Loads
3.3. Optimization Analysis of B20 Biodiesel under Different Loads
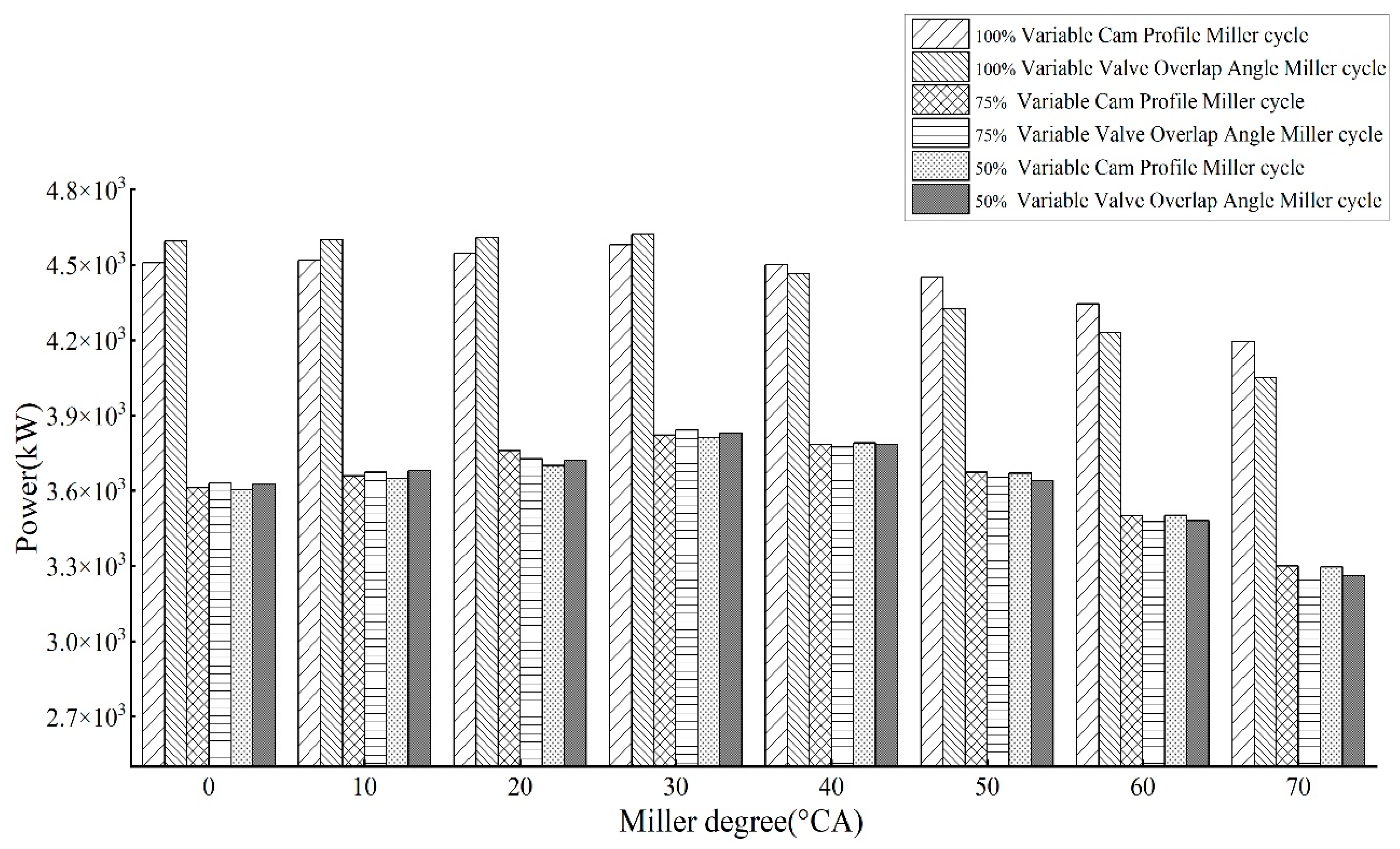
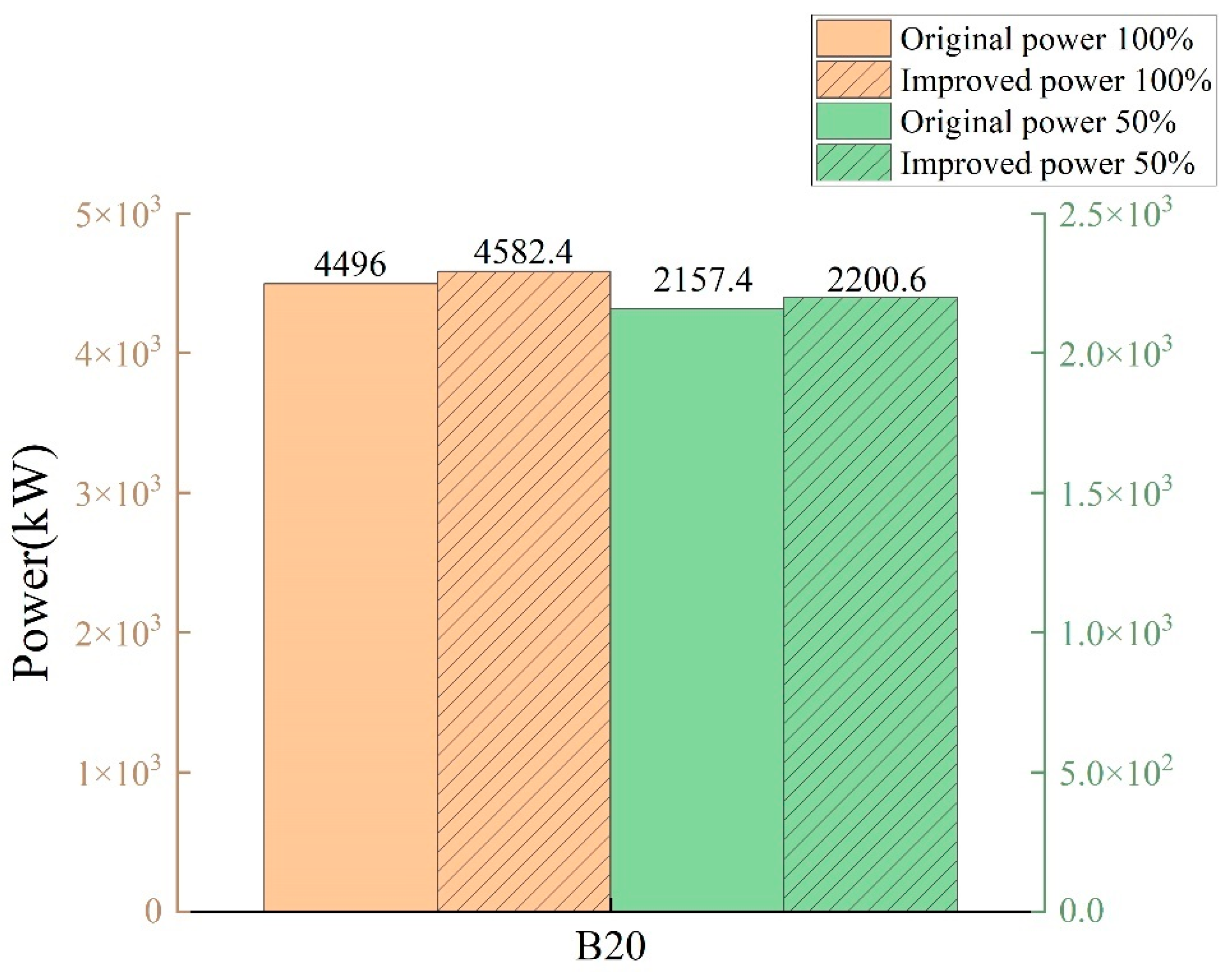
3.3.1. Power Optimization Analysis of B20 Biodiesel under Different Loads
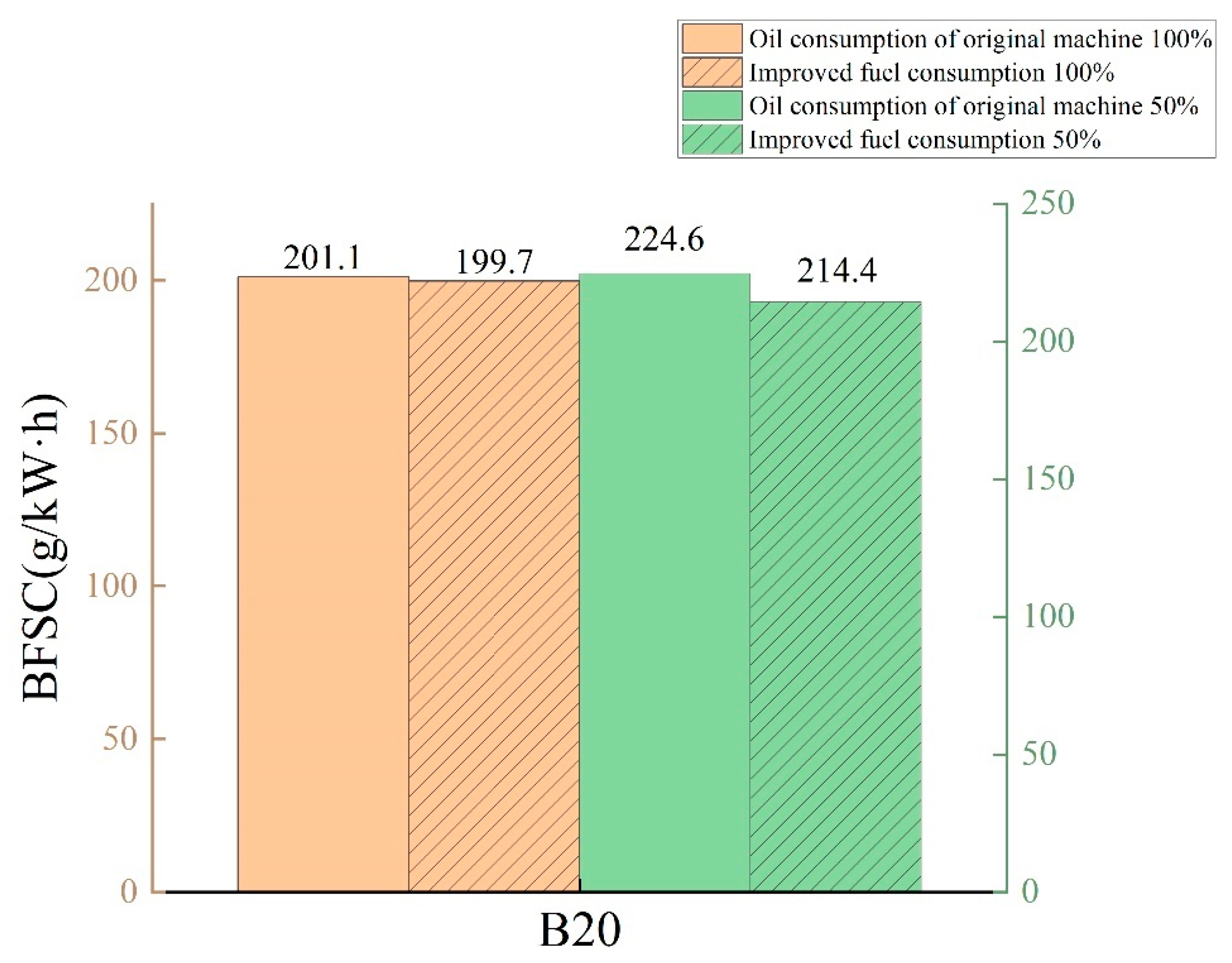
3.3.2. Fuel Consumption Optimization Analysis of B20 Biodiesel under Different Loads
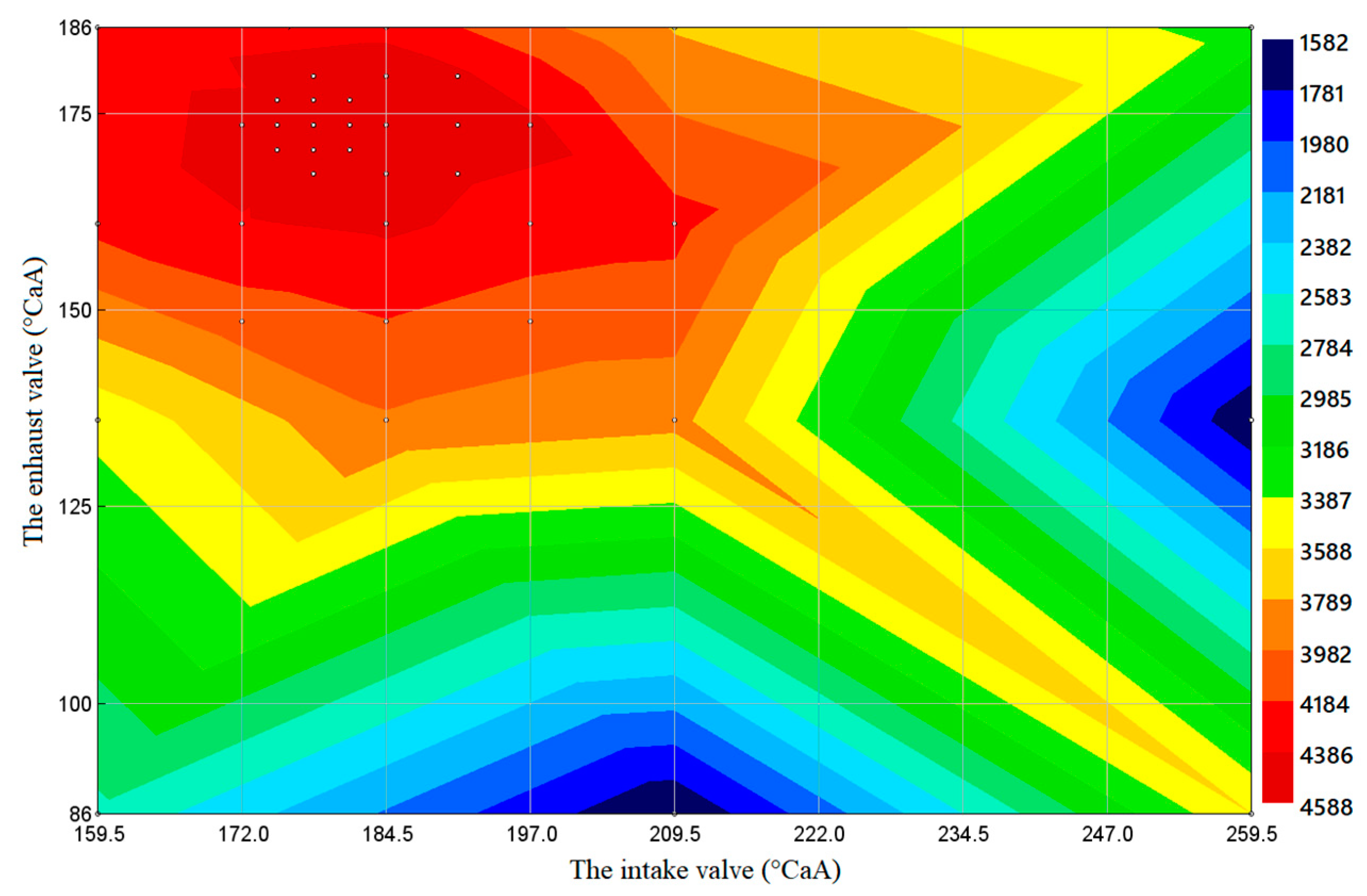
3.3.3. Soot Optimization Analysis of B20 Biodiesel under Different Loads
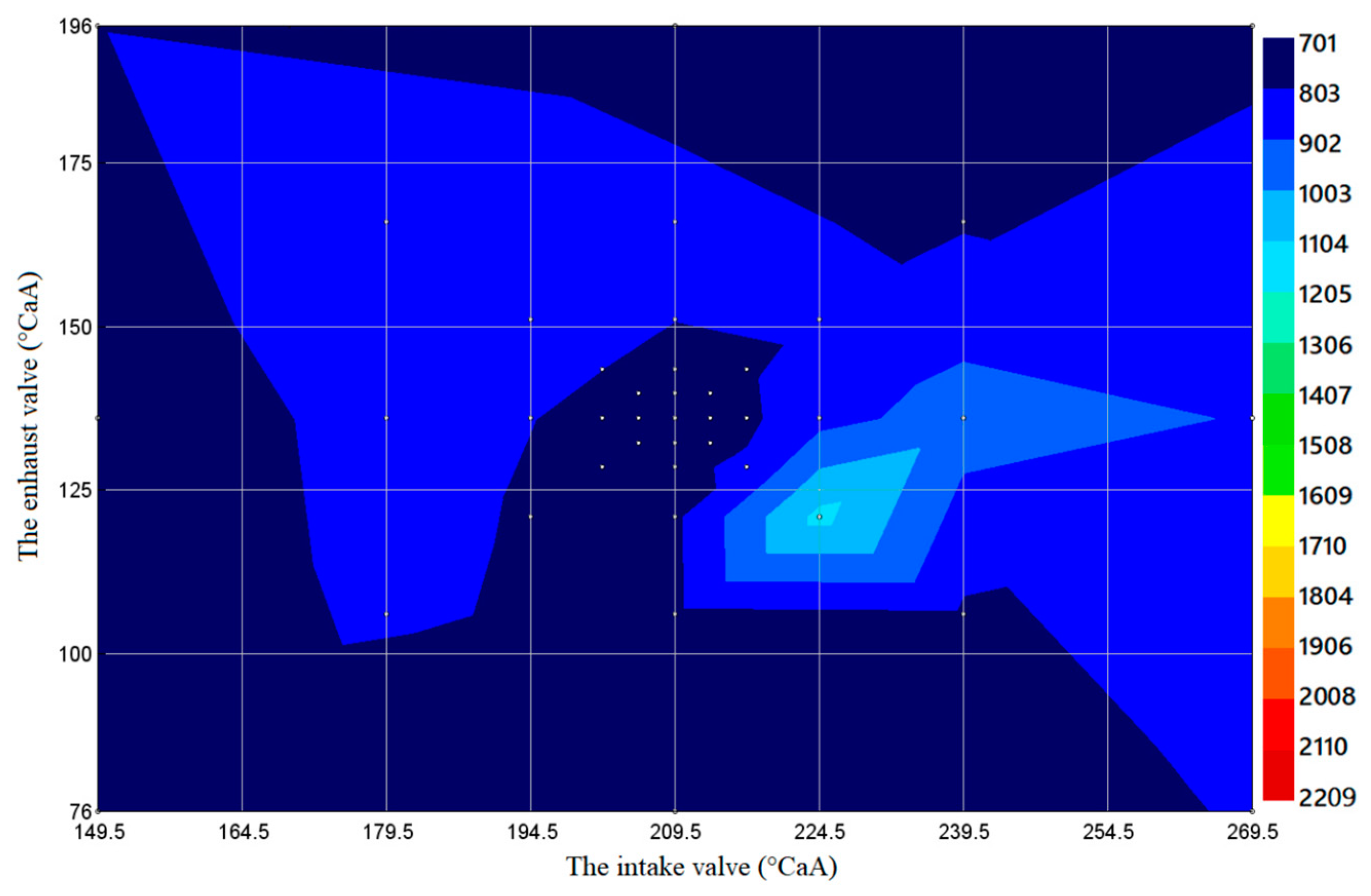
3.3.4. NOX Optimization Analysis of B20 Biodiesel under Different Loads
4. Conclusions
- (1)
- When the Miller degree increases to 0–30 °CA, the power of the VCA is lower than that of the VVA and the fuel consumption and emission are slightly higher than that of the VVA. When the Miller degree continues to increase to the range of 40–70 °CA, the power generated by both Miller cycles decreases at the same time and the former decreases less than the latter; the former has lower fuel consumption and soot than the latter and has better performance in fuel consumption and soot emission, but the NOX emission is slightly higher than the latter;
- (2)
- It can be seen from the analysis that the effect of the VVA on improving the comprehensive performance of the locomotive diesel engines is significantly better than the VCA. From the optimization results of various performance indexes under 100%, 75%, and 50% load conditions, the best optimization scheme combination of a diesel engine can be determined as follows: the effect of improving the performance of diesel engines by using the VVA and Miller degree 30 °CA is the best;
- (3)
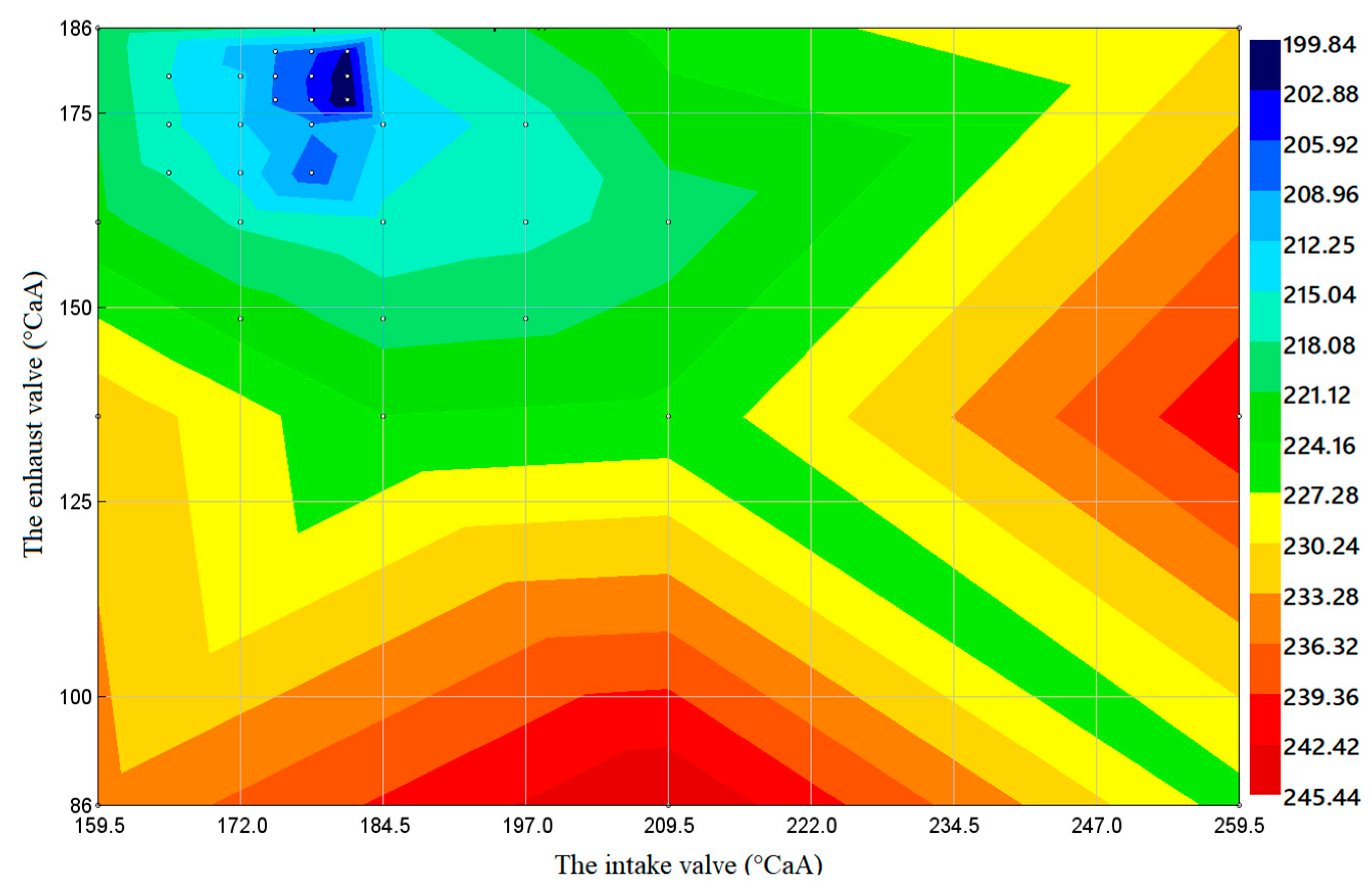
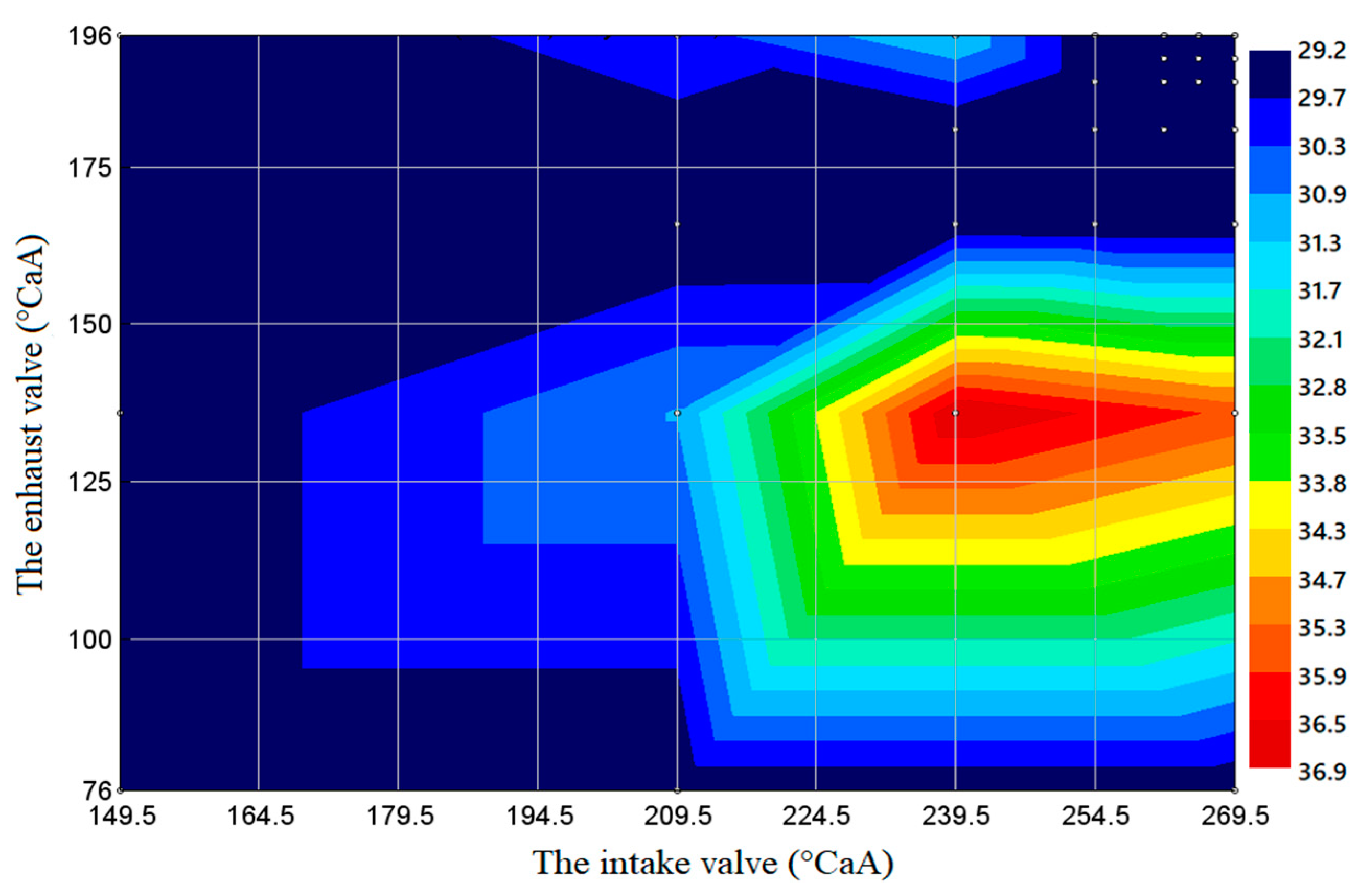
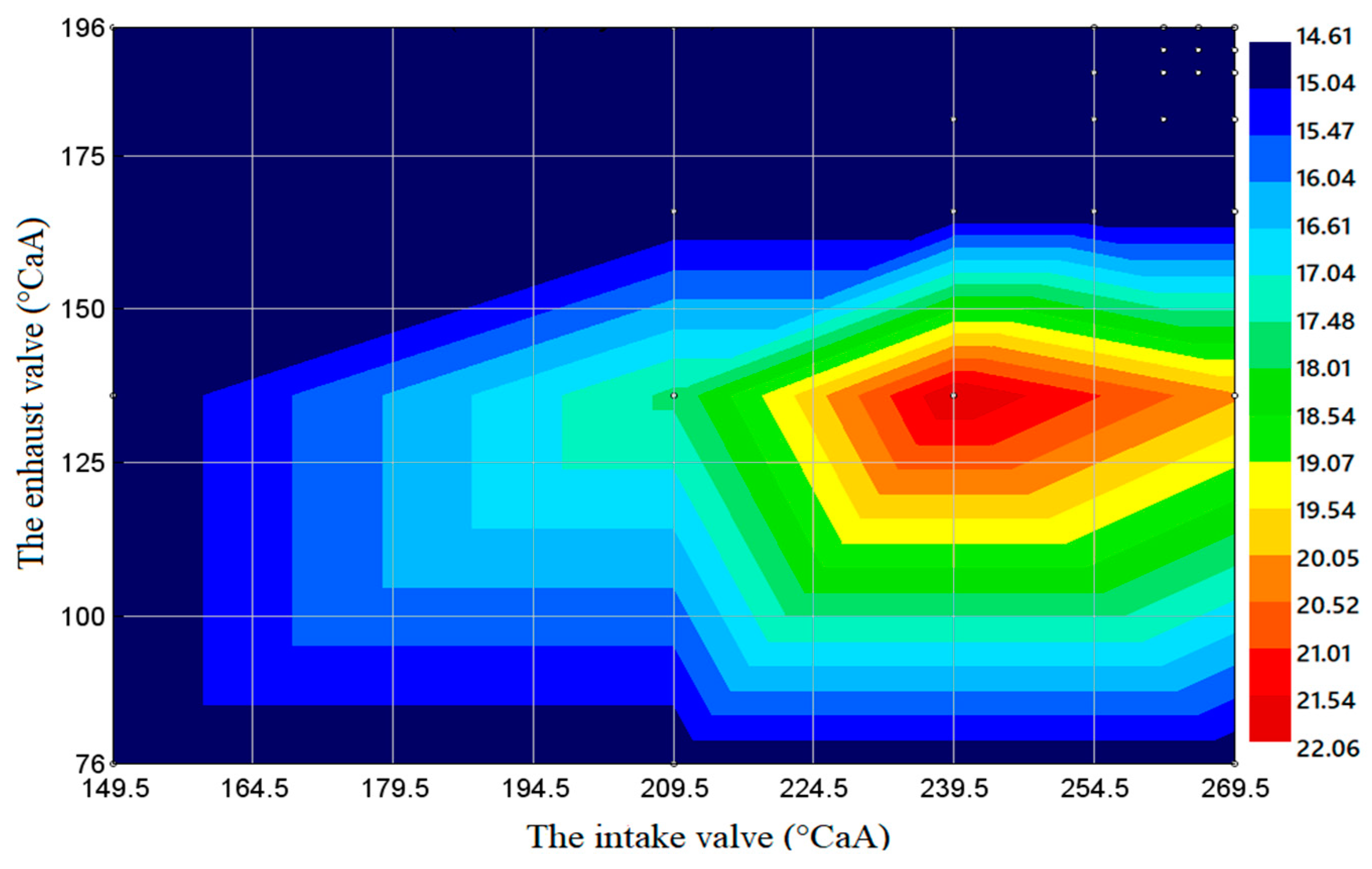
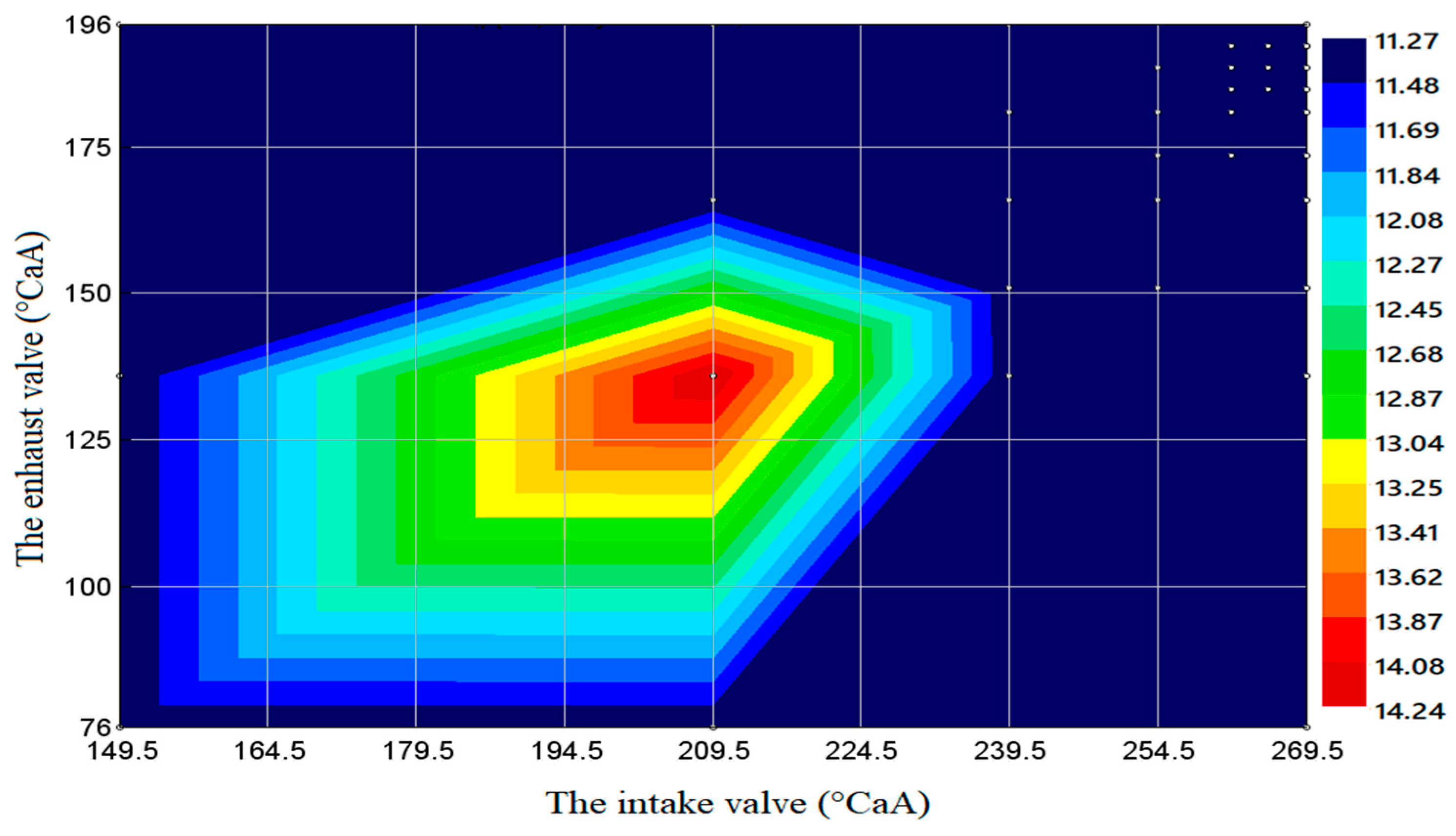
- When using B20 biodiesel under 100% load conditions, when the intake valve closing needs to be delayed by about 30 °CAA and the exhaust valve opening needs to be advanced by about 28 °CAA (near the intake valve timing 179 °CAA and the exhaust valve timing 174 °CAA), the output power of the diesel engine has a maximum area. When the intake valve closing is delayed by about 29 °CAA and the exhaust valve opening is advanced by about 44 °CAA (near the intake valve timing 180 °CAA and the exhaust valve timing 180 °CAA), the fuel consumption is the lowest. The soot emission is the lowest in the area around 264.5 °CAA of intake valve timing and 191 °CAA of exhaust valve timing. Near 232 °CAA of intake valve timing and 189 °CAA of exhaust valve timing is the area where NOX emission has a minimum value.
- (4)
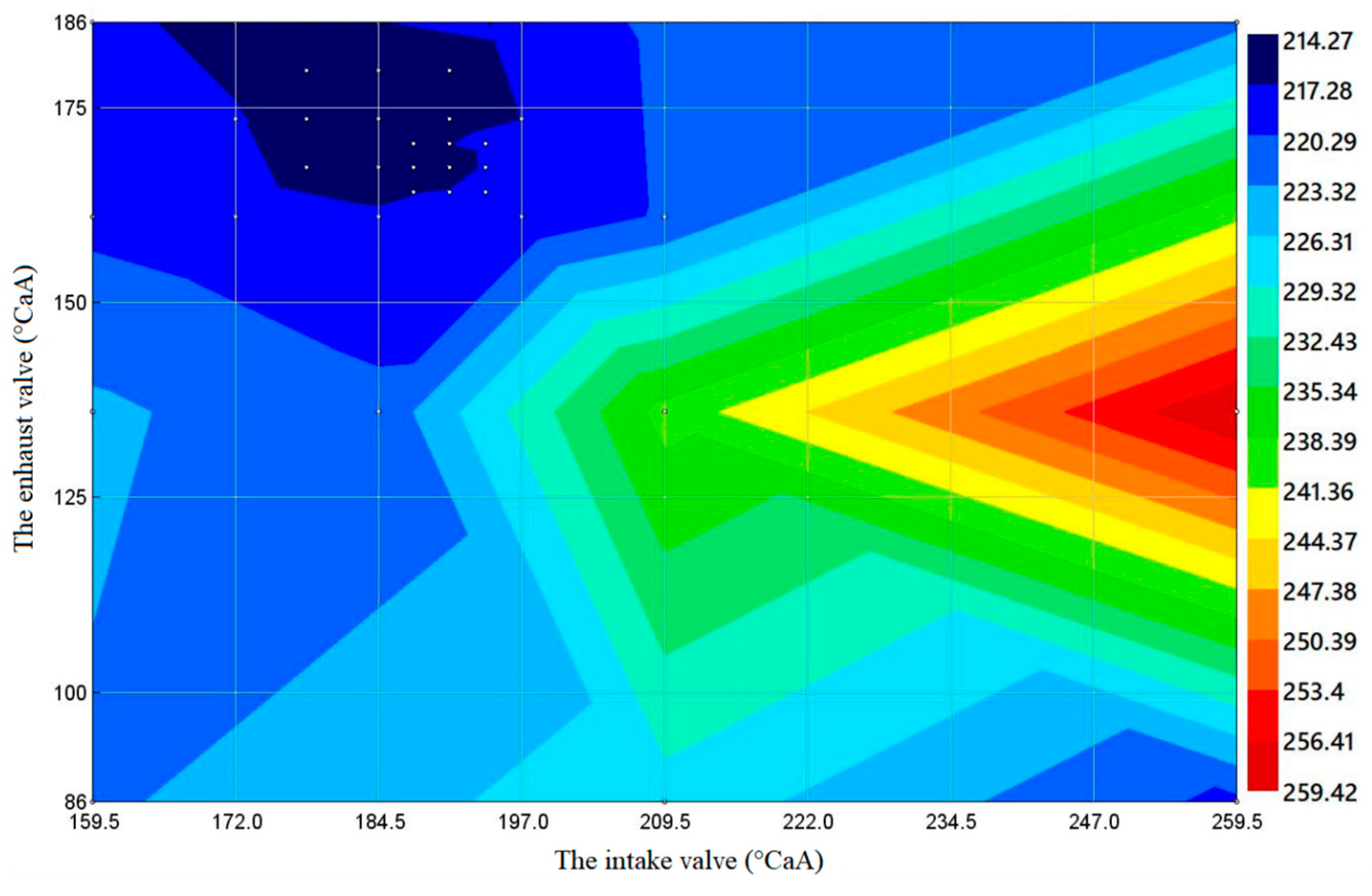
- When using B20 biodiesel under 50% load condition the diesel engine has the maximum output power when the intake valve closing needs to be delayed by about 15 °CAA and the exhaust valve opening needs to be advanced by about 17 °CAA (near 224.5 °CAA of intake valve timing and 119 °CAA of exhaust valve timing). Near 187.5 °CAA of intake valve timing and 170 °CAA of exhaust valve timing (when intake valve closing needs to be delayed by about 22 °CAA and exhaust valve opening needs to be advanced by about 34 °CAA), the lowest fuel consumption area appears. The area around 239.5 °CAA of intake valve timing and 136 °CAA of exhaust valve timing is the area with maximum soot emission. The lowest NOX emission area appears in the area centered around 202 °CAA of intake valve timing and 98 °CAA of exhaust valve timing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| B20 | 80% diesel + 20% biodiesel |
| NOx | Nitrogen Oxides |
| BTE | Brake Thermal Efficiency |
| BSFC | Brake Specific Fuel Consumption |
| EGR | Exhaust Gas Re-circulation |
| DFP | Davidon–Fletcher–Powell Algorithm |
| RLT | Reformulation-Linearization-Technique |
| VCP | Variable Cam Profile Miller Cycle |
| VVA | Variable Valve Overlap Angle Miller Cycle |
| CO | Carbon Monoxide |
| BFSC | Brake Specific Fuel Consumption |
References
- Tian, Z.; Wang, Y.; Zhen, X.; Liu, Z. The effect of methanol production and application in internal combustion engines on emissions in the context of carbon neutrality: A review. Fuel 2022, 320, 123902. [Google Scholar] [CrossRef]
- Xie, B.; Peng, Q.; Yang, W.; Li, S.; E, J.; Li, Z.; Tao, M.; Zhang, A. Effect of pins and exit-step on thermal performance and energy efficiency of hydrogen-fueled combustion for micro-thermophotovoltaic. Energy 2022, 239, 122341. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, J.; Tan, D.; Feng, Z.; Luo, J.; Tan, Y.; Huang, Y. The effects of Fe2O3 based DOC and SCR catalyst on the combustion and emission characteristics of a diesel engine fueled with biodiesel. Fuel 2021, 290, 120039. [Google Scholar] [CrossRef]
- Zhang, Z.; Lv, J.; Xie, G.; Wang, S.; Ye, Y.; Huang, G.; Tan, D. Effect of assisted hydrogen on combustion and emission characteristics of a diesel engine fueled with biodiesel. Energy 2022, 254, 124269. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Xie, G.; Li, J.; Xu, W.; Jiang, F.; Huang, Y.; Tan, D. Investigation on the combustion and emission characteristics of diesel engine fueled with diesel/methanol/n-butanol blends. Fuel 2022, 314, 123088. [Google Scholar] [CrossRef]
- E, J.; Zuo, W.; Gao, J.; Peng, Q.; Zhang, Z.; Hieu, P.M. Effect analysis on pressure drop of the continuous regeneration-diesel particulate filter based on NO2 assisted regeneration. Appl. Therm. Eng. 2016, 100, 356–366. [Google Scholar] [CrossRef]
- Chen, S.; Tian, J.; Li, J.; Li, W.; Zhang, Z. Investigation of the Performance and Emission Characteristics of a Diesel Engine with Different Diesel–Methanol Dual-Fuel Ratios. Processes 2021, 9, 1944. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, J.; Lv, J.; Xu, W.; Tan, D.; Jiang, F.; Huang, H. Investigation on the effects of non-uniform porosity catalyst on SCR characteristic based on the field synergy analysis. J. Environ. Chem. Eng. 2022, 10, 107056. [Google Scholar] [CrossRef]
- Li, J.; Ji, L.; Xu, Y.; Xie, J. The Valve Timing Optimization of the Diesel Engine Based on Response Surface Methodology. Stud. Eng. Technol. 2013, 1, 44. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Cheng, F.; Zhang, T.; Liu, G.; Yuan, J.; Mao, P. Visible-light photoredox-promoted desilylative allylation of α-silylamines: An efficient route to synthesis of homoallylic amines. Tetrahedron Lett. 2021, 81, 153357. [Google Scholar] [CrossRef]
- Peng, Q.; Xie, B.; Yang, W.; Tang, S.; Li, Z.; Zhou, P.; Luo, N. Effects of porosity and multilayers of porous medium on the hydrogen-fueled combustion and micro-thermophotovoltaic. Renew. Energy 2021, 174, 391–402. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Q.; Yang, R.; Zhu, T.; Zhao, R.; Wang, Y. Investigation on the effects of pilot injection on low temperature combustion in high-speed diesel engine fueled with n-butanol-diesel blends. Energy Convers. Manag. 2015, 106, 748–758. [Google Scholar] [CrossRef] [Green Version]
- E, J.; Xie, L.; Zuo, Q.; Zhang, G. Effect analysis on regeneration speed of continuous regeneration-diesel particulate filter based on NO2-assisted regeneration. Atmos. Pollut. Res. 2016, 7, 9–17. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Q.; Teng, W.; Pan, M.; Liu, C.; Wang, Q. Improvement of combustion performance and emissions in diesel engines by fueling n-butanol/diesel/PODE3-4 mixture. Appl. Energy 2017, 227, 38–48. [Google Scholar] [CrossRef]
- Pan, M.; Huang, R.; Liao, J.; Ouyang, T.; Zheng, Z.; Lv, D.; Huang, H. Effect of EGR dilution on combustion, performance and emission characteristics of a diesel engine fueled with n-pentanol and 2-Ethylhexyl nitrate additive. Energy Convers. Manag. 2018, 176, 246–255. [Google Scholar] [CrossRef]
- Pan, M.; Huang, R.; Liao, J.; Jia, C.; Zhou, X.; Huang, H.; Huang, X. Experimental study of the spray, combustion, and emission performance of a diesel engine with high n-pentanol blending ratios. Energy Convers. Manag. 2019, 194, 1–10. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Li, J.; Lv, J.; Wang, S.; Zhong, Y.; Dong, R.; Gao, S.; Cao, C.; Tan, D. Investigation on combustion, performance and emission characteristics of a diesel engine fueled with diesel/alcohol/n-butanol blended fuels. Fuel 2022, 320, 123975. [Google Scholar] [CrossRef]
- Lou, D.; Qi, B.; Zhang, Y.; Fang, L. Study on the Emission Characteristics of Urban Buses at Different Emission Standards Fueled with Biodiesel Blends. ACS Omega 2022, 7, 7213–7222. [Google Scholar] [CrossRef]
- Pan, X.; Zhao, Y.; Lou, D.; Fang, L. Study of the Miller Cycle on a Turbocharged DI Gasoline Engine Regarding Fuel Economy Improvement at Part Load. Energies 2020, 13, 1500. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Zhou, J.; Hu, J.; Tan, X.; Cao, W.; Tan, Z. Study on Performance of Locomotive Diesel Engine Fueled with Biodiesel Using Two Miller Cycle Technologies. Processes 2022, 10, 372. [Google Scholar] [CrossRef]
- Georgiou, C.; Azimov, U. Analysis and Multi-Parametric Optimisation of the Performance and Exhaust Gas Emissions of a Heavy-Duty Diesel Engine Operating on Miller Cycle. Energies 2020, 13, 3724. [Google Scholar] [CrossRef]
- Jahanbakhshi, A.; Karami-Boozhani, S.; Yousefi, M.; Ooi, J.B. Performance of bioethanol and diesel fuel by thermodynamic simulation of the miller cycle in the diesel engine. Results Eng. 2021, 12, 100279. [Google Scholar] [CrossRef]
- Guan, W.; Pedrozo, V.B.; Wang, X.; Zhao, H.; Ban, Z.; Lin, T. Exploring the Potential of Miller Cycle with and without EGR for Maximum Efficiency and Minimum Exhaust Emissions in a Heavy-Duty Diesel Engine. SAE Int. J. Engines 2019, 12, 579–595. [Google Scholar] [CrossRef] [Green Version]
- Sürmen, A.; Arslan, R.; Kopmaz, O.; Avci, A.; Karagöz, I.; Karamangil, I. Development of a variable-profile cam to enhance the volumetric efficiency of IC engines. Int. J. Veh. Des. 2017, 73, 63–75. [Google Scholar] [CrossRef]
- Perceau, M.; Guibert, P.; Guilain, S. Zero-dimensional turbulence modeling of a spark ignition engine in a Miller cycle « Dethrottling » approach using a variable valve timing system. Appl. Therm. Eng. 2021, 199, 117535. [Google Scholar] [CrossRef]
- Wang, J.; Duan, X.; Wang, W.; Guan, J.; Li, Y.; Liu, J. Effects of the continuous variable valve lift system and Miller cycle strategy on the performance behavior of the lean-burn natural gas spark ignition engine. Fuel 2021, 297, 120762. [Google Scholar] [CrossRef]
- Milov, K.V. Computational studies of the influence of variable valve timing on the performance of a gas engine with Miller’s thermodynamic cycle. J. Phys. Conf. Ser. 2021, 2061, 012066. [Google Scholar] [CrossRef]
- Xing, K.; Huang, H.; Guo, X.; Wang, Y.; Tu, Z.; Li, J. Thermodynamic analysis of improving fuel consumption of natural gas engine by combining Miller cycle with high geometric compression ratio. Energy Convers. Manag. 2022, 254, 115219. [Google Scholar] [CrossRef]
- Wang, D.; Shi, L.; Zhang, H.; Li, X.; Qian, Y.; Deng, K. Research on influence and demand of Miller cycle based on the coupling of marine low-speed engine and turbocharger. Appl. Therm. Eng. 2022, 200, 117624. [Google Scholar] [CrossRef]
- Sun, X.; Liang, X.; Zhou, P.; Yu, H.; Cao, X. Computational study of NO x reduction on a marine diesel engine by application of different technologies. Energy Procedia 2019, 158, 4447–4452. [Google Scholar] [CrossRef]
- Zhou, S.; Gao, R.; Feng, Y.; Zhu, Y. Evaluation of Miller cycle and fuel injection direction strategies for low NOx emission in marine two-stroke engine. Int. J. Hydrogen Energy 2017, 42, 20351–20360. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Jia, B.; Roskilly, A.P. Application of Miller cycle with turbocharger and ethanol to reduce NOx and particulates emissions from diesel engine—A numerical approach with model validations. Appl. Therm. Eng. 2019, 150, 904–911. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, Q.; Ma, Q.; Chen, Z.; Zheng, Z. Effect of various ethanol/diesel cosolvents addition on combustion and emission characteristics of a CRDI heavy diesel engine. Energy Rep. 2022, 8, 735–748. [Google Scholar] [CrossRef]
- Huang, Z.; Shen, K.; Wang, L.; Chen, W.; Pan, J. Experimental study on the effects of the Miller cycle on the performance and emissions of a downsized turbocharged gasoline direct injection engine. Adv. Mech. Eng. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Roper, E.; Wang, Y.; Zhang, Z. Numerical Investigation of the Application of Miller Cycle and Low-Carbon Fuels to Increase Diesel Engine Efficiency and Reduce Emissions. Energies 2022, 15, 1783. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, Z.; Li, X.; Wu, C.; Yang, F. Simulation Analysis of Fuel Economy of the GDI Engine with a Miller Cycle and EGR Based on GT-Power. Processes 2022, 10, 319. [Google Scholar] [CrossRef]
- Allami, H.A.; Nayebzadeh, H. The assessment of the engine performance and emissions of a diesel engine fueled by biodiesel produced using different types of catalyst. Fuel 2021, 305, 121525. [Google Scholar] [CrossRef]
- Hasan, A.O.; Osman, A.I.; Al-Muhtaseb, A.A.H.; Al-Rawashdeh, H.; Abu-jrai, A.; Ahmad, R.; Gomaa, M.R.; Deka, T.J.; Rooney, D.W. An experimental study of engine characteristics and tailpipe emissions from modern DI diesel engine fuelled with methanol/diesel blends. Fuel Process. Technol. 2021, 220, 106901. [Google Scholar] [CrossRef]
- Tong, Q.; Chen, H.; He, J.; Su, X.; Wei, Z.; Sun, F.; Xu, H.; Wang, F. Experimental studies of combustion and emission characteristics of diesel engine fueled with diesel/cyclopentanone blend. Energy Rep. 2021, 7, 6756–6768. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Tian, J.; Zhong, Y.; Zou, Z.; Dong, R.; Gao, S.; Xu, W.; Tan, D. The effects of Mn-based catalysts on the selective catalytic reduction of NOx with NH3 at low temperature: A review. Fuel Process. Technol. 2022, 230, 107213. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Tian, J.; Dong, R.; Zou, Z.; Gao, S.; Tan, D. Performance, combustion and emission characteristics investigations on a diesel engine fueled with diesel/ethanol/n-butanol blends. Energy 2022, 249, 123733. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Teng, W.; Huang, R.; Liu, Q. Effects of EGR rates on combustion and emission characteristics in a diesel engine with n-butanol/PODE3-4/diesel blends. Appl. Therm. Eng. 2018, 146, 212–222. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Teng, W.; Liu, Q.; Zhou, C.; Wang, Q. Combustion performance and emission characteristics of a diesel engine under low-temperature combustion of pine oil-diesel blends. Energy Convers. Manag. 2016, 128, 317–326. [Google Scholar] [CrossRef]
- Huang, J.; Xiao, H.; Yang, X.; Guo, F.; Hu, X. Effects of methanol blending on combustion characteristics and various emissions of a diesel engine fueled with soybean biodiesel. Fuel 2020, 282, 118734. [Google Scholar] [CrossRef]
- Taib, N.M.; Zainuddin, M.S.; Mansor, M.R.A.; Ilham, Z. Performance and emission opacity of canola and soybean biodiesel fuel in a diesel engine. J. Mech. Eng. Sci. 2018, 12, 3689–3699. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Q.; Wang, Q.; Zhou, C.; Mo, C. Experimental investigation of particle emissions under different EGR ratios on a diesel engine fueled by blends of diesel/gasoline/n-butanol. Energy Convers. Manag. 2016, 121, 212–223. [Google Scholar] [CrossRef]
- Huang, H.; Teng, W.; Li, Z.; Liu, Q.; Wang, Q. Improvement of emission characteristics and maximum pressure rise rate of diesel engines fueled with n-butanol/PODE3-4/diesel blends at high injection pressur. Energy Convers. Manag. 2017, 152, 45–56. [Google Scholar] [CrossRef]
- Ma, B.; Yao, A.; Yao, C.; Wu, T.; Wang, B.; Gao, J.; Chao, C. Exergy loss analysis on diesel methanol dual fuel engine under different operating parameters. Appl. Energy 2020, 261, 114483. [Google Scholar] [CrossRef]
- Yadav, J.; Ramesh, A. Injection strategies for reducing smoke and improving the performance of a butanol-diesel common rail dual fuel engine. Appl. Energy 2018, 212, 1–12. [Google Scholar] [CrossRef]
- Hong, C.; Estefen, S.F.; Lourenço, M.I.; Wang, Y. A nonlinear constrained optimization model for subsea pipe route selection on an undulating seabed with multiple obstacles. Ocean. Eng. 2019, 186, 106088. [Google Scholar] [CrossRef]
- Sangeetha, V.; Thirisangu, K.; Elumalai, P. Dual Simplex Method Based solution for a Fuzzy Transportation Problem. J. Phys. Conf. Ser. 2021, 1947, 01201. [Google Scholar] [CrossRef]
- Jiang, F.; Cao, W.; Tan, X.; Hu, J.; Zhou, J.; Tan, Z. Optimization Analysis of Locomotive Diesel Engine Intake System Based on Matlab-Simulink and GT-Power. Processes 2022, 10, 157. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Li, J.; Cao, C.; Wang, S.; Lv, J.; Zheng, W.; Tan, D. The development of diesel oxidation catalysts and the effect of sulfur dioxide on catalysts of metal-based diesel oxidation catalysts: A review. Fuel Process. Technol. 2022, 233, 107317. [Google Scholar] [CrossRef]
- Oxenham, L.; Wang, Y. A Study of the Impact of Methanol, Ethanol and the Miller Cycle on a Gasoline Engine. Energies 2021, 14, 4847. [Google Scholar] [CrossRef]
- Jeya Jeevahan, G.; Mageshwaran, G.; Britto Joseph, R.B.; Durai Raj, R.; Kannan, R.T. Various strategies for reducing NOx emissions of biodiesel fuel used in conventional diesel engines: A review. Chem. Eng. Commun. 2017, 204, 1202–1223. [Google Scholar] [CrossRef]
- Guan, W.; Pedrozo, V.B.; Zhao, H.; Ban, Z.; Lin, T. Variable valve actuation–based combustion control strategies for efficiency improvement and emissions control in a heavy-duty diesel engine. Int. J. Engine Research. 2020, 21, 578–591. [Google Scholar] [CrossRef]
- Wang, P.; Hu, Z.; Shi, L.; Tang, X.; Liu, Y.; Deng, K. Experimental investigation of the effects of Miller timing on performance, energy and exergy characteristics of two-stage turbocharged marine diesel engine. Fuel 2021, 292, 120252. [Google Scholar] [CrossRef]
- Ge, J.; Wu, G.; Yoo, B.; Choi, N. Effect of injection timing on combustion, emission and particle morphology of an old diesel engine fueled with ternary blends at low idling operation. Energy 2022, 253, 124150. [Google Scholar] [CrossRef]
- Ge, J.; Wu, G.; Choi, N. Comparative study of pilot–main injection timings and diesel/ethanol binary blends on combustion, emission and microstructure of particles emitted from diesel engines. Fuel 2022, 313, 122658. [Google Scholar] [CrossRef]
- Ge, J.; Kim, H.; Yoon, S.; Choi, N. Optimization of palm oil biodiesel blends and engine operating parameters to improve performance and PM morphology in a common rail direct injection diesel engine. Fuel 2020, 260, 116236. [Google Scholar] [CrossRef]
- Zhang, Z.; Lv, J.; Li, W.; Long, J.; Wang, S.; Tan, D.; Yin, Z. Performance and emission evaluation of a marine diesel engine fueled with natural gas ignited by biodiesel-diesel blended fuel. Energy 2022, 256, 124662. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, Y.; He, J.; Fang, D.; Zhu, J.; Meng, X. Effect of friction stir processing parameters on the microstructure and properties of ZK60 magnesium alloy. Mater. Res. Express 2022, 8, 016508. [Google Scholar] [CrossRef]
- Tan, D.; Chen, Z.; Li, J.; Luo, J.; Yang, D.; Cui, S.; Zhang, Z. Effects of Swirl and Boiling Heat Transfer on the Performance Enhancement and Emission Reduction for a Medium Diesel Engine Fueled with Biodiesel. Processes 2021, 9, 568. [Google Scholar] [CrossRef]
- Tan, Y.; E, J.; Chen, J.; Liao, G.; Zhang, F.; Li, J. Investigation on combustion characteristics and thermal performance of a three rearward-step structure micro combustor fueled by premixed hydrogen/air. Renew. Energy 2022, 186, 486–504. [Google Scholar] [CrossRef]

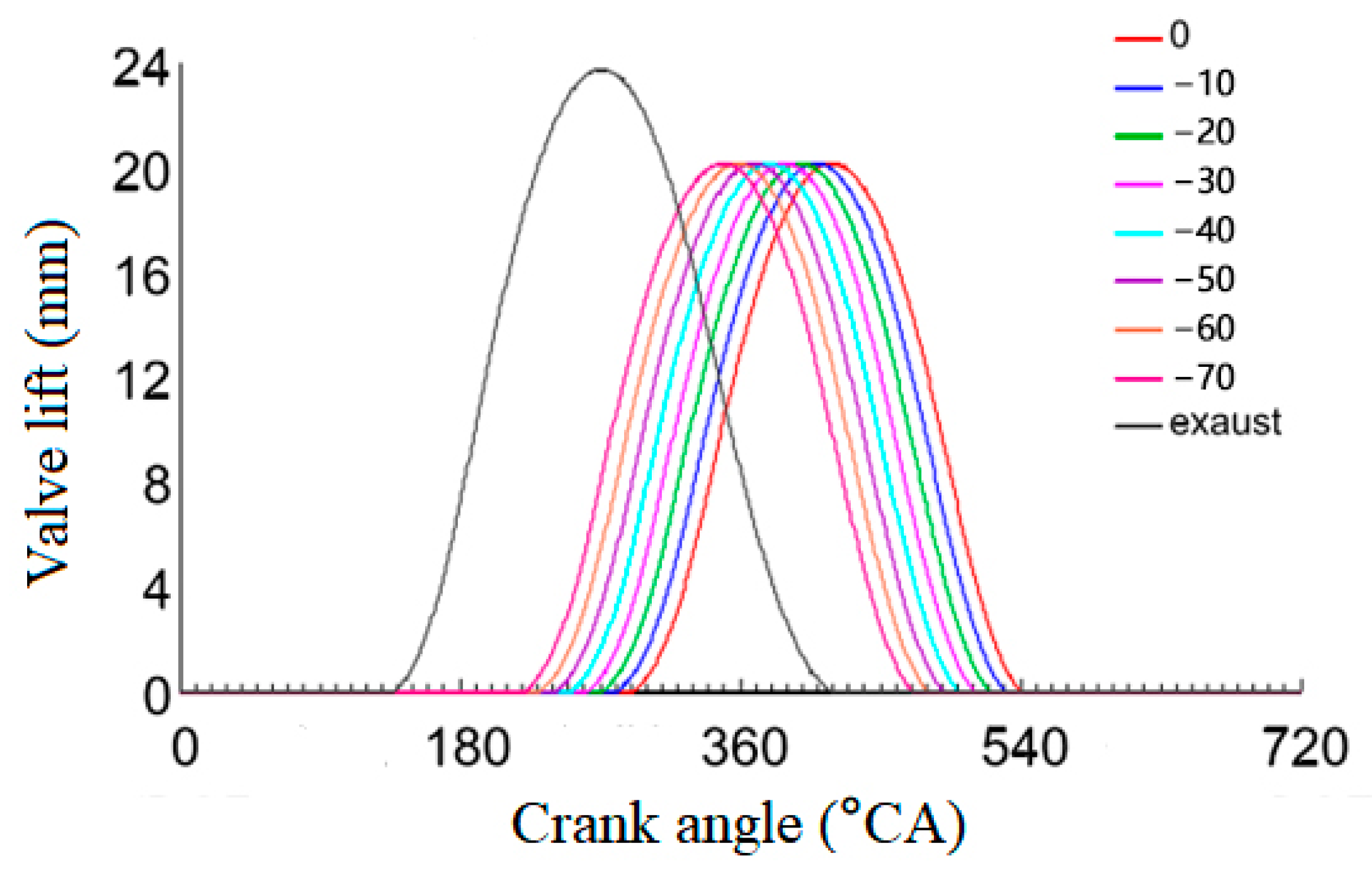



| Miller Degree (°CA) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Translation angle of intake valve lift curve (°CA) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Intake valve closing time (°CA) | 540 | 530 | 520 | 510 | 500 | 490 | 480 | 470 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Zhou, J.; Hu, J.; Tan, X.; Mo, Q.; Cao, W. Performance Comparison and Optimization of 16V265H Diesel Engine Fueled with Biodiesel Based on Miller Cycle. Processes 2022, 10, 1412. https://doi.org/10.3390/pr10071412
Jiang F, Zhou J, Hu J, Tan X, Mo Q, Cao W. Performance Comparison and Optimization of 16V265H Diesel Engine Fueled with Biodiesel Based on Miller Cycle. Processes. 2022; 10(7):1412. https://doi.org/10.3390/pr10071412
Chicago/Turabian StyleJiang, Feng, Junming Zhou, Jie Hu, Xueyou Tan, Qinglie Mo, and Wentong Cao. 2022. "Performance Comparison and Optimization of 16V265H Diesel Engine Fueled with Biodiesel Based on Miller Cycle" Processes 10, no. 7: 1412. https://doi.org/10.3390/pr10071412





