In this section we assess the reliability of our nanosensor under both nanowire probability models. First we define n × m to be the size of the nanosensor. For all lattice types n and m refer to the number of vertices that could potentially be in the row and column, respectively. For a nanosensor of size n × m we define Xn × m, XEn × m, and XHn × m to be the random variables that represent the number of cycles of H2 that a nanosensor with SL, ETL, and HL structure, respectively, will last through before they no longer percolate. We then define Rn × m(x), REn × m(x), and RHn × m(x) to be the reliability functions for nanosensors with SL, ETL, and HL structure, respectively. Similarly, E(Xn × m), E(XEn × m), and E(XHn × m) are the expected lifetimes.
2.1. Model 1: p1=p2=...=p
In [
5] and [
7] the authors presented exact formulas for the reliability functions and expected lifetimes of 2
× m nanosensors with SL structure, 3
× m nanosensors with ETL structure, and 4
× m nanosensors with HL structure when the movement of the electrical current was restricted. These formulas still hold when the electrical current can move in all directions, because percolation on these specific structures does not benefit from the electrical current being able to move right to left. Specifically for 2
× m nanosensors with SL structure and 4
× m nanosensors with HL structure, right to left movement would only occur after percolation was complete. For 3
× m nanosensors with ETL structure there are opportunities for the electrical current to move right to left before percolation completes, however these opportunities create redundancy. Right to left movement would either occur after percolation was complete or would take the electrical current back to the left contact.
In general when the electrical current can move in all directions, the reliability functions and expected lifetimes of
n × m sized nanosensors will be the same as or higher than when movement is restricted. To see the difference between the two scenarios we use the following algorithm, which is a slight modification of the algorithm proposed in [
5,
6,
7]. Here we use the algorithm to obtain estimates for the exact value of the reliability function and expected lifetime when the electrical current can move in all directions.
Algorithm to Simulate the Lifetime of a Nanosensor A chosen lattice (SL, ETL, or HL) is generated.
Under each model a sequence of iid Bernoulli(pi) random variables are generated and assigned to the nanowires to determine their status as functioning or broken during cycle i,
i = 1,2,3,...
Any nanowires that break are removed from consideration, and the remaining nanowires are sorted into open clusters (any connected component of the lattice in which all of the nanowires are functioning).
The clusters are tested for percolation. If no clusters percolate, then the algorithm is stopped. The result is recorded, and the next simulation starts.
If one of the clusters percolates, then the remaining open nanowires are assigned new Bernoulli random variables and steps (c) and (d) are repeated. Example 1 demonstrates the accuracy of our algorithm and presents several cases where there is no increase in reliability or expected lifetime.
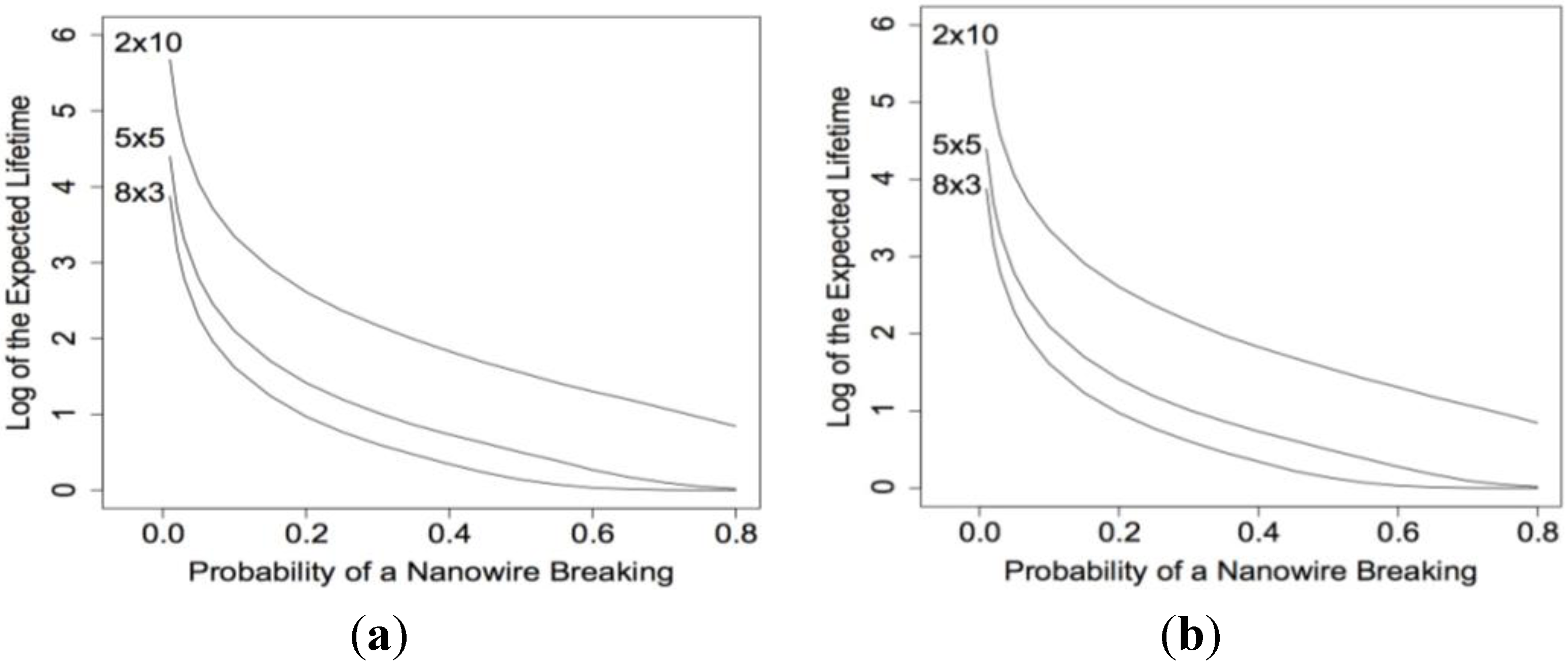
Example 1: The lifetime of the nanosensor was simulated 10,000 times for each of three nanosensors with the SL structure for several values of
p.
Figure 3a shows the log of the expected lifetime for these three nanosensors when the electrical current can move in all directions. For comparison,
Figure 3b shows the log of the expected lifetime for the same three nanosensors when movement is restricted. As can be seen, there is very little difference between the two Figures. As previously stated, the expected lifetime for the 2
× 10 nanosensor will be the same in both scenarios. This also allows us to look at the accuracy of our algorithm. Comparing the values for the expected lifetime for the 2
× 10 nanosensor in both scenarios, we see that our algorithm appears to be accurate. The two figures also show us that the expected lifetimes of the 5
× 5 and 8
× 3 sized nanosensors do not benefit from the electrical current moving in all directions. Similarly, the reliability functions do not benefit either.
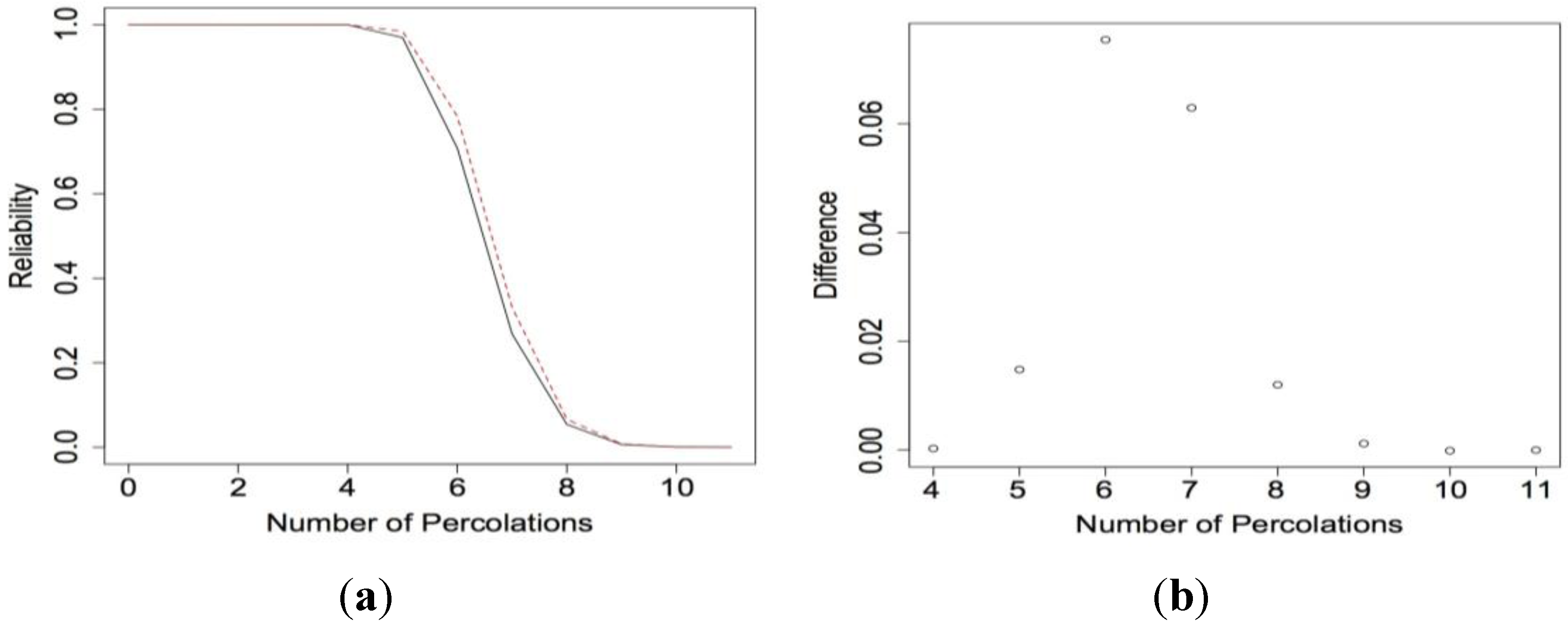
Figure 4a shows the reliability function for the 5
× 5 nanosensor for both scenarios when
p = 0.95. Since the difference between the two functions is not discernible, we have plotted the differences in
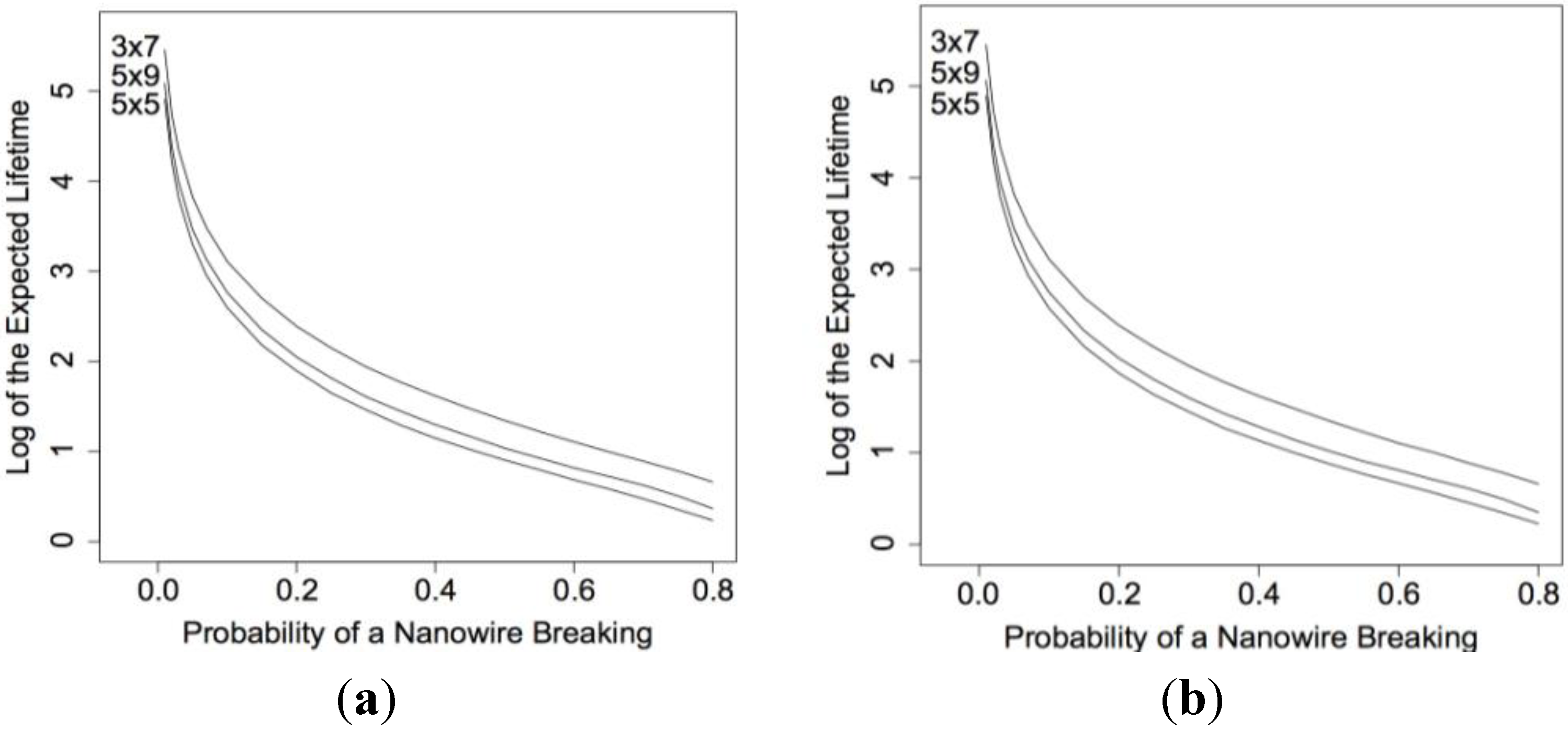
Figure 4b. They are all very close to zero. We repeated this example for three nanosensors with ETL structure and for three nanosensors with HL structure. Comparing the two scenarios we again see that with smaller sized nanosensors there is little difference in the expected lifetimes. See
Figure 5a and
Figure 6b.
In general, we find that larger nanosensors benefit more from the electrical current moving in all directions. This is due to the fact that allowing the electrical current to move right to left creates more percolation paths when the nanosensor is larger. Example 2 provides a rational for this claim, while Example 3 illustrates two scenarios where the reliability of a nanosensor increases when the electrical current can move in all directions.
Figure 3.
log E(Xn × m) calculated using our algorithm for various values of n and m when (a) the electrical current can move in all directions and when (b) movement is restricted.
Figure 3.
log E(Xn × m) calculated using our algorithm for various values of n and m when (a) the electrical current can move in all directions and when (b) movement is restricted.
Figure 4.
(a) R5 × 5(x) calculated using our algorithm when the electrical current can move in all directions and when movement is restricted when p = 0.95 and (b) the difference between the R5 × 5(x).
Figure 4.
(a) R5 × 5(x) calculated using our algorithm when the electrical current can move in all directions and when movement is restricted when p = 0.95 and (b) the difference between the R5 × 5(x).
Figure 5.
log E(XEn × m) calculated using our algorithm for various values of n and m when (a) the electrical current can move in all directions and when (b) movement is restricted.
Figure 5.
log E(XEn × m) calculated using our algorithm for various values of n and m when (a) the electrical current can move in all directions and when (b) movement is restricted.
Figure 6.
log E(XHn × m) calculated using our algorithm for various values of n and m when (a) the electrical current can move in all directions and when (b) movement is restricted.
Figure 6.
log E(XHn × m) calculated using our algorithm for various values of n and m when (a) the electrical current can move in all directions and when (b) movement is restricted.
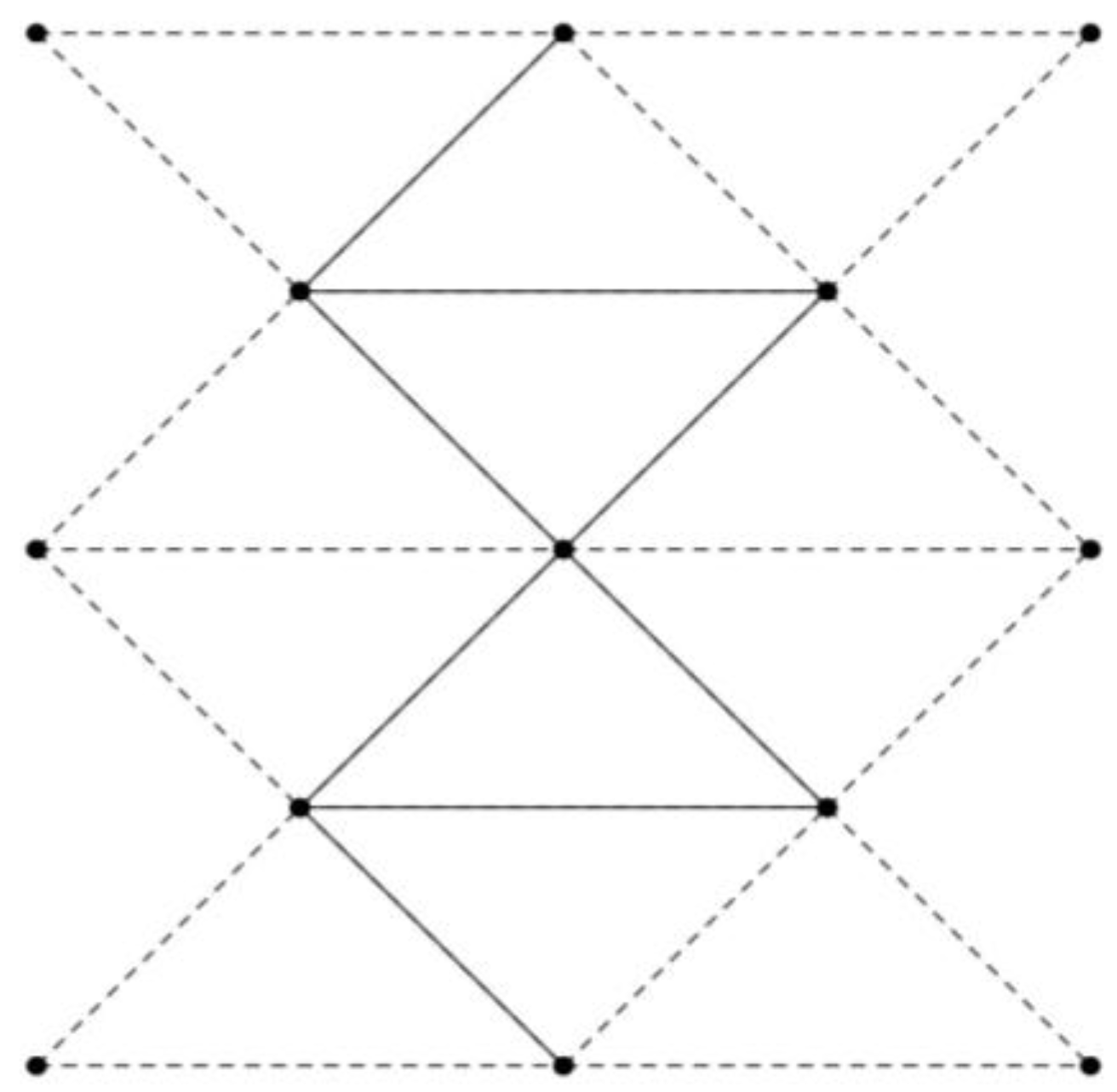
Example 2: Consider the 5
× 5 nanosensor with ETL structure shown in
Figure 7. The nanowires drawn with dashed lines do not create new percolation paths when the electrical current is allowed to move right to left. Right to left movement through the dashed nanowires would occur after percolation was complete, cause the current to return to the left contact, or cause the percolation path to unnecessarily form a loop on itself. Only the solid nanowires can create new percolation paths. However, the nanosensor will percolate without requiring the electrical current to move right to left in most cases. So the 5
× 5 nanosensor with ETL structure will not have as much of an increase in reliability as a larger nanosensor would.
Figure 7.
5 × 5 nanosensor with ETL structure. Dashed lines do not benefit percolation when the electrical current can move in all directions.
Figure 7.
5 × 5 nanosensor with ETL structure. Dashed lines do not benefit percolation when the electrical current can move in all directions.
Example 3: Consider a 10
× 10 and a 20
× 20 nanosensor with SL structure.
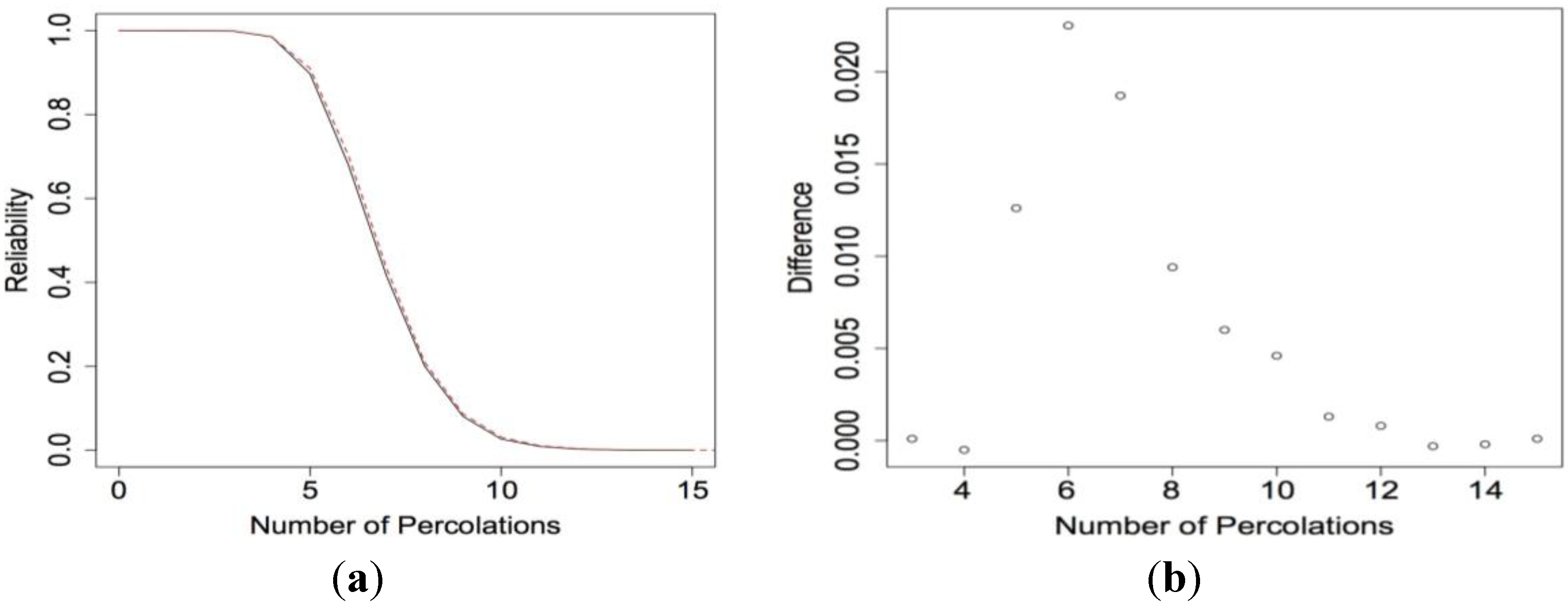
Figure 8a shows the reliability functions for the 10
× 10 nanosensor when
p = 0.90 for both scenarios. The dashed line represents the reliability when the electrical current can move in all directions. Here we begin to see a slight increase in the reliability. The largest increase occurs when
x = 6, where the difference between the two reliability functions is 0.0225. Since the differences are still hard to discern, we plotted the differences in
Figure 8b. The expected lifetime for the 10
× 10 nanosensor when
p = 0.90 is 7.3737 when the electrical current can move in all directions and 7.2985 when movement is restricted. Even though the reliability increased, the expected lifetime did not significantly change.
Figure 8.
(a) R10 × 10(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.90 and (b) the difference between the R10 × 10(x).
Figure 8.
(a) R10 × 10(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.90 and (b) the difference between the R10 × 10(x).
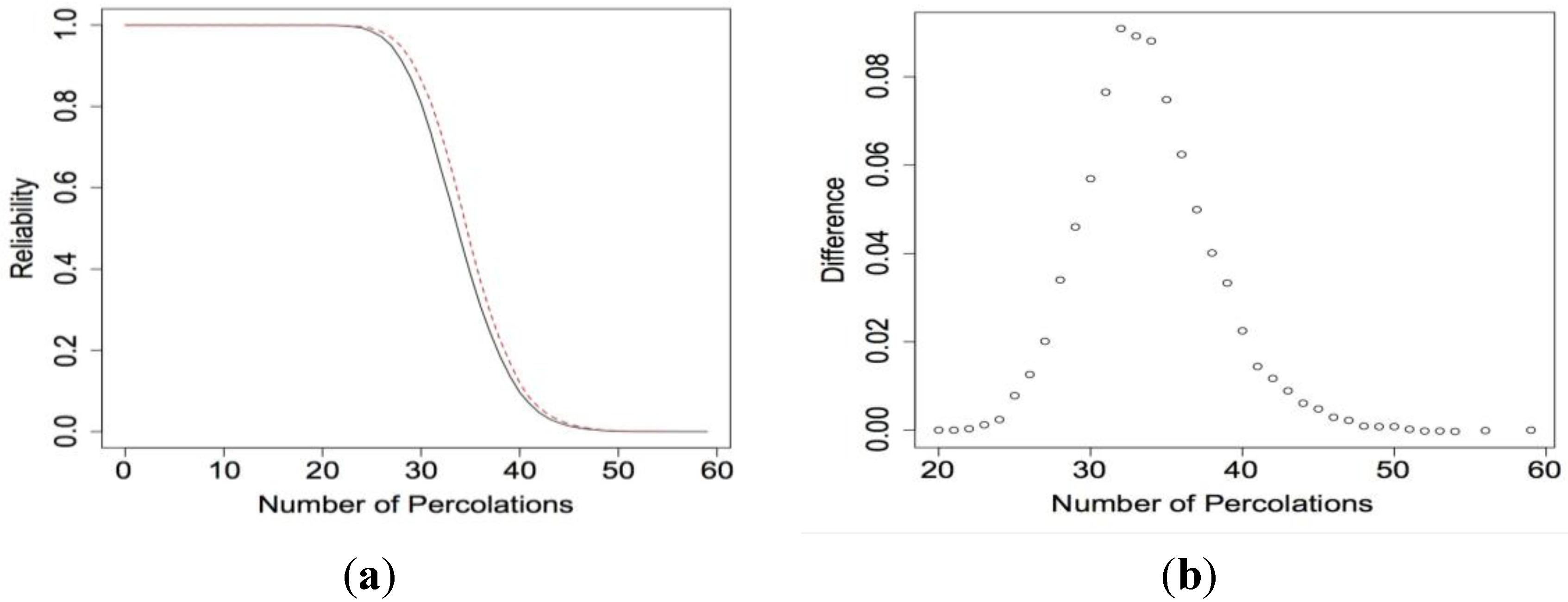
Next,
Figure 9a shows the reliability functions for the 20
× 20 nanosensor when
p = 0.90 for both scenarios. With the increase in the size of the nanosensor, the increase in reliability becomes more obvious. When
x = 32 the reliability increases by 0.0754. This is quite a large increase. Furthermore, we find that the increase in reliability is even larger for larger values of
p. See
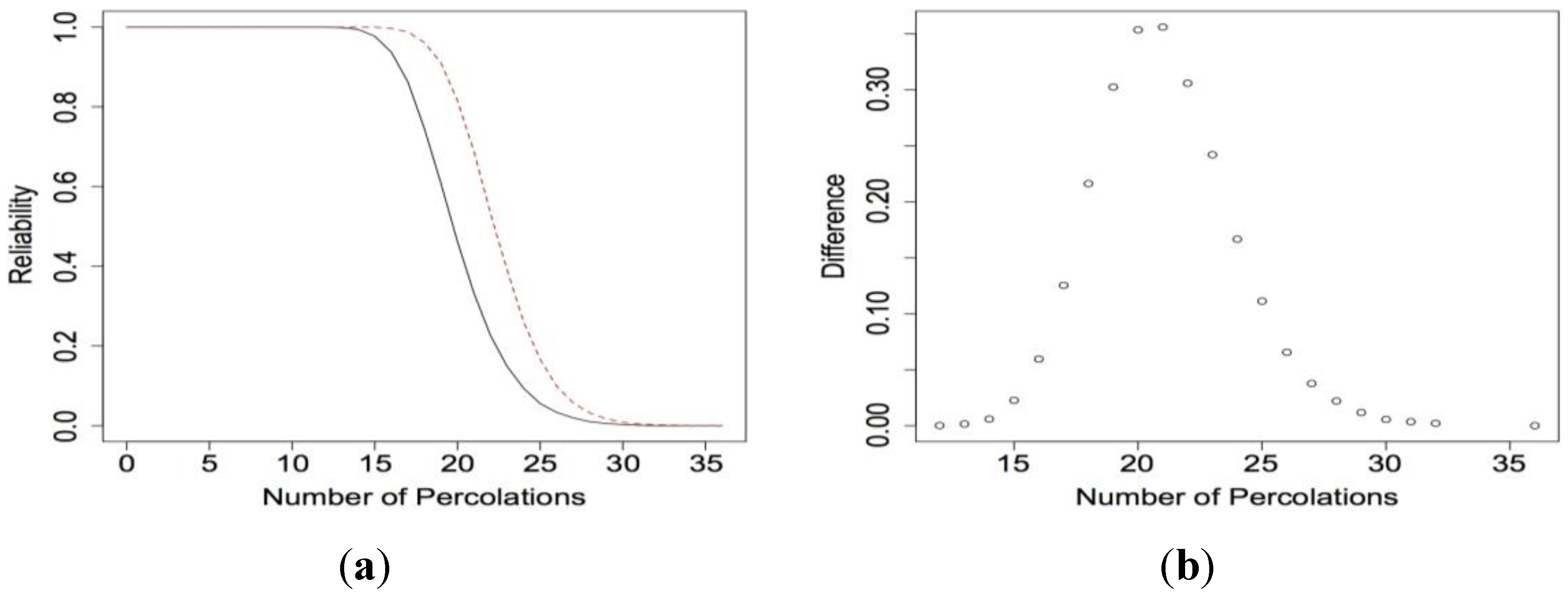
Figure 10a for the reliability functions for the 20
× 20 nanosensor when
p = 0.98. Here the largest increase in reliability is 0.0909. The expected lifetime for the nanosensor when
p = 0.98 is 35.3291 when the electrical current can move in all directions and 34.4678 when movement is restricted. Again, although the reliability increased, the expected lifetime did not change as significantly.
Figure 9.
(a) R20 × 20(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.90 and (b) the difference between the R20 × 20(x).
Figure 9.
(a) R20 × 20(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.90 and (b) the difference between the R20 × 20(x).
We can also show that a significant increase in reliability occurs for nanosensors with ETL and HL structures of larger sizes.
Figure 11a shows the reliability functions for a 21
× 21 nanosensor with ETL structure when
p = 0.95, and
Figure 12a shows the reliability functions for a 9
× 9 nanosensor with HL structure when
p = 0.90. For both figures the dashed lines represent the reliability when the electrical current can move in all directions.
Figure 10.
(a) R20 × 20(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.98 and (b) the difference between the R20 × 20(x).
Figure 10.
(a) R20 × 20(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.98 and (b) the difference between the R20 × 20(x).
Figure 11.
(a) RE21 × 21(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.95 and (b) the difference between the RE21 × 21(x).
Figure 11.
(a) RE21 × 21(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.95 and (b) the difference between the RE21 × 21(x).
Figure 12.
(a) RH9 × 9(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.90 and (b) the difference between the RH9 × 9(x).
Figure 12.
(a) RH9 × 9(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p = 0.90 and (b) the difference between the RH9 × 9(x).
2.2. Model 2: Dynamic p
In [
6] and [
7] the authors presented exact formulas for the reliability functions and expected lifetimes for
2 × m nanosensors with SL structure, 3
× m nanosensors with ETL structure, and 4
× m nanosensors with HL structure operating in dynamic environments. These formulas still hold when the electrical current can move in all directions. For general
n × m nanosensors under Model 2, we experience the same phenomena as in Model 1: the reliability increase is more substantial for larger sized nanosensors when the electrical current can move in all directions. Examples 4 and 5 support this claim.
Example 4. Using the algorithm presented in
Section 2.1 we simulated the lifetime of the nanosensor 10,000 times for a 5
× 5 nanosensor with SL structure, a 5
× 15 nanosensor with ETL structure, and a 6
× 13 nanosensor with HL structure. We assumed that these nanosensors were operating under uniform decay. Mathematically, we let
log(
pi/pi-1)
= −β,
i = 2,3,4
,... Equivalently,
pi = pi-1e−β,
i = 2,3,4,
... Here
β is the non-negative uniform decay factor. For the 5
× 5 nanosensor with SL structure and the 6
× 13 nanosensor with HL structure, we let
β = 0.01. For the 5
× 15 nanosensor with ETL structure, we let
β = 0.005.
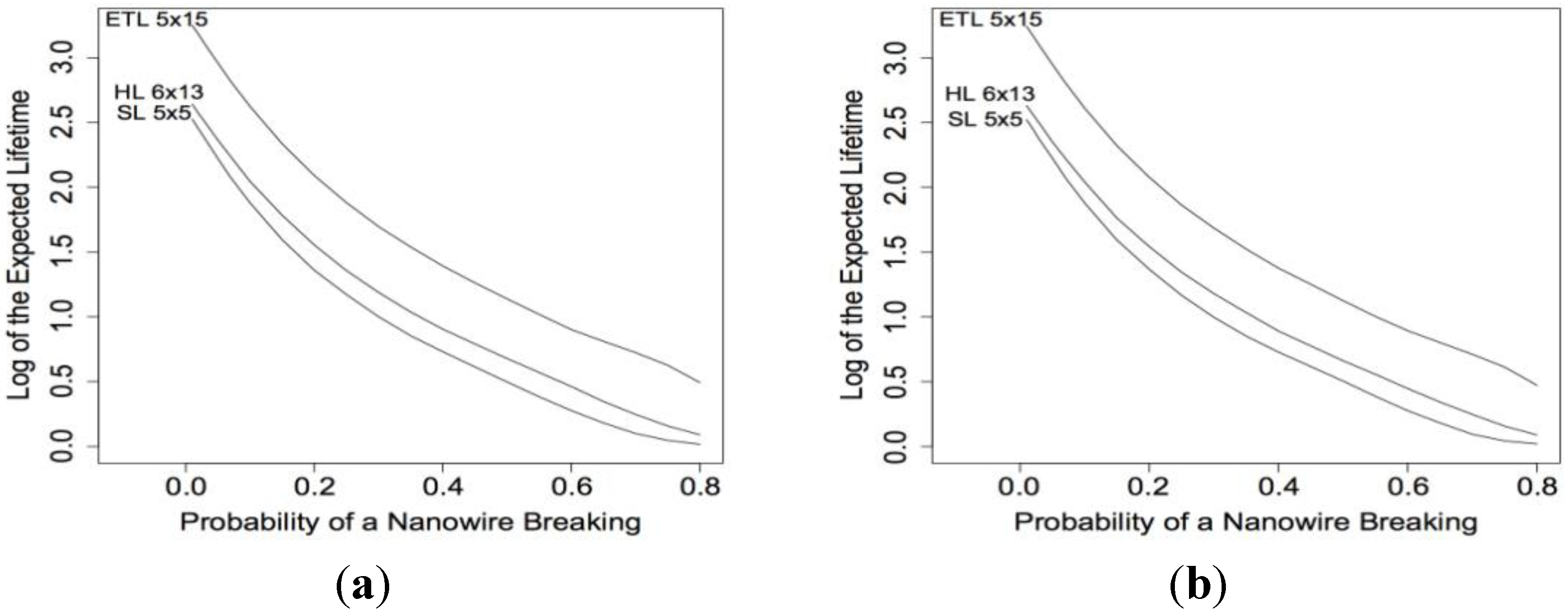
Figure 13a shows the log of the expected lifetimes for these nanosensors for several values of
p1. For comparison,
Figure 13b shows the log of the expected lifetimes when the movement of the electrical current is restricted. The nanosensors in this example are too small to benefit from the electrical current being able to move right to left, so there is little difference between the two figures.
Figure 13.
log E(X5 × 5), log E(XE5 × 15), and log E(XH6 × 13) calculated using our algorithm when β = 0.01, β = 0.005, and β = 0.01, respectively when (a) the electrical current can move in all directions and when (b) movement is restricted.
Figure 13.
log E(X5 × 5), log E(XE5 × 15), and log E(XH6 × 13) calculated using our algorithm when β = 0.01, β = 0.005, and β = 0.01, respectively when (a) the electrical current can move in all directions and when (b) movement is restricted.
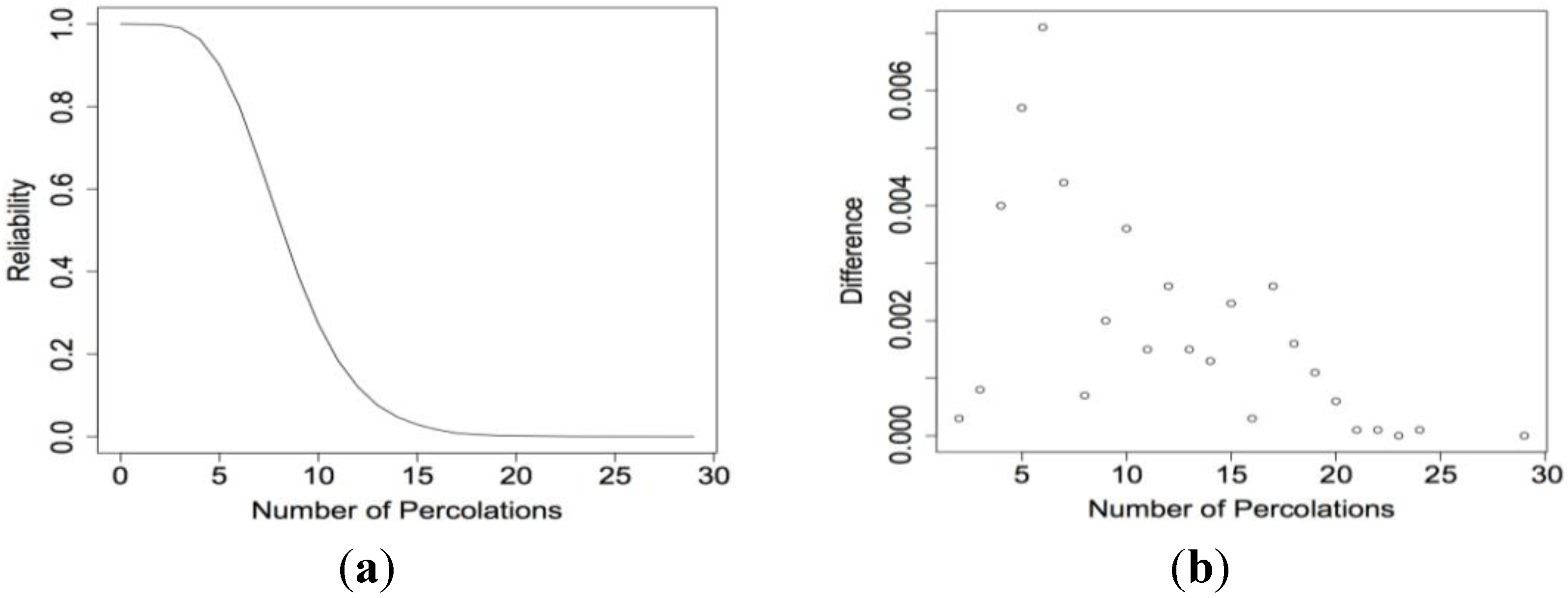
Example 5. We examined the reliability functions for three nanosensors with different structures operating under uniform decay.
Figure 14a shows the reliability functions for a 3
× 5 nanosensor with SL structure when
p1 = 0.90 and
β = 0.01 for both scenarios. For this specific nanosensor the reliability functions are exactly the same. So we can use this example to assess the accuracy of our algorithm under Model 2. The differences between the two reliability functions are shown in
Figure 14b. The differences are very small, so we conclude that our algorithm works well. Next
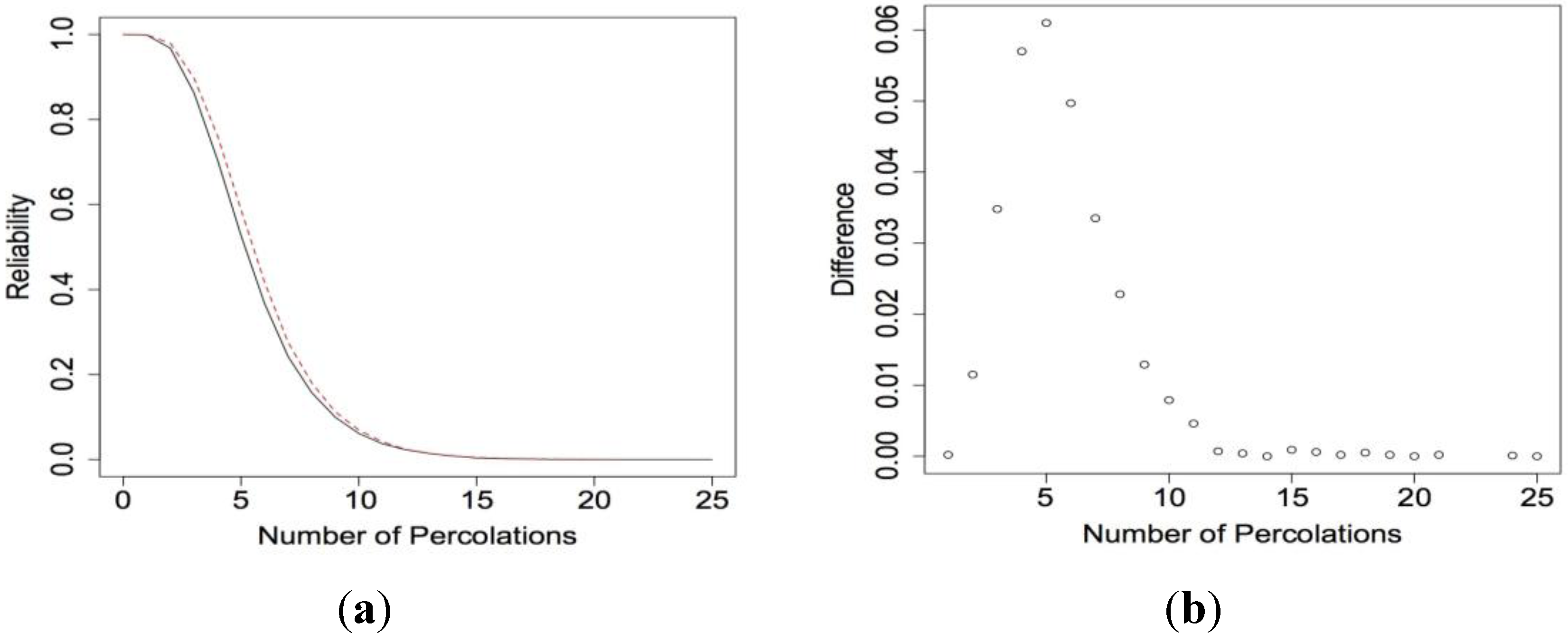
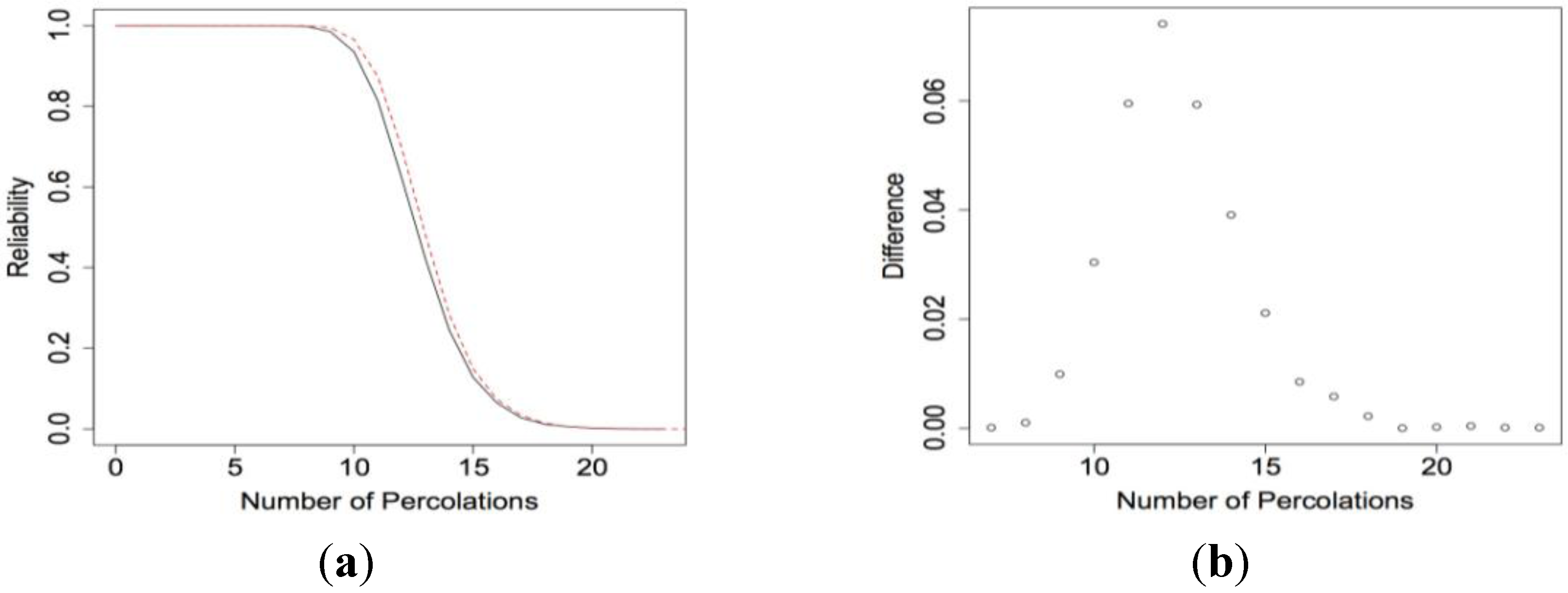
Figure 15a shows the reliability functions for a 7
× 13 nanosensor with ETL structure when
p1 = 0.95 and
β = 0.01. The reliability increases by as much as 0.0741 when the electrical current can move in all directions. However, the expected lifetime only increases from 13.26 to 13.57.
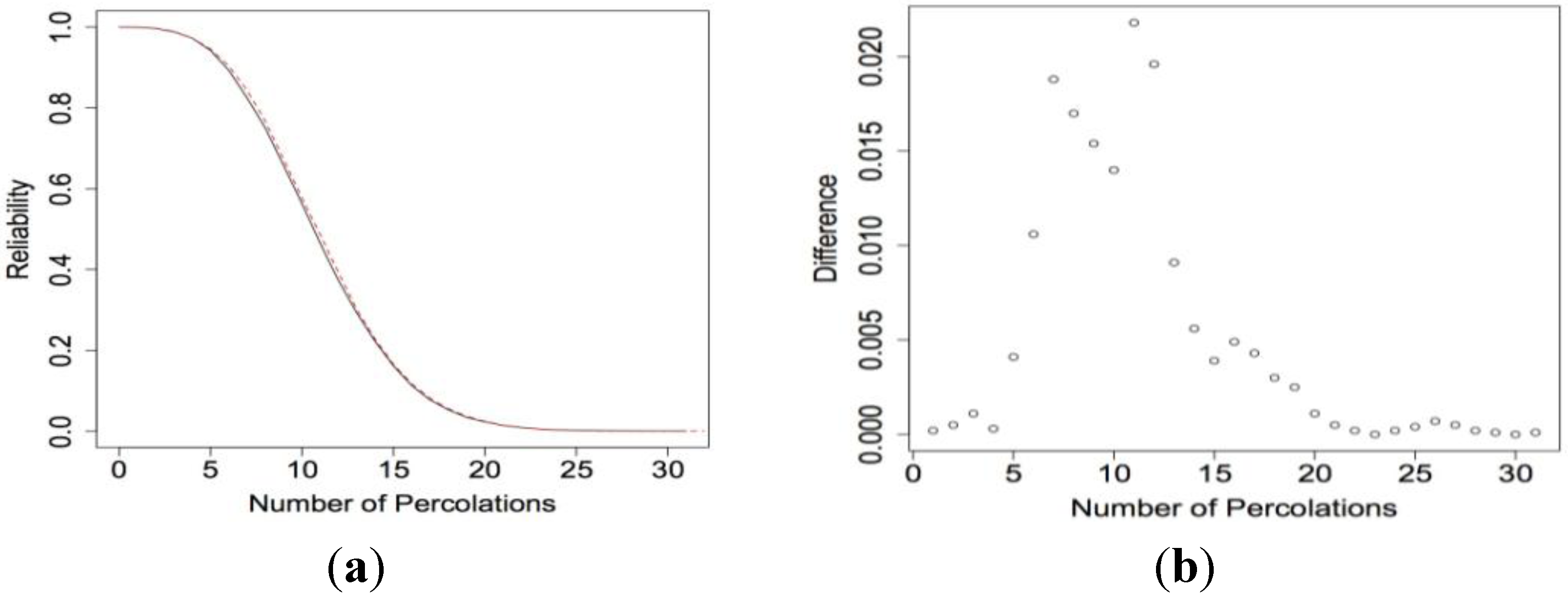
Figure 16a shows the reliability functions for a 7
× 5 nanosensor with HL structure when
p1 = 0.98 and
β = 0.005. Here the reliability increases by as much as 0.0218.
Figure 14.
(a) R3 × 5(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p1 = 0.90 and β = 0.01 and (b) the difference between the R3 × 5(x).
Figure 14.
(a) R3 × 5(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p1 = 0.90 and β = 0.01 and (b) the difference between the R3 × 5(x).
Figure 15.
(a) RE7 × 13(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p1 = 0.95 and β = 0.01 and (b) the difference between the RE7 × 13(x).
Figure 15.
(a) RE7 × 13(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p1 = 0.95 and β = 0.01 and (b) the difference between the RE7 × 13(x).
Figure 16.
(a) RH7 × 5(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p1 = 0.98 and β = 0.005 and (b) the difference between the RH7 × 5(x).
Figure 16.
(a) RH7 × 5(x) calculated using our algorithm when the electrical current can move in all directions (top curve) and when movement is restricted (bottom curve) when p1 = 0.98 and β = 0.005 and (b) the difference between the RH7 × 5(x).