2. Literature on Internet Education and Economic Growth
Education in Internet skills enhances the productivity of the future labor force, which, in turn, helps promote economic growth. These days, more countries are increasing investments in information and communication technologies (ICT). New investments in such high-tech industries may require more capital than labor, and hence, the marginal rate of technical substitution (MRTS), which is the ratio of marginal productivities of labor and capital, would be relatively high. The high MRTS suggests that labor is more productive in such capital-intensive countries. The high productivity of labor is largely due to human capital, such as being educated Internet skills. In this case, marketing and management skills are also highly developed in industrialized countries, and thus the production process will be more efficient. The Internet skills of the labor force are thus treated here as human capital which is regarded as an advancement in total factor productivity.
More specifically, average Internet usage rates can be used as a measure of Internet skills in each country. A rapid increase of computer-related technology in recent years makes the Internet a central force of technology advancement. For example, most industrialized countries that have a rapid growth in frontier technologies are closely related to higher usage rates of the Internet. Late comers, such as East Asian economies with a higher percentage of the labor force that utilizes the Internet, also tend to learn advanced technologies overseas faster than other countries. This suggests that the percentage of Internet users in each country can be used as a quality measure of human capital alongside Hanushek and Kimko’s [
12] index of math and science skills. Litan and Rivlin [
13] described the benefits of the Internet at an industry level; Czernich,
et al. [
14] investigated the significant effects of broadband infrastructure on economic growth; Miranda and Lima [
15] quantitatively analyzed the evolution of the Internet over the past two decades. No studies have discussed the role of Internet education in the growth of nations.
1This paper thus investigates empirically the effects of Internet skills on economic growth employing a cross-section of 36 high-income countries. The average annual usage rates of Internet over time are employed here as a proxy for different levels of Internet skills of the labor force across countries. Employing the Internet usage rates as a quality measure of human capital offers two large advantages. First, most empirical studies in the growth literature used schooling—the quantity measure of education, assuming that the quality of education is constant across countries (Barro, [
17]; Mankiw,
et al. [
18]; Islam, [
19], among others). However, Internet skills—the quality measure of education—differ across countries and suggest why some countries have a rapid growth in advanced technologies and thus a subsequent economic growth faster than other countries. Second, we can directly compare a relative size of the growth effects of two different quality measures of human capital: one is the growth effect of proficiency in high school math and science (Hanushek and Kimko [
12]; Hanushek and Woessmann [
20,
21]); the other is the growth effect of Internet usage rates that are used here as a measure of the Internet skills of the future labor force.
3. Empirical Model and Dataset
Following Bosworth and Collins [
22], our empirical model is specified based on a Cobb-Douglas production function in which output is a function of capital, labor, and a term for total factor productivity:
Y is a measure of output. A represents total factor productivity. K stands for physical capital with its share of income, α. Labor L is now adjusted for improvements in educational attainment E, and hence, LE represents the educated labor force. The educated labor force’s share of income is assumed equal to (1 − α). With this assumption, along with capital share α, the output Y shows the constant returns to scale of all inputs used.
We divide both sides of the production function by labor L:
After taking logarithms of both sides, we take first the differences of the variables to report the results in terms of growth rates:
With this framework, the growth in output per worker is decomposed of the contributions of an improvement in total factor productivity, growth in capital per worker and increases in educational attainment per worker. Because total factor productivity is not directly observable, it is measured indirectly. That is, total factor productivity is the amount of output growth that remains after we have accounted for the determinants of growth that we can measure directly. This is sometimes called the Solow residual.
The capital-labor ratio is replaced by the initial level of income that determines the speed of convergence. The convergence hypothesis is based upon diminishing returns to reproducible capital. In other words, poor countries with low capital-labor ratios are able to grow faster than rich countries, because the marginal productivity of capital is relatively high in lower-income economies. The higher productivity of capital induces the low-income countries to grow faster than rich countries. Therefore, a country’s growth rate of real per capita GDP has a negative relationship with its initial level of income per person.
In addition, the educational attainment E is not only achieved by the number of years of schooling (i.e., educational quantity), but also improved by the quality of the future labor force (i.e., educational quality). Therefore, our empirical model includes two types of educational attainments (quantity of schooling and quality of education), in addition to the initial level of income which replaces the capital-labor ratio that determines the speed of convergence. That is,
where GR80-05 = the average annual growth rates of real per capita GDP over the period 1980–2005; GDP80 = the real per capita GDP of the initial year 1980; SCHOOL = the arithmetic mean of primary and secondary school net enrollment rates in 1980; INTNET = the average annual percentage of Internet users over the period 1995–2004;
2 and ε
i represents serially uncorrelated white noise residuals.
As noted earlier, residuals ε
i are treated as the estimates of total factor productivity, which are best interpreted as gains in efficiency when all factor inputs are used. Thus, regression models may include all other factors that determine the efficiency of factor usage: government spending on R&D, government policies on economic openness and property rights, tax burden, life expectancies and even geographical variables (Sala-i-Martin [
23]). If all these variables are included, our model clearly suffers from the degrees of freedom problem. Rather than controlling for all possible determinants of growth, we merely focus on two important aspects of educational attainments: one is the quantity measure of schooling (SCHOOL) and another the quality measure of computer proficiency (INTNET).
The initial level of income (GDP80) is included in the model to test for the convergence hypothesis in which a country’s growth rate of real per capita GDP has a negative relationship with its initial level of income per person (Solow, [
24]; Cass, [
25]; and Koopmans, [
26]). The correlation coefficient between GDP growth and the initial level of GDP appears to be negative, but virtually zero (
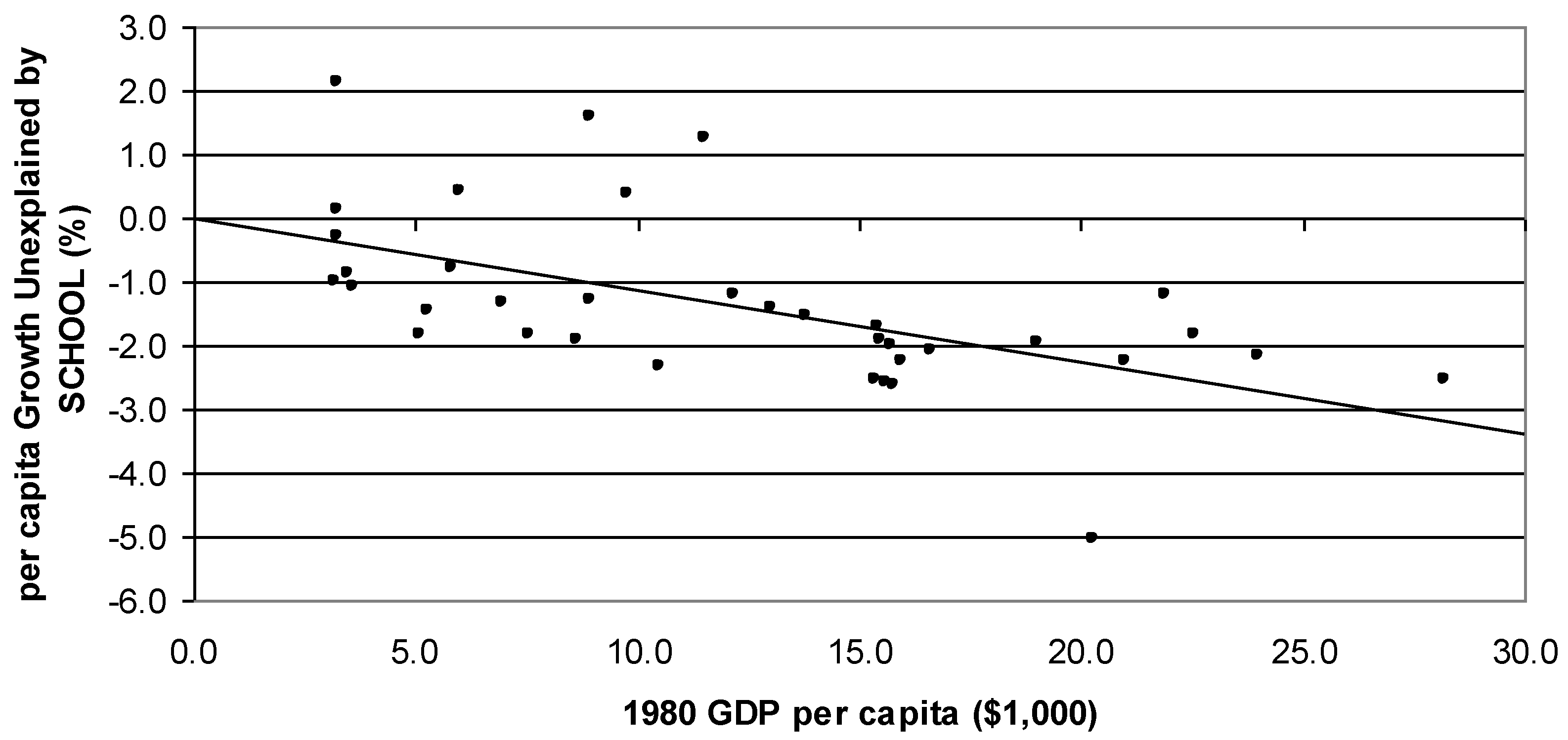
r = −0.06). The insignificant relationship found here is perhaps due to the fact that economic growth is, in fact, explained by other relevant variables, as well. For example, the GDP growth rates are first allowed to be explained by school enrollment rates (SCHOOL). The predicted GDP growth rates are subtracted from actual growth rates, and the remaining unexplained portion of GDP growth is plotted with the initial level of income (GDP80).
Figure 1 shows that the inclusion of school enrollment rates as an explanatory variable for GDP growth significantly strengthens the convergence hypothesis. The partial correlation coefficient between GDP growth rates and the initial level of income appears to be −0.57. The results are, in general, consistent with the convergence hypothesis found in Barro [
17], among others.
Figure 1.
Partial association between per capita GDP growth rates and 1980 per capita GDP.
Figure 1.
Partial association between per capita GDP growth rates and 1980 per capita GDP.
Data source:
World Development Indicators (World Bank) [
27].
Hanushek and Kimko [
12] further included in the model international math and science exam scores (MATH&SCI) as a proxy for the quality measure of labor force. While math and science are important for the development of science and technology in a hardware context, computer-related technologies these days prevail in all types of industries, especially in the service sector, which uses technologies in a soft form, such as management and marketing skills, as well as logistics. Internet usage rates (INTNET) are, therefore, used here as a proxy for another quality measure of human capital, which is our major contribution to the literature.
It is, however, noted that measuring a country’s computer proficiency is relevant only for the countries to which the use of the Internet has been influential. For less developed countries that are still using lower-level technologies, computer-related advanced technologies may not be sufficiently used to develop light industries, such as textiles and home appliances, compared to heavy chemical industries that use high tech intensely. This is similar to the case of an early stage in the process of economic development. For low-income countries, the standard deviation of Internet usage rates was also observed to be greater than the mean value, and thus, measurement errors were unavoidable if low-income countries were included. This contrasts with the use of 36 high-income countries, in which the mean value appears to be 20.1% and its standard deviation 11.8% (
Table 1). In addition, the Internet these days has been used extensively in low-income countries, like Nigeria, to generate spam emails and defraud money online. According to a report by the Message Anti-Abuse Working Group [
28], about 88%–90% of emails are estimated to be spam. These harmful Internet activities may incorrectly show up as a positive correlation with economic growth in such low-income countries. This paper thus includes 36 high-income countries only, in which an initial income level is higher than US$3000 in the year 1980.
3Table 1 reports the summary statistics of the key variables used. The mean growth rate of real GDP per capita across countries in our sample appears to be 1.76% on average. South Korea had the highest growth rate of GDP (5.52%) in our sample over the period, while Kuwait had a negative annual average growth rate (−2.15%). It is also noted that real GDP per capita of the initial year 1980 ranges from the lowest of US$3180 in Panama to the highest of US$28,210 in Switzerland. The average income in our sample at that time appears to be US$12,130. For Barro’s [
17] schooling, Belgium has the highest average of primary and secondary school enrollment rates with 98% (100% in a primary and 96% in a secondary school). The lowest school enrollment rate is found in Venezuela, with an average of 53.5%. Hanushek and Kimko’s [
12] math and science quality measure appears to be 48.4 points on average. The lowest score is found in Kuwait with 28.4 points, while Japan has the highest score of 60.7 points. Japan is also among the highest in school enrollment rates with an average of 96.5%.
Table 1.
Descriptive Statistics.
Table 1.
Descriptive Statistics.
| Variables | Mean | Median | SD | Minimum | Maximum |
|---|
| GR80-05 (%) | 1.76 | 1.68 | 1.36 | −2.15 | 5.52 |
| GDP80 (US$1000) | 12.13 | 11.86 | 6.83 | 3.18 | 28.21 |
| SCHOOL (%) | 85.3 | 88.8 | 10.7 | 53.5 | 98.0 |
| MATH&SCI (Score) | 48.4 | 48.9 | 7.5 | 28.4 | 60.7 |
| INTNET (%) | 20.1 | 20.0 | 11.8 | 3.4 | 40.6 |
In addition, the level of computer proficiency fluctuates about the mean value of 20.1%, ranging from the lowest of 3.4% in Venezuela to the highest of 40.6% in Sweden.
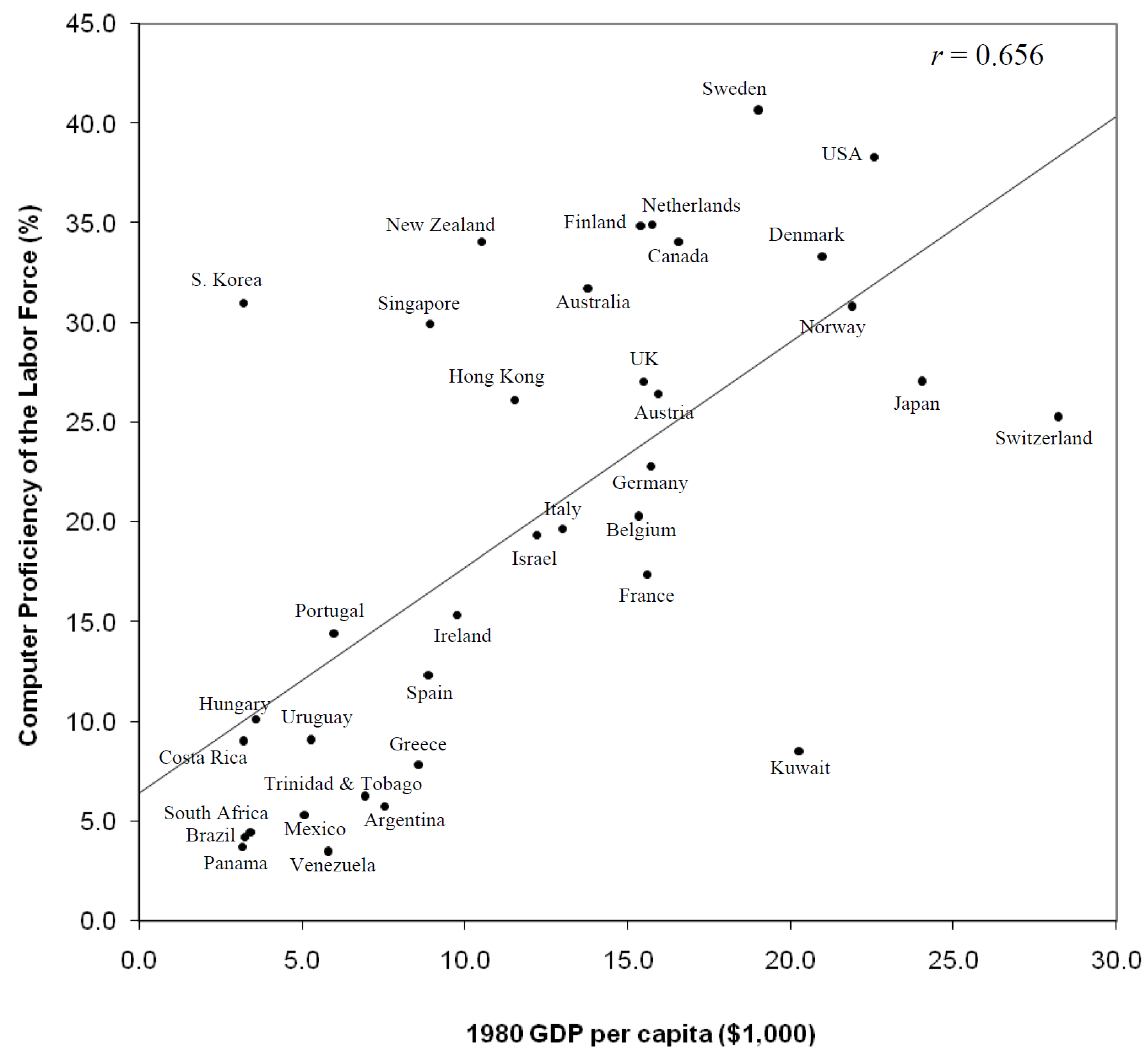
Figure 2 further shows that rich countries were closely related to higher usage rates of the Internet, while the Internet usage rates of lower-income countries were relatively low. Internet usage rates would be even lower if low-income countries were included in our sample. Notice, however, that South Korea’s real per capita GDP in 1980 (US$3220) was among the lowest in our sample, but the average Internet usage rate was notably high (31.0%). South Korea is thus a seemingly extreme value in our sample, but the high Internet usage rate reflects South Korea’s early investment in information technology, which facilitated the country in quickly catching up with the advanced technologies of the U.S. and Japan in recent decades. In contrast, Kuwait had a high income level in 1980 (US$20,300), but was unusually low in its Internet usage rate (8.5%). As an oil producing country, Kuwait could be exclusively driven by exports of oil, and its high income would be mainly due to oil revenue. Its low rate of Internet usage indicates that computer proficiency in Kuwait might have little impact on its economy, and hence, Kuwait could be regarded as a potential outlier. Except for these few extremes, rich countries generally show high computer proficiencies.
4
Figure 2.
Per capita GDP in 1980 versus computer proficiency.
Figure 2.
Per capita GDP in 1980 versus computer proficiency.
Data Source:
World Development Indicators (World Bank) [
27].
4. Basic Results
Prior to estimation of the regression model, correlation coefficients among independent variables are reported to check with a potential multicollinearity problem.
Table 2 shows that the quantity measure of schooling is moderately correlated with the quality measure of math and science skills; the quality measure is also moderately correlated with another quality measure of computer skills in the Internet. However, the degree of a linear relationship is less than 0.8, a rule of thumb, and hence, a multicollinearity problem may not be serious. The symptom of multicollinearity has been further checked with the regression results. All parameter estimates appear to have correct signs, and
t-values are generally consistent with the size of the adjusted
R2. The standard error estimates also remain relatively stable when other explanatory variables are included in the model. We therefore conclude that multicollinearity problems may not be serious in this model specification.
Table 2.
Correlation coefficients among independent variables.
Table 2.
Correlation coefficients among independent variables.
| | GDP80 | SCHOOL | MATH&SCI | INTNET |
|---|
| GDP80 | 1 | | | |
| SCHOOL | 0.657 | 1 | | |
| MATH&SCI | 0.357 | 0.606 | 1 | |
| INTNET | 0.656 | 0.681 | 0.587 | 1 |
Table 3 shows basic regression results. In Regression (1), GDP growth rates are explained by the initial level of income (GDP80) and school enrollment rates (SCHOOL). This is simply a replication of Barro [
17]. Although slightly different sample periods and a smaller sample size of countries are used, our findings are similar to Barro [
17]. The estimated coefficient of GDP80 appears to be negative and significant at the 1% significance level. The convergence hypothesis is well supported, in which an increase in per capita income by US$1000 will reduce the subsequent growth rates by approximately 0.11 percentage points on average. The quantity measure of education, SCHOOL, is also positively and significantly related to GDP growth rates. The parameter estimate of schooling suggests that an increase of one standard deviation in both primary and secondary school enrollment rates will generate 1.03 percentage points of GDP growth on average (i.e., 0.096 × 10.7 = 1.03). The results are generally consistent with the findings in Barro [
17].
Table 3.
Basic regression results.
Table 3.
Basic regression results.
| | (1) | (2) | (3) | (4) | (5) | (6) |
|---|
| Dependent variable | GR80-05 | GR80-05 | GR80-05 | GR80-05 | GR80-05 | GR80-05 |
| Constant | −5.089 (1.783) | −6.111 (1.561) | −5.902 (1.458) | −2.828 (1.603) | −4.090 (1.546) | −4.291 (1.568) |
| GDP80 | −0.112 (0.038)** | −0.104 (0.032)** | −0.103 (0.031)** | −0.162 (0.034)** | −0.144 (0.032)** | −0.136 (0.033)** |
| SCHOOL | 0.096 (0.024)** | 0.051 (0.024)* | 0.057 (0.021)** | 0.058 (0.022)** | 0.035 (0.022) | 0.046 (0.021)* |
| MATH&SCI | | 0.099 (0.028)** | | | 0.071 (0.027)** | |
| MATH&SCI 2 | | | 0.076 (0.018)** | | | 0.053 (0.020)** |
| INTNET | | | | 0.079
(0.020)** | 0.060 (0.020)** | 0.048
(0.022)* |
| Observations | 36 | 36 | 36 | 36 | 36 | 36 |
| Adjusted R2 | 0.292 | 0.475 | 0.535 | 0.503 | 0.582 | 0.583 |
Regression (2) replicates Hanushek and Kimko [
12], who additionally include a math and science quality measure (MATH&SCI). The effect of math and science skills on GDP growth appears to be positive and significant. The parameter estimate of MATH&SCI suggests that an increase of one standard deviation in MATH&SCI improves GDP growth rates by 0.74 percentage points on average (i.e., 0.099 × 7.5 = 0.74). It is, however, noted that the inclusion of a quality measure in the same model mitigates the size of the growth effect of schooling, but the growth effect of schooling remains significant at the 5% significance level. The result appears to be at odds with the findings in Hanushek and Kimko [
12] in which the smaller effect of schooling was statistically insignificant.
For the robustness of our results, Regression (3) further employs Hanushek and Kimko’s [
12] second quality measure (MATH&SCI2) in that the math and science scores of each country were normalized to a yearly U.S. performance. In this case, the growth effect of schooling (0.057 × 10.7 = 0.61) is similar to the growth effect of math and science skills (0.076 × 7.5 = 0.57) if one standard deviation is raised for both variables. The result thus suggests that, unlike the findings in Hanushek and Kimko [
12], which critically emphasized the weak evidence of Barro’s [
17] schooling effect on economic growth, both quantity and quality measures of education are equally important for the growth of nations.
Regression (4) further includes Internet usage rates (INTNET) as an alternative quality measure of labor force. The growth effect of INTNET appears to be significant, and an increase in computer proficiency by one standard deviation enhances GDP growth rates by 0.92 percentage points on average (i.e., 0.079 × 11.8 = 0.92). The size of the effect is greater than the growth effect of SCHOOL (i.e., 0.058 × 10.7 = 0.62).
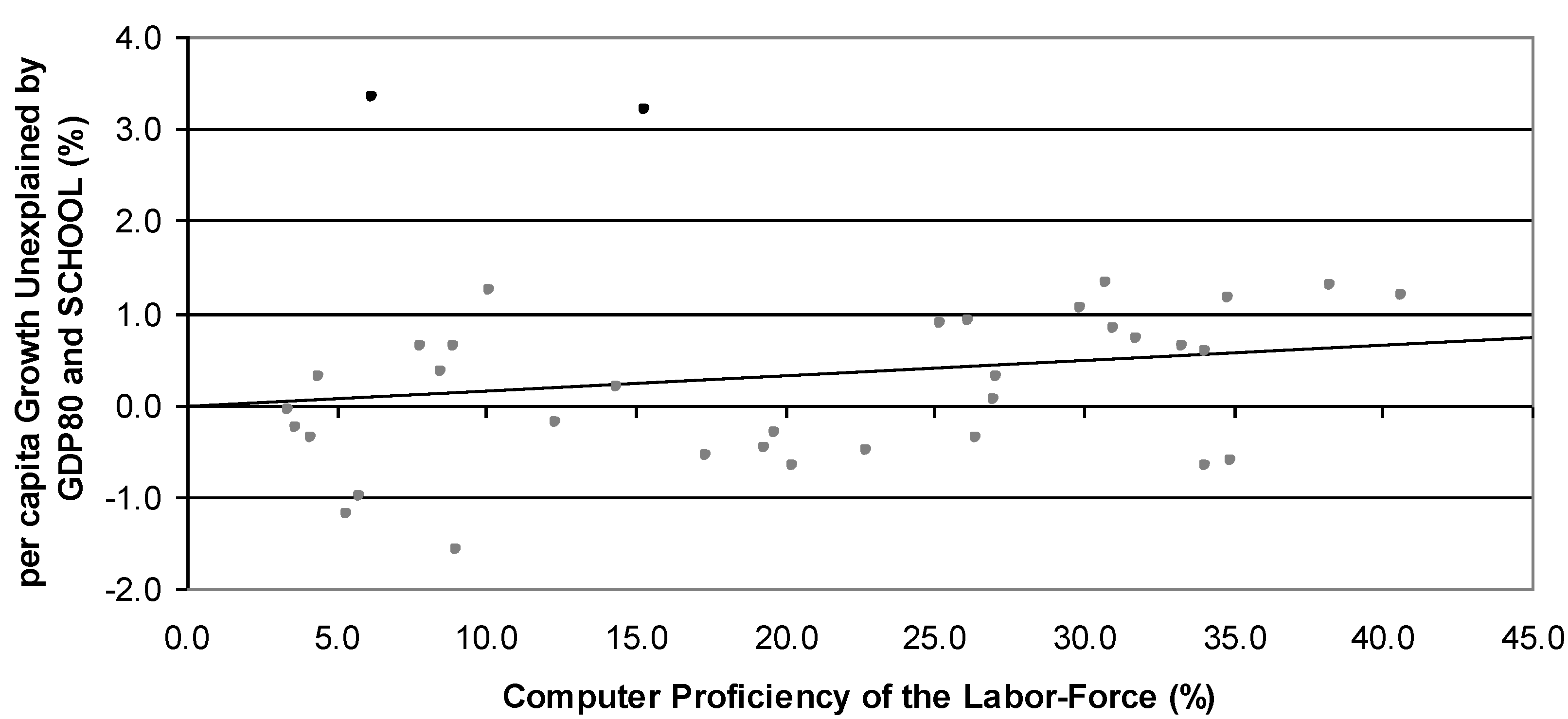
Figure 3 further shows a partial association between the two variables, holding other variables constant. In other words, the GDP growth rates predicted by all explanatory variables other than INTNET are subtracted from the actual growth rates. The unexplained portion of GDP growth is now plotted with INTNET. The stronger association (
r = 0.71) re-confirms the significant growth effect of INTNET found in Regression (4).
Figure 3.
Partial association between per capita GDP growth and the computer proficiency of the labor force.
Figure 3.
Partial association between per capita GDP growth and the computer proficiency of the labor force.
Data source:
World Development Indicators (World Bank) [
27].
Furthermore, Regression (5) directly compares the relative size of the growth effects of INTNET and MATH&SCI within a model. Both quality measures are strongly related to GDP growth rates. A one standard deviation rise in MATH&SCI will generate 0.53 additional percentage points of GDP growth on average, whereas a one standard deviation increase in INTNET will improve the GDP growth rates by 0.71 percentage points. The growth effect of computer proficiency is even greater than the one with math and science skills if one standard deviation is raised in each variable. Similar results are found in Regression (6), which uses the second measure of math and science skills.
5. The Notion of Causality
For the robustness of the results,
Table 4 further estimates regression models.
Table 4.
Further estimation.
Table 4.
Further estimation.
| | (7) | (8) | (9) | (10) | (11) | (12) |
|---|
| Dependent variable | GR95-05 | GR95-05 | GR80-05 | GR80-05 | GR80-05 | GR80-05 |
| Constant | −3.348 (1.798) | −1.178 (1.170) | −3.132 (1.578) | −7.630 (7.441) | −2.122
(1.938) | −3.195 (1.296) |
| GDP80 | −0.142 (0.038)** | −0.118 (0.024)** | −0.342 (0.118)** | −0.156 (0.035)** | −0.163 (0.034)** | −0.137 (0.028)** |
| GDP80SQ | | | 0.595 (0.375) | | | |
| SCHOOL | 0.081 (0.025)** | 0.043 (0.017)** | 0.073 (0.024)** | 0.185 (0.193) | 0.052 (0.025)* | 0.062 (0.018)** |
| SCHOOLSQ | | | | −0.083 (0.125) | | |
| INTNET | 0.016 (0.023) | 0.046 (0.015)** | 0.083 (0.020)** | 0.080 (0.021)** | 0.075 (0.021)** | 0.054 (0.017)** |
| LATIN | | | | | −0.376 (0.569) | |
| ASIA | | | | | | 1.870 (0.438)** |
| Observations | 36 | 34 | 36 | 36 | 36 | 36 |
| Adjusted R2 | 0.307 | 0.479 | 0.525 | 0.494 | 0.494 | 0.677 |
Regression (7) changes the sample period for GDP growth rates from 1980–2005 to more recent years, 1995–2005. In this way, we can examine the notion of causality that may run from schooling one decade earlier to the growth of GDP afterwards (Barro, [
17]). In other words, the primary and secondary school enrollment rates of the initial year, 1980 (SCHOOL), are now allowed to have a causal impact on the GDP growth rates one decade afterwards, 1995–2005. The result shows that schooling leads the subsequent decade’s GDP growth. Schooling causes the growth of GDP. However, the effect of INTNET turns out to be insignificant. This would be largely due to the outliers observed in our sample.
Figure 4 shows a partial relationship between GDP growth rates and INTNET, holding other variables constant. The correlation coefficient appears to be positive, but relatively small (
r = 0.18), because of two notable outliers (in a dark color): one is identified as Ireland, another as Trinidad and Tobago.
Figure 4.
Partial association between per capita GDP growth and the computer proficiency of the labor force.
Figure 4.
Partial association between per capita GDP growth and the computer proficiency of the labor force.
Data source:
World Development Indicators (World Bank) [
27].
Ireland, once referred to as a Celtic Tiger, experienced an exceptionally rapid economic growth between 1995 and 2005. The average annual GDP growth rate of Ireland over the period 1995–2005 was 6.2%, compared with 4.4% over the whole sample period 1980–2005. While this economic boom was once credited to effective government policies and economic reform in the early 1990s, a recent collapse of the Irish economy following the 2008 global financial crisis suggests that the previous growth rates were driven by factors other than ‘real’ economic development, such as housing and credit bubbles.
5 Trinidad and Tobago also experienced a rapid economic growth between 1995 and 2005, with an average annual growth rate of 5.7%. This rapid growth was highly related with an increase in exports, particularly of petrochemicals, such as methanol, ammonia and liquefied natural gas; the tourist boom was another important reason for economic growth. However, high-tech was less used for such development of natural resources and inbound tourism. Like the case of Ireland, computer proficiency did not amply explain the recent economic boom of Trinidad and Tobago.
Therefore, Regression (8) further estimates without using the two outliers mentioned above. As expected, the computer skills of the labor force are found to be significantly related to GDP growth, and a one standard deviation rise in INTNET is now associated with 0.54 percentage points of GDP growth rates on average.
7. Quadratic Relations
The negative relationship between the initial level of income and a subsequent growth rate may attenuate higher income (Barro, [
17]). In other words, the relationship will be negative, but at a decreasing rate. Regression (9) includes the squares of the initial income (GDP80SQ, measured in US$100 million) to check with this non-linear relationship. The estimated coefficient of GDP80 remains negative and significant, and the quadratic term is, as expected, positive, although statistically insignificant. The relationship is plotted in the following way. The growth rates predicted by the explanatory variables other than GDP80 and GDP80SQ are subtracted from the actual growth rates to obtain the unexplained GDP growth on the
y-axis. A negative but slightly weakening relationship is found in
Figure 6, although the upward rising force does not appear to be statistically significant.
Figure 6.
Partial association between per capita GDP growth and 1980 GDP per capita.
Figure 6.
Partial association between per capita GDP growth and 1980 GDP per capita.
Data source: World Development Indicators (World Bank) [
27].
Regression (10) estimates a quadratic relationship between school enrollment rates and GDP growth. Since the enrollment rates are measured in percentages, their effects on GDP growth may be non-linear, that is, the marginal growth effects of SCHOOL may diminish as schooling approaches 100%. To allow for this possibility of non-linearity, SCHOOL has been squared. The estimated coefficient of SCHOOLSQ is found negative, but appears to be insignificant. In other words, the growth effect of schooling increases at a decreasing rate, but the diminishing non-linear relationship due to schooling is not prominent.
8. Regional Differences
To observe regional differences in economic performances, Regression (11) includes a dummy variable for seven Latin American countries (LATIN): Argentina, Brazil, Costa Rica, Panama, Trinidad and Tobago, Uruguay and Venezuela. The estimated coefficient of the dummy variable is negative, but not significant. This means that Latin American countries have GDP growth rates slightly less than the world average, but the difference is not large enough to reject the null hypothesis of a zero difference.
Similarly, Regression (12) includes an Asian dummy (ASIA): Hong Kong, Japan, Singapore and South Korea. These economies had notably higher growth rates in the past decades. For instance, Hong Kong’s actual growth rate over the sample period used was 4.1%, but the predicted growth rate was 1.8% worldwide. Likewise, the actual growth rates of Japan, Singapore and South Korea exceeded the predicted growth rate by 1.0%, 2.1% and 2.0%, respectively.
Figure 7 graphically compares the actual GDP growth rates
versus the growth rates predicted by all other explanatory variables. The four Asian economies are marked in a darker color. The effect of the Asian dummy is found to be positive and significant. This extra average growth rate attributed to the four Asian economies is identified as a vertical distance between two regression lines (the upper line as a best-fit for Asian economies; the lower line as a best-fit for all other countries). This prominent difference is consistent with a significant positive effect of the Asian dummy in regression (12).
Figure 7.
Per capita GDP growth versus predicted per capita GDP growth.
Figure 7.
Per capita GDP growth versus predicted per capita GDP growth.
Data source: World Development Indicators (World Bank) [
27].
9. Conclusions
This paper empirically investigates the growth effects of Internet education using a cross-section of 36 high-income countries. Following Barro [
17], school enrollment rates are used as a proxy for the quantity measure of primary and secondary education across countries. For the quality measure of secondary education, Hanushek and Kimko’s [
12] math and science skills are employed. As another quality measure of the future labor force, our model includes Internet usage rates, which is a major contribution of this paper to the literature.
Regression results show that both schooling and math and science skills are significantly related to the growth rates of real GDP. Internet usage rates, a proxy for different levels of Internet education across countries, also have a positive and significant effect on real GDP growth. The estimated growth effects remain significant when other relevant variables are included in the model. The relative size of the growth effects caused by the two quality measures of education shows that, if one standard deviation is increased in each variable, the growth effect of Internet skills is even greater than the growth effect of math and science skills. The results are, in general, robust across different model specifications.
One policy implication is that Internet education, as well as math and science education, will improve labor productivity which in turn helps promote economic growth. In particular, students in high-income countries are more exposed to computer facilities, and hence the future labor force will be well equipped with Internet skills. Middle-income economies especially in Asia also have been able to absorb new technologies overseas within a short period of time by increasing the Internet skills of the workforce.
Besides, Internet education can be enhanced without many trade-offs. As long as universities and colleges are well equipped with high-tech Internet facilities on campus, students are more exposed to computer-related advanced technologies, and more students will have an opportunity to enhance their Internet skills. It is, however, noted that this policy implication may not be appropriate for generalizing to low-income countries, because high technologies are not sufficiently used in the process of economic development. For low-income countries, increasing school enrollment rates would rather be more effective in economic growth.