Applications of Optical Interferometer Techniques for Precision Measurements of Changes in Temperature, Growth and Refractive Index of Materials
Abstract
:1. Introduction
1.1. Survey Optical Techniques for Growth Rate Measurements
1.2. Survey of Optical Sensor Technologies for Temperature Measurement
2. Experimental Details
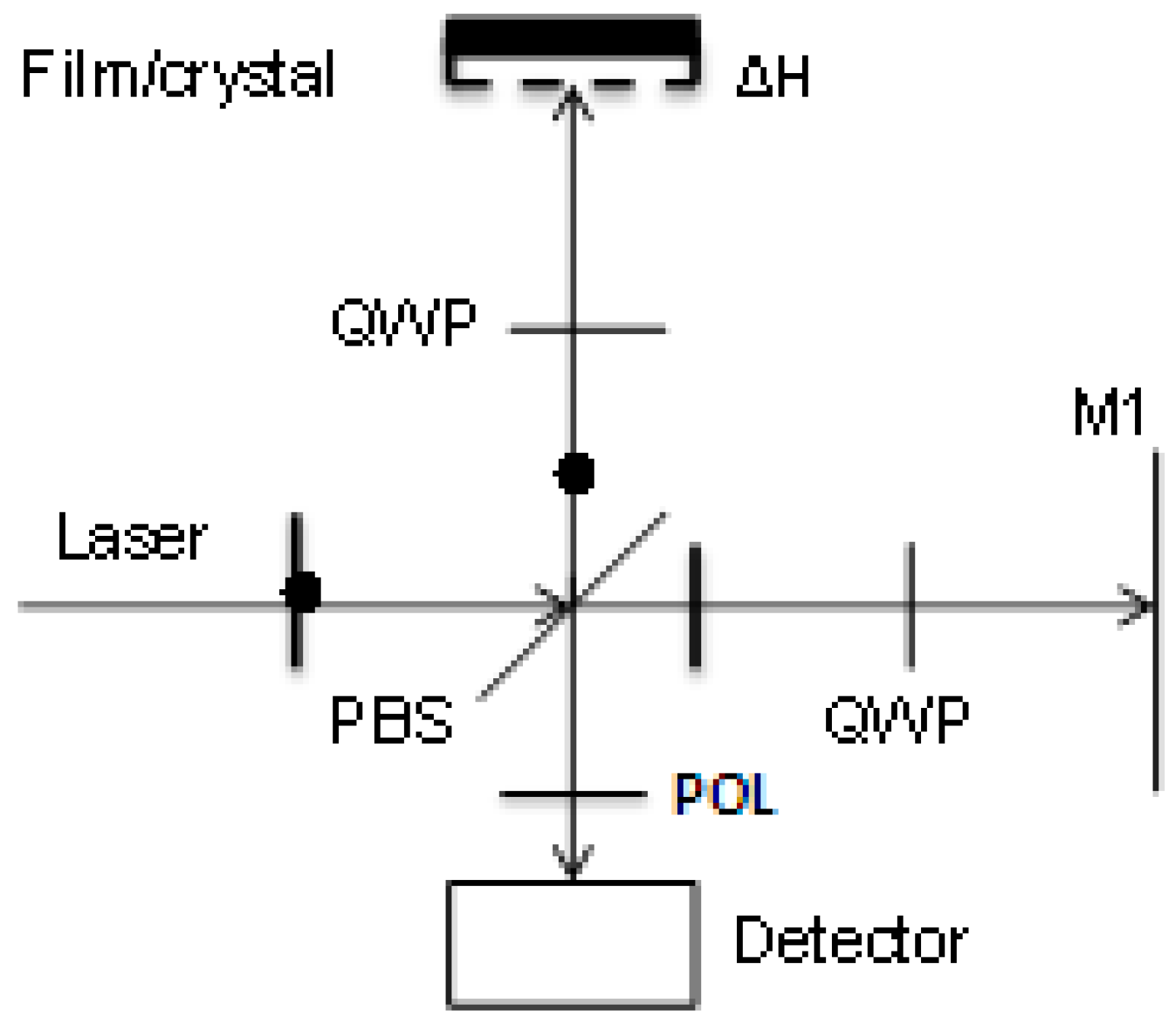
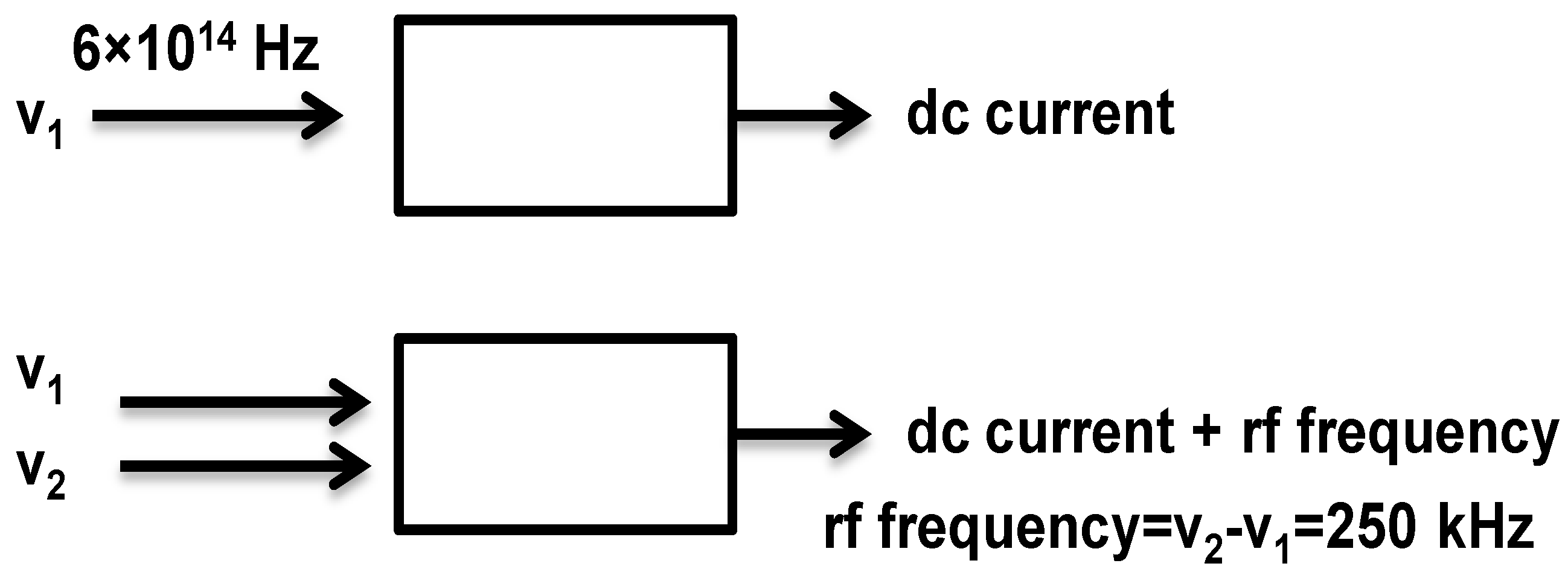
2.1. Optical Heterodyne Technique
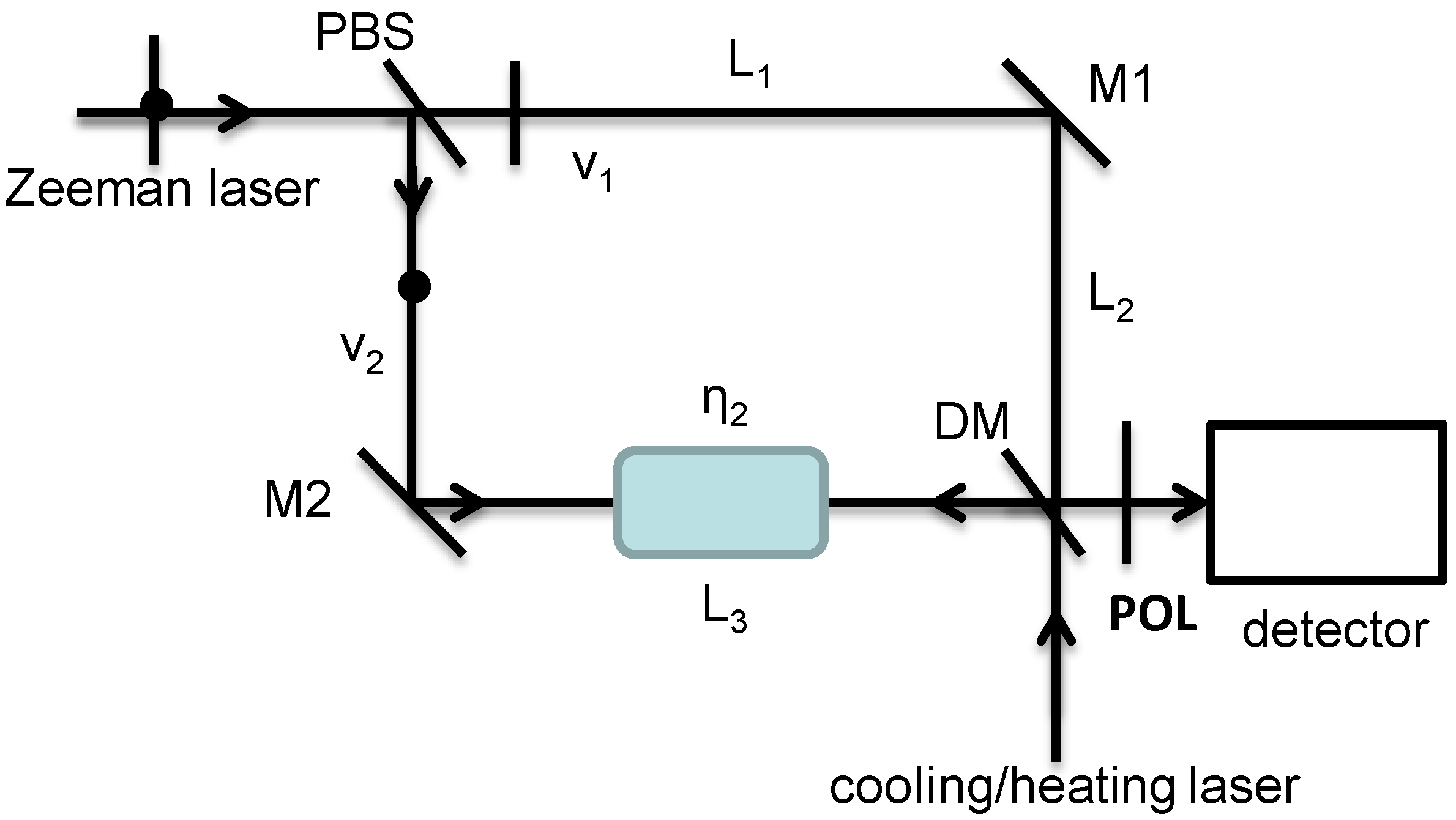
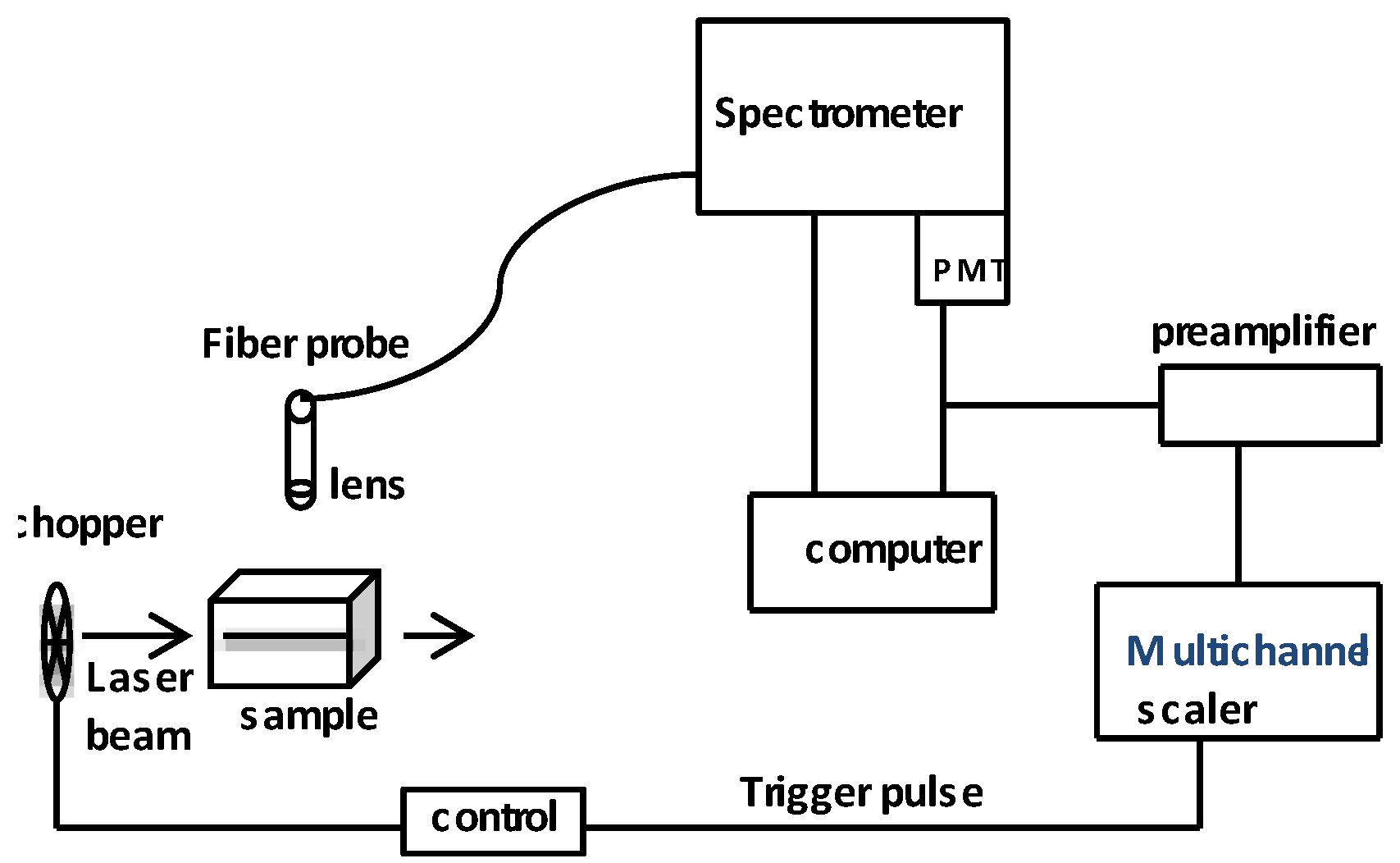
2.2. Rare-Earth Luminescence Measurements

3. Principle of the Optical Heterodyne Detection Technique
3.1. Application of Optical Heterodyne Detection Technique for in situ Measurement of Crystal Growth
3.2. Application of Optical Heterodyne Detection Technique for Surface Roughness Measurement

4. Measurement of Temperature Changes
4.1. Application of Optical Heterodyne Detection Technique to Laser Cooling/Heating of Solids
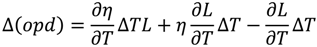
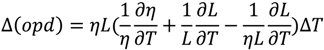
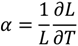
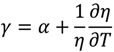
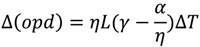
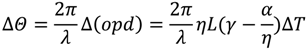
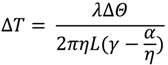
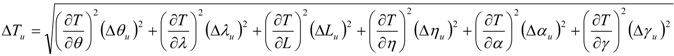
4.2. Rare-Earth Luminescence Sensors for Temperature Measurement
4.2.1. Fluorescence Lifetime Sensors
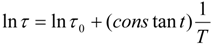
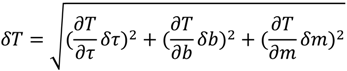
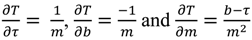
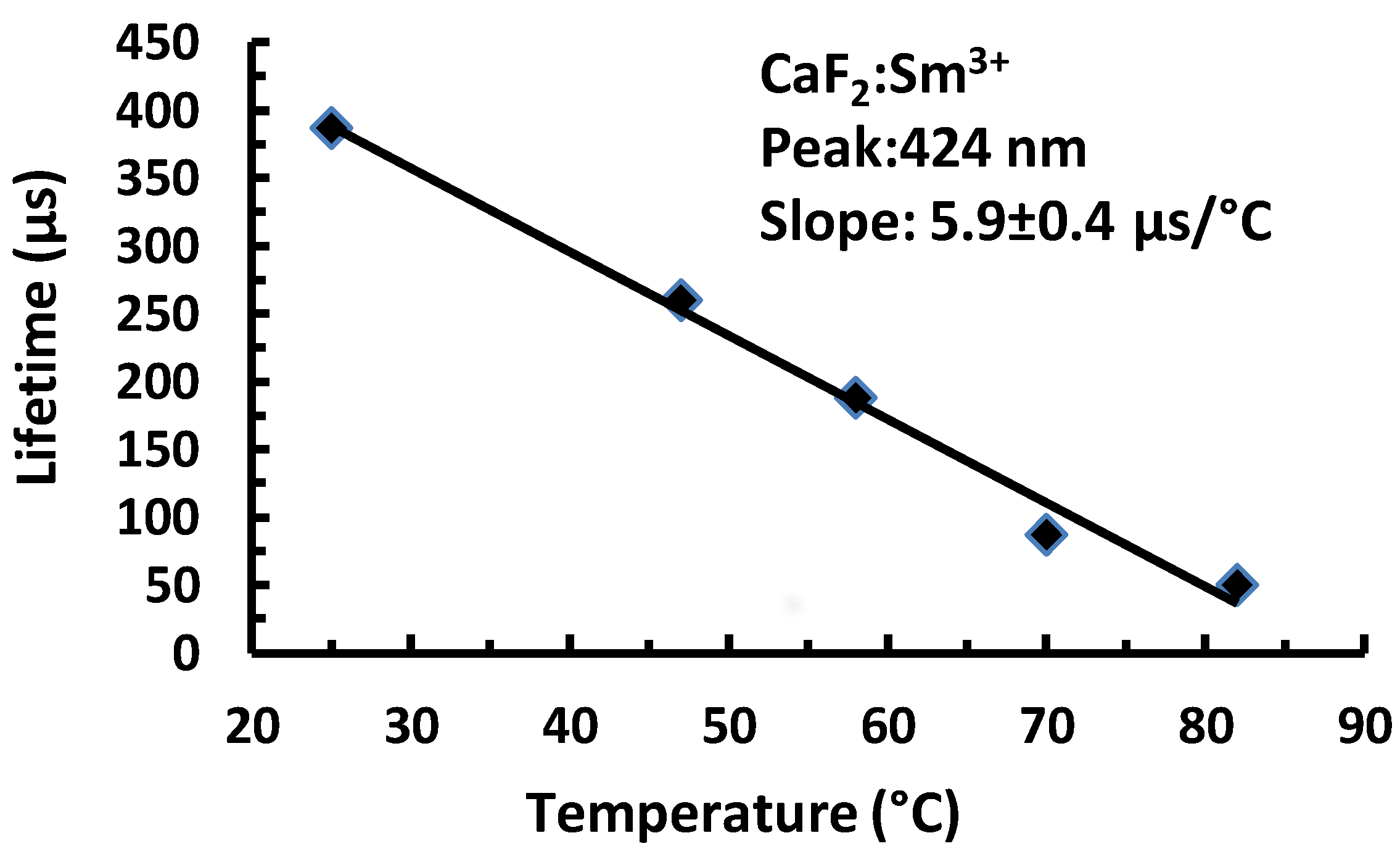
4.2.2. Fluorescence Ratio Method
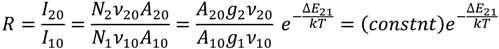


4.3. Application of Michelson and Mach-Zehnder Interferometers to Measure Temperature Changes
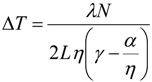
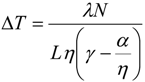
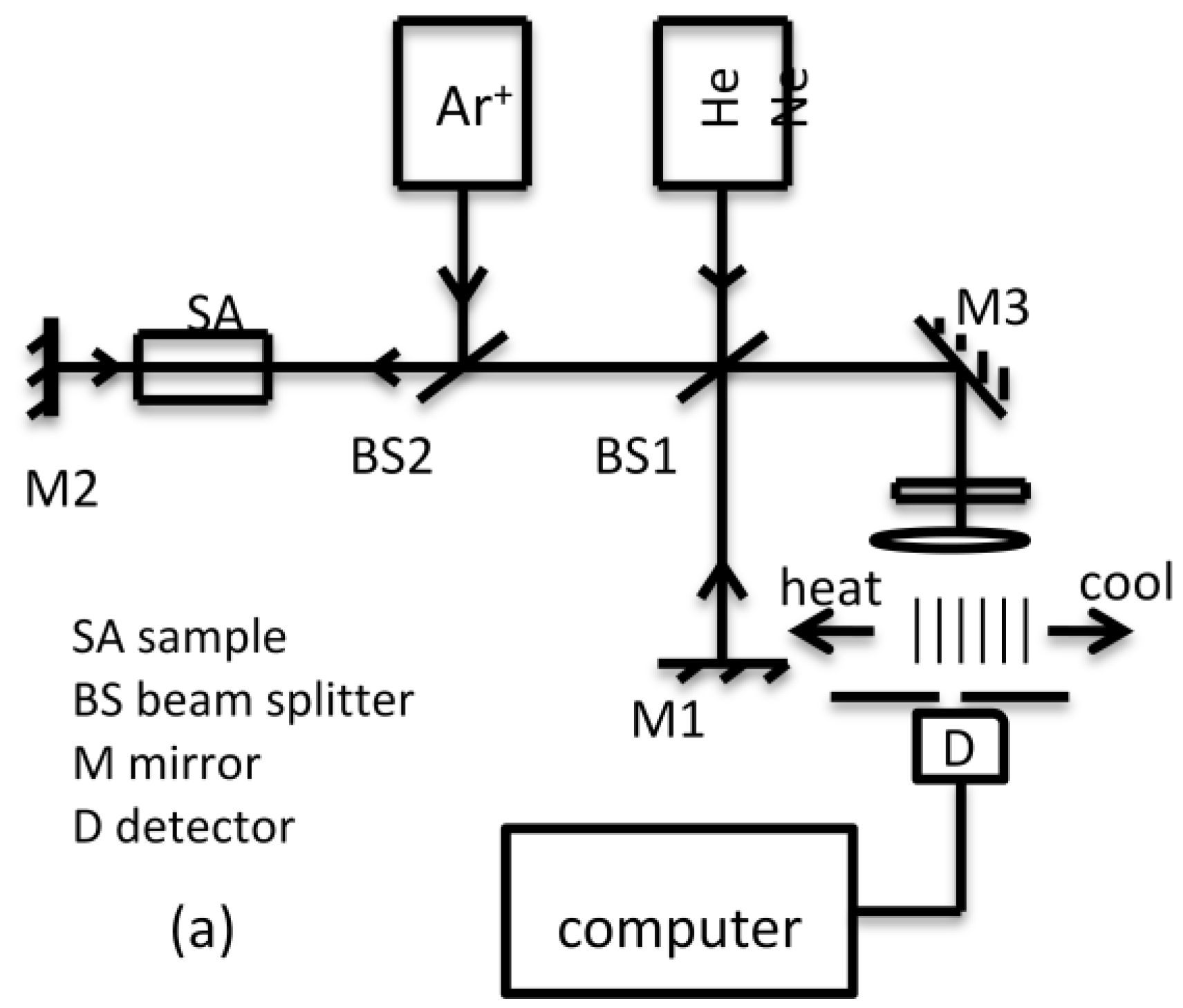
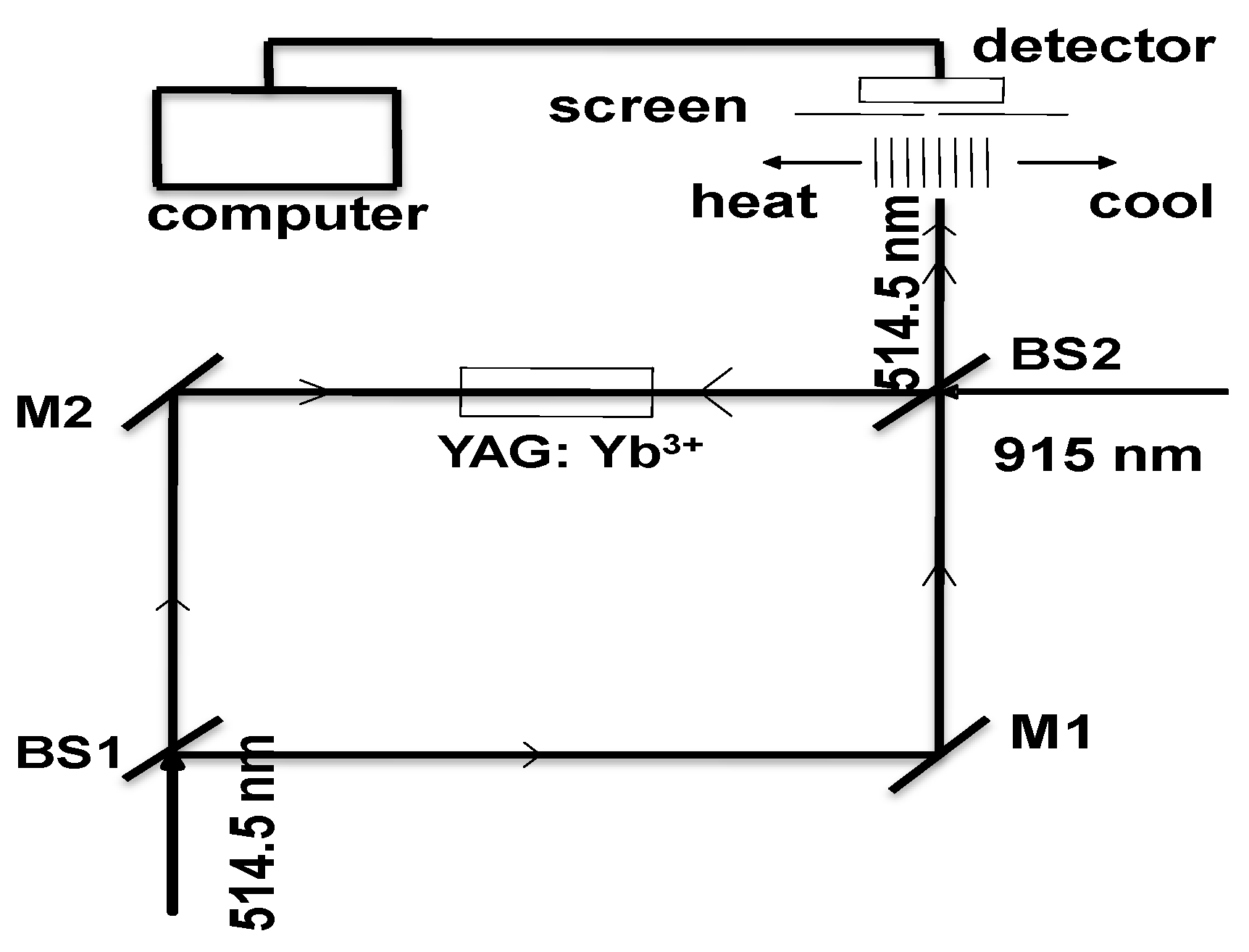


5. Application of Mach-Zehnder Interferometer Technique for the Measurement of Changes in Solution Concentration or Refractive Index in a Crystal Growth Experiment
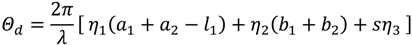
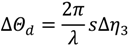
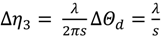

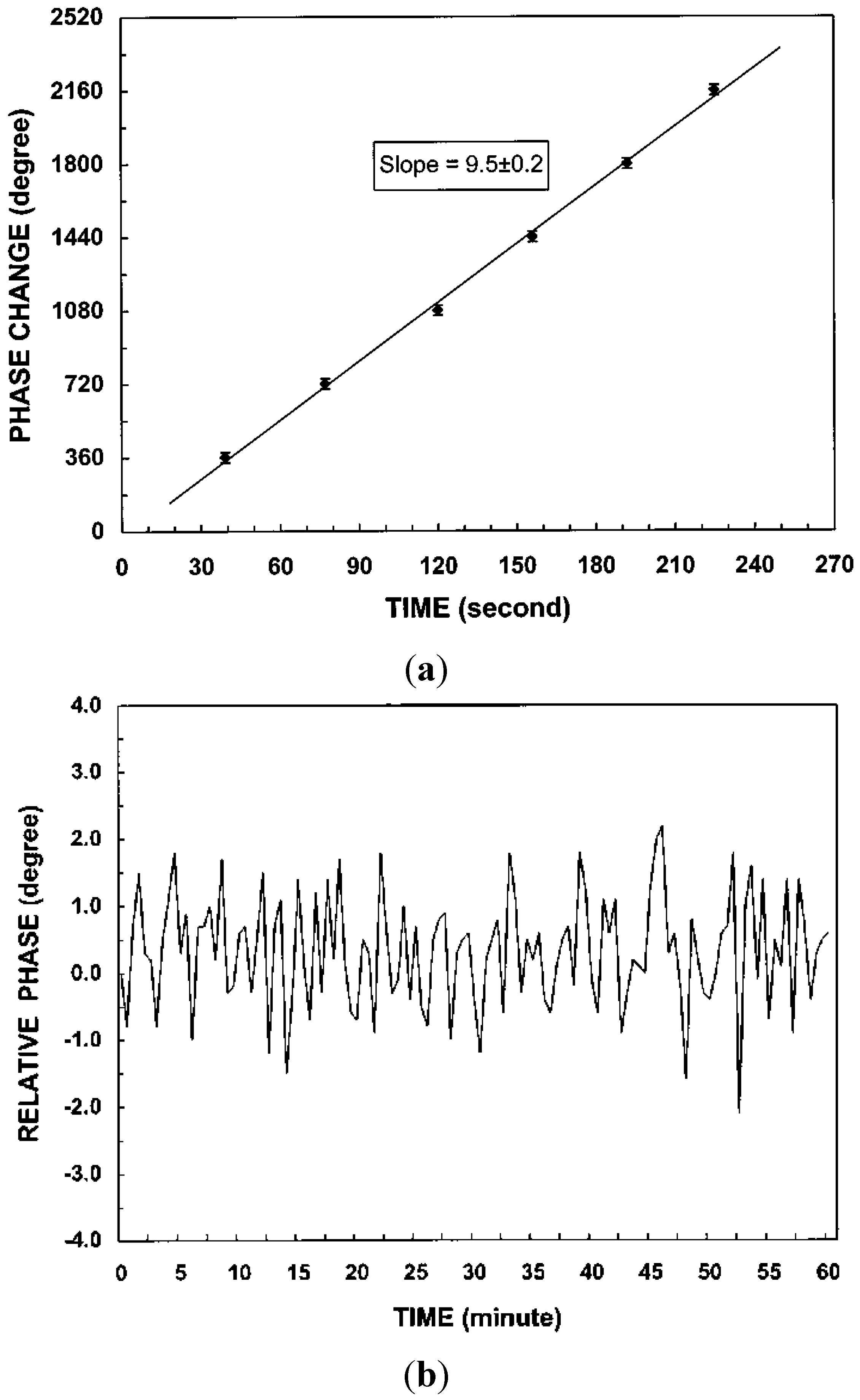
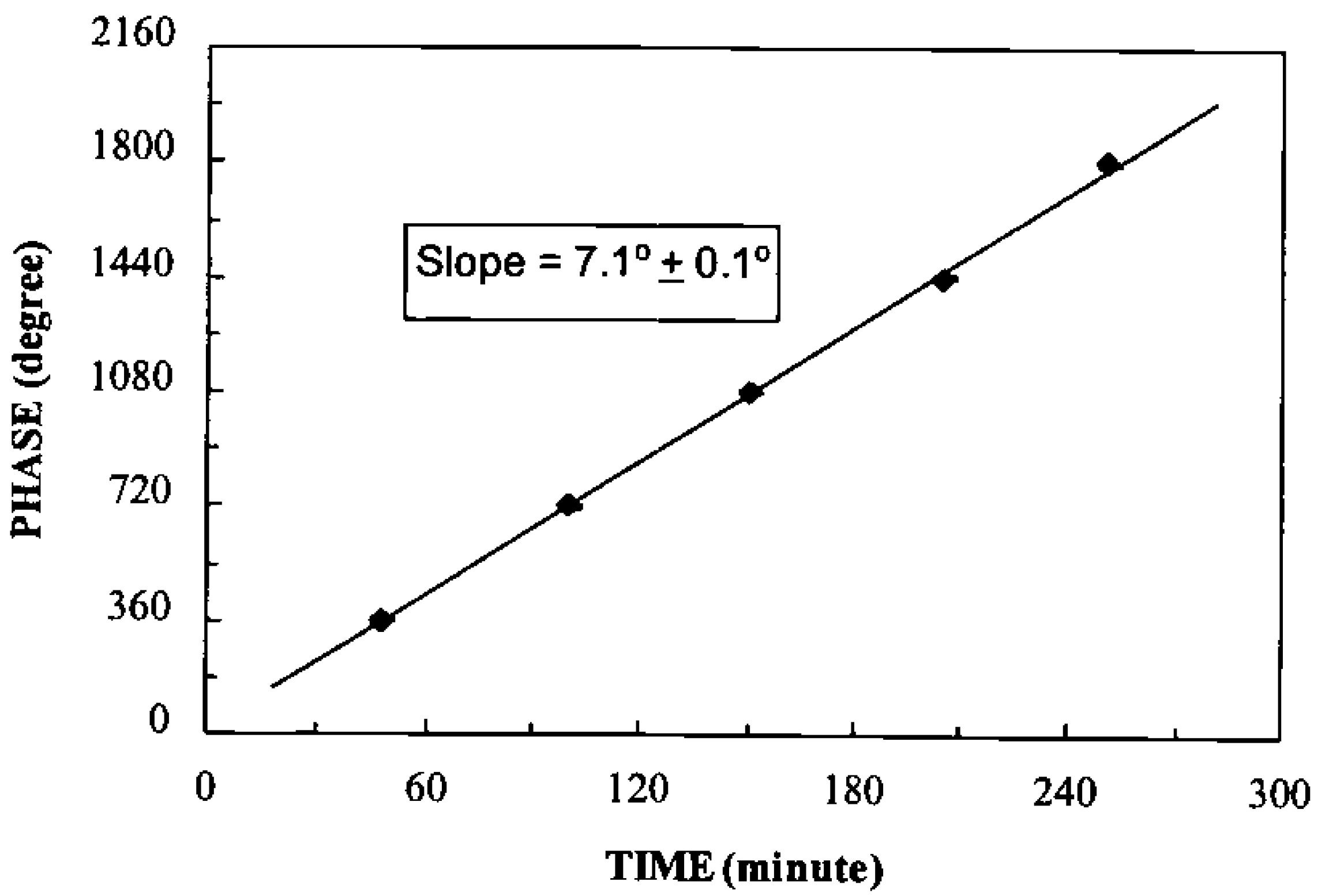
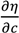 can be measured experimentally. For a 2π phase change (ΔΘd = 2π), the concentration change can be estimated as
can be measured experimentally. For a 2π phase change (ΔΘd = 2π), the concentration change can be estimated as
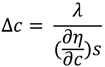
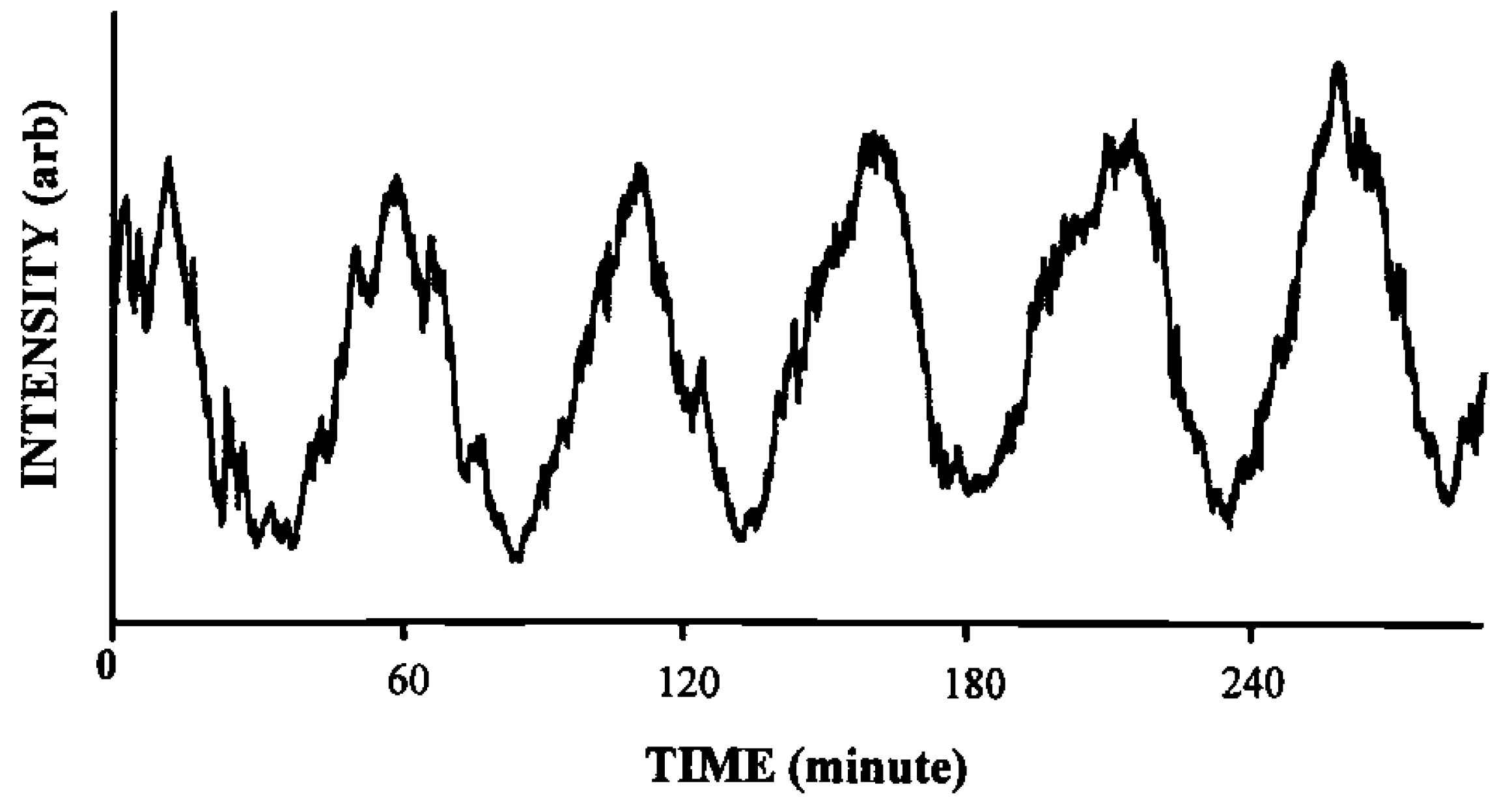
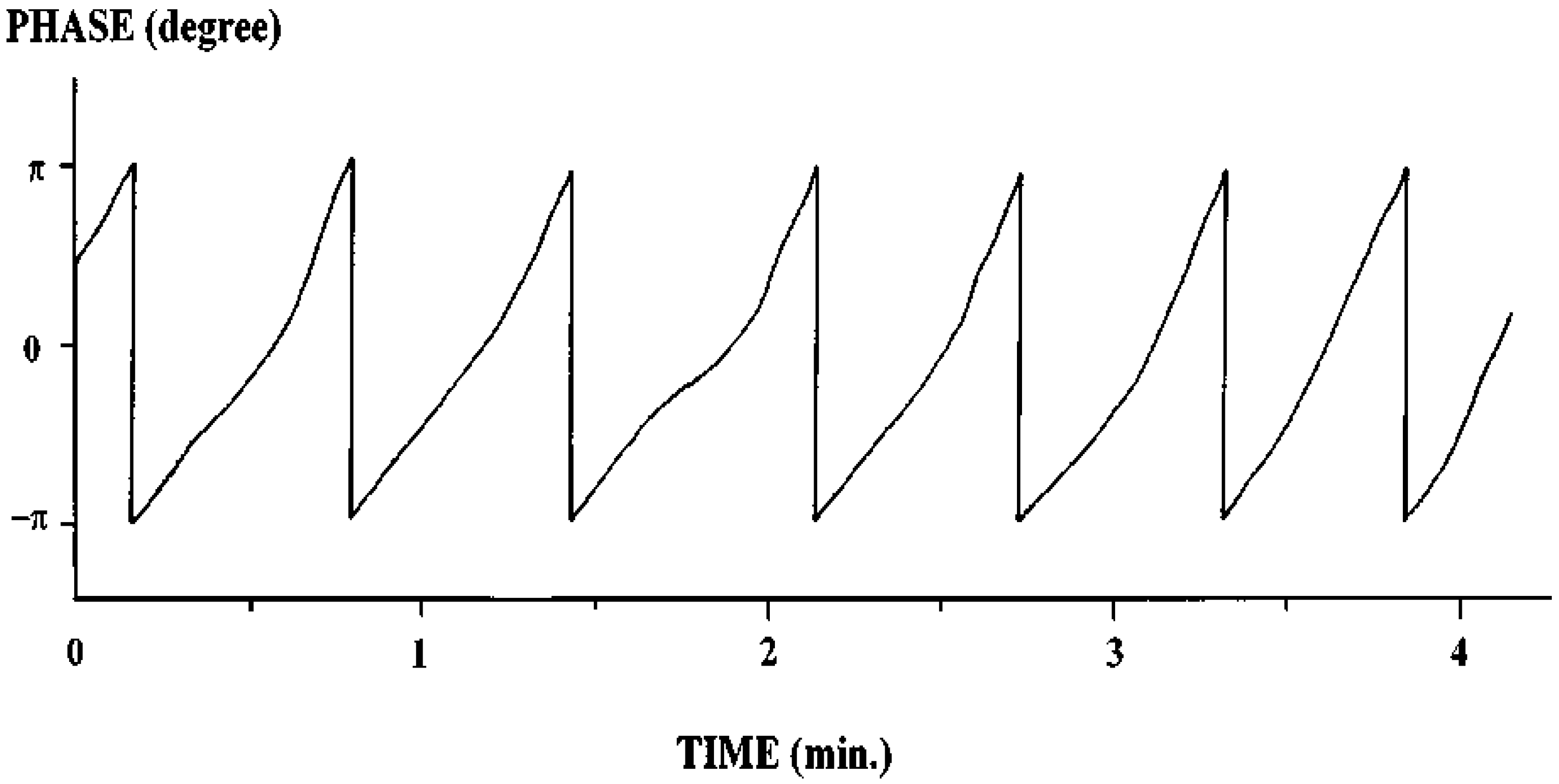
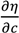 was measured. According to Equation (35) Δη3 equals λ/s if ΔΘd = 2π. The optical mounts/beams are subjected to random vibrations. So the fringe intensity and hence the electrical output of the detector fluctuates (Figure 16). That is why the fringes shown in Figure 16 are not uniform in shape. This will result in a maximum error of 10% in the estimation of Δη3. So the maximum error in the estimation of change in concentration is likewise 10%.
was measured. According to Equation (35) Δη3 equals λ/s if ΔΘd = 2π. The optical mounts/beams are subjected to random vibrations. So the fringe intensity and hence the electrical output of the detector fluctuates (Figure 16). That is why the fringes shown in Figure 16 are not uniform in shape. This will result in a maximum error of 10% in the estimation of Δη3. So the maximum error in the estimation of change in concentration is likewise 10%.
6. Conclusions
Conflicts of Interest
References
- Hariharan, P. Optical Inteferometry; Elsevier/Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Zhou, J.J.; Li, Y.; Thompson, P.; Chu, R.; Lee, H.P. Continuous in situ growth rate extraction using pyrometric interferometry and laser reflectance measurement during molecular beam epitaxy. J. Electron. Mater. 1997, 26, 1083–1089. [Google Scholar] [CrossRef]
- Allison, S.W.; Gillies, G.T. Remote thermometry with thermographic phosphors: Instrumentation and applications. Rev. Sci. Instrum. 1997, 68, 2615–2650. [Google Scholar] [CrossRef]
- Koechner, W.; Bass, M. Solid State Lasers; Springer-Verlag: New York, NY, USA, 2003. [Google Scholar]
- Gasvik, K.J. Optical Metrology; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Hilfiker, J. Emerging applications of spectroscopic ellipsometry. Glass Coatings 2007, 1, 24–27. [Google Scholar]
- Hariharan, P.; Oreb, B.F.; Eiju, T. Digital phase-shifting interferometry: A simple error-compensating phase calculation algorithm. Appl. Opt. 1987, 26, 2504–2506. [Google Scholar] [CrossRef]
- Kanzaki, N.; Onuma, K.; Ito, A.; Teraoka, K.; Tateishi, T; Tsutsumi, S. Direct growth rate measurement of Hydroxyapatite single crystal by Moiré phase shift interferometry. J. Phys. Chem. 1998, 102, 6471–6476. [Google Scholar] [CrossRef]
- Hariharan, P. Optical Holography: Principles, Techniques, and Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Gao, F.; Muhamedsalih, H.; Jiang, X. Surface and thickness measurement of a transparent film using wavelength scanning interferometry. Opt. Express 2012, 20, 21450–21456. [Google Scholar] [CrossRef]
- Zuiker, C.D.; Gruen, D.M.; Krauss, A.R. In situ laser reflectance interferometry measurement of diamond film growth. J. Appl. Phys. 1996, 79, 3541–3546. [Google Scholar] [CrossRef]
- Yoshizaki, I.; Tsukamoto, K.; Yamazaki, T.; Murayama, K.; Oshi, K.; Fukuyama, S.; Shimaoka, T.; Suzuki, Y.; Tachibana, M. Growth rate measurements of lysozyme crystals under microgravity conditions by laser interferometry. Rev. Sci. Instr. 2013, 84. [Google Scholar] [CrossRef]
- Masuda, K.; Erskine, D.; Anderson, O. Differential laser interferometer for thermal expansion measurements. Am. Mineral. 2000, 85, 279–282. [Google Scholar]
- Farahani, M.A.; Torsten Gogolla, T. Spontaneous raman scattering in optical fibers with modulated probe light for distributed temperature raman remote sensing. J. Lightw. Technol. 1999, 17, 1379–1383. [Google Scholar] [CrossRef]
- Zhan, Y.; Wu, H.; Yang, Q.; Xiang, S.; He, H. Fiber Bragg grating sensors for high temperature measurement. Opt. Lasers Eng. 2008, 46, 349–354. [Google Scholar] [CrossRef]
- Liao, S.C.; Xu, Z.; Izatt, J.A.; Alcala, J.R. Real-time frequency domain temperature and O2 sensor with a single optical fiber. IEEE Trans. Biomed. Eng. 1997, 44, 1114–1121. [Google Scholar]
- Patterson, W.M.; Seletskiy, D.V.; Sheik-Bahae, M.; Epstein, R.I.; Hehlen, M.P. Measurement of solid-state optical refrigeration by two-band differential luminescence thermometry. J. Opt. Soc. Am. B 2010, 27, 611–618. [Google Scholar] [CrossRef]
- Chubb, D.L.; Wolford, D.S. Rare-earth optical temperature sensor. Rev. Sci. Instrum. 2000, 71, 2233–2240. [Google Scholar] [CrossRef]
- Sommergren, G.E. Optical heterodyne profilometry. Appl. Opt. 1981, 20, 610–618. [Google Scholar] [CrossRef]
- Kim, Y.; Reddy, B.R.; George, T.G.; Lal, R.B. Optical heterodyne interferometry technique for solution crystal growth rate measurement. Opt. Eng. 1998, 37, 616–621. [Google Scholar] [CrossRef]
- George, M.C.; Reddy, B.R.; Jagannath, H.; Perera, G.M.; Venkateswarlu, P. Measurement of Surface Roughness Using a Noncontact Profilometer. In Laser Spectroscopy and Nonlinear Optics of Solids; Radhakrishna, S., Tan, B.C., Eds.; Narosa Publishing House: Delhi, India, 1991; pp. 147–152. [Google Scholar]
- Kamma, I.; Kommidi, P.; Reddy, B.R. Design of a high temperature sensing system using luminescent lifetime measurement. Rev. Sci. Instrum. 2008, 79. [Google Scholar] [CrossRef]
- Fan, T.Y.; Daneu, J.L. Thermal coefficients of the optical path length and refractive index in YAG. Appl. Opt. 1998, 37, 1635–1637. [Google Scholar] [CrossRef]
- Farley, C.W.; Reddy, B.R. Interferometric measurement of laser heating in Praseodymium doped YAG crystal. Appl. Opt. 2011, 50, 526–531. [Google Scholar] [CrossRef]
- Weber, M.J. Probabilities for radiative and non-radiative decay of Er3+ in LaF3. Phys. Rev. 1967, 157, 262–272. [Google Scholar] [CrossRef]
- Layne, C.B.; Lowdermilk, W.H.; Weber, M.J. Multiphonon relaxation of rare-earth ions in glasses. Phys. Rev. 1977, B16, 10–20. [Google Scholar]
- Shepard, C.L.; Cannon, B.D.; Khaleel, M.A. Determination of temperature in glass with a fluorescence method. Int. J. Heat Mass Transfer 2001, 44, 4027–4034. [Google Scholar] [CrossRef]
- Kamma, I.; Kommidi, P.; Reddy, B.R. High temperature measurement using luminescence of Pr3+ doped YAG and Ho3+ doped CaF2. Phys. Stat. Sol. C 2009, 6, S187–S190. [Google Scholar] [CrossRef]
- Kommidi, P.; Reddy, B.R. Fluorescence lifetime sensing of temperature. Proc. SPIE 2006, 6377. [Google Scholar] [CrossRef]
- Wade, S.A.; Collins, S.F.; Baxter, D.W. Fluorescence intensity ratio technique for optical fiber point temperature sensing. J. Appl. Phys. 2003, 94, 4743–4756. [Google Scholar] [CrossRef]
- Messias, D.N.; Vermelho, M.V.D.; Gouveia-Neto, A.S.; Aitchison, J.S. All optical integrated upconversion fluorescence based point temperature sensing system using Er3+ doped silica-on-silicon waveguides. Rev. Sci. Instrum. 2002, 73, 476–479. [Google Scholar] [CrossRef]
- Forsyth, D.I.; Sun, T.; Grattan, K.T.V.; Wade, S.A.; Collins, S.F. Characteristics of doped optical fiber for fluorescence-based fiber optic temperature systems. Rev. Sci. Instrum. 2003, 74, 5212–5218. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; He, H.; Lin, Y.; Nan, C. Temperature sensing with fluorescence intensity ratio technique in epoxy-based nanocomposite filled with Er3+-doped 7YSZ. Compos. Sci. Technol. 2012, 72, 1008–1011. [Google Scholar] [CrossRef]
- Paez, G.; Strojnik, M. Erbium-doped optical fiber fluorescence temperature sensor with enhanced sensitivity, a high signal-to-noise ratio and a power ratio in the 520–530- and 550–560-nm bands. Appl. Opt. 2003, 42, 3251–3258. [Google Scholar] [CrossRef]
- Reddy, B.R.; Kamma, I.; Kommidi, P. Optical sensing techniques for temperature measurement. Appl. Opt. 2013, 52, B33–B39. [Google Scholar] [CrossRef]
- Farley, C.W.; Reddy, B.R. Mach-Zehnder interferometric measurement of laser heating/cooling in Yb3+: YAG. Proc. SPIE 2011, 7951. [Google Scholar] [CrossRef]
- Kim, Y.K.; Reddy, B.R.; Lal, R.B. Laser and Mach-Zehnder interferometry for solution crystal growth rate and concentration variation measurement, in “Laser interferometry IX: Applications”. Proc. SPIE 1998, 3479, 172–180. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bommareddi, R.R. Applications of Optical Interferometer Techniques for Precision Measurements of Changes in Temperature, Growth and Refractive Index of Materials. Technologies 2014, 2, 54-75. https://doi.org/10.3390/technologies2020054
Bommareddi RR. Applications of Optical Interferometer Techniques for Precision Measurements of Changes in Temperature, Growth and Refractive Index of Materials. Technologies. 2014; 2(2):54-75. https://doi.org/10.3390/technologies2020054
Chicago/Turabian StyleBommareddi, Rami Reddy. 2014. "Applications of Optical Interferometer Techniques for Precision Measurements of Changes in Temperature, Growth and Refractive Index of Materials" Technologies 2, no. 2: 54-75. https://doi.org/10.3390/technologies2020054