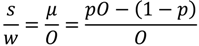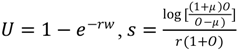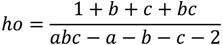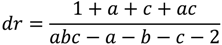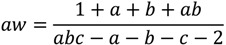Systematic Positive Expected Returns in the UK Fixed Odds Betting Market: An Analysis of the Fink Tank Predictions

Abstract

We report striking evidence of semi-strong inefficiency in the UK fixed-odds football betting market using a reputable newspaper tipster which offers probabilities of match outcomes rather than simple result indicators. Betting on the Fink Tank probabilities of home wins across 10 bookmakers, when there are positive expected returns, would have generated positive returns in each of the seasons from 2006–07 to 2011–12 for a variety of different betting strategies. These returns could have been enhanced by employing the best odds from a greater number of bookmakers. However, the fact that pure arbitrage bets have existed for years and appear to last for several hours or days suggest they are in practice not exploitable to a magnitude that poses any threat to bookmakers.

1. Introduction

It is now well recognized in the literature that betting markets are important for testing market efficiency as pointed out by Thaler and Ziemba [1], they possess the property that each asset or bet has a well-defined termination point at which its value becomes certain. As a consequence, the problems that arise in determining the expected value of future fundamentals are mitigated. Betting markets share many of the other characteristics of asset markets, in particular large numbers of investors (bettors), with readily available cheap sources of information.

There have been numerous studies of the efficiency of the fixed odds football betting market in the UK and elsewhere since the first study of the efficiency of the fixed odds betting in the UK market by Pope and Peel [2]. These authors examined odds from four bookmakers in the 1981–82 season and reported evidence of weak form inefficiency, that is the profitability of a trading rule based purely on bookmakers’ posted odds. They also reported the apparent existence of a few pure arbitrage opportunities in the absence of the 10% betting tax at that time. That entails placing bets on the home, away and draw outcome with different bookmakers and winning with certainty, assuming payout is honoured.

Subsequent analyses have documented the existence of mispricing as well as the apparent existence of pure arbitrage possibilities in European fixed-odds football betting markets [3,4,5,6,7,8,9]. There are numerous papers that have investigated market efficiency in other sports betting markets such as horse racing, National Football League, greyhounds, National Hockey League, Major League Baseball and National Basketball Association (see Sauer [10] and Williams [11] for surveys). The broad conclusion of the empirical studies is that market efficiency appears violated in various periods but there were no systematic violations and that overall the markets analyzed appear efficient when attitude to risk is appropriately accounted for.

Overall, the reported results from the literature on European football betting suggest that mispricing of odds has occurred over many seasons, particularly in the latter period. However Levitt [12] shows that by systematically setting the “wrong” prices in a manner that takes advantage of bettor preferences, bookmakers can increase profits (see also Humphreys [13], and Paul and Weinbach [14]). However, Levitt also notes that there are constraints on the magnitude of this distortion, since bettors who know the “correct” price can generate positive returns if the posted price deviates too much from the true odds. Consequently, evidence of mispricing that does not lead to betting strategies that can generate positive expected returns is irrelevant from the bookmakers’ perspective.

Overall, the view of Forrest and Simmons [15] on statistical models of fixed-odds betting markets seems a good summary of previous work. Forrest wrote “Notwithstanding the apparent potential for employing a statistical model to secure positive returns late in the season, the literature reviewed so far has tended to find difficulty in establishing potential for using statistical modelling to secure positive as opposed to merely less negative returns” ([15], p. 436).

Our purpose in this paper is to provide more striking and firm evidence of semi-strong inefficiency in the UK fixed odds betting market than has been previously reported. We find evidence of systematic positive returns in the English Premier League football based on the predictions of the Fink Tank, (also presented as Castrol Predictor) published weekly in the The Times (on Saturday and online at [16]). Constantinou and Fenton [17] analyse data for the Fink Tank for the 2011/12 season as a predictor of outcomes of matches relative to other predictors. However, they do not examine the potential for generating abnormal returns.

The Fink Tank predictions are based on a statistical model that uses time-weighted shots and goals data to generate an attack and defence ranking for each club. The number of goals scored by a club in a match depends on the attack rating of the club and the defence rating of the opposition. There is also a home advantage rating, which allows for the fact that clubs score more goals when playing at home. An early version of the Fink Tank model appeared as Graham and Stott [18].

The Fink Tank predictions are reported in the form of the probabilities of the home, draw and away outcome. This is unusual as tipsters normally just report ‘most likely’ match outcomes. Forrest and Simmons [5] reported remarkably poor predictive performance of three newspaper tipsters. Later, Forrest et al. [19] demonstrated the superior predictive ability of UK bookmakers over an elaborate statistical model in forecasting English League match results across all four tiers of English football.

We examine Fink Tank probabilities in conjunction with the odds of 10 bookmakers over the 2006–07 to 2011–12 Premier League seasons. We find systematic positive returns in each year obtained from a variety of different betting strategies based on betting on the home win. Given that the predictions of Fink Tank are readily available and positive returns have persisted for so many years, so that bettors or bookmakers have had time to learn of the value of the predictions, our findings appear to be of interest.

We also examine in more detail bets that appear to offer pure, paper, arbitrage profits. Numerous such bets exist each week and can be readily found by employing free internet comparisons of fixed-odds bookmaker sites. Of course, if these opportunities were exploitable they would constitute evidence of inefficiency under any definition and raise issues about both bookmaker and bettor rationality. However, it is well known that bookmakers need only balance their books to make a risk-free profit. With a balanced book, bookmakers do not necessarily care about odds from other bookmakers and arbitrage does not necessarily imply irrationality [9]. We should stress, though, that the balanced book assumption has been challenged recently [13].

2. Expected Returns from the Fink Tank Model

Our data set comprises the Fink Tank predicted probabilities of all possible outcomes of 1669 matches in the English Premier League, the top division of English football, over the 2006–07 to 2001–12 seasons together with the odds set by 10 bookmakers (Bet365, BWin, Gamebookers, Interwetten, Ladbrokes, Sportingbet, William Hill, StanJames, BETVICTOR, Blue Square). In Table 1 we report some summary statistics for the difference in maximum and minimum odds as a proportion of minimum odds.

Table 1. Differences in maximum and minimum odds as a ratio of minimum odds.

Statistics	Home odds	Away odds	Draw odds
N	1669	1669	1669
Mean	0.232	0.289	0.158
St. deviation	0.115	0.161	0.099

Table 1. Differences in maximum and minimum odds as a ratio of minimum odds.

Statistics	Home odds	Away odds	Draw odds
N	1669	1669	1669
Mean	0.232	0.289	0.158
St. deviation	0.115	0.161	0.099

We note that there is a mean difference of 23.2%, 28.9% and 15.8% between the best and worst odds posted for home, away and draw odds respectively. Clearly, placing bets with more than one bookmaker can increase expected returns or decrease losses substantially, ceteris paribus. To illustrate we randomly assumed we bet solely with either William Hills or Ladbrokes. In Table 2 we report the number of times they had the best odds.

Table 2. William Hill’s and Ladbrokes’s odds versus best odds by other bookmakers.

WH or LB versus other bookmakers	N
WH or LB’s home odds > other BM’s	75
WH or LB’s away odds > other BM’s	51
WH or LB’s draw odds > other BM’s	87

LB—Ladbrokes, WH—William Hill, and BM—best bookmaker’s odds.

Table 2. William Hill’s and Ladbrokes’s odds versus best odds by other bookmakers.

WH or LB versus other bookmakers	N
WH or LB’s home odds > other BM’s	75
WH or LB’s away odds > other BM’s	51
WH or LB’s draw odds > other BM’s	87

LB—Ladbrokes, WH—William Hill, and BM—best bookmaker’s odds.

The expected return, for a one unit stake based on the Fink Tank probabilities is given by

μ = pO − (1 − p)

(1)

where p is the Fink Tank probability and O is the highest odds of the 10 bookmakers. In Table 3 we report the summary statistics for the expected returns for a one unit stake based on the Fink Tank probabilities for home, away and draw employing the best bookmaker odds for our data sample. We follow the literature on European football betting in offering average returns from simulations rather than statistical tests as applied in the literature on North American sports betting.

Table 3. Expected returns—for home win, away win and draw.

	N	Mean	Median	St. dev.	Minimum	Maximum
Home
Expected return ≤ 0	837	−0.118	−0.096	0.098	−0.674	0.000
Expected return > 0	832	0.164	0.110	0.183	0.000	1.880
Expected return	1669	0.023	0.000	0.203	−0.670	1.880
Away
Expected return ≤ 0	746	−0.149	−0.120	0.125	−0.890	0.000
Expected return > 0	923	0.251	0.170	0.263	0.000	2.825
Expected return	1669	0.072	0.035	0.292	−0.890	2.825
Draw
Expected return ≤ 0	1519	−0.157	−0.150	0.089	−0.813	0.000
Expected return > 0	150	0.125	0.050	0.277	0.000	2.650
Expected return	1669	−0.131	−0.142	0.143	−0.813	2.650

Table 3. Expected returns—for home win, away win and draw.

	N	Mean	Median	St. dev.	Minimum	Maximum
Home
Expected return ≤ 0	837	−0.118	−0.096	0.098	−0.674	0.000
Expected return > 0	832	0.164	0.110	0.183	0.000	1.880
Expected return	1669	0.023	0.000	0.203	−0.670	1.880
Away
Expected return ≤ 0	746	−0.149	−0.120	0.125	−0.890	0.000
Expected return > 0	923	0.251	0.170	0.263	0.000	2.825
Expected return	1669	0.072	0.035	0.292	−0.890	2.825
Draw
Expected return ≤ 0	1519	−0.157	−0.150	0.089	−0.813	0.000
Expected return > 0	150	0.125	0.050	0.277	0.000	2.650
Expected return	1669	−0.131	−0.142	0.143	−0.813	2.650

Over the sample period the Fink Tank probabilities and best bookmaker odds implied that we would bet on 832 home matches with an average expected return of 16.4%, 923 away matches with an expected return of 25.1% and 150 draws with an expected return of 12.5%. The largest expected home return of 18.8% occurred in the match Swansea versus Manchester United when the Fink Tank probability of a home win was p = 0.36 and best odds 7/1. In fact Manchester United won the match with a 1-0 away win.

For matches where the expected return is greater than zero we consider a number of betting strategies. The first betting strategy is to stake one unit on each outcome where expected return is positive. We report the results for each season and actual returns to this betting strategy in Table 4.

We observe that betting on one unit on each home team when expected return was positive would have generated a positive return in all seasons except 2008/9 with an average return of 10.75%. The actual returns to a one unit stake on away matches were negative (mean of −8.1%) but positive for draws with volatile returns across seasons. We conjecture that the Fink Tank probabilities deal with home advantage differently to bookmakers. Since home teams win in almost 50% of games, they are more likely to be favourites than away teams. Some studies have found evidence for favourite-longshot bias in European fixed odds betting markets [3]. To the extent that bookmakers are prone to this bias and the Fink Tank predictions avoid such bias then it is possible to derive positive returns from betting on home teams using the Fink Tank. However, the Fink Tank predictions deliver substantial losses from betting on away teams and this may be due to misclassification of results between draws and away wins.

Table 4. Returns to a unit stake on home, away and draw when expected returns are positive and bet on home team benchmark.

Season	Stake	Winning bets	Losing bets	Wins	Profit	Return (%)
Home
2006–07	132	65	67	85.04	18.04	13.67
2007–08	143	63	80	86.75	6.75	4.72
2008–09	122	53	69	68.59	−0.41	−0.34
2009–10	151	68	83	101.24	18.24	12.08
2010–11	150	74	76	100.49	24.49	16.33
2011–12	134	61	73	95.33	22.33	16.66
Total	832	384	448	537.44	89.44	10.75
Away
2006–07	130	31	99	75.08	–23.92	−18.40
2007–08	189	47	142	91.66	−50.34	−26.63
2008–09	133	44	89	122.05	33.05	24.85
2009–10	145	27	118	64.54	−53.46	−36.87
2010–11	161	34	127	132.18	5.18	3.22
2011–12	165	39	126	140.75	14.75	8.94
Total	923	222	701	626.26	−74.74	−8.10
Draw
2006–07	41	12	29	30.85	1.85	4.51
2007-08	19	8	11	30.90	19.9	104.74
2008–09	12	3	9	9.00	0.00	0.00
2009–10	25	3	22	9.8	−12.2	−48.80
2010–11	20	6	14	19.90	5.90	29.50
2011–12	33	10	23	36.65	13.65	41.36
Total	150	42	108	137.10	29.10	19.40
Unit bet on home team “benchmark”
2006–07	300	143	157	169.83	12.83	4.28
2007–08	326	150	176	159.38	−16.62	−5.10
2008–09	226	92	134	111.62	−22.38	−9.90
2009–10	271	134	137	161.80	24.80	9.15
2010–11	282	131	151	160.15	9.15	3.24
2011–12	264	124	140	141.22	1.22	0.46
Total	1669	774	895	904.00	9.00	0.54

Table 4. Returns to a unit stake on home, away and draw when expected returns are positive and bet on home team benchmark.

Season	Stake	Winning bets	Losing bets	Wins	Profit	Return (%)
Home
2006–07	132	65	67	85.04	18.04	13.67
2007–08	143	63	80	86.75	6.75	4.72
2008–09	122	53	69	68.59	−0.41	−0.34
2009–10	151	68	83	101.24	18.24	12.08
2010–11	150	74	76	100.49	24.49	16.33
2011–12	134	61	73	95.33	22.33	16.66
Total	832	384	448	537.44	89.44	10.75
Away
2006–07	130	31	99	75.08	–23.92	−18.40
2007–08	189	47	142	91.66	−50.34	−26.63
2008–09	133	44	89	122.05	33.05	24.85
2009–10	145	27	118	64.54	−53.46	−36.87
2010–11	161	34	127	132.18	5.18	3.22
2011–12	165	39	126	140.75	14.75	8.94
Total	923	222	701	626.26	−74.74	−8.10
Draw
2006–07	41	12	29	30.85	1.85	4.51
2007-08	19	8	11	30.90	19.9	104.74
2008–09	12	3	9	9.00	0.00	0.00
2009–10	25	3	22	9.8	−12.2	−48.80
2010–11	20	6	14	19.90	5.90	29.50
2011–12	33	10	23	36.65	13.65	41.36
Total	150	42	108	137.10	29.10	19.40
Unit bet on home team “benchmark”
2006–07	300	143	157	169.83	12.83	4.28
2007–08	326	150	176	159.38	−16.62	−5.10
2008–09	226	92	134	111.62	−22.38	−9.90
2009–10	271	134	137	161.80	24.80	9.15
2010–11	282	131	151	160.15	9.15	3.24
2011–12	264	124	140	141.22	1.22	0.46
Total	1669	774	895	904.00	9.00	0.54

The bottom panel of Table 4 shows a benchmark set of returns from betting on home teams. In some seasons, betting purely on home teams would have generated a profit (4.3% in 2006/07 and 9.1% in 2009/10) but returns are volatile across seasons the average return over the whole sample is negligible at +0.54%. In every season, the Fink Tank predictions generate higher returns from backing home teams where expected returns are positive compared to a naive strategy of just backing home teams.

Of course a one unit bet on every outcome where expected return is positive does not make allowance for either the magnitude of the expected return or the probability of occurrence. A standard staking system in the betting literature is to employ the variable Kelly stake as a proportion of wealth as a solution to this problem. See Sung and Johnson [20,21] for applications of Kelly investment strategies to the horse race betting market.

The Kelly stake is the optimal stake for an expected utility maximiser who has a logarithmic utility function. Expected utility, Eu, is given by

Eu = p log(w + sO) + (1 − p) log(w − s)

(2)

where w is the agent’s betting wealth, s is the stake, O are odds and p is the probability of winning. Differentiating (1) with respect to s we obtain the optimal stake as

(3)

Our second betting strategy, is to determine returns based on staking s = μ/o on each match where μ is positive and assuming betting wealth is fixed at w = 1. The returns are reported in Table 5. The important point to note from Table 5 is that actual returns to betting homes matches where expected returns are positive generates a positive return in each season with an average return of 10.53%. Actual returns to betting on away wins or draws were both negative.

Table 5. Returns on home, away and draw bets when using Kelly single stake.

Season	Winning bets	Losing bets	Winning stakes	Losing stakes	Wins	Profit	Return (%)
Home
2006–07	65	67	82.95	82.95	88.36	5.41	3.26
2007–08	63	80	64.81	63.07	69.98	6.91	5.40
2008–09	53	69	58.84	45.26	63.25	17.99	17.28
2009–10	68	83	76.66	73.18	93.93	20.75	13.85
2010–11	74	76	92.43	74.01	94.16	20.15	12.11
2011–12	61	73	58.05	60.69	77.18	16.49	13.89
Total	384	448	433.74	399.17	486.86	87.69	10.53
Away
2006–07	31	99	35.91	79.35	79.97	0.62	0.54
2007–08	47	142	33.55	83.63	55.55	−28.08	−23.96
2008–09	44	89	36.73	53.21	76.37	23.17	25.76
2009–10	27	118	14.36	79.73	33.55	−46.18	−49.08
2010–11	34	127	32.38	97.85	104.64	6.8	5.22
2011–12	39	126	26.66	78.17	74.68	−3.48	−3.32
Total	222	701	179.58	471.93	424.77	−47.15	−7.24
Draw
2006–07	12	29	3.81	13.96	11.92	−2.04	−11.48
2007–08	8	11	1.09	1.56	6.03	4.46	168.30
2008–09	3	9	0.26	1.57	0.80	−0.770	−42.08
2009–10	3	22	1.58	14.14	4.34	−9.80	−62.34
2010–11	6	14	1.39	3.17	4.01	0.84	18.42
2011–12	10	23	1.47	3.66	6.06	2.40	46.78
Total	42	108	9.61	38.06	33.15	−4.91	−10.30

Table 5. Returns on home, away and draw bets when using Kelly single stake.

Season	Winning bets	Losing bets	Winning stakes	Losing stakes	Wins	Profit	Return (%)
Home
2006–07	65	67	82.95	82.95	88.36	5.41	3.26
2007–08	63	80	64.81	63.07	69.98	6.91	5.40
2008–09	53	69	58.84	45.26	63.25	17.99	17.28
2009–10	68	83	76.66	73.18	93.93	20.75	13.85
2010–11	74	76	92.43	74.01	94.16	20.15	12.11
2011–12	61	73	58.05	60.69	77.18	16.49	13.89
Total	384	448	433.74	399.17	486.86	87.69	10.53
Away
2006–07	31	99	35.91	79.35	79.97	0.62	0.54
2007–08	47	142	33.55	83.63	55.55	−28.08	−23.96
2008–09	44	89	36.73	53.21	76.37	23.17	25.76
2009–10	27	118	14.36	79.73	33.55	−46.18	−49.08
2010–11	34	127	32.38	97.85	104.64	6.8	5.22
2011–12	39	126	26.66	78.17	74.68	−3.48	−3.32
Total	222	701	179.58	471.93	424.77	−47.15	−7.24
Draw
2006–07	12	29	3.81	13.96	11.92	−2.04	−11.48
2007–08	8	11	1.09	1.56	6.03	4.46	168.30
2008–09	3	9	0.26	1.57	0.80	−0.770	−42.08
2009–10	3	22	1.58	14.14	4.34	−9.80	−62.34
2010–11	6	14	1.39	3.17	4.01	0.84	18.42
2011–12	10	23	1.47	3.66	6.06	2.40	46.78
Total	42	108	9.61	38.06	33.15	−4.91	−10.30

If we examine the actual proportions of home away and draws outcomes and the proportions predicted obtained from best bookmaker odds and the Fink Tank we observe in Table 6 that the average of the Fink Tank probability exactly matched the proportion of outcomes but was too high and too low for away wins and draws respectively.

Table 6. Actual Proportions of Outcomes and Predicted based on best bookmaker’s odds (BM) and Fink Tank (FT).

	Home win	Home probability (BM)	Home probability (FT)
N	1669	1669	1669
Mean	0.464	0.452	0.464
St. dev.	0.499	0.183	0.185
Minimum	0.000	0.052	0.040
Maximum	1.000	0.869	0.930
	Away win	Away probability (BM)	Away probability (FT)
N	1669	1669	1669
Mean	0.268	0.289	0.305
St. dev.	0.443	0.163	0.162
Minimum	0.000	0.033	0.020
Maximum	1.000	0.824	0.850
	Draw	Draw probability (BM)	Draw probability (FT)
N	1669	1669	1669
Mean	0.268	0.259	0.231
St. dev.	0.443	0.045	0.049
Minimum	0.000	0.097	0.030
Maximum	1.000	0.315	0.730

Table 6. Actual Proportions of Outcomes and Predicted based on best bookmaker’s odds (BM) and Fink Tank (FT).

	Home win	Home probability (BM)	Home probability (FT)
N	1669	1669	1669
Mean	0.464	0.452	0.464
St. dev.	0.499	0.183	0.185
Minimum	0.000	0.052	0.040
Maximum	1.000	0.869	0.930
	Away win	Away probability (BM)	Away probability (FT)
N	1669	1669	1669
Mean	0.268	0.289	0.305
St. dev.	0.443	0.163	0.162
Minimum	0.000	0.033	0.020
Maximum	1.000	0.824	0.850
	Draw	Draw probability (BM)	Draw probability (FT)
N	1669	1669	1669
Mean	0.268	0.259	0.231
St. dev.	0.443	0.045	0.049
Minimum	0.000	0.097	0.030
Maximum	1.000	0.315	0.730

Of course punters may not be expected utility maximizers with a logarithmic utility function or may be non-expected utility maximizers. They could, for example, be better described as expected utility maximizers with a power or exponential utility function or non-expected utility maximizers of either Tversky and Kahneman’s cumulative prospect theory [22] or Markowitz [23]. We therefore computed returns for a variety of alternative expected utility or non-expected value functions. The results were qualitatively similar to those reported for stakes based on the Kelly ratio. For example, in Table 7 we report the returns from betting on home teams with positive expected values for an expected utility maximiser with an exponential utility function as follows:

(4)

The parameter r cancels in computation of actual returns.

The actual returns in Table 4, Table 5, Table 7, and Table 8 were computed employing the best odds from 10 bookmakers. In Table 8, we report the returns if agents bet solely with William Hill or Ladbrokes when expected returns were positive employing the Kelly ratio. We observe by comparing Table 5 and Table 8 that the average return to betting on home wins is some 4% lower, while returns are negative in the season 2006–07 (−4.19%) but positive for this season (3.26%) across the 10 bookmakers. Clearly, choosing bets from more bookmaker accounts will increase returns, ceteris paribus and without considering transactions costs of choices.

Formal evidence of the incremental value in the Fink Tank prediction of home win outcomes but not away wins or draws relative to the probability based on the best bookmaker odds is shown by the probit regressions reported in Table 9. Our analysis shows that a betting strategy based on the Fink Tank probabilities of home wins would have generated positive expected returns in the last six seasons of Premier League matches. It is clear that betting at the best odds on matchday would increase expected returns by perhaps 2%–3% at the cost of having a greater number of bookmaker accounts. Overall, our results provide a striking example of semi-strong inefficiency.

Table 7. Constant Absolute Risk Aversion.

Season	Winning bets	Losing bets	Winning stakes	Losing stakes	Wins	Profit	Return (%)
2006–07	66	67	85.12	85.23	85.60	0.37	0.22
2007–08	65	78	68.50	60.82	70.23	9.42	7.28
2008–09	53	70	61.30	44.66	62.63	17.97	16.96
2009–10	68	83	76.81	69.73	89.97	20.23	13.81
2010–11	73	77	102.53	73.81	97.38	23.57	13.37
2011–12	61	72	56.80	56.33	73.58	17.25	15.25
Total	386	447	451.07	390.58	479.39	88.81	10.55

Table 7. Constant Absolute Risk Aversion.

Season	Winning bets	Losing bets	Winning stakes	Losing stakes	Wins	Profit	Return (%)
2006–07	66	67	85.12	85.23	85.60	0.37	0.22
2007–08	65	78	68.50	60.82	70.23	9.42	7.28
2008–09	53	70	61.30	44.66	62.63	17.97	16.96
2009–10	68	83	76.81	69.73	89.97	20.23	13.81
2010–11	73	77	102.53	73.81	97.38	23.57	13.37
2011–12	61	72	56.80	56.33	73.58	17.25	15.25
Total	386	447	451.07	390.58	479.39	88.81	10.55

The Fink Tank predictions are now available online during the week preceding a match. As a consequence, this will enable a bettor employing the Fink Tank home predictions far more opportunities to bet on home wins with positive expected value as the different bookmakers odds change over the course of the week. The adjustment of betting odds on football matches by bookmakers up to kick-off is a relatively recent phenomenon in the UK. Forrest [24] records how bookmakers in the 1990s and early 2000s used to keep odds fixed and stationary in the two or three days before a match. Such a position became untenable with the emergence of internet betting combined with increased global competition in betting markets. Of course, if bettors who were able to stake between them relatively large amounts were to employ the Fink Tank predictions, with consequent systematic and persistent returns, then at some point the bookmakers would have to set odds that reflected more closely the predictions of Fink Tank.

Table 8. Returns on home, away and draw bets using Kelly stake with Ladbrokes or William Hill when expected returns is positive.

Season	Winning bets	Losing bets	Winning stakes	Losing stakes	Wins	Profit	Return (%)
Home
2006–07	52	55	62.10	64.14	58.85	−5.29	−4.19
2007–08	49	50	41.01	37.46	37.66	0.20	0.25
2008–09	44	62	44.52	36.59	46.93	10.34	12.75
2009–10	57	80	61.28	62.32	76.99	14.67	11.87
2010–11	65	65	81.85	64.29	78.29	14.01	9.59
2011–12	57	67	50.50	53.11	62.26	9.15	8.83
Total	324	379	341.25	317.91	360.98	43.08	6.54
Away
2006–07	28	75	27.34	58.88	55.52	−3.35	−3.89
2007–08	31	74	19.76	44.83	28.32	−16.50	−25.55
2008–09	35	72	29.18	39.87	54.92	15.05	21.80
2009–10	22	108	11.20	67.61	25.79	−41.82	−53.06
2010–11	32	112	27.63	79.82	83.78	3.96	3.69
2011–12	35	116	21.61	63.62	52.94	−10.69	−12.54
Total	183	557	136.73	354.63	301.27	−53.36	−10.86
Draw
2006–07	6	14	1.21	9.03	3.11	−5.91	−57.71
2007–08	1	1	0.51	0.90	3.60	2.70	191.49
2008–09	1	5	0.10	0.78	0.35	−0.43	−48.86
2009–10	3	17	1.48	12.72	3.90	−8.82	−62.11
2010–11	5	9	1.27	1.76	3.67	1.91	63.04
2011–12	3	8	0.65	0.87	2.67	1.80	118.42
Total	19	54	5.23	26.06	17.31	−8.75	−27.96

Table 8. Returns on home, away and draw bets using Kelly stake with Ladbrokes or William Hill when expected returns is positive.

Season	Winning bets	Losing bets	Winning stakes	Losing stakes	Wins	Profit	Return (%)
Home
2006–07	52	55	62.10	64.14	58.85	−5.29	−4.19
2007–08	49	50	41.01	37.46	37.66	0.20	0.25
2008–09	44	62	44.52	36.59	46.93	10.34	12.75
2009–10	57	80	61.28	62.32	76.99	14.67	11.87
2010–11	65	65	81.85	64.29	78.29	14.01	9.59
2011–12	57	67	50.50	53.11	62.26	9.15	8.83
Total	324	379	341.25	317.91	360.98	43.08	6.54
Away
2006–07	28	75	27.34	58.88	55.52	−3.35	−3.89
2007–08	31	74	19.76	44.83	28.32	−16.50	−25.55
2008–09	35	72	29.18	39.87	54.92	15.05	21.80
2009–10	22	108	11.20	67.61	25.79	−41.82	−53.06
2010–11	32	112	27.63	79.82	83.78	3.96	3.69
2011–12	35	116	21.61	63.62	52.94	−10.69	−12.54
Total	183	557	136.73	354.63	301.27	−53.36	−10.86
Draw
2006–07	6	14	1.21	9.03	3.11	−5.91	−57.71
2007–08	1	1	0.51	0.90	3.60	2.70	191.49
2008–09	1	5	0.10	0.78	0.35	−0.43	−48.86
2009–10	3	17	1.48	12.72	3.90	−8.82	−62.11
2010–11	5	9	1.27	1.76	3.67	1.91	63.04
2011–12	3	8	0.65	0.87	2.67	1.80	118.42
Total	19	54	5.23	26.06	17.31	−8.75	−27.96

3. Apparent Pure Arbitrage Possibilities

In our analysis we employed the best odds from 10 bookmakers available to us over our sample period. The website [25] supplied the odds for 18 bookmakers and two betting exchanges. The website highlights the best home, draw and away odds available and the over round based on these odds. The over round is the sum of probability implied by the odds. This sum is typically greater than unity but on rare occasions can be below unity which would indicate the potential for a pure arbitrage gain.

Bookmakers quote odds that are fixed for the bettor at the time of placing the wager. This means that the terms of the bettor’s wager are unaltered before the finish of the match. Significant changes in the bookmakers’ quoted odds tend to occur frequently from the first listing of odds, about three weeks before the match until the end of the match. The odds will change over the betting period in response to a number of factors. These include protection against insider trading activity [26] and public news about fundamentals such as player injuries [27]. Bookmakers will change their subjective probability of match outcomes as they attempt to maximize their objective function. This could involve deliberately setting the “wrong” prices on some outcomes to exploit sentiment or as “loss leaders” [7,15].

Table 9. Probit models with marginal effects for home win, away win and draw.

Home win
	(1)	(2)	(3)
Home probability (BM)	1.060 ***		0.571 ***
	(14.460)		(3.043)
Home probability (FT)		1.043 ***	0.523 ***
		(14.350)	(2.807)
Observations	1669	1669	1669
Pseudo R2	0.097	0.096	0.100
Away win
	(4)	(5)	(6)
Away probability (BM)	1.006 ***		0.873 ***
	(15.078)		(5.284)
Away probability (FT)		0.955 ***	0.146
		(14.210)	(0.872)
Observations	1669	1669	1669
Pseudo R2	0.121	0.106	0.121
Draw
	(7)	(8)	(9)
Draw probability (BM)	1.144 ***		0.979 ***
	(4.484)		(2.660)
Draw probability (FT)		0.836 ***	0.201
		(3.576)	(0.627)
Observations	1669	1669	1669
Pseudo R2	0.010	0.007	0.011

BM—Best bookmaker’s odds, FT—Fink Tank; *** denotes significance at 1 percent.

Table 9. Probit models with marginal effects for home win, away win and draw.

Home win
	(1)	(2)	(3)
Home probability (BM)	1.060 ***		0.571 ***
	(14.460)		(3.043)
Home probability (FT)		1.043 ***	0.523 ***
		(14.350)	(2.807)
Observations	1669	1669	1669
Pseudo R2	0.097	0.096	0.100
Away win
	(4)	(5)	(6)
Away probability (BM)	1.006 ***		0.873 ***
	(15.078)		(5.284)
Away probability (FT)		0.955 ***	0.146
		(14.210)	(0.872)
Observations	1669	1669	1669
Pseudo R2	0.121	0.106	0.121
Draw
	(7)	(8)	(9)
Draw probability (BM)	1.144 ***		0.979 ***
	(4.484)		(2.660)
Draw probability (FT)		0.836 ***	0.201
		(3.576)	(0.627)
Observations	1669	1669	1669
Pseudo R2	0.010	0.007	0.011

BM—Best bookmaker’s odds, FT—Fink Tank; *** denotes significance at 1 percent.

The over round for a particular bookmaker and the over round employing the best odds across bookmakers, from the punters perspective, each tends to fall as match day approaches. The over round of an individual bookmaker on a given match at kick-off is always above unity at approximately 8% (1.08). Previous studies have reported over rounds of around 10% to 12% [23] and the lower current figure is most likely a consequence of competition from betting exchanges such as Betfair [28]. The over round across bookmakers is typically around 1 to 2% (1.01 to 1.02). In the week leading up to kick off, it is not unusual to observe an over round less than unity in up to three Premier League matches per day, with a few others in lower divisions, based on the best odds of typically three to four out of 20 bookmakers. The identities of bookmakers involved in these apparent pure arbitrage possibilities vary from day to day.

The possibility of pure arbitrage profits was identified in a number of earlier papers and has clearly not disappeared over two decades since first noted by Pope and Peel [2]. However, we are highly quizzical about whether pure arbitrage profits of any economically significant amount can be systematically realized. It is possible that bookmakers are unaware when the over round across bookmakers becomes negative, as a necessary condition for pure arbitrage, but we doubt this if only because of the existence of internet comparison sites such as Betrescue [25], which has direct links to all bookmakers quoted in our sample, together with the apparent existence of such pure arbitrage bets since at least 1989.

An over round of below unity is necessary, but not sufficient, for a pure arbitrage opportunity. There are direct costs associated with undertaking an arbitrage. An arbitrage will not be riskless. In order to undertake arbitrage bets, it will be necessary for the bettor to have funds deposited in a number of bookmaker accounts since inspection suggests that arbitrage possibilities are not concentrated across a few bookmakers. Clearly, the less the number of bookmaker accounts covered the fewer the arbitrage opportunities available. It appears that at least 10 accounts would be needed to achieve a reasonable number of arbitrage possibilities. An arbitrage gain of £10 would appear to require an outlay typically of £500 or more so a large capital base is required. Also, there are costs and delays in depositing and withdrawing funds. While specialist methods for fund transfers do exist, such as eWallets, withdrawals are often limited to a particular amount per month or to a specific number of free monthly withdrawals. Withdrawals tend to be charged for on the eWallet side. For many bettors with medium sized stakes, these transactions costs could amount to 2% to 3% of the stake which would wipe out positive returns from arbitrage trades. For very large traders, the very existence of their accounts with large deposits and withdrawals draw the attention of bookmakers to arbitrage attempts. Bookmakers can then suddenly suspend bettor accounts imposing potentially large losses on the arbitrageur.

The formulae for the stakes on the home, ho, draw, dr, and away, aw, to obtain a pure arbitrage gain of 1 when the over round across bookmakers is less than one and the home odds are a, draw odds, b, and away odds, c, are given by

(5)

(6)

(7)

A necessary condition for a pure arbitrage gain is that abc – a – b – c – 2 > 0. If one of the outcomes is heavily odds on the amounts required to be bet to earn one unit can be relatively large. For example the pure arbitrage odds a = 1/5, b = 17/2 and c = 18/1 (Manchester City versus Southampton opening day of the 2012/13 Premier League season) required a total bet of £113 to win one £1. (home = £95, draw = £12, away = £6). Consequently, large outlays would typically be needed to generate an arbitrage paper gain of £10. Our estimate is typically around is £500. As noted above, if the arbitrageur’s capital base is large enough this profit can be realized but a bookmaker can impose maximum limits on the size of a stake without warning, leaving the arbitrageur with costs as she attempts to cover the bet with other bookmakers.

Overall, it seems scarcely credible that bookmakers are unaware of arbitrage opportunities given that they are linked to comparison web sites such as Betrescue [25]. Bookmakers have expressed a dim view of arbitrage attempts. They can close accounts or refuse bets without warning and thus potentially impose substantial costs on arbitrageurs as they remove the arbitrage possibility after some of the components have been bet. We should add that the odds can also change for fundamental reasons so that the arbitrage opportunity disappears after one or two components of the arbitrage bet have been placed.

Case Studies of Pure Arbitrage

We followed an apparent arbitrage possibility through from their first appearance on Betrescue [25] to their removal. The typical pattern is shown by the following two examples of arbitrage opportunity. On Monday October 1st 2012 at 6:40 p.m. the best odds for the forthcoming Swansea versus Reading match on October 6th included 1/1 for the home win (quoted by three of 19 bookmakers on Betrescue [25], namely Stan James, BLUESQ, and Boyesports). The best draw odds were quoted by BETVICTOR at 29/10. The best away odds were quoted by BETVICTOR and Panbet at 7/2. For this match it would be necessary to stake a total of £45.8 to obtain a £1 gain. (home = £23.4, draw = £12, away = £10.4). We noted that bookmaker BETVICTOR was posting the worst odds on the home at this time but the best odds available for the draw and away. On Tuesday at 10am this arbitrage possibility had disappeared with a new over round of 1.008. The best home odds of 1/1 were still being quoted by Stan James and BLUESQ. Boyesports and BETVICTOR were quoting 23/10 the draw, (the best draw odds were 13/5 with 32RED, BET365 or bodog). The best away odds were now 10/3 quoted by Panbet.

West Bromwich Albion versus Queens Park Rangers, to be played on October 12th 2012 also offered a pure arbitrage possibility again on Monday October 1st 2012 at 6.40 p.m. 21/20 (home win) quoted by Stan James, 11/4 (draw) quoted by 32RED, BETVICTOR and Bodog and 7/2 (away) quoted by Panbet. £42 stake was required to win £1 i.e., home win bet of £20.93, draw bet of £11.44 and away win bet of £9.53 with an over round of 0.977. Note that the draw odds in this arbitrage example were the same on Tuesday at 11.40 am as on Monday at 6 40 pm, the previous day. However, by Tuesday at 12.10 pm this arbitrage opportunity had gone. Best odds were now 19/20 home win (Skybet), 11/4/ draw (32RED) and 10/3 away win (Panbet) giving an over round of 1.01.

Clearly, these arbitrage possibilities could have disappeared due to pure arbitrage dealing staggered over time. Arbitrage opportunities signalled by a below-unity over round may fall under the heading of ‘limits to arbitrage’ proposed by Shleifer and Vishny [29] who suggested that arbitrage possibilities may not quickly disappear. Alternatively, Kondor [30] developed a model of competition between arbitrageurs in standard asset markets. An arbitrageur faces the risk that the opportunity may disappear as she tries to exploit it. The arbitrageur may leave the opportunity ‘on the table’ in order to exploit future (more lucrative) arbitrage possibilities.

In our examples, the arbitrage possibilities did not disappear quickly. Most money has to be wagered on the favourite in a pure arbitrage bet, In the Swansea-Reading match the odds for the home outcome of the three bookmakers offering the best home odds were unchanged at 1/1. This is suggestive of a persistent arbitrage opportunity. Rather, some bettors appear to have bet on draw and away win outcomes at the more favourable odds. Similarly, in the West Bromwich Albion-Queens Park Rangers match the draw odds remained unchanged over the duration of the arbitrage possibility.

4. Conclusions

Previous literature has reported some evidence of inefficiency in bookmakers’ pricing of odds in fixed odds betting, including the potential for pure arbitrage gains betting with different bookmakers. In this paper we add to this literature and report striking evidence that betting on the Fink Tank probability of home wins across 10 bookmakers when there are positive expected returns, would have generated positive returns in each of the seasons from 2006–07 to 2011–12 for a variety of different betting strategies. These returns could have been enhanced by employing the best odds from a greater number of bookmakers. The inefficiency associated with Fink Tank match outcome probability is unlikely to be due to systematic mistakes. Bookmakers will change their subjective probability of match outcomes as they attempt to maximize their objective function. This could involve deliberately setting the “wrong” prices on some outcomes to exploit sentiment or as “loss leaders”. The extent to which the inefficiencies derived here from Fink Tank probability can be attributed to either or both of these sources of mispricing is a useful topic for further research.

We noted that paper pure arbitrage opportunities occur quite frequently, perhaps a handful a day, as bookmakers change odds in response to betting flows and news or possibly in an attempt to induce betting flows. The fact that these pure arbitrage bets have existed for years and appear to last for several hours or even days suggest they are in practice not exploitable to a magnitude that poses any threat to bookmakers. Similar remarks apply to betting strategies based on the Fink Tank probability of home win.

Bookmakers appear to set prices that are informationally (semi-strong) inefficient. However, the degree of inefficiency has clearly not been exploited to date on a scale that presents a probability problem for bookmakers. The transactions costs and risks attached to trading on the mispricing, revealed by Fink Tank probability and from other sources, appear to insulate bookmakers to a large degree from arbitrageurs.