1. Introduction
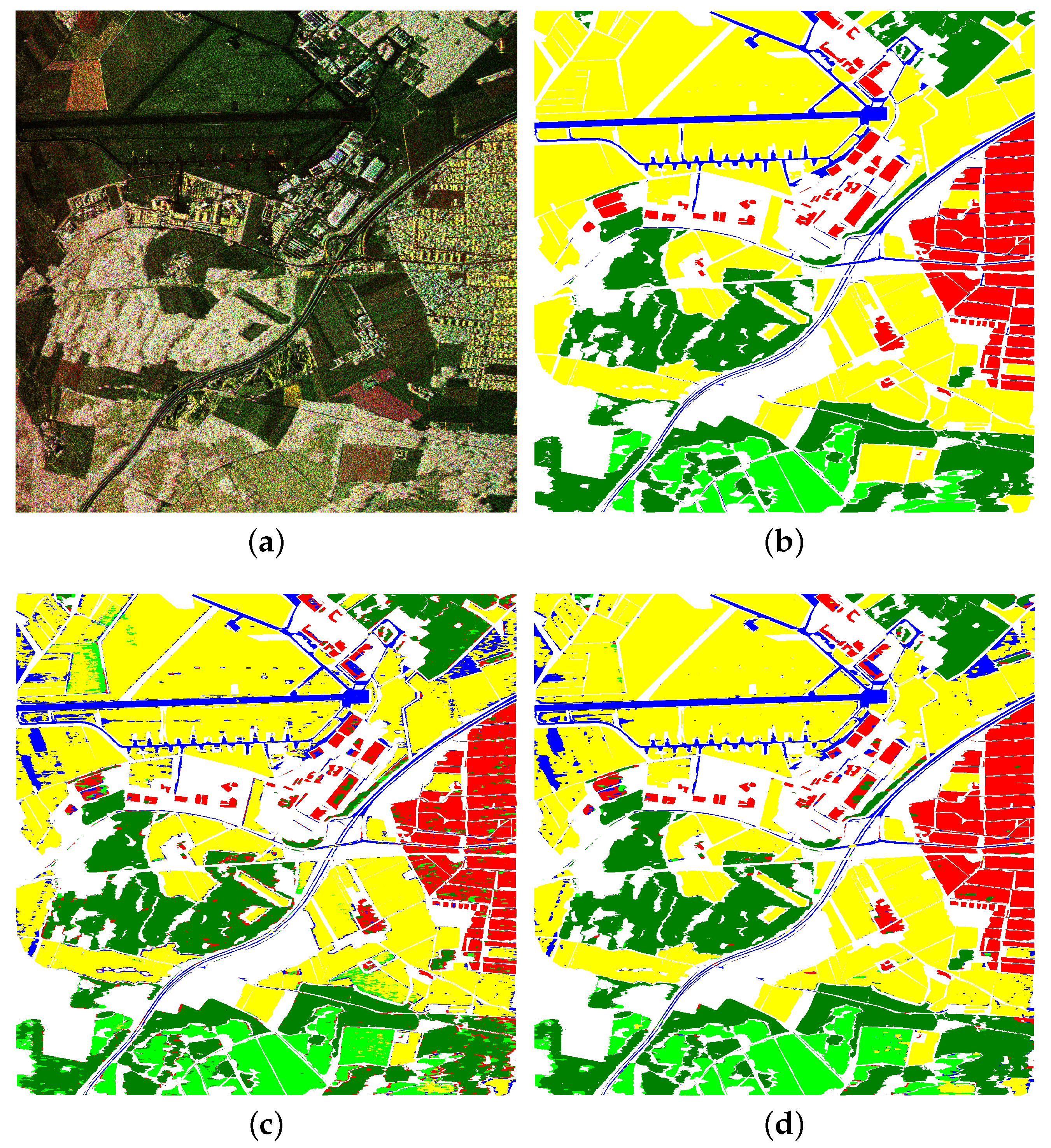
As active air- or space-borne sensor Synthetic Aperture Radar (SAR) transmits microwaves and records the backscattered echo. It is independent of daylight, only marginally influenced by weather conditions, and is able to penetrate clouds, dust, and to some degree and, depending on the used wavelength, even vegetation. Those unique properties render it complementary to optical and hyperspectral sensors. Polarimetric SAR (PolSAR) uses different polarisations during emission and reception leading to multi-channel images such as the one shown on the left of
Figure 1 (a small detail of a larger seen acquired by the E-SAR sensor of the German Aerospace Center (DLR) (see
Section 4.1)). The change of polarization in orientation as well as degree depends on several surface properties including moisture, roughness, as well as object geometry. Consequently, the recorded data contains valuable cues about physical processes as well as semantic object classes on the illuminated ground. Nowadays, there are many modern sensors that acquire PolSAR data, i.e., images that contain complex-valued vectors in each pixel (see
Section 2).
The increasing amount of these data makes manual interpretation infeasible and justifies the need for methods of automatic analysis of PolSAR images. One of the most important examples of typical applications is the creation of semantic maps, i.e., the assignment of a semantic label to each pixel within the image(s) (an example is shown on the right of
Figure 1 with semantic classes as introduced in
Section 4.1). If the goal is fully automatic interpretation, this task is addressed by supervised machine learning methods that aim to change the internal parameters of a generic model in such a way that the system provides (on average) the correct label when given a training sample, i.e., a sample for which the true class is known. On the one hand, there are several works that approach this problem by modelling the relationship between the data and the class by probabilistic distributions (or mixtures thereof) (e.g., [
1,
2,
3]) On the other hand, there are discriminative approaches as they have been shown to be easier trained and more robust as generative models. These methods usually extract (often hand-crafted and class-specific) image features, which focus on class-relevant aspects of the data and apply typical classifiers such as Support Vector Machines (SVMs, e.g., in [
4]), Multi-Layer Perceptrons (MLPs, e.g., in [
5]), or Random Forests (RFs, e.g., in [
6]). This feature extraction step is highly non-trivial. It involves hand-crafting and preselecting operators that are discriminative for a specific classification task and thus requires expert knowledge. While there is a large set of features available that capture polarimetric (e.g., [
7]) or textural (e.g., [
8]) information, it is still an ongoing field of research as to which combination leads to the best results.
A few approaches avoid the extraction of real-valued features by adapting the involved classifier to work directly on the complex-valued PolSAR data, e.g., by using complex-valued MLPs [
9] or SVMs with kernels defined over the complex-domain [
10]. Other methods rely on quasi-exhaustive feature sets that at least potentially contain all information necessary to solve a given classification problem. As the high dimensionality of those feature sets is usually problematic for most modern classifiers, a common preprocessing step is to reduce the set by dimensionality reduction techniques such as principal component analysis [
11], independent component analysis [
12], or linear discriminant analysis [
13]. Other methods apply classifiers that are able to handle high-dimensional and partially undescriptive feature sets. One example are Random Forests (RFs), which are not prone to the curse of dimensionality due to their inbuilt feature selection. A recent review of RFs in the context of classifying remotely sensed data in general and PolSAR images in particular can be found e.g., in [
14].
In [
15], hundreds of real-valued features are computed based on a given PolSAR image and used as input for an RF which uses only the most descriptive ones to solve the specific classification task. In [
16], this approach is extended by the extraction of thousands of simple features. Boosted decision stumps select a relevant feature subset and apply it for the task of land cover classification from optical images. While those methods are less likely to be biased towards specific classification tasks, the large amount of features consumes a huge amount of memory and computation time.
Feature learning techniques avoid the precomputation of features by including feature extraction into the optimization problem of the classifier. A well known example are Convolutional Networks (ConvNets), which—in the case of PolSAR data—are either applied to simple real-valued features (e.g., [
17]), or adapted to the complex domain (e.g., [
18,
19]). Another example of modern feature learning approaches are RFs that are tailored towards the labelling of images: while standard RFs are—as all multi-purpose classifiers—defined over the space of
n-dimensional vectors, i.e.,
, these specific RF variants are applied to image or feature patches (i.e., elements of
with patch size
w and
c channels) [
15,
20,
21]. Recently, these RFs have been adapted to work directly on the complex-valued data of PolSAR images by defining the internal node tests over the space of image patches containing Hermitian matrices [
22].
RFs are a specific instance of Ensemble Learning, i.e., the general approach to create multiple (suboptimal) classifiers and to combine their output instead of striving to create a single optimal model. RFs consist of multiple (mostly binary) decision trees that are independently trained and used for prediction. Each of the trees will provide its own estimate of the target variable, e.g., a class label or class posterior. Those individual estimates are subsequently fused, mostly by simple majority vote (in the case of a single label) or averaging (in the case of a posterior distribution).
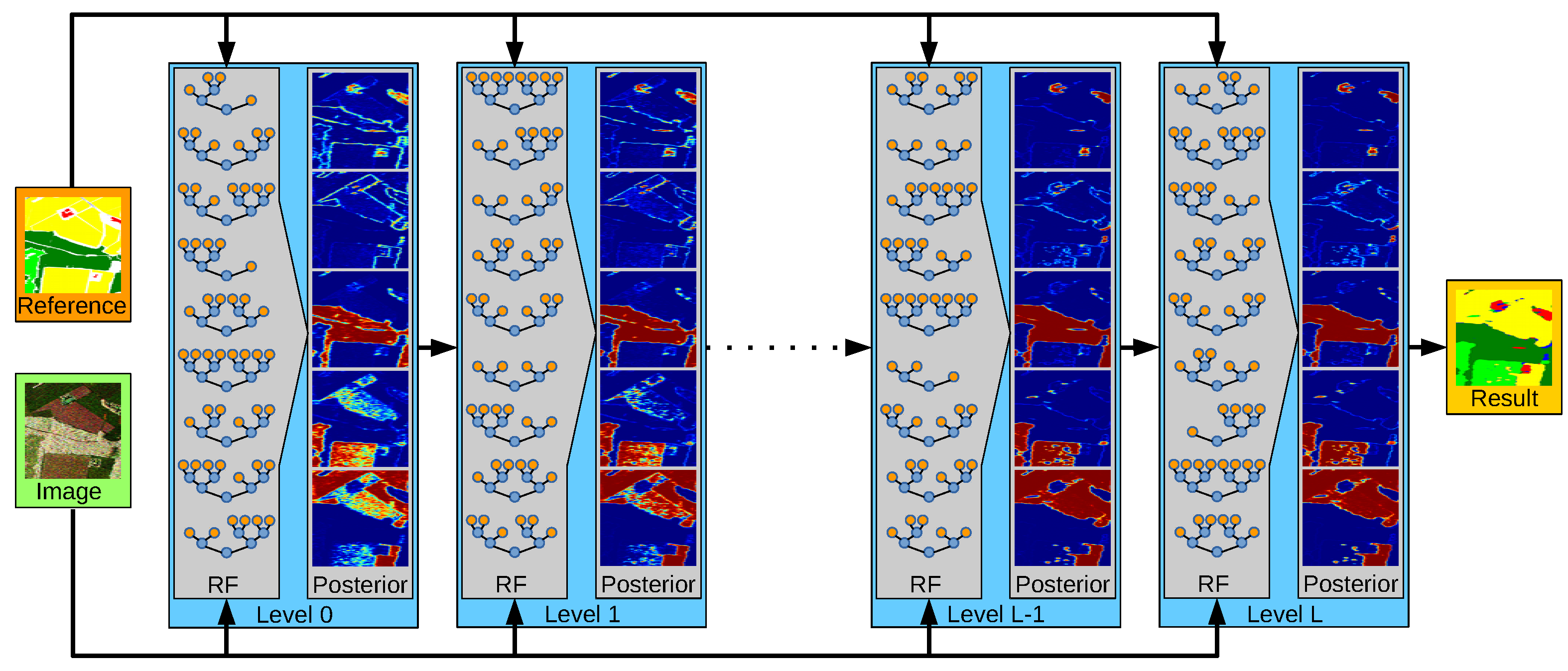
In this work, we extend the work in [
22] by applying a second Ensemble technique: Stacking (sometimes also called blending, stacked generalization [
23], stacked regression [
24], or super learning [
25]). Stacking usually consists of two steps: the first stage involves the training of multiple base learners (the socalled Tier-1 models) similar to the individual decision trees within the RF framework. However, in contrast to RFs, their individual output is not fused by simple averaging. Instead, they are used as input feature to another classifier (the socalled Tier-2 model) during the second stage. On the one hand, the Tier-2 model applies a more sophisticated fusion rule than simple averaging by learning when to ignore which of the Tier-1 models. On the other hand, consistent errors of the Tier-1 models might actually provide descriptive information about the true class, which can subsequently be exploited by the Tier-2 model. Stacking, originally proposed in 1992 [
23], has been shown to be an asymptotically optimal learning model [
25] and was the winning method of the Netflix Grand Prize in 2009 [
26]. The work of [
15] uses a two stage framework very similar to stacking: the first stage applies an RF to low-level image features for pixel-wise image labeling. The outcome of this stage is used together with the original image data for a semantic segmentation process. The second stage applies an RF for a segment-wise classification and uses spectral (e.g., textural properties of the segments), geometric (e.g., shape properties of the segments), as well as semantic features—the latter defined as the class distribution within a segment as estimated by the RF of the first stage.
We slightly differ from the original formulation of stacking in two major points: first, we do not train multiple Tier-1 models, but only train one single RFs, in particular, the RF variant proposed in [
22], as it can directly be applied to PolSAR data and is sufficiently efficient as well as accurate. As a probabilistic model, it provides a class posterior as output, which contains a high level of semantic information. This class posterior is subsequently used by the Tier-2 model as input additionally to the original image data. As a Tier-2 model, we use the same RF framework as for the Tier-1 model with the extension that the internal node tests can either be applied to the PolSAR image data as before (see
Section 3.1), or to the class posterior (see
Section 3.3). The second difference is that this procedure is repeated multiple times, i.e., an RF at the
i-th level obtains the original image data as well as the posterior estimate of the RF at level
. In this way, the posterior is more and more refined as the RFs learn which previous decisions are consistent with the reference labels of the training data and which parts still need refinement. The left side of the second column in
Figure 1 shows the uncertainty of the RF at the first level in its classification decision. While red indicates the existence of a dominant class (i.e., a class with significant higher probability than all other classes), blue illustrates high uncertainty (i.e., the existence of at least one other class with similar probability to the class with maximum probability). The ride part of this figure illustrates the uncertainty of the RF in the 9th level and shows that the final RF is significantly more certain in its decision then the initial RF. The third column of
Figure 1 shows the corresponding label maps of the two RFs. The left side contains many misclassifications in particular at object boundaries. Many of those errors have been corrected in the label map on the ride side, which appears much smoother, more consistent, and less noisy (Figure 3 provides larger versions of those images).
The following
Section 2 briefly repeats the basics of PolSAR images as needed to follow the explanations of the polarimetric node tests of the RF introduced in [
22] and briefly explained in
Section 3.1.
Section 3.3 discusses the proposed stacking techniques, in particular it introduces the family of node test functions designed to analyse the spatial structure of the posterior estimates.
Section 4 evaluates the proposed method on two very different PolSAR datasets and discusses the influence of stacking on the classification result.
Section 5 concludes the paper by summarizing its main findings and providing an outlook to future work.
3. Stacked Random Forests
Random Forest (RF, [
35,
36]) are ensembles of multiple, usually binary decision trees. Single decision trees have many advantages as, for example, being applicable to different kinds of data, having high interpretability, and—despite being based on rather simple algorithms—performing well on many different classification as well as regression tasks. Their disadvantages, however, let them fall out of favor, mainly due to their high variance and their tendency to easily overfit the data. RFs aim at keeping the advantages, while avoiding those limitations.
The core idea is to apply a random process during the training procedure of the individual trees. This leads to similarly accurate trees that will agree on the correct estimate of the target variable (e.g., class label) for most samples. However, since they will also be slightly different, their mistakes will not be consistent. In this case, a certain fraction of the trees will agree on the right answer, while the others disagree about the wrong answers. Consequently, the correct answer obtains the majority of all votes on average. For an in-depth discussion of Decision Trees, Random Forests, and Ensemble Learning, the interested reader is referred to e.g., [
15,
20].
The following
Section 3.1 provides a brief explanation of random decision trees as defined in [
22], while the stacking procedure is discussed in
Section 3.3.
3.1. Tree Creation and Training
A tree in an RF is a graph consisting of a single root node as well as multiple internal and terminal nodes (leafs). In a supervised framework, trees are created based on a training set of N samples with known value of the corresponding target variable , e.g., a class label (i.e., ).
The training data is resampled into
T bags
(
) for each of the
T trees within the RF (Bagging, [
37]). The corresponding data enters each tree at the root node. Each internal node applies a binary test to every sample and propagates it either to the left or right child node depending on the test outcome. If certain stopping criteria are met (e.g., reaching the maximum tree height), this recursive procedure stops and a terminal node is created. This leaf then estimates the value of the target variable based on the samples that reached it.
If an RF serves as general purpose classifier, the samples
are usually assumed to be a real-valued feature vector, i.e.,
. In this case, node tests are mostly defined as axis-align splits, i.e., “
,” where
is the
i-th component of
and the threshold
is determined by a variety of methods (see, e.g., [
38] for an overview).
For images more sophisticated, node tests have been proposed that are defined on image patches and analyse the local spatial structure [
21,
39] by computing distances between (e.g., color) intensities between random pairs of pixels. This idea is applied to PolSAR images in [
22], where image patches contain Hermitian matrices, i.e.,
(with
w as the spatial patch size and
k is the number of channels of the PolSAR image). Each node test samples either one, two, or four regions
of size
inside a patch
(where
). An operator
selects one covariance matrix from each region, e.g., by taking the center value or the region element with minimal/maximal span. These matrices are subsequently compared to each other by Equations (
10)–(12) by means of a distance measure
d between Hermitian matrices (see
Section 2 for examples):
Each internal node creates multiple such tests by randomly selecting the number of regions, region position and size, the operator, as well as the distance measure. All of the resulting split candidates are evaluated by the drop of impurity
(measured by the Gini impurity (Equation (14)) of the corresponding local class posteriors), i.e., the information gain obtained by splitting the current set of samples
into two subsets subsets
,
(with
and
) for the left and right child node
,
with
:
3.2. Prediction
During prediction, each query sample starts at the root node of every tree. Every internal node applies the node tests defined during tree creation and, depending on the test outcome, the sample is shifted to the left or right child node. It will reach exactly one terminal node
in every tree
t, which stores the class posterior
as estimated during tree training. The final class posterior
of the Random Forest is obtained by averaging the estimates of the individual trees:
3.3. Stacking
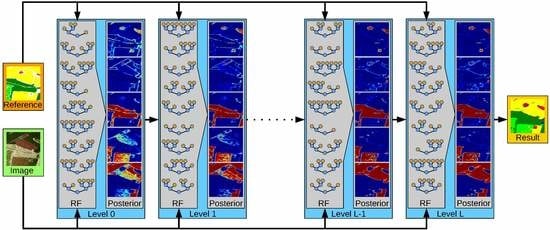
The basic principle of stacking as used in this work is illustrated in
Figure 2. At the first level (i.e., the 0-level), an RF is trained as described in
Section 3.1. It has only access on the image data, i.e., on the sample covariance matrices in each pixel, as well as to the reference data. Once this RF is created and trained, it is applied to the training data and predicts the class posterior for each sample, i.e., for each pixel within the image. This completes the first level.
An RF in a level l (with ) has access to the image data and the reference data, but also to the class posterior as estimated by the RF at level . This enables it to refine the class decisions and possibly correct errors made by the RF of the previous level. In the case of the correct label, it will learn to trust the decision of its predecessor if the data (and the posterior) have certain properties. In the case of an incorrect label, it will aim to learn how to correct it. One intuitive example of this effect are pixels showing double bounce backscattering. Due to the geometric structure of buildings, double bounce happens very frequently within urban areas. It does rarely happen at roads, fields, or shrublands (with few possible exceptions, e.g., power poles on the agricultural fields, etc.). However, it also happens frequently within a forest due to the stems of the trees. The RF of the first stage might have learnt that double bounce scattering is a strong indication of urban areas and consequently labels a forest pixel as belonging to a city. The RF in the next stage now has the chance to correct that by recognizing that isolated double bounce pixels labelled as city but surrounded by forest are rarely correct but mostly belong to the forest class. Thus, the combination of spectral and semantic information leads to an improvement.
In order to enable the RF to analyze the local class posterior estimate, similar node tests as defined in
Section 3.1 for PolSAR data have to be designed for patches of class posteriors, i.e., where each pixel in the sample
contains a probability distribution
describing that this pixel belongs to a class
. As before (see
Section 3.1, Equations (
10)–(12)), each node test randomly samples several regions within a patch and selects one of the pixels based on an operator (for example, by taking the center value or the region element with minimal/maximal margin defined in Equation (25)). These probability distributions are then compared by a proper distance measure
d. Distances that are directly defined over real-valued vectors in general or probability distributions in particular are suitable, such as histogram intersection
(Equation (
16)), the city-block distance
(Equation (17)), the Euclidean distance
(Equation (18)), the Kullback–Leibler divergence
(Equation (19)), the Bhattacharyya distance
(Equation (20)), and the Matusita distance
(Equation (21)):
Of course, it is also possible to compute simple properties of the posteriors and compare them. Examples are the dominant
and second strongest
class, which can be tested for identity by
(Equation (24), where
is the Kronecker delta). Other examples are the margin (Equation (25)), i.e., the distance between the probability of the two strongest classes, the entropy (Equation (26)), or the Gini index (Equation (27)) of the posterior, as well as the probability of misclassification (Equation (28)). These real-valued characteristics can be simply compared by the signed distance
(Equation (29)) between them:
While node tests as discussed in
Section 3.1 allow the analysis of local spectral and textural properties within the image space, the usage of the distance measures above allow the node tests to analyse the local structure of the label space within a probabilistic framework. In this way, not only the final classification decision of the RF of the previous level can be taken into account, but also its certainty into the label as well as their spatial distributions. Thus, the resulting RFs are able to analyse spectral, spatial, as well as semantic information to a high degree.
Each node generates multiple split candidates by randomly selecting which feature should be taken into account as well as how many and which regions should be considered and which distance measures should be used. From all the generated tests, the one with the highest drop of impurity (Equation (
13)) is selected and applied in order to propagate the current samples further up the trees.
In order to avoid overfitting of the stacked RFs, incomplete training data is used at each level. Instead, a certain amount of samples is randomly drawn from the training area of each class. The semantic features, however, i.e., the class posterior are computed for the whole training regions so that they are available for the RFs at higher levels.
5. Conclusions
This paper proposes using RFs within the stacking meta-learning framework for the classification of PolSAR data. It thus combines two ensemble learning strategies, i.e., the well established approach to average the output of several base learners (the individual trees within the RF) on the one hand, and, on the other hand, the lesser known but very successful method of stacking, i.e., including the estimates of the base learners as features for a subsequent model. The usage of the RF allows a seamless integration of both techniques: it not only provides a probabilistic estimate, i.e., the class posterior, which serves as optimal semantic feature, but also allows using this new feature without changing the overall framework simply by designed node tests that are defined over spatial-semantic probability distributions.
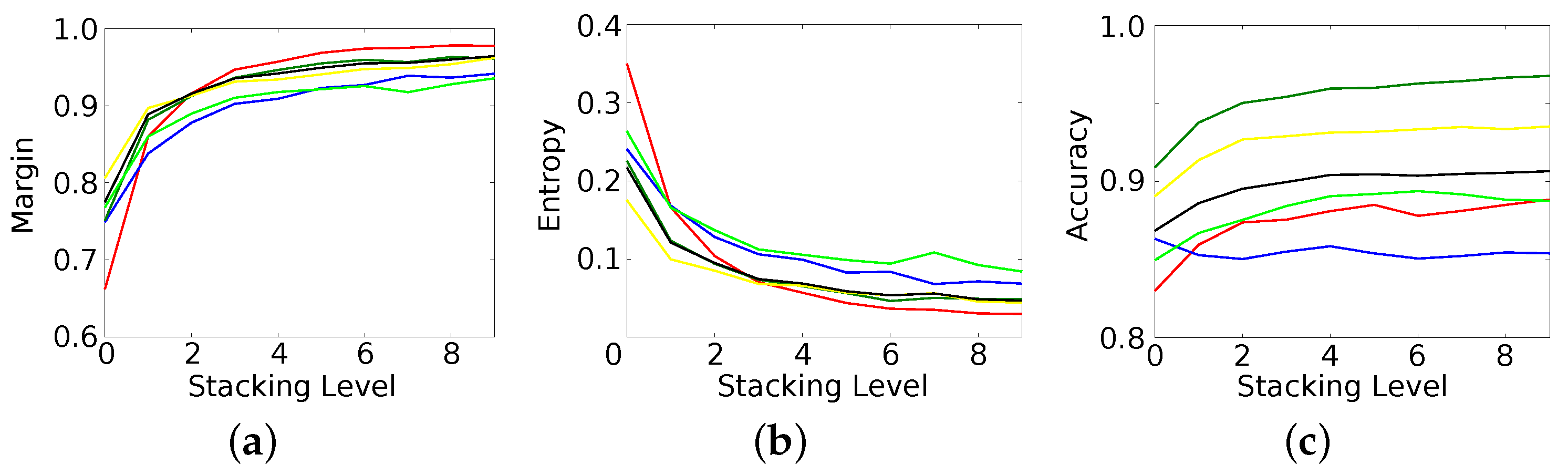
The performance on both datasets and for all classes are consistently improved over the different stacking levels, i.e., the results of each level are at least as good but mostly better than the results of the preceding level. The final results are more accurate by a significant margin, contain considerably less label noise, show smoother object boundaries, and have a higher degree of certainty of the classifier in its decision. Furthermore, the method itself converges, which makes a manual tuning of the number of stacking levels obsolete. The largest improvements happen within the first couple of levels, while performance saturates quickly (e.g., after four levels). This keeps the additional computational load at a limit and justifies the gain in performance.
It should be noted that this gain in accuracy comes basically for free, i.e., only at the cost of an increased training and prediction time—both increase (roughly) linear with the number of levels. However, neither more (e.g., more training samples) nor different (e.g., different sensors) data is needed. Furthermore, the same framework is used in all levels, i.e., the proposed method does not require several training and/or preprocessing procedures for different classifiers. Instead, no preprocessing and no explicit feature computation are performed, but the proposed stacked RF is directly applied to the local sample covariance matrices of the PolSAR data as well as to the probabilistic class estimates of previous levels.
Future work will focus on exploiting more information generated by the preceding RFs. The path a sample takes through each tree can serve as a powerful descriptor of local texture and thus complements to some extent the spectral and semantic properties used in this work. Furthermore, the estimated label maps provide not only local, but also more global context, which is currently ignored but can easily be included by node tests that sample large and more distant regions. Finally, the computational load of the stacking procedure can be decreased by more efficient node tests and by the fact that RFs in the first levels do not necessarily need to provide highly accurate estimations.
A second line of future work addresses the applicability of the proposed Stacked Random Forests to other types of remotely sensed data. This only requires an adaption of the applied node tests to the different data domains. In general, every image-based classification problem that can be solved by RFs sufficiently accurate should benefit from the proposed stacking framework.