Effect of Turbulence on Line Shapes in Astrophysical and Fusion Plasmas
Abstract
:1. Introduction
2. Wave Collapse and Strong Turbulence
3. Line Shape Model for Wave Collapse
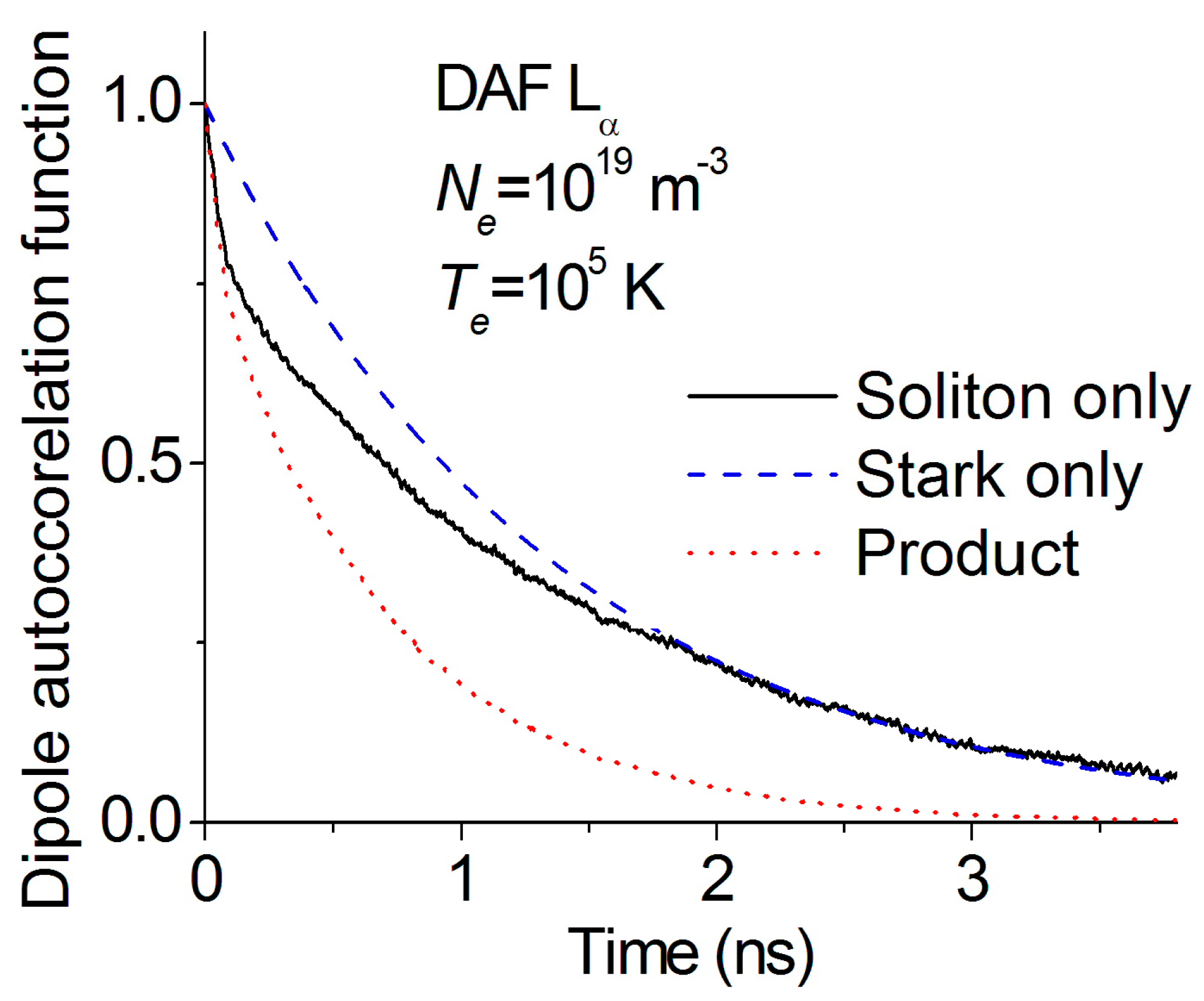
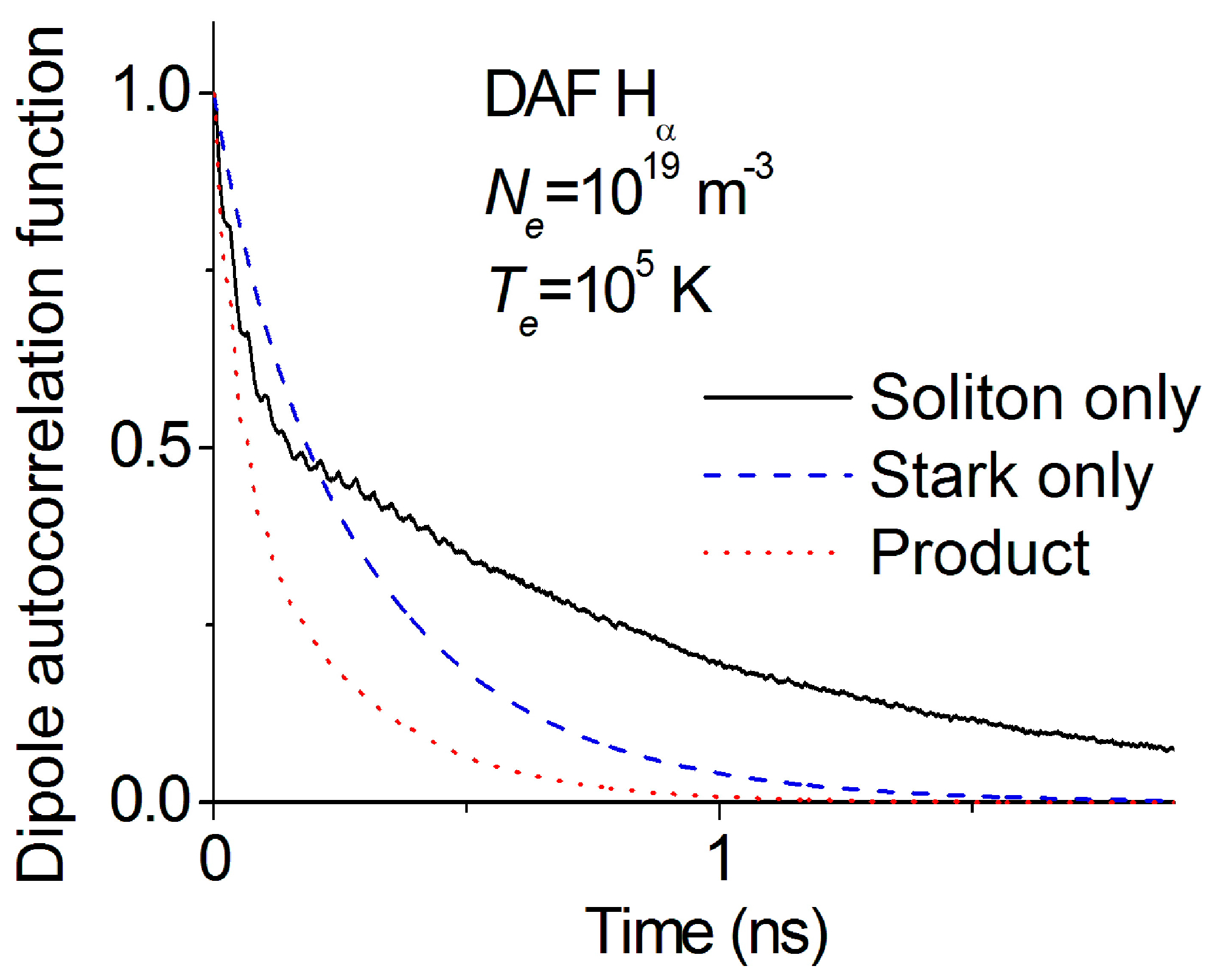
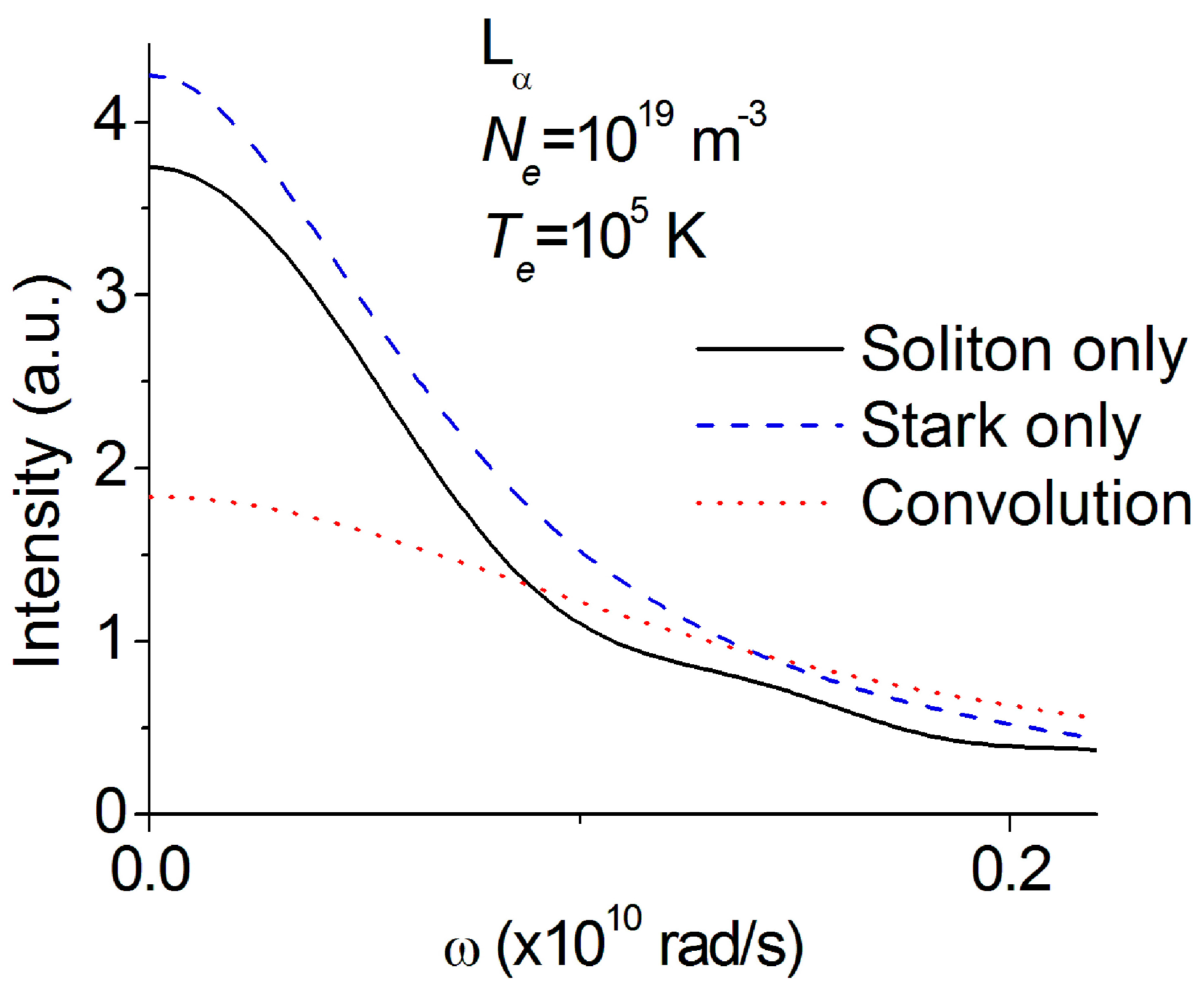
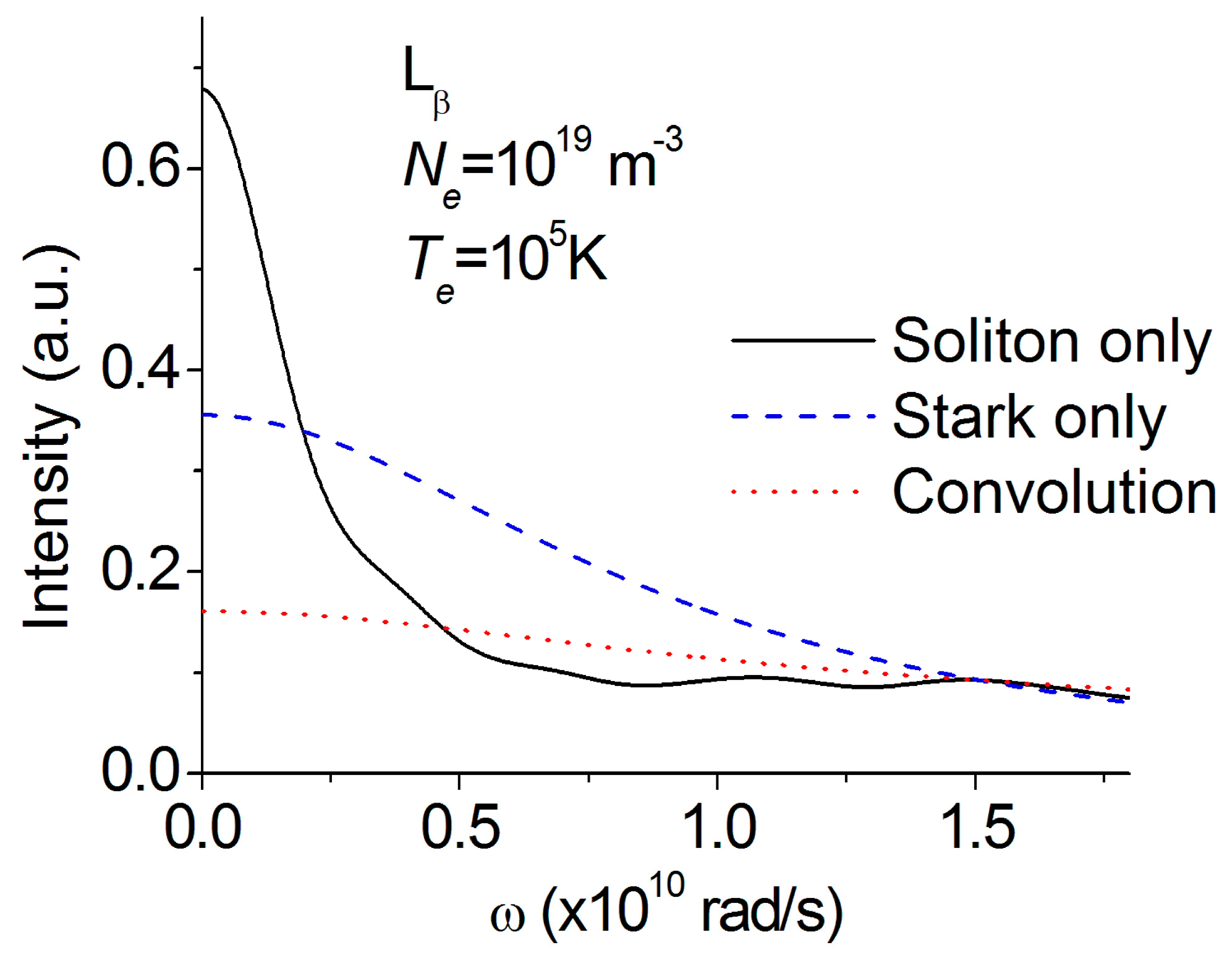
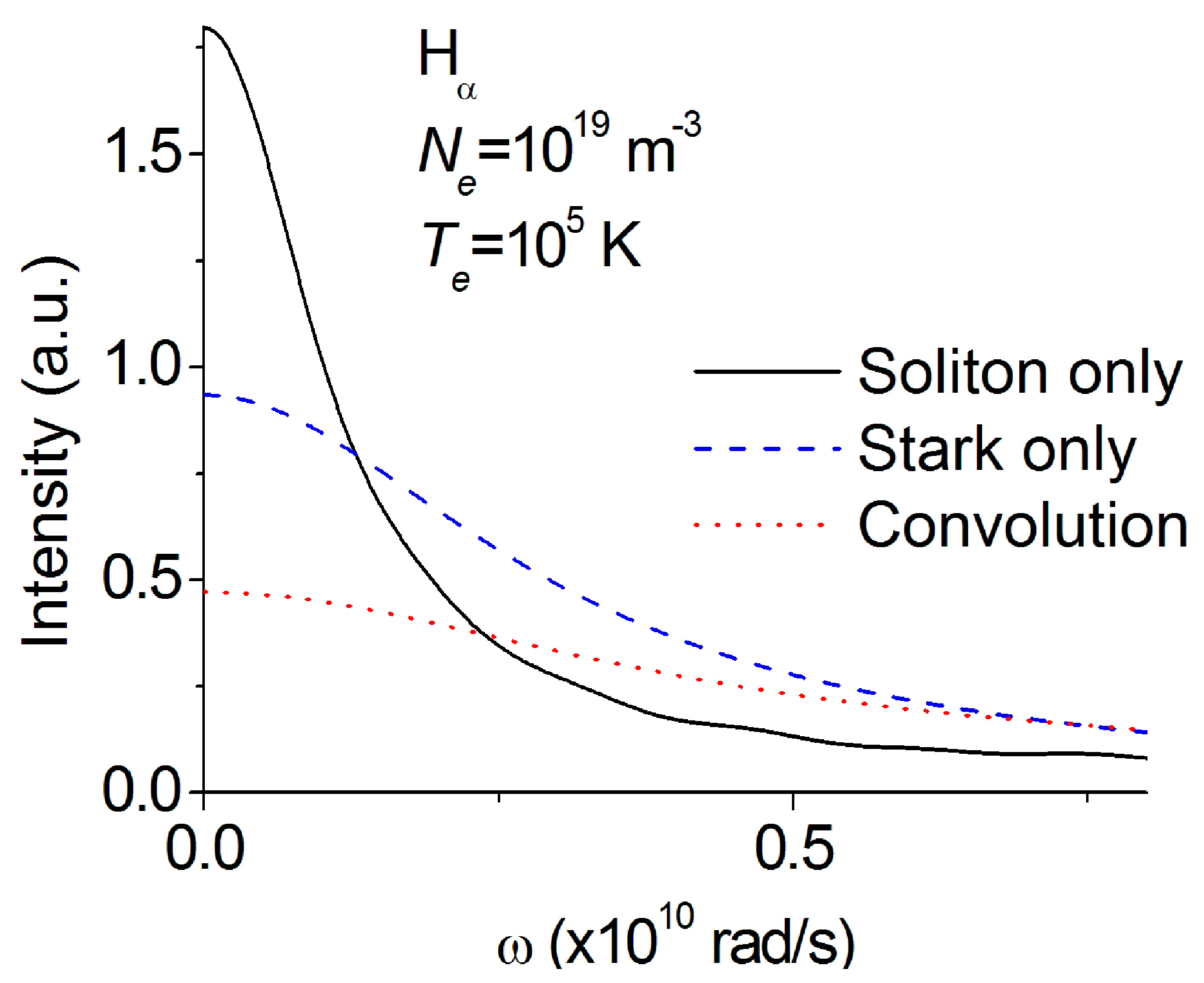
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rosseland, S. Viscosity in the Stars. Mon. Not. R. Astron. Soc. 1928, 89, 49–53. [Google Scholar] [CrossRef]
- Struve, O. Thermal Doppler effect and turbulence in stellar spectra of early class. Proc. Natl. Acad. Sci. USA 1932, 18, 585–589. [Google Scholar] [CrossRef] [PubMed]
- Hannachi, I.; Stamm, R.; Rosato, J.; Marandet, Y. Effect of nonlinear wave collapse on line shapes in a plasma. Europhys. Lett. 2016, 114, 23002. [Google Scholar] [CrossRef]
- Stamm, R.; Hannachi, I.; Meireni, M.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Rosato, J.; Marandet, Y.; Dimitrijević, M.; Simić, Z. Line shapes in turbulent plasmas. Eur. Phys. J. D 2017, 71, 68. [Google Scholar] [CrossRef]
- Robinson, P.A. Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 1997, 69, 507–574. [Google Scholar] [CrossRef]
- Miller, H.; Wiita, P. Active Galactic Nuclei; Springer: Berlin, Germany, 1987. [Google Scholar]
- Asseo, E.; Porzio, A. Strong Langmuir turbulence in a pulsar emission region: Statistical analysis. Mon. Not. R. Astron. Soc. 2006, 369, 1469–1490. [Google Scholar] [CrossRef]
- Sigsbee, K.; Kletzing, C.A.; Gurnett, D.A.; Pickett, J.S.; Balogh, A.; Lucek, E. Statistical behavior of foreshock Langmuir waves observed by the cluster wideband data plasma wave receiver. Ann. Geophys. 2004, 22, 2337–2344. [Google Scholar] [CrossRef]
- Ratcliffe, H.; Kontar, E.P.; Reid, A.S. Large-scale simulations of solar type III radio bursts: Flux density, drift rate, duration, and bandwidth. Astron. Astrophys. 2014, 572, A111. [Google Scholar] [CrossRef]
- Kruer, W.L. The Physics of Laser-Plasma Interactions; Addison-Wesley: Redwood City, CA, USA, 1988. [Google Scholar]
- Bauer, B.; Wong, A.; Scurry, L.; Decyk, V. Efficiency of caviton Formation as a function of plasma density gradient. Phys. Fluids B 1990, 2, 1941. [Google Scholar] [CrossRef]
- Paz-Soldan, C.; Eidietis, N.; Granetz, R.; Hollmann, E.; Moyer, R.; Wesley, J.; Zhang, J.; Austin, M.; Crocker, N.; Winger, A.; et al. Growth and decay of runaway electrons above the critical electric field under quiescent conditions. Phys. Plasmas 2014, 21, 022514. [Google Scholar] [CrossRef]
- Zakharov, V.; Musher, S.; Rubenchik, A. Weak Langmuir turbulence of an isothermal plasma. Sov. Phys. JETP 1975, 42, 80–86. [Google Scholar]
- Zakharov, V. Collapse of Langmuir waves. Sov. Phys. JETP 1972, 35, 908–914. [Google Scholar]
- Bellan, P.M. Fundamental of Plasma Physics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Griem, H.R. Spectral Line Broadening by Plasmas; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Vesely, F. Computational Physics, an Introduction; Plenum Press: New York, NY, USA, 1994. [Google Scholar]
- IMSL. 2012. Available online: http://www.roguewave.com (accessed on 12 August 2017).
- Rosato, J.; Reiter, D.; Kotov, V.; Marandet, Y.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Stamm, R. Progress Radiative Transfer modelling in Optically Thick Divertor plasmas. Contrib. Plasma Phys. 2010, 50, 398–403. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hannachi, I.; Meireni, M.; Génésio, P.; Rosato, J.; Stamm, R.; Marandet, Y. Effect of Turbulence on Line Shapes in Astrophysical and Fusion Plasmas. Atoms 2017, 5, 34. https://doi.org/10.3390/atoms5040034
Hannachi I, Meireni M, Génésio P, Rosato J, Stamm R, Marandet Y. Effect of Turbulence on Line Shapes in Astrophysical and Fusion Plasmas. Atoms. 2017; 5(4):34. https://doi.org/10.3390/atoms5040034
Chicago/Turabian StyleHannachi, Ibtissem, Mutia Meireni, Paul Génésio, Joël Rosato, Roland Stamm, and Yannick Marandet. 2017. "Effect of Turbulence on Line Shapes in Astrophysical and Fusion Plasmas" Atoms 5, no. 4: 34. https://doi.org/10.3390/atoms5040034




