Two Photon Processes in an Atom Confined in Gaussian Potential
Abstract
:1. Introduction
2. Theory
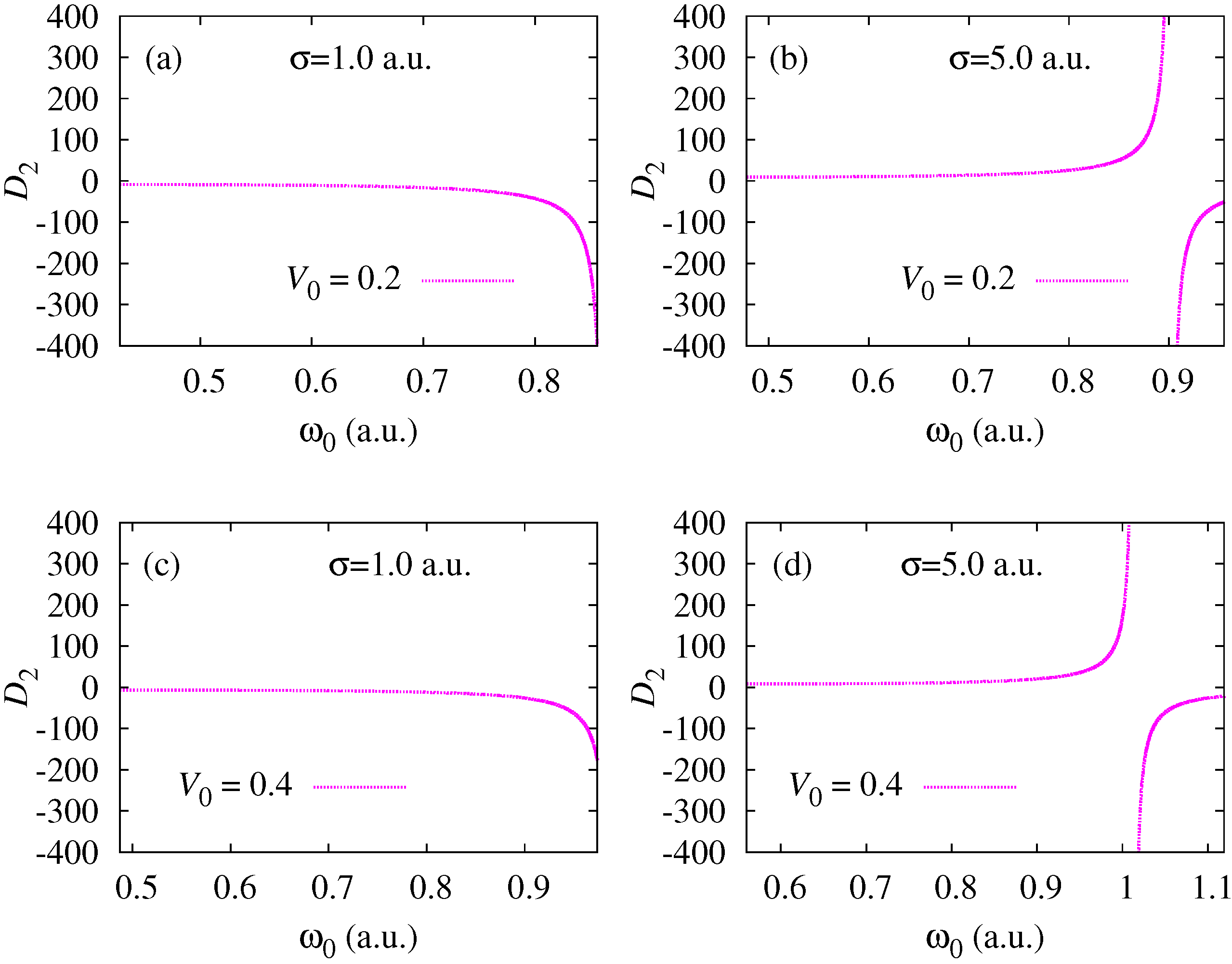
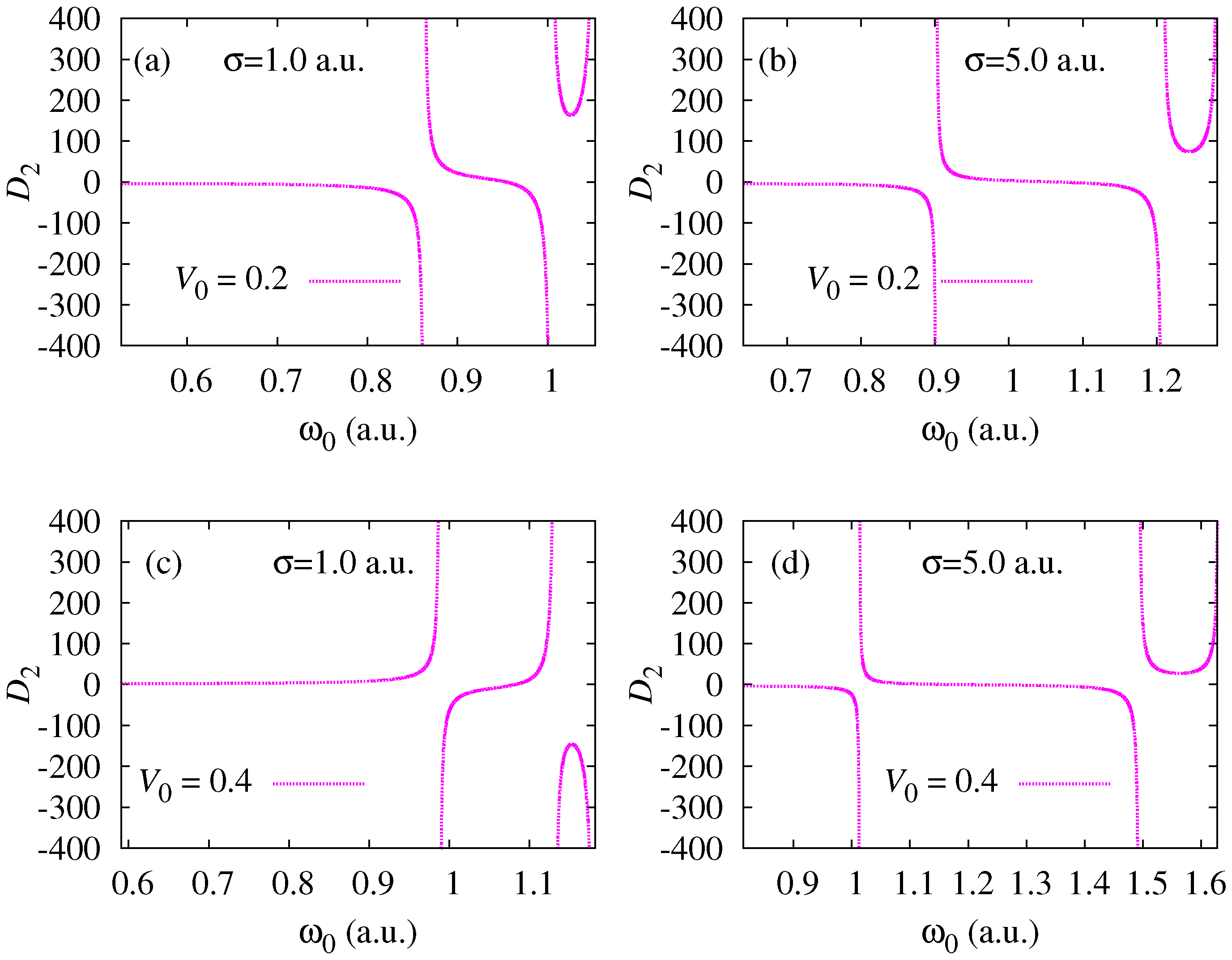
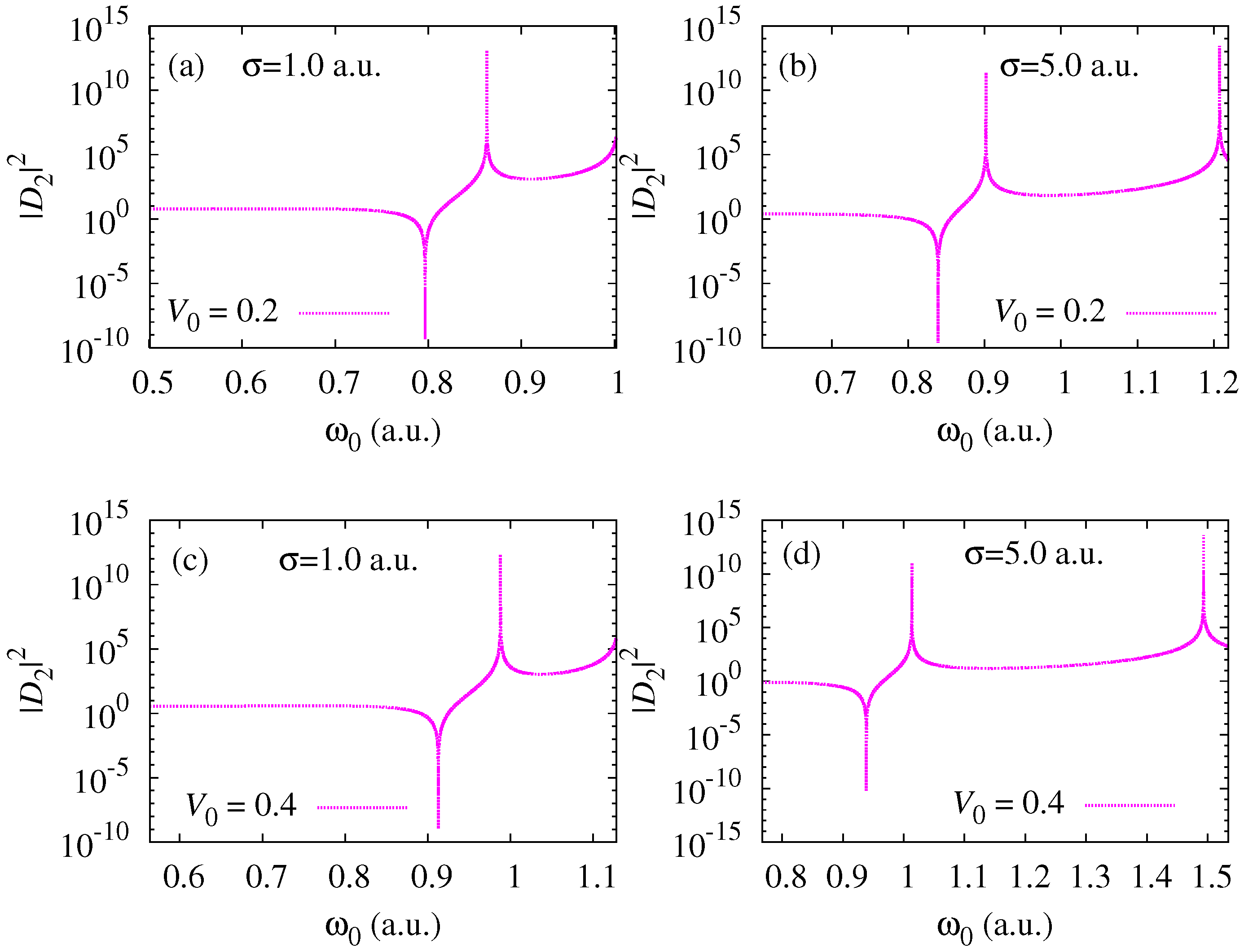
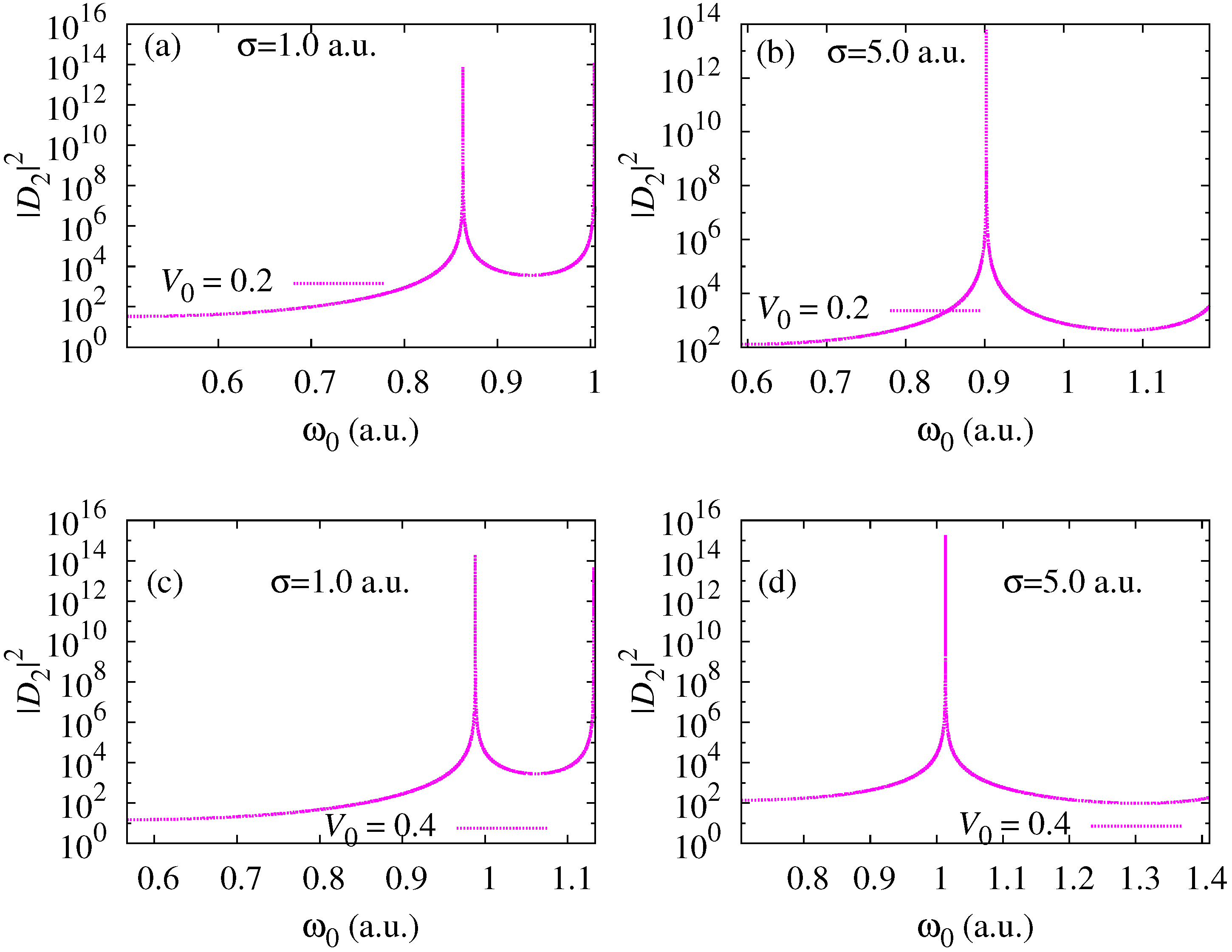
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kundliya, R.; Prasad, V.; Mohan, M. The two-photon process in an atom using the pseudostate summation technique. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 5263–5274. [Google Scholar] [CrossRef]
- Joshi, R. Two-photon transitions to Rydberg states of hydrogen. Phys. Lett. A 2007, 361, 352–355. [Google Scholar] [CrossRef]
- Basu, J.; Ray, D. Dynamic polarizability of an atomic ion within a dense plasma. Phys. Rev. E 2011, 83, 016407. [Google Scholar] [CrossRef] [PubMed]
- Achtstein, A.W.; Ballester, A.; Movilla, J.L.; Hennig, J.; Climente, J.I.; Prudnikau, A.; Antanovich, A.; Scott, R.; Artemyev, M.V.; Planelles, J.; et al. One- and Two- Photon Absorption in CdS Nanodots and Wires: The Role of Dimensionality in the One- and Two-Photon Luminescence Excitation Spectrum. J. Phys. Chem. C 2015, 119, 1260–1267. [Google Scholar] [CrossRef]
- Dakovski, G.L.; Shan, J. Size dependence of two-photon absorption in semiconductor quantum dots. J. App. Phys. 2013, 114, 014301. [Google Scholar] [CrossRef]
- Khatei, J.; Sandeep, C.S.S.; Philip, R.; Rao, K.S.R.K. Near-resonant two-photon absorption in luminescent CdTe quantum dots. App. Phys Lett. 2012, 100, 081901. [Google Scholar] [CrossRef]
- Xia, C.; Spector, H.N. Nonlinear Franz-Keldysh effect: Two photon absorption in semiconducting quantum wires and quantum boxes. J. App. Phys. 2009, 106, 124302. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Three-photon transitions in the hydrogen atom immersed in Debye plasmas. Phys. Rev. A 2009, 79, 032714. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Effects of Debye plasmas on two-photon transitions in lithium atoms. Phys. Rev. A 2008, 78, 042711. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Two-colour three-photon transitions in a hydrogen atom embedded in Debye plasmas. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 065701. [Google Scholar] [CrossRef]
- Chang, T.N.; Fang, T.K.; Ho, Y.K. One- and two-photon ionization of hydrogen atom embedded in Debye plasmas. Phys. Plasmas 2013, 20, 092110. [Google Scholar] [CrossRef]
- De Wild, J.; Meijerink, A.; Rath, J.K.; van Sarka, W.G.J.H.M.; Schropp, R.E.I. Upconverter solar cells: Materials and applications. Energy Environ. Sci. 2011, 4, 4835–4848. [Google Scholar] [CrossRef]
- Lin, Z.; Vučković, J. Enhanced two-photon processes in single quantum dots inside photonic crystal nanocavities. Phys. Rev. B 2010, 81, 035301. [Google Scholar] [CrossRef]
- Amaro, P.; Surzhykov, A.; Parente, F.; Indelicato, P.; Santos, J.P. Calculation of two-photon decay rates of hydrogen-like ions by using B-polynomials. J. Phys. A Math. Theor. 2011, 44, 245302. [Google Scholar] [CrossRef]
- Prasad, V.; Dahiya, B. Modifications of laser field assisted intersubband transitions in the coupled quantum wells due to static electric field. Phys. Status Solidi B 2011, 248, 1727–1734. [Google Scholar] [CrossRef]
- Lahon, S.; Gambhir, M.; Jha, P.K.; Mohan, M. Multiphoton excitation of disc shaped quantum dot in presence of laser (THz) and magnetic field for bioimaging. Phys. Status Solidi B 2010, 247, 962–967. [Google Scholar] [CrossRef]
- Larson, D.R.; Zipfel, W.R.; Williams, R.M.; Clark, S.W.; Bruchez, M.P.; Wise, F.W.; Webb, W.W. Water-Soluble Quantum Dots for Multiphoton Fluorescence Imaging in Vivo. Science 2003, 300, 1434–1436. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.E.; Blanton, S.A.; Hines, M.A.; Guyot-Sionnest, P. Size-dependent two-photon excitation spectroscopy of CdSe nanocrystals. Phys. Rev. B 1996, 53, 12629–12632. [Google Scholar] [CrossRef]
- Cotter, D.; Burt, M.G.; Manning, R.J. Below-band-gap third-order optical nonlinearity of nanometer-size semiconductor crystallites. Phys. Rev. Lett. 1992, 68, 1200–1203. [Google Scholar] [CrossRef] [PubMed]
- Banfi, G.P.; Degiorgio, V.; Ghigliazza, M.; Tan, H.M.; Tomaselli, A. Two-photon absorption in semiconductor nanocrystals. Phys. Rev. B 1994, 50, 5699–5702. [Google Scholar] [CrossRef]
- Padilha, L.; Fu, J.; Hagan, D.; van Stryland, E.; Cesar, C.; Barbosa, L.; Cruz, C. Two-photon absorption in CdTe quantum dots. Opt. Express 2005, 13, 6460–6467. [Google Scholar] [CrossRef] [PubMed]
- Padilha, L.A.; Fu, J.; Hagan, D.J.; van Stryland, E.W.; Cesar, C.L.; Barbosa, L.C.; Cruz, C.H.B.; Buso, D.; Martucci, A. Frequency degenerate and nondegenerate two-photon absorption spectra of semiconductor quantum dots. Phys. Rev. B 2007, 75, 075325. [Google Scholar] [CrossRef]
- Lad, A.D.; Kiran, P.P.; More, D.; Kumar, G.R.; Mahamuni, S. Two-photon absorption in ZnSe and ZnSe/ ZnS core/shell quantum structures. App. Phys. Lett. 2008, 92, 043126. [Google Scholar] [CrossRef]
- Nyk, M.; Szeremeta, J.; Wawrzynczyk, D.; Samoc, M. Enhancement of Two-Photon Absorption Cross Section in CdSe Quantum Rods. J. Phys. Chem. C 2014, 118, 17914–17921. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Munjal, D.; Prasad, V. Intense field induced excitation and ionization of an atom confined in a dense quantum plasma. Phys. Scr. 2015, 90, 1–10. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Static polarizability of an atom confined in Gaussian potential. Eur. Phys. J. Plus 2015, 130, 149–160. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Photoexcitation and ionization of hydrogen atom confined in Debye environment. Eur. Phys. J. D 2015, 69, 176–184. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Photoexcitation and ionization of a hydrogen atom confined by a combined effect of a spherical box and Debye plasma. Phys. Lett. A 2015, 379, 1263–1269. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Photoionization of confined hydrogen atom by short laser pulses. Indian J. Phys. 2015, 89, 13–21. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Laser-induced excitation and ionization of a confined hydrogen atom in an exponential-cosine-screened Coulomb potential. Phys. Rev. A 2014, 90, 1–9. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Dynamics of Particle in Confined-Harmonic Potential in External Static Electric Field and Strong Laser Field. J. Mod. Phys. 2013, 4, 1139–1148. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Response of a Harmonically Confined System to Short Laser Pulses. Quantum Matter 2013, 2, 314–320. [Google Scholar] [CrossRef]
- Salzmann, D. Atomic Physics in Hot Plasmas; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Sen, S.; Mandal, P.; Mukherjee, P.K.; Fricke, B. Hyperpolarizabilities of one and two electron ions under strongly coupled plasma. Phys. Plasmas 2013, 20, 013505. [Google Scholar] [CrossRef]
- Sen, S.; Mandal, P.; Mukherjee, P.K. Positronium formation in positron-helium collisions with a screened Coulomb interaction. Eur. Phys. J. D 2012, 66, 230–241. [Google Scholar] [CrossRef]
- Montgomery, H.E., Jr.; Sen, K.D. Dipole polarizabilities for a hydrogen atom confined in a penetrable sphere. Phys. Lett. A 2012, 376, 1992–1996. [Google Scholar] [CrossRef]
- Ichimaru, S. Strongly coupled plasmas: High-density and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017–1059. [Google Scholar] [CrossRef]
- Lai, H.F.; Lin, Y.C.; Ho, Y.K. Two-photon transitions in the He+ ion embedded in strongly-coupled plasmas. J. Phys. Conf. Ser. 2009, 163, 012096. [Google Scholar] [CrossRef]
- Ho, Y.K.; Lai, H.F.; Lin, Y.C. Two-photon 1s-3d and 1s-4d transitions in the He+ ion embedded in strongly-coupled plasmas with ion-sphere model. J. Phys. Conf. Ser. 2009, 194, 022023. [Google Scholar] [CrossRef]
- Nascimento, E.M.; Prudente, F.V.; Guimarães, M.N.; Maniero, A.M. A study of the electron structure of endohedrally confined atoms using a model potential. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 1–7. [Google Scholar] [CrossRef]
- Quattropani, A.; Bassani, F.; Carillo, S. Two-photon transitions to excited states in atomic hydrogen. Phys. Rev. A 1982, 25, 3079–3089. [Google Scholar] [CrossRef]
- Tung, J.H.; Ye, X.M.; Salamo, G.J.; Chan, F.T. Two-photon decay of hydrogenic atoms. Phys. Rev. A 1984, 30, 1175–1184. [Google Scholar] [CrossRef]
- Bhatti, M.I.; Perger, W.F. Solutions of the radial Dirac equation in a B-polynomial basis. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 553–558. [Google Scholar] [CrossRef]
- Bhatta, D.D.; Bhatti, M.I. Numerical solution of KdV equation using modified Bernstein polynomials. Appl. Math. Comput. 2006, 174, 1255–1268. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Two-photon transitions in hydrogen atoms embedded in weakly coupled plasmas. Phys. Plasmas 2008, 15, 1–7. [Google Scholar] [CrossRef]
- Lumb, S.; Lumb, S.; Prasad, V. Multi-photon transitions in confined atoms. 2016; in prepareation. [Google Scholar]





| ( → ) | ( → ) | |||
|---|---|---|---|---|
| Present Study | Reference [45] | Present Study | Reference [45] | |
| 0.3750 | 11.780338 | 11.7805 | 3.235425 | 3.2354 |
| 0.5250 | 14.731690 | 14.7319 | ||
| 0.6750 | 41.147800 | 41.1484 | 1.669316 | 1.6693 |
| 0.6875 | 49.686983 | 49.6878 | 0.696330 | 0.6963 |
| 0.7000 | 62.658358 | 62.6595 | 0.984604 | 0.9847 |
| 0.7125 | 84.523402 | 84.5252 | 4.158088 | 4.1583 |
| 0.7250 | 128.680019 | 128.6835 | 11.215759 | 11.2162 |
| 0.7375 | 262.153248 | 262.1654 | 34.224314 | 34.2263 |
| 0.7475 | 1334.059059 | 1334.3261 | 226.765862 | 226.8138 |
| 0.7650 | 58.200900 | 58.2000 | ||
| 0.8000 | 38.309623 | 38.3099 | ||
| 0.8250 | 46.579090 | 46.5797 | ||
| 0.8500 | 74.418968 | 74.4204 | ||
| 0.8750 | 219.974861 | 219.9847 | ||
| 0.8860 | 1117.033823 | 1117.2380 | ||
| σ | ||||
|---|---|---|---|---|
| 0.2 | 0.2 | 0.6966575 | 0.6943135 | 0.8417985 |
| 0.8748915 | ||||
| 0.4 | 0.6997875 | 0.6974305 | 0.8455535 | |
| 0.8784775 | ||||
| 0.6 | 0.7029685 | 0.7005985 | 0.8493665 | |
| 0.8821205 | ||||
| 0.8 | 0.7062005 | 0.7038175 | 0.8532385 | |
| 0.8858195 | ||||
| 1.0 | 0.7094835 | 0.7070865 | 0.8571695 | |
| 0.8895765 | ||||
| 1.0 | 0.2 | 0.7966715 | 0.7946135 | 0.9540155 |
| 0.9837665 | ||||
| 0.4 | 0.9129015 | 0.9111615 | 1.0823305 | |
| 1.1088085 | ||||
| 0.6 | 1.0413755 | 1.0399605 | 1.2221895 | |
| 1.2456185 | ||||
| 0.8 | 1.1810825 | 1.1799705 | 1.3726705 | |
| 1.3932485 | ||||
| 1.0 | 1.3309895 | 1.3301425 | 1.5328565 | |
| 1.5507545 | ||||
| 2.0 | 0.2 | 0.9120575 | 0.9100275 | 1.0821115 |
| 1.1100905 | ||||
| 0.4 | 1.1385265 | 1.1359635 | 1.3399855 | |
| 1.3627115 | ||||
| 0.6 | 1.3661185 | 1.3623365 | ||
| 1.6253105 | ||||
| 0.8 | 1.5894415 | 1.5839235 | 1.8820885 | |
| 1.8955715 | ||||
| 1.0 | 1.8046355 | 1.7971595 | 2.1605405 | |
| 2.1721445 | ||||
| 5.0 | 0.2 | 0.8393165 | 0.8325805 | 1.0656265 |
| 1.1942105 | ||||
| 0.4 | 0.9385475 | 0.9232605 | 1.1849155 | |
| 1.4908805 | ||||
| 0.6 | 1.0136965 | 1.7431005 | 1.2573295 | |
| 0.8 | 1.9660075 | |||
| 1.0 | 1.4822535 | |||
| 2.1662075 |
| σ | |||||
|---|---|---|---|---|---|
| 0.2 | 0.2 | 0.7536975 | 0.7536975 | 0.7536975 | 0.7536975 |
| 0.8925875 | 0.8925875 | 0.8925875 | |||
| 0.4 | 0.7574475 | 0.7574475 | 0.7574475 | 0.7574475 | |
| 0.8963405 | 0.8963405 | 0.8963405 | |||
| 0.6 | 0.7612565 | 0.7612565 | 0.7612565 | 0.7612565 | |
| 0.9001505 | 0.9001505 | 0.9001505 | |||
| 0.8 | 0.7651245 | 0.7651245 | 0.7651245 | 0.7651245 | |
| 0.9040205 | 0.9040205 | 0.9040205 | |||
| 1 | 0.7690515 | 0.7690515 | 0.7690515 | 0.7690515 | |
| 0.9079485 | 0.9079485 | 0.9079485 | |||
| 1 | 0.2 | 0.8630055 | 0.8630055 | 0.8630055 | 0.8630055 |
| 1.0038595 | 1.0038595 | 1.0038595 | |||
| 1.0530765 | |||||
| 0.4 | 0.9880245 | 0.9880245 | 0.9880245 | 0.9880245 | |
| 1.1311185 | 1.1311185 | 1.1311185 | |||
| 1.1809445 | |||||
| 0.6 | 1.1241155 | 1.1241155 | 1.1241155 | 1.1241155 | |
| 1.2697875 | 1.2697875 | 1.2697875 | |||
| 1.3203075 | |||||
| 0.8 | 1.2702465 | 1.2702465 | 1.2702465 | 1.2702465 | |
| 1.4189135 | 1.4189135 | 1.4189135 | |||
| 1.4702285 | |||||
| 1 | 1.4253685 | 1.4253685 | 1.4253685 | 1.4253685 | |
| 1.5775475 | 1.5775475 | 1.5775475 | |||
| 1.6297795 |
| σ | ||||||
|---|---|---|---|---|---|---|
| 2 | 0.2 | 0.9625345 | 0.9625345 | 0.9625345 | 0.9625345 | 0.9625345 |
| 1.1264855 | 1.1264855 | 1.1264855 | 1.1264855 | |||
| 1.1802345 | 1.1802345 | |||||
| 0.4 | 1.1717755 | 1.1717755 | 1.1717755 | 1.1717755 | 1.1717755 | |
| 1.3771515 | 1.3771515 | 1.3771515 | 1.3771515 | |||
| 1.4370505 | 1.4370505 | |||||
| 0.6 | 1.3696755 | 1.3696755 | 1.3696755 | 1.3696755 | 1.3696755 | |
| 1.6383765 | 1.6383765 | 1.6383765 | 1.6383765 | |||
| 1.7046825 | 1.7046825 | |||||
| 0.8 | 1.5528565 | 1.5528565 | 1.5528565 | 1.5528565 | 1.5528565 | |
| 1.9086325 | 1.9086325 | 1.9086325 | 1.9086325 | |||
| 1.9809315 | 1.9809315 | |||||
| 1 | 1.7214035 | 1.7214035 | 1.7214035 | 1.7214035 | 1.7214035 | |
| 2.1863955 | 2.1863955 | 2.1863955 | 2.1863955 | |||
| 2.2641365 | 2.2641365 | |||||
| 5 | 0.2 | 0.9017875 | 0.9017875 | 0.9017875 | 0.9017875 | 0.9017875 |
| 1.2076625 | 1.2076625 | 1.2076625 | ||||
| 1.2833555 | ||||||
| 0.4 | 1.0133065 | 1.0133065 | 1.0133065 | 1.0133065 | 1.0133065 | |
| 1.4933425 | 1.4933425 | 1.4933425 | ||||
| 1.6303775 | ||||||
| 0.6 | 1.1047275 | 1.1047275 | 1.1047275 | 1.1047275 | 1.1047275 | |
| 1.7368975 | 1.7368975 | 1.7368975 | ||||
| 1.9763745 | ||||||
| 0.8 | 1.1844925 | 1.1844925 | 1.1844925 | 1.1844925 | 1.1844925 | |
| 1.9540065 | 1.9540065 | 1.9540065 | ||||
| 2.3162335 | ||||||
| 1 | 1.2556685 | 1.2556685 | 1.4262795 | 1.2556685 | 1.2749545 | |
| 2.1478855 | 2.1478855 | 2.1478855 | ||||
| 2.6377985 |
| n | l | ||||
|---|---|---|---|---|---|
| 1 | 0 | 1.0 | −0.500000 | −0.557966 | −0.622137 |
| 2 | 0 | −0.125000 | −0.130189 | −0.135136 | |
| 2 | 1 | −0.125000 | −0.126463 | −0.128125 | |
| 3 | 0 | −0.055556 | −0.057016 | −0.058382 | |
| 3 | 1 | −0.055556 | −0.056037 | −0.056578 | |
| 3 | 2 | −0.055556 | −0.055564 | −0.055573 | |
| 4 | 0 | −0.031204 | −0.031818 | −0.032386 | |
| 4 | 1 | −0.031216 | −0.031428 | −0.031665 | |
| 4 | 2 | −0.031233 | −0.031238 | −0.031244 | |
| 4 | 3 | −0.031246 | −0.031246 | −0.031246 | |
| 1 | 0 | 5.0 | −0.679948 | −0.861344 | |
| 2 | 0 | −0.202437 | −0.301700 | ||
| 2 | 1 | −0.229055 | −0.354691 | ||
| 3 | 0 | −0.070459 | −0.094417 | ||
| 3 | 1 | −0.076117 | −0.114672 | ||
| 3 | 2 | −0.087940 | −0.155671 | ||
| 4 | 0 | −0.036800 | −0.043339 | ||
| 4 | 1 | −0.038271 | −0.046155 | ||
| 4 | 2 | −0.038904 | −0.047266 | ||
| 4 | 3 | −0.033498 | −0.044919 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lumb, S.; Lumb, S.; Prasad, V. Two Photon Processes in an Atom Confined in Gaussian Potential. Atoms 2016, 4, 6. https://doi.org/10.3390/atoms4010006
Lumb S, Lumb S, Prasad V. Two Photon Processes in an Atom Confined in Gaussian Potential. Atoms. 2016; 4(1):6. https://doi.org/10.3390/atoms4010006
Chicago/Turabian StyleLumb, Sonia, Shalini Lumb, and Vinod Prasad. 2016. "Two Photon Processes in an Atom Confined in Gaussian Potential" Atoms 4, no. 1: 6. https://doi.org/10.3390/atoms4010006
APA StyleLumb, S., Lumb, S., & Prasad, V. (2016). Two Photon Processes in an Atom Confined in Gaussian Potential. Atoms, 4(1), 6. https://doi.org/10.3390/atoms4010006






