A Study on Input Power Factor Compensation Capability of Matrix Converters
Abstract
1. Introduction
2. SVM Method for MCs
- (1)
- Group I includes 18 active-vector states,
- (2)
- Group II includes three zero-vector states,
- (3)
- Group III includes six rotating-vector states.
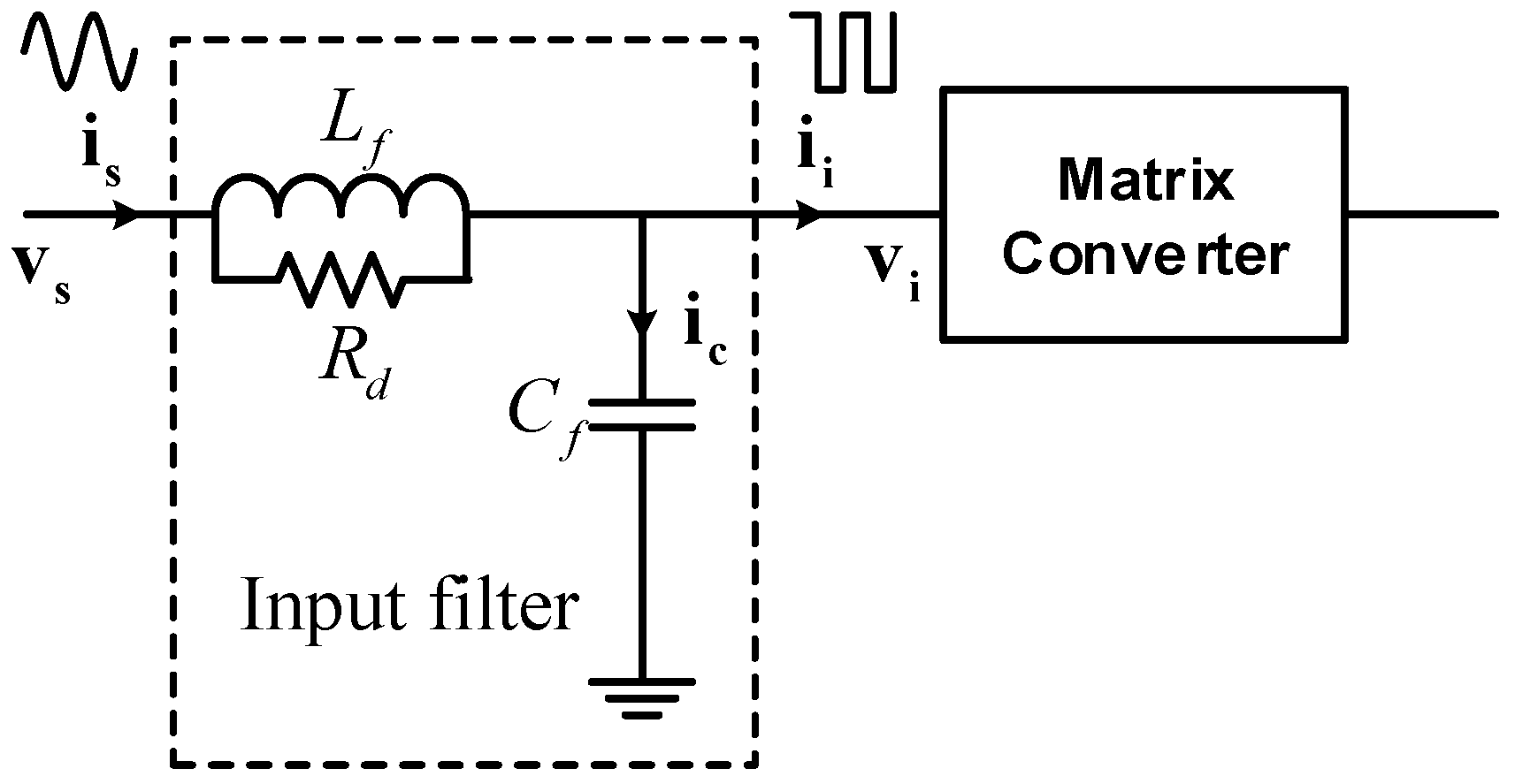
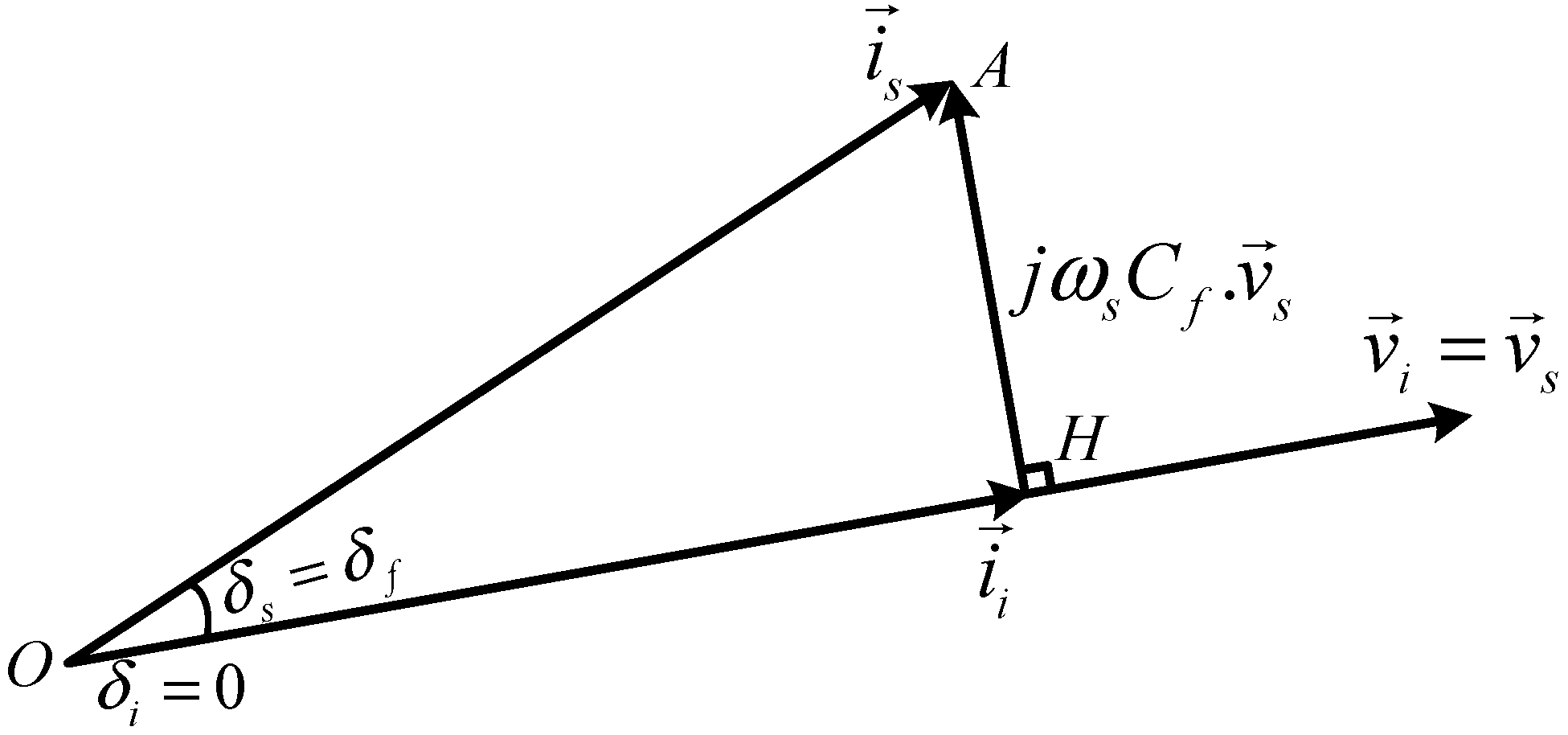
3. Input Filter Analysis
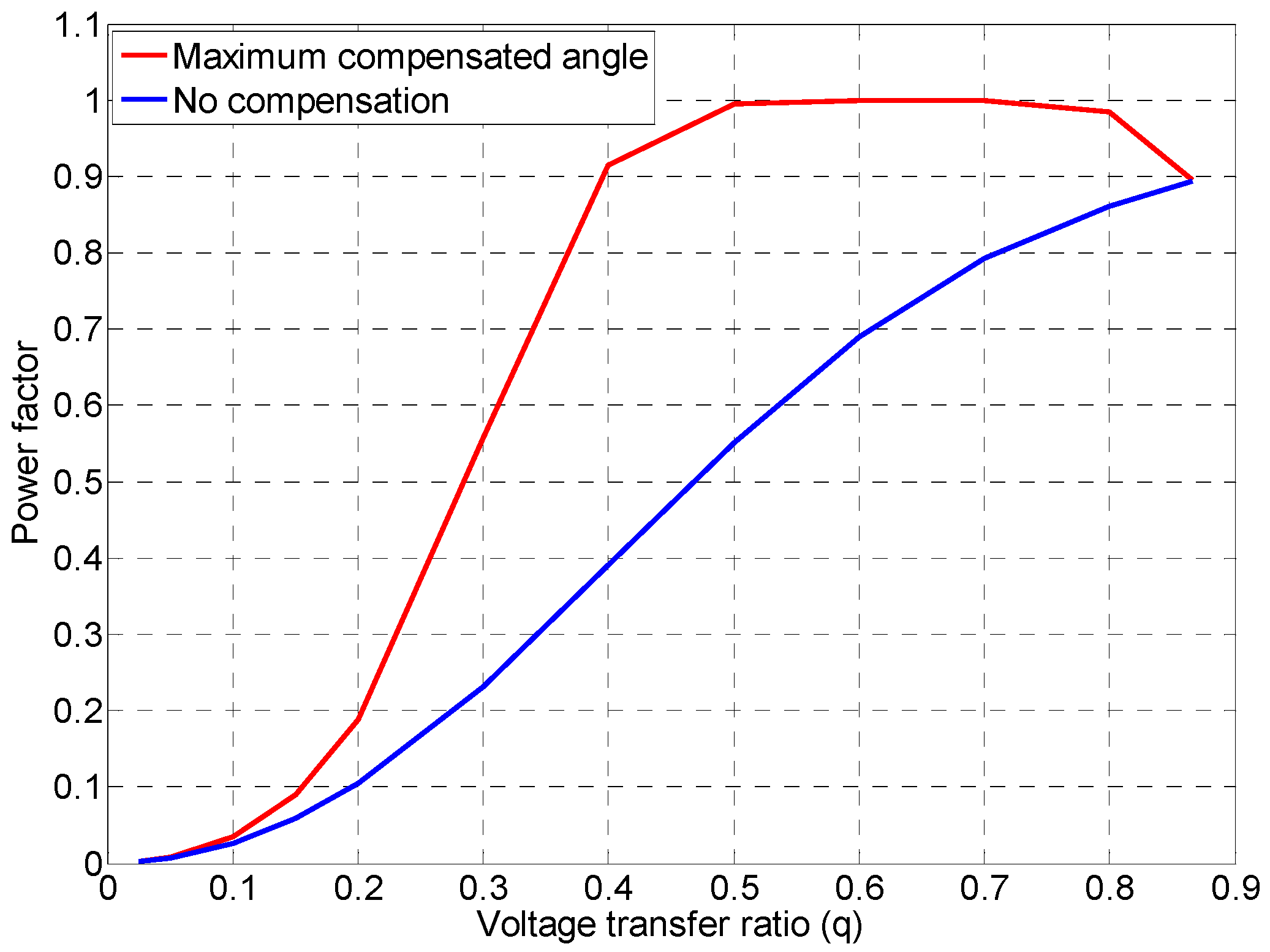
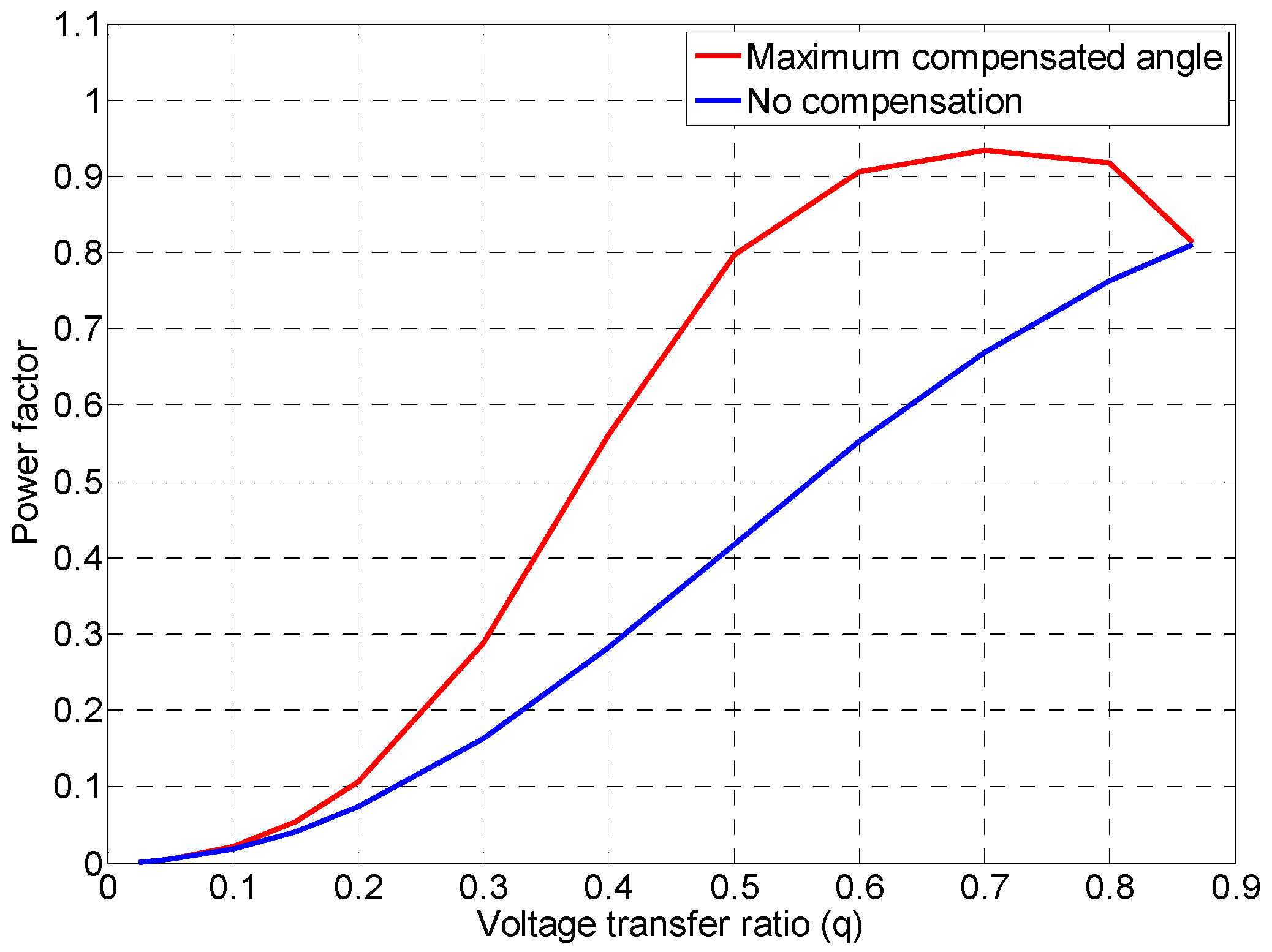
4. Study on IPF Compensation
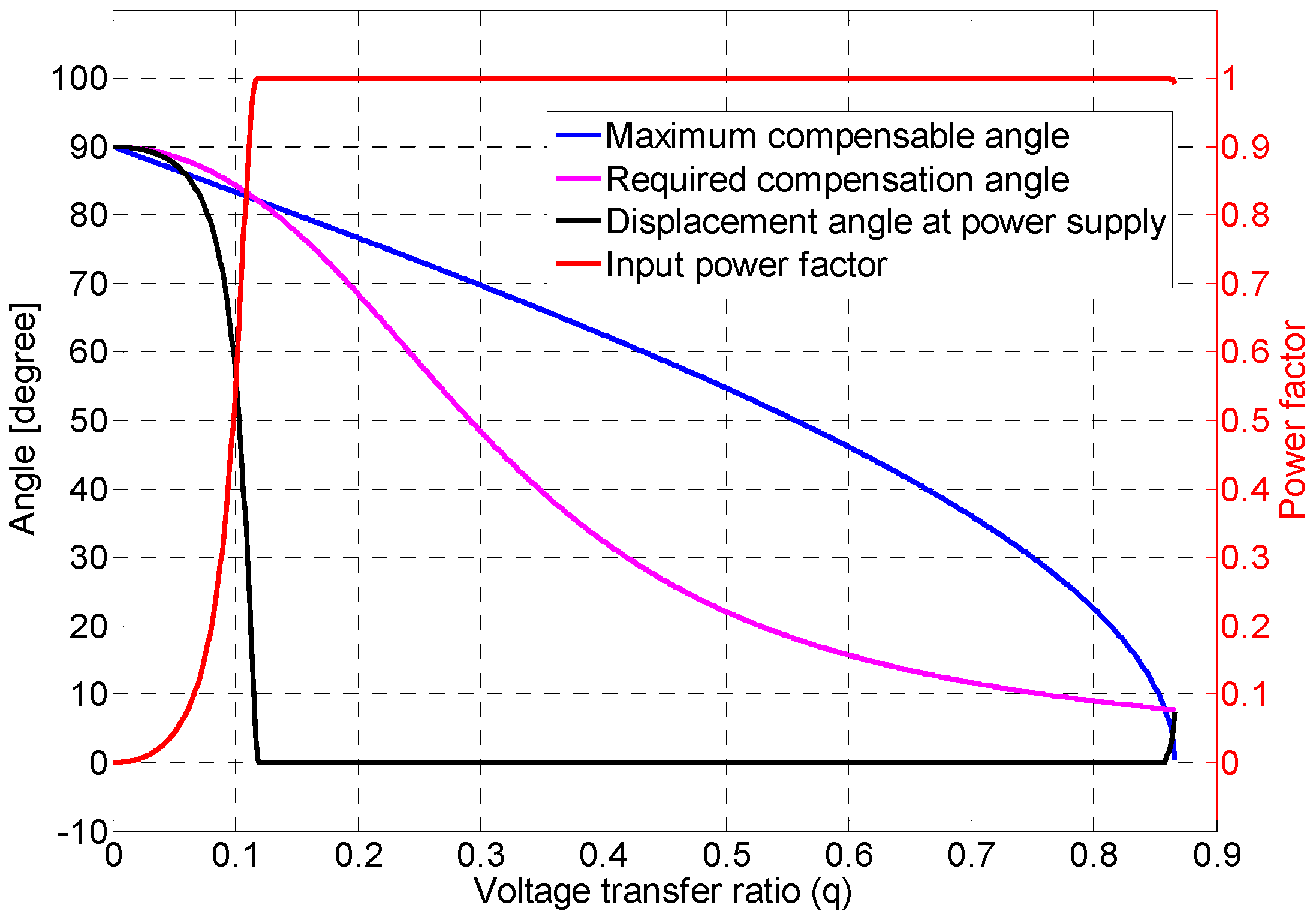
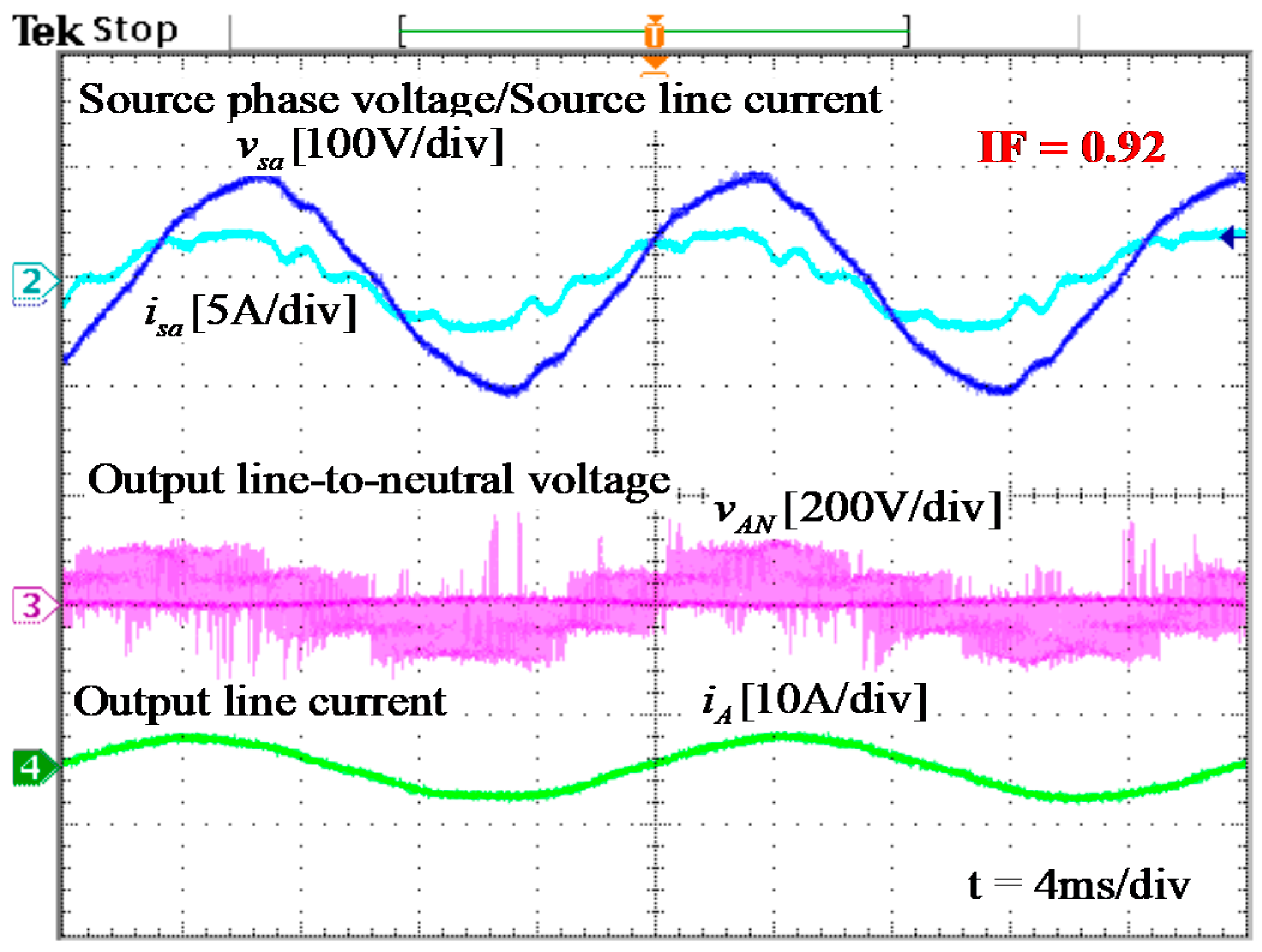
4.1. No Compensation
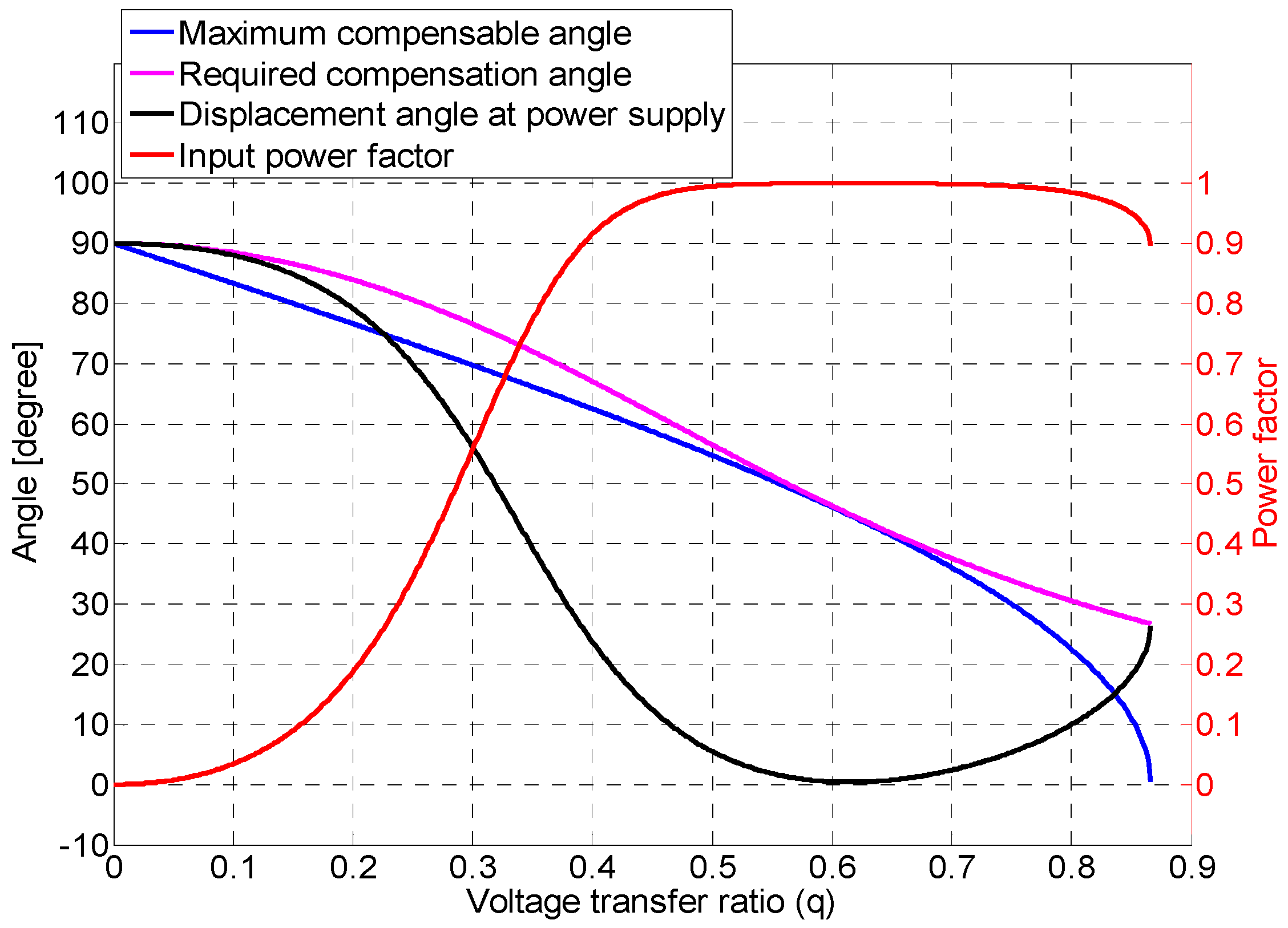
4.2. General Compensation
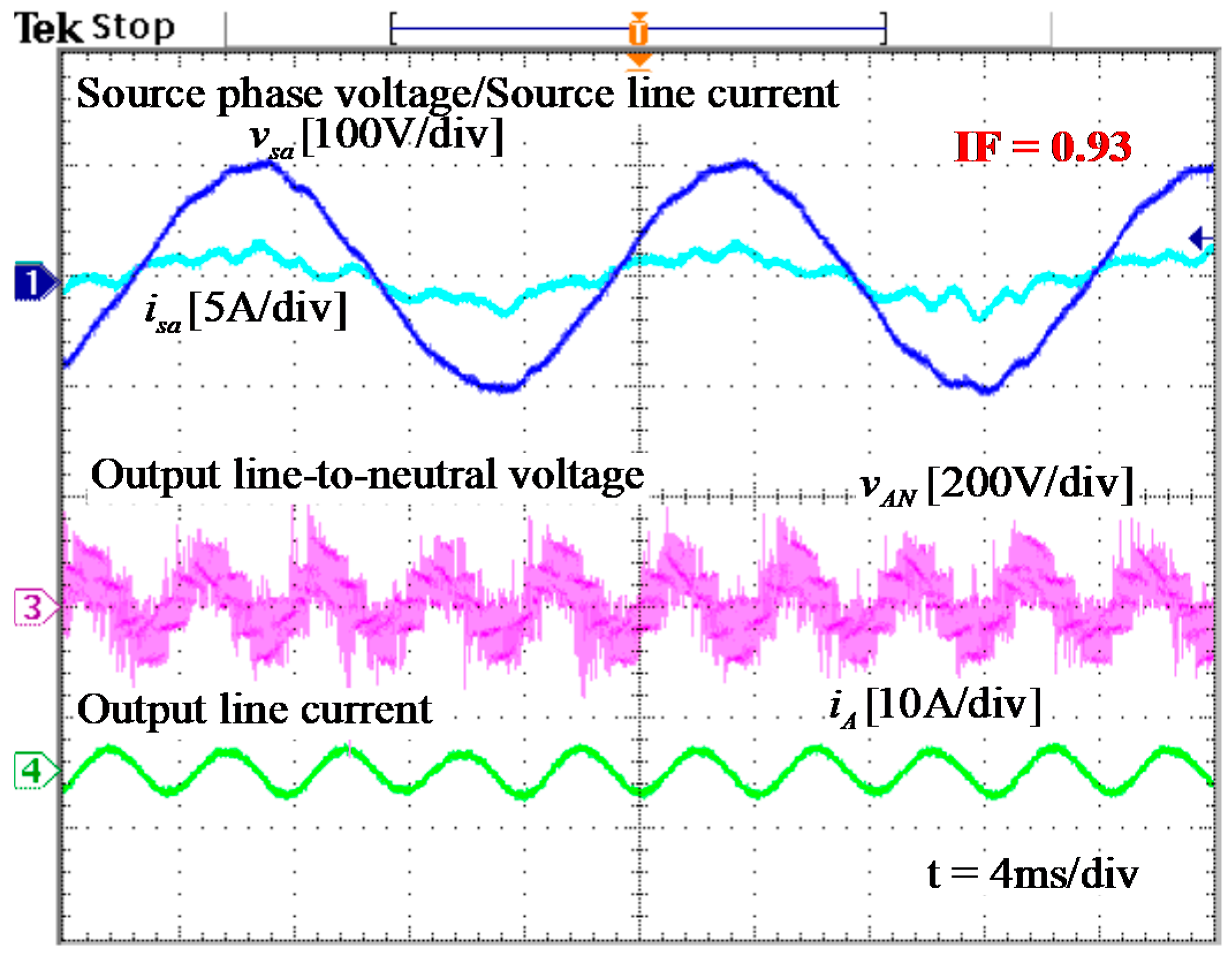
4.3. Unity IPF
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Three-phase source voltage vector, | |
| , , | Instantaneous source phase voltages |
| Source voltage amplitude | |
| Angular frequency of source voltage | |
| Initial phase angle of source voltage | |
| Space vector of three-phase source voltage | |
| Space vector of three-phase source current | |
| Amplitude of source current, | |
| , , | Instantaneous input phase voltages of MC |
| , , | Instantaneous output phase voltages of MC |
| , | Amplitudes of MC input and output voltages |
| , | Phase angles of MC input and output voltages |
| , | Space vectors of MC input and output voltages |
| , , | Instantaneous input line currents of MC |
| , , | Instantaneous output line currents of MC |
| , | Amplitudes of MC input and output currents |
| , | Phase angles of MC input and output currents |
| , | Space vectors of MC input and output currents |
| Sampling period | |
| Duty cycles of zero and active vectors | |
| Voltage transfer ratio of MC, | |
| Output voltage sector | |
| Input current sector | |
| , | Inductance and capacitance of input filter |
| Damping resistance of input filter | |
| Displacement angle due to input filter, | |
| Compensated angle, | |
| Displacement angle at main power supply, | |
| Displacement angle at main power supply with no compensated angle | |
| Load displacement angle at output frequency, | |
| , , | Load resistance, inductance and impedance |
| Output frequency | |
| Output angular frequency |
References
- Empringham, L.; Kolar, J.W.; Wheeler, P.W.; Clare, J.C. Technological issues and industrial application of matrix converters: A review. IEEE Trans. Ind. Electron. 2013, 60, 4260–4271. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T.; Rodriguez, J.; Wheeler, P.W. Review of three-phase PWM ac–ac converter topologies. IEEE Trans. Ind. Electron. 2011, 58, 4988–5006. [Google Scholar] [CrossRef]
- Villalba, L.R.M.; Lozano-Garcia, J.M.; Gutierrez-Torres, D.A.J.; Avina-Cervante, J.G.; Pizano-Martinez, A. Four-step current commutation strategy for a matrix converter based on enhanced-PWM MCU peripherals. Electronics 2019, 8, 547. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Lee, H.H. A DSVM Method for Matrix Converters to Suppress Common-mode Voltage with Reduced Switching Losses. IEEE Trans. Power Electron. 2016, 31, 4020–4030. [Google Scholar] [CrossRef]
- Wheeler, P.W.; Rodríguez, J.; Clare, J.C.; Empringham, L.; Weinstein, A. Matrix converters: A technology review. IEEE Trans. Ind. Electron. 2002, 49, 276–288. [Google Scholar] [CrossRef]
- Rodriguez, J.; Rivera, M.; Kolar, J.W.; Wheeler, P.W. A review of control and modulation methods for matrix converters. IEEE Trans. Ind. Electron. 2012, 59, 58–70. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Lee, H.H. An enhanced SVM method to drive matrix converters for zero common-mode voltage. IEEE Trans. Power Electron. 2015, 30, 1788–1792. [Google Scholar] [CrossRef]
- Friedli, T.; Kolar, J.W.; Rodriguez, J.; Wheeler, P.W. Comparative evaluation of three-phase ac–ac matrix converter and voltage dc-link back-to-back converter systems. IEEE Trans. Ind. Electron. 2012, 59, 4487–4510. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Lee, H.H. A modulation scheme for matrix converters with perfect zero common-mode voltage. IEEE Trans. Power Electron. 2016, 31, 5411–5422. [Google Scholar] [CrossRef]
- Kwak, S.S. Investigation of fault-mode behaviors of matrix converters. J. Power Electron. 2009, 9, 949–959. [Google Scholar]
- Friedli, T.; Kolar, J.W. Milestones in matrix converter research. IEEJ J. Ind. Appl. 2012, 1, 2–14. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Dorrell, D.G. Control and applications of direct matrix converters: A review. Chin. J. Electr. Eng. 2018, 4, 18–27. [Google Scholar]
- Lei, J.; Feng, S.; Zhou, B.; Nguyen, H.; Zhao, J.; Chen, W. A simple modulation scheme with zero common-mode voltage and improved efficiency for direct matrix converter fed PMSM drives. IEEE J. Emerg. Sel. Topics Power Electron. 2019. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Nguyen, T.D.; Lee, H.H. A modulation strategy to eliminate CMV for matrix converters with input power factor compensation. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6237–6242. [Google Scholar]
- Dasgupta, A.; Sensarma, P. Filter design of direct matrix converter for synchronous applications. IEEE Trans. Ind. Electron. 2014, 61, 6483–6493. [Google Scholar] [CrossRef]
- Varajao, D.; Araujo, R.E.; Miranda, L.M.; Lopes, J.A.P. EMI filter design for a single-stage bidirectional and isolated AC–DC matrix converter. Electronics 2018, 7, 318. [Google Scholar] [CrossRef]
- Klumpner, C.; Nielsen, P.; Boldea, I.; Blaabjerg, F. A new matrix converter-motor (MCM) for industry applications. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference, Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy, Rome, Italy, 8–12 October 2000; Volume 3, pp. 1394–1402. [Google Scholar]
- Trentin, A.; Zanchetta, P.; Clare, J.; Wheeler, P. Automated optimal design of input filters for direct ac/ac matrix converters. IEEE Trans. Ind. Electron. 2012, 59, 2811–2833. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Basu, K.; Mohan, N. Systematic input filter design of matrix converter by analytical estimation of RMS current ripple. IEEE Trans. Ind. Electron. 2015, 62, 132–143. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Lee, H.H.; Chun, T.W. Input power factor compensation algorithms using a new direct-SVM method for matrix converter. IEEE Trans. Ind. Electron. 2011, 58, 232–243. [Google Scholar] [CrossRef]
- Schafmeister, F.; Kolar, J.W. Novel hybrid modulation schemes significantly extending the reactive power control range of all matrix converter topologies with low computational effort. IEEE Trans. Ind. Electron. 2012, 59, 194–210. [Google Scholar] [CrossRef]
- Li, X.; Su, M.; Sun, Y.; Dan, H.; Xiong, W. Modulation strategy based on mathematical construction for matrix converter extending the input reactive power range. IEEE Trans. Power Electron. 2014, 29, 654–664. [Google Scholar]
- Li, X.; Sun, Y.; Zhang, J.; Su, M.; Huang, S. Modulation methods for indirect matrix converter extending the input reactive power range. IEEE Trans. Power Electron. 2017, 32, 4852–4863. [Google Scholar] [CrossRef]
- Das, D.; Basak, A.; Mukherjee, K.; Syam, P. Degradation of input displacement power factor by input current filter and its compensation for a matrix converter. In Proceedings of the PEDES, Chennai, India, 18–21 December 2018. [Google Scholar]
- Malekjamshidi, Z.; Jafari, M.; Zhu, J.; Xiao, D. Comparative analysis of input power factor control techniques in matrix converters based on model predictive and space vector control schemes. IEEE Access. 2019, 7, 139150–139160. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Trentin, A.; Zarri, L.; Calvini, M. Experimental analysis of a matrix converter prototype based on new IGBT modules. In Proceedings of the IEEE International Symposium on Industrial Electronics, Dubrovnik, Croatia, 20–23 June 2005; Volume 2, pp. 559–564. [Google Scholar]











| Switching Configuration | Output Voltage | Input Current | ||||||
|---|---|---|---|---|---|---|---|---|
| No | A | B | C | Vo | αo | Ii | βi | |
| GroupI | +1 | a | b | b | 2vab/3 | 0 | 2iA/√3 | −π/6 |
| −1 | b | a | a | −2vab/3 | 0 | −2iA/√3 | −π/6 | |
| +2 | b | c | c | 2vbc/3 | 0 | 2iA/√3 | π/2 | |
| −2 | c | b | b | −2vbc/3 | 0 | −2iA/√3 | π/2 | |
| +3 | c | a | a | 2vca/3 | 0 | 2iA/√3 | 7π/6 | |
| −3 | a | c | c | −2vca/3 | 0 | −2iA/√3 | 7π/6 | |
| +4 | b | a | b | 2vab/3 | 2π/3 | 2iB/√3 | −π/6 | |
| −4 | a | b | a | −2vab/3 | 2π/3 | −2iB/√3 | −π/6 | |
| +5 | c | b | c | 2vbc/3 | 2π/3 | 2iB/√3 | π/2 | |
| −5 | b | c | b | −2vbc/3 | 2π/3 | −2iB/√3 | π/2 | |
| +6 | a | c | a | 2vca/3 | 2π/3 | 2iB/√3 | 7π/6 | |
| −6 | c | a | c | −2vca/3 | 2π/3 | −2iB/√3 | 7π/6 | |
| +7 | b | b | a | 2vab/3 | 4π/3 | 2iC/√3 | −π/6 | |
| −7 | a | a | b | −2vab/3 | 4π/3 | −2iC/√3 | −π/6 | |
| +8 | c | c | b | 2vbc/3 | 4π/3 | 2iC/√3 | π/2 | |
| −8 | b | b | c | −2vbc/3 | 4π/3 | −2iC/√3 | π/2 | |
| +9 | a | a | c | 2vca/3 | 4π/3 | 2iC/√3 | 7π/6 | |
| −9 | c | c | a | −2vca/3 | 4π/3 | −2iC/√3 | 7π/6 | |
| GroupII | 0a | a | a | a | 0 | x | 0 | x |
| 0b | b | b | b | 0 | x | 0 | x | |
| 0c | c | c | c | 0 | x | 0 | x | |
| GroupIII | r1 | a | b | c | Vi | αi | Io | βo |
| r2 | a | c | b | Vi | −αi | Io | −βo | |
| r3 | c | a | b | Vi | 2π/3 + αi | Io | −2π/3+βo | |
| r4 | b | a | c | Vi | 2π/3 – αi | Io | 2π/3–βo | |
| r5 | b | c | a | Vi | −2π/3 + αi | Io | 2π/3+βo | |
| r6 | c | b | a | Vi | −2π/3 – αi | Io | −2π/3–βo | |
| Input Current Vector Sector | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Output Voltage Vector | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||||||
| –7 | +9 | +1 | –3 | +9 | –8 | –3 | +2 | –8 | +7 | +2 | –1 | +7 | –9 | –1 | +3 | –9 | +8 | +3 | –2 | +8 | –7 | –2 | +1 | |
| +4 | –6 | –7 | +9 | –6 | +5 | +9 | –8 | +5 | –4 | –8 | +7 | –4 | +6 | +7 | –9 | +6 | –5 | –9 | +8 | –5 | +4 | +8 | –7 | |
| –1 | +3 | +4 | –6 | +3 | –2 | –6 | +5 | –2 | +1 | +5 | –4 | +1 | –3 | –4 | +6 | –3 | +2 | +6 | –5 | +2 | –1 | –5 | +4 | |
| +7 | –9 | –1 | +3 | –9 | +8 | +3 | –2 | +8 | –7 | –2 | +1 | –7 | +9 | +1 | –3 | +9 | –8 | –3 | +2 | –8 | +7 | +2 | –1 | |
| –4 | +6 | +7 | –9 | +6 | –5 | –9 | +8 | –5 | +4 | +8 | –7 | +4 | –6 | –7 | +9 | –6 | +5 | +9 | –8 | +5 | –4 | –8 | +7 | |
| +1 | –3 | –4 | +6 | –3 | +2 | +6 | –5 | +2 | –1 | –5 | +4 | –1 | +3 | +4 | –6 | +3 | –2 | –6 | +5 | –2 | +1 | +5 | –4 | |
| Duty cycles | d1 | d2 | d3 | d4 | d1 | d2 | d3 | d4 | d1 | d2 | d3 | d4 | d1 | d2 | d3 | d4 | d1 | d2 | d3 | d4 | d1 | d2 | d3 | d4 |
| Power Supply | Input Filter | Output Load |
|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.-N.; Nguyen, M.-K.; Duong, T.-D.; Tran, T.-T.; Lim, Y.-C.; Choi, J.-H. A Study on Input Power Factor Compensation Capability of Matrix Converters. Electronics 2020, 9, 82. https://doi.org/10.3390/electronics9010082
Nguyen H-N, Nguyen M-K, Duong T-D, Tran T-T, Lim Y-C, Choi J-H. A Study on Input Power Factor Compensation Capability of Matrix Converters. Electronics. 2020; 9(1):82. https://doi.org/10.3390/electronics9010082
Chicago/Turabian StyleNguyen, Huu-Nhan, Minh-Khai Nguyen, Truong-Duy Duong, Tan-Tai Tran, Young-Cheol Lim, and Joon-Ho Choi. 2020. "A Study on Input Power Factor Compensation Capability of Matrix Converters" Electronics 9, no. 1: 82. https://doi.org/10.3390/electronics9010082
APA StyleNguyen, H.-N., Nguyen, M.-K., Duong, T.-D., Tran, T.-T., Lim, Y.-C., & Choi, J.-H. (2020). A Study on Input Power Factor Compensation Capability of Matrix Converters. Electronics, 9(1), 82. https://doi.org/10.3390/electronics9010082









