As evident from the above discussions, there is no scheme in the current literature that can correct more than two random output bit errors including those in the correction block. This section explains the BCH error correction scheme to mitigate radiation induced temporal errors in detail along with its efficient hardware implementation. To the best of our knowledge, the technique presented in this paper is first to investigate such a scheme for fault tolerant Galois field circuits. However the scope of the proposed technique here is to focus on the error that are happening on the internal nodes of the circuit. Hence we assume that the primary input is error free.
4.1. Bose–Choudhury–Hocquenghem Code
The Bose–Choudhury–Hocquenghem (BCH) codes belong to the family of cyclic codes in which the message block is encoded using a polynomial
g(
x), called the
generator polynomial. The generator polynomial is the least common multiplier (LCM) of the minimal polynomial for the selected powers with respect to GF(2
m), provided that each of the minimal polynomial should appear only once in the product. Here, the message is treated as a whole block and encoded one at a time rather than encoding continuously as in the case of convolution codes. The encoder block possesses no memory, hence no information of the previous message blocks. This style of encoding can be thought of as sliding an encoding window over the message bits. In the conventional BCH codes, the LFSR structure is used to encode incoming message bits one at a time. Hence, the present encoded bit depends on the previous bit, which shows that a memory is being used. In the proposed scheme, a parallel implementation of the BCH encoder is introduced which encodes the message as a whole block and uses no memory. The binary BCH codes are generalized Hamming codes. The BCH codes detect and correct randomly located bit errors in a stream of information bits according to its error correction capability (
t). The burst error correcting codes, such as the Reed–Solomon codes, correct multiple errors within a symbol or multiple symbols, but all the bit errors must be within the
same symbol. The most interesting aspect of the BCH codes over Reed–Solomon codes for our purpose is the simplicity in decoding the codewords. In this case, the bit’s location only needs to be determined and not the correct value, as in the case of Reed–Solomon codes. The basic block diagram of the generic multiple bit error correction circuit using the binary BCH code is shown in
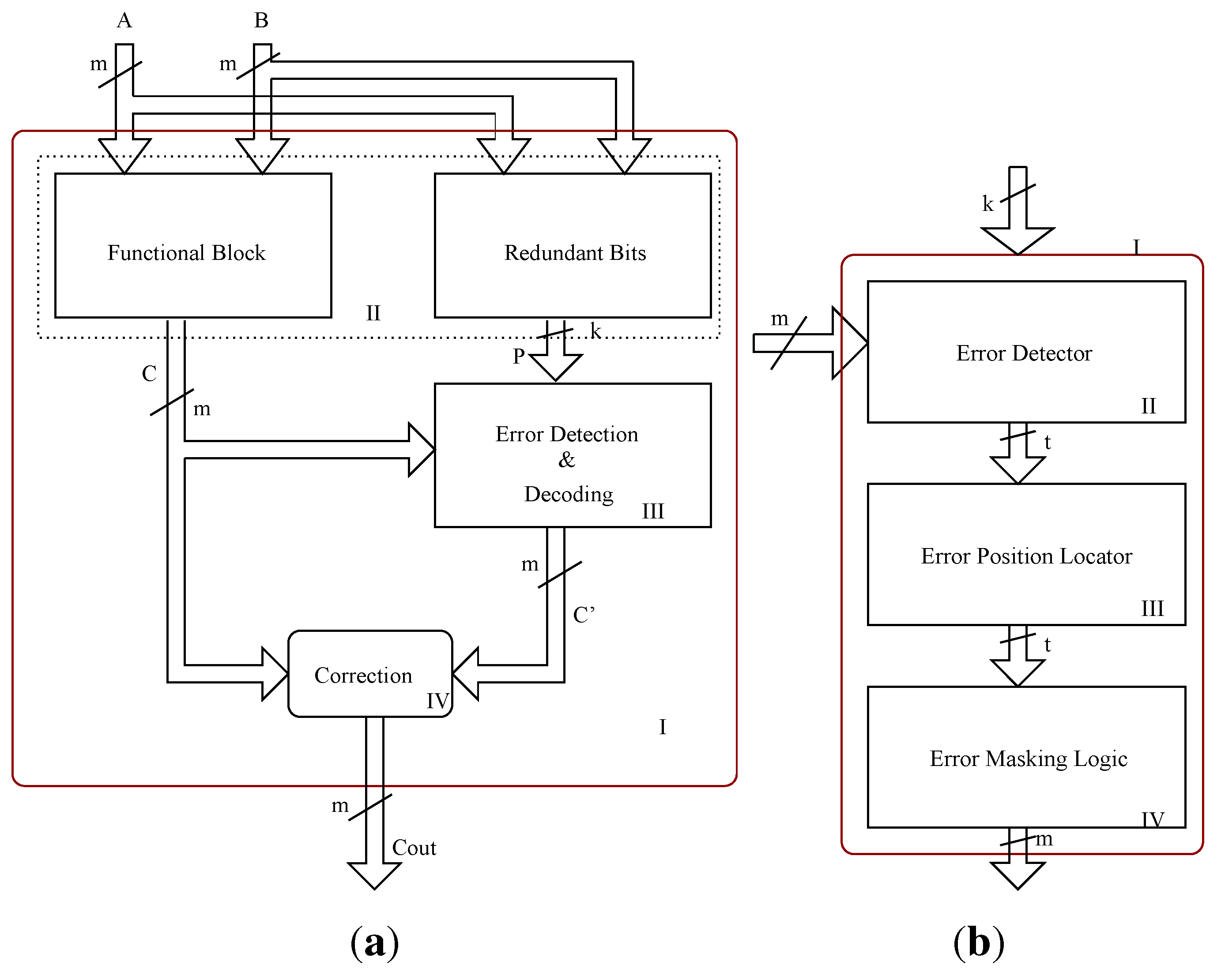
Figure 1(a). The overall design contains a redundant bit generation block that works in parallel with the functional block, an error detection and decoding block that detects the occurrence of an error and its location, and finally a decoder, apart from the bit parallel multiplier functional block.
Figure 1.
BCH code based multiple detection and correction architectures. (a) Multiple error correction architecture; (b) Error detection and correction block.
Figure 1.
BCH code based multiple detection and correction architectures. (a) Multiple error correction architecture; (b) Error detection and correction block.
4.2. BCH Encoder and Decoder Design
The complete design of a BCH parallel encoder and decoder with an example is now discussed. The bit parallel multiplier architecture is adopted from [
19]. The general representation of BCH code is
BCH(
n,
k,
d), where
n is the size of the codeword or, in other words, it is the sum of the message length
k, and the number of parity bits
p used for encoding, and
d is the minimum distance (dmin) between the codewords. The possible BCH codes for
m ≥ 3 and
t < 2
m−1 is given by the following expressions:
The codeword is formed by adding the remainder after dividing the shifted message block by a generator polynomial
g(
x). All the codewords are multiples of the generator polynomial. The generator polynomial is not just a minimal primitive polynomial, but a combination of several polynomials corresponding to the powers of the primitive element
α in GF(2
m). In other words,
g(
x) is the least common multiple of the minimal polynomials over the various powers of the primitive element
α (powers from
α,
α2, …,
α2t, where
t is the error correction capability of the code). Then,
where
m1(
x),
m2(
x), …
m2t(
x) are the minimal polynomials corresponding to the various powers of
α. It is also noted that every even power of a primitive element has the same minimal polynomial. Hence Equation (
4) is simplified to the following:
The basic principle and design of the bit-parallel BCH code based multiple error correction scheme is explained with an example as follows. Let us consider a simple case of
BCH(15, 5, 7), where
n = 15 and
k = 5. In this fairly small example, we consider bit-parallel PB multiplier over GF(2
5). Let
c = [
co,
c1,
c2,
c3,
c4] be the outputs of the multiplier. Then,
as in this case
n = 15 and
k = 5.
The redundant bits are generated by the following:
Let
α be the primitive element of GF(2
4). Here,
P(
x) =
x4 +
x + 1 is the primitive polynomial. The three minimal polynomials
m1(
x),
m3(
x), and
m5(
x) are given by:
For three bit error correction (
t = 3), the generator polynomial for constructing the codeword is then given by the following:
Substituting the minimal polynomials, the following expression is obtained:
Substituting the generating polynomial, the following expression is obtained:
where,
p0 =
c0 +
c2 +
c4,
p0 =
d0 +
d2 +
d4 +
e0 +
e1 +
e2 +
e3,
p1 =
c0 +
c1 +
c2 +
c3 +
c4 p1 =
d0 +
d1 +
d2 +
d3 +
d4,
p2 =
c0 +
c1 +
c3,
p2 =
d0 +
d1 +
d3 +
e1 +
e2 +
e3,
p3 =
c1 +
c2 +
c4,
p3 =
d1 +
d2 +
d4 +
e0 +
e2 +
e3,
p4 =
c0 +
c3 +
c4,
p4 =
d0 +
d3 +
d4 +
e0 +
e2,
p5 =
c0 +
c1 +
c2,
p5 =
d0 +
d1 +
d2 +
e2,
p6 =
c1 +
c2 +
c3,
p6 =
d1 +
d2 +
d3 +
e0 +
e3,
p7 =
c2 +
c3 +
c4,
p7 =
d2 +
d3 +
d4 +
e1,
p8 =
c0 +
c2 +
c3,
p8 =
d0 +
d2 +
d3 +
e0 +
e1 +
e3,
p9 =
c1 +
c3 +
c4,
p9 =
d0 +
d3 +
d4 +
e0 +
e2, where the
d and
e terms are the inner product terms of the multiplier [
19]. Hence, the final BCH encoded codeword for the bit parallel GF multiplier circuit is given as the following expression:
The redundant bits (check bits) are generated by a parallel redundant bit generation unit as shown in
Figure 1(a). The resulting parity bits along with the multiplier outputs are passed on to the error detection and correction block (syndrome generation and decoding) as shown in
Figure 1(b). For three bit error correction capability (
t = 3), six (2 ×
t) syndromes need to be generated. The syndromes help us to determine whether the computed multiplication results are error free or not. In case of error free computation, the syndromes will be evaluate to zero. If the syndromes are nonzero, then that flags us the erroneous computation. The syndromes are calculated using the following expression:
The syndrome decoding is done by using the well known Peterson–Gorenstein–Zierler algorithm. In our work we use only three syndromes to predict and correct errors instead of 6 syndromes in case of classical BCH scheme. This would reduce area of the whole implementation. Here for three bit error correction we need to calculate only syndromes
S1,
S3, and
S5. The generalized equation for syndromes for the given example of
BCH(15, 5, 7) are given as follows:
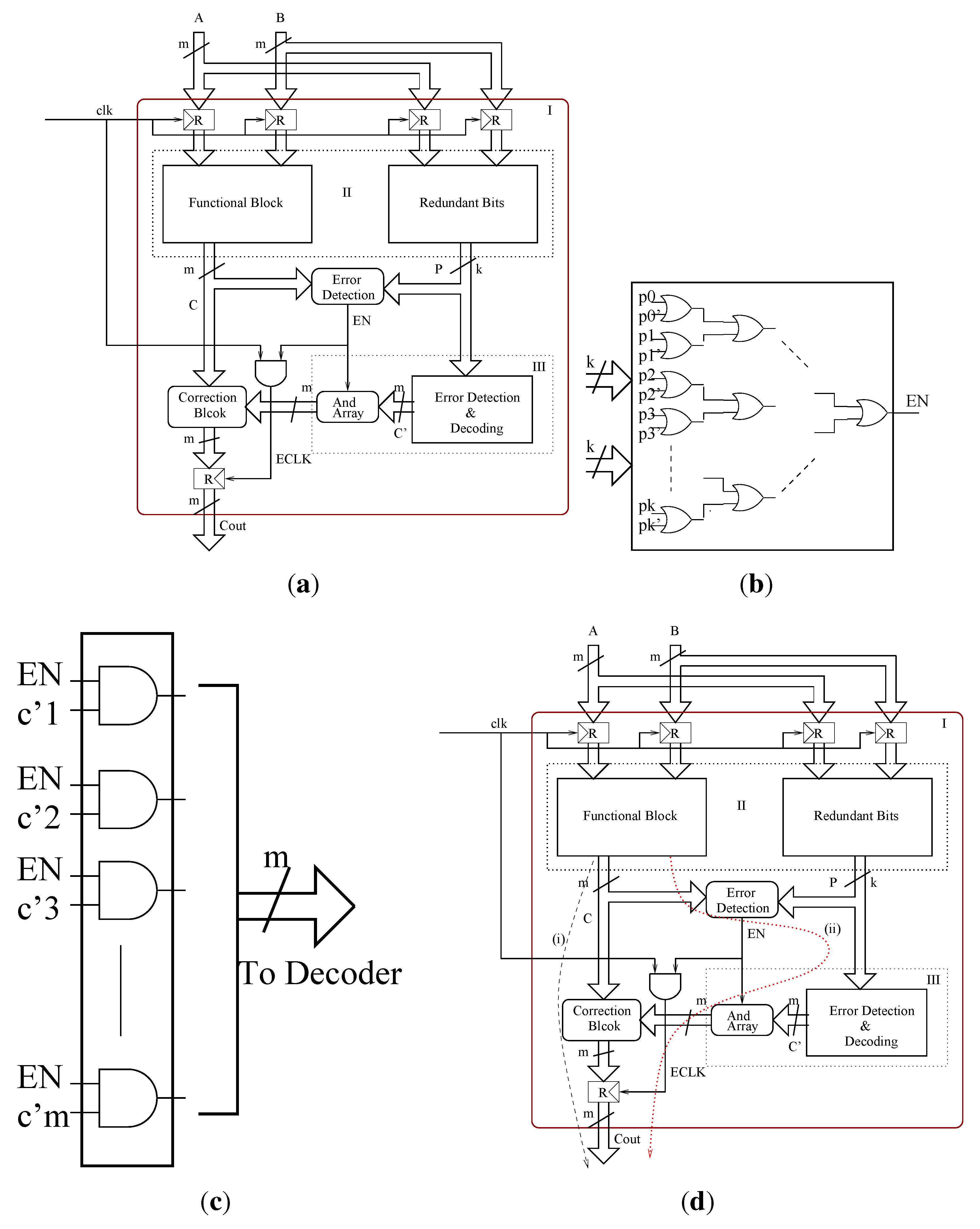
Determining whether the computation is error free is not sufficient; we also need to correct these errors in case if they are present. For this, we need to compute the error positions or error locations of the erroneous bits. To determine the error positions effectively, we need to decode the syndromes. The syndrome decoding block (error detection and correction block) of the BCH based error correction technique contains an error locator polynomial generator block that finds the root of the error locator polynomial and a decoder that eventually corrects the erroneous bits based on the computed error position. For this purpose the computed syndrome values are passed on to the error locator polynomial computation block, as shown in
Figure 2. For the three (
t = 3) bit error correction, we have three (
t = 3) coefficients for the error locator polynomial. Let
σ1,
σ2, and
σ3 be the three coefficients of the error locator polynomial. Then they are calculated as follows:
4.3. Improved Error Locator Design
Once we have the error locator polynomial, the roots of the polynomial will give the error locations. The traditional algorithms for finding the roots of the error locator polynomial are based on exhaustive search methods. Another scheme for finding the roots is the Chien search algorithm, in which all the possible values of the primitive element α, ranging from α0, α, … α2m−1, are inserted into the error locator polynomial to check if they satisfy the polynomial. In the proposed design, a bit parallel implementation of the area optimized Chien search algorithm is proposed. In particular, we proposed a scheme in which the root of the error locator polynomial is checked only among the powers of the primitive element α corresponding to the bit positions of the message bits, i.e., the multiplier output bits. The roots of the error locator polynomial corresponding to the parity bits are omitted in order to reduce the hardware complexity and hence the chip area. For a 5-bit multiplier, we check whether α1, α2, α3, α4, α5 are roots of the error locator polynomial, which in turn corresponds to the bit positions c4, c3, c2, c1 and c0 in the output of the multiplier. In other words, if α is a root of the error locator polynomial, it says that the bit c4 of the multiplier is erroneous, etc. The decoder corrects the erroneous bit(s) corresponding to the information provided by the parallel root search block. Based on this design principle, we have also extended the design to a 16-bit parallel PB multiplier over GF(216) and to a 45-bit parallel PB multiplier over GF(245).
4.4. ASIC Prototyping
The design was simulated in Modelsim™ .
Figure 2 shows the snapshot of a typical Modelsim™ simulation result. During the simulations, the faults are introduced into the multiplier outputs randomly for checking the error correction capability of the proposed scheme. The highlighted parts in
Figure 2 show one of the many testing values. The errors are introduced in the intermediate stages of the multiplier, which in turn gave multiple bit errors at the multiplier output. In this case we have errors at bit positions 1, 2, and 16, however the
cout values show the corrected final output from the BCH decoder. Although the example designs considered 2 to 5-bit error correction capability, based on the theory presented in this paper, the capability can be extended to more than five bits and also to any digital circuit in general.
Figure 2.
Simulation results of BCH code based multiple error correction.
Figure 2.
Simulation results of BCH code based multiple error correction.
4.5. Comparison with Existing Approaches
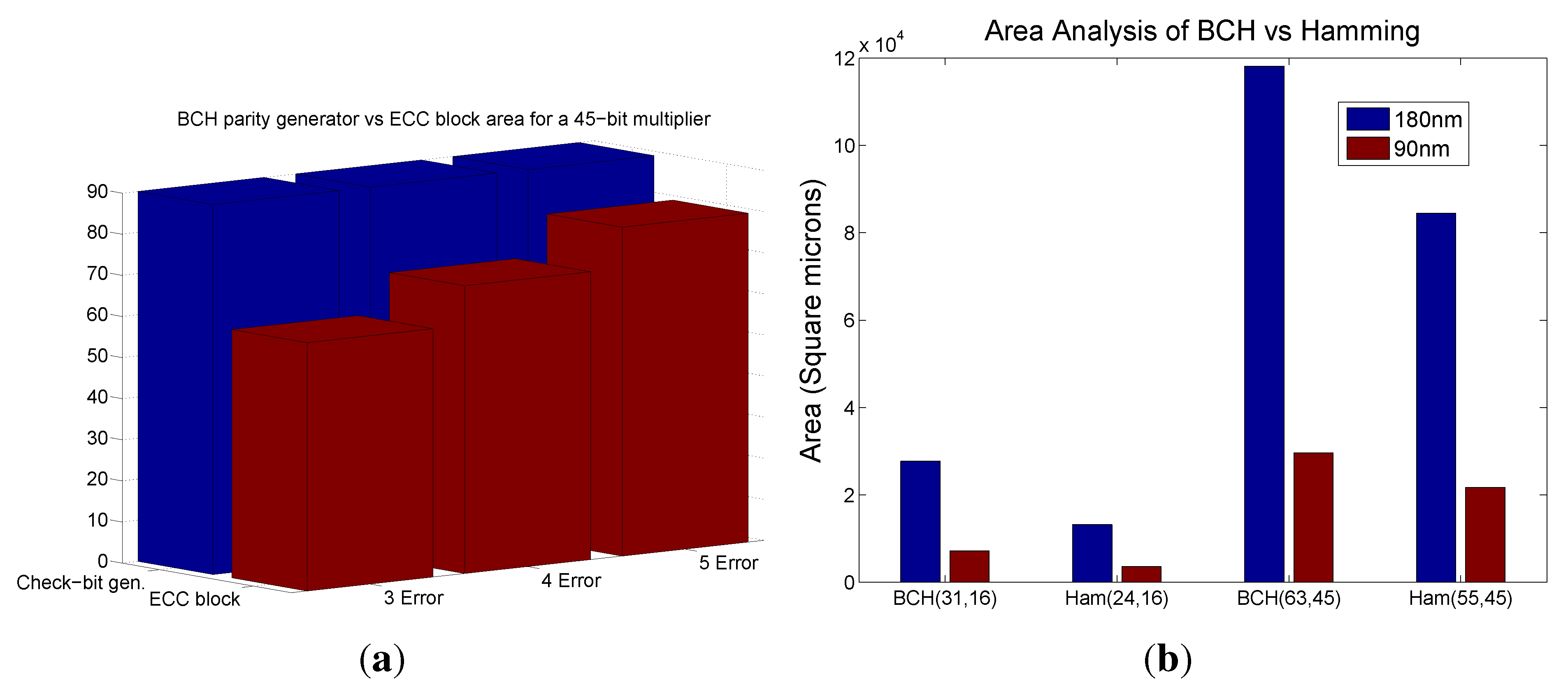
The area overhead for the various designs with 2, 3, 4 and 5 error correction for a 45-bit multiplier is shown in
Figure 3(a). It is observed that for a fixed size multiplier, the area increases with the number of bit error correction.
Figure 3.
Area overhead analysis for comparative perspective. (a) Overhead analysis of BCH based error correction scheme; (b) Block wise area of a 45-bit GF multiplier with 3-bit error correction.Error LocatrorError Locator
Figure 3.
Area overhead analysis for comparative perspective. (a) Overhead analysis of BCH based error correction scheme; (b) Block wise area of a 45-bit GF multiplier with 3-bit error correction.Error LocatrorError Locator
The area of the various blocks in the proposed multiple error correction scheme is shown in
Figure 3(b). The additional area contribution to the over all design is due to the parity predictor block and the Chien search root finding block.
Table 1 compares the area overhead of our approach with other existing related error detection or correction methods appeared in existing literature.
Table 1.
Comparison with Other Approaches for 45-bit multiplier.
Table 1.
Comparison with Other Approaches for 45-bit multiplier.
| Property | TMR | Mathew et al. 2008 [13] | Mathew et al. 2008 [14] | Proposed | Proposed | Proposed |
|---|
| #errors correction | multiple | single | single | 3 Errors | 4 Errors | 5 Errors |
| Coding technique | Voting | Hamming | LDPC | BCH | BCH | BCH |
| Overhead | >200% | >130% | 120% | 150.4% | 164.04% | 170.4% |
Further, for a given error correction capability, the extra hardware comes down significantly for larger and more practical designs. For example, for the 5-, 16-, and 45-bit multipliers we observed that the extra hardware is 600%, 240%, and 150.4%, respectively, for 3-bit error correction capability.