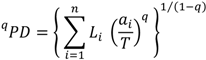Climate Change Impacts on the Tree of Life: Changes in Phylogenetic Diversity Illustrated for Acropora Corals
Abstract
:1. Introduction
2. The Phylogenetic Diversity Measure, PD
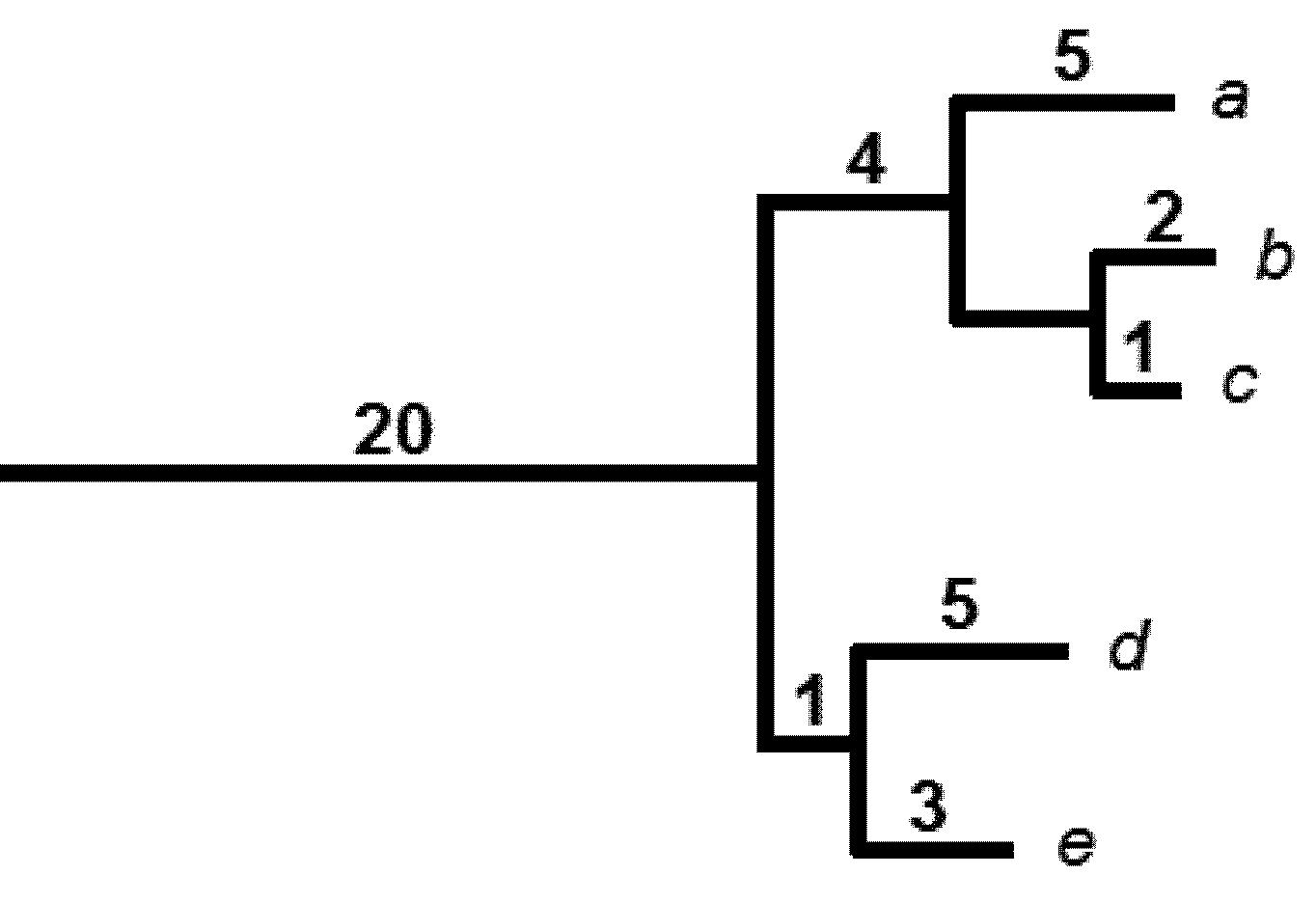
3. A Brief Review of Climate Change Impacts on PD
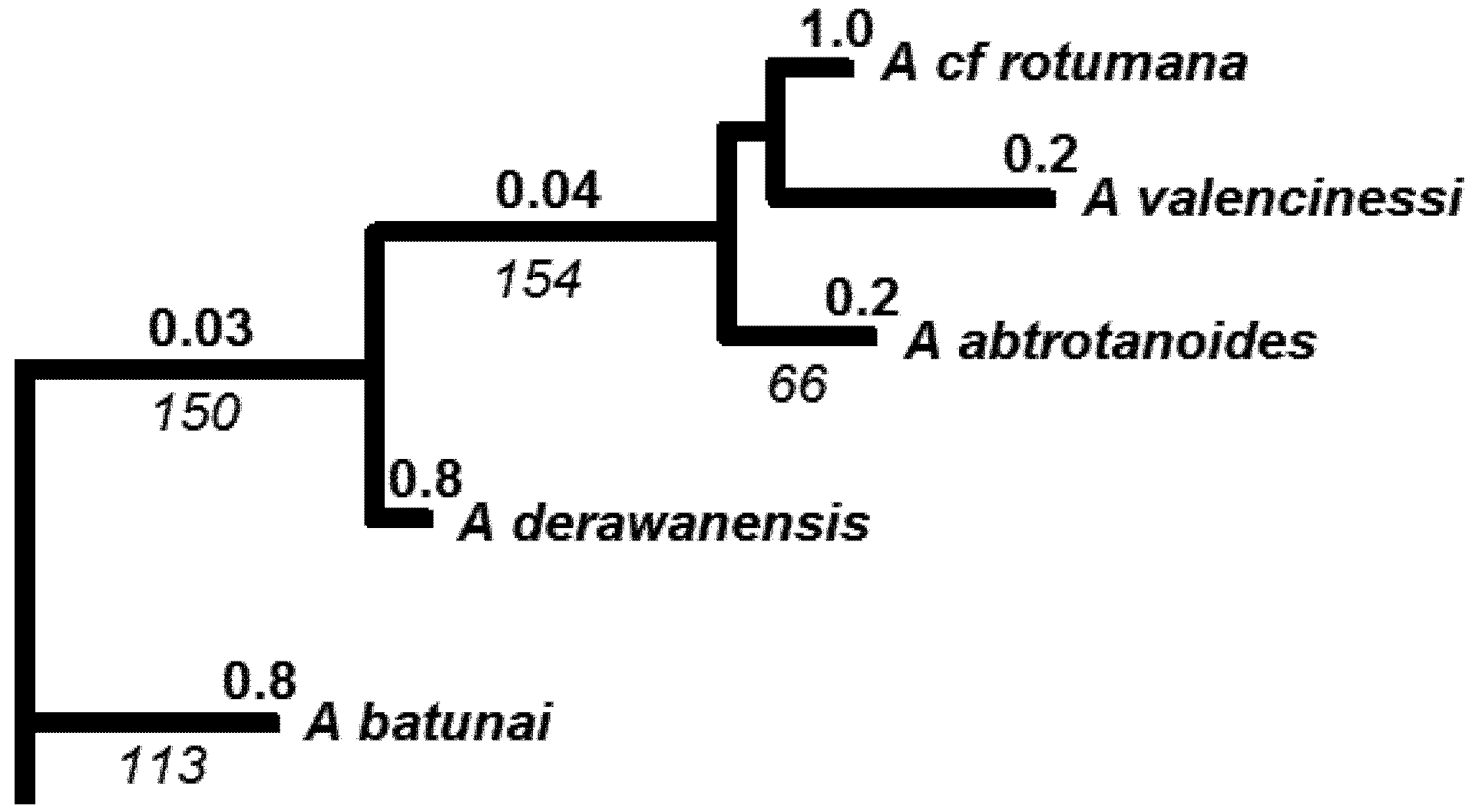
4. Phylogeny of Acropora — Rationale and Methods
4.1. Introduction to Acropora as a Model Group for Extinction Risk Studies
| IUCN Category | Number of Acropora species (n = 173) | Percentage of Acropora species | Conversion to extinction probability |
|---|---|---|---|
| Critically Endangered (CE) | 2 | 1.2% | 0.99 |
| Endangered (E) | 3 | 1.7% | 0.9 |
| Vulnerable (V) | 49 | 28.3% | 0.8 |
| Near Threatened (NT) | 22 | 12.7% | 0.4 |
| Least Concern (LC) | 27 | 15.6% | 0.2 |
| Data Deficient (DD) | 64 | 37% | - |
| Not Assessed | 6 | 3.5% | - |
4.2. Phylogenetically-Informative Markers
4.3. Molecular Phylogenetic Analysis by Maximum Likelihood Method
| Species (Authority) | GENBANK Accession No. | Source | Species Group in Wallace 1999 | IUCN status |
|---|---|---|---|---|
| Acropora abrotanoides (Lamarck, 1816) | FJ899076.1 | [77] | robusta group | LC |
| Acropora aculeus (Dana, 1846) | aculeus2_39IF | [78] | latistella group | V |
| Acropora acuminata (Verrill, 1864) | acuminata2_13IF | [78] | muricata group | V |
| Acropora aspera (Dana, 1846) | EU918267 | [62] | aspera group | V |
| Acropora austera (Dana, 1846) | EU918228.1 | [62] | rudis group | NT |
| Acropora batunai (Wallace, 1997) | EU918250.1 | [62] | echinata group | V |
| Acropora carduus (Dana, 1846) | carduus1_10IF | [78] | echinata group | NT |
| Acropora caroliniana (Nemenzo, 1976) | EU918264.1 | [62] | loripes group | V |
| Acropora cerealis (Dana, 1846) | EU918248.1 | [62] | nasuta group | LC |
| Acropora cervicornis (Lamarck, 1816) | GQ863996 | [79] | cervicornis group | CE |
| Acropora chesterfieldensis (Veron and Wallace, 1984) | EU918279.1 | [62] | loripes group | LC |
| Acropora cytherea (Dana, 1846) | cythereaD7hetplasIF | [78] | hyacinthus group | LC |
| Acropora derewanensis (Wallace, 1997) | EU918263.1 | [62] | horrida group | V |
| Acropora digitifera (Dana, 1846) | EF206519 | [80] | humilis group | NT |
| Acropora divaricata (Dana, 1846) | AY026432 | [60] | divaricata group | NT |
| Acropora donei (Veron and Wallace, 1984) | donei1_121IF | [78] | selago group | V |
| Acropora elseyi (Brook, 1892) | elseyi2_22IF | [78] | echinata group | LC |
| Acropora florida (Dana, 1846) | AY026435.1 | [60] | florida group | NT |
| Acropora muricata(Dana, 1846) | AY026436.1 | [60] | muricata group | NT |
| Acropora gemmifera (Brook, 1892) | EU918256.1 | [62] | humilis group | LC |
| Acropora globiceps (Dana, 1846) | EF206434.1 | [80] | humilis group | V |
| Acropora granulosa (Milne Edwards and Haime, 1860) | EU918286 | [62] | loripes group | NT |
| Acropora horrida (Dana, 1846) | horridaIF | [78] | horrida group | V |
| Acropora humilis (Dana, 1846) | EU918282.1 | [62] | humilis group | NT |
| Acropora hyacinthus (Dana, 1846) | AB361095.1 | [81] | hyacinthus group | NT |
| Acropora jacquelineae (Wallacew, 1994) | EU918284.1 | [62] | loripes group | V |
| Acropora kimbeensis (Wallace, 1999) | EU918268.1 | [62] | nasuta group | V |
| Acropora kirstyae (Veron and Wallace, 1984) | EU918215.1 | [62] | horrida group | V |
| Acropora latistella (Brook, 1891) | AY026443.1 | [60] | latistella group | LC |
| Acropora loisetteae (Wallace, 1994) | EU918273.1 | [62] | selago group | V |
| Acropora lokani (Wallace, 1994) | EU918270.1 | [62] | loripes group | V |
| Acropora longicyathus (Milne Edwards and Haime, 1860) | EU918221.1 | [62] | echinata group | LC |
| Acropora loripes (Brook, 1892) | EU918205.1 | [62] | loripes group | NT |
| Acropora microphthalma (Verrill, 1859) | EU918203.1 | [80] | horrida group | LC |
| Acropora millepora (Ehrenberg, 1834) | AY026449.1 | [60] | aspera group | LNT |
| Acropora monticulosa (Brüggemann, 1879) | EF206471.1 | [80] | humilis group | NT |
| Acropora multiacuta (Nemenzo, 1967) | EF206547.1 | [80] | humilis group | V |
| Acropora nasuta (Dana, 1846) | AY026450.1 | [60] | nasuta group | NT |
| Acropora intermedia (Dana, 1846) | AY026451.1 | [60] | robusta group | LC |
| Acropora palmata (Lamarck, 1816) | AF505257.1 | [73] | cervicornis group | CE |
| Acropora papillare (Latypov, 1992) | EU918211.1 | [62] | aspera group | V |
| Acropora pichoni (Wallace, 1999) | EU918236.1 | [62] | elegans group | NT |
| Acropora prolifera (Lamarck, 1816) | AF507266.1 | [73] | cervicornis group | NOT ASSESSED |
| Acropora pruinosa (Brook, 1893) | AB638782.1 | [82] | cf. divaricata group | DD |
| Acropora pulchra (Brook, 1891) | EU918230.1 | [62] | aspera group | LC |
| Acropora retusa (Dana, 1846) | EF206537.1 | [80] | humilis group | V |
| Acropora robusta (Dana, 1846) | FJ8990765 | [77] | robusta group | LC |
| Acropora rongelapensis (Richards and Wallace, 2004) | EU918210.1 | [62] | cf. loripes group | DD |
| Acropora rotumana cf. (Richards, Wallace, Miller, 2010) | FJ899069.1 | [77] | cf. robusta group | NOT ASSESSED |
| Acropora samoensis (Brook, 1891) | AY364093.1 | [80] | humilis group | LC |
| Acropora sarmentosa (Brook, 1892) | AY026455.1 | [60] | florida group | LC |
| Acropora selago (Studer, 1878) | selago 1_25IF | [78] | selago group | NT |
| Acropora solitaryensis (Veron and Wallace, 1984) | AB638798.1 | [82] | divaricata group | V |
| Acropora spathulata (Brook, 1891) | EU918242.1 | [62] | aspera group | LC |
| Acropora speciosa (Quelch, 1886) | EU918244.1 | [62] | loripes group | V |
| Acropora spicifera (Dana, 1846) | AY083881.1 | [61] | aspera group | V |
| Acropora tenella (Brook, 1892) | EU918239.1 | [62] | elegans group | V |
| Acropora tenuis (Dana, 1846) | AY026457.1 | [60] | selago group | NT |
| Acropora tortuosa (Dana, 1846) | EU918238.1 | [62] | horrida group | LC |
| Acropora valenciennesi (Milne Edwards and Haime, 1860) | val2_33IF | [78] | muricata group | LC |
| Acropora valida (Dana, 1846) | EU918235.1 | [62] | nasuta group | LC |
| Acropora vaughani (Wells, 1954) | EU918224.1 | [62] | horrida group | V |
| Acropora walindii (Wallace, 1999) | EU918234.1 | [62] | elegans group | V |
| Acropora yongei (Veron and Wallace, 1984) | youngei2_15IF | [78] | selago group | LC |
| Isopora cuneata (Dana, 1846) | AY026429.1 | [60] | Genus Isopora (included as outgroup) | V |
5. Indices Providing Information about Climate Change Impacts on Aspects of PD
5.1. PD and Probabilities of Extinction — “Expected PD” Calculations

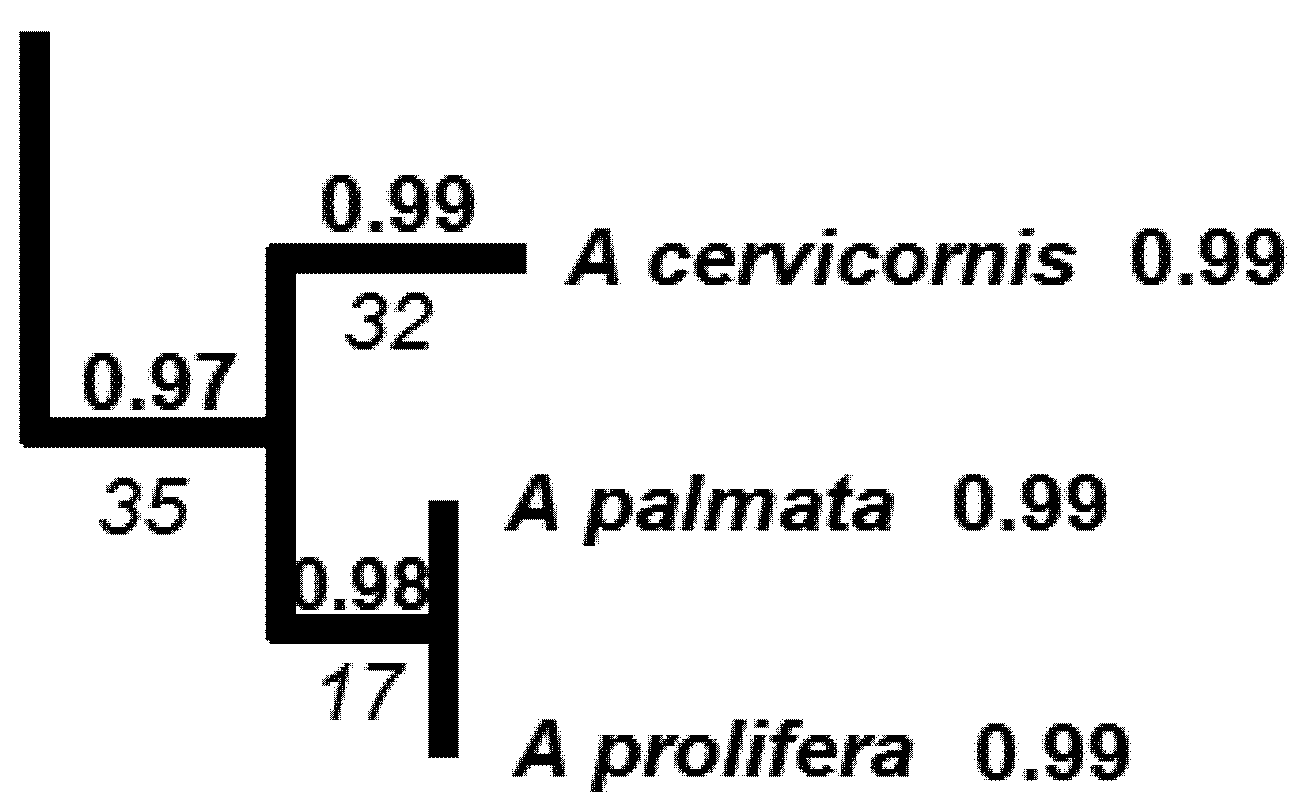

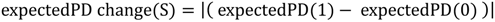
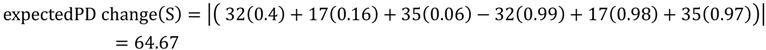
5.2. Phylogenetic Risk Analysis
5.3. Phylogenetic Spatial Homogeneity and Heterogeneity Analyses
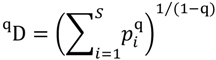
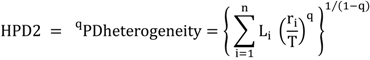
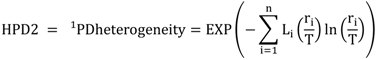


| Li | A | B | C |
|---|---|---|---|
| 32 | 2 | 1 | 2 |
| 17 | 8 | 8 | 8 |
| 35 | 9 | 9 | 9 |
| HPD2 | 67.7 | 64.6 | 68.2 |
6. Discussion
References
- Kappelle, M.; van Vuuren, M.M.I.; Baas, P. Effects of climate change on biodiversity: A review and identification of key research issues. Biodiv. Conserv. 1999, 8, 1383–1397. [Google Scholar] [CrossRef]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar] [CrossRef]
- Koh, L.P.; Dunn, R.R.; Sodhi, N.S.; Colwell, R.K.; Proctor, H.C.; Smith, V.S. Species co-extinctions and the biodiversity crisis. Science 2004, 305, 1632–1634. [Google Scholar]
- Botkin, D.B.; Saxe, H.; Araujo, M.B.; Betts, R.; Bradshaw, R.H.W.; Cedhagen, T.; Chesson, P.; Dawson, T.P.; Etterson, J.R.; Faith, D.P.; et al. Forecasting the effects of global warming on biodiversity. Bioscience 2007, 57, 227–236. [Google Scholar] [CrossRef]
- Kannan, R.; James, D.A. Effects of climate change on global biodiversity: A review of key literature. Trop. Ecol. 2009, 50, 31–39. [Google Scholar]
- Barnosky, A.D.; Matzke, N.; Tomiya, S.; Wogan, G.O.U.; Swartz, B.; Quental, T.B.; Marshall, C.; McGuire, J.L.; Lindsey, E.L.; Maguire, K.C.; et al. Has the Earth’s sixth mass extinction already arrived? Nature 2011, 471, 51–57. [Google Scholar]
- Bellard, C.; Bertelsmeier, C.; Leadley, P.; Thuiller, W.; Courchamp, F. Impacts of climate change on the future of biodiversity. Ecol. Lett. 2012, 15, 365–377. [Google Scholar] [CrossRef]
- Faith, D.P. Conservation evaluation and phylogenetic diversity. Biol. Conserv. 1992a, 61, 1–10. [Google Scholar] [CrossRef]
- Mace, G.M.; Gittleman, J.L.; Purvis, A. Preserving the tree of life. Science 2003, 300, 1707–1709. [Google Scholar] [CrossRef]
- Special Issue "Biological Implications of Climate Change". Available online: https://www.mdpi.com/journal/biology/special_issues/implications_climate (accessed on 11 December 2012).
- Sterling, E.J.; Gomez, A.; Porzecanski, A.L. A systemic view of biodiversity and its conservation: Processes, interrelationships, and human culture. Bioessays 2010, 32, 1090–1098. [Google Scholar] [CrossRef]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, A.; Chapin, F.S.; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. A safe operating space for humanity. Nature 2009, 461, 472–475. [Google Scholar] [CrossRef]
- Australian Academy of Science. To live within Earth’s limits. Australian Academy of Science: Canberra, Australia. Available online: http://www.science.org.au/natcoms/nc-ess/documents/ess-report2010.pdf (accessed on 11 December 2012).
- Faith, D.P. Biodiversity. The Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2007, Fall 2008 ed. Available online: http://plato.stanford.edu/archives/fall2008/entries/biodiversity (accessed on 29 June 2012).
- Future Earth — Research for Global Sustainability: Draft Research Framework. Available online: http://www.icsu.org/future-earth/whats-new/4th-transition-team-meeting/documents-2/research-framework (accessed on 11 December 2012).
- Sterman, J.D. Sustaining sustainability: Creating a systems science in a fragmented academy and polarized world. In Sustainability Science: The Emerging Paradigm and the Urban Environment; Springer: New York, NY, USA, 2012; pp. 21–58. [Google Scholar]
- International Union for Conservation of Nature World Conservation Strategy: Living Resource Conservation for Sustainable Development, International Union for Conservation of Nature and Natural Resources (IUCN): Gland, Switzerland, 1980.
- Faith, D.P.; Magallón, S.; Hendry, A.P.; Conti, E.; Yahara, T.; Donoghue, M.J. Evosystem Services: An evolutionary perspective on the links between biodiversity and human-well-being. Curr. Opin. Environ. Sustain. 2010, 2, 1–9. [Google Scholar] [CrossRef]
- Faith, D.P. Biodiversity and ecosystem services: Similar but different. Bioscience 2012, 62, 785. [Google Scholar]
- Faith, D.P. Common ground for biodiversity and ecosystem services: The "partial protection" challenge. F1000 Res. 2012, 1, 30. [Google Scholar]
- Faith, D.P. Regional Sustainability Analysis; CSIRO: Canberra, Australia, 1995. Available online: http://australianmuseum.net.au/document/Biodiversity-and-regional-sustainability-analysis/ (accessed on 11 December 2012).
- Faith, D.P. Biodiversity transcends services. Science 2010, 330, 1744–1745. [Google Scholar] [CrossRef]
- Carpenter, K.E.; Abrar, M.; Aeby, G.; Aronson, R.B.; Banks, S.; Bruckner, A.; Chiriboga, A.; Cortes, J.; Delbeek, J.C.; DeVantier, L.; et al. One-third of reef-building corals face elevated extinction risk from climate change and local impacts. Science 2008, 321, 560–563. [Google Scholar]
- Hughes, T.P.; Baird, A.H.; Bellwood, D.R.; Card, M.; Connolly, S.R.; Folke, C.; Grosberg, R.; Hoegh-Guldberg, O.; Jackson, J.B.C.; Kleypas, J.; et al. Climate change, human impacts, and the resilience of coral reefs. Science 2003, 301, 929–933. [Google Scholar]
- Mooney, H.; Larigauderie, A.; Cesario, M.; Elmquist, T.; Hoegh-Guldberg, O.; Lavorel, S.; Mace, G.M.; Palmer, M.; Scholes, R.; Yahara, T. Biodiversity, climate change, and ecosystem service. Cur.Opin. Environ. Sust. 2009, 1, 46–54. [Google Scholar] [CrossRef]
- Faith, D.P. Systematics and conservation: On predicting the feature diversity of subsets of taxa. Cladistics 1992, 8, 361–373. [Google Scholar] [CrossRef]
- Forest, F.; Grenyer, R.; Rouget, M.; Davies, T.J.; Cowling, R.M.; Faith, D.P.; Balmford, A.; Manning, J.C.; Proches, S.; van der Bank, M.; et al. Preserving the evolutionary potential of floras in biodiversity hotspots. Nature 2007, 445, 757–760. [Google Scholar]
- Faith, D.P. Phylogenetic diversity: A general framework for the prediction of feature diversity. In Systematics and Conservation Evauation; Clarendon Press: Oxford, UK, 1994; pp. 251–268. [Google Scholar]
- Faith, D.P.; Reid, C.A.M.; Hunter, J. Integrating phylogenetic diversity, complementarity, and endemism for conservation assessment. Conserv. Biol. 2004, 18, 255–261. [Google Scholar] [CrossRef]
- Bordewich, M.; Semple, C. Budgeted nature reserve selection with biodiversity feature loss and arbitrary split systems. J. Math. Biol. 2012, 64, 69–85. [Google Scholar] [CrossRef]
- Morlon, H.; Dylan, W.; Schwilk, J.A.; Bryant, P.A.; Marquet, A.G.; Rebelo, C.T.; Bohannan, B.J.M.; Green, J.L. Spatial patterns of phylogenetic diversity. Ecol. Lett. 2010, 14, 141–149. [Google Scholar]
- Smith, M.A.; Fisher, B.L. Invasions, DNA barcodes, and rapid biodiversity assessment using ants of Mauritius. Front. Zool. 2009, 6, 31. [Google Scholar] [CrossRef]
- Davies, T.J.; Buckley, L.B. Phylogenetic diversity as a window into the evolutionary and biogeographic histories of present-day richness gradients for mammals. Phil. Trans. R. Soc. B 2011, 366, 2414–2425. [Google Scholar]
- Nee, S.; May, R.M. Extinction and the loss of evolutionary history. Science 1997, 278, 692–694. [Google Scholar] [CrossRef]
- Parhar, R.K.; Mooers, A.O. Phylogenetically clustered extinction risks do not substantially prune the tree of life. PLoS One 2011, 6, e23528. [Google Scholar]
- Rodrigues, A.S.L.; Gaston, K.J. Maximising phylogenetic diversity in the selection of networks of conservation areas. Biol. Conserv. 2002, 105, 103–111. [Google Scholar] [CrossRef]
- Faith, D.P.; Williams, K.J. Phylogenetic diversity and biodiversity conservation. In McGraw-Hill Yearbook of Science and Technology; McGraw-Hill: New York, NY, USA, 2006; pp. 233–235. [Google Scholar]
- Thuiller, W.; Lavergne, S.; Roquet, C.; Boulangeat, I.; Lafourcade, B.; Araujo, M.B. Consequences of climate change on the tree of life in Europe. Nature 2011, 470, 531–534. [Google Scholar]
- Potter, K.M.; Woodall, C.W. Trends over time in tree and seedling phylogenetic diversity indicate regional differences in forest biodiversity change. Ecol. Appl. 2012, 22, 517–531. [Google Scholar] [CrossRef]
- Yesson, C.; Culham, A. A phyloclimatic study of cyclamen. BMC Evol. Biol. 2006, 6, 72. [Google Scholar]
- Sander, J.; Wardell-Johnson, G. Fine-scale patterns of species and phylogenetic turnover in a global biodiversity hotspot: Implications for climate change vulnerability. J. Vege. Sci. 2011, 22, 766–780. [Google Scholar] [CrossRef]
- Huang, S.; Davies, T.J.; Gittleman, J.L. How global extinctions impact regional biodiversity in mammals. Biol. Lett. 2011. [Google Scholar] [CrossRef]
- Willis, C.G.; Ruhfel, B.; Primack, R.B.; Miller-Rushing, A.J.; Davis, C.D. Phylogenetic patterns of species loss in Thoreau’s woods are driven by climate change. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 17029–17033. [Google Scholar]
- Baillie, J.E.M.; Hilton-Taylor, C.; Stuart, S.N. IUCN Red List of Threatened Species. A Global Species Assessment; IUCN: Gland, Switzerland and Cambridge, UK, 2004; p. 191. [Google Scholar]
- Huang, D. Threatened reef corals of the world. PLoS One 2012, 7, e34459. [Google Scholar] [CrossRef]
- Veron, J.E.N.; Wallace, C.C. Scleractinia of Eastern Australia, Part V. Family Acroporidae. AIMS Monograph Series 1984, 6, 485. [Google Scholar]
- Wallace, C.C. Staghorn Corals of the World: A Revision of the Genus Acropora; CSIRO Publishing: Melbourne, Australia, 1999. [Google Scholar]
- Veron, J.E.N. A biogeographic database of hermatypic corals. Aust. Inst. Marine Sci. Monogr. Ser. 1993, 10, 433. [Google Scholar]
- Veron, J.E.N. Corals of the World; Australian Institute of Marine Science: Townsville, Australia, 2012. Available online: http://coral.aims.gov.au/ (accessed on 11 December 2012).
- Wallace, C.C.; Richards, Z.; Suharsono. Regional distribution patterns of Acropora in Indonesia and their use in conservation. Indones. J. Coast. Mar. Res. 2001, 1, 40–58. [Google Scholar]
- Marshall, P.A.; Baird, A.H. Bleaching of corals on the Great Barrier Reef: Differential susceptibilities among taxa. Coral Reefs 2000, 19, 155–163. [Google Scholar] [CrossRef]
- Sutherland, K.P.; Porter, J.; Torres, C. Disease and immunity in Caribbean and Indo-Pacific zooxanthellate corals. Mar. Ecol. Prog. Ser. 2004, 266, 273–302. [Google Scholar] [CrossRef]
- Bruno, J.F.; Selig, E.R.; Casey, K.S.; Page, C.A.; Willis, B.L.; Harvell, C.D.; Sweatman, H.; Melendy, A.M. Thermal stress and coral cover as drivers of coral disease outbreaks. PLoS Biol. 2007, 5, e124. [Google Scholar] [CrossRef]
- Wallace, C.C.; Done, B.J.; Muir, P.R. Revision and catalogue of worldwide staghorn corals of Acropora and Isopora (Scleractinia: Acroporidae) in the Museum of Tropical Queensland. Mem. Queensl. Mus. Nat. 2012, 57, 1–255. [Google Scholar]
- International Commission of Zoological Nomenclature. Coral taxon names published in 'Corals of the world' by J.E.N. Veron (2000): Potential availability confirmed under Article 86.1.2. Bull. Zool. Nom. 2011, 68, 162–166.
- Ditlev, H. New scleractinian corals (Cnidaria: Anthozoa) from Sabah, North Borneo. Description of one new genus and eight new species, with notes on their taxonomy and ecology. Zool. Meded. Leiden 2003, 77, 193–219. [Google Scholar]
- Richards, Z.T.; Wallace, C.C. Acropora rongelapensis sp. nov., a new species of Acropora from the Marshall Islands (Scleractinia: Astrocoeniina: Acroporidae). Zootaxa 2004, 590, 1–5. [Google Scholar]
- Claereboudt, M.R. Reef Corals and the Coral Reefs of the Gulf of Oman; Al-Roya Publishing: Muscat, Oman, 2006; p. 344. [Google Scholar]
- Wallace, C.C.; Phongsuwan, N.; Muir, P.R. A new species of staghorn coral, Acropora sirikitiae sp. Nov. (Scleractinia: Astrocoeniina: Acroporidae) from western Thailand. Phuk. Mar. Biol. Cent. Res. Bull. 2012, 71, 117–124. [Google Scholar]
- Van Oppen, M.J.H.; McDonald, B.J.; Willis, B.L.; Miller, D.J. The evolutionary history of the coral genus Acropora (Scleractinia, Cnidaria) based on a mitochondrial and a nuclear marker: Reticulation, incomplete lineage sorting, or morphological convergence? M. Biol. Evol. 2001, 18, 1315–1329. [Google Scholar] [CrossRef]
- Márquez, L.M.; van Oppen, M.J.H.; Willis, B.L.; Reyes, A.; Miller, D.J. The highly cross-fertile coral species, Acropora hyacinthus and A. cytherea, constitute statistically distinguishable lineages. Mol. Ecol. 2002, 11, 1339–1349. [Google Scholar] [CrossRef]
- Richards, Z.T.; van Oppen, M.J.H.; Wallace, C.C.; Willis, B.L.; Miller, D.J. Some rare Indo-Pacific coral species are probable hybrids. PLoS One 2008, 3, e3240. [Google Scholar]
- The IUCN red list of threatened species. Available online: http://www.iucnredlist.org/ (accessed on 11 December 2012).
- Status of the Coral Reefs of the World: 2004; Wilkinson, C. (Ed.) Global Coral Reef Monitoring Network and Australian Institute of Marine Science: Townsville, Qld, Australia, 2004.
- Mooers, A.O.; Faith, D.P.; Maddison, W.P. Converting endangered species categories to probabilities of extinction for phylogenetic conservation prioritization. PLoS One 2008, 3, e3700. [Google Scholar]
- Ordorico, D.M.; Miller, D.J. Variation in the ribosomal internal transcribed spacers and 5.8S rDNA among five species of Acropora (Cnidaria; Scleractinia): Patterns of variation consistent with reticulate evolution. Mol. Biol. Evol. 1997, 14, 465–473. [Google Scholar] [CrossRef]
- Van Oppen, M.J.H.; Willis, B.L.; van Rheede, T.; Miller, D.J. Spawning times, reproductive compatibilities and genetic structuring in the Acropora aspera group: Evidence for natural hybridisation and semi-permeable species boundaries in corals. Mol. Ecol. 2002, 11, 1363–1376. [Google Scholar] [CrossRef]
- Márquez, L.M.; Miller, D.J.; MacKenzie, J.B.; van Oppen, M.J.H. Pseudogenes Contribute to the Extreme diversity of nuclear ribosomal DNA in the Hard Coral Acropora. Mol. Biol. Evol. 2003, 20, 1077–1086. [Google Scholar] [CrossRef]
- Wei, N.V.; Wallace, C.C.; Dai, C.F.; Moothien Pillay, K.R.; Chen, C.A. Analysis of the roboomal internal transcribed spacers (ITS) and the 5.8S Gene indicate that extremely high rDNA heterogeneity is a unique feature in the scleractinian coral genus Acropora (Scleractinia: Acroporidae). Zool. Stud. 2006, 45, 404–418. [Google Scholar]
- Vollmer, S.V.; Palumbi, S.R. Testing the utility of internally transcribed spacer sequences in coral phylogenetics. Mol. Ecol. 2004, 13, 2763–2772. [Google Scholar] [CrossRef]
- Wang, W.; Omori, M.; Hayashibara, T.; Shimoike, K.; Hatta, M.; Sugiyama, T.; Fujisawa, T. Isolation and characterization of a mini-collagen gene enconding a nematocyst capsule protein from a reef-building coral, Acropora donei. Gene 1995, 152, 195–200. [Google Scholar] [CrossRef]
- Hayward, D.C.; Catmul, J.; Reece-Hoyes, J.S.; Berghammer, H.; Dodd, H.; Hann, S.J.; Miller, D.J.; Ball, E.E. Gene structure and larval expression of cnox-2Am from the coral Acropora millepora. Dev. Genes Evol. 2001, 211, 10–19. [Google Scholar] [CrossRef]
- Vollmer, S.V.; Palumbi, S.R. Hybridization and the evolution of coral reef diversity. Science 2002, 296, 2023–2025. [Google Scholar] [CrossRef]
- Tavare, S. Lines of descent and genealogical processes, and their application in population genetics models. Theor. Pop. Biol. 1984, 26, 119–164. [Google Scholar] [CrossRef]
- Nucleotide. Available online: http://www.ncbi.nlm.nih.gov/nuccore/ (accessed on 11 December 2012).
- Tamura, K.; Peterson, D.; Peterson, N.; Stecher, G.; Nei, M.; Kumar, S. EGA5: Molecular evolutionary genetics analysis using maximum likelihood, evolutionary distance, and maximum parsimony methods. Mol. Biol. Evol. 2011, 28, 2371–2739. [Google Scholar] [CrossRef]
- Richards, Z.T.; Wallace, C.C.; Miller, D.J. Archetypal ‘elkhorn’ coral discovered in the Pacific Ocean. Syst. Biol. 2010, 8, 281–288. [Google Scholar]
- Fleury, I.M.S. Genetic Isolation and spawning times of some mass-spawning Acropora species: Coincidence or correlation? Ph.D. Thesis, Zoological Institute of Basel, Basel, Switzerland, 2004. [Google Scholar]
- Hemond, E.M.; Vollmer, S.V. Genetic diversity and connectivity in the threatened staghorn coral (Acropora cervicornis) in Florida. PLoS One 2010 5, e8652.
- Wolstenholme, J.K.; Wallace, C.C.; Chen, C.A. Species boundaries within the Acropora humilis species group (Cnidaria; Scleractinia): A morphological and molecular interpretation of evolution. Coral Reefs 2003, 22, 155–166. [Google Scholar] [CrossRef]
- Suzuki, G.; Hayashibara, T.; Shirayama, Y.; Fukami, H. Evidence of species-specific habitat selectivity of Acropora corals based on identification of new recruits by two molecular markers. Mar. Ecol. Prog. Ser. 2008, 355, 149–159. [Google Scholar] [CrossRef]
- Suzuki, G.; Fukami, H. Evidence of genetic and reproductive isolation between two morphs of a subtropical coral Acropora solitaryensis in the non-reef region of Japan. Zool. Sci. 2012, 29, 134–140. [Google Scholar] [CrossRef]
- Kimura, M. A simple method for estimating evolutionary rate of base substitutions through comparative studies of nucleotide sequences. J. Mol. Evol. 1980, 16, 111–120. [Google Scholar] [CrossRef]
- Isaac, N.J.B.; Turvey, S.T.; Collen, B.; Waterman, C.; Baillie, J.E.M. Mammals on the EDGE: Conservation priorities based on threat and phylogeny. PLoS One 2007, 2, e296. [Google Scholar] [CrossRef]
- Faith, D.P. Threatened species and the preservation of phylogenetic diversity (PD): Assessments based on extinction probabilities and risk analysis. Conserv. Biol. 2008, 22, 1461–1470. [Google Scholar] [CrossRef]
- Witting, L.; Loeschcke, V. The optimization of biodiversity conservation. Biol. Conserv. 1995, 71, 205–207. [Google Scholar] [CrossRef]
- Faith, D.P. Phylogenetic diversity and conservation. In Conservation Biology: Evolution in Action; Carroll, S.P., Fox, C., Eds.; Oxford University Press: New York, NY, USA, 2008; pp. 99–115. [Google Scholar]
- Weitzman, M.L. The Noah’s Ark problem. Econometrica 1998, 66, 1279–1298. [Google Scholar] [CrossRef]
- Olden, J.D.; Poff, N.L.; Marlis, R.; Douglas, M.E.; Douglas, K.; Fausch, D. Ecological and evolutionary consequences of biotic homogenization. Tr. Ecol. Evol. 2004, 19, 18–24. [Google Scholar] [CrossRef]
- Lozupone, C.; Knight, R. UniFrac: A new phylogenetic method for comparing microbial communities. Appl. Envir. Microbiol. 2005, 71, 8228–8235. [Google Scholar] [CrossRef]
- Nipperess, D.A.; Faith, D.P.; Barton, K. Resemblance in phylogenetic diversity among ecological assemblages. J. Veg. Sci. 2010, 21, 809–820. [Google Scholar] [CrossRef]
- Veron, J.E.N.; Turak, E.; DeVantier, L.M.; Stafford-Smith, M.G.; Kininmonth, S. Coral Geographic, version 1.1. Available online: http://www.coralgeographic.com (accessed on 7 June 2012).
- Chao, A.; Chiu, C.; Jost, L. Phylogenetic diversity measures based on Hill numbers. Phil. Trans. R. Soc. B 2010, 365, 3599–3609. [Google Scholar] [CrossRef]
- Hill, M.O. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Winter, M.; Devictor, V.; Schweiger, O. Phylogenetic diversity and nature conservation: Where are we? Tr. Ecol. Evol. 2012, in press. [Google Scholar]
- Srivastava, D.S.; Cadotte, M.W.; Andrew, A.; MacDonald, M.; Marushia, R.G.; Mirotchnick, N. Phylogenetic diversity and the functioning of ecosystems. Ecol. Lett. 2012, 15, 637–648. [Google Scholar] [CrossRef]
- Walker, P.A.; Faith, D.P. Diversity-PD: Procedures for conservation evaluation based on phylogenetic diversity. Biodiv. Lett. 1994, 2, 132–139. [Google Scholar] [CrossRef]
- Billionnet, A. Solution of the generalized Noah’s Ark problem. Syst. Biol. 2012. [Google Scholar] [CrossRef]
- May-Collado, L.J.; Agnarsson, I. Phylogenetic analysis of conservation priorities for aquatic mammals and their terrestrial relatives, with a comparison of methods. PLoS One 2011, 6, e22562. [Google Scholar] [CrossRef]
- Swenson, N.G. Phylogenetic resolution and quantifying the phylogenetic diversity and dispersion of communities. PLoS One 2009, 4, e4390. [Google Scholar] [CrossRef]
- Jones, R.T.; Robeson, M.S.; Lauber, C.L.; Hamady, M.; Knight, R.; Fierer, N. A comprehensive survey of soil acidobacterial diversity using pyrosequencing and clone library analyses. ISME J. 2009, 3, 442–453. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Faith, D.P.; Richards, Z.T. Climate Change Impacts on the Tree of Life: Changes in Phylogenetic Diversity Illustrated for Acropora Corals. Biology 2012, 1, 906-932. https://doi.org/10.3390/biology1030906
Faith DP, Richards ZT. Climate Change Impacts on the Tree of Life: Changes in Phylogenetic Diversity Illustrated for Acropora Corals. Biology. 2012; 1(3):906-932. https://doi.org/10.3390/biology1030906
Chicago/Turabian StyleFaith, Daniel P., and Zoe T. Richards. 2012. "Climate Change Impacts on the Tree of Life: Changes in Phylogenetic Diversity Illustrated for Acropora Corals" Biology 1, no. 3: 906-932. https://doi.org/10.3390/biology1030906
APA StyleFaith, D. P., & Richards, Z. T. (2012). Climate Change Impacts on the Tree of Life: Changes in Phylogenetic Diversity Illustrated for Acropora Corals. Biology, 1(3), 906-932. https://doi.org/10.3390/biology1030906