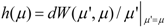An Eco-Evolutionary Model for Demographic and Phenological Responses in Migratory Birds
Abstract
:1. Introduction
2. Model and Methods
2.1. Model for Population Dynamics and Phenological Adaptation









2.2. Analysis




2.3. Ecological and Evolutionary Equilibrium
2.4. Studying Effects of Environmental Change in This System
3. Results
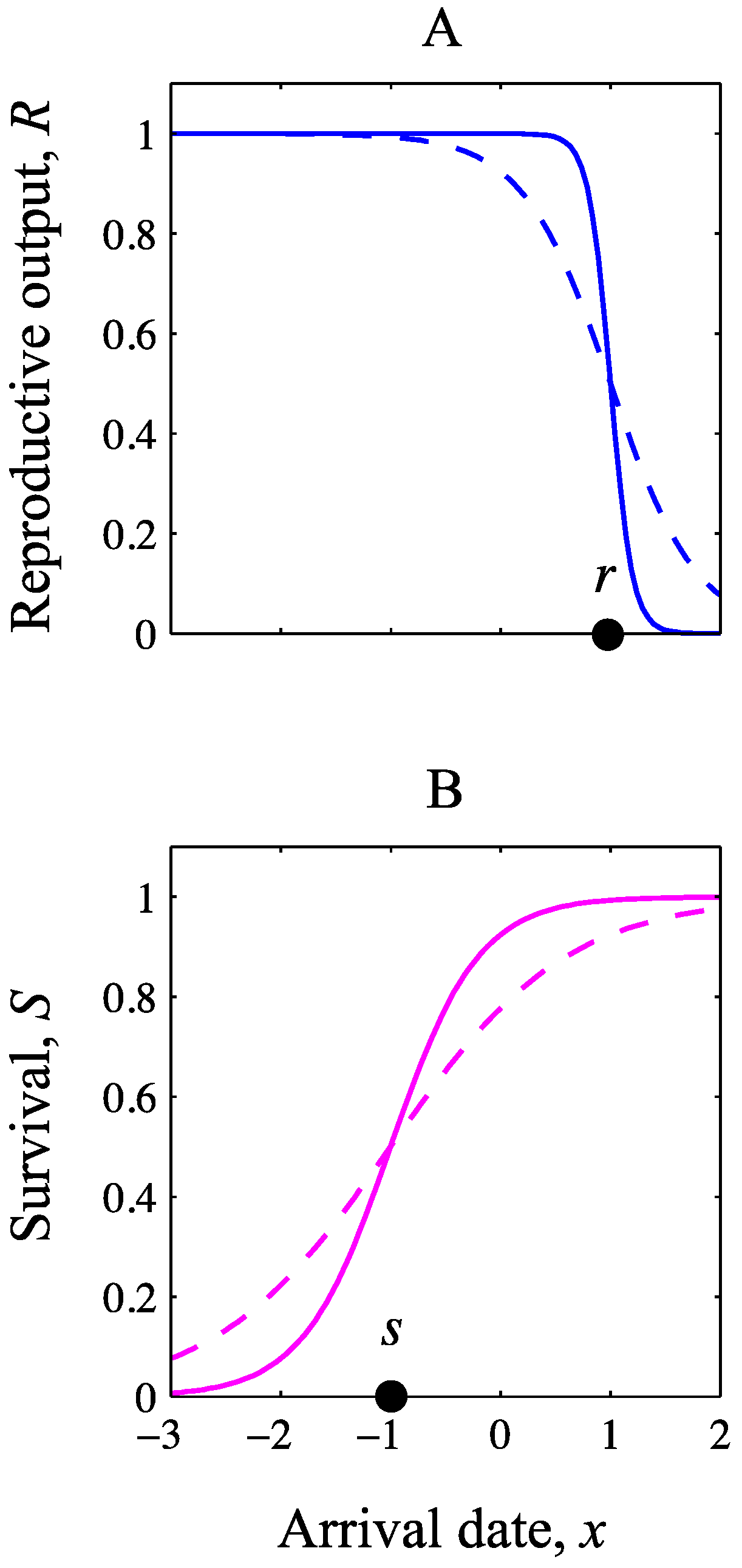
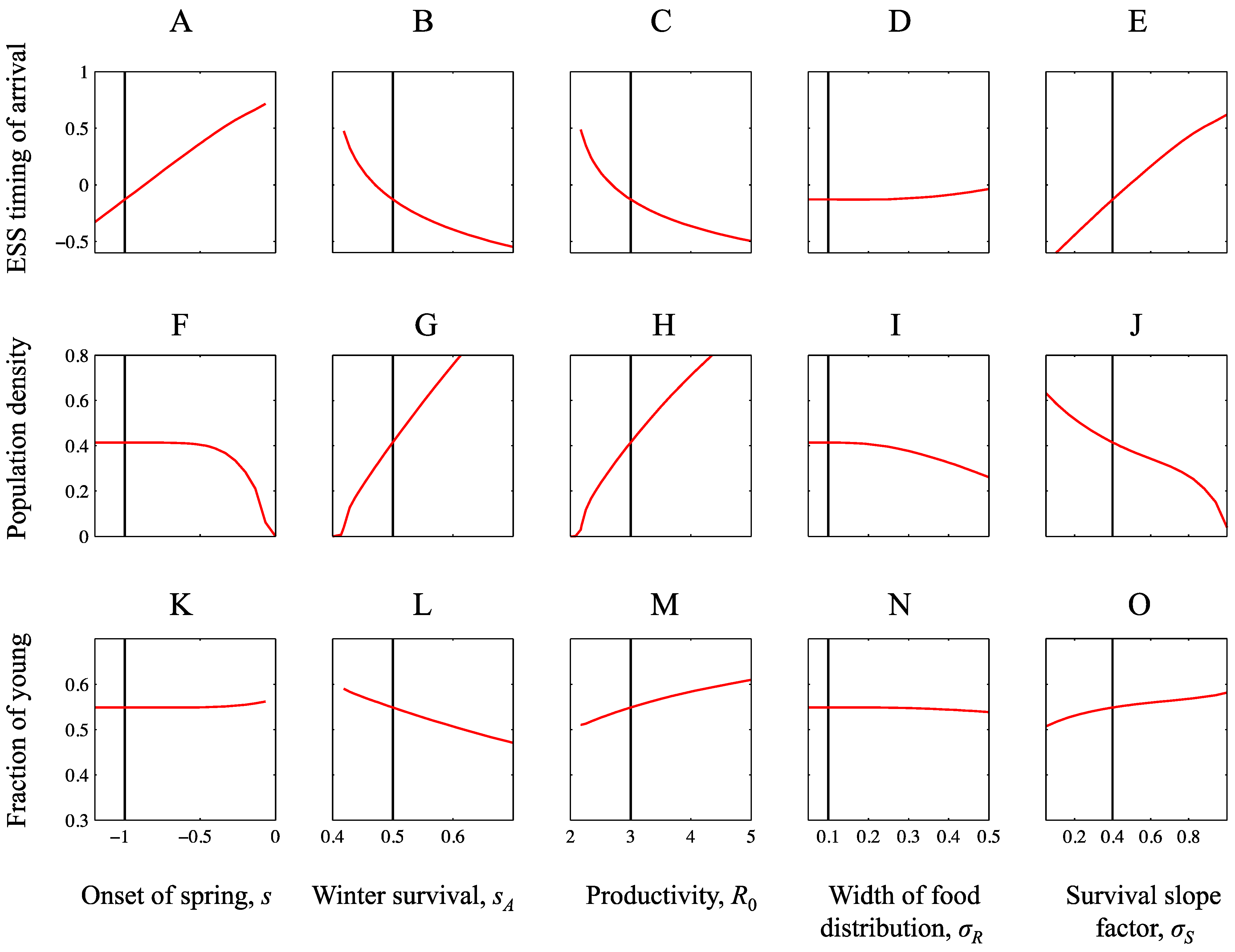
3.1. Ensuing Selection Pressures after Seasonal Changes

3.2. Equilibrium Population Density after Seasonal Changes
3.3. Equilibrium Population Structure after Seasonal Changes
4. Discussion
4.1. Summary of the Results and Their Significance
4.2. Comparisons with Observed Patterns of Phenological Adaptation
5. Future Research on Eco-Evolutionary Dynamics in Phenological Shifts
Acknowledgments
References and Notes
- Lehikoinen, E.; Sparks, T.H.; Zalakevicius, M. Arrival and departure dates. Adv. Ecol. Res. 2004, 35, 1–31. [Google Scholar] [CrossRef]
- Parmesan, C. Ecological and evolutionary responses to recent climate change. Ann. Rev. Ecol. Evol. Syst. 2006, 37, 637–669. [Google Scholar] [CrossRef]
- Gordo, O. Why are bird migration dates shifting? A review of weather and climate effects on avian migratory phenology. Clim. Res. 2007, 35, 37–58. [Google Scholar] [CrossRef]
- Rubolini, D.; Møller, A.P.; Rainio, K.; Lehikoinen, E. Intraspecific consistency and geographic variability in temporal trends of spring migration phenology among European bird species. Clim. Res. 2007, 35, 135–146. [Google Scholar] [CrossRef]
- Both, C.; Visser, M.E. Adjustment to climate change is constrained by arrival date in a long-distance migrant bird. Nature 2001, 411, 296–298. [Google Scholar]
- Møller, A.P.; Rubolini, D.; Lehikoinen, E. Populations of migratory bird species that did not show a phenological response to climate change are declining. Proc. Natl. Acad. Sci. USA 2008, 105, 16195–16200. [Google Scholar] [CrossRef]
- Jones, T.; Cresswell, W. The phenology mismatch hypothesis: Are declines of migrant birds linked to uneven global climate change? J. Appl. Ecol. 2010, 79, 98–108. [Google Scholar] [CrossRef]
- Saino, N.; Ambrosini, R.; Rubolini, D.; von Hardenberg, J.; Provenzale, A.; Hüppop, K.; Hüppop, O.; Lehikoinen, A.; Lehikoinen, E.; Rainio, K.; et al. Climate warming, ecological mismatch at arrival and population decline in migratory birds. Proc. R. Soc. Lond. B 2011, 278, 835–842. [Google Scholar] [CrossRef]
- Miller-Rushing, A.J.; Høye, T.T.; Inouye, D.W.; Post, E. The effects of phenological mismatches on demography. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 3177–3186. [Google Scholar] [CrossRef]
- Ådahl, E.; Lundberg, P.; Jonzén, N. From climate change to population change: The need to consider annual life cycles. Glob. Change Biol. 2006, 12, 1627–1633. [Google Scholar] [CrossRef]
- Singer, M.C.; Parmesan, C. Phenological asynchrony between herbivorous insects and their hosts: Signal of climate change or pre-existing adaptive strategy? Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 3161–3176. [Google Scholar] [CrossRef]
- Goodenough, A.E.; Elliot, S.L.; Hart, A.G. The challenges of conservation for declining migrants: Are reserve-based initiatives during the breeding season appropriate for the pied flycatcher Ficedula hypoleuca? Ibis 2009, 151, 429–439. [Google Scholar]
- Both, C.; Te Marvelde, L. Climate change and timing of avian breeding and migration throughout Europe. Clim. Res. 2007, 35, 93–105. [Google Scholar] [CrossRef]
- Goodenough, A.E.; Hart, A.G.; Stafford, R. Is adjustment of breeding phenology keeping pace with the need for change? Linking observed response in woodland birds to changes in temperature and selection pressure. Clim. Change 2010, 102, 687–697. [Google Scholar] [CrossRef] [Green Version]
- Visser, M.E.; Both, C. Shifts in phenology due to global climate change: The need for a yardstick. Proc. R. Soc. Lond. B 2005, 272, 2561–2569. [Google Scholar] [CrossRef]
- McNamara, J.M.; Houston, A.I. Optimal annual routines:behaviour in the context of physiology and ecology. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2008, 363, 301–319. [Google Scholar] [CrossRef]
- Hedenström, A.; Barta, Z.; Helm, B.; Houston, A.I.; McNamara, J.M.; Jonzén, N. Migration speed and scheduling of annual events by migrating birds in relation to climate change. Clim. Res. 2007, 35, 79–91. [Google Scholar] [CrossRef]
- Barta, Z.; McNamara, J.M.; Houston, A.I.; Weber, T.P.; Hedenström, A.; Feró, O. Optimal moult strategies of migratory birds. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2008, 363, 211–230. [Google Scholar] [CrossRef]
- Kokko, H. Competition for early arrival in migratory birds. J. Anim. Ecol. 1999, 68, 940–950. [Google Scholar] [CrossRef]
- Jonzén, N.; Hedenström, A.; Lundberg, P. Climate change and the optimal arrival of migratory birds. Proc. R. Soc. Lond. B 2007, 274, 269–274. [Google Scholar] [CrossRef]
- Johansson, J.; Jonzén, N. Effects of territory competition and climate change on timing of arrival to breeding grounds: A game-theory approach. Am. Nat. 2012, 179, 463–474. [Google Scholar] [CrossRef]
- Johansson, J.; Jonzén, N. Game theory sheds new light on ecological responses to current climate change when phenology is historically mismatched. Ecol. Lett. 2012, 15, 881–888. [Google Scholar] [CrossRef]
- Lack, E. Breeding season and clutch-size of the wood warbler. Ibis 1950, 92, 95–98. [Google Scholar] [CrossRef]
- Wiklund, C.; Fagerström, T. Why do males emerge before females? A hypothesis to explain the incidence of protandry in butterflies. Oecologia 1977, 31, 153–158. [Google Scholar] [CrossRef]
- Zonneveld, C.; Metz, J.A.J. Models on butterfly protandry: Virgin females are at risk to die. Theor. Pop. Biol. 1991, 40, 308–321. [Google Scholar] [CrossRef]
- Knudsen, E.; Lindén, A.; Ergon, T.; Jonzén, N.; Vik, J.O.; Knape, J.; Røer, J.E.; Stenseth, N.C. Characterizing bird migration phenology using data from standardized monitoring at bird observatories. Clim. Res. 2007, 35, 59–77. [Google Scholar] [CrossRef]
- Geritz, S.A.H.; Kisdi, É.; Meszéna, G.; Metz, J.A.J. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 1998, 12, 35–57. [Google Scholar]
- McGill, B.J.; Brown, J.S. Evolutionary game theory and adaptive dynamics of continuous traits. Ann. Rev. Ecol. Evol. Syst. 2007, 38, 403–435. [Google Scholar] [CrossRef]
- Abrams, P.A.; Matsuda, H.; Harada, Y. Evolutionarily unstable fitness maxima and stable fitness minima of continuous traits. Evol. Ecol. 1993, 7, 465–487. [Google Scholar] [CrossRef]
- Waxman, D.; Gavrilets, S. Issues of terminology, gradient dynamics, and the ease of sympatric speciation in Adaptive Dynamics. J. Evol. Biol. 2005, 18, 1214–1219. [Google Scholar] [CrossRef]
- Johansson, J. Evolutionary responses to environmental changes: How does competition affect adaptation? Evolution 2008, 62, 421–435. [Google Scholar] [CrossRef]
- Marino, G.P.; Kaiser, D.P.; Gu, L.; Ricciuto, D.M. Reconstruction of false spring occurrences over the southeastern United States, 1901–2007: An increasing risk of spring freeze damage? Environ. Res. Lett. 2011, 6, 93–101. [Google Scholar]
- Both, C.; Artemyev, A.V.; Blaauw, B.; Cowie, R.J.; Dekhuijzen, A.J.; Eeva, T.; Enemar, A.; Gustafsson, L.; Ivankina, E.V.; Järvinen, A.; et al. Large-scale geographical variation confirms that climate change causes birds to lay earlier. Proc. R. Soc. Lond. B 2004, 271, 1657–1662. [Google Scholar] [CrossRef]
- Curry-Lindahl, K. Bird Migration in Africa; Academic Press: London, UK, 1981. [Google Scholar]
- Lundberg, A.; Alatalo, R.V. The Pied Flycatcher. In Mating and Reproductive Strategies; Academic Press: London, UK, 1992. [Google Scholar]
- Both, C.; Bouwhuis, S.; Lessells, C.M.; Visser, M.E. Climate change and population declines in a long-distance migratory bird. Nature 2006, 441, 81–83. [Google Scholar]
- Laaksonen, T.; Ahola, M.; Eeva, T.; Väisänen, R.A.; Lehikoinen, E. Climate change, migratory connectivity and changes in laying date and clutch size of the pied flycatcher. Oikos 2006, 114, 277–290. [Google Scholar] [CrossRef]
- Ahola, M.P.; Laaksonen, T.; Sippola, K.; Eeva, T.; Rainio, K.; Lehikoinen, E. Variation in climate warming along the migration route uncouples arrival and breeding dates. Glob. Change Biol. 2004, 10, 1610–1617. [Google Scholar] [CrossRef]
- Goodenough, A.E.; Hart, A.G.; Elliot, S.L. What prevents phenological adjustment to climate change in migrant bird species? Evidence against the “arrival constraint” hypothesis. Int. J. Biometeorol. 2011, 55, 97–102. [Google Scholar]
- McCleery, R.H.; Perrins, C.M. Temperature and egglaying trends. Nature 1998, 391, 30–31. [Google Scholar] [CrossRef]
- Forsman, J.T.; Thomson, R.L.; Seppanen, J.T. Mechanisms and fitness effects of interspecific information use between migrant and resident birds. Behav. Ecol. 2007, 18, 888–894. [Google Scholar] [CrossRef]
- Török, J.; Tóth, L. Asymmetric competition between two tit species: A reciprocal removal experiment. J. Anim. Ecol. 1999, 68, 338–345. [Google Scholar] [CrossRef]
- Visser, M.E.; Caro, S.P.; van Oers, K.; Schaper, S.V.; Helm, B. Phenology, seasonal timing and circannual rhythms: Towards a unified framework. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 3113–3127. [Google Scholar]
- Dieckmann, U.; Law, R. The dynamical theory of coevolution: A derivation from stochastic ecological processes. J. Math. Biol. 1996, 34, 579–612. [Google Scholar] [CrossRef]
- Bürger, R.; Lynch, M. Evolution and extinction in changing environment: A quantitative genetic analysis. Evolution 1995, 49, 151–163. [Google Scholar] [CrossRef]
- Vincent, T.L.; Brown, J.S. Evolutionary Game Theory, Natural Selection and Darwinian Dynamics; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Johansson, J.; Smallegange, I.M.; Jonzén, N. An Eco-Evolutionary Model for Demographic and Phenological Responses in Migratory Birds. Biology 2012, 1, 639-657. https://doi.org/10.3390/biology1030639
Johansson J, Smallegange IM, Jonzén N. An Eco-Evolutionary Model for Demographic and Phenological Responses in Migratory Birds. Biology. 2012; 1(3):639-657. https://doi.org/10.3390/biology1030639
Chicago/Turabian StyleJohansson, Jacob, Isabel M. Smallegange, and Niclas Jonzén. 2012. "An Eco-Evolutionary Model for Demographic and Phenological Responses in Migratory Birds" Biology 1, no. 3: 639-657. https://doi.org/10.3390/biology1030639