Computational Tools and Approaches for Design and Control of Coating and Composite Color, Appearance, and Electromagnetic Signature
Abstract
:1. Introduction
1.1. Direct versus Inverse Solutions to Electromagnetic Radiation Transport Problems
1.2. The Geometric Limit and Its Implications
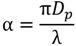
1.3. Defining a Computational Photon
2. Surface Scattering Approaches
2.1. Kirchhoff Scattering, Davies Scattering, and Beckmann Scattering
2.2. Geometric Optics Ray Tracing and Nanoscale Surface Roughness
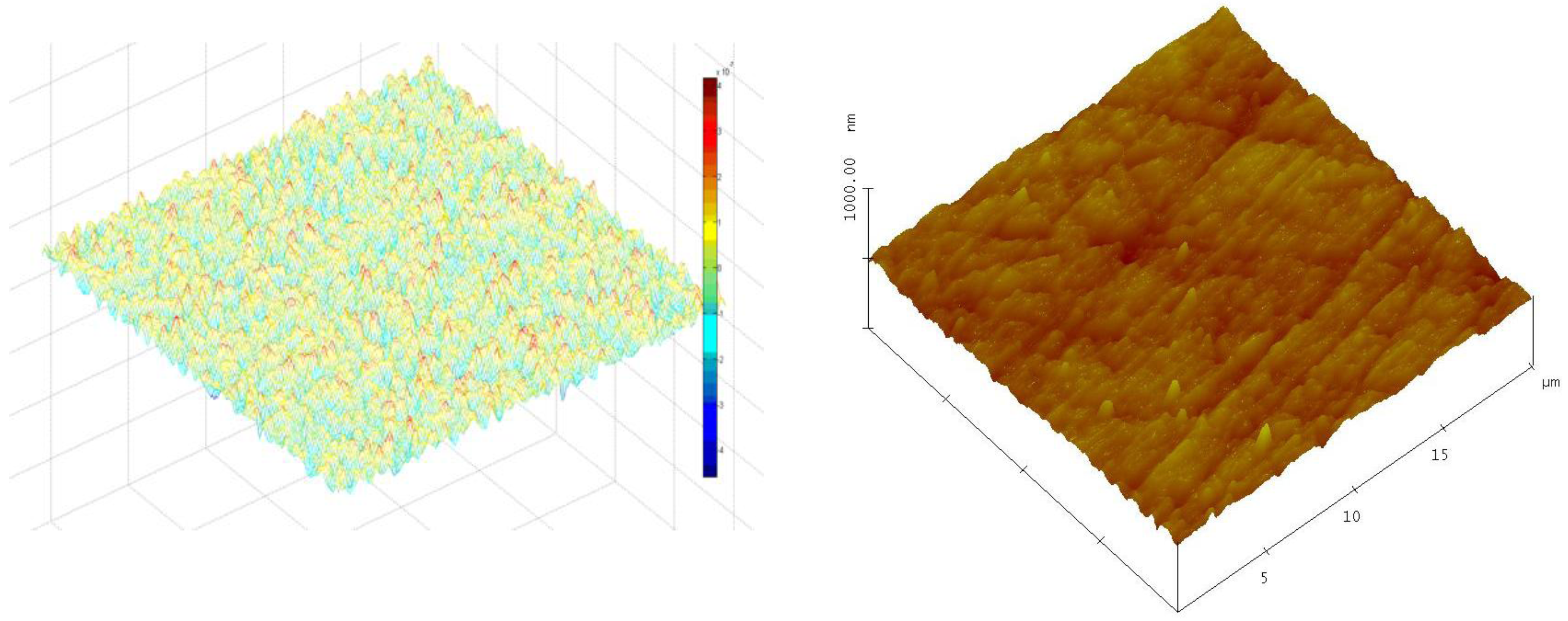
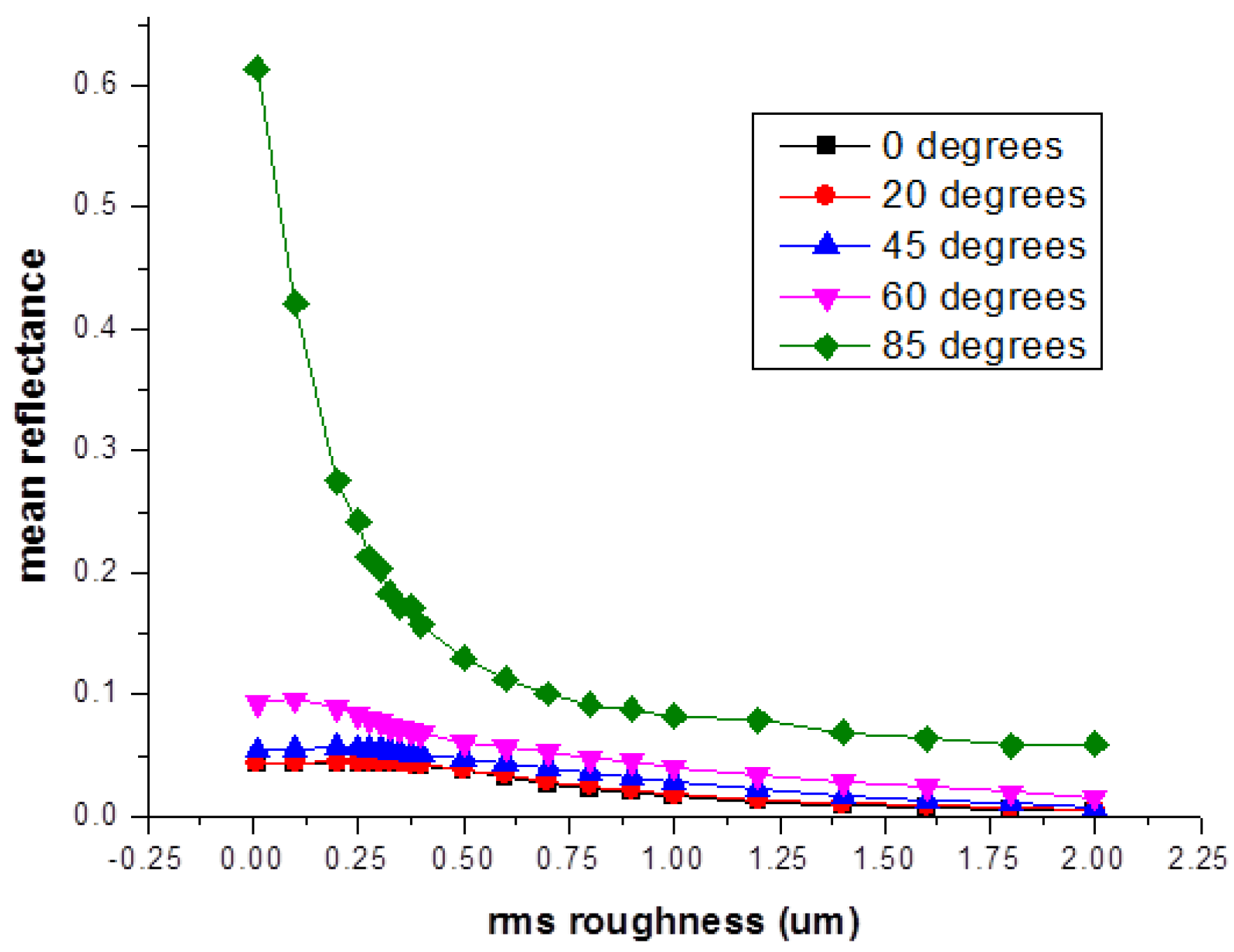
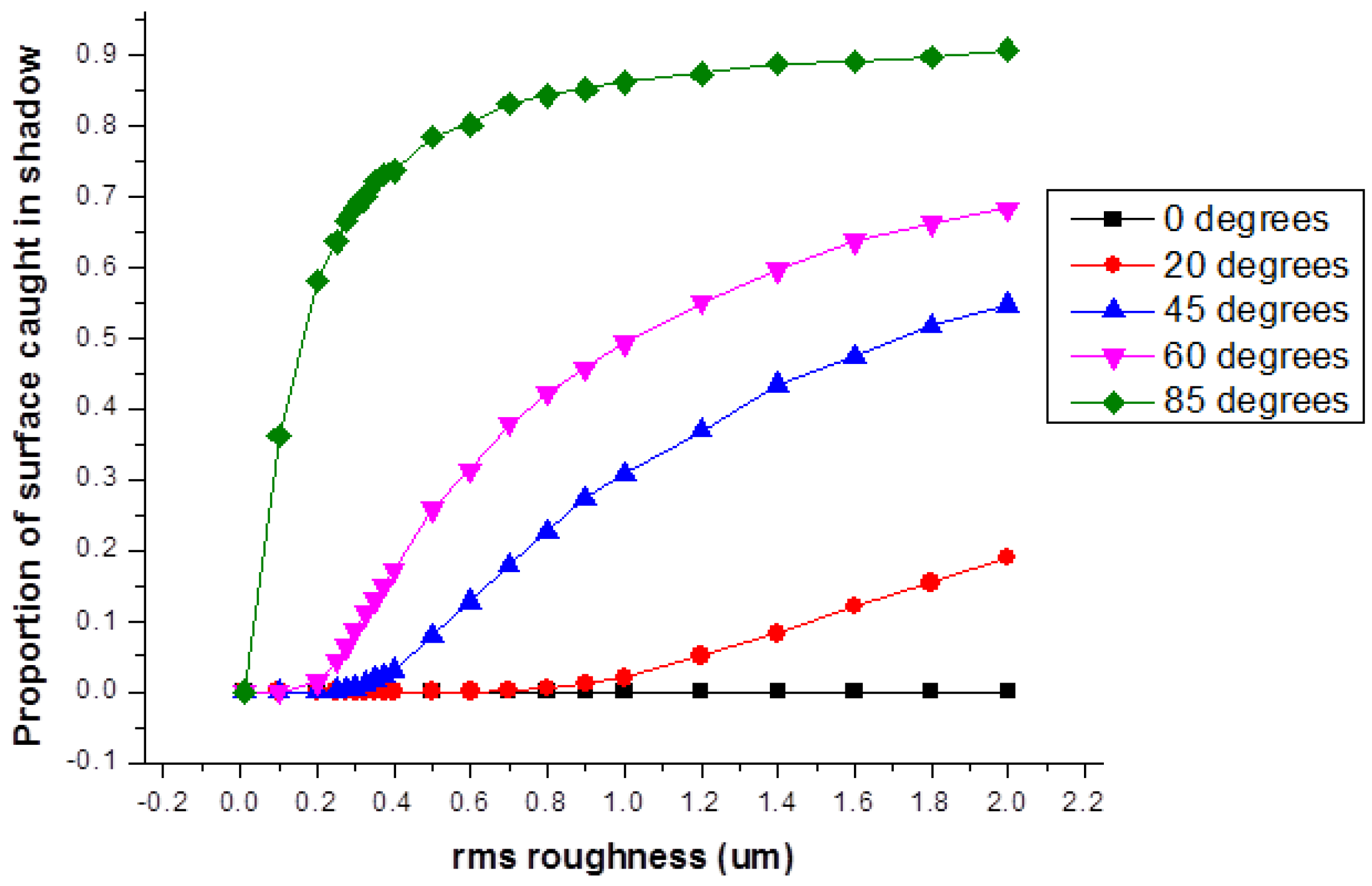
2.3. Surface Scattering Simulation Results
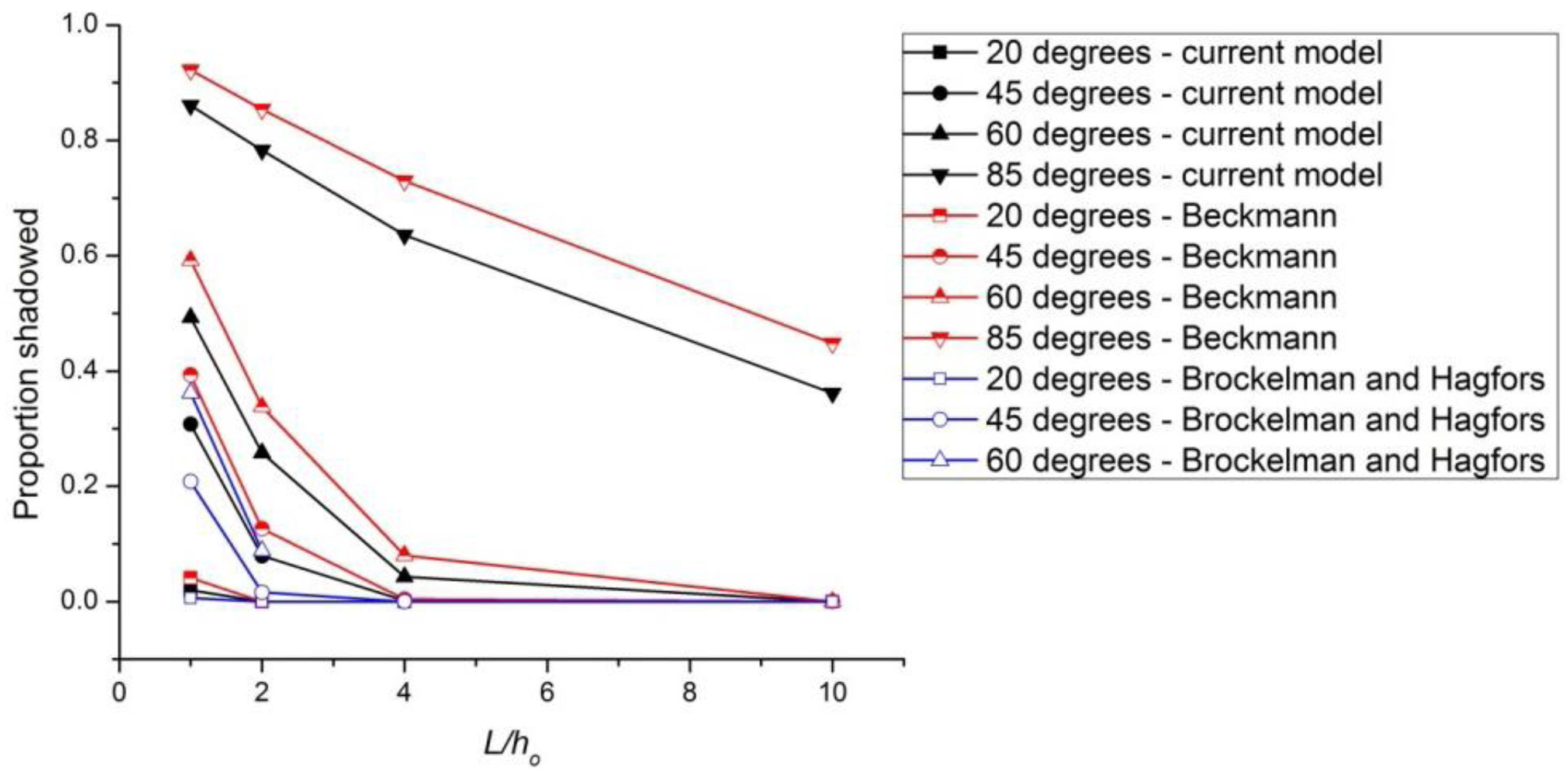
2.4. Further Reading
3. Bulk Scattering Approaches
3.1. Mie Theory Scattering
3.2. Kubelka-Munk Theory: A Two-Flux Scattering Model
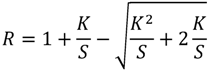
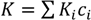 ,
, 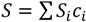 .
.3.3. Finite Element Solutions to Maxwell’s Equations
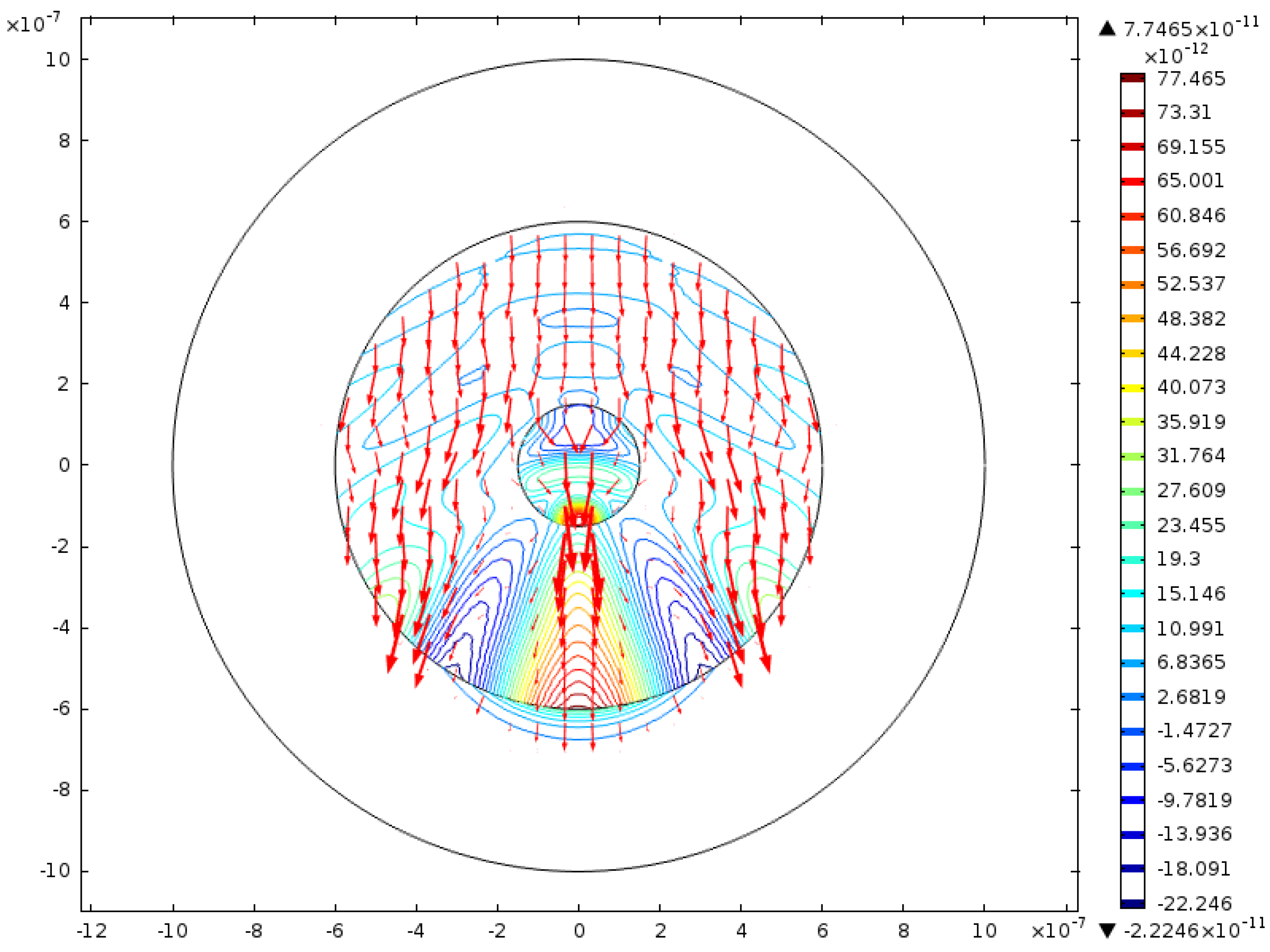
3.4. Inclusions to Consider in a Finite Element Scattering Module
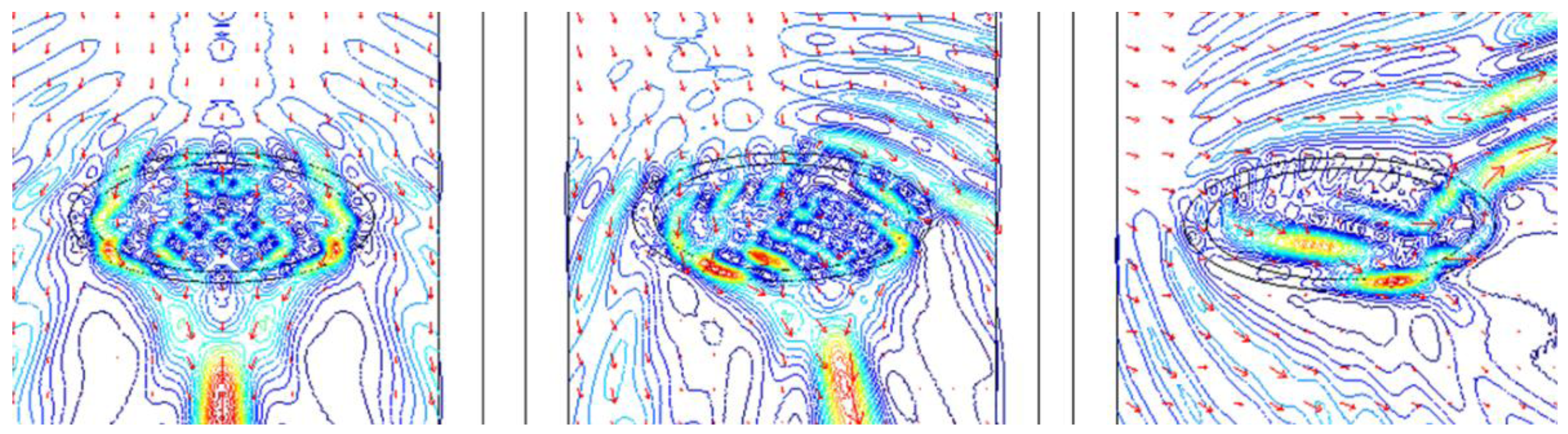
3.5. Further Reading
4. Hybrid or Multiscale Approaches to Omniscale Electromagnetic Radiation Transport
4.1. Discrete versus Statistical Material Approaches
4.2. Hybrid Scattering in an Ideal, Discrete Material
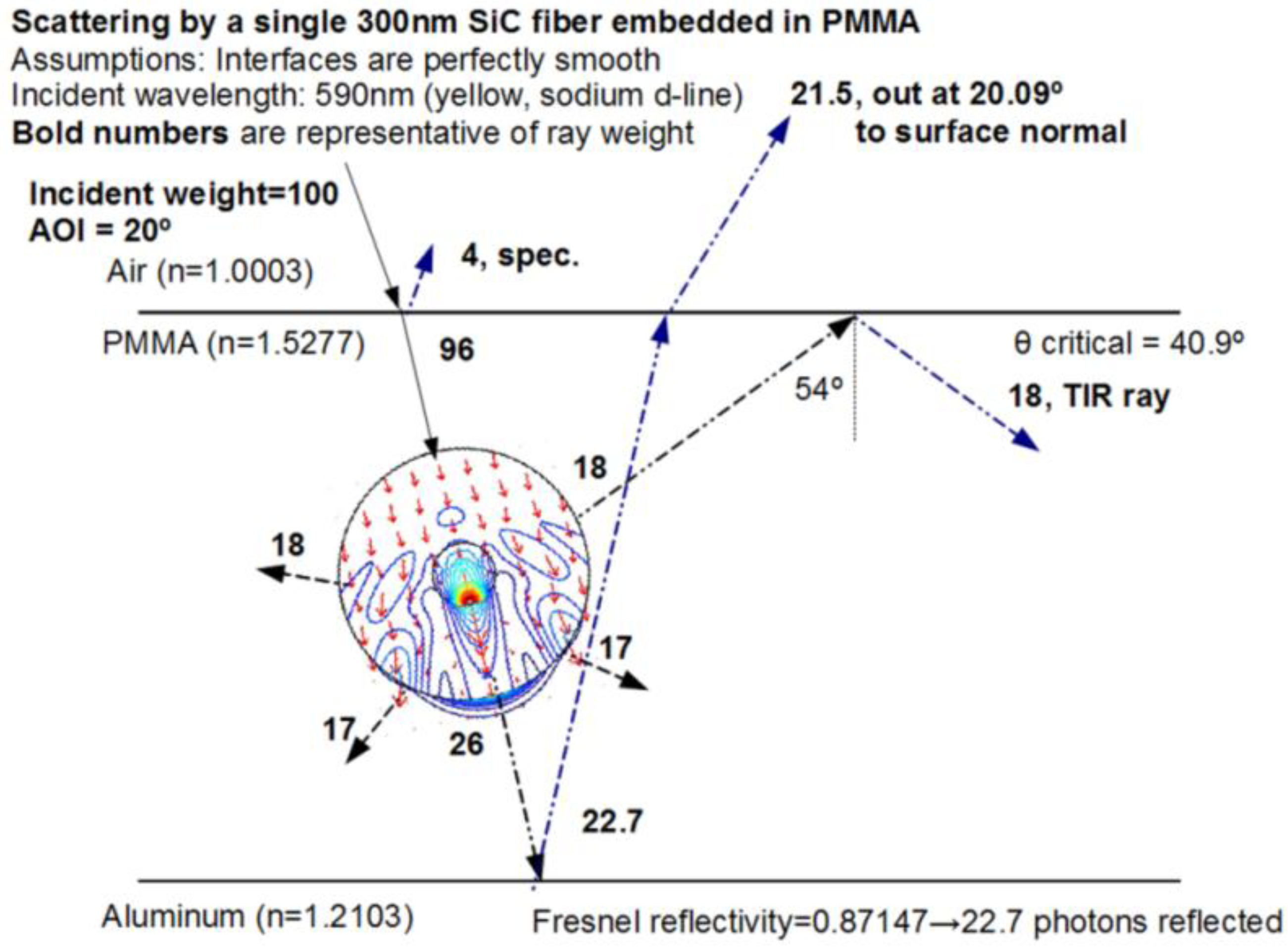
5. Extension to Color, Color Matching, and Metamerism Prediction and Visualization
5.1. The Color of Purely Diffuse Scattering Systems
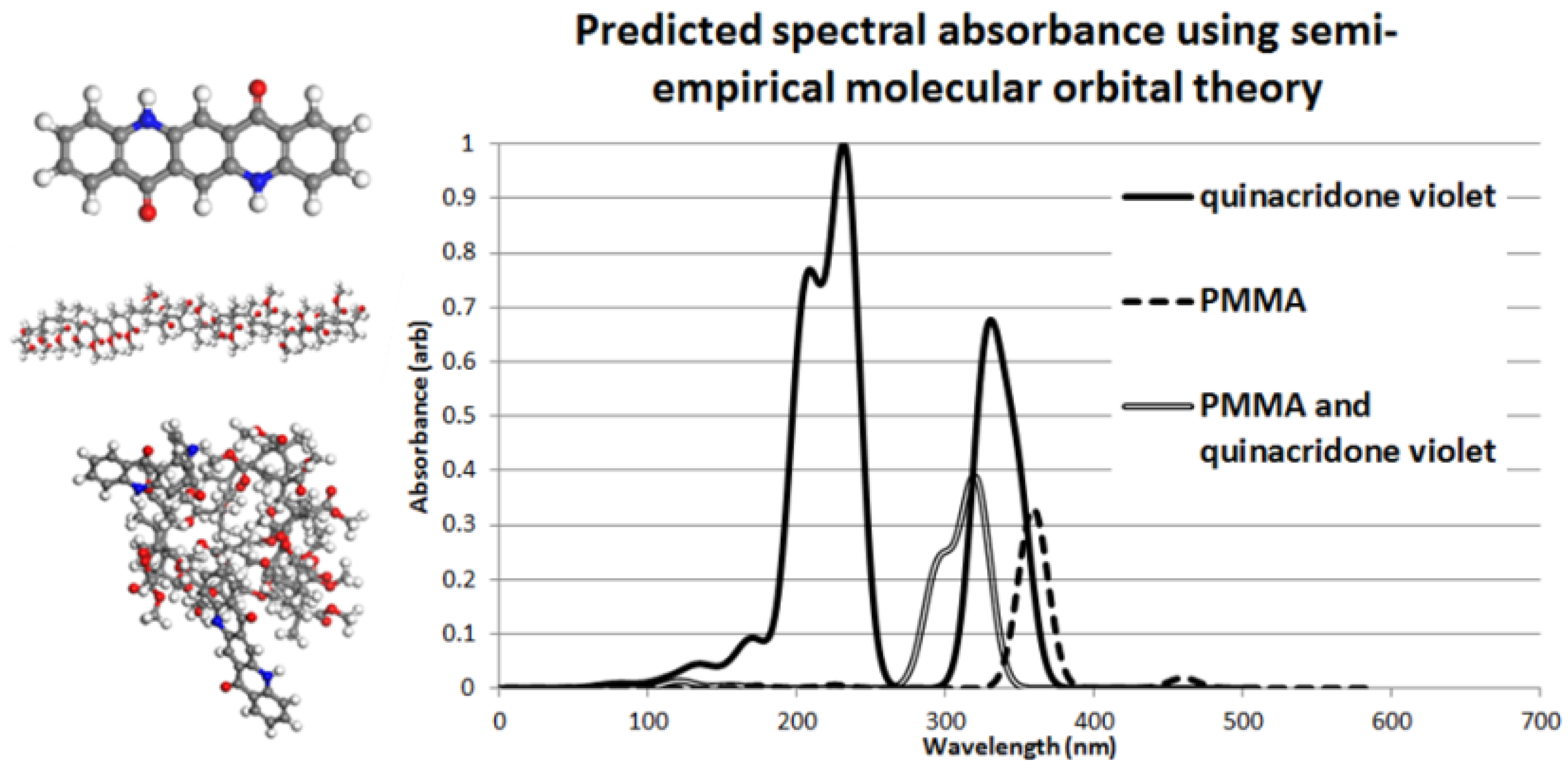
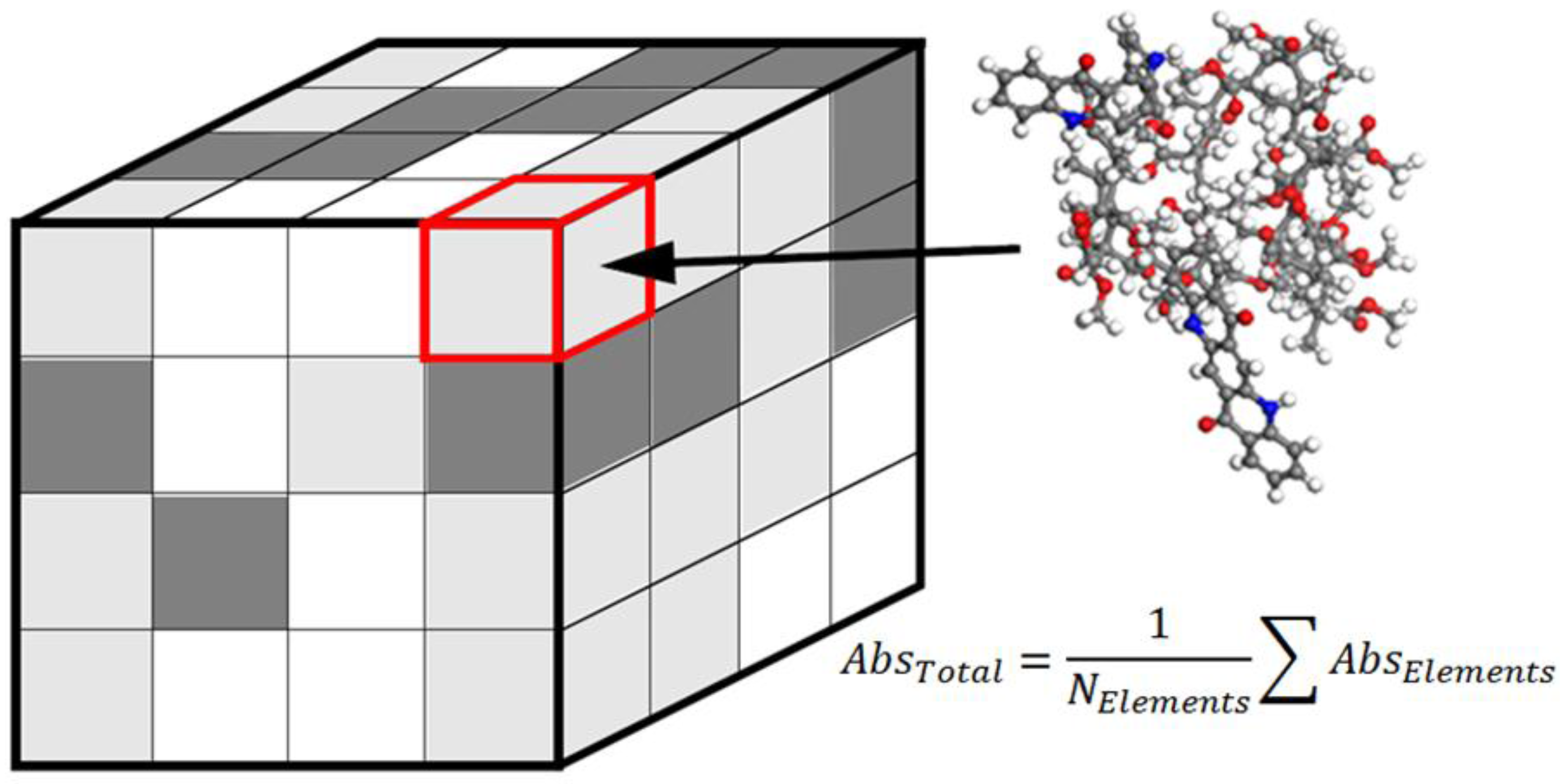
5.2. Kubelka-Munk Theory and Application to Multiscale Light Scattering Simulations
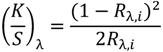
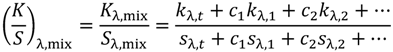
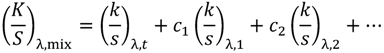
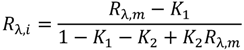
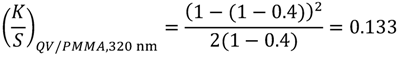
5.3. Color Prediction of Scattering Systems with Diffuse and Directional Components
5.4. Simulating Metamerism
6. Conclusions
Acknowledgments
References
- Martelli, F.; Del Bianco, S.; Ismaelli, A.; Zaccanti, G. Light Propagation through Biological Tissue and Other Diffusive Media; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar]
- Tishkovets, V.P. Incoherent and coherent backscattering of light by a layer of densely packed random medium. J. Quant. Spectrosc. Radiat. Transfer 2007, 108, 454–463. [Google Scholar] [CrossRef]
- Tishkovets, V.P. Light scattering by closely packed clusters: Shielding of particles by each other in the near field. J. Quant. Spectrosc. Radiat. Transfer 2008, 109, 2665–2672. [Google Scholar] [CrossRef]
- Tishkovets, V.P.; Jockers, K. Multiple scattering of light by densely packed random media of spherical particles: Dense media vector radiative transfer equation. J. Quant. Spectrosc. Radiat. Transfer 2006, 101, 52–74. [Google Scholar]
- Light Scattering and Nanoscale Surface Roughness; Maradudin, A.A. (Ed.) Nanostructure Science and Technology Series XXIV; Springer: New York, NY, USA, 2007.
- Van de Hulst, H.C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1983; p. 530. [Google Scholar]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Oxford: New York, NY, USA, 1963; p. 503. [Google Scholar]
- Chen, M.F.; Fung, A.K. A numerical study of the regions of validity of the Kirchhoff and small-perturbation rough surface scattering models. Radio Sci. 1988, 23, 163–170. [Google Scholar] [CrossRef]
- Thorsos, E.I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum. J. Acoust. Soc. Am. 1988, 83, 78–92. [Google Scholar] [CrossRef]
- Davies, H. The reflection of electromagnetic waves from a rough surface. Proc. IEE 1954, 101, 209–214. [Google Scholar]
- Beckmann, P. A new approach to the problem of reflection from a rough surface. Acta Techn. CSAV 1957, 2, 311–355. [Google Scholar]
- Thomas, T.R. Rough Surfaces, 2nd ed; Imperial College Press: London, UK, 1999. [Google Scholar]
- Dorsey, J.; Rushmeier, H.; Sillion, F. Digital Modeling of Material Appearance; Elsevier: New York, NY, USA, 2008. [Google Scholar]
- Tang, K.; Buckius, R.O. The geometric optics approximation for reflection from two-dimensional random rough surfaces. Int. J. Heat Mass Transfer 1998, 41, 2037–2047. [Google Scholar]
- Tang, K.; Dimenna, R.A.; Buckius, R.O. Regions of validity of the geometric optics approximation for angular scattering from very rough surfaces. Int. J. Heat Mass Transfer 1997, 40, 49–59. [Google Scholar]
- Warnick, K.F.; Arnold, D.V. Generalization of the geometrical-optics scattering limit for a rough conduting surface. Opt. Soc. Am. 1998, 15, 2355–2361. [Google Scholar]
- Bergstrom, D.; Powell, D.; Kaplan, A.F.H. A ray-tracing analysis of the absorption of light by smooth and rough metal surfaces. J. Appl. Phys. 2007, 101, 113504. [Google Scholar] [CrossRef]
- Nicodemus, F.E. Directional reflectance and emissivity of an opaque surface. Appl. Opt. 1965, 4, 767–773. [Google Scholar] [CrossRef]
- Parvianen, H.; Muinonen, K. Bidirectional reflectance of rough particualte media: Ray-tracing solution. J. Quant. Spectrosc. Radiat. Trans. 2009, 110, 1418–1440. [Google Scholar] [CrossRef]
- Brockelman, R.A.; Hagfors, T. Note on the effect of shadowing on the backscattering of waves from a random rough surface. IEEE Trans. Ant. Prop. 1966, 14, 621–626. [Google Scholar] [CrossRef]
- Sapper, E.; Hinderliter, B. A Hybrid Computational Approach for Simulation the Scattering of Electromagnetic Radiation in Coatings and Composite Materials. CoatingsTech Conference, Rosemont, IL, USA, 2013.
- Bennett, J.M.; Mattsson, L. Introduction to Surface Roughness and Scattering; Optical Society of America: Washington, D.C., WA, USA, 1989; p. 110. [Google Scholar]
- Tsang, L.; Kong, J.A.; Ding, K.-H.; Ao, C.O. Scattering of Electromagnetic Waves: Numerical Simulations; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Stover, J.C. Optical Scattering: Measurement and Analysis; SPIE Press: Bellingham, WA, USA, 1995. [Google Scholar]
- Bergstrom, D. The Absorption of Laser Light by Rough Metal Surfaces. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2008. [Google Scholar]
- Mishenko, M.I.; Travis, L.D. Gustav Mie and the evolving discipline of electromagnetic scattering by particles. Bull. Am. Meteorol. Soc. 2008, 89, 1853–1861. [Google Scholar] [CrossRef]
- Wiscombe, W.J. Improved Mie scattering algorithms. Appl. Opt. 1980, 19, 1505–1509. [Google Scholar]
- Rother, T.; Schmidt, K. The discretized Mie-formalism—A novel algorithm to treat scattering on axisymmetric particles. J. Electromag. Wav. Appl. 1996, 10, 273–297. [Google Scholar] [CrossRef]
- Rother, T.; Schmidt, K. The discretized Mie-formalism for plane wave scattering on dielectric objects with non-separable geometries. J. Quant. Spectrosc. Radiat. Transfer 1996, 55, 615–625. [Google Scholar] [CrossRef]
- Berns, R.S. Billmeyer and Saltzman’s Principles of Color Technology, 3rd ed; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Phillips, D.G.; Billmeyer, F.W. Predicting reflectance and color of paint films by Kubelka-Munk analysis. J. Coat. Technol. 1976, 48, 30–36. [Google Scholar]
- Kubelka, P. New contributions to the optics of intensely light-scattering material, part I. J. Opt. Soc. Am. 1948, 38, 448. [Google Scholar] [CrossRef]
- Kubelka, P. New contributions to the optics of intensely light-scattering material, part II. J. Opt. Soc. Am. 1954, 44, 330. [Google Scholar] [CrossRef]
- Kubelka, P.; Munk, F. Ein beitrag zur optik der farbanstriche. Z. Tech. Physik. 1931, 12, 330. [Google Scholar]
- Bierwagen, G.P. Estimation of film thickness nonuniformity effects on coating optical properties. Col. Res. Appl. 1992, 17, 284–292. [Google Scholar] [CrossRef]
- Billmeyer, F.W.; Chassaigne, P.G.; Dubois, J.F. Determining pigment optical properties for use in the mie and many-flux theories. Col. Res. Appl. 1980, 5, 108–112. [Google Scholar] [CrossRef]
- Maxwell, J.C. On physical lines of force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1861, 21, 161–175, 281–291, 338–348. [Google Scholar]
- COMSOL, COMSOL Multiphysics RF Module User’s Guide; COMSOL AB: Burlington, MA, USA, 2006.
- Jackson, J. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Shadowitz, A. The Electromagnetic Field. In Dover Books on Physics; Dover: New York, NY, USA, 2010. [Google Scholar]
- Westland, S.; Ripamonti, C. Computaitonal Colour Science Using MATLAB; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]
- Leach, A. Molecular Modeling: Principles and Applications, 2nd ed; Prentice Hall: New York, NY, USA, 2001. [Google Scholar]
- Pople, J.A.; Santry, D.P.; Segal, G.A. Approximate self-consistent molecular orbital theory. I. Invariant procedures. J. Chem. Phys. 1965, 43, S129. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar]
- Mahnaz, M.; Mahdi, N.; Lawrence, T.; Roy, B. Pigment selection using Kubelka-Munk turbid media theory and non-negative least square technique. Available online: https://ritdml.rit.edu/handle/1850/4353 (accessed on 3 April 2013).
- Latimer, P.; Noh, S.J. Light propagation in moderately dense particle systems: A reexamination of the Kubelka-Monk theory. Appl. Opt. 1987, 26, 514–523. [Google Scholar] [CrossRef]
- Molenaar, R.; Bosch, J.J.T.; Zijp, J.R. Determination of Kubelka-Munk scattering and absorption coefficients by diffuse illumination. Appl. Opt. 1999, 38, 2068–2077. [Google Scholar] [CrossRef]
- Murphy, A.B. Modified Kubelka-Munk model for calculation of the reflectance of coatins with optically-rough surfaces. J. Phys. D 2006, 39, 3571–3581. [Google Scholar] [CrossRef]
- Vargas, W.E.; Niklasson, G.A. Applicability conditions of the Kubelka-Munk theory. Appl. Opt. 1997, 36, 5580–5586. [Google Scholar] [CrossRef]
- Saunderson, J.L. Calculation of the color of pigmented plastics. J. Opt. Soc. Am. 1942, 32, 727–736. [Google Scholar] [CrossRef]
- HunterLab. The Kubelka-Monk theory and K/S. Available online: http://www.hunterlab.com/appnotes/an07_06.pdf (accessed on 3 April 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sapper, E.D.; Hinderliter, B.R. Computational Tools and Approaches for Design and Control of Coating and Composite Color, Appearance, and Electromagnetic Signature. Coatings 2013, 3, 59-81. https://doi.org/10.3390/coatings3020059
Sapper ED, Hinderliter BR. Computational Tools and Approaches for Design and Control of Coating and Composite Color, Appearance, and Electromagnetic Signature. Coatings. 2013; 3(2):59-81. https://doi.org/10.3390/coatings3020059
Chicago/Turabian StyleSapper, Erik D., and Brian R. Hinderliter. 2013. "Computational Tools and Approaches for Design and Control of Coating and Composite Color, Appearance, and Electromagnetic Signature" Coatings 3, no. 2: 59-81. https://doi.org/10.3390/coatings3020059



